Next Article in Journal
Artificial Intelligence, Accelerated in Parallel Computing and Applied to Nonintrusive Appliance Load Monitoring for Residential Demand-Side Management in a Smart Grid: A Comparative Study
Next Article in Special Issue
Influence of Grit Size and Wood Species on the Granularity of Dust Particles during Sanding
Previous Article in Journal
Improvement of Microwave Electric Field Measurement Sensitivity via Multi-Carrier Modulation in Rydberg Atoms
Previous Article in Special Issue
Tropical Wood Dusts—Granulometry, Morfology and Ignition Temperature
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 10
Issue 22
10.3390/app10228113
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Optimization of Parameters for the Cutting of Wood-Based Materials by a CO2 Laser

by
Ivan Kubovský
,
Ľuboš Krišťák
*,
Juraj Suja
,
Milada Gajtanska
,
Rastislav Igaz
,
Ivan Ružiak
and
Roman Réh
Faculty of Wood Sciences and Technology, Technical University in Zvolen, T. G. Masaryka 24, SK-960 01 Zvolen, Slovakia
*
Author to whom correspondence should be addressed.
Appl. Sci. 2020, 10(22), 8113; https://doi.org/10.3390/app10228113
Submission received: 15 October 2020 / Revised: 4 November 2020 / Accepted: 12 November 2020 / Published: 16 November 2020
(This article belongs to the Special Issue Application of Wood Composites)
Browse Figures
Versions Notes

Abstract

:
This article deals with the laser cutting of wood and wood composites. The laser cutting of wood and wood composites is widely accepted and used by the wood industry (due to its many advantages compared to, e.g., saw cutting). The goal of this research was to optimize the cutting parameters of spruce wood (Pices abies L.) by a low-power CO2 laser. The influence of three factors was investigated, namely, the effect of the laser power (100 and 150 W), cutting speed (3, 6, and 9 mm·s−1), and number of annual rings (3–11) on the width of the cutting kerf on the top board, on the width of the cutting kerf on the bottom board, on the ratio of the cutting kerf width on the top and bottom of the board, on the width of the heat-affected area on both sides of the cutting kerf (this applies to the top and bottom of the board), and on the degree of charring. Analysis of variance (ANOVA) and correlation and regression analysis were used for developing a linear regression model without interactions and a quadratic regression model with quadratic interactions. Based on the developed models, the optimization of parameter settings of the investigated process was performed in order to achieve the final kerf quality. The improvement in the quality of the part ranged from 3% to more than 30%. The results were compared with other research dealing with the laser cutting of wood and wood composites.

1. Introduction

The cutting of materials is one of the most widely used laser machining processes. The principle consists of the movement of a focused laser beam perpendicular to the plane of the machined surface. The absorption of high energy laser radiation causes the material to melt and subsequently evaporate, creating the desired cut. For this purpose, a powerful CO2 laser is still very frequently used, producing a beam with a wavelength of 10.6 µm [1]. In the past, CO2 lasers were by far the most widely used devices for laser cutting. In recent years, the laser with the largest market for industry use has been the fiber laser, with a wavelength of 1064 nm. In industrialized countries, such as Japan, material cutting operations performed by beam radiation are very widespread and have grown significantly in recent years [2,3]. Due to their unique efficiency and accuracy, these technologies have become the center of attraction in various fields of application [4]. The cutting process is fast, non-contact, and highly automated and there is only thermal stress in a very limited area, allowing the cutting of a wide range of materials. Additionally, low operating costs are achieved, despite the high initial investment and the requirement for qualified staff [5].
In the case of wood and wood-based products, laser machining is widely accepted by the wood industry [6,7,8]. The laser processing of wood was one of the earliest applications of laser use in the 1970s [9,10]. The advantage of the laser system is its ability to cut complicated patterns. The application of lasers in the furniture industry for automated cutting processes us also well-known [11,12]. In addition to cutting, CO2 lasers are also used for the irradiation or engraving of a wood surface [13,14,15,16,17]. The main advantages of the laser cutting of wood in comparison with conventional cutting methods are the highly precise cut, flexibility to start and finish cutting at any point of the board, narrow kerf width (0.1–0.3 mm compared to saw cut of 3–6 mm), and extremely smooth surfaces [18,19,20,21,22,23]. Other advantages of laser wood cutting are the absence of tool wear, low noise emission and vibration, low sensitivity to very variable processing properties [23,24,25,26], reduced amount of sawdust [27,28,29,30,31], and low mechanical stress in the workpiece [32,33].
Factors influencing the process of cutting wood and wood composites by a laser can be divided into three groups [34,35,36], namely, the properties of the radiation beam, the properties of the laser device and the characteristics of the cutting process, and the properties of the workpiece, specifically, the effects of the beam power, mode, and polarization as aspects of optics; the location of the focal point; the feed speed; the gas-jet assist system and workpiece thickness; the density; and the moisture content [37,38,39,40,41,42,43,44].
In the case of wood composites, Lum et al. [45] investigated the parameters of the process of MDF board cutting with a beam of radiation generated by a CO2 laser with a power of 520–530 W in pulse and continuous mode. The optimal setting of the parameters for the MDF board cutting was achieved by the experimental change of the cutting speed, the composition of the auxiliary gas and its pressure, and the change of the position of the radiation beam focusing in the material. The results showed that narrow kerf widths are achievable for MDF laser-cut boards, particularly for pulse mode cutting. Striation patterning, although masked by external charring, is evident, but this is of little significance to the overall quality of cut, as evidenced by the low surface roughness values obtained. Burnout was also minimal, even for angular profile cuts of small internal angles. These results were also in agreement with Powell [46]. Eltawahni et al. [47] investigated a means for selecting the process parameters for the laser cutting of MDF based on the design of experiments. They defined a methodology according to which we can partially evaluate the efficiency and quality of radiation beam cutting by the proportion of the cutting joint width on the cut upper workpiece surface to the cutting joint width on the cut workpiece bottom (the so-called ratio). The focal point position and laser power are the principal factors affecting the ratio. In the case of the upper board’s surface kerf, the focal point position has the main role, and in the case of the lower kerf, the laser power and cutting speed have the main effect on the lower kerf width. The roughness of the cut section decreases as the focal point position and laser power increase. The roughness increases as the cutting speed and air pressure increase. Smoother cut sections could be processed, but with an increase in the processing operating cost. Barnekov et al. [48] investigated the effect of different focal point positions on the cut surface quality. They found that a smooth surface of the workpiece middle can be achieved with less charring with the focal point at or slightly above the middle. Most of these results are in harmony with previous published research in the case of wood and wood composites [49,50,51]. The focal point position was also investigated by Barnekov et al. [40]. In their research, they achieved the best quality of particleboard laser cutting when the beam was focused on the surface of the composite material.
In the case of wood, Tayal et al. investigated the significance of the focus position of the CO2 laser optical system when hardwood cutting [52]. They concluded that the focal point should be at a location Z/2 below the surface to achieve a maximum average laser power density, where Z is the focal length (depth of focus). They verified these results by experimental observations. Nukman et al. [53] used a CO2 laser to cut a wide range of Malaysian wood and plywood. The processing variables taken into account were the laser power, focal point position, nozzle size, assist gas pressure, types of assist gas, cutting speed, and delay time. The wood properties observed were the thickness, density, and moisture content of wood. The analyses considered the geometric and dimensional accuracy (straight sideline length, diameter of the circle, kerf width, and percent over cut), material removal rate, and severity of burning. A guideline for cutting a wide range of Malaysian wood has been outlined. The influence of the laser power, cutting speed, and shield gas on the cut quality in the case of hard and soft timber was confirmed by Khan et al. [6]. McMillin [54] dealt with the moisture content and its influence on the process of pine wood cutting by a beam of radiation generated by a CO2 laser in his work. He found that the cutting speed of wetter wood is slower compared to drier wood. The reason for this is that the moisture content in wood increases the thermal conductivity, which results in energy loss in the heating zone. Grad and Mozina [41] showed that the CO2 laser beam is almost completely absorbed by wood. This result has been confirmed by Hattori [42], who claimed that a CO2 laser is most suitable for wood processing due to the wavelength used. The authors of the research [55,56] proved that a cut section quality with less roughness results from an increasing beam power.
The optimal conditions for laser cutting were determined by several authors using theoretical models. Zhou and Mahdavian [57] explored the possibilities of cutting wood and particleboards with various levels of laser power and different workpiece cutting speeds. They introduced a theoretical model that estimates the depth of the cut in terms of the material properties and cutting speed. The experimental cutting results were compared with theoretical predictions. Two correction parameters were introduced in the analysis to improve the theoretical model. Numerous other theoretical models for laser machining have been developed by other researchers, among them, Moradi et al. [58], Choudhury et al. [59], Yang et al. [60], Elsheikh et al. [61], Alizadeh and Omrani, and others [62,63,64]. Various modes of heat transfer, phase changes, workpiece motions, and material properties have been taken into account in these analysis.
There are also several simulations and mathematical and statistical models, in addition to theoretical models. Statistical and experimental analyses of the multiple-pass laser cutting of wet and dry pine wood were presented by Castaneda et al. [65]. The parameters investigated were the laser power, traverse speed, focal plane position, gas pressure, number of passes, direction of cut (normal or parallel to the wood´s tracheids), and moisture content. The experimental results were compared against process responses defining the efficiency (i.e., kerf depth and energy consumption) and quality of the cut section (i.e., kerf width, heat-affected zone, edge surface roughness, and perpendicularity). An energy balance-based simple analytical model was developed and validated with experimental results by Prakash Kumar [66]. The optimal properties of the cutting process can also be determined by suitable simulation methods. Jianying and Yun [67] developed a simulation technique with ANSYS software using the finite element method in order to propose the optimal parameters of the wood beam cutting process. Polak et al. [68] used ANSYS and the numerical finite element method to model the radiation beam cutting and drilling process. Yang et al. [69,70] analyzed the influence of the ablative mechanism of wood processed with a nanosecond laser on the cutting quality and established a prediction model through multiple linear regression equations. Hardalov et al. [71] used the finite element method in their work to quantify the temperature gradient on the surface of ceramic material in the process of irradiation with pulsed and continuous beams using FEMLAB software. In the research by Modest [72], a previously developed three-dimensional conduction model for the scribing of a thick solid was extended to predict the transient temperature distribution inside a finite thickness slab that was irradiated by a moving laser source. The governing equations were solved for both constant and variable thermophysical properties using a finite-difference method on a boundary-fitted coordinate system. An evaluation of the radiation beam cutting quality was also addressed by Rogerro et al. [73], whose method is a combination of neural networks and traditional algorithmic techniques. Bianco et al. [74] used COMSOL Multiphysics 3.2 software to solve a transient two- and three-dimensional temperature field irradiated by a beam of radiation. Babiak et al. [75] dealt with the analysis of temperature profiles created by a moving Gaussian energy beam on a wood surface. Yilbas et al. [76] analyzed both mathematical and numerical solutions of material heating by a beam of radiation.
The aim of this research was to find the optimal combination of parameters of the cutting process of an 8 mm thick spruce board with a moisture content of 12% by a CO2 laser. The required cut quality was determined by the minimum width of the heat-affected zone, the minimum value of the degree of charring, and the ratio of the cutting joint width on the upper and bottom board´s surface. The parameters were the laser power, cutting speed, and number of annual rings intersecting the area of the cutting kerf.

2. Materials and Methods

The experiments were carried out on Norway spruce (Picea abies (L.) H.Karst). Wood was harvested from the Polana region in Slovakia. Cutting kerf was created by the cutting of tangential spruce lumber with dimensions of 8 mm x 100 mm x 1000 mm (tangential x radial x longitudinal), with a relative moisture content w = 12 ± 1% and average density ρ = 428.4 ± 27.9 kg·m−3. The moisture content of the samples was determined according to ISO 13061-1 [77]. The wood density was determined according to ISO 13061-2 [78]. The CO2 laser LCS 400-1/W (TST Strojárne Piesok, Piesok, Slovakia) was used for cutting with a wavelength of 10.6 μm operated at a continuous mode output power of 100 and 150 W. Three speeds of cutting were used, with values 3, 6, and 9 mm·s−1. A power of 150 W and speed of cutting of 9 mm·s−1 were used as a reference, since this combination is used in practice due to the speed of production. The focal length was 127 mm (5”), beam diameter was 10 mm, and spot diameter was 0.3 mm. The focal point position of the laser beam was set to 1/2 of the sample thickness (measured from the upper surface of the board). The process gas was supplied via a laval contour nozzle with 0.25 MPa pressured air.
All cuts were made parallel to the wood fibers in the tangential direction (Figure 1). The quality of the cut section of the wood was examined using Digital Microscopy (DM).
The Response Surface Method (RSM) was used to prepare the experiment. The influence of three factors was investigated, namely, the effect of the laser power P, cutting speed V, and number of annual rings AR (Table 1) on the width of the cutting kerf WKU (width of the cutting kerf on the upper board´s surface) and WKD (cutting kerf width on the board bottom), on their ratio WKR (ratio of the cutting kerf width on the upper and bottom board´s surface), on the width of the heat-affected areas on the spruce board surface WHAZx (width of the heat-affected area on both sides of the cutting kerf is equal, and this applies to the upper board´s surface, as well as to the bottom of the board), and on the degree of charring B.
Measuring of the cutting kerf width WKU, WKD, and WHAZx was observed by DM using the K-means clustering segmentation method [79]. The K-means clustering algorithm is an unsupervised algorithm and it clusters or partitions the given data into K-clusters based on the K-centroids. The algorithm is used when we have unlabeled data (without defined categories) and the objective is to minimize the sum of squared distances between all points and the cluster center. In our case, three different color-coded regions were searched in image processing software, namely, the area of the unaffected workpiece, the area of the heat-affected zone, and the area of the cutting kerf. The mean values of the width of the cutting kerf and especially the width of the heat-affected zones were determined from the segmented photos by applying the theorem on the mean value theorem for integrals (Figure 2).
The measuring of the degree of charring consisted of an analysis of cutting kerf in a direction perpendicular to the surface and a subsequent analysis of the morphology (texture) of the examined surface. Surface charred areas are amorphous areas of cutting kerf without a visible texture with a damaged anatomical wood structure due to the thermal degradation of wood. The bimodal histogram was modeled as a mixture of two Gaussian density functions. The use of adaptive particle swarm optimization for the suboptimal estimation of the means and variances of these two Gaussian density functions, and then the computation of the optimal threshold value, was straightforward [80]. The result of this analysis was obtained as the degree of charring in %.
The Shapiro–Wilk test was used to test the normality of measured data, followed by Box-Cox nonlinear normalizing transformation. For greater data clarity of the response, variables were transformed into variables that also passed the normality test. Analysis of variance (ANOVA) and correlation and regression analysis were used for developing a linear regression model without interactions and a quadratic regression model with quadratic interactions. Based on the developed models, the optimization of parameter settings of the investigated process was performed in order to achieve the required response.

3. Results and Discussion

The total number of measurements was 108 in one block, with 864 measured or calculated data. Due to the random factor AR, nine measurements were performed at each monitored cutting speed. The WKR ratio was calculated and the degree of charring was subsequently determined from the measured data. The data were then tested by the Shapiro–Wilk test of good agreement of the measured data, with the normal distribution at a significance level of 0.05. Due to the fact that the measured data did not meet the assumption of a normal distribution, a normal distribution was achieved by a nonlinear Box-Cox transformation (Table 2).
The results of the measured data after the transformation enabled the use of parametric mathematical-statistical methods of experimental evaluation (in the next parts asterisk symbol * is used for transformed values). Descriptive statistics were subsequently produced for all monitored transformed responses (Table 3).
It follows from the descriptive statistics tables for each monitored transformed response that the cutting kerf width at the board top is larger than the cutting kerf width at the board bottom. The term “upper board´s surface” refers to the side where the primary radiation beam interacts with the material. The values of the variation coefficients are smaller on the upper board´s surface compared to the values of the variation coefficients of the observed responses on the board bottom. This is related to the properties of the wood from the point of view of heat transfer, as well as to the power of the radiation beam required for thermal decomposition of the wood in the cutting process. Larger values of variation coefficients also point to defects in the form of burns on the surface of the board bottom, which are caused by the sudden blowing of burns from the space of the cutting kerf with auxiliary gas (air).

3.1. Analysis of Variance and Regression Analysis

A three-factor experimental model without interactions was used to primarily determine the influence of the investigated factors AR, P, and V for responses WKU*, WHAZU*, WKD*, WHAZD*, WKR*, and B*, with an evaluation of the variability degree of the investigated response (Table 4). Additional information on the influence of interactions between factors was analyzed by a second-degree polynomial model with first-order interactions (Table 5). The coefficients of the factors of the examined responses are marked in gray, which are significant in terms of impact at the significance level of 0.05. The force measures of the models are also marked in gray, which can be considered as sufficiently explanatory of the spruce board cutting process. The coefficients of the regression function were determined by the least squares method. The significance of the investigated factors was evaluated by analysis of variance (F test, p test, R2, standard deviation, PACH analysis, and percentage error of the model were performed in all cases), graphically by a Pareto diagram, and by a graphical analysis of their influence (Figure 3).
It follows from the table of results on the analysis of variance for WKU* for the transformed values of the cutting kerf width (Table 4) that the influence of the cutting speed factor V and the laser power P is statistically significant. The influence of the AR factor was not confirmed by the mathematical-statistical analysis, which is related to the wood density. The reason for this may be the fact that the thermal conductivity of wood only plays a major role in heat transfer in the phase of penetration of the energy beam into the material, while on the surface, respectively in the phase of energy contact with the board surface, the surface properties of wood are more pronounced, e.g., color, roughness, reflectivity, and the properties of the laboratory environment. The cutting speed has the greatest influence on the value of the width size of the cutting kerf on the upper board´s surface. However, this effect is disproportionate, and the width of the cutting kerf WKU* decreases with an increasing cutting speed. We can explain this phenomenon by the decreasing amount of energy interacting with the board material per unit time. For this reason, it is necessary to include the interactions between the investigated factors in the model, which correlates with the results of Hernandez [65] in the case of Scots pine, with Ready [81] in the case of Silver fir, and with Liu et al. [82] in case of cherry wood. On the contrary, the width of the cutting kerf increases with an increasing laser power, which was confirmed in the work of Nukman et al. [53] in their research on selected Malaysian wood cutting. If we consider the factor AR, then its effect on WKU*, although negligible, is directly proportional. In the case of the interaction model of factors for WKU*, in addition of the factors P and V, the interactions P*V and V2 are also statistically significant. This confirmed the assumption of the mutually important influence of V and P on the cutting kerf width, so these factors significantly affect the amount of absorbed and reflected energy in the board structure, as pointed out by Hernandez in his work [65] on pine wood cutting, as well as Barnekov [48]. A statistically significant factor AR in the form of the self-interaction AR2 already appeared in the interactions model. This is indicated by the fact that the wood density affects the properties of the cutting kerf, which is also stated in the work of Asibu [83].
It follows from the results of the analysis of variance for the transformed values of WHAZU* that the influence of the cutting speed factor V and the laser power factor P is statistically significant. The influence of the factor AR, which is related to the wood density, was not confirmed by the mathematical-statistical analysis. The significant influence of the speed factor V points to the fact that the cutting speed significantly affects the energy distribution in the cutting process by the radiation beam on the workpiece surface at the point of energy interaction with the material. This is consistent with Hernandez’s results [65]. This follows from a detailed analysis showing that the cutting speed V and laser power P have the greatest influence on the width value of the heat-affected area on the upper board´s surface in comparison with the other investigated factors. In the case of the cutting speed V, the effect is directly proportional, and the width of the heat-affected area WHAZU* increases with an increasing cutting speed. The result obtained is in contrast to the findings published in the work of Asibu [83], Barcikowsky [7], and Lum [45]. The reason for this is that these authors examined the heat-affected area below the surface of cut wood, while the subject of our research was the size of the heat-affected area on the board surface. This reduces the amount of energy in the process of decomposing the material below its surface by increasing the cutting speed, as well as increasing the amount of energy on the board surface. Therefore, it is clear that it increases the area affected by heat due to energy excess on the board surface, which is consistent with the results of Arai and Hayashi, [84,85]. The width of the heat-affected zone increases as the power of the laser P increases, as Barcikowski [7] also pointed out. If we also take into account the factor AR, then its effect on WHAZU*, although also negligible, is directly proportional. All model quality indicators improved after the inclusion of interactions in the model WHAZU*, but not so significantly that we can consider this model as credible. However, we can use it to explain the influence of the investigated factors and their interactions on the investigated response, in this case, WHAZU*. The mutual interaction between the laser power P and the cutting speed V determines the degree and form of energy distribution, as in the case of the WKU* or WHAZU*; this causes the wood chemical decomposition and thus determines the width of the heat-affected area. The cutting speed also affects the properties at the same time, and in particular, the distribution of the flowing auxiliary gas on the board surface.
It follows from the results of the analysis of variance for the transformed values of the cutting kerf width on the board bottom of the WKD* that the influence of the cutting speed factor V, the laser power P, and the factor AR is statistically significant. These results are in harmony with Ready [79]. The reason for this is again that the wood thermal conductivity plays an important role in heat transfer in the phase of penetration of the energy beam into the material, while on the surface, respectively in the phase of energy contact with the board surface, the surface properties of wood are manifested analogously, as in the case of WKU* and WHAZU*. It is clear that the cutting speed V increase, as well as the density increase, and respectively the number of annual rings AR, results in a reduction in the cutting kerf width on the board bottom. The results correspond to the results of Mahdavian and Zhou [57] or Lum and Black [45,49] in a cutting depth analysis. On the contrary, an increase in the power P of the laser results in an increase in the value of the cutting kerf width WKD* on the board bottom, which is in accordance with the published results, e.g., Eltawahni et al. [47]. It was found, by comparing the effect of the factors for both widths WKU* and WKD*, that the power factor P and the speed factor V act in the same direction on the width values of the WKU* and WKD*. However, the factor AR, respectively the wood density, acts to increase the cutting kerf width on the board surface, in contrast to the effect on the board bottom, where it reduces this width by its influence. The extent value of the variance explanation only improved insignificantly in the case of the interaction model for WKD*, so the model without interactions sufficiently and simply describes the influence of the factors P, V, and AR on WKD*.
The effect of the factor AR could not be confirmed by the results of the variance analysis for WHAZD*; however, a significant effect was confirmed by the cutting speed factors V and laser power P. It is clear that the value of WHAZD* increases with an increasing laser power P and, conversely, the value of the width of the heat-affected zone on the surface of the board bottom decreases with an increasing speed V. It follows from the results of a detailed analysis that a significant improvement in all properties of the model will not be achieved, even when considering the interactions between the investigated factors. Considering this, it is necessary to include other factors in the analysis in the case of continuing research, e.g., the auxiliary gas flow rate.
It follows from the results of the variance analysis for the transformed values of the width ratio of the cutting kerf WKR* that the influence of the cutting speed factor V, the laser power P, and also the factor AR is statistically significant. Analogous to WKD*, the wood thermal conductivity plays an important role in the material, while the wood surface properties are reflected on the surface. A speed increase, as well as density increase, causes the WKR* value to decrease, while a power increase causes the WKR* value to increase. The results are in line with the results obtained for the analysis of WKU* and WKD*, as well as the works dealing with the joint assessment of the cutting kerf width on the upper and bottom board´s surface in the case of other softwoods, e.g., those by Ready [81] and Eltawahni et al. [47]. It improved all the indicators in the model in the case of the model with interactions for WKR* and this was mainly due to the mutual interaction between power P and speed V, while the factor of power P and speed V had the most significant effect on WKR*.
Analysis of variance did not confirm a statistically significant effect of the investigated factors AR, P, and V in the case of B*. Nevertheless, it is clear from a physical point of view that the power factor P, together with the cutting speed V, i.e., feed of the energy source, determines the amount of energy absorbed by the wood, and thus the amount of energy needed to create the burns. Peters and Banas [86] and Barnekov et al. [48] also reached analogous conclusions. This is due to a decrease in the reaction time of the radiation beam interaction on the workpiece material. It evaporates the material at the upper board´s surface just below the surface due to the uneven distribution of energy supplied to the board material. Below the area, where the material evaporates, is the area where there is less energy, and thus the wood is decomposed by burning. The interactions between the laser power P and the cutting speed V are statistically significant, highlighted by the interaction V*V in the case of the interaction model.

3.2. Optimal Parameter Settings of the Investigated Process

It is desirable to minimize the subsequent post processing due to minimizing the cost of the cutting process by the energy beam. It is possible to achieve cost minimization by optimally setting the parameters of the investigated process, in order to achieve the required values of process responses based on a mathematical-statistical model. The goal is to reach a minimum value in the case of WKU*, WHAZU*, WKD*, WHAZD*, and B*, and in the case of WKR*, the goal is to achieve the value 1 and at the same time to find the optimal values of the factors P, V, and AR. There are six polynomial functions based on Table 5, five of which need to be minimized and one of which needs to be normalized, i.e., needs to be equal to one:
WKU* = 1.96353 + 0.00695·V2 + 0.08847·P*V + 0.00032·AR*V − 0.00745·AR*P + 0.00526·AR2
− 0.25323·V − 0.29207·P − 0.05862·AR = min,
WHAZU* = 0.23073 − 0.00193·V2 − 0.02749·P*V − 0.00108·AR*V + 0.00257·AR*P − 0.00142·AR2 +
0.08067·V + 0.19104·P + 0.02398·AR = min,
WKD* = −0.13999 − 0.00489·V2 − 0.02015·P*V − 0.00208·AR*V − 0.05651·AR*P + 0.00034·AR2 +
0.03693·V + 0.81739·P + 0.06392·AR = min,
WHAZD* = −0.78817 + 0.00099·V2 + 0.01778·P*V + 0.00121·AR*V + 0.02135·AR*P − 0.00349·AR2 −
0.05375·V + 0.00574·P + 0.01209·AR = min,
B* = 1.04444 + 0.00467·V2 + 0.06385·P*V + 0.00172·AR*V + 0.01333·AR*P + 0.00107·AR2 − 0.15057·V
− 0.51849·P – 0.03579·AR = min,
WKR* = −1.01551 − 0.09964·V2 − 0.09821·P*V − 0.00352·AR*V − 0.05468·AR*P − 0.00263·AR2 +
0.23656·V + 1.17681·P + 0.10382·AR = 1.
The modeling was performed by the method of linear programming, which determined the optimal values of the investigated factors (based on a set of solutions of a system of six linear equations and inequations using the simplex method of solving the general problem of linear programming).
The results of joint optimization of the investigated factor settings reached values of AR = 3, P = 100 W, and v = 9 mm·s−1. The suitability of the joint optimization reached the value of 0.92. We can conclude that we can approach the optimal parameters of the cutting process of a given board by increasing the cutting speed at the optimal performance based on the analysis of the response area (Figure 4 left). It is possible to achieve the same or a similar result by reducing the power of the radiation beam at the optimum cutting speed of a given board (Figure 4 right).
The correctness of the optimization was also confirmed by Table 6. From this table, it is clear to see that the chosen parameters of cutting after optimization (AR = 3, P = 100 W, and v = 9 mm·s−1) are improved over the reference parameters of cutting (AR = 3, P = 150 W, and v = 9 mm·s−1) by 3% to 30%.
In case we need to optimize only one parameter separately, we can achieve even better results, since, in the case of joint optimization, the values are related to each other. The obtained values of separate optimization for all parameters are given in Table 7. In practice, in the case of laser wood cutting, it is not always necessary to achieve the optimized quality of all parameters at the same time. In some cases, with specific requirements for the cutting zone created in laser cutting, optimization of the cutting zone for only one parameter is needed, e.g., the maximum surface flatness is required for subsequent gluing (WKR = 1); in case of increased requirements for the tensile shear strength of the glue joint, minimization of charring is required (B = min); and in the case of subsequent edging and the requirement of one viewing area, minimization of the HAZ is required (WHAZxU alebo WHAZxD = min). In some cases, the perfect surface is counterproductive (in the case of adhesion of the glue, etc.). Alternatively, there is a requirement to combine the optimization of two parameters, e.g., at subsequent edging and the requirement of two viewing surfaces (WHAZxU and WHAZxD = min). These requirements are applied, especially in the case of wood composites (plywood, particleboard, fiberboard, etc.), in the production of furniture elements. In practice, in most cases, the second optimization is more important due to the above reasons.
The obtained results show a high correlation with experimentally measured results, despite the difficulties largely resulting from the anisotropy of spruce wood, and at the same time, they are comparable with the results of authors investigating cutting by a radiation beam generated by a CO2 laser for other wood species, as well as wood composites [53,65,81,82,83].

4. Conclusions

The goal of our research was to find the optimal combination of parameters of the cutting process with a beam of a CO2 laser energy of a 8 mm thick spruce board with a moisture content of 12% and thus to achieve the required quality of cutting. The targets of past research were mainly equivalent homogeneous wood material. The target of this research was highly anisotropic material. Therefore, parameter AR was considered and discussed, in addition to standard parameters, such as the effect of the cutting speed V and beam power output P, and the influence of these parameters on responses was also analyzed too, including the cutting kerf width on the upper board´s surface WKU, cutting kerf width on the board bottom WKD, the width of the heat-affected area on the upper board’s surface WHAZU and the board bottom WHAZD, the ratio of the cutting kerf width on the board bottom to the width on the upper board´s surface WKR, and the degree of char B. Using a mathematical-statistical model, we achieved the optimal parameters (AR = 3, 100 W, and 9 mm·s−1). These parameters of cutting are much better than the non-optimized control parameters (AR = 3, 150 W, and 9 mm·s−1). The improvement in the quality ranged from 3% to more than 30%. The results exhibit a high correlation with experimental measurements and they are also comparable to the results of research on the cutting of more homogeneous wood and wood composite materials cut with a CO2 laser.
Research has further shown that even inhomogeneous materials such as spruce wood can be cut with a low power laser. However, in order to make this process more predictable, further research should focus on assessing the impact of other factors, such as the spruce moisture content and composition and flow rate of the auxiliary gas, and extending the ranges of factors considered, especially the beam power output and the cutting speed. We can use the method of measuring the cutting kerf width in other areas, where we require a fast and inexpensive method to measure small lengths, which are determined by the resolution of the scanning device. At the same time, this method is suitable for the proposal of electronic equipment that would perform the measurements of small two-dimensional objects. The used method of char measuring can be applied in the mass identification of errors or characteristic properties of the surface of the scanned workpiece by division into characteristic areas.
As mentioned in the introduction, from a comprehensive point of view, the cutting process of wood and wood-based products with a CO2 laser can be evaluated as a fast, highly-automated, and workpiece-friendly approach that is suitable for cutting homogeneous and inhomogeneous wood and wood composite materials. Other benefits include the highly precise cut, the narrow kerf width, the smooth surface, no tool wear, and the reduced amount of sawdust.
Innovative solutions are essential for sustaining the market position in the competitive business environment. This clearly supports the position of the wood-working industry among the sectors completely fulfilling the requirements of green business products and principles of sustainable development [87,88,89,90,91].

Author Contributions

Conceptualization, I.K. and R.I.; methodology, M.G.; formal analysis, Ľ.K. and J.S.; investigation, J.S. and M.G.; resources, Ľ.K.; data curation, I.R.; writing—original draft preparation, Ľ.K. and R.R.; writing—review and editing, Ľ.K. and R.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Slovak Research and Development Agency under contract no. APVV-18-0378, APVV-19-0269, and VEGA 1/0717/19.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Masoud, F.; Sapuan, S.; Mohd Ariffin, M.K.A.; Nukman, Y.; Bayraktar, E. Cutting Processes of Natural Fiber-Reinforced Polymer Composites. Polymers 2020, 12, 1332. [Google Scholar] [CrossRef] [PubMed]
  2. Yoshida, K.; Yahagi, H.; Wada, M.; Kameyama, T.; Kawakami, M.; Furukawa, H.; Adachi, K. Enormously Low Frictional Surface on Tough Hydrogels Simply Created by Laser-Cutting Process. Technologies 2018, 6, 82. [Google Scholar] [CrossRef] [Green Version]
  3. Yang, L.; Wei, J.; Ma, Z.; Song, P.; Ma, J.; Zhao, Y.; Huang, Z.; Zhang, M.; Yang, F.; Wang, X. The Fabrication of Micro/Nano Structures by Laser Machining. Nanomaterials 2019, 9, 1789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Abidou, D.; Yusoff, N.; Nazri, N.; Awang, M.A.O.; Hassan, M.A.; Sarhan, A.A.D. Numerical simulation of metal removal in laser drilling using radial point interpolation method. Eng. Anal. Bound. Elem. 2017, 77, 89–96. [Google Scholar] [CrossRef]
  5. Mukherjee, K.T.; Grendzwell, P.A.A.; McMillin, C.W. Gas-flow parameters in laser cutting of wood–nozzle design. For. Prod. J. 1990, 40, 39–42. [Google Scholar]
  6. Khan, P.A.A.; Cherif, M.; Kudapa, S.; Barnekov, V.; Mukherjee, K. High Speed, High Energy Automated Machining of Hardwoods by Using a Carbon Dioxide Laser: ALPS; Laser Institute of America: Orlano, FL, USA, 1991; Volume 2, pp. 238–252. [Google Scholar]
  7. Barcikowski, S.; Koch, G.; Odermatt, J. Characterisation and modification of the heat affected zone during laser material processing of wood and wood composites. Holz Roh Werkst. 2006, 64, 94–103. [Google Scholar] [CrossRef]
  8. Huber, H.E.; McMillin, C.W.; Rasher, A. Economics of cutting wood parts with a laser under optical image analyzer control. For. Prod. J. 1982, 32, 16–21. [Google Scholar]
  9. Belforte, D.A. Non-metal cutting. Ind. Laser Rev. 1998, 13, 11–13. [Google Scholar]
  10. Powell, J.; Ellis, G.; Menzies, I.A.; Scheyvaerts, P.F. CO2 laser cutting of non-metallic materials. In Proceedings of the 4th International Conference Lasers in Manufacturing, Birmingham, UK, 12–14 May 1987. [Google Scholar]
  11. Wieloch, G.; Pohl, P. Use of laser in the furniture industry. In Proceedings of the Laser Technology IV: Research Trends, Instrumentation, and Applications in Metrology and Materials Processing, Szczecin, Poland, 1 March 1995; Volume 2202, pp. 604–607. [Google Scholar]
  12. Pires, M.C. Plywood inlays through CO2 laser cutting. In Proceedings of the CO2 Laser and Applications, Los Angeles, CA, USA, 28 July 1989; Volume 1042, pp. 97–102. [Google Scholar]
  13. Kúdela, J.; Kubovský, I.; Andrejko, M. Surface properties of beechwood after CO2 laser engraving. Coatings 2020, 10, 77. [Google Scholar] [CrossRef] [Green Version]
  14. Kúdela, J.; Kubovský, I.; Andrejko, M. Impact of different radiation forms on beech wood discolouration. Wood Res. 2018, 63, 923–934. [Google Scholar]
  15. Kubovský, I.; Kačík, F.; Veľková, V. The effects of CO2 laser irradiation on color and major chemical component changes in hardwoods. Bioresources 2018, 13, 2515–2529. [Google Scholar] [CrossRef]
  16. Kubovský, I.; Kačík, F.; Reinprecht, L. The impact of UV radiation on the change of colour and composition of the surface of lime wood treated with a CO2 laser. J. Photochem. Photobiol. A Chem. 2016, 322, 60–66. [Google Scholar] [CrossRef]
  17. Kubovský, I.; Kačík, F. Colour and chemical changes of the lime wood surface due to CO2 laser thermal modification. Appl. Surf. Sci. 2014, 321, 261–267. [Google Scholar] [CrossRef]
  18. Sinn, G.; Chuchala, D.; Orlowski, K.; Tauble, P. Cutting model parameters from frame sawing of natural and impregnated Scots Pine (Pinus sylvestris L.). Eur. J. Wood Wood Prod. 2020, 78, 777–784. [Google Scholar] [CrossRef]
  19. Očkajová, A.; Kučerka, M.; Kminiak, R.; Krišťák, L’.; Igaz, R.; Réh, R. Occupational Exposure to Dust Produced When Milling Thermally Modified Wood. Int. J. Environ. Res. Public Health 2020, 17, 1478. [Google Scholar]
  20. Kučerka, M.; Očkajová, A. Thermowood and granularity of abrasive wood dust. Acta Fac. Xylologiae Zvolen 2018, 60, 43–51. [Google Scholar]
  21. Gaff, M.; Razaei, F.; Sikora, A.; Hýsek, Š.; Sedlecký, M.; Ditommaso, G.; Corleto, R.; Kamboj, G.; Sethy, A.; Vališ, M.; et al. Interactions of monitored factors upon tensile glue shear strength on laser cut wood. Compos. Struct. 2020, 234, 111679. [Google Scholar] [CrossRef]
  22. Martinez-Conde, A.; Krenke, T.; Frybort, S.; Muller, U. Review: Comparative analysis of CO2 laser and conventional sawing for cutting of lumber and wood-based materials. Wood Sci. Technol. 2017, 51, 943–966. [Google Scholar] [CrossRef]
  23. Pinkowski, A.; Krauss, A.; Sydor, M. The effect of spiral grain on energy requirement of plane milling od Scots pine (Pinus sylvestris L.) wood. Bioresources 2016, 11, 1930–2126. [Google Scholar]
  24. Vlckova, M.; Gejdos, M.; Nemec, M. Analysis of vibration in wood chipping process. Akustika 2017, 28, 106–110. [Google Scholar]
  25. Suchomel, J.; Belanova, K.; Gejdos, M.; Nemec, M.; Danihelova, A.; Maskova, Z. Analysis of Fungi in Wood Chip Storage Piles. Bioresources 2014, 9, 4410–4420. [Google Scholar] [CrossRef]
  26. Sydor, M.; Rogozinski, T.; Stuper-Szablewska, K.; Starczewski, K. The Accuracy of Holes Drilled in the Side Surface of Plywood. Bioresources 2020, 15, 117–129. [Google Scholar]
  27. Barcík, Š.; Kvietková, M.; Gašparík, M.; Kminiak, R. Influence of technological parameters on lagging size in cutting process of solid wood by abrasive water jet. Wood Res. 2013, 58, 627–636. [Google Scholar]
  28. Igaz, R.; Kminiak, R.; Krišťák, L’.; Němec, M.; Gergel’, T. Methodology of Temperature Monitoring in the Process of CNC Machining of Solid Wood. Sustainability 2018, 11, 95. [Google Scholar] [CrossRef] [Green Version]
  29. Eltawahni, H.A.; Rossini, N.S.; Dassisti, M.; Alrashed, K.; Aldaham, T.A.; Benyounis, K.Y.; Olabi, A.G. Evaluation and optimization of laser cutting parameters for plywood materials. Opt. Lasers Eng. 2013, 51, 1029–1043. [Google Scholar] [CrossRef] [Green Version]
  30. Orlowski, K.; Chuchala, D.; Muzinski, T.; Barariski, J.; Banski, A.; Rogozinski, T. The effect of wood drying method on the granularity of sawdust obtained during the sawing process using the frame sawing machine. Acta Fac. Xylologiae Zvolen 2019, 61, 83–92. [Google Scholar]
  31. Rogozinski, T.; Wilkowski, J.; Gorski, J.; Szymanowski, K.; Podziewski, P.; Czarniak, P. Technical note: Fine particles content in dust created in CNC milling of selected wood composites. Wood Fiber Sci. 2017, 49, 461–469. [Google Scholar]
  32. Hlaskova, L.; Orlowski, K.; Kopecky, Z.; Jedinak, M. Sawing Processes as a Way of Determining Fracture Toughness and Shear Yield Stresses of Wood. Bioresources 2015, 10, 5381–5394. [Google Scholar] [CrossRef] [Green Version]
  33. Marková, I.; Mračková, E.; Očkajová, A.; Ladomerský, J. Granulometry of selected wood dust species of dust from orbital sanders. Wood Res. 2016, 61, 983–992. [Google Scholar]
  34. Igaz, R.; Gajtanska, M. The influence of water vapour concentration in CO2 laser active region on output power of emited beam. Acta Fac. Tech. 2014, 19, 35–40. [Google Scholar]
  35. Gajtanska, M.; Igaz, R.; Krišťák, L’.; Ružiak, I. Contamination of CO2 Laser Mixture; Technical University in Zvolen Publishing: Zvolen, Slovakia, 2014. [Google Scholar]
  36. Gajtanska, M.; Suja, J.; Igaz, R.; Krišťák, L’.; Ružiak, I. CO2 Laser Cutting of Spruce Wood; Technical University in Zvolen Publishing: Zvolen, Slovakia, 2015. [Google Scholar]
  37. Antov, P.; Neykov, N. Costs of occupational accidents in the Bulgarian woodworking and furniture industry. In Proceedings of the 3rd International Scientific Conference Wood Technology & Product Design, Ohrid, Republic of Macedonia, 11–14 September 2017; Volume III, pp. 213–221. [Google Scholar]
  38. Brezin, V.; Antov, P. Engineering Ecology, 1st ed.; Publishing House of the UF: Sofia, Bulgaria, 2015; 259p. [Google Scholar]
  39. Li, L.; Mazumder, J. A study of the mechanism of laser cutting of wood. For. Prod. J. 1992, 41, 53–59. [Google Scholar]
  40. Barnekov, V.G.; Huber, H.A.; McMillin, C.W. Laser machining wood composites. For. Prod. J. 1989, 39, 76–78. [Google Scholar]
  41. Grad, L.; Mozina, J. Optodynamic studies of Er: YAG laser interaction with wood. Appl. Surf. Sci. 1998, 127, 973–986. [Google Scholar] [CrossRef]
  42. Hattori, N. Laser processing of wood. Mokuzai Gakkaishi 1995, 41, 703–709. [Google Scholar]
  43. Riveiro, A.; Quintero, F.; Boutinguiza, M.; del Val, J.; Comesana, R.; Lusquinos, F.; Pou, J. Laser Cutting: A Review on the Influence of Assist Gas. Materials 2019, 12, 157. [Google Scholar] [CrossRef] [Green Version]
  44. Piili, H.; Hirvikaki, M.; Salminen, A. Repeatability of laser cutting of uncoated and coated boards. In Proceedings of the NOLAMP, Copenhagen, Denmark, 24–26 August 2009. [Google Scholar]
  45. Lum, K.C.P.; Hg, S.L.; Black, I. CO2 laser cutting of MDF: Determination of process parameter settings. Opt. Laser Technol. 2000, 32, 67–76. [Google Scholar] [CrossRef]
  46. Powell, J. CO2 Laser Cutting, 2nd ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
  47. Eltawahni, H.A.; Olabi, A.G.; Benyounis, K.Y. Investigating the CO2 laser cutting parameters of MDF wood composite material. Opt. Laser Technol. 2011, 43, 648–659. [Google Scholar] [CrossRef] [Green Version]
  48. Barnekov, V.G.; McMillin, C.W.; Huber, H.A. Factors influencing laser cutting of wood. For. Prod. J. 1986, 36, 55–58. [Google Scholar]
  49. Lum, K.C.P.; Hg, S.L.; Black, I. CO2 laser cutting of MDF, Estimation of power distribution. J. Opt. Laser Technol. 2000, 32, 77–87. [Google Scholar] [CrossRef]
  50. Antov, P.; Mantanis, G.I.; Savov, V. Development of Wood Composites from Recycled Fibres Bonded with Magnesium Lignosulfonate. Forests 2020, 11, 613. [Google Scholar] [CrossRef]
  51. Antov, P.; Savov, V.; Mantanis, G.; Neykov, N. Medium-density fibreboards bonded with phenol-formaldehyde resin and calcium lignosulfonate as an eco-friendly additive. J. Wood Mater. Sci. Eng. 2020. [Google Scholar] [CrossRef]
  52. Tayal, M.; Barnekov, V.; Mukherjee, K. Focal point location in laser machining of thick hard wood. J. Mater. Sci. Lett. 1994, 13, 644–646. [Google Scholar] [CrossRef]
  53. Nukman, Y.; Saiful, R.I.; Azuddin, M.; Aznijar, A.Y. Selected Malaysian Wood CO2 Laser Cutting Parameters and Cut Quality. Am. J. Appl. Sci. 2008, 5, 990–996. [Google Scholar]
  54. McMillin, W.C.; Harry, J.E. Laser Machining of Southern Pine. For. Prod. J. 1971, 21, 24–37. [Google Scholar]
  55. Quintero, F.; Riveiro, A.; Lusquinos, F.; Comesana, R.; Pou, J. CO2 laser cutting of phenolic resin boards. J. Mater. Process. Technol. 2011, 211, 1710–1718. [Google Scholar] [CrossRef]
  56. Quintero, F.; Riveiro, A.; Lusquinos, F.; Comesana, R.; Pou, J. Feasibility study on the laser cutting of phenolic resin boards. Phys. Procedia 2011, 12, 578–583. [Google Scholar] [CrossRef] [Green Version]
  57. Zhou, B.H.; Mahdavian, S.M. Experimental and theoretical analyses of cutting nonmetallic materials by low power CO2 laser. J. Mater. Process. Technol. 2004, 146, 188–192. [Google Scholar] [CrossRef]
  58. Moradi, M.; Mehrabi, O.; Azdast, T.; Benyounis, K.Y. Enhancement of low power CO2 laser cutting process for injection molded polycarbonate. Opt. Laser Technol. 2017, 96, 208–218. [Google Scholar] [CrossRef]
  59. Choudhury, I.A.; Shirley, S. Laser cuting of polymeric materials: An experimental investigation. Opt. Laser Technol. 2010, 42, 503–508. [Google Scholar] [CrossRef]
  60. Yang, C.B.; Deng, C.S.; Chiang, H.L. Combining the Taguchi method with artificial neural network to construct a prediction model of a CO2 laser cutting experiment. Int. J. Adv. Manuf. Technol. 2012, 59, 1103–1111. [Google Scholar] [CrossRef]
  61. Elsheikh, A.H.; Shehabeldeen, T.A.; Zhou, J.; Showaib, E.; Elaziz, M.A. Prediction of laser cutting parameters for polymethylmethacrylate sheets using random vector functional link network integrated with equilibrium optimizer. J. Intell. Manuf. 2020. [Google Scholar] [CrossRef]
  62. Alizadeh, A.; Omrani, H. An integrated multi response Taguchi- neural network- robust data envelopment analysis model for CO2 laser cutting. Measurement 2019, 131, 69–78. [Google Scholar] [CrossRef]
  63. Dubey, A.K.; Yadava, V. Laser beam machining: A review. Int. J. Mach. Tools Manuf. 2008, 48, 609–628. [Google Scholar] [CrossRef]
  64. Radovanovic, M.; Madic, M. Experimental investigations of CO2 laser cut quality: A review. Nonconv. Technol. Rev. 2011, 4, 35–42. [Google Scholar]
  65. Hernandez-Castaneda, C.J.; Sezer, K.H.; Li, L. The effect of moisture content in fibre laser cutting of pine wood. Opt. Lasers Eng. 2011, 49, 1139–1152. [Google Scholar] [CrossRef]
  66. Prakash, S.; Kumar, S. Experimental investigation and analytical modeling of multi-pass CO2 laser processing on PMMA. Precis. Eng. 2017, 49, 220–234. [Google Scholar] [CrossRef]
  67. Jianying, S.; Yun, Z. FEM Simulation Technologies of Laser Cutting Wood Board Based on ANSYS. Adv. Mater. Res. 2010, 113, 1629–1631. [Google Scholar]
  68. Polak, M.; Chmelickova, H.; Vasicek, L. Numerical modeling of laser treatment of metal and nonmetal materials. In Proceedings of the 13th Polish-Czech-Slovak Conference on Wave and quantum Aspects of Contemporary Optics, Krzyzowa, Poland, 21 November 2003; Volume 5259, pp. 303–307. [Google Scholar] [CrossRef]
  69. Yang, C.; Jiang, T.; Yu, Y.; Dun, G.; Ma, Y.; Liu, J. Study of surface quality of wood processed by water-jet assisted nanosecond laser. Bioresources 2018, 13, 3125–3134. [Google Scholar] [CrossRef]
  70. Yang, C.; Jiang, T.; Yu, Y.; Bai, Y.; Song, M.; Miao, Q.; Ma, Y.; Liu, J. Water-jet assisted nanosecond laser microcutting of norheast China ash wood: Experimental study. Bioresources 2019, 14, 128–138. [Google Scholar]
  71. Hardalov, C.M.; Christov, C.G.; Mihalev, M.S. Numerical modeling of laser machining on the ceramic surface. AU J. Technol. 2006, 9, 163–171. [Google Scholar]
  72. Modest, F.M. Laser Machining of Ablating/Decomposing Materials–Through Cutting and Drilling Models; ICALEO: Quebec, Canada, 1996. [Google Scholar]
  73. Roggero, G.; Scotti, F.; Piuri, V. Quality analysis measurement for laser cutting. In Proceedings of the 2001 International Workshop on Virtual and Intelligent Measurement Systems, Budapest, Hungary, 20–20 May 2001. [Google Scholar]
  74. Bianco, N.; Manca, O.; Nardini, S.; Tamburino, S. Transient Heat Conduction in Solids Irradiated by a Moving Heat Source. Defect Diffus. Forum 2009, 283, 358–363. [Google Scholar] [CrossRef]
  75. Babiak, M.; Orech, J.; Kleskeňová, M. Temperature distribution in wood heated by scanning gaussian laser beam. Wood Res. 1986, 108, 1–15. [Google Scholar]
  76. Yilbas, B. Laser Cutting Qualitz Assesment and Thermal Efficiency Analysis. J. Mater. Process. Technol. 2004, 155, 2106–2115. [Google Scholar] [CrossRef]
  77. ISO 13061-1:2014. Physical and Mechanical Properties of Wood. Test Methods for Small Clear Wood Specimens. Part 1: Determinantion of Moisture Content for Physical and Mechanical Tests; International Organization for Standardization: Geneva, Swittzerland, 2014. [Google Scholar]
  78. ISO 13061-2:2014. Physical and Mechanical Properties of Wood. Test Methods for Small Clear Wood Specimens. Part 2: Determination of Density for Physical and Mechanical Tests; International Organization for Standardization: Geneva, Swittzerland, 2014. [Google Scholar]
  79. Dhanachandra, N.; Manglem, K.; Chanu, Y.J. Image Segmentation Using K–means Clustering Algorithm and Subtractive Clustering Algorithm. Procedia Comput. Sci. 2015, 54, 764–771. [Google Scholar] [CrossRef] [Green Version]
  80. Moallem, P.; Razmjooy, N. Adaptive Particle Swarm Optimization. J. Appl. Res. Technol. 2012, 5, 703–712. [Google Scholar]
  81. Ready, J.F.; Farson, D.F.; Feeley, T. LIA Handbook of Laser Materials Processing; Laser Institute of America, Magnolia Publishing: Orlando, FL, USA; Springer Nature: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
  82. Liu, Q.; Yang, C.; Xue, B.; Miao, Q.; Liu, J. Processing Technology and Experimental Analysis of Gas-assisted Laser Cut Micro Thin Wood. Bioresources 2020, 15, 5366–5378. [Google Scholar]
  83. Asibu, E.K. Principles of Laser Materials Processing; John Wiley and Sons: New York, NY, USA, 2009. [Google Scholar]
  84. Arai, T.; Hayashi, D. Factors affecting the Laser processing of wood. 1. Effects of mechanical laser parameters on machinability. Mokuzai Gakkaishi 1992, 38, 350–356. [Google Scholar]
  85. Arai, T.; Hayashi, D. Factors affecting the Laser processing of wood. 2. Effects of material parameters on machinability. Mokuzai Gakkaishi 1994, 40, 497–503. [Google Scholar]
  86. Peters, C.C.; Banas, C.M. Cutting wood and wood-base products with a multikilowatt CO2 laser. For. Prod. J. 1977, 27, 41–45. [Google Scholar]
  87. Pędzik, M.; Bednarz, J.; Kwidziński, Z.; Rogoziński, T.; Smardzewski, J. The Idea of Mass Customization in the Door Industry Using the Example of the Company Porta KMI Poland. Sustainability 2020, 12, 3788. [Google Scholar] [CrossRef]
  88. Potkany, M.; Gejdoš, M.; Debnár, M. Sustainable Innovation Approach for Wood Quality Evaluation in Green Business. Sustainability 2018, 10, 2984. [Google Scholar] [CrossRef] [Green Version]
  89. Němec, F.; Lorincová, S.; Hitka, M.; Turinská, L. The Storage Area Market in the Particular Territory. Nase More 2015, 62, 131–138. [Google Scholar] [CrossRef] [Green Version]
  90. Lorincová, S.; Schmidtová, J.; Balážová, Z. Perception of the corporate culture by managers and blue collar workers in Slovak wood-processing businesses. Acta Fac. Xylologiae Zvolen 2016, 58, 149–163. [Google Scholar]
  91. Potkany, M.; Hitka, M. Utilization of contribution margin in the costing system in the production of components for wood working machines. Drv. Ind. 2009, 60, 101–110. [Google Scholar]
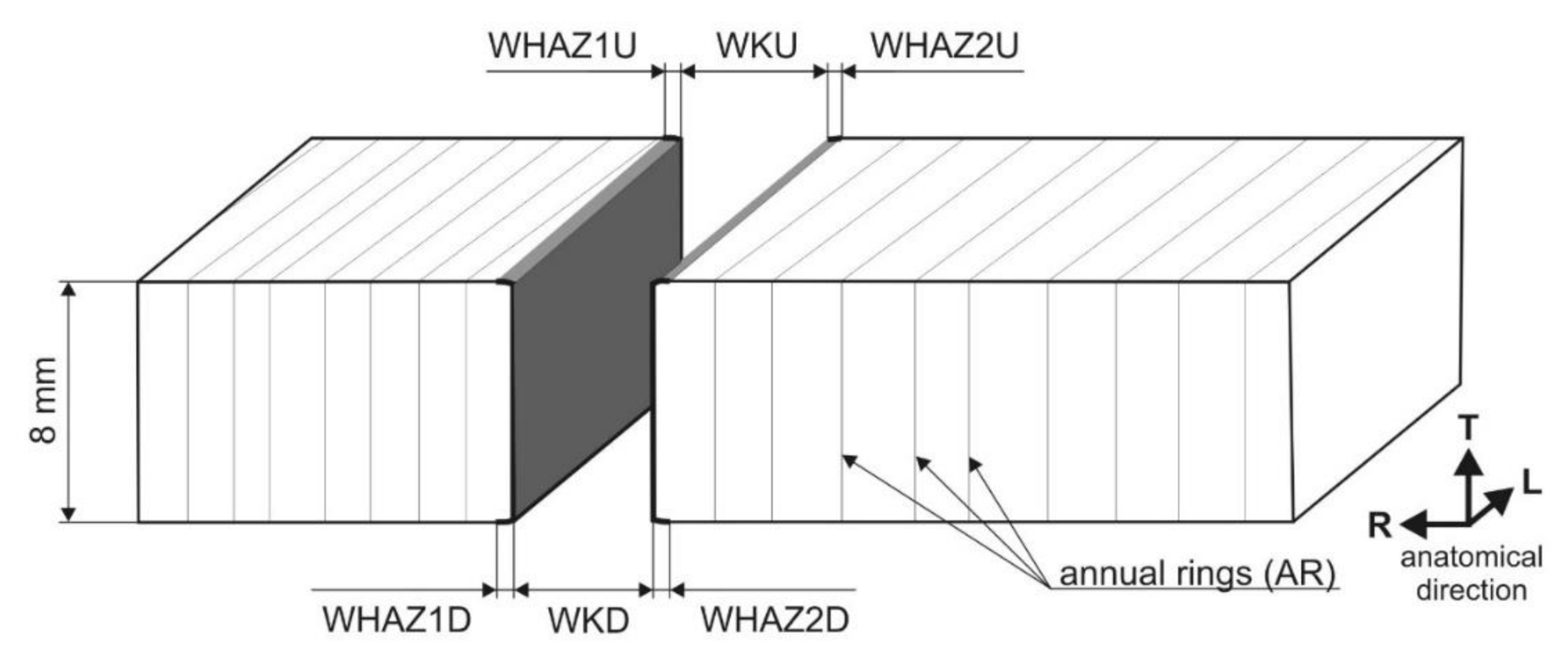
Applsci 10 08113 g001 550
Figure 1. Cutting scheme.
Figure 1. Cutting scheme.
Applsci 10 08113 g001
Applsci 10 08113 g002 550
Figure 2. Photo used for measuring the width of the cutting kerf and heat-affected zone (left), and photo edited by segmentation (right) by Digital Microscopy (DM).
Figure 2. Photo used for measuring the width of the cutting kerf and heat-affected zone (left), and photo edited by segmentation (right) by Digital Microscopy (DM).
Applsci 10 08113 g002
Applsci 10 08113 g003 550
Figure 3. Influence of the main factors: First line (left) WKU* and (right) WHAZU*; second line (left) WKD* and (right) WHAZD*; and last line (left) WKR* and (right) B*.
Figure 3. Influence of the main factors: First line (left) WKU* and (right) WHAZU*; second line (left) WKD* and (right) WHAZD*; and last line (left) WKR* and (right) B*.
Applsci 10 08113 g003
Applsci 10 08113 g004 550
Figure 4. Response areas for joint optimization in the case of fixed power P = 100 W (left) and in the case of fixed cutting speed V = 9 mm·s−1 (right).
Figure 4. Response areas for joint optimization in the case of fixed power P = 100 W (left) and in the case of fixed cutting speed V = 9 mm·s−1 (right).
Applsci 10 08113 g004
Table
Table 1. Experimental factors.
Table 1. Experimental factors.
FactorMin. ValueMax. ValueLevels NumberFactor LevelsUnitType
AR31193, 4, 5, 6, 7, 8, 9, 10, 11-random
P1001502100, 150Wcontrolled
V3933, 6, 9mm·s−1controlled
Table
Table 2. Box-Cox transformation.
Table 2. Box-Cox transformation.
ReactionBox-Cox Transformation
WKU*1 + (WKU−0.569 − 1)/(−0.569·0.847226−1.569)
WHAZU*1 + (WHAZU0.134 − 1)/(0.134·0.172185−0.866)
WKD*1 + (WKD0.206 − 1)/(0.206·0.460085−0.794)
WHAZD*1 + (WHAZD−0.605 − 1)/(−0.605·0.169228−1.605)
WKR*1 + (WKR0.372 − 1)/(0.372·0.543049−0.628)
B*1 + (B2.049 − 1)/(2.049·46.42581.049)
Table
Table 3. Descriptive statistics for transformed values of all parameters.
Table 3. Descriptive statistics for transformed values of all parameters.
WKU*WHAZU*WKD*WHAZD*WKR*B*
Average0.85660.17410.55240.21920.63370.4688
Standard deviation0.17610.06570.20930.14710.17090.0079
Variation coefficient20.55%37.75%37.88%67.14%26.97%16.74%
Displacement coefficient−0.422.3441.9644.6851.452−1.328
Peak coefficient−1.256−0.1885−0.52222.288−1.079−0.657
95% confidence interval for the average<0.8085; 0.9046><0.1561; 0.1920><0.4953; 0.6095><0.1179; 0.2593><0.5870; 0.6803><0.4474; 0.4902>
95% confidence interval for the standard deviation<0.148; 0.2174><0.0553; 0.0811><0.1759; 0.2583><0.1237; 0.1816><0.1437; 0.2110><0.0660; 0.0969>
Table
Table 4. Summary of linear models without interactions (e.g., WKU* = 0.9691 + 0.0031·AR + 0.1762·P − 0.0586·V). Background color was used for statistically significant values for 99% confidence interval.
Table 4. Summary of linear models without interactions (e.g., WKU* = 0.9691 + 0.0031·AR + 0.1762·P − 0.0586·V). Background color was used for statistically significant values for 99% confidence interval.
ResponseWKU*WHAZU*WKD*WHAZD*WKR*B*
FactorCoeff.Coeff.Coeff.Coeff.Coeff.Coeff.
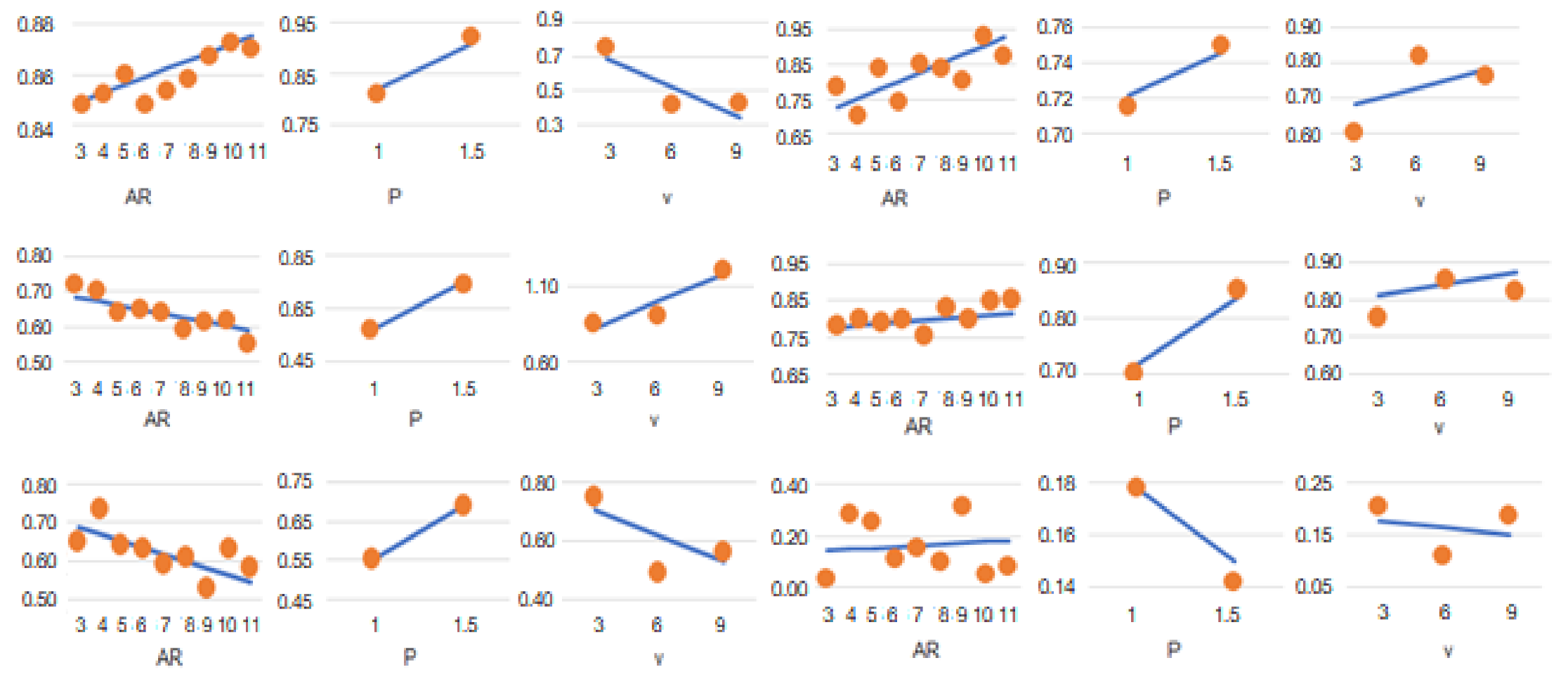
AR0.00310.0021−0.01120.0003−0.01770.00487
P0.17620.04510.35010.25830.2847−0.05437
V−0.05860.0168−0.061−0.0110−0.0304−0.00415
Constant0.96910.56130.64860.51890.56990.22126
R271.76%49.14%84.65%46.51%46.74%2.73%
Table
Table 5. Summary of linear models with interactions (e.g., WKU*= 1.96353 + 0.00695·V2 + 0.08847·P*V + 0.00032·AR*V − 0.00745·AR*P + 0.00526·AR2 − 0.25323·V − 0.29207·P − 0.05862·AR). Background color was used for statistically significant values for 99% confidence interval.
Table 5. Summary of linear models with interactions (e.g., WKU*= 1.96353 + 0.00695·V2 + 0.08847·P*V + 0.00032·AR*V − 0.00745·AR*P + 0.00526·AR2 − 0.25323·V − 0.29207·P − 0.05862·AR). Background color was used for statistically significant values for 99% confidence interval.
ResponseWKU*WHAZU*WKD*WHAZD*WKR*B*
FactorCoeff.Coeff.Coeff.Coeff.Coeff.Coeff.
AR−0.058620.023980.063920.012090.10382−0.03579
P−0.292070.191040.817390.005741.17681−0.51849
V−0.253230.080670.03693−0.053750.23656−0.15057
AR20.00526−0.001420.00034−0.00349−0.002630.00107
AR*P−0.007450.00257−0.056510.02135−0.054680.01333
AR*V0.00032−0.00108−0.002080.00121−0.003520.00172
P*V0.08847−0.02749−0.020150.01778−0.098210.06385
V20.00695−0.00193−0.004890.00099−0.099640.00467
Constant1.963530.23073−0.13999−0.78817−1.015511.04444
R285.88%56.49%87.93%50.50%62.53%29.40%
Table
Table 6. A table presenting the parameters at 150 W power (reference) and 100 W power (optimal), for a cutting speed of 9 mm·s−1 and AR = 3.
Table 6. A table presenting the parameters at 150 W power (reference) and 100 W power (optimal), for a cutting speed of 9 mm·s−1 and AR = 3.
ParameterGoalCutting Kerf Width (mm) ReferenceCutting Kerf Width (mm) OptimalImprovement (%)
WKU*min0.7150.62712.3
WKD*min0.5910.41629.6
WKR*10.5280.67021.1
WHAZU*min0.7860.7642.7
WHAZD*min0.8080.67916
B*min0.1170.144-
Table
Table 7. Results of separate optimization of the investigated factor settings.
Table 7. Results of separate optimization of the investigated factor settings.
GoalCutting Kerf Width (mm)SuitabilityARP (W)V (mm·s−1)
WKU* (WKU)min0.627 (0.565)0.9231009
WKD* (WKD)min0.327 (0.334)0.92111009
WKR* (WKR)10.853 (0.853)0.9231503
WHAZU* (WHAZU)min0.663 (0.113)0.9231003
WHAZD* (WHAZD)min0.679 (0.093)0.8831009
B* (B)min0.117 (33.245)0.6931509
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Kubovský, I.; Krišťák, Ľ.; Suja, J.; Gajtanska, M.; Igaz, R.; Ružiak, I.; Réh, R. Optimization of Parameters for the Cutting of Wood-Based Materials by a CO2 Laser. Appl. Sci. 2020, 10, 8113. https://doi.org/10.3390/app10228113

AMA Style

Kubovský I, Krišťák Ľ, Suja J, Gajtanska M, Igaz R, Ružiak I, Réh R. Optimization of Parameters for the Cutting of Wood-Based Materials by a CO2 Laser. Applied Sciences. 2020; 10(22):8113. https://doi.org/10.3390/app10228113

Chicago/Turabian Style

Kubovský, Ivan, Ľuboš Krišťák, Juraj Suja, Milada Gajtanska, Rastislav Igaz, Ivan Ružiak, and Roman Réh. 2020. "Optimization of Parameters for the Cutting of Wood-Based Materials by a CO2 Laser" Applied Sciences 10, no. 22: 8113. https://doi.org/10.3390/app10228113

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop