Design of an Isolated Bidirectional Symmetric Resonant Converter

Abstract

An isolated type bidirectional resonant converter is presented in this paper. Using a dual active bridge as the main topology and integrating symmetric resonant mechanism, the developed converter features an isolated type bidirectional resonant converter with bidirectional power conversion and electrical isolation capabilities to ensure working security and stability. The application of a symmetric resonant scheme enables the control range of input and output voltages to be widened and achieves soft switching during bidirectional power conversion. A converter design process covering all the bases is exhibited in this work. With the digital signal processor (DSP) TMS320F28335 being employed as the control core, the developed isolated bidirectional resonant converter can effectively handle the power conversion between the simulated 400 V DC grid and the energy storage battery ranging from 280 to 403 V. Based on a 1 kW capacity design, the test data reveal that the forward conversion efficiency from grid to battery can reach 93.25%, and the reverse conversion efficiency from battery to grid is as high as 94.60%.

1. Introduction

Most of the conventional renewable energy storage system is made up of multiple converters [1] with at least one for storage and another for supply. The essential power conversion circuits lead to cost and size increase. The introduction of a bidirectional converter [2,3] with bidirectional power propagation ability can effectively overcome these problems and enhance the conversion efficiency.

Refs. [4,5,6] are articles regarding dual active bridge (DAB) design; these circuits are featured with simple structure, easy control, and bidirectional power flow. However, there exist some problems in a single-phase shift controller, such as a narrower voltage range at light load and curtailed efficiency owing to hard switching. In the case of renewable energy regulation applications, hard switching might usually yield the current waveform to be square or sawtooth, thus invoking high-frequency electromagnetic interference (EMI) and excessive switching loss.

Resonant converters possess a soft switching feature and thus have merits of power loss reduction, with the inductor-inductor-capacitor (LLC) resonant topology being the most popular one. In charger applications, various schemes including LCC, LLC, CLLC, CLLLC, etc., have been proposed [7,8,9,10]. Owing to the advantages of soft-switching characteristic and easy control, the LCC and/or CLLC converter are popularly used in many applications. However, due to the low voltage gain in reverse operation, they are not suitable for bidirectional converter designs [11,12,13]. In the bidirectional power transfer applications [14,15,16], the LLC resonant converter is forced to turn into LC resonant, owing to the magnetizing inductance being clamped by the output voltage. Thus, the voltage gain is limited to be less than 1 in the backward power transfer mode, and only zero-voltage switching (ZVS) of power switches can be achieved. The lack of zero-current switching (ZCS) on the secondary rectifying devices leads to a reduction of conversion efficiency and is unsuitable for wide voltage range applications. Plus, the bidirectional LLC resonant converter is always unsymmetrical and thus results in the difficulty of a bidirectional design. Moreover, LLC only possesses the LC feature in the reverse operating mode and has limited operating range, with the voltage gain being less than 1.0. Therefore, the CLLLC design is more suitable for a bidirectional converter with wider wide operating range [17].

An isolated type bidirectional resonant converter is developed in this paper to tackle the inherited problems faced. Compared with the bidirectional LLC resonant topology, the developed bidirectional symmetric resonant converter allows the voltage gain to be greater than 1 in the reverse mode and achieves soft switching at a full range of load as well as keeps high conversion efficiency in large power applications. Moreover, the symmetric circuit topology makes the circuit design easier and suits the bidirectional operation and wide voltage range applications.

This research principally aims at realizing a CLLLC topology, which is more suitable than LLC in accomplishing bidirectional conversion. A detailed bidirectional resonant converter design procedure is revealed, and the component parameters are derived theoretically and then validated in practice. Finally, an isolated type bidirectional resonant converter is implemented with its performance being exhibited.

2. Circuit Structure and Operation Analysis

2.1. Circuit Structure

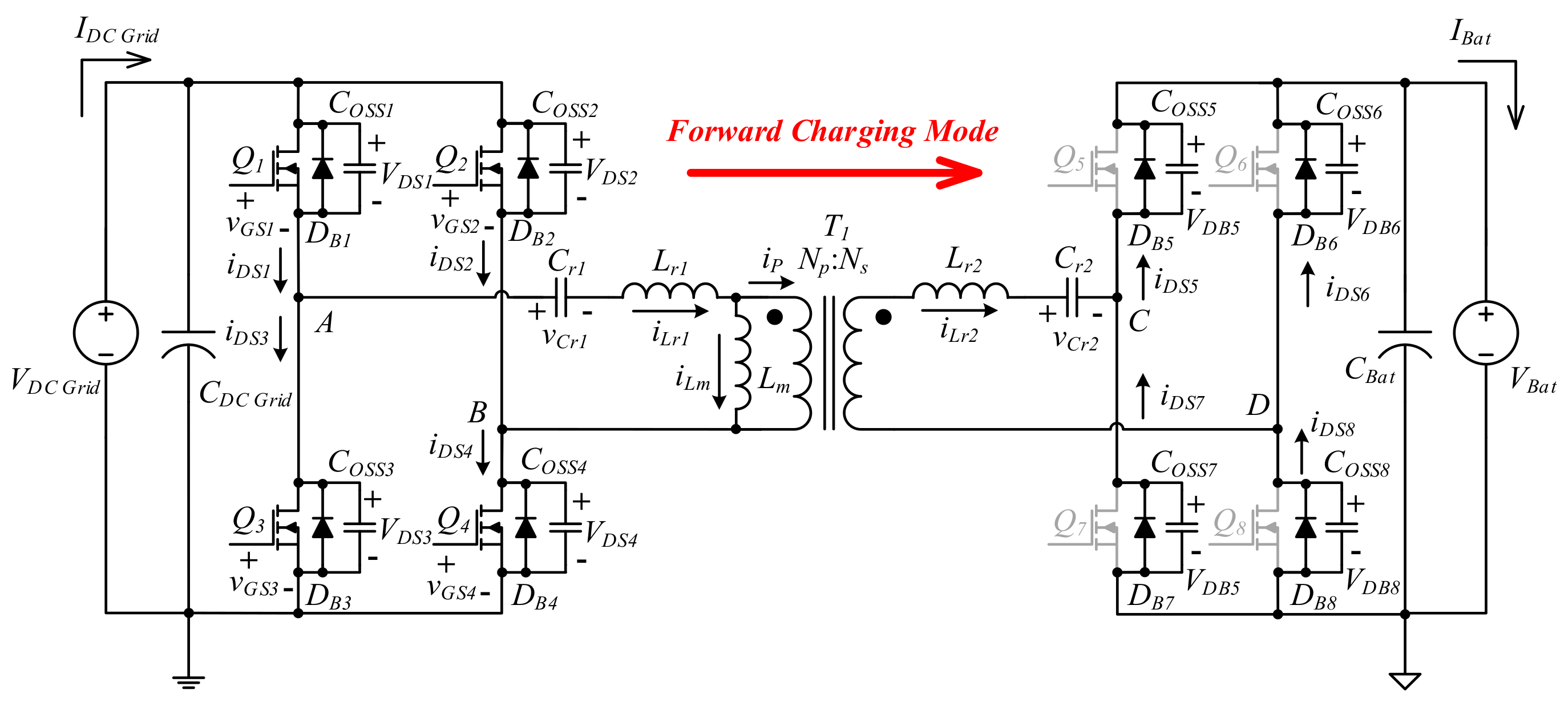
Evolved from an LLC resonant converter, rectification diodes of the transformer secondary side are replaced by active power switches, and an inductor is introduced into the secondary side to form a resonant tank along with the resonant capacitor. Figure 1 shows the realized topology of the isolated bidirectional symmetric resonant converter with a dual active full bridge. In definition, forward charging mode is the power transfer from power grid V_{DC_Grid} to battery port V_Bat, and reverse discharging mode marks the power transfer reversely. With the usage of the symmetric resonant scheme, the power switches can achieve soft switching in either direction of power transfer and thus reduce the switching losses and EMI. Figure 2 illustrates the voltage gain curves of the traditional LLC resonant converter; the reverse-mode voltage gain is limited to be less than 1.

2.2. Description of Operating Range

Figure 3 shows the voltage gain profile in the forward mode of the proposed isolated bidirectional symmetric resonant converter. It is conducted and completed by applying Mathcad and simulated software. The magnitude of voltage gain depends on the ratio of the switching frequency with respect to the resonant frequency. According to the frequency ratio, Region I only ensures ZVS. Region II ensures ZVS of power switches and ZCS of the diodes. Region III exhibits large voltage variation with only ZCS of the diodes. Therefore, Region III should be avoided for voltage control consideration [18]. Due to the symmetric feature, the description is suitable for the reverse mode as well.

2.3. Description of Operating Range

Figure 4 shows the power propagation of the forward charging mode. The energy on the DC grid V_{DC_Grid} supplies energy via power switches Q₁, Q₂, Q₃, and Q₄; it passes from the transformer primary side to the secondary side and thus is rectified by the intrinsic diodes D_B5, D_B6, D_B7, and D_B8 to charge the battery V_Bat. By adjusting the switching frequency, the output voltage and output power are controlled accordingly. The trigger signals of Q₁–Q₄ are a pair of symmetric square waves with each being around a 50% duty ratio. With Q₁ and Q₄ being a group and Q₂ and Q₃ being another, the trigger signals of Q₁ and Q₂ are displaced by 180°, and an appropriate dead time is introduced therein. Due to the symmetric feature, the reverse discharging mode will apply the same operation. Therefore, only the forward mode operating in Region II is used to describe the operating principle. Figure 5 illustrates the important theoretic waveforms. For simplifying the analysis, the following assumptions must be made:

• The circuit operates in the steady state.
• Only intrinsic diode D_B and parasitic capacitance C_OSS are taken into account with others being ignored.
• The effect of the parasitic capacitances C_OSS1–C_OSS8 is neglected.
• All devices are ideal.
• The output capacitances C_{DC_Grid} and C_Bat are large enough to look upon V_{DC_Grid} and V_Bat as the ideal voltage source.

2.3.1. Stage I [t₁ < t ≤ t₂]

In this stage, Figure 6a shows that Q₁, Q₂, Q₃, and Q₄ are all cut off. At the secondary side, D_B5 and D_B8 conduct, while D_B6 and D_B7 remain cut off. At the primary side, the resonant current i_Lr1 passes through D_B1 and D_B4 to keep the resonant current flow and prevent the devices from voltage spike damage. In addition, the circuit is ready for the ZVS of Q₁ and Q₄. At t = t₂, as gate signals v_GS1 and v_GS4 turn from low level to high, the next stage follows.

2.3.2. Stage II [t₂ < t ≤ t₃]

As shown in Figure 6b, Q₁–Q₄ remain at the cut-off state. The intrinsic diodes D_B5 and D_B8 keep on conducting while D_B6 and D_B7 remain at the cut-off state. The resonant current i_Lr1 flows via intrinsic diodes D_B1 and D_B4 to retain the conduction loop. As the power switch turns on at the end at t = t₃, the ZVS is realized, whereas due to the magnetizing inductor L_m being clamped by the output voltage V_Bat and the secondary resonant capacitor voltage V_Cr2, L_m is absent from resonating, and thus i_Lm keeps on rising linearly. At t = t₃, resonant current i_Lr1 approaches 0, and this stage ends.

2.3.3. Stage III [t₃ < t ≤ t₄]

As shown in Figure 6c, Q₁ and Q₄ turn on at t = t₃ and achieve ZVS while Q₂ and Q₃ remain at the cut-off state. In this stage, V_{DC_Grid} passes the energy through C_r1, L_r1, C_r2, and L_r2, and it delivers the energy to the battery side via the isolated transformer. After being rectified by intrinsic diodes D_B5 and D_B8, the energy charges the battery, whereas L_m is absent from resonating due to the magnetizing inductor L_m being clamped by the output voltage V_Bat and the secondary resonant capacitor voltage V_Cr2, and thus i_Lm keeps on rising linearly. At t = t₄, i_Lr1 equals i_Lm, and this stage terminates. In the meantime, current i_DB5,8 falls to 0, and thus ZVS is achieved.

2.3.4. Stage IV [t₄ < t ≤ t₅]

As shown in Figure 6d, Q₁ and Q₄ remain conducting while Q₂ and Q₃ remain at the cut-off state. As i_Lr1 equals i_Lm at t = t₄, the transformer is decoupled, and electromagnetic induction takes a break. The secondary side bridge is temporarily disabled without current flow. The D_B5 and D_B8 is naturally cut off and gets ready for ZCS. In this mode, the transformer does not transfer energy to the load, and the magnetizing inductor L_m is not clamped by the output voltage V_Bat and the secondary resonant capacitor voltage V_Cr2. The magnetizing inductor L_m, L_r1, and C_r1 constitute a resonant circuit while L_r2 and C_r2 are idle. As the gating signals v_GS1 and v_GS4 turn from high to low at t = t₅, Q₁ and Q₄ cut off, and this stage ends.

2.3.5. Stage V [t₅ < t ≤ t₆]

As shown in Figure 6e, Q₁ and Q₄ are cut off at t = t₅ while Q₂, Q₃ still remain at the cut-off state. This exactly marks the dead time region with resonant current i_Lr1 charging the parasitic capacitors C_OSS1 and C_OSS4 as well as helping C_OSS2 and C_OSS3 to discharge. In the secondary side, D_B6 and D_B7 conduct, and D_B5 and D_B8 cut off. When the voltages on C_OSS2 and C_OSS3 are discharged to 0 and simultaneously C_OSS1 and C_OSS4 are charged to V_{DC_Grid}, this stage terminates.

The abovementioned process from Stage I to Stage V constitutes the whole operation procedure during the positive cycle. The negative cycle has similar operating stages and thus is omitted here.

3. Equivalent Circuit and Mathematic Formulation

For obtaining the voltage gain and its relationship with respect to frequency, the fundamental harmonic approximation method (FHA) [19] was used to build the equivalent circuit model of the forward charging mode as illustrated in Figure 7 [20]. Here, V_{DC_Grid_FHA} is the fundamental component of the square voltage waveform at the primary side. V_oe is the fundamental component of the square voltage waveform of the resonant tank and transformer. The resonant capacitance at the primary side, resonant inductance at the primary side, magnetizing inductance, resonant capacitance at the secondary side, and resonant capacitance at the secondary side are designated as C_r1, L_r1, L_m, C_r2′, and L_r2′, respectively. Moreover, power equivalent load resistance R_oe is the AC load resistance of the energy storage battery referred to the primary side and is expressed as (1).

$$R_{oe}=\frac{8N^2}{{\pi }^2}·\frac{V_{Bat}}{I_{Bat}}=\frac{8N^2}{{\pi }^2}{R}_{Bat}$$

(1)

where N is the transformer turn ratio, and R_Bat is the equivalent resistance of battery pack. For obtaining the transfer function of voltage gain, the Laplace transform of the ratio between the output voltage and the input voltage is derived as follows.

First, the node voltage on the transformer is assigned as v_x, and based on basic circuit theory, (2) is obtained.

$$\begin{gathered} v_x\left(s\right)=v_{DC Grid\_FHA}\left(s\right)·\frac{Z_2\left(s\right)}{Z_1\left(s\right)} \\ {v}_{oe}\left(s\right)=v_x\left(s\right)·\frac{Z_4\left(s\right)}{Z_3\left(s\right)} \end{gathered}$$

(2)

In (2), Z₁(s), Z₂(s), Z₃(s), and Z₄(s) are the Laplace forms of Z₁, Z₂, Z₃, and Z₄, respectively, looking from different positions, and are as expressed by (3).

$$\begin{gathered} Z_1\left(s\right)=\mathrm{s}{L}_{r1}+\frac{1}{s{C}_{r1}}+Z_2\left(s\right) \\ {Z}_2\left(s\right)=\frac{s{L}_m·\left(s{L}_{r2}^{\prime }+\frac{1}{s{C}_{r2}\prime }+R_{oe}\right)}{s{L}_m+s{L}_{r2}\prime +\frac{1}{s{C}_{r2}\prime }+R_{oe}} \\ {Z}_3\left(s\right)=s{L}_{r2}\prime +\frac{1}{s{C}_{r2}\prime }+R_{oe} \\ {Z}_4\left(s\right)=R_{oe} \end{gathered}$$

(3)

By properly rearranging (2) and (3), the voltage gain function of the forward charging mode can be given as (4).

$$M_{vr\_Forward}\left(s\right)=\frac{v_{oe}\left(s\right)}{v_{DC Grid\_FHA}\left(s\right)}=\frac{\mathrm{s}{L}_m//\left(s{L}_{r2}\prime +\frac{1}{s{C}_{r2}\prime }+R_{oe}\right)}{\mathrm{s}{L}_{r1}+\frac{1}{s{C}_{r1}}+\left[\mathrm{s}{L}_m//\left(s{L}_{r2}\prime +\frac{1}{s{C}_{r2}\prime }+R_{oe}\right)\right]}·\frac{R_{oe}}{\mathrm{s}{L}_{r2}\prime +\frac{1}{s{C}_{r2}\prime }+R_{oe}}$$

(4)

In addition, for simplifying the mathematic operation and for easily observing the gain curve, some definitions are described as follows: f_s is the switching frequency of power switches; f_{r1_F} is the first resonant frequency; f_{n_F} is the ratio of f_s and f_{r1_F}, referred to as normalized frequency; Q₁ represents quality factor; k₁ is the ratio of L_m and L_r1; g₁ and m₁ represent the resonant capacitor ratio and resonant inductance ratio, respectively, with reference to the primary side. These are written as follows:

$$f_{r1\_F}=\frac{1}{2\pi \sqrt{L_{r1}{C}_{r1}}},f_n=\frac{f_s}{f_{r1\_F}},Q_1=\frac{\sqrt{\frac{L_{r1}}{C_{r1}}}}{R_{oe}},k_1=\frac{L_m}{L_{r1}},g_1=\frac{C_{r2}\prime }{C_{r1}},m_1=\frac{L_{r2}\prime }{L_{r1}}$$

(5)

$$C_{r1}=\frac{1}{2\pi f_{r1\_F}{Q}_1{R}_{oe}}$$

(6)

$$L_{r1}=\frac{Q_1{R}_{oe}}{2\pi f_{r1\_F}}$$

(7)

By substituting the above defined quantities into (4), it yields (8), where C_r1 and L_r1 are expressed as (6) and (7).

$$\begin{gathered} M_{vr\_Forward}\left(f_{n\_F}\right)= \\ \frac{1}{\sqrt{{\left[1+\frac{1}{k_1}-\frac{1}{k_1{(f_{n\_F})}^2}\right]}^2+Q_1{}^2{\left[f_{n\_F}-\frac{1}{k_1{g}_1{f}_{n\_F}}-\frac{1}{f_{n\_F}}-\frac{1}{g_1{f}_{n\_F}}+\frac{1}{k_1{g}_1{(f_{n\_F})}^3}+\frac{m_1{f}_{n\_F}}{k_1}-\frac{m_1}{k_1{f}_{n\_F}}+f_{n\_F}{m}_1\right]}^2}} \end{gathered}$$

(8)

Similarly, the voltage gain of the reverse discharging mode can be derived as well. The FHA AC equivalent circuit model of reverse mode is shown in Figure 8.

By applying the same conduction, the voltage gain transfer function of the reverse discharging mode can be expressed by (9).

$$\begin{gathered} M_{vr\_Reverse}\left(f_{n\_R}\right) \\ \frac{1}{\sqrt{{\left[1+\frac{1}{k_2}-\frac{1}{k_2{(f_{n\_R})}^2}\right]}^2+Q_2{}^2{\left[f_{n\_R}-\frac{1}{k_2{g}_2{f}_{n\_R}}-\frac{1}{f_{n\_R}}-\frac{1}{g_2{f}_{n\_R}}+\frac{1}{k_2{g}_2{(f_{n\_R})}^3}+\frac{m_2{f}_{n\_R}}{k_2}-\frac{m_2}{k_2{f}_{n\_R}}+f_{n\_R}{m}_2\right]}^2}} \end{gathered}$$

(9)

where the simplified parameters f_{n_R}, Q₂, k₂, g₂, and m₂ are defined below.

$$f_{r1\_R}=\frac{1}{2\pi \sqrt{L_{r2}{C}_{r2}}},f_{n\_R}=\frac{f_s}{f_{r1\_R}},Q_2=\frac{\sqrt{\frac{L_{r2}}{C_{r2}}}}{R_{oe}\prime },k_2=\frac{L_m\prime }{L_{r2}},g_2=\frac{C_{r1}\prime }{C_{r2}},m_2=\frac{L_{r1}\prime }{L_{r2}}$$

(10)

4. The Design Procedure of Circuit Component Parameters

For meeting the performance requirements of the developed converter, some design prerequisites are listed as follows:

• It must have a wide voltage range.
• There must be soft switching of power switches.
• Cost and size should be reduced under high frequency operation.

A good circuit design of resonant circuits is founded on selecting appropriate resonance parameters. Figure 9 illustrates a complete design flowchart of the bidirectional symmetric resonant converter with the step-by-step design procedures being described in the following.

4.1. Step 1: Determining the Specification of Converter

Based on the circuit topology, an isolated type bidirectional symmetric resonant converter with 1 kW output power was implemented to test the validity of the conception. The specification of the converter is listed in

Table 1. Converter specifications.

Parameters	Specifications
DC grid voltage VDC_Grid	400 V
Battery port voltage VBat	280–403 V
Max. conversion power P	1000 W
Series resonant frequency fr1	100 kHz
Power switching range fs	70–150 kHz

.

4.2. Step 2: Calculating the Transformer Turn Ratio

Following the determination of converter specifications, the proper transformer turn ratio was chosen immediately. For obtaining the flexibility of the tuning range, the transformer parameter design as expressed by (11) is based on the rated output voltage of the energy storage/supply port according to the battery nominal voltage.

$$N=\frac{N_P}{N_S}=\frac{V_{DC Grid\_nom}}{V_{Bat\_nom}}$$

(11)

4.3. Step 3: Calculating the Maximum and the Minimum Voltage Gains of Forward Mode

Step 2 determines the transformer turn ratio to be approximately at 1.2. By applying (12) and (13), the maximum and the minimum gains of the forward charging mode are obtained.

$$M_{vr\_max}=\frac{N·V_{Bat\_max}}{V_{DC Grid\_nom}}=\frac{1.2·403}{400}\cong 1.21$$

(12)

$$M_{vr\_min}=\frac{N·V_{Bat\_min}}{V_{DC Grid\_nom}}=\frac{1.2·280}{400}=0.84$$

(13)

4.4. Step 4: Selecting Parameters of Q₁, k₁, g₁, and m₁ to Meet the Forward Voltage Gain Requirement

Initially, a set of proper parameter quantity was selected. Figure 10 shows the forward voltage gain with k₁, g₁, and m₁ being fixed and the forward mode quality factor Q₁ being adjusted. It clearly shows that the voltage gain curve is not a monotonic one and Q₁ with 0.6–2 cannot realize the maximum and minimum gain requirement. Moreover, if Q₁ = 0.4, the operating range of switching frequency is too wide and will result in longer response time. Therefore, a value of Q₁ = 0.2 is suitable for the forward charging mode. With the same consideration, the selection of k₁, g₁, and m₁ is to meet the maximum and minimum gain as the primary priority.

Due to the bidirectional operation of the proposed circuit, the resonant parameters must meet the voltage regulation of both the forward and reverse charging modes. The parameter design can only be fulfilled by an iterative process. Finally, the design parameters are Q₁ = 0.2, k₁ = 3.5, g₁ = 1, and m₁ = 1, as shown in Figure 11.

4.5. Step 5: Checking the Maximum and the Minimum Gains of the Forward Charging Mode

If the maximum and the minimum gains of the forward charging mode are not met, the design has to return to Step 4 to update the parameters Q₁, k₁, g₁, and m₁. As the conditions are met, the design can go on to the next step.

4.6. Step 6: Calculating the Resonant Device Parameters

After the quantities Q₁, k₁, g₁, and m₁ are determined, the parameters of the associated resonant devices with device parameters R_oe, C_r1, L_r1, L_m, C_r2, and L_r2 can be obtained by (14) to (19).

$$R_{oe}=\frac{8N^2}{{\pi }^2}·\frac{V_{Bat}}{I_{Bat}}=\frac{8·{1.2}^2}{{\pi }^2}·\frac{403}{2.5}\cong 188.16\Omega$$

(14)

$$C_{r1}=\frac{1}{2·\pi ·f_{r1\_F}·Q_1·R_{oe}}=\frac{1}{2·\pi ·100k·0.2·188.16}\cong 42.29nF$$

(15)

$$L_{r1}=\frac{1}{{\left(2\pi f_{r1\_F}\right)}^2·C_{r1}}=\frac{1}{{\left(2·\pi ·100k\right)}^2·42.29n}\cong 59.90\mu H$$

(16)

$$L_m=k_1·L_{r1}=3.5·59.9\mu =209.65\mu H$$

(17)

$$C_{r2}=g_1·N^2·C_{r1}=1·{1.2}^2·42.29n\cong 60.90nF$$

(18)

$$L_{r2}=\frac{L_{r1}·m_1}{N^2}=\frac{59.89u·1}{{1.2}^2}\cong 41.60uH$$

(19)

4.7. Step 7: Calculating the Maximum and the Minimum Voltage Gains of Reverse Mode

According to (20) and (21), the maximum and the minimum gains of the reverse charging mode can be achieved.

$$M_{max}=\frac{V_{DC Grid\_nom}}{N·V_{Bat\_min}}=\frac{400}{1.2·280}\cong 1.19$$

(20)

$$M_{min}=\frac{V_{DC Grid\_nom}}{N·V_{Bat\_max}}=\frac{400}{1.2·403}\cong 0.83$$

(21)

4.8. Step 8: Using the Resonant Device Parameters of Step 6 to Reversely Obtain the Parameters Q₂, k₂, g₂, and m₂ of the Reverse Discharging Mode

Employing the resonant device parameters obtained from the forward charging mode and backwards, we can calculate the parameters Q₂, k₂, g₂, and m₂ of the reverse discharging mode.

4.9. Step 9: Checking the Maximum and the Minimum Gains of the Reverse Charging Mode

Mathcad is applied to examine whether the gains meet the maximum and minimum gain requirements illustrated in Figure 12. If the gain curves of reverse charging mode cannot satisfy the maximum and minimum gains condition, we will need to return to Step 4 to readjust the amount of Q₁, k₁, g₁, and m₁ recursively until the voltage gains of both forward and backward mode meet the requirements.

4.10. Step 10: Determining the Maximum and Minimum Operating Frequencies of the Forward and Reverse Charging Modes

By inspecting Figure 12, the maximum and minimum operating frequencies of the forward (f_{s_max_Forward} and f_{s_min_Forward}) and reverse (f_{s_max_Reverse} and f_{s_min_Reverse}) charging modes can be calculated.

4.11. Step 11: Determining the Duration of Dead Time (t_dead)

The duration of dead time plays the key role of success or failure of ZVS of power switches. Too short of a dead time will lead to the unsuccessful removal of the charge on the parasitic capacitors of the power switches and yield ZVS failure while too long of a dead time would sacrifice the energy propagation time and thus increase the current stress on the primary side [21]. Therefore, the silicon carbide (SiC) NMOS power switches C2M0160120D manufactured by the CREE Inc. with very small parasitic capacitance C_OSS being equal to 55 pF are used, and thus the ZVS is easily accomplished. By using (22), the required dead time can be attained.

$$t_{dead}\ge 8·C_{OSS}·f_{s\_max}·L_m=8·55p·145k·209.65u\cong 13.38ns$$

(22)

Because the stray capacitance and parasitic inductance are not taken into account, the dead-time interval was kept up to 200 ns for more tolerance.

5. The Structure of the Digital Signal Control System

Figure 13 shows the control system structure of the developed isolated bidirectional symmetric resonant converter. The digital signal processor (DSP) IC TMS320F28335 of Texas Instruments was employed as the control core of this bidirectional converter system to manipulate the bidirection power flow approach. In comparison with the analog scheme, the digital signal approach can effectively reduce the amount of circuit component and thus decrease the size and cost accordingly.

5.1. Control Strategy

In this research, the constant current–constant voltage control is determined as the charging strategy of battery storage. In the battery discharging mode, the constant voltage control is applied to keep the stability and reliability of the DC power grid.

Taking the battery storage as an example, Figure 14 shows the control system block diagram of the battery storage [22,23], with the reference voltage signal V_{b_ref} being 95% of the upper limit battery voltage and I_{b_ref} being the reference current signal according to the battery charging current. When the battery is charged in the constant-current mode, the analog-to-digital converter (ADC) of the DSP will fetch the output signal I_b and compare it with the reference current signal I_{b_ref} to obtain the difference. With the compensation by a Proportional integrator (PI) controller and modulation by a frequency modulation generator (FM generator), a frequency modulated pulse-width modulation (PWM) is achieved to accomplish the constant current control.

5.2. The Step Response Test of the Charging Current

Although the constant current–constant voltage control is the charging strategy, most of the charging time is based on the constant current charging. Thus, an abrupt constant current charging fluctuation is proposed to validate the developed scheme.

Figure 15 shows the voltage and current curves under a step load current change. In Figure 15a, the battery voltage is kept constant when load current is drastically increased, while Figure 15b reveals that the battery voltage remains unchanged under an abrupt load current drop. It can be clearly observed that the battery voltage remains constant when load current fluctuates.

6. The Measurements and Operating Efficiency Analysis

Based on the parameters, the resonant components are calculated with L_r1 = 59.9 µH, Lr2 = 41.6 µH, L_m = 209.65 µH, C_r1 = 42.29 nF, and C_r2 = 60.9 nF. Owing to the winding transformer’s windings and resonant inductor being handmade, there definitely exists some differences from the calculated ones. Indeed, the transformer magnetizing inductance L_m was measured to be 219.85 µH, and the primary and secondly leakage inductances are L_lk1 = 6 µH and L_lk2 = 4 µH, respectively. Moreover, two resonant inductances are L_r1 = 55.2 µH and L_r2 = 40.36 µH. The resonant capacitors are connected in parallel; it not only can divert the current flow, but it also can reduce the current stress of each capacitor and decrease equivalent series resistance (ESR) loss with C_r1 = 41.4 nF and C_r2 = 53.7 nF.

Table 2. Selected parameters of the important devices.

Device Symbol	Quantity
Transformer turn ratio NP:NS	1.2:1
Magnetizing inductance Lm	219.85 µH
Resonant inductance Lr1 (including primary leakage inductance)	61.2 µH
Resonant inductance Lr2 (including secondary leakage inductance)	44.36 µH
Resonant capacitance (primary) Cr1	41.4 nF
Resonant capacitance (secondary) Cr2	53.7 nF
DC grid capacitor tank CDC_Grid	540 µF
Battery capacitor tank CBat	540 µF
Power switches Q1–Q8	C2M0160120D
Trigger controller	TMS320F28335

lists the selected parameters of the important devices in the practical circuit. The microcontroller unit (MCU) TMS320F28335 developed by TI was selected as the control core of bidirectional power flow to effectively dwindle the amount of device and reduce the size and cost. Considering the cost and the fast switching feature, the wide-band gap SiC (C2M0160120D) is used to serve the power switches (Q₁–Q₈) to promote the converter’s performance.

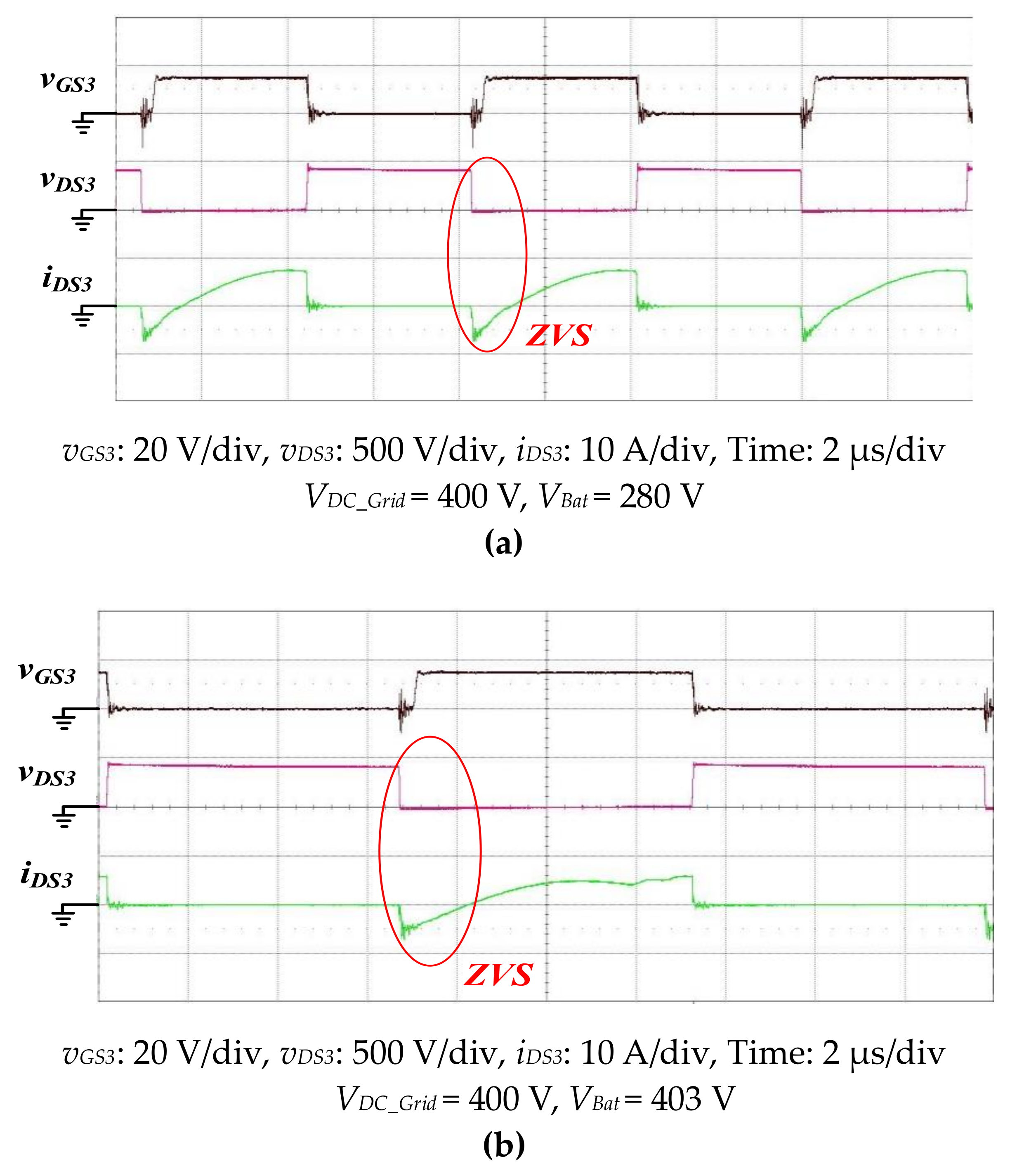
6.1. Critical Measurements for the Forward Charging Mode

Figure 16 shows the measurement results of v_GS3, v_DS3, and i_DS3 in the cases where V_{DC_Grid} = 400 V and charging battery voltages are V_Bat = 280 V and V_Bat = 403 V respectively. It is obvious that there appears a reverse current i_DS3 inside the power switch both in Figure 16a,b which helps remove the energy on the parasitic capacitance and rapidly decline V_DS3 to 0V, thus achieving ZVS.

Figure 17 shows the measurement results of v_DB7 and i_DB7 in the cases where V_{DC_Grid} = 400 V and charging battery voltages are V_Bat = 280 V and V_Bat = 403 V, respectively. By observing Figure 17a, the diode current i_DB7 has not fallen to 0 A prior to the cut-off of diode D_B7 and thus leads to diode ZCS failure. Figure 17b shows that the diode current i_DB7 has reached 0 A before diode D_B7 turns off and thus succeeds in the ZCS of D_B7. It is worth noting that the oscillation of v_DB7 at the switching instant resulted from the resonance of parasitic capacitance and resonant inductance.

6.2. Critical Measurements for the Reverse Discharging Mode

Figure 18 shows the measurement results of v_GS8, v_DS8, and i_DS8 in the cases where the discharging battery voltages are V_Bat = 280 V and V_Bat = 403 V, respectively, and V_{DC_Grid} = 400 V. It is obvious that there appears a reverse current i_DS8 inside the power switch both in Figure 18a,b, which helps remove the energy on the parasitic capacitance and rapidly decline v_DS8 to 0 V, thus achieving ZVS.

Notably, Figure 19a clearly exhibits the advantage of a symmetric dual resonant converter in that the voltage gain is obviously greater than 1.

Figure 19 shows the measurement results of v_DB4 and i_DB4 in the cases where the discharging battery voltages are V_Bat = 280 V and 403 V, respectively, and the DC grid voltage V_{DC_Grid} = 400 V. By observing Figure 19a, the diode current i_DB4 has fallen to 0 A prior to the cut-off of diode D_B4 and thus leads to diode ZCS being successful. It is worth noting that there appears oscillation of v_DB4 at the switching instant, which resulted from the resonance of parasitic capacitance and the secondary resonant inductance. Due to the resonant converter working at Region I, Figure 19b shows that the diode current i_DB4 has not reached 0 A before diode D_B4 turns off and thus fails in ZCS of D_B4.

6.3. Efficiency Plots for Forward Mode and Reverse Mode

Figure 20 shows the efficiency curves with battery voltages V_Bat being 280, 340, and 403 V and charging currents ranging from 0.5 to 2.5 A. This reveals that the maximum conversion efficiency is 91.96% at the lowest battery voltage 280 V, and the maximum conversion efficiency is 93.25% at the highest battery voltage 403 V. The maximal efficiency of 93.67% appears in the case of the 340 V battery voltage because it gets near to the resonant point, and the total impedance is nearly 0. In the forward charging mode, the voltage of DC grid is 400 V, and the designed resonant frequency is around 100 kHz at the 340 V battery voltage, thus getting higher efficiency due to the switching instants of the turn-on and cut-off being near the zero-crossing point. When the discharging current is low, although possessing both ZVS and ZCS, the effect is not obvious due to low current. As the current rises to 1.5A, the efficiency at battery voltage 403 V apparently surpasses that with 280 V battery voltage.

Figure 21 shows the efficiency curves with discharging voltages V_Bat being 280, 340, and 403 V and discharging currents ranging from 0.5 to 2.5 A. In the reverse discharging mode, the voltage of DC grid is 400 V as well. For low battery voltage level, it needs more voltage gain to fulfill DC grid charging and operates in the Region II due to low operating frequency. At different voltage levels of the battery, low battery voltage conditions need more current to discharge the constant voltage DC grid to achieve the identical power level and thus experience more relative power loss. In the case of a 280 V battery voltage, despite the converter operating in Region II and possessing ZCS on the rectifier side, its power loss rate is relatively higher. Operating at a 340 V battery voltage, even though the converter works near the resonant frequency and possesses the advantage of ZVS and ZCS, the conversion efficiency is better than that of the 403 V battery voltage due to more discharging current being needed for the identical power conversion. In fact, when the battery voltage is 403 V and operates at high frequency in Region I with only a ZVS mechanism, it achieves similar efficiency with that of 340 V. This reveals that the maximum conversion efficiency is 91.3% at the lowest discharging voltage 280 V, and the maximum conversion efficiency is 94.6% at the highest discharging voltage 403 V.

7. Conclusions

This research accomplished and realized an isolated type bidirectional symmetric resonant converter with a wide voltage range. By modifying the traditional LLC resonant topology, the secondary side rectifying diodes were replaced by active power switches to constitute a dual active bridge topology. With the introduction of a second set of resonant devices to the secondary side, the symmetric structure enabled the voltage gain to be greater than 1. Indeed, the developed converter is featured with a wide voltage range due to symmetric topology and good conversion efficiency due to ZVS and ZCS functionality. Finally, a 1 kW bidirectional power flow converter that assigns one port with voltage 400 V and another port with voltage ranging from 280 to 403 V was accomplished. The measurements indicate that the maximum conversion efficiency can reach 93.25% in the forward charging mode and is as high as 94.60% in the reverse discharging mode.