Evolution Characteristics of Separated Vortices and Near-Wall Flow in a Centrifugal Impeller in an Off-Designed Condition
Abstract
:1. Introduction
2. Numerical Setup
2.1. Physical Model
2.2. Mesh Generation
2.3. Numerical Methods
2.4. Mesh Independence Study and Validation
3. Results and Discussion
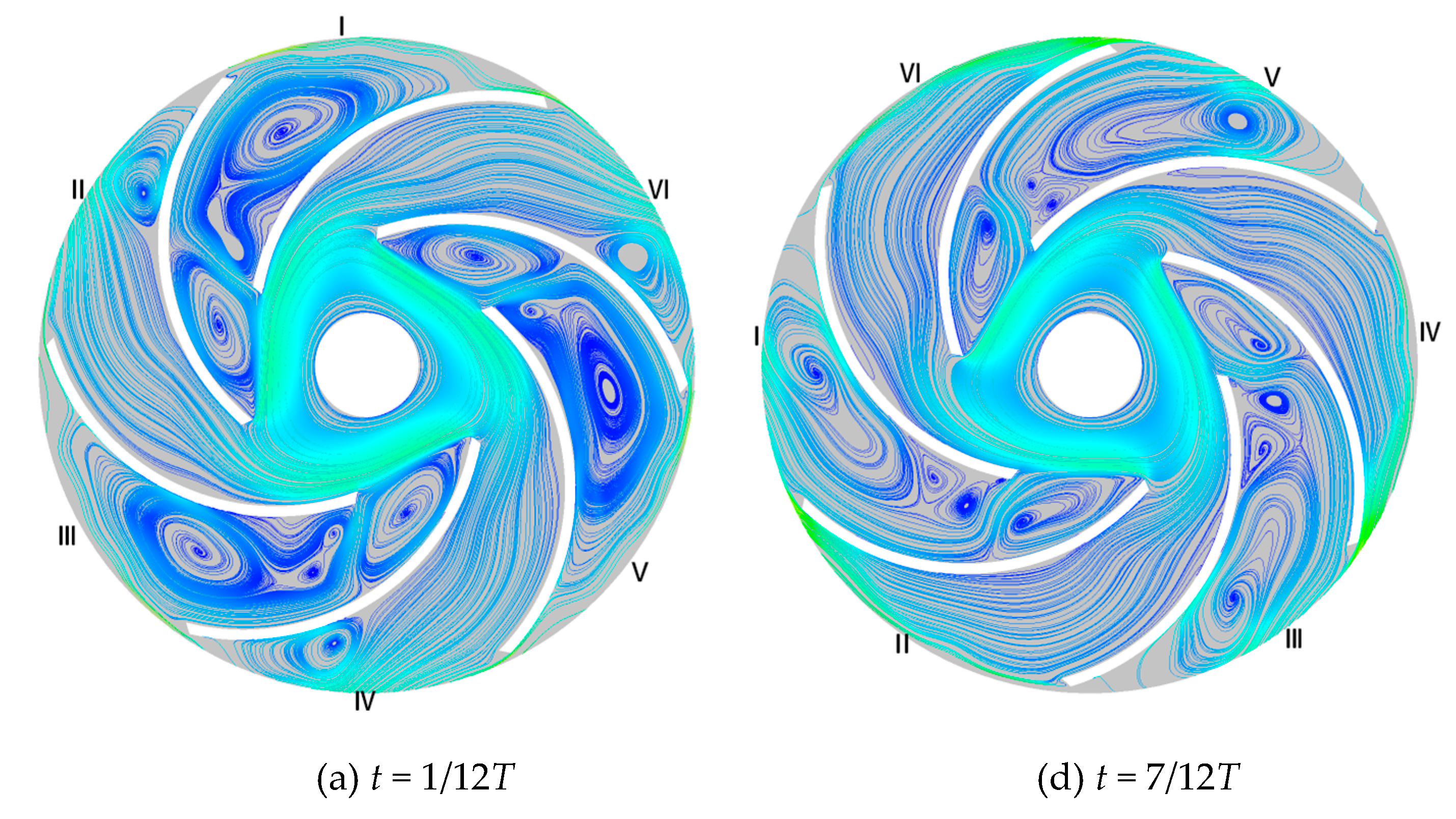
3.1. General Description of the Evolution of Vortices
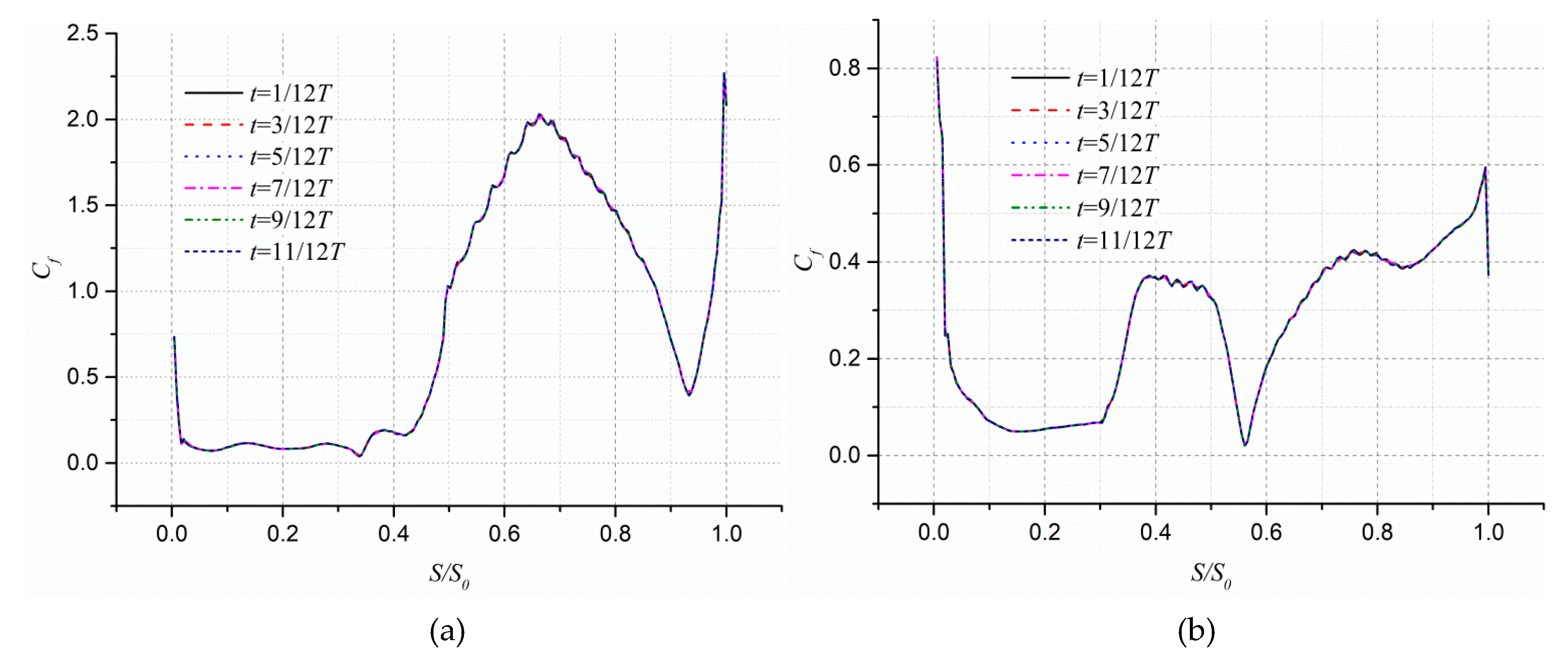
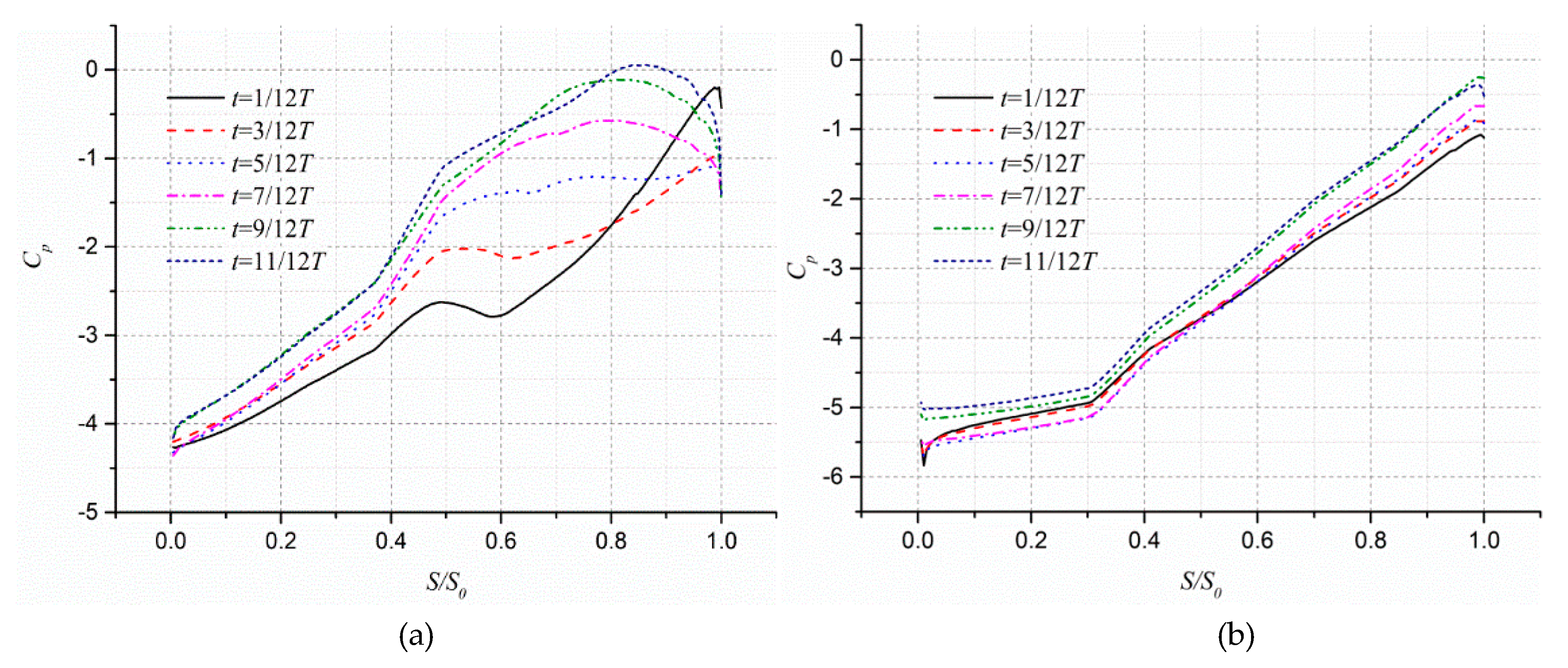
3.2. Boundary Layer Flow in the Stalled Passage
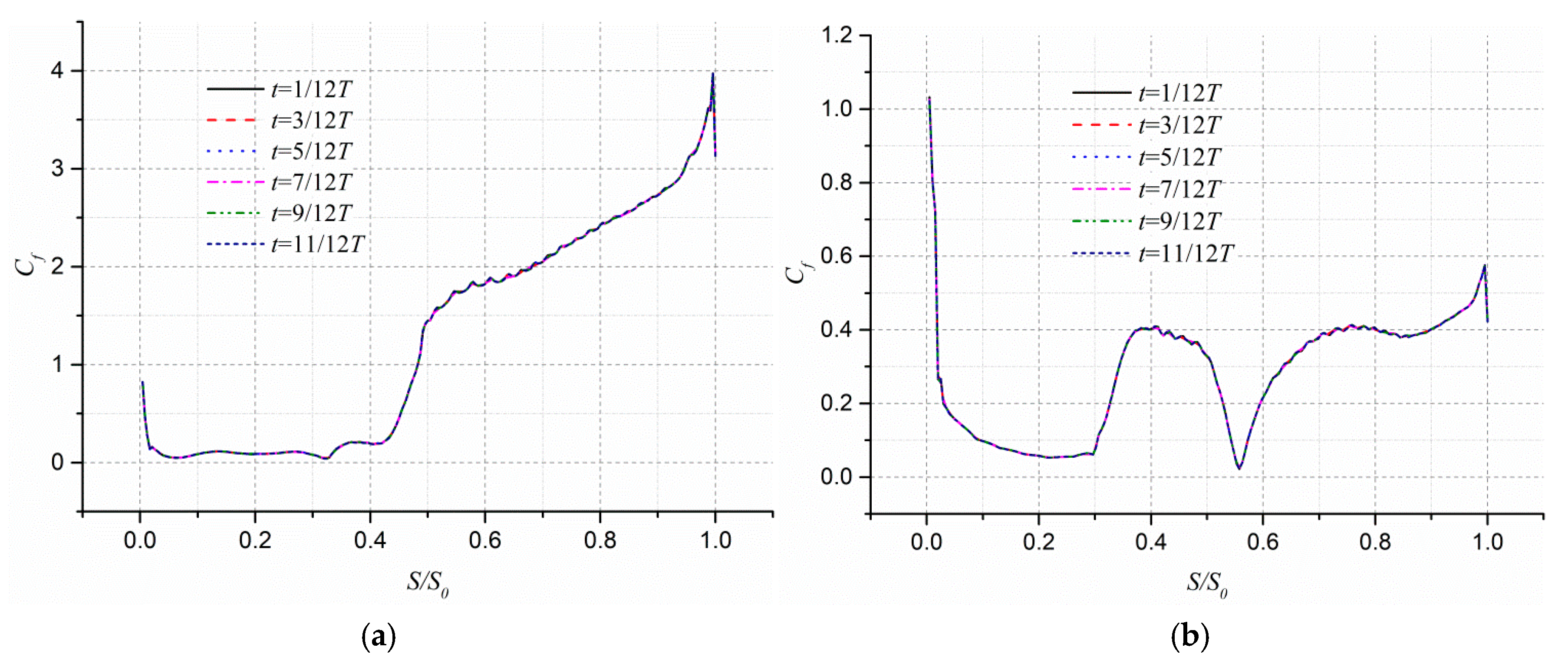
3.3. Boundary Layer Flow in the Unstalled Passage
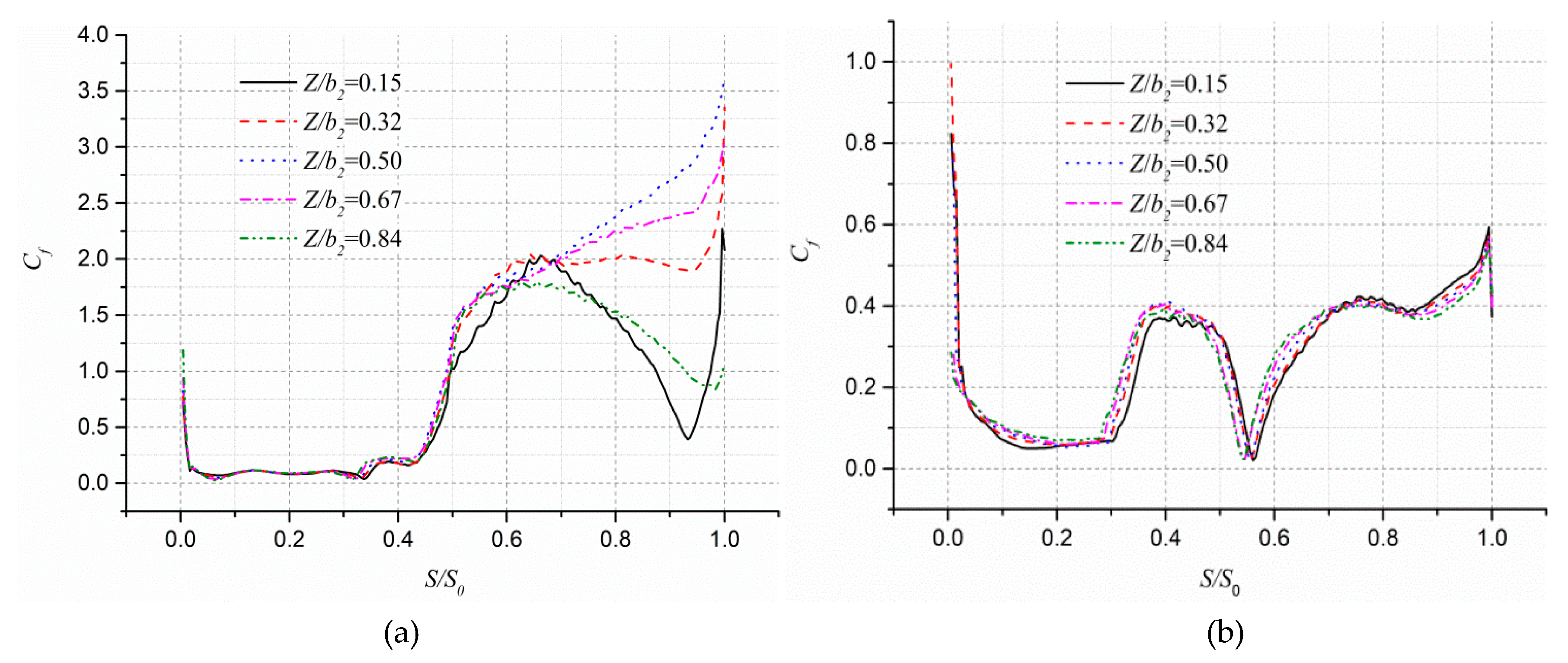
3.4. Three-Dimensionality of Main Flow in Stalled and Unstalled Passages
4. Conclusions
- (1)
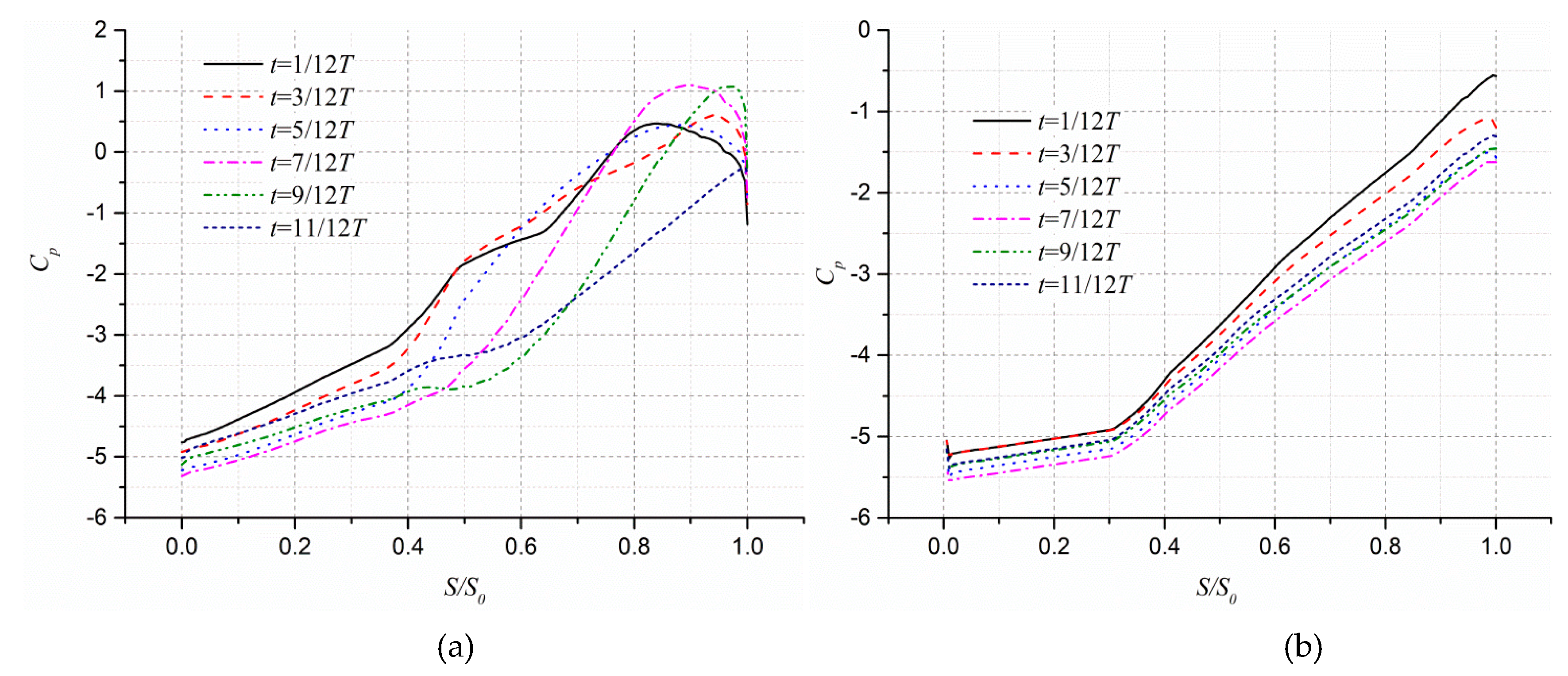
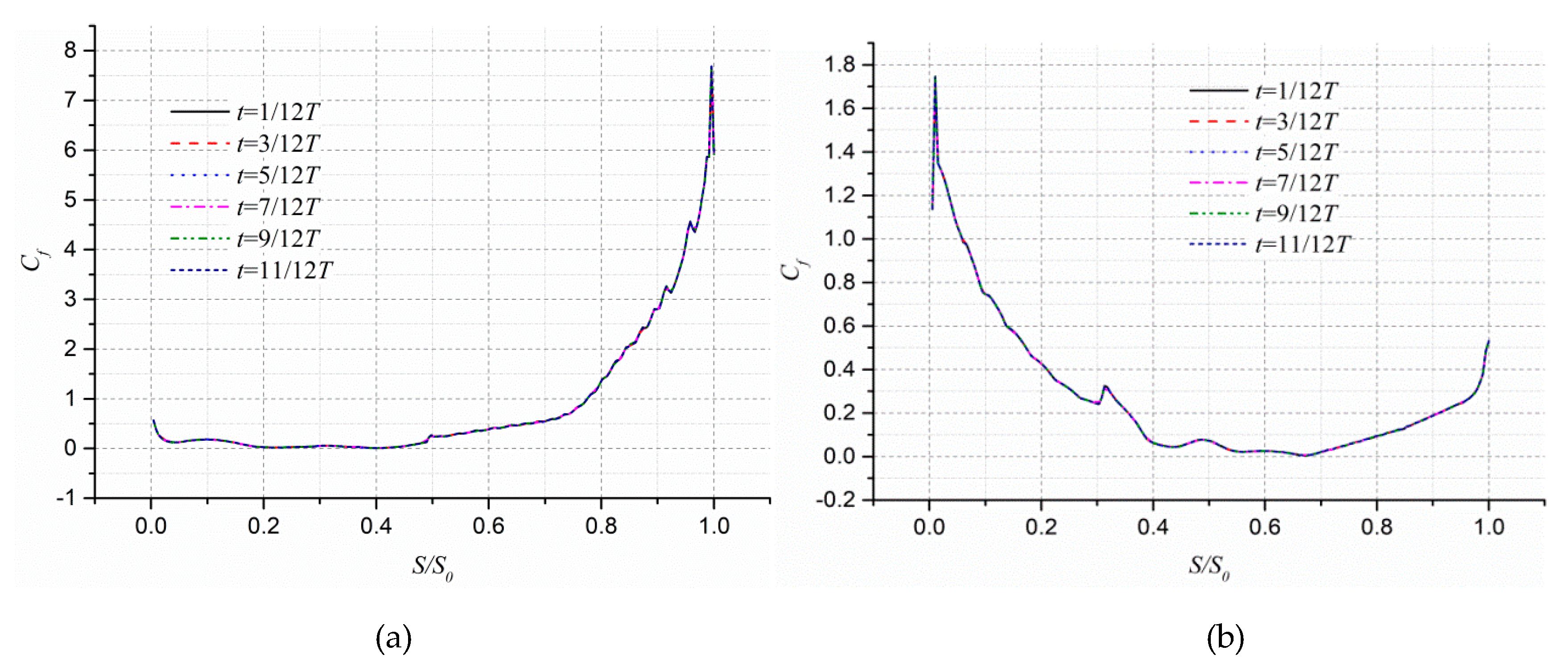
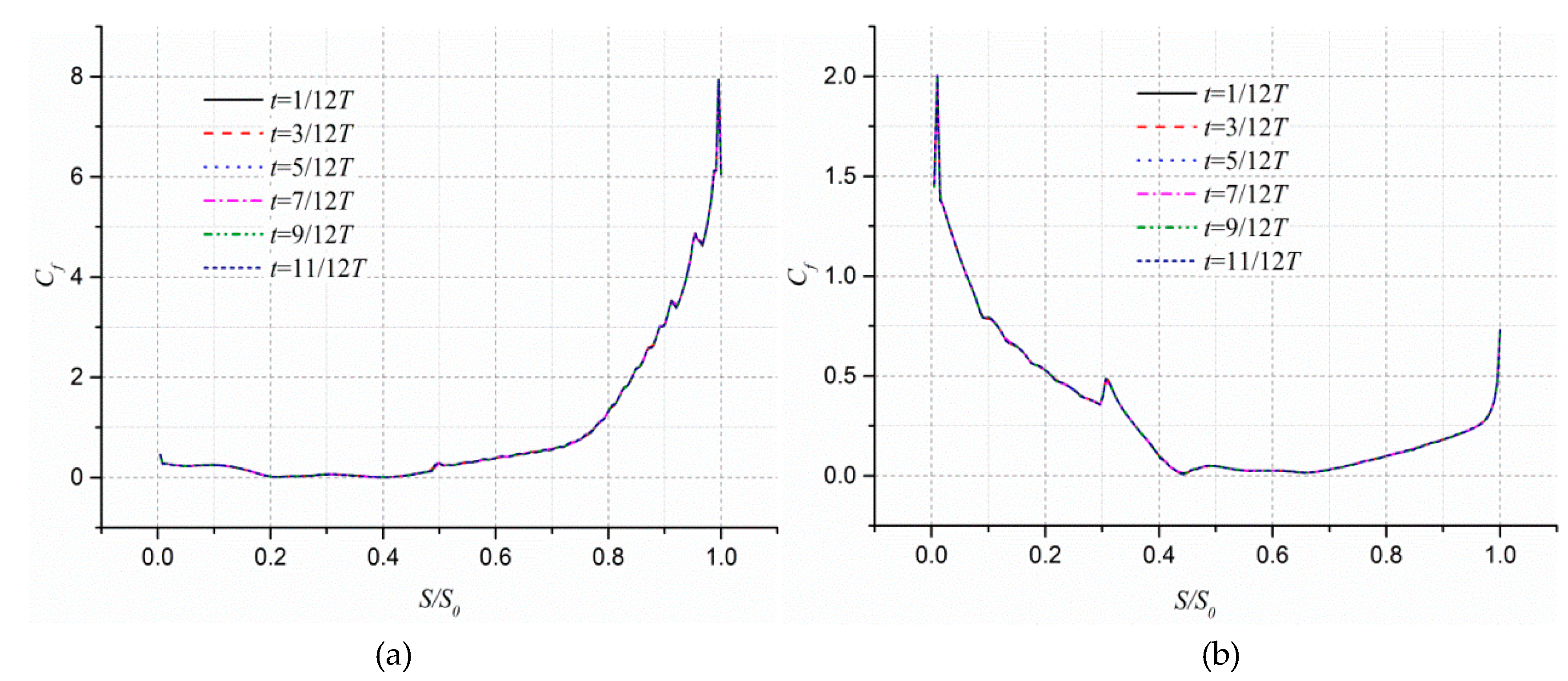
- At the axial cross section Z/b2 = 0.15, the APG of the pressure surface of the stalled passage at the beginning of the blade generally shows a sharp increase, while the magnitude of APG on the suction surface shows a slight increase within a vortex formation period. At S/S0 = 0.4, the wall shear stress of the blade pressure surface also increases sharply, and the peak value reaches about 2.0. The wall shear stress of the suction surface of the blade slowly increases, and the peak value reaches about 7.5 at the impeller outlet section. The large-scale vortex is seen almost blocking the flow channel which decays, merges, sheds, and grows in time.
- (2)
- At the axial cross section Z/b2 = 0.5, the AFG of the pressure surface and suction surface of the stalled passage are similar to the variation at Z/b2 = 0.15. However, the wall shear stress of the pressure surface increases rapidly at first and then slowly increases near S/S0 = 0.4. The peak value of wall shear stress reaches about 4.0. Although the variation trend of the wall shear stress of the suction surface also exhibits peaks and valleys, the peak value reaches about 0.8. Comparing the wall shear stress of the same pressure surface at different axial positions, it is found that the wall shear stress increases the most at the beginning of S/S0 = 0.6.
- (3)
- At the axial cross section Z/b2 = 0.15, the APG of the pressure surface of the unstalled passage is at around the inlet of the impeller (S/S0 = 0.4), in which FPG generally shows a decreasing trend, while the FPG of the suction surface shows a slow decrease. The wall shear stress of the pressure surface shows an increasing trend near S/S0 = 0.5, and its peak value reaches about 7.5. A large-scale vortex can be seen at the impeller outlet. At the entrance of the impeller, the wall shear stress of the suction surface varies from 1.5 to 1.7. The velocity gradient is hardly disturbed; thus, the near-wall flow of the suction surface is relative stable.
- (4)
- At the axial cross-section Z/b2 = 0.5, the FPG of the pressure and suction surfaces of the unstalled passage show similar distributions. The wall shear stress of the pressure surface is approximately the same as that of Z/b2 = 0.15. At the entrance of the impeller, the wall shear stress of the suction surface varies from 1.5 to 2.0, which is slightly higher. Although the peak value has increased by about 0.2, the flow in the vicinity of the suction surface is relatively stable.
- (5)
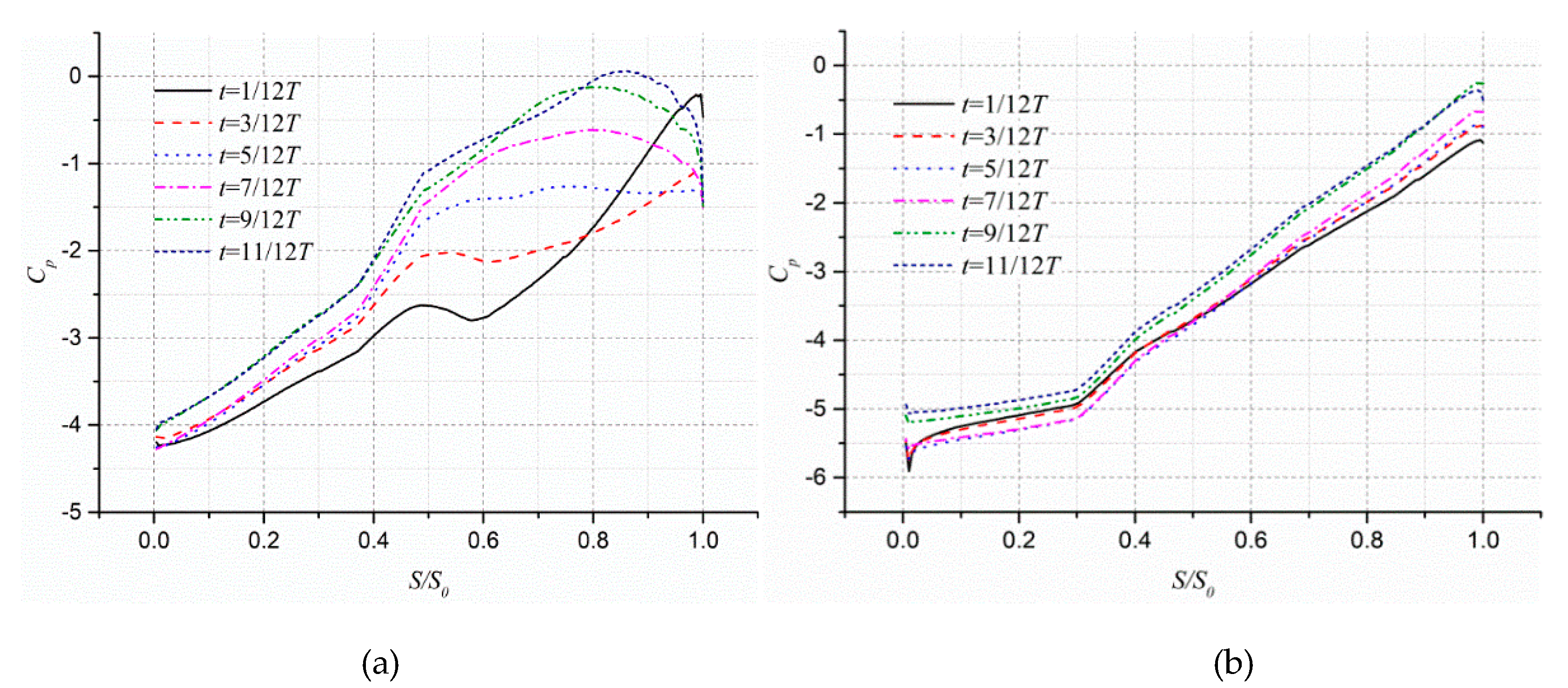
- From the inlet to outlet of the stalled passage, the peak positive value of radial velocity gradually approaches the suction side, and the reversed flow zone gradually expands, indicating that a large area of the vortex appears in the outlet area and deteriorates the through-flow capacity of the passage.
Author Contributions
Funding
Conflicts of Interest
References
- Xia, X.J.; Deng, X.Y. Engineering Separation Dynamics, 1st ed.; Beihang University Press: Beijing, China, 1991; pp. 233–235. [Google Scholar]
- Zhou, P.J.; Dai, J.C.; Li, Y.F. Unsteady flow structures in centrifugal pump under two types of stall conditions. J. Hydrodyn. 2018, 30, 1038–1044. [Google Scholar] [CrossRef]
- Andreas, L.; Gunther, B. Numerical simulation and evaluation of velocity Fluctuations during rotating stall of a centrifugal pump. J. Fluids Eng. 2011, 133, 081102. [Google Scholar]
- Byskov, R.K.; Jacobsen, C.B.; Pedersen, N. Flow in a centrifugal pump impeller at design and off-design conditions-Part I: Particle image velocimetry(PIV) and laser Doppler velocimery(LDV) measurements. J. Fluids Eng. 2003, 125, 61–72. [Google Scholar] [CrossRef]
- Tan, L.; Zhu, B.S.; Cao, S.L. Numerical simulation of unsteady cavitation flow in a centrifugal pump at off-design conditions. Proc. Inst. Mech. Eng. Part C J. Eng. Mech. 2014, 228, 1994–2006. [Google Scholar]
- Olivier, P.; Hakan, N. Numerical investigations of unsteady flow in a centrifugal pump with a vaned diffuser. Int. J. Rotating Mach. 2013, 2013, 961580. [Google Scholar]
- Huang, X.B.; Liu, Z.Q.; Li, Y.J. Study of the internal characteristics of the stall in a centrifugal pump with a cubic non-linear SGS model. J. Hydrodyn. 2019, 31, 788–799. [Google Scholar] [CrossRef]
- Ren, X.M.; Fan, H.G.; Xie, Z.F. Stationary stall phenomenon and pressure fluctuation in a centrifugal pump at partial load condition. Heat Mass Transf. 2019, 55, 2277–2288. [Google Scholar] [CrossRef]
- Akiha, S.; Hideto, H.; Shutaro, K. Study of flow instability in off design operation of a multistage centrifugal pump. J. Mech. Sci. Technol. 2016, 30, 493–498. [Google Scholar]
- Manish, S.; Ali, P.; Joseph, K. The flow structure during onset and developed states of rotating stall with a vaned diffuser of a centrifugal pump. J. Fluids Eng. 2001, 123, 490–499. [Google Scholar]
- Akin, O.; Rokwell, D. Interaction of zones of flow separation in a centrifugal impeller-stationary vane system. Exp. Fluids 1994, 17, 427–433. [Google Scholar] [CrossRef]
- Elias, S.; Bernhard, S.; Mihai, M. Generation mechanisms of rotating stall and surge in centrifugal compressors. Flow Turbul. Combust. 2018, 100, 705–719. [Google Scholar]
- Taher, H.; Mohamed, A.; Mohamed, S.G. Numerical investigation of rotating stall in compressor with vaned and vaneless diffuser. J. Therm. Sci. 2015, 24, 323–333. [Google Scholar]
- Zhang, L.; He, R.Y.; Wang, S.L.; Zhang, Q. A review of rotating stall in vaneless diffuser of centrifugal compressor. J. Therm. Sci. 2020, 29, 323–342. [Google Scholar] [CrossRef]
- Nobumichi, F.; Shotaro, H.; Yutaka, O. Unsteady behavior of leading-edge vortex and diffuser stall in a centrifugal compressor with vaned diffuser. J. Therm. Sci. 2016, 25, 13–21. [Google Scholar]
- Dazin, A.; Coutier-Delgosha, O.; Dupont, P. Rotating instability in the vaneless diffuser of a radial flow pump. J. Thermal Sci. 2008, 17, 368–374. [Google Scholar] [CrossRef]
- Feng, J.; Benra, F.; Dohmen, H.J. Unsteady flow visualization at part load conditions of a radial diffuser pump: By PIV and CFD. J. Vis. 2009, 12, 65–72. [Google Scholar] [CrossRef]
- Krause, N.; Zähhringer, K.; Pap, E. Time-solved particle imaging velocimetry for the investigation of rotating stall in a radial pump. Exp. Fluids. 2005, 39, 192–201. [Google Scholar] [CrossRef]
- Li, W.; Li, E.D.; Ji, L.L.; Zhou, L.; Shi, W.; Zhu, Y. Mechanism and propagation characteristics of rotating stall in a mixed flow pump. Renew. Energy 2020, 153, 74–92. [Google Scholar] [CrossRef]
- Kan, K.; Zheng, Y.; Chen, Y.J.; Xie, Z.S.; Yang, G.; Yang, C. Numerical study on the internal flow characteristics. J. Mech. Sci. Technol. 2018, 32, 4683–4695. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, C.; Yang, D.; Wang, W.; Yang, C.; Qi, M. Investigation on the Stall Inception Circumferential Position and Stall Process Behavior in a Centrifugal Compressor with Volute. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference & Exposition, Oslo, Norway, 11–15 June 2018; ASME: New York, NY, USA, 2018. [Google Scholar]
- Ceyrowsky, T.; Hildebrandt, A.; Schwarze, R. Numerical investigation of the circumferential pressure distortion induced by a centrifugal compressor’s external volute. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference & Exposition, Oslo, Norway, 11–15 June 2018; ASME: New York NY, USA, 2018. [Google Scholar]
- Cravero, C.; Marsano, D. Criteria for the stability limit prediction of high-speed centrifugal compressors with vaneless diffuser. Part I: Flow structure analysis. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual Conference, London, UK, 21–25 September 2020; ASME: New York, NY, USA, 2020. [Google Scholar]
- Cravero, C.; Marsano, D. Criteria for the stability limit prediction of high-speed centrifugal compressors with vaneless diffuser. Part II: The development of prediction criteria. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual Conference, London, UK, 21–25 September 2020; ASME: New York, NY, USA, 2020. [Google Scholar]
- Fu, S.; Launder, B.E.; Leschziner, M.A. Modeling strongly swirling recirculating jet flow with Reynolds-stress transport closures. In Proceedings of the 6th Symposium on Turbulent Shear Flows, Toulouse, France, 7–9 September 1987; Springer: Berlin, Germany, 1987. [Google Scholar]
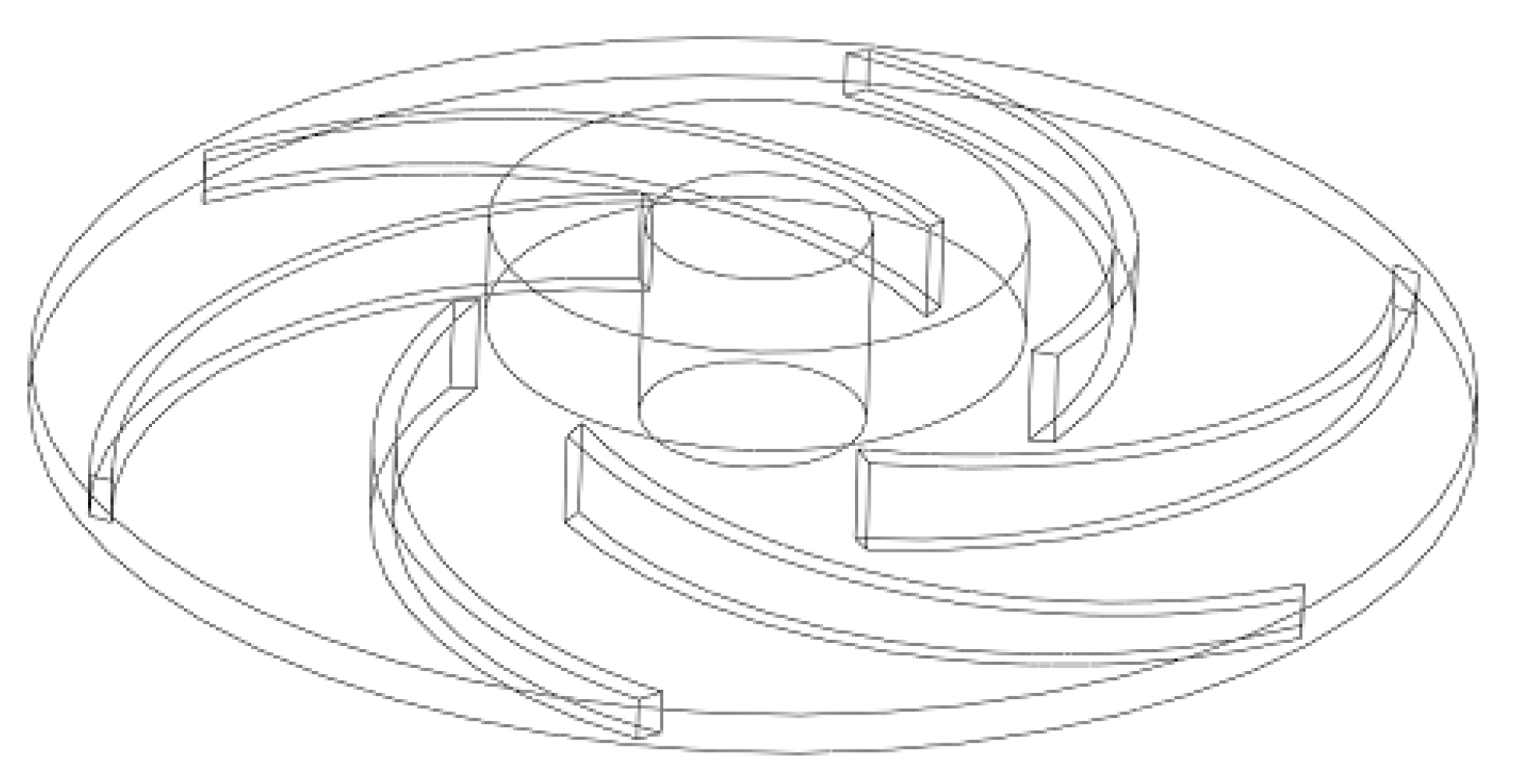




| Parameter | Value |
|---|---|
| Inlet Diameter D1 | 71.0 mm |
| Outlet Diameter D2 | 190.0 mm |
| Inlet Height b1 | 13.8 mm |
| Outlet Height b2 | 5.8 mm |
| Number of Blades Z | 6 |
| Blade Thickness t | 3.0 mm |
| Inlet Blade Angle β1 | 19.7° |
| Outlet Blade Angle β2 | 18.4° |
| Blade Curvature Radius Rb | 70.0 mm |
| Specific Speed Ns | 26.3 |
| Mesh Number | H/m | |
|---|---|---|
| Mesh 1 | 4,740,324 | 2.42 |
| Mesh 2 | 5,598,924 | 2.51 |
| Mesh 3 | 7,642,362 | 2.31 |
| Mesh 4 | 9,185,268 | 2.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Lin, P.; Zhang, W.; Zhu, Z. Evolution Characteristics of Separated Vortices and Near-Wall Flow in a Centrifugal Impeller in an Off-Designed Condition. Appl. Sci. 2020, 10, 8209. https://doi.org/10.3390/app10228209
Zhou S, Lin P, Zhang W, Zhu Z. Evolution Characteristics of Separated Vortices and Near-Wall Flow in a Centrifugal Impeller in an Off-Designed Condition. Applied Sciences. 2020; 10(22):8209. https://doi.org/10.3390/app10228209
Chicago/Turabian StyleZhou, Shihao, Peifeng Lin, Wei Zhang, and Zuchao Zhu. 2020. "Evolution Characteristics of Separated Vortices and Near-Wall Flow in a Centrifugal Impeller in an Off-Designed Condition" Applied Sciences 10, no. 22: 8209. https://doi.org/10.3390/app10228209
APA StyleZhou, S., Lin, P., Zhang, W., & Zhu, Z. (2020). Evolution Characteristics of Separated Vortices and Near-Wall Flow in a Centrifugal Impeller in an Off-Designed Condition. Applied Sciences, 10(22), 8209. https://doi.org/10.3390/app10228209





