Sequence-to-Sequence Video Prediction by Learning Hierarchical Representations
Abstract
:1. Introduction
2. Related Work
3. Methods
3.1. Model
3.2. Training
4. Experiments
- Bouncing Balls dataset contains videos of 4 balls randomly bouncing off the walls and the other balls. The emphasis is mostly on capturing the complex dynamics of high-level features in an interactive enviroment, e.g., the center positions and velocity of the balls.
- Moving MNIST (MMNIST) dataset contains 2 hand-written digits moving independently. The focus is on tracking the dynamics of both high-level (digit position) and mid- to low-level features (digit shapes).
- KTH action dataset contains several classes of human actions. For predicting future frames, one needs to capture high-level features such as the person’s positions; but the focus is largely on low-level features representing details of body parts.
4.1. Bouncing Balls
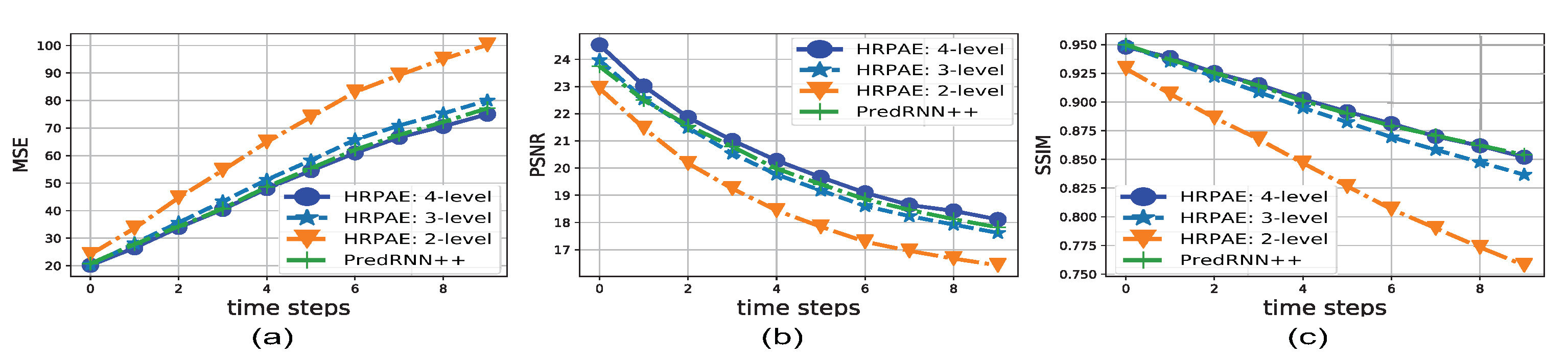
4.2. Moving MNIST
- The default 4-level HRPAE as shown in Figure 1a with the output channel sizes given by 32, 64, 128 and 256.
- The 3-level HRPAE which contains the first 3 levels of CNN blocks and convLSTMs from the network in Figure 1a (e.g., uses EncCNN 1–3, LSTM 1–3, and DecCNN 1–3) with the output channel sizes given by 32, 64 and 128.
- The 2-level HRPAE which consists of the first 2 layers of CNN blocks and convLSTMs with output channel sizes given by 32 and 64.
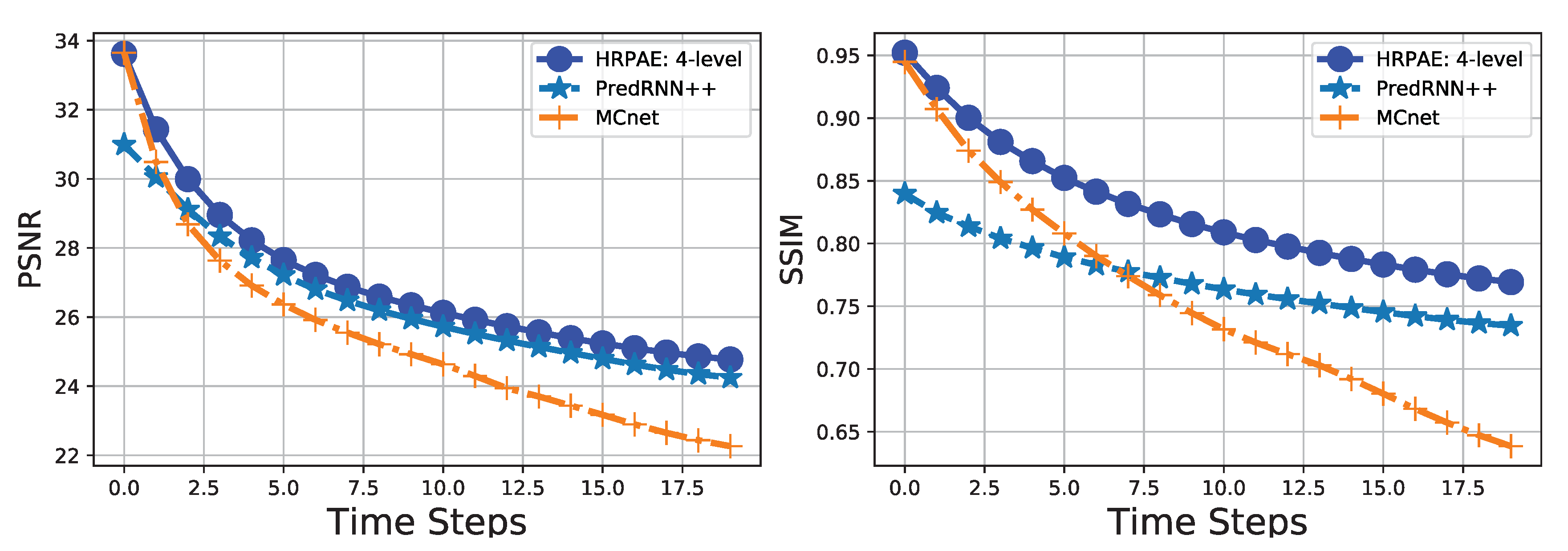
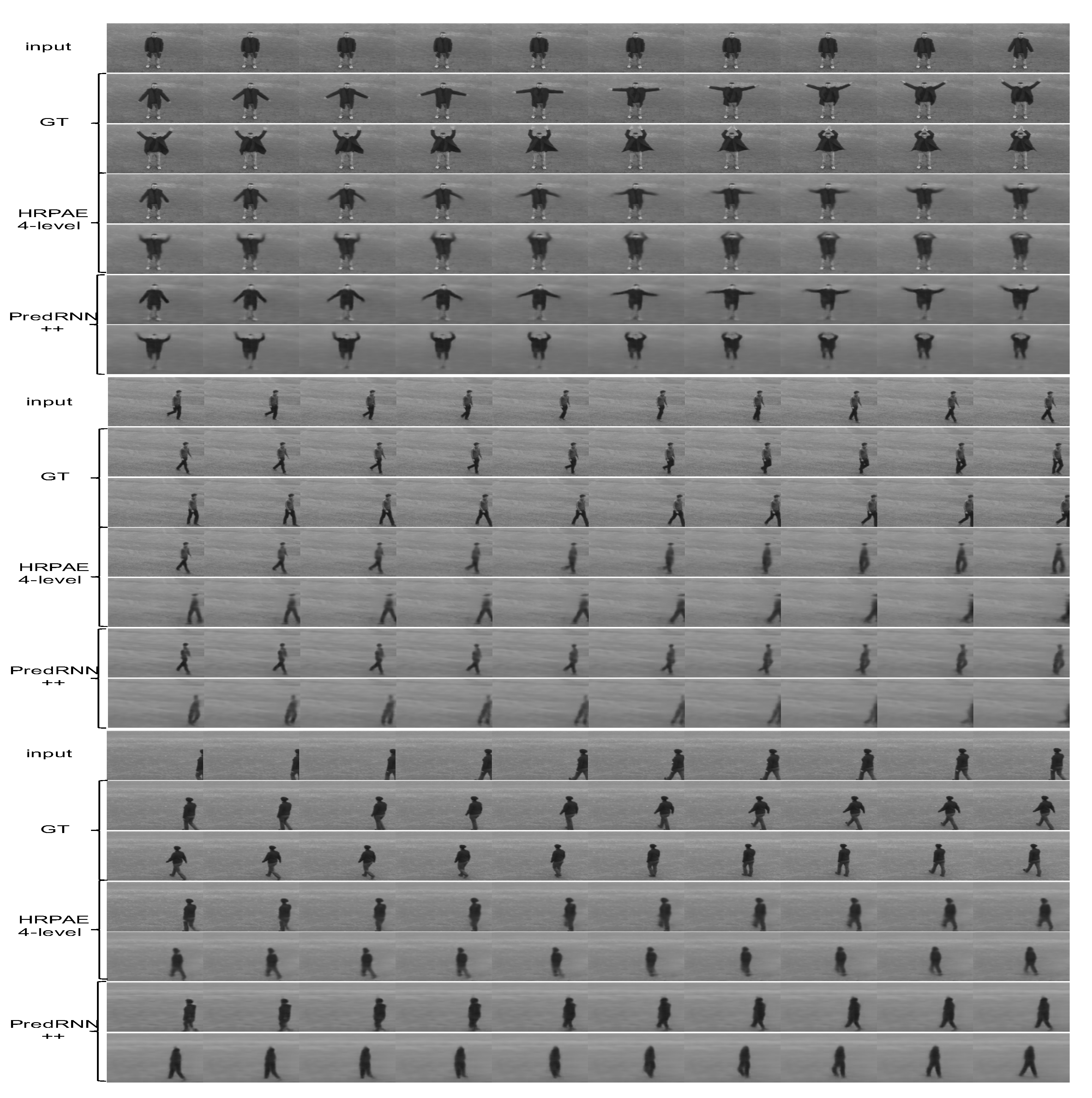
4.3. KTH Action Dataset
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Li, C.; Zhang, Z.; Lee, W.S.; Lee, G.H. Convolutional Sequence to Sequence Model for Human Dynamics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Foxlin, E. Pedestrian tracking with shoe-mounted inertial sensors. IEEE Comput. Graph. Appl. 2005, 25, 38–46. [Google Scholar] [PubMed]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Chun Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Srivastava, N.; Mansimov, E.; Salakhudinov, R. Unsupervised learning of video representations using LSTMs. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 843–852. [Google Scholar]
- Mathieu, M.; Couprie, C.; LeCun, Y. Deep multi-scale video prediction beyond mean square error. In Proceedings of the International Conference on Learning Representations, San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Oh, J.; Guo, X.; Lee, H.; Lewis, R.L.; Singh, S. Action-conditional video prediction using deep networks in atari games. Adv. Neural Inf. Process. Syst. 2015, 28, 2863–2871. [Google Scholar]
- Kalchbrenner, N.; van den Oord, A.; Simonyan, K.; Danihelka, I.; Vinyals, O.; Graves, A.; Kavukcuoglu, K. Video pixel networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1771–1779. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2012, 60, 84–90. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 2, 2672–2680. [Google Scholar]
- Denton, E.L. Unsupervised learning of disentangled representations from video. Adv. Neural Inf. Process. Syst. 2017, 1, 4414–4423. [Google Scholar]
- Villegas, R.; Yang, J.; Hong, S.; Lin, X.; Lee, H. Decomposing motion and content for natural video sequence prediction. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Villegas, R.; Yang, J.; Zou, Y.; Sohn, S.; Lin, X.; Lee, H. Learning to generate long-term future via hierarchical prediction. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3560–3569. [Google Scholar]
- Walker, J.; Marino, K.; Gupta, A.; Hebert, M. The pose knows: Video forecasting by generating pose futures. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3332–3341. [Google Scholar]
- Wichers, N.; Villegas, R.; Erhan, D.; Lee, H. Hierarchical Long-term Video Prediction without Supervision. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Newell, A.; Yang, K.; Deng, J. Stacked hourglass networks for human pose estimation. In European Conference on Computer Vision; Springer: Amsterdam, The Netherlands, 2016; pp. 483–499. [Google Scholar]
- Battaglia, P.; Pascanu, R.; Lai, M.; Rezende, D.J. Interaction networks for learning about objects, relations and physics. Adv. Neural Inf. Process. Syst. 2016, 1, 4502–4510. [Google Scholar]
- Chang, M.B.; Ullman, T.; Torralba, A.; Tenenbaum, J.B. A Compositional Object-Based Approach to Learning Physical Dynamics. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Fragkiadaki, K.; Agrawal, P.; Levine, S.; Malik, J. Learning visual predictive models of physics for playing billiards. In Proceedings of the International Conference on Learning Representations, San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Schüldt, C.; Laptev, I.; Caputo, B. Recognizing human actions: A local SVM approach. In Proceedings of the 17th International Conference on Pattern Recognition ( ICPR), St. Petersburg, Russian, 18–23 October 2004; Volume 3, pp. 32–36. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar]
- Wang, Y.; Jiang, L.; Yang, M.H.; Li, L.J.; Long, M.; Fei-Fei, L. Eidetic 3D LSTM: A Model for Video Prediction and Beyond. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Xue, T.; Wu, J.; Bouman, K.; Freeman, B. Visual dynamics: Probabilistic future frame synthesis via cross convolutional networks. Adv. Neural Inf. Process. Syst. 2016, 1, 91–99. [Google Scholar]
- Babaeizadeh, M.; Finn, C.; Erhan, D.; Campbell, R.H.; Levine, S. Stochastic Variational Video Prediction. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent Neural Networks for Predictive Learning using Spatiotemporal LSTMs. Adv. Neural Inf. Process. Syst. 2017, 1, 879–888. [Google Scholar]
- Oliu, M.; Selva, J.; Escalera, S. Folded Recurrent Neural Networks for Future Video Prediction. In ECCV; Springer: Munich, Germany, 2018. [Google Scholar]
- Lakhal, M.I.; Lanz, O.; Cavallaro, A. View-LSTM: Novel-View Video Synthesis Through View Decomposition. In Proceedings of the 2019 ICCV, Seoul, Korea, 27 October–2 November 2019; pp. 7576–7586. [Google Scholar]
- Gao, H.; Xu, H.; Cai, Q.Z.; Wang, R.; Yu, F.; Darrell, T. Disentangling Propagation and Generation for Video Prediction. In Proceedings of the 2019 ICCV, Seoul, Korea, 27 October–2 November 2019; pp. 9005–9014. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. Adv. Neural Inf. Process. Syst. 2014, 2, 3104–3112. [Google Scholar]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning Precise Timing with LSTM Recurrent Networks. J. Mach. Learn. Res. 2002, 3, 115–143. [Google Scholar]
- Finn, C.; Goodfellow, I.; Levine, S. Unsupervised learning for physical interaction through video prediction. Adv. Neural Inf. Process. Syst. 2016, 1, 64–72. [Google Scholar]
- Lotter, W.; Kreiman, G.; Cox, D. Deep predictive coding networks for video prediction and unsupervised learning. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Eslami, S.A.; Heess, N.; Weber, T.; Tassa, Y.; Szepesvari, D.; Hinton, G.E. Attend, infer, repeat: Fast scene understanding with generative models. Adv. Neural Inf. Process. Syst. 2016, 29, 3225–3233. [Google Scholar]
- Kosiorek, A.; Kim, H.; Teh, Y.W.; Posner, I. Sequential attend, infer, repeat: Generative modelling of moving objects. Adv. Neural Inf. Process. Syst. 2018, 1, 8615–8625. [Google Scholar]
- Hsieh, J.T.; Liu, B.; Huang, D.A.; Fei-Fei, L.F.; Niebles, J.C. Learning to decompose and disentangle representations for video prediction. Adv. Neural Inf. Process. Syst. 2018, 1, 515–524. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Yu, P.S. PredRNN++: Towards A Resolution of the Deep-in-Time Dilemma in Spatiotemporal Predictive Learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Pan, J.; Wang, C.; Jia, X.; Shao, J.; Sheng, L.; Yan, J.; Wang, X. Video Generation From Single Semantic Label Map. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Wang, T.H.; Cheng, Y.C.; Lin, C.H.; Chen, H.T.; Sun, M. Point-to-Point Video Generation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, South Korea, 27 October–2 November 2019. [Google Scholar]
- Vondrick, C.; Pirsiavash, H.; Torralba, A. Generating videos with scene dynamics. Adv. Neural Inf. Process. Syst. 2016, 1, 613–621. [Google Scholar]
- Tulyakov, S.; Liu, M.Y.; Yang, X.; Kautz, J. MoCoGAN: Decomposing Motion and Content for Video Generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1526–1535. [Google Scholar]
- Denton, E.; Fergus, R. Stochastic video generation with a learned prior. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Ohnishi, K.; Yamamoto, S.; Ushiku, Y.; Harada, T. Hierarchical video generation from orthogonal information: Optical flow and texture. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Liang, X.; Lee, L.; Dai, W.; Xing, E.P. Dual Motion GAN for Future-Flow Embedded Video Prediction. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1762–1770. [Google Scholar]
- Lee, A.X.; Zhang, R.; Ebert, F.; Abbeel, P.; Finn, C.; Levine, S. Stochastic Adversarial Video Prediction. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Ba, J.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:abs/1607.06450. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar]
- Bengio, S.; Vinyals, O.; Jaitly, N.; Shazeer, N. Scheduled sampling for sequence prediction with recurrent neural networks. Adv. Neural Inf. Process. Syst. 2015, 1, 1171–1179. [Google Scholar]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image analysis using mathematical morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 4, 532–550. [Google Scholar]
- Srivastava, N.; Mansimov, E.; Salakhudinov, R. Moving MNIST Download Link. 2015. Available online: http://www.cs.toronto.edu/~nitish/unsupervised_video/ (accessed on 6 May 2019).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]




| Methods | MSE | PSNR | Parameters |
|---|---|---|---|
| PredRNN++ | 27.22 | 27.87 | 31,565 K |
| HRPAE | 20.25 | 29.36 | 9391 K |
| Method | MSE | PSNR | SSIM |
|---|---|---|---|
| DRNet [15] | 207.9 | 13.2 | 0.42 |
| MCnet [16] | 172.2 | 13.9 | 0.66 |
| PredRNN++ [41] | 50.66 | 20.12 | 0.8984 |
| 2-level HRPAE | 66.36 | 18.75 | 0.839 |
| 3-level HRPAE | 52.91 | 19.99 | 0.891 |
| 4-level HRPAE | 49.67 | 20.47 | 0.8987 |
| PredRNN++ | 3-Level | 4-Level | |
|---|---|---|---|
| LSTM 1 | 5921 K | 74 K | 74 K |
| LSTM 2 | 3359 K | 295 K | 295 K |
| LSTM 3 | 2261 K | 1180 K | 1180 K |
| LSTM 4 | 2261 K | 0 | 4719 K |
| Total | 15,441 K | 2313 K | 9391 K |
| Ratio | 1 | 0.15 | 0.61 |
| Methods | PSNR | SSIM |
|---|---|---|
| MCnet | 25.439 | 0.756 |
| PredRNN++ | 26.400 | 0.772 |
| HRPAE: 4-level | 27.029 | 0.828 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, K.; Joung, C.; Baek, S. Sequence-to-Sequence Video Prediction by Learning Hierarchical Representations. Appl. Sci. 2020, 10, 8288. https://doi.org/10.3390/app10228288
Fan K, Joung C, Baek S. Sequence-to-Sequence Video Prediction by Learning Hierarchical Representations. Applied Sciences. 2020; 10(22):8288. https://doi.org/10.3390/app10228288
Chicago/Turabian StyleFan, Kun, Chungin Joung, and Seungjun Baek. 2020. "Sequence-to-Sequence Video Prediction by Learning Hierarchical Representations" Applied Sciences 10, no. 22: 8288. https://doi.org/10.3390/app10228288
APA StyleFan, K., Joung, C., & Baek, S. (2020). Sequence-to-Sequence Video Prediction by Learning Hierarchical Representations. Applied Sciences, 10(22), 8288. https://doi.org/10.3390/app10228288




