Integrated Control and Protection Architecture for Islanded PV-Battery DC Microgrids: Design, Analysis and Experimental Verification
Abstract
:1. Introduction
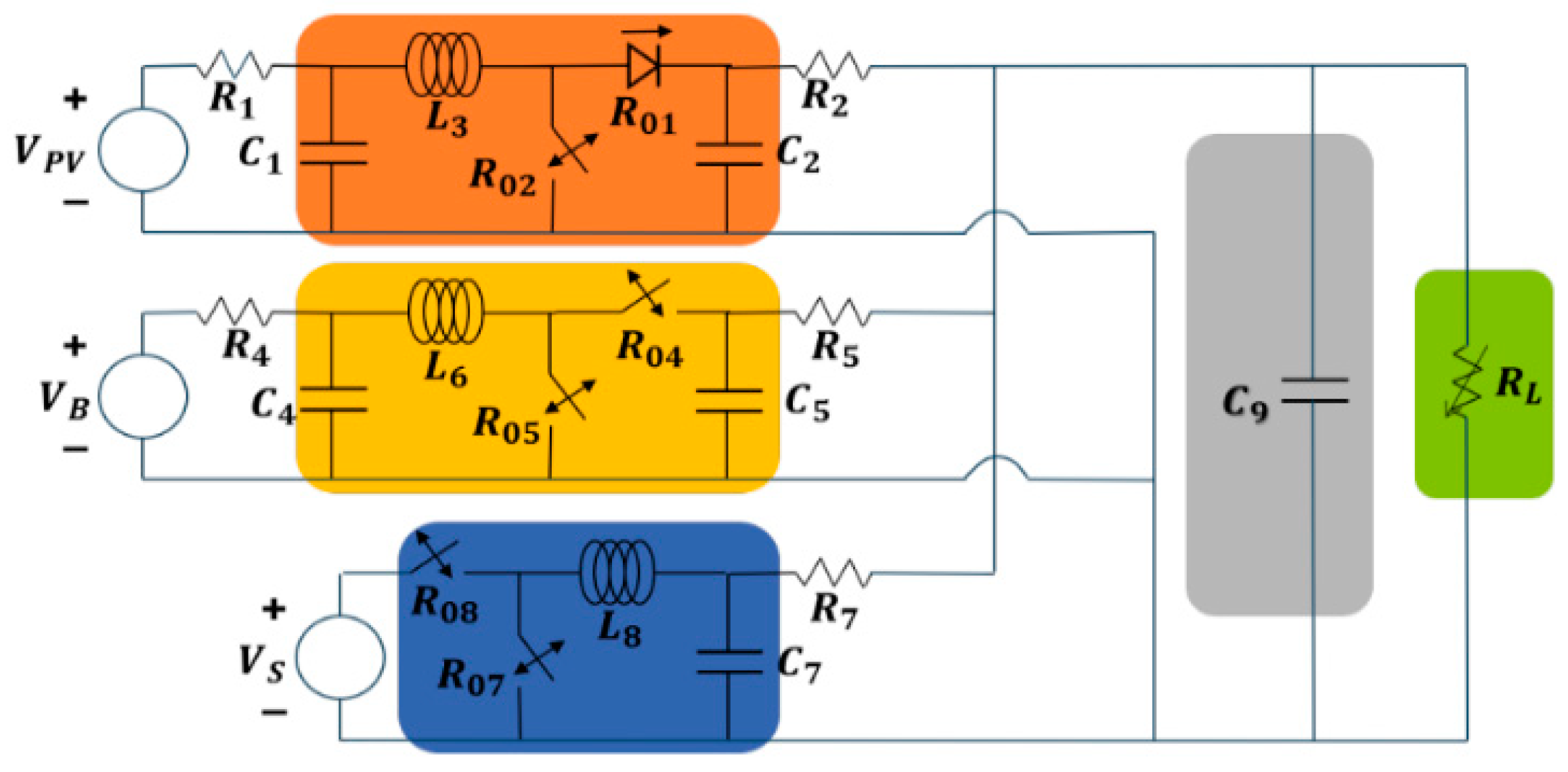
2. Proposed PV-Battery Islanded DC Microgrid
2.1. PV System, Battery and Capacitor Bank Modeling
2.2. DC Microgrid Modeling
3. Proposed SDRE Nonlinear Observer-Controller
3.1. SDRE Controller
3.2. SDRE Observer
4. Simulation Results
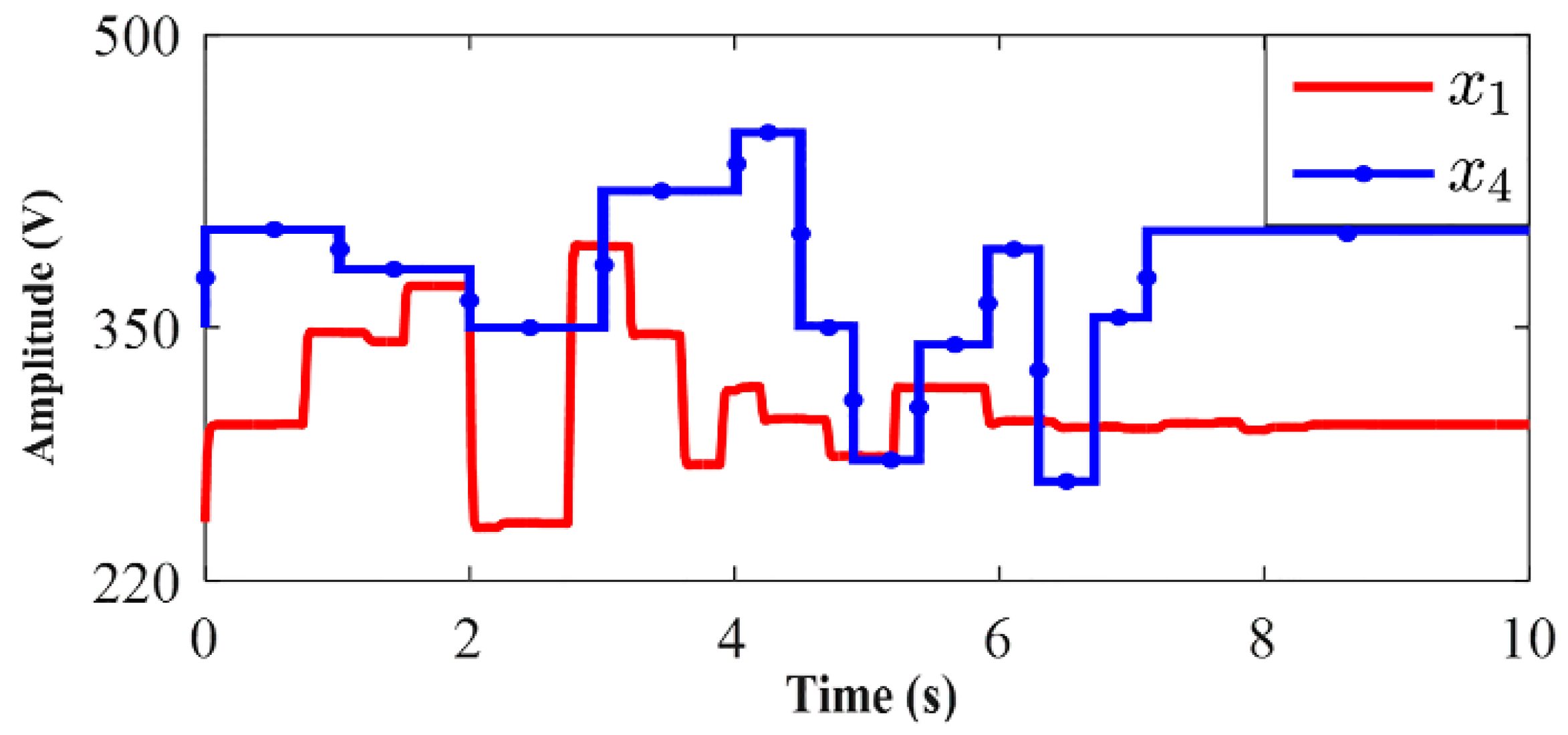
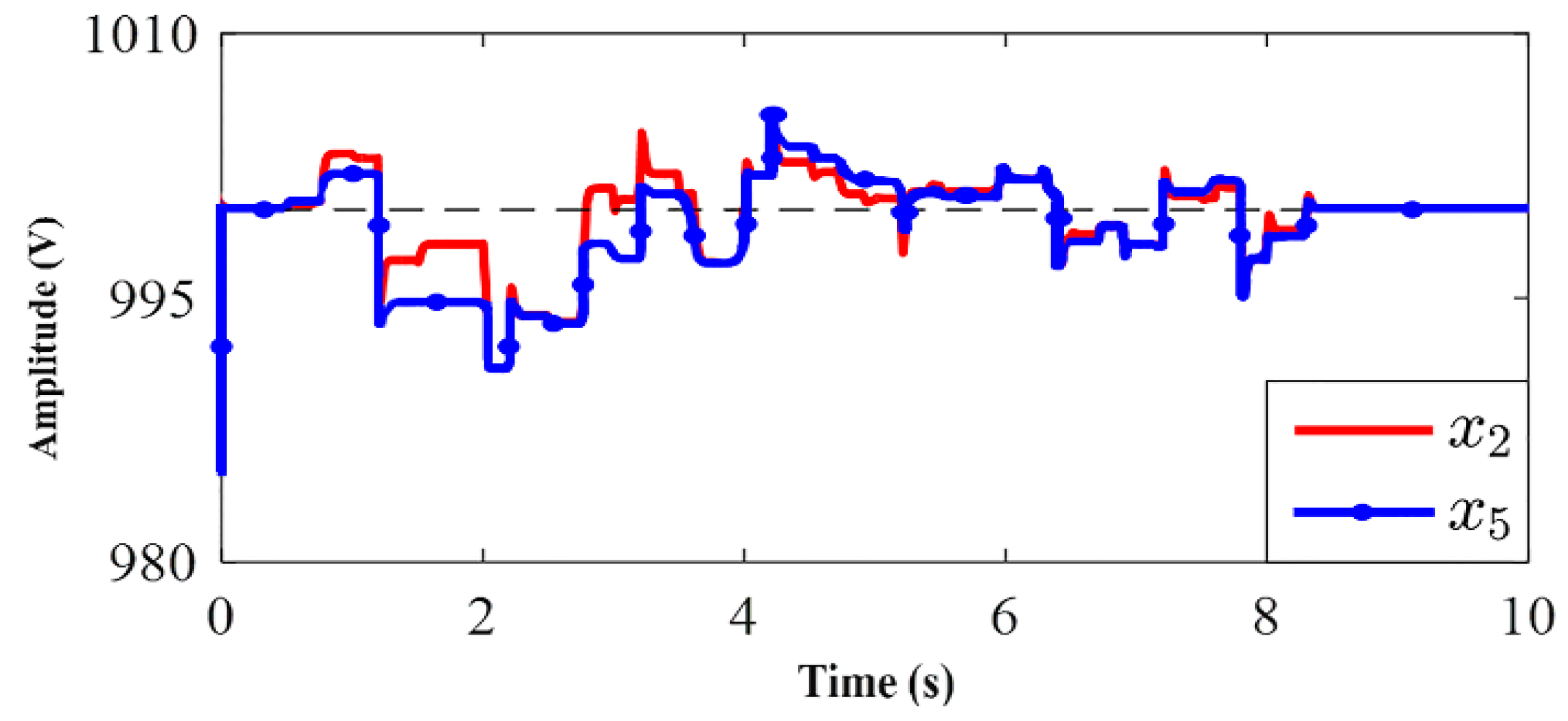
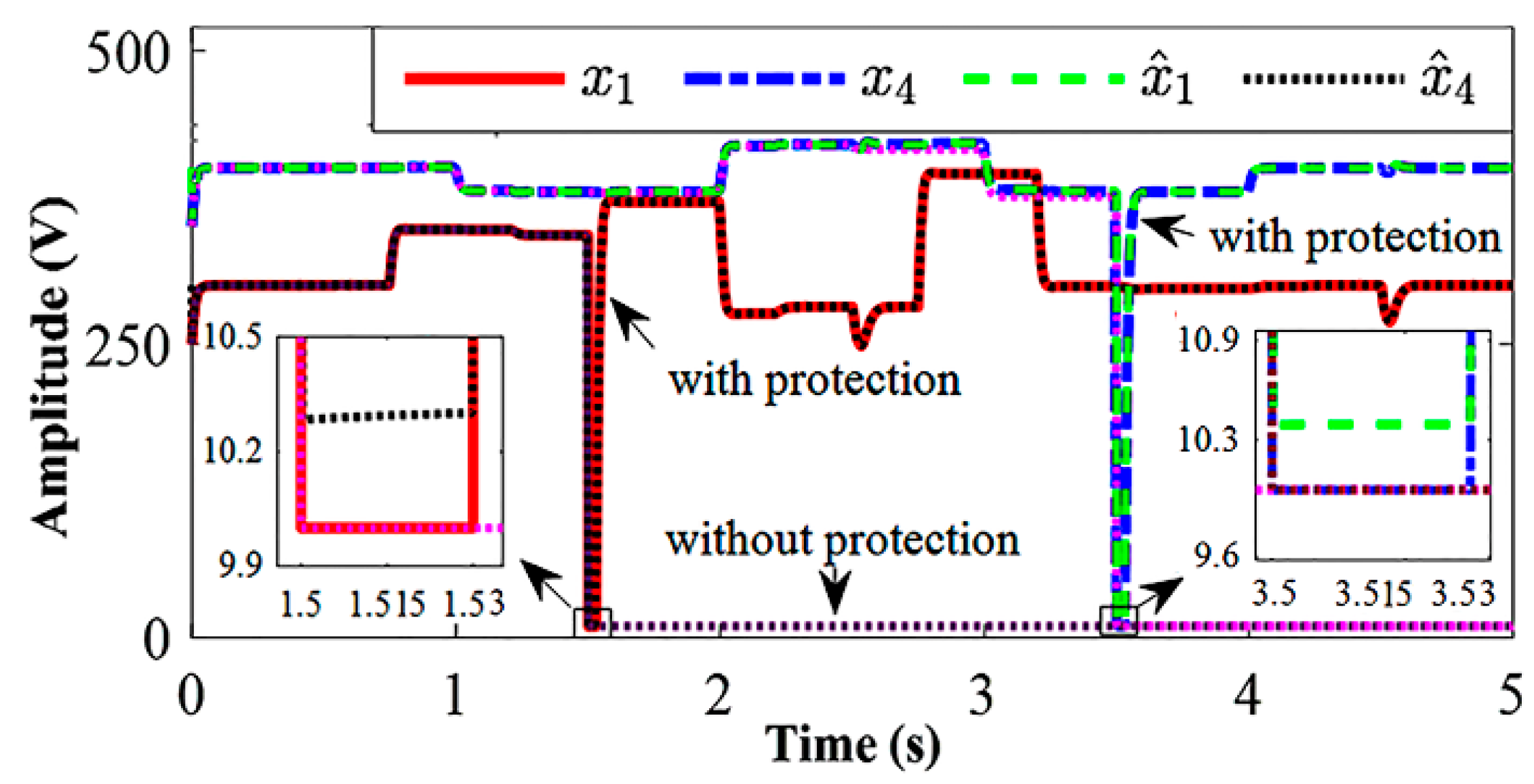
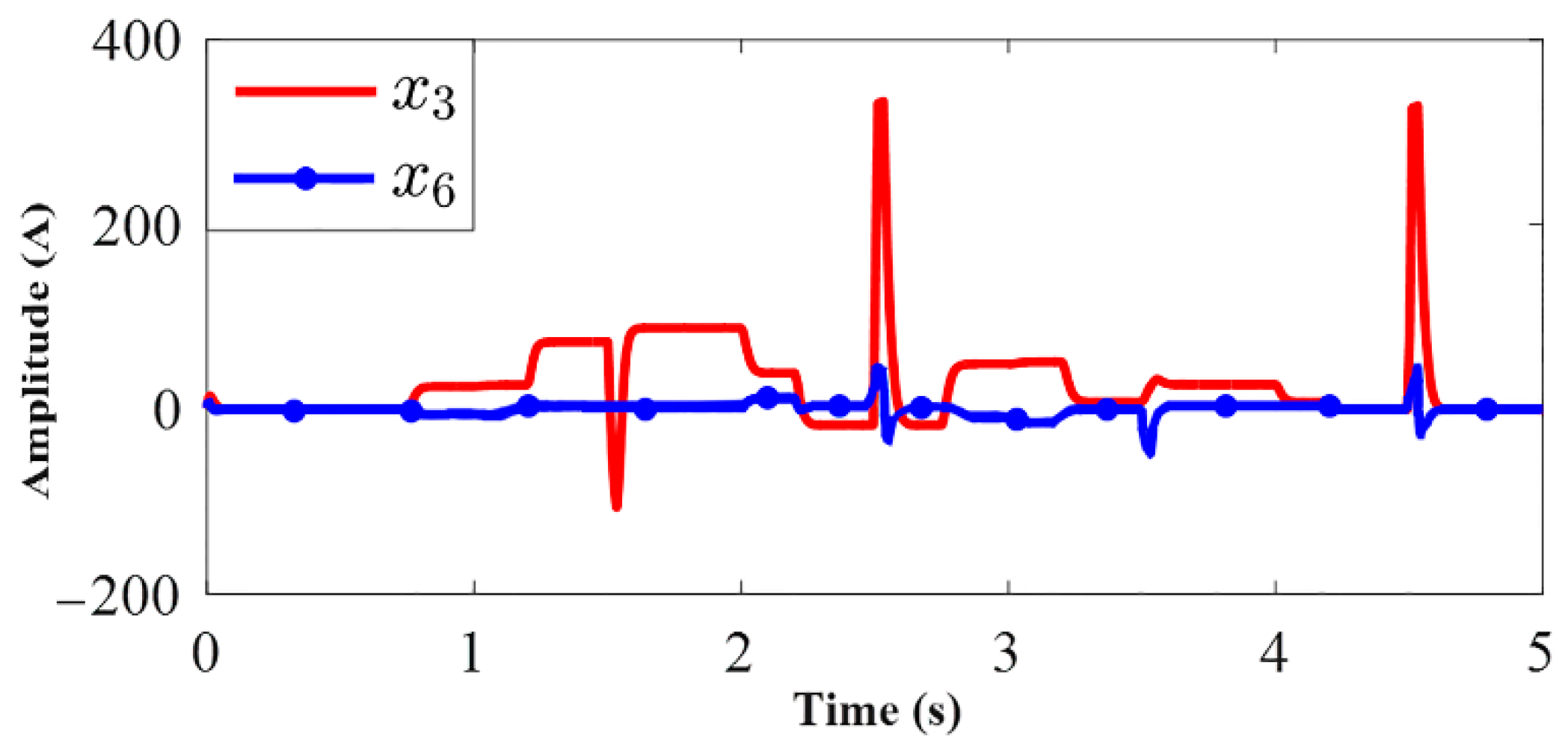
4.1. SDRE Controller
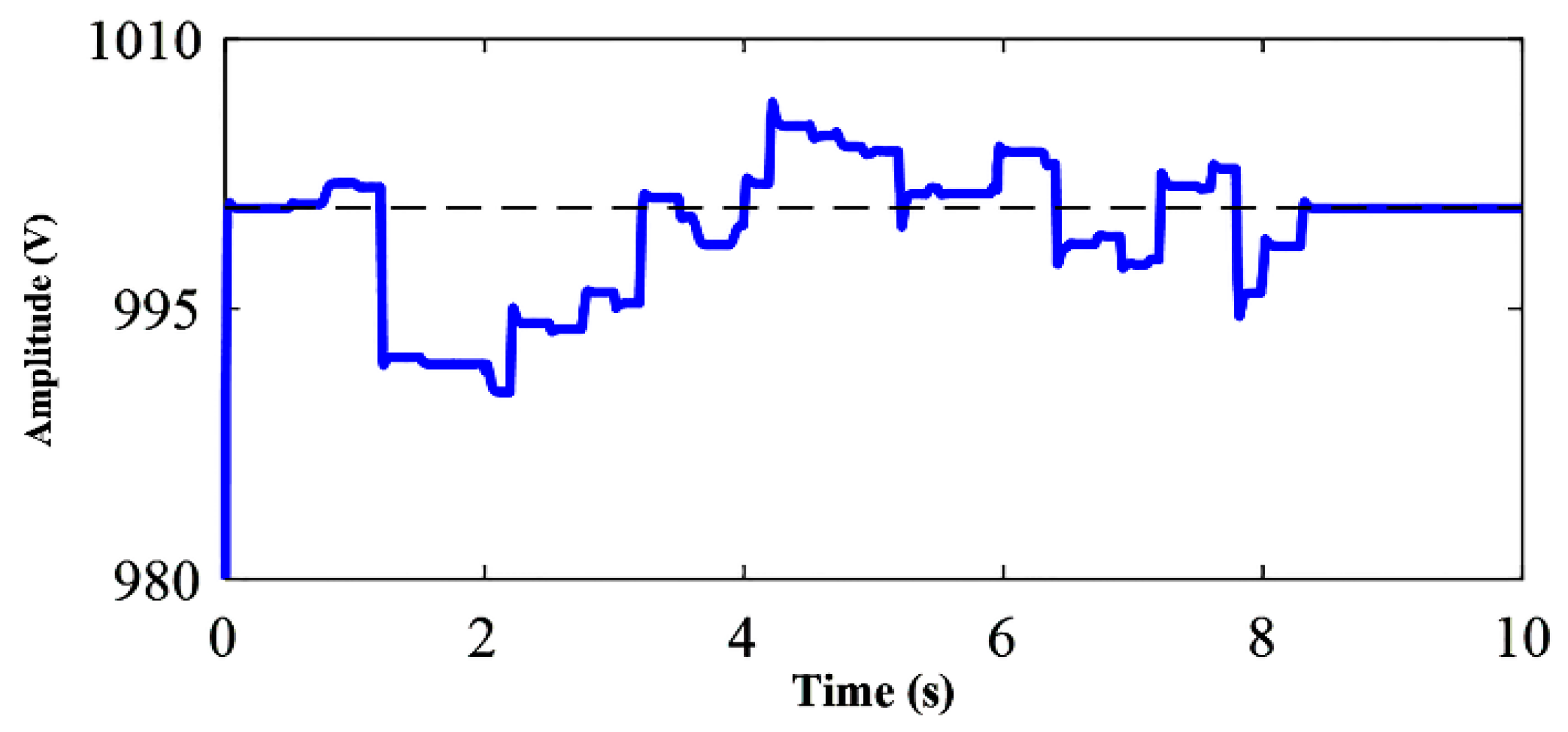
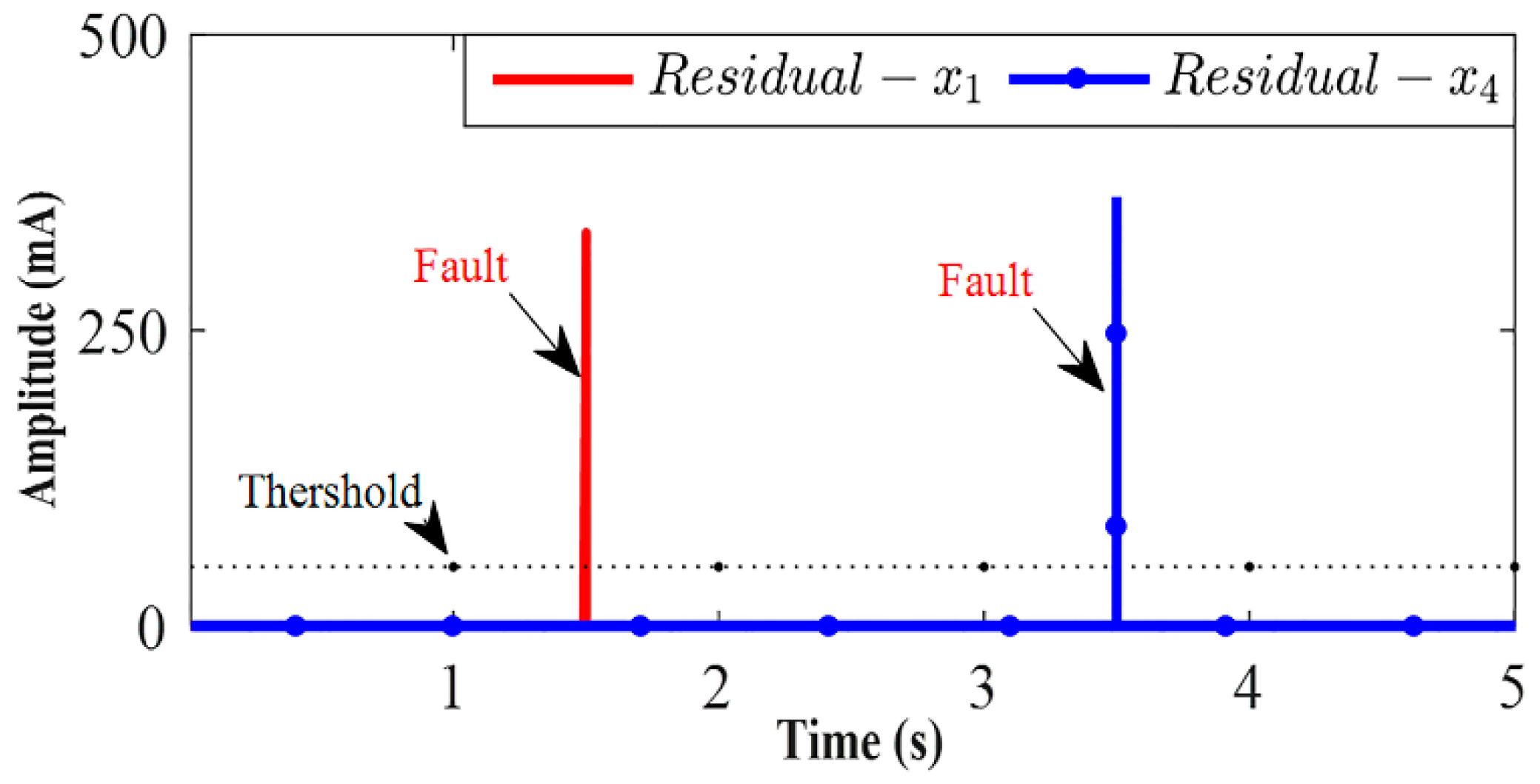
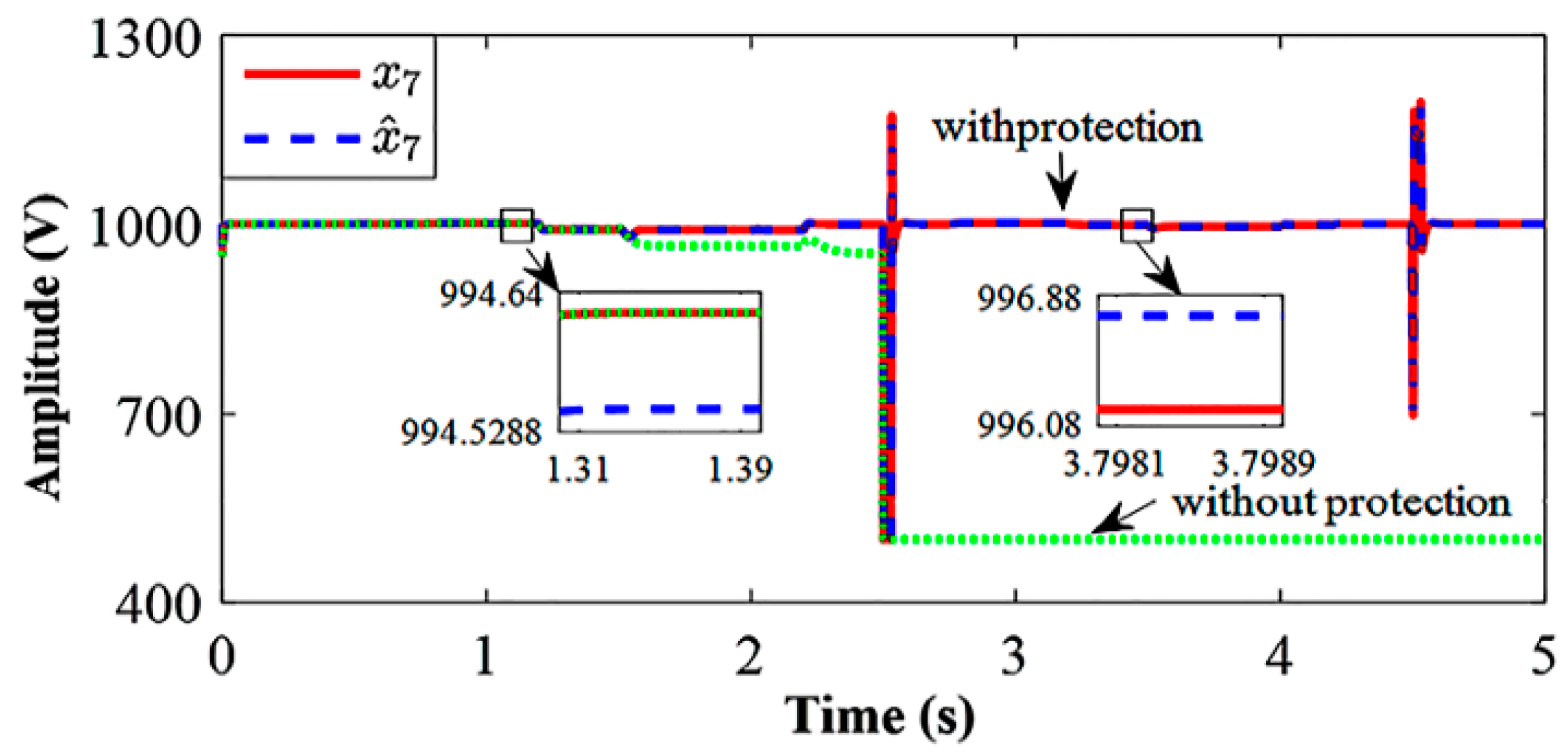
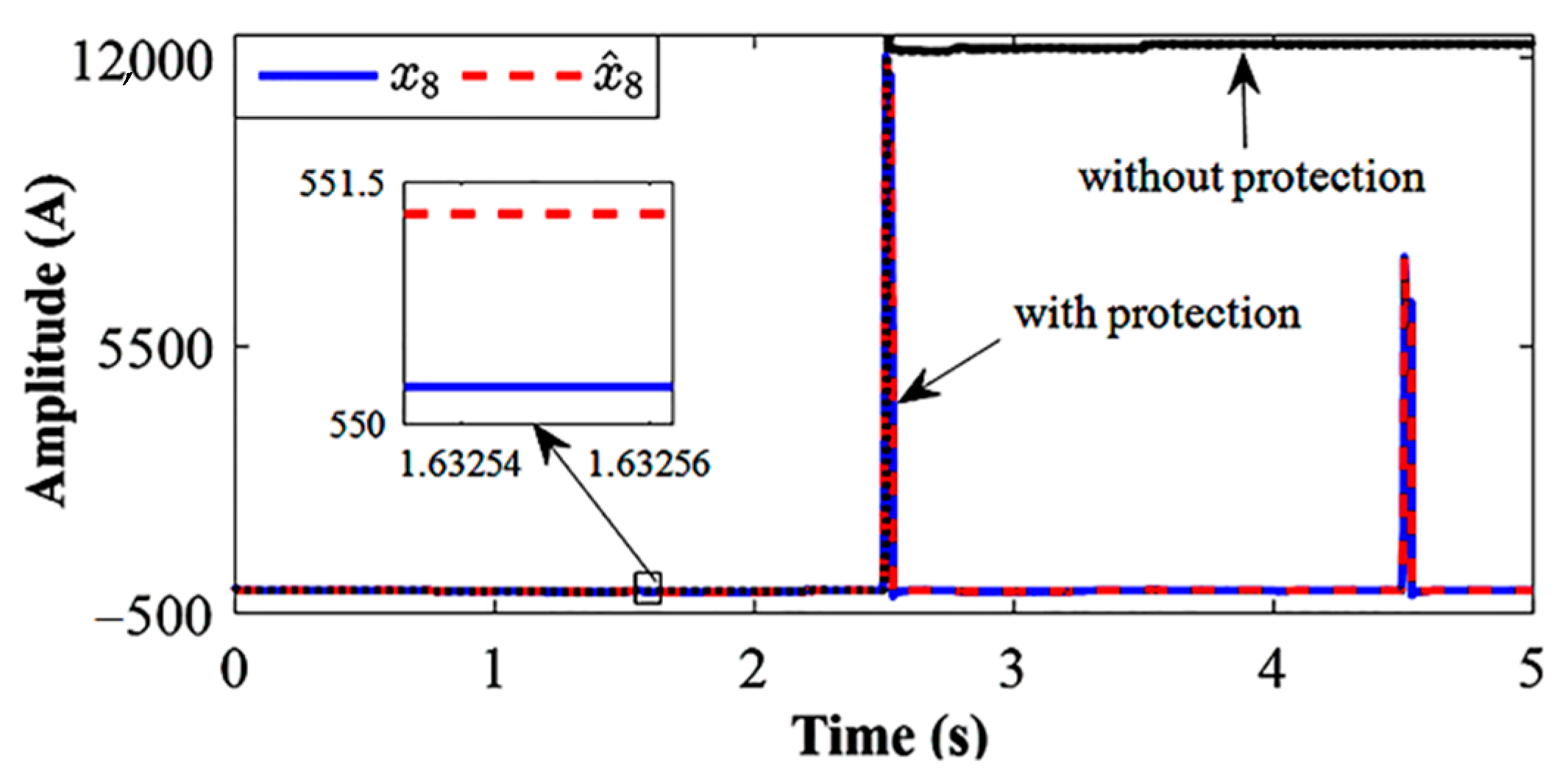
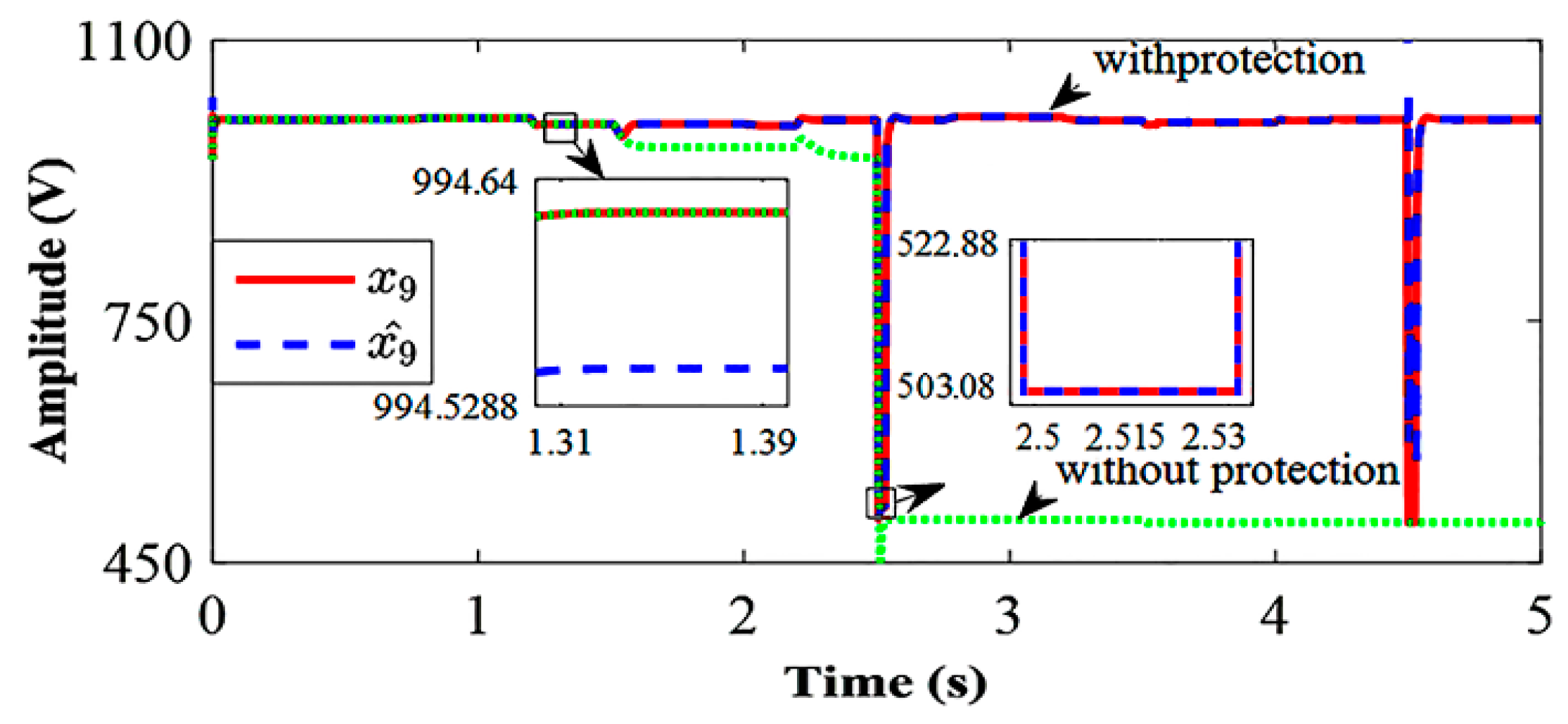
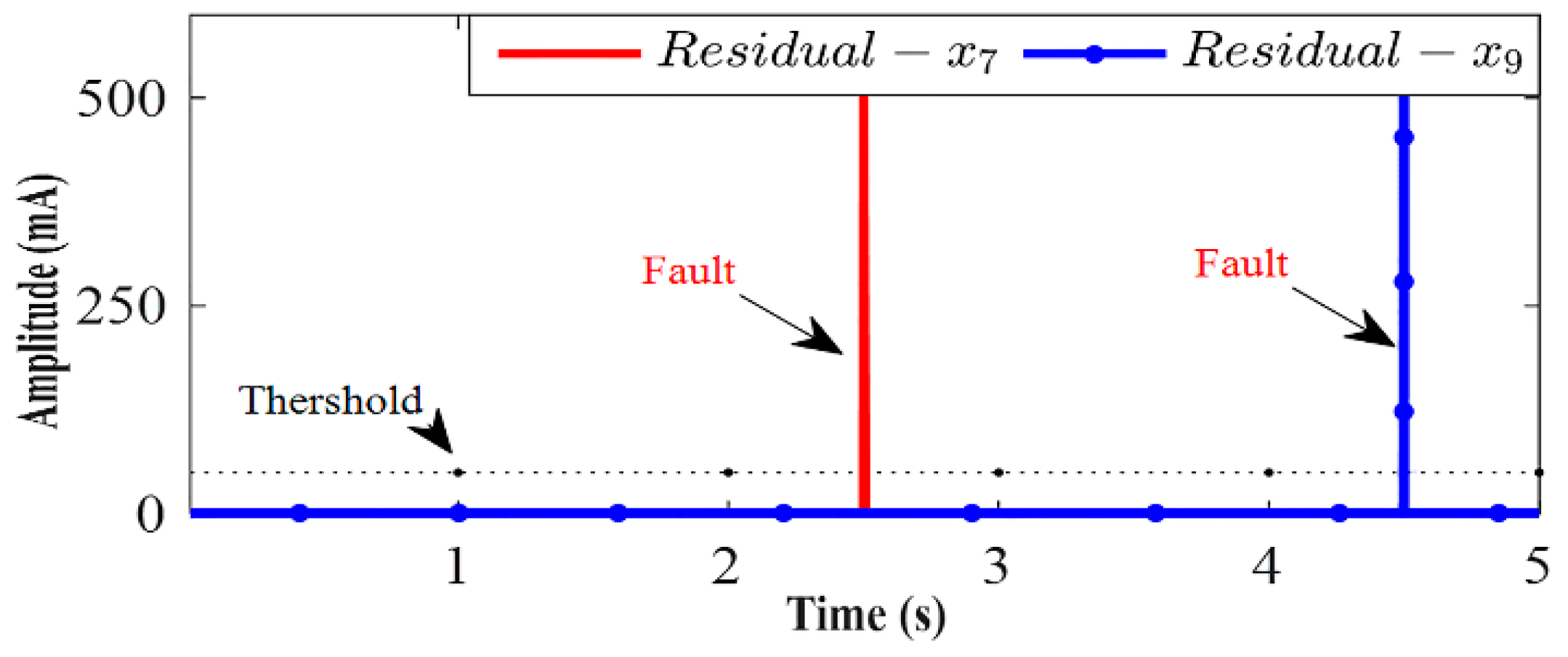
4.2. SDRE Observer
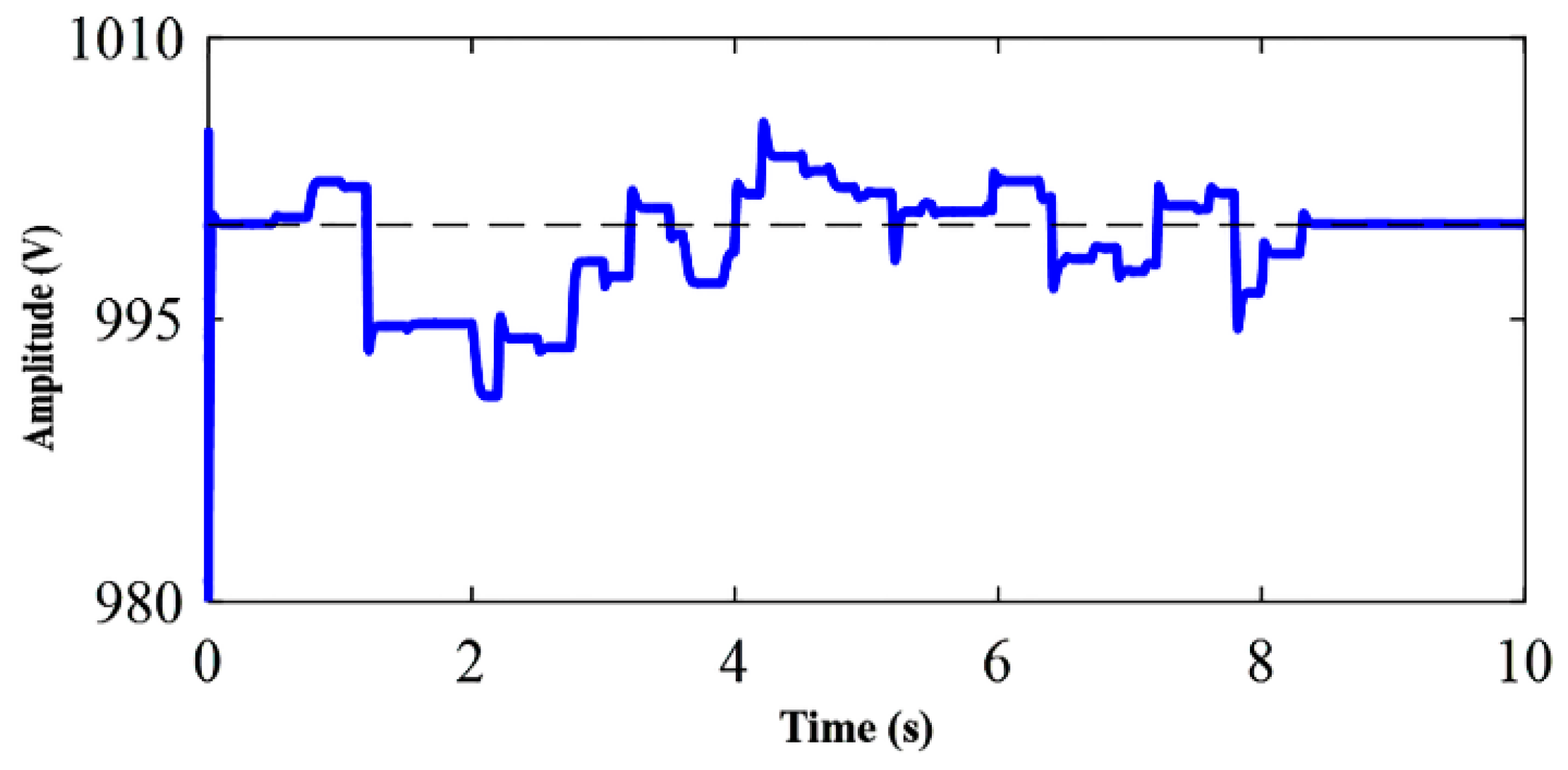
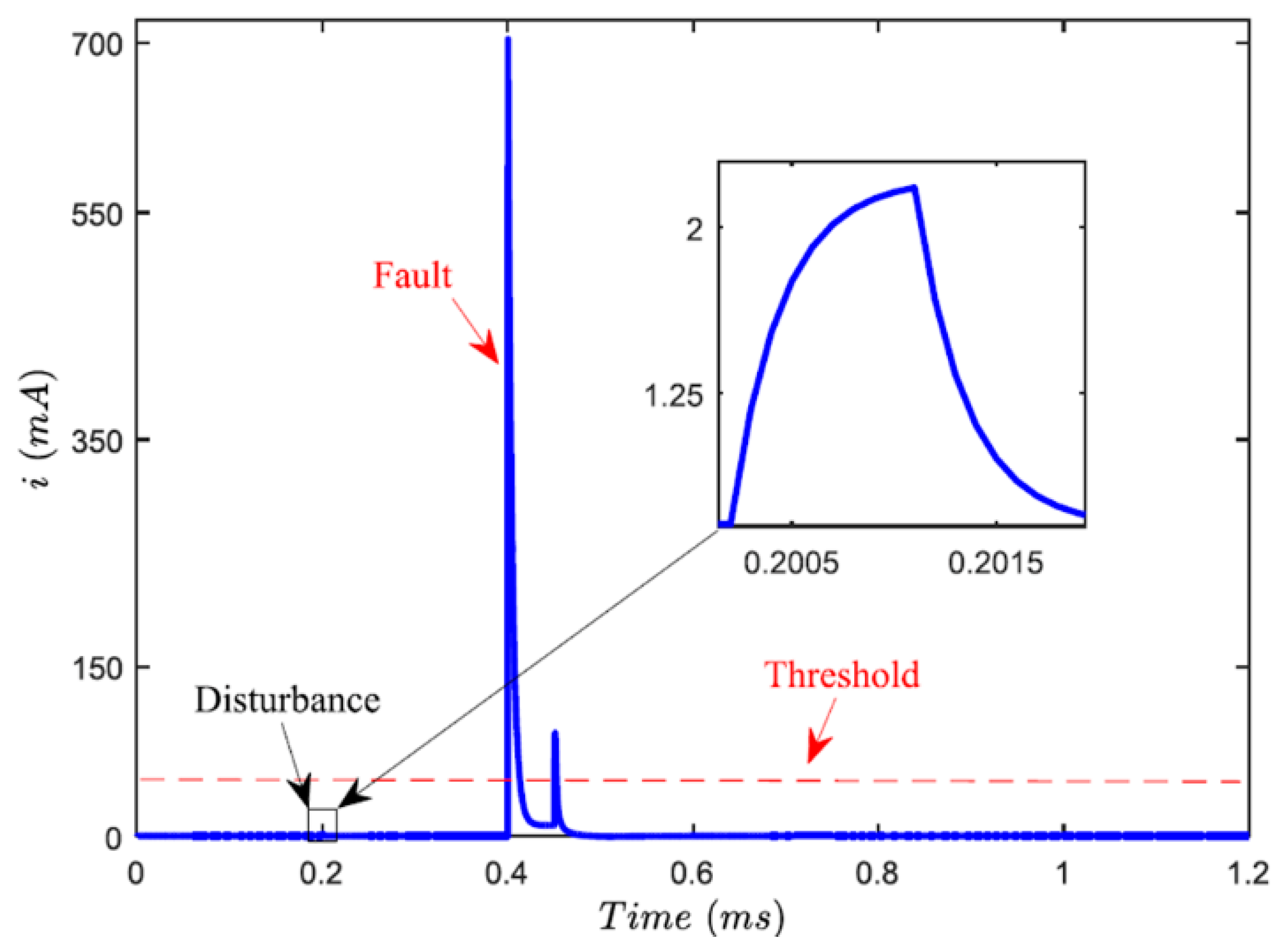
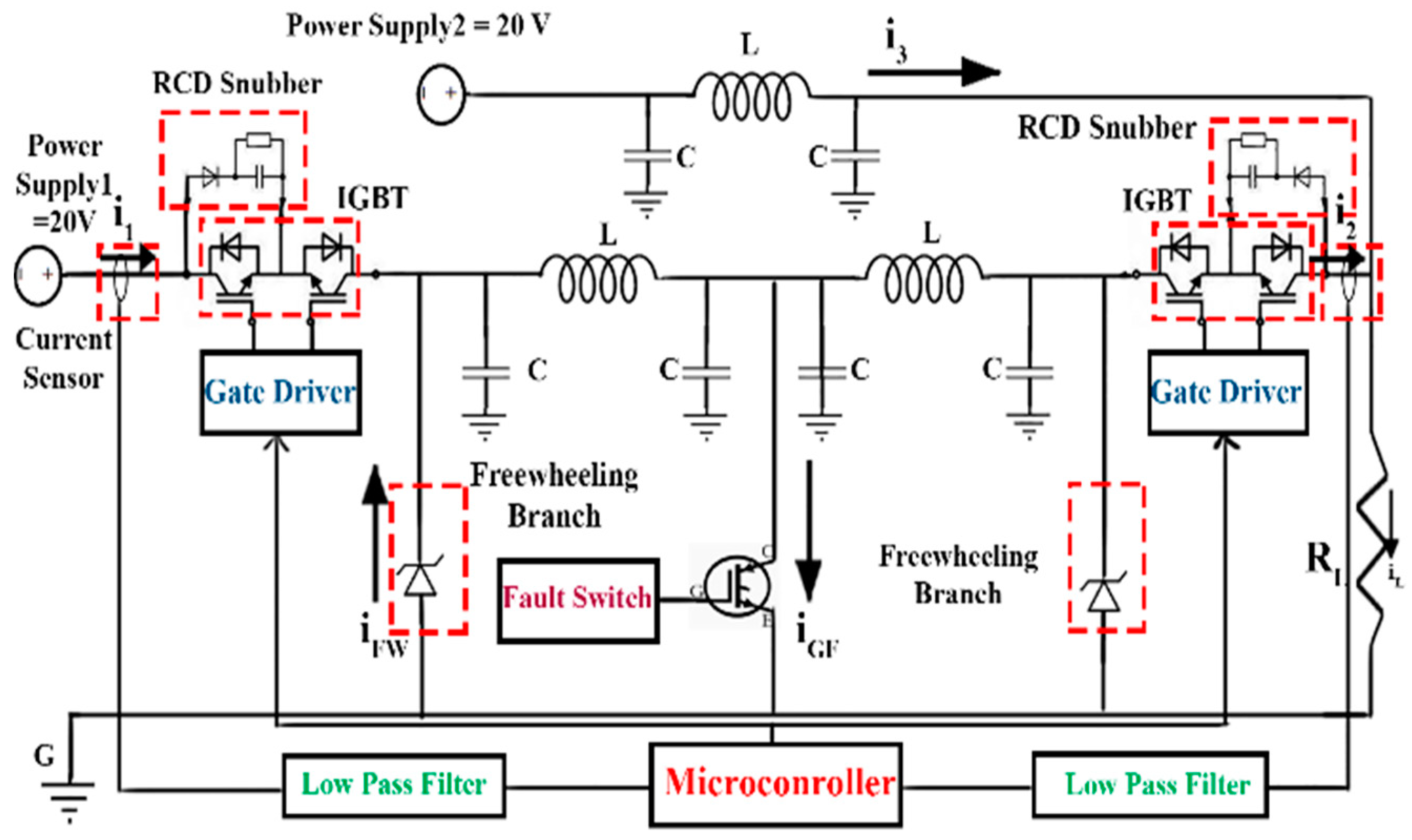
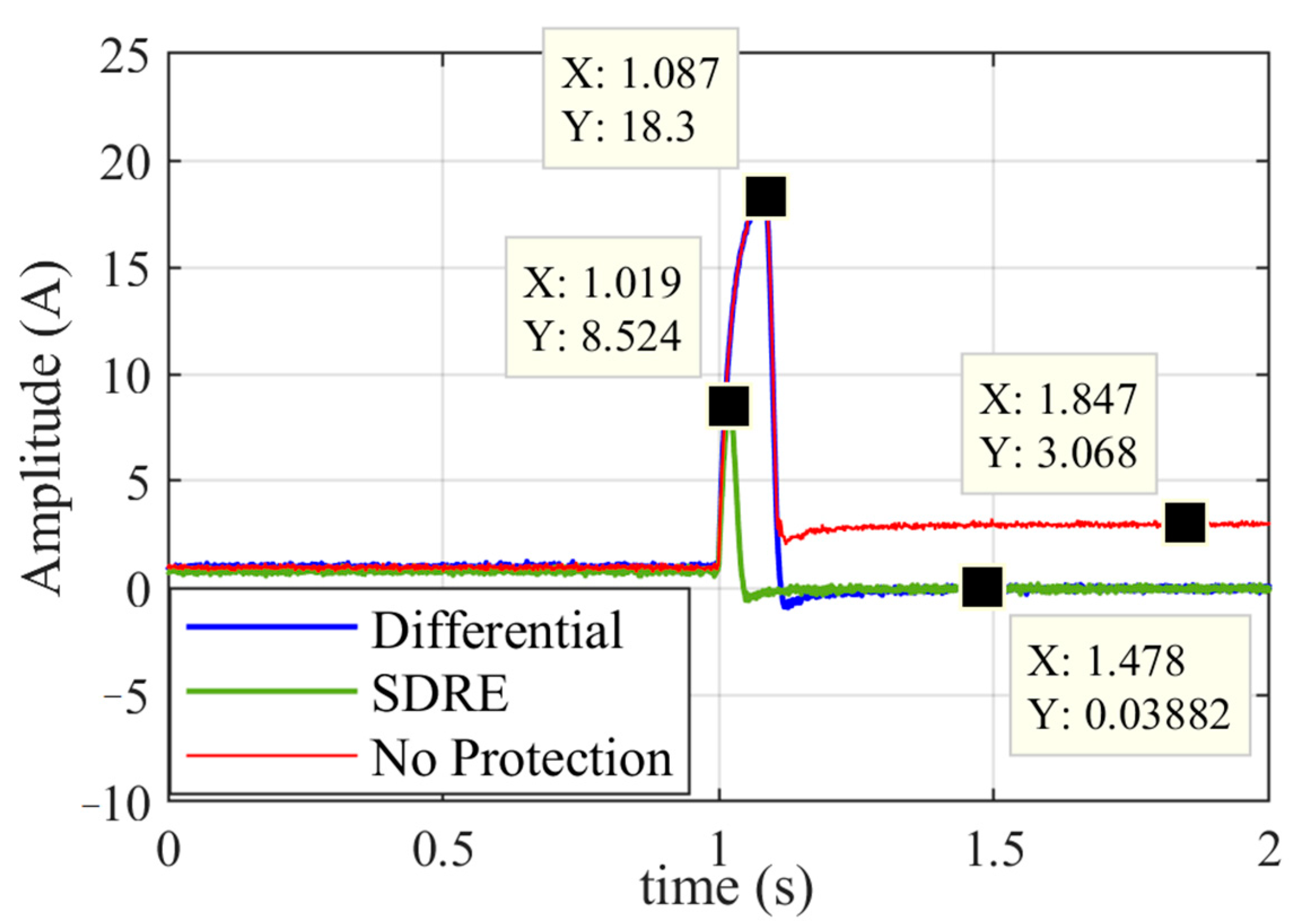
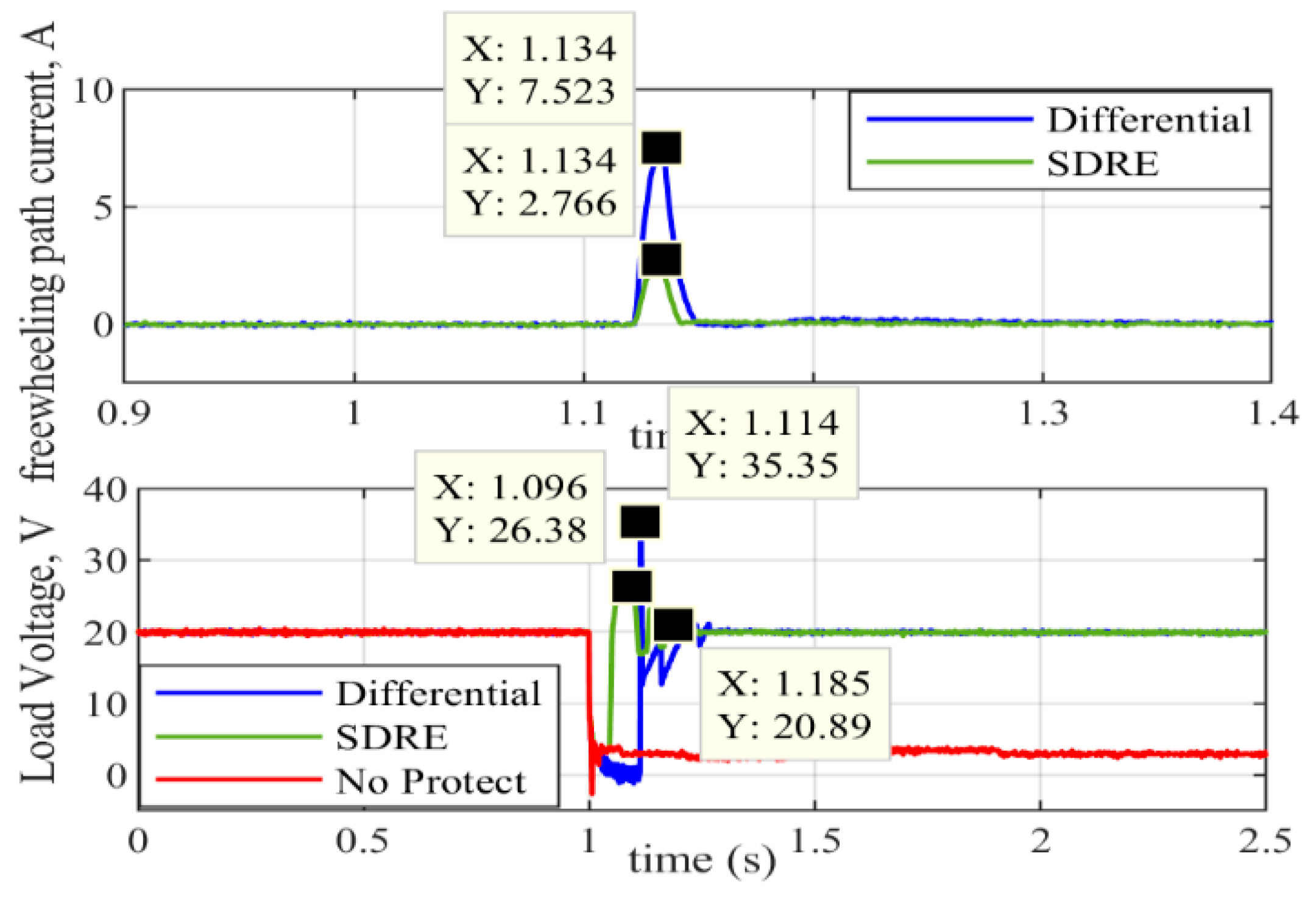
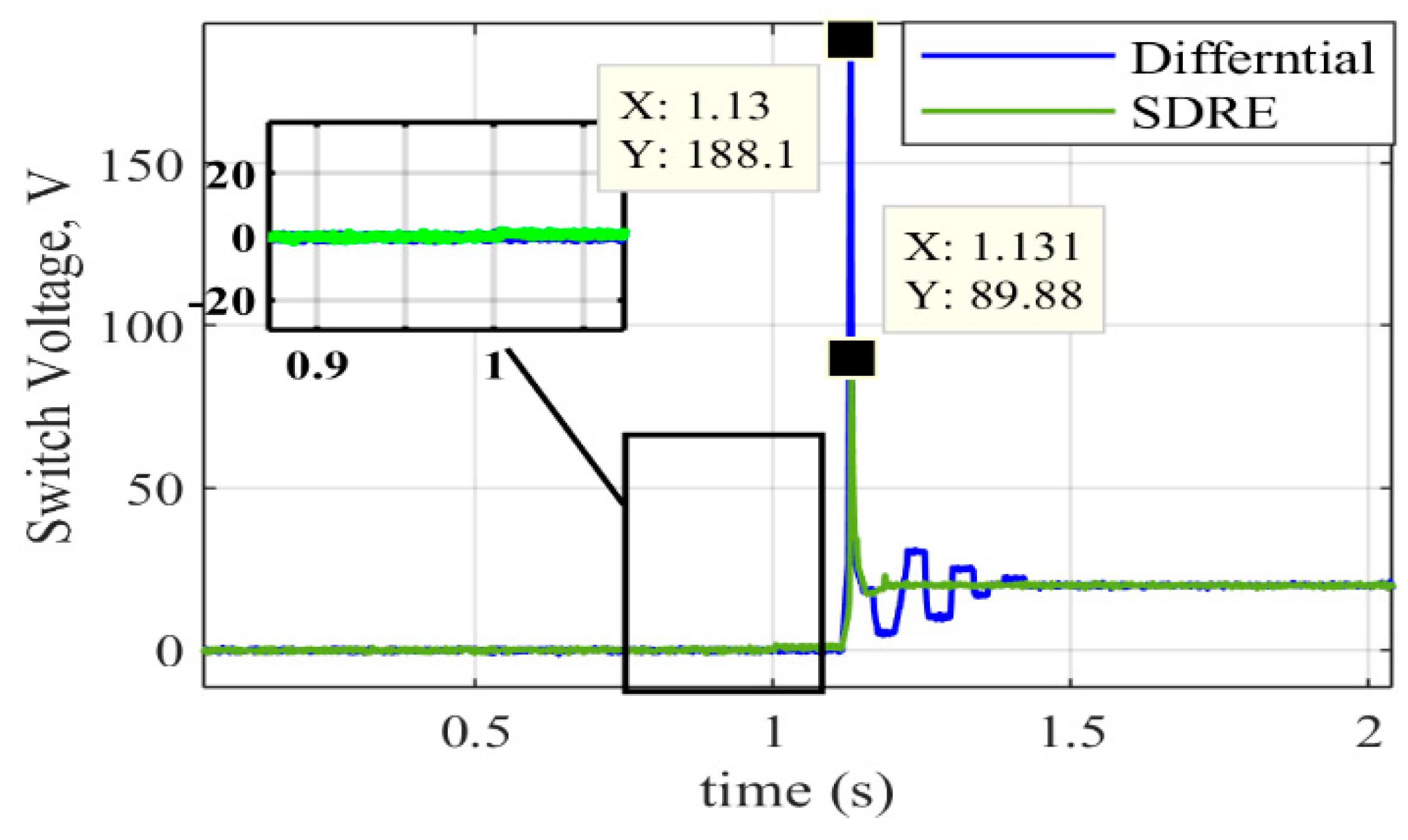
5. Experimental Verification
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, Z.; Zheng, T.; Wang, Y.; Yang, C. A Hierarchical Coordinative Control Strategy for Solid State Transformer Based DC Microgrids. Appl. Sci. 2020, 10, 6853. [Google Scholar] [CrossRef]
- Saponara, S.; Saletti, R.; Mihet-Popa, L. Recent Trends in DC and Hybrid Microgrids: Opportunities from Renewables Sources, Battery Energy Storages and Bi-Directional Converters. Appl. Sci. 2020, 10, 4388. [Google Scholar] [CrossRef]
- Adi, F.S.; Lee, Y.J.; Song, H. State Estimation for DC Microgrids using Modified Long Short-Term Memory Networks. Appl. Sci. 2020, 10, 3028. [Google Scholar] [CrossRef]
- Yin, C.; Wu, H.; Sechilariu, M.; Locment, F. Power management strategy for an autonomous DC microgrid. Appl. Sci. 2018, 8, 2202. [Google Scholar] [CrossRef] [Green Version]
- Abdali, A.; Mazlumi, K.; Noroozian, R. Novel Method of Low and High Impedance Fault Detection in LVDC Microgrids. In Proceedings of the 11th International Conference on Protection and Automation of Power System, Tehran, Iran, 18–19 January 2017. [Google Scholar]
- Yaqobi, M.A.; Matayoshi, H.; Danish, M.S.S.; Lotfy, M.E.; Howlader, A.M.; Tomonobu, S. Low-Voltage Solid-State DC Breaker for Fault Protection Applications in Isolated DC Microgrid Cluster. Appl. Sci. 2019, 9, 723. [Google Scholar] [CrossRef] [Green Version]
- Salomonsson, D.; Soder, L.; Sannino, A. Protection of low-voltage DC microgrids. IEEE Trans. Power Deliv. 2009, 24, 1045–1053. [Google Scholar] [CrossRef]
- Abdali, A.; Mazlumi, K.; Noroozian, R. Fast fault detection and isolation in low-voltage DC microgrids using fuzzy inference system. In Proceedings of the 5th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS), Qazvin, Iran, 7–9 March 2017; pp. 172–177. [Google Scholar]
- Lv, C.; Zheng, X.; Tai, N.; Chen, S. Single-ended protection scheme for VSC-based DC microgrid lines. Energies 2018, 11, 1440. [Google Scholar] [CrossRef] [Green Version]
- Abdali, A.; Mazlumi, K.; Noroozian, R. A precise fault location scheme for low-voltage dc microgrids systems using multi-layer perceptron neural network. Sigma J. Eng. Nat. Sci. 2018, 36, 821–834. [Google Scholar]
- Abdali, A.; Noroozian, R.; Mazlumi, K. Simultaneous control and protection schemes for DC multi microgrids systems. Int. J. Electr. Power Energy Syst. 2019, 104, 230–245. [Google Scholar] [CrossRef]
- Abdali, A.; Mazlumi, K.; Noroozian, R. High-speed fault detection and location in DC microgrids systems using Multi-Criterion System and neural network. Appl. Soft Comput. 2019, 79, 341–353. [Google Scholar] [CrossRef]
- Farhadi, M.; Mohammed, O.A. Event-based protection scheme for a multiterminal hybrid DC power system. IEEE Trans. Smart Grid 2015, 6, 1658–1669. [Google Scholar] [CrossRef]
- Fletcher, S.D.; Norman, P.J.; Fong, K.; Galloway, S.J.; Burt, G.M. High-speed differential protection for smart DC distribution systems. IEEE Trans. Smart Grid 2014, 5, 2610–2617. [Google Scholar] [CrossRef] [Green Version]
- Park, J.D.; Candelaria, J. Fault detection and isolation in low-voltage DC-bus microgrid system. IEEE Trans. Power Deliv. 2013, 28, 779–787. [Google Scholar] [CrossRef]
- Esreraig, M.; Mitra, J. An observer-based protection system for microgrids. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar]
- Esreraig, M.; Mitra, J. Microgrid protection using system observer and minimum measurement set. Int. Trans. Electr. Energy Syst. 2015, 25, 607–622. [Google Scholar] [CrossRef]
- Hwas, A.; Katebi, R. Nonlinear observer-based fault detection and isolation for wind turbines. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 870–875. [Google Scholar]
- Xu, L.; Chen, D. Control and operation of a DC microgrid with variable generation and energy storage. IEEE Trans. Power Deliv. 2011, 26, 2513–2522. [Google Scholar] [CrossRef]
- Çimen, T. Systematic and effective design of nonlinear feedback controllers via the state-dependent Riccati equation (SDRE) method. Annu. Rev. Control 2010, 34, 32–51. [Google Scholar] [CrossRef]
- Chen, W.; Saif, M. An iterative learning observer for fault detection and accommodation in nonlinear time-delay systems. Int. J. Robust Nonlinear Control IFAC Affil. J. 2006, 16, 1–19. [Google Scholar] [CrossRef]





| Parameters | Value | Parameters | Value | Parameters | Value |
|---|---|---|---|---|---|
| Equipment | Description |
|---|---|
| MASTECH HY3005-2, 30-V 3-A power supply, 2 channels | Utilized for 20 V VPV and VB |
| MASTECH HY3005-2, 30-V 3-A power supply, 2 channels | Utilized for 20 V VS |
| 10 Ω, 30-Watt resistor | Utilized for resistive dc load |
| Three 15 μH inductor | Utilized for the inductance of VPV, VB and Vs |
| Six 220 pF capacitor | Utilized for capacitance of VPV, VB and Vs |
| Two STGW38IH130D IGBT modules | Utilized to for circuit breaker |
| One IKW40N120H3 IGBT | Utilized to employ the line to ground (LG) fault |
| FEP30GP Diode, 2 Ω resistor | Utilized for freewheeling branches |
| FEP30GP Diode, 10 μF capacitor, 12 Ω resistor | Utilized for Resistance Capacitance Diode (RCD) snubber |
| ATMEGA8L-8PU Microcontroller | Implemented for the protective system |
| Three ACS 712-30 and ADS1115 modules | Utilized for sampling current, 3rd low-pass filter, A/D |
| Three TC427CPA microchips, ULN2003 APC buffer | Utilized for insulated-gate bipolar transistors (IGBTs) gate drivers |
| Two HCPL-7840 optocoupler | Utilized for differentiation of analog and digital grounds, noise decrement, isolation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdali, A.; Mazlumi, K.; Guerrero, J.M. Integrated Control and Protection Architecture for Islanded PV-Battery DC Microgrids: Design, Analysis and Experimental Verification. Appl. Sci. 2020, 10, 8847. https://doi.org/10.3390/app10248847
Abdali A, Mazlumi K, Guerrero JM. Integrated Control and Protection Architecture for Islanded PV-Battery DC Microgrids: Design, Analysis and Experimental Verification. Applied Sciences. 2020; 10(24):8847. https://doi.org/10.3390/app10248847
Chicago/Turabian StyleAbdali, Ali, Kazem Mazlumi, and Josep M. Guerrero. 2020. "Integrated Control and Protection Architecture for Islanded PV-Battery DC Microgrids: Design, Analysis and Experimental Verification" Applied Sciences 10, no. 24: 8847. https://doi.org/10.3390/app10248847







