1. Introduction
The use of anthropomorphic robots, which offer a more affordable cost, has spread widely for the development of more flexible and reconfigurable manufacturing systems for handling, assembly, welding, and painting, among others. In other manufacturing processes, such as industrial machining operations, robotic systems are less widespread used because process forces generate significant path deviations from the programmed path, which limit their use in the production of parts with acceptable manufacturing tolerances in sectors such as automation, aeronautics and naval application [
1].
At the industrial level, there is a trend towards directly applying a conventional machining approach to robotic systems [
2]. Using this philosophy, there have been many failures, since the substantial difference between the two manufacturing systems requires prior study to guide the solutions of each application. Knowledge of robotics and machining technology must be properly combined to obtain an acceptable degree of success [
3].
Robotic cell operators who were previously used in machining centers are subjected to steep learning curves due to the lack of methods and procedures what provide working guidelines to allow production of parts within an acceptable manufacturing tolerance range and surface quality. An example of these type of working guidelines is a manual that defines machining conditions based on the cutting tool selected for removing material [
4,
5], since other robotic machining reference documents do not exist.
The lack of machining rules for robotic cell users results in higher uncertainty in the possible results of the production process, and consequently the selection of strategies and cutting conditions is left to the judgment of the operator or leading into the undesirable process of trial-and-error. Fortunately, CAM tools [
6] have been developed allowing programming and simulating tool paths in robotic cells for different manufacturing processes. These CAM software facilitate the path generation of the cutting tool and usually incorporate industrial robot movement simulators. This allows to evaluate the possibility of achieving a certain space position, singularities and limits in axes, movement indeterminacies, etc. Even so, there are certain limitations that affect the smoothness of the robot’s path or functional redundancy in 5-axis robotic machining that have been studied by different authors. Peng, J. et al. [
7] have developed a sequential linearization programming method that generates a smoother robot path in which a significant reduction in the magnitude of the maximum joint acceleration is obtained and leads to better quality surface area and greater machining efficiency. Schneider, U. et al. [
8] have developed an offline predictive compensation method for machining errors, an innovative programming system, based on kinematic and dynamic robot models. The compensation of machining errors is adaptive in real time and allows to improve the results in terms of robotic machining accuracy.
During the last three decades, robotic machining has aroused great research interest due to the benefit provided by the industrial robot in terms of economic profitability, flexibility of operations and multifunctionality, identifying its main limitations [
9,
10]. The low stiffness of robots has not been a particularly limiting technical barrier in the development of industrial solutions meant for handling, welding, component assembly, or other operations in which the external system forces are mainly due to the robot’s own acceleration and gravity effects [
11,
12,
13]. However, in applications in which the robot is subjected to periodic forces characteristic of the manufacturing process, such as machining forces, an analysis of robotic system behavior [
14,
15,
16], specifically, the robot’s structural strength as a function of the programmed path, is required [
17,
18,
19]. Klimchik, A. et al. [
20] have developed a model to demonstrate that the precision of series industrial robots in the machining operation of circular grooves depends on its structural rigidity. Janez, G. et al. [
21] has shown that the manipulability, structural rigidity, structural inertia, damping ratios and natural frequencies of industrial robots are kinematic, static and dynamic properties that determine the precision result of robotic machining. Gotlih, J. et al. [
22] delved a little deeper in this field and developed a calibrated model used to generate a substitute model the structural rigidity of the robot considering other properties such as inaccurate geometry of model, friction, component wear and other effects. Another notable scientific contribution is that made by Jiao, J. et al. [
23], who propose a variable parameter stiffness model to achieve the simultaneous identification of the robot’s kinematics and the stiffness parameters. They also provide a model-based error prediction and compensation method through online detection of external load.
In robotic machining operations, under certain defined machining and path conditions the deviation and tool chatter will depend strongly on the robot’s axes’ configuration [
24,
25]. In other words, the deviation of the real path with respect to the programmed path, and the chatter of the tool during the machining operations, depend essentially on the interrelation between the stiffness of the robot and the magnitude and direction of the machining forces [
26,
27].
The published literature verifies that the tool’s path deviation and vibration depend fundamentally on the robot’s stiffness, the cutting force magnitude and the predominant direction of action. Some authors have researched into this phenomenon [
28,
29,
30] and have provided tools that help to address this issue from a workshop-oriented perspective. A correct selection of robots, cutting tools and optimum machining conditions is decisive in order to produce parts with suitable dimensional tolerances and surface quality in robotic machining systems. The machined surface quality generated during machining is correlated closely with milling conditions, mainly diameter–length of tool, feed rate, depth of cut, cutting speed, etc. [
31,
32,
33]. Among the most notable advances, we must highlight the machining tool path deviation predictive methodology (PREMET) developed by I. Iglesias et al. [
34] in which the robot’s structural dynamics are reduced to the cutting Tool’s Center Point (TCP) to evaluate and compare the deviations between different robot structural configurations in order to select the lowest deviation of the cutting path. PREMET has been applied for the case of the grooving operation in soft materials and the errors obtained are smaller than 12%.
Factorial design of experiments has been identified as a very useful tool to evaluate the influence of different factors on precision in robotic machining without having to execute a long and tedious experimental phase. For example, Grisol de Melo, E. et al. [
35] used a factorial design to evaluate the performance of the industrial robot with respect to the precision of movements in function of the geometry of the tool, feed rate and spindle speed. Previously, Antunes Simões, J.F.C.P. et al. [
36] used the design of experiments through factorial techniques to evaluate surface quality and geometric precision function of lead/lag angle, advance speed and robot arm extension.
Considering the background, the main motivation of this investigation is to present novel factorial procedure that allows preliminary study of critical factors in robotic machining operations. This development represents a novel analytical tool for studying of the main cutting conditions of the robotic machining process, facilitating the evaluation of critical factors not previously addressed by the scientific community. The factorial procedure identifies and classifies the main conditions of robotic machining and uses the factorial design of experiments to make viable the execution of the experimental tests. Furthermore, this procedure contemplates the use of PREMET, that allows the determining of path deviations during the machining process in the robotic system without the need for extensive experimental tests. PREMET establishes and defines a simulation model for predicting the dynamic structural behavior for any industrial robot of up to six degrees of freedom, which is used to analyze of the correct use of the robot’s stiffness and the adequate selection of the main machining constraints in soft, metallic and nonmetallic materials compared to cutting conditions in conventional machine tools. Then, this novel factorial procedure facilitates the study and analysis of the main critical factors in robotic machining cells and it represents an unprecedented advance as a prior tool for designers and users of robotic manufacturing system.
2. Factorial Procedure for Preliminary Study of Critical Factors in Robotic Machining
The factorial procedure was designed to establish the relationship between the main machining conditions imposed on the robot and the simulate deviation of the cutting tool path through the PREMET, and in this way to determine which are the critical factors that most affect the machining path of any robotic cell. This factorial procedure allows the evaluation of the most influential factors in robotic machining in order to obtain the process conditions with lower path deviations. Machinable materials can be grouped into three sections: metallic, plastic and ceramic. This factorial procedure was applied in the field of soft material machining (metallic, plastic or composite materials formed by a combination of the above) in which the material hardness values do not exceed 110 HB.
The factorial procedure consists of the following phases:
Phase 1: Factorial design
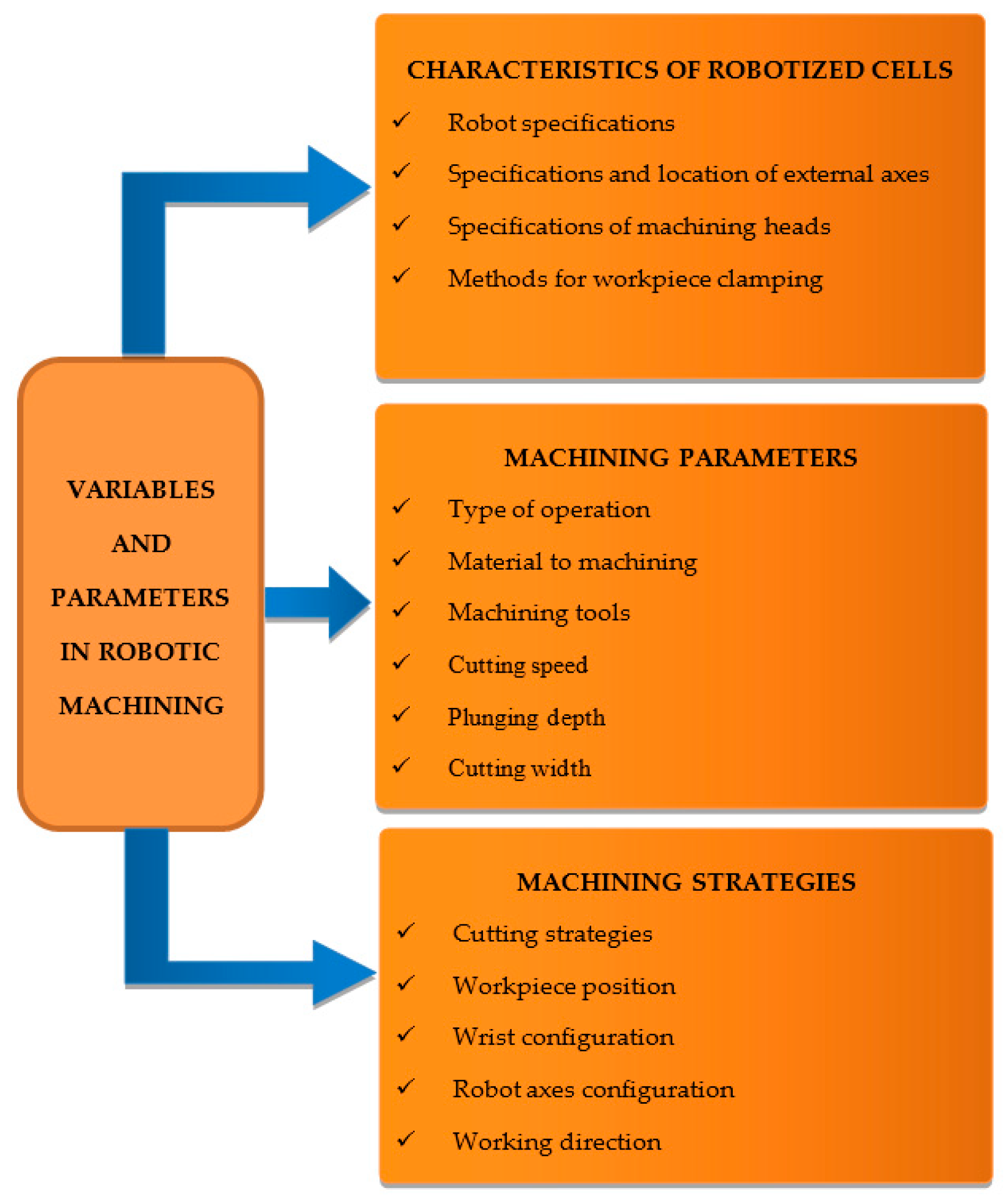
A factorial design was performed to study the effects of different variables and parameters on the machining tool’s path precision. By simultaneously varying the levels of all factors, instead of one at a time, it is possible to assess the interaction between them and rank them accordingly to their influence on the part’s dimensional quality. The factorial procedure raises the classification of the variables and machining parameters that affect robotic machining depending on whether they affect the rigidity of the robot, the cutting force vector or the interaction between both. The conditions related to the characterization of the robotic cell affect the precision of the tool path because they modify the rigidity of the robotic machining system, while the machining parameters influence the cutting force vector. Finally, the machining strategy also conditions the machining precision due to the interaction between the rigidity of the robot and the cutting force vector of the machining tool, multiple combinations are possible with different precision results. Some of the main variables and parameters that condition robot machining have been identified and can be classified into three groups, as shown in
Figure 1:
The specifications of robot, external axes, machining heads or methods for workpiece clamping can be considered as initial data or variables and parameters of the robotic machining cell design process. For this reason, certain specifications such as the robot structural rigidity are studied as a factor or simply as a starting point.
- 2.
Machining parameters.
Type of operation, material to machining, machining tools, cutting speed, plunging depth, cutting width and other machining parameters can be initial data. It is very common, for example, that in order to evaluate the machinability of a part in a robotic cell, the material of the part and the required machining operation are classified as initial data. In the same way, it is also usual to optimize variables and machining parameters that allow parts to be produced with adequate tolerances in order to reduce manufacturing times and costs. For this reason, the study of these conditions is of special interest to users of robotic machining cells.
- 3.
Machining strategies.
The cutting strategies, workpiece position, wrist configuration, robot axes configuration or working direction are some variables and parameters of robotic machining that can remain fixed during the process or they can be studied for making the most of the performance of robotic machining cells. Therefore, some of these constraints can be considered initial data and others factors of study in order to obtain the cutting tool path that provides smaller deviations with respect to the programmed tool path.
Prior to the analysis and selection of variables and machining parameters, it is necessary to know what type of operation is carried out, robotic cell to be used and the manufacturing strategy to follow. Depending on the conditioning factors of each robotic machining application, there will be some batch data and other variables customizable by operator. From among these variables and machining parameters to be defined, the conditions that will be included in the design of the factorial study will be chosen before the simulated model execution.
Stage 1: Set initial data
The initial data are the values or parameters of robotic machining that cannot be changed during the study—these are the starting conditions of the process whose effect is not studied for a specific application. Considering the classification of variables and machining parameters carried out in
Figure 1, the necessary initial data must be defined.
Stage 2: Selection of the variables and parameters to study
The values or parameters to be studied are the factors whose influence on robotic machining must be evaluated; they are the conditioning factors on which to act, in order to reduce the machining tool path deviation. Considering the classification made in
Figure 1 again, scoping factors should be selected for each study.
Stage 3: Development of the test tables.
If it is proposed to obtain complete real data, an experimental phase that includes
number of trials is necessary, where k represents the levels to be evaluated and j the factors to study. The large number of experiments that would be needed if we are interested in evaluating many factors with many levels, as in the case of robotized machining operations can be unapproachable because of the high cost that may involve experimentation. The literature recommends in these cases to use the factorial design in order to optimize the cost of the experiments [
37]. The usual strategy is to carry out the factorial design of experiments considering the evaluation of only two levels for j factors, resulting
trials. This procedure is based on this strategy to be able to approach the experimental phase. According to the variables and parameters of study, the factorial design resulted a 2xj matrix. In
Table 1 is shown the factorial design of j factors in the two levels proposed for this study.
Phase 2: Methodology applied for determination of the simulated cutting tool path deviation
PREMET, the predictive methodology developed by I. Iglesias et al. [
34], has been validated and can be applied in any six degrees of freedom industrial robot to calculate the path deviations of the machining tool, and it is used in this factorial procedure to predict the simulated path deviation.
Stage 1: Characterization of the reduced equivalent model
The stiffness matrix
Kr and the damping matrix
Cr for the different path points is determined for representing the robot’s mechanics through the next equation:
where
- -
Mr(
) is the equivalent matrix of the mass of the robot’s axes and machining head,
- -
Kr(
) is the stiffness matrix equivalent to the mechanical structure of the robot for a point
Pi of the space. The TCP deviations under the action of a known static force was measured with a deflection gauge.
- -
Cr(
) is the damping equivalent to the mechanical structure of the robot for a specific point
Pi of the space. It was calculated through a hammer impact test and considering the Rayleigh equation.
Stage 2: Cutting force modeling
The standard cutting force model based on Altintas [
38] is used to simulate the cutting force vector for the flat end milling. The equation for calculating the force
Fxyz,tool on the TCP is,
Stage 3: Modeling of the interactions between the cutting forces and the robot mechanics
Therefore, the interaction between the cutting forces and the robot’s mechanics is represented by the equation:
Stage 4: Evaluation and comparison of different structural configurations
The different structural configurations of the robot must be evaluated and compared based on the simulated maximum path deviation values. It is recommended to graph and to tabulate the deviations of simulated paths to analyze in depth the data obtained with PREMET.
Stage 5: Selection of the lowest-deviation structural configuration
Finally, the structural configuration with the lowest path deviation prediction result must be selected, and therefore the machining conditions that give the best corresponding prediction results.
Phase 3: Evaluation and identification of the most influential factors in robotic machining
In order to determine the robotic cell configuration and the machining conditions that provide the least tool path deviation and the best cutting parameters, the different machining possibilities are evaluated and it is determined which allows the least tool path deviations and the best machining time for obtaining the required part accuracies.
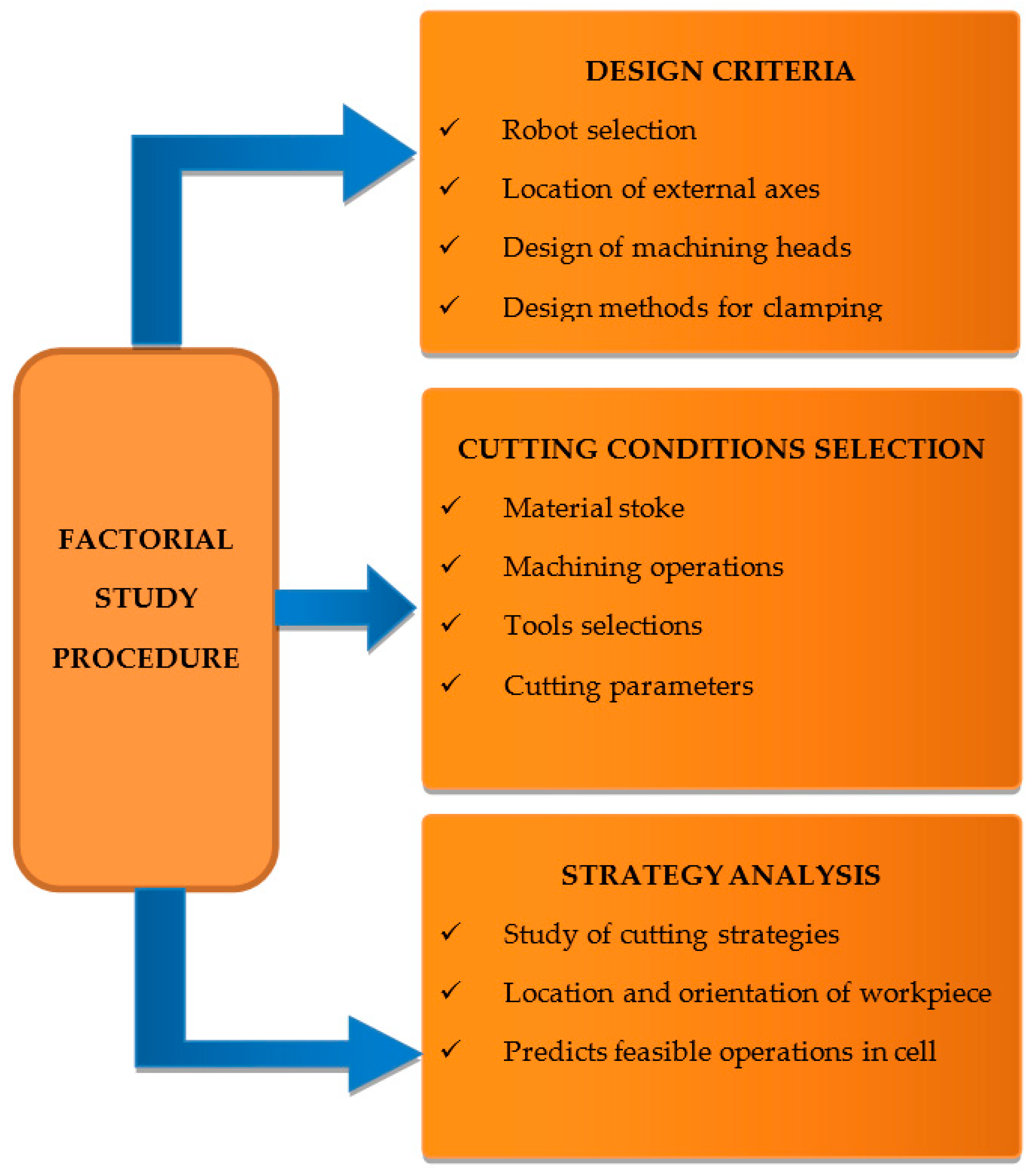
After determining the simulated cutting tool path deviation for these specific machining variables and parameters, the user of the robotic machining cells must evaluate the results obtained in order to identify the most critical factors and make a decision according to the criteria shown in
Figure 2:
Establish design criteria for the robotic cell, in cases where robot selection, location of external axes, machining head configuration or workpiece clamping methods are necessary.
Determine whether a specific machining operation can be performed in the robotic cell, depending on the work material, machining operation, cutting tool and process parameters.
Select the most convenient cutting strategy by defining the location and orientation of the part and determining the most favorable robot axis configuration, which guarantees the correct execution of the machining operation, complying with the required manufacturing tolerances of the part.
3. Experimental Validation of the Factorial Procedure
Set initial data
In order to validate the factorial procedure, all variables and parameters defined through the different phases need to be applied in the machining of soft materials. Considering the classification of variables and machining parameters carried out, the initial data are:
The machining tests were performed in a robotic cell with an IRB 6660 robot, an MTC 2000 turning unit, a Peron speed machining head and also used mechanical clamping devices.
- 2.
Machining parameters.
Certain initial conditions are established:
- ○
A grooving operation was chosen for its simple cutting force vector representation.
- ○
To perform the machining tests, a KENDU hard metal burr-cutting tool with a 10 mm diameter, 150 mm length, two cutting edges, and a 30º helix angle was chosen.
- 3.
Machining strategies.
A rectilinear cutting path was programmed, in which the machining tool axis is perpendicular to the worktable. The existing trend in the use of path programming software for robotic machining systems, which facilitate the linearization of curved paths through the selection of smoothing and tolerance parameters, allow to calculate the path of the cutting tool as a set of movements rectilinear from point to point with sufficient proximity without need to use programming with complex cycles such as circular interpolations. For the validation of this factorial procedure, the calculation, simulation and analysis of rectilinear machining paths have been considered, where rectilinear movements from point to point are the basic element to evaluate in any trajectory.
Selection of the variables and parameters to study
With the objective of evaluating the influence of certain machining conditions on the machining tool path deviation, the following variables and parameters were considered:
The evaluation of any variable corresponding to the robotic cell has not been considered because all the validation tests will be carried out on the same robot, machining head, worktable and clamps. In further studies these variables can be considered.
- 2.
Machining parameters.
Selection of the workpiece material type: To evaluate the influence of the hardness of the material to be machined on the prediction of the robotic system, two materials with very different properties were selected: Aluminum EN AW—5083 (Al) and 300 kg/cm3 rigid polyurethane foam (PUR 300).
Cutting parameter selection, based on the conventional machining manual for KENDU machine tool:
- ○
To study the influence of cutting speed on path precision, two rotational tool speeds (n) were defined: 6000 rpm and 8000 rpm.
- ○
To evaluate the influence of cutting depth on the tool’s path deviation, two values (ap) were defined: 1 mm and 1.5 mm.
- 3.
Machining strategies.
To assess the importance of the cutting force vector orientation with respect to robot’s mechanics, two different machining directions are defined, one longitudinal (L) and one transverse (T) to the worktable, as shown in
Figure 4. The feed direction of the cutting tool L corresponds to the X direction of the robot’s base coordinate system, while T direction corresponds to one parallel direction to the axis Y of the base coordinate system of the robot.
Development of the test tables
According to the variables and parameters the study selected, the factorial design was carried out, summarized in
Table 2, resulting in a 2 × 5 matrix.
The compiled test tables are shown in
Table 3a,b below:
Experimental tests
Actual experiments with a robot were performed, and the cutting tool path deviation values obtained from the simulation were compared with those obtained during real machining. In
Figure 5 it can see the Al and PUR 300 pieces used in the experimental test, as well as the robotic cell at the beginning of machining.
Measurement of robotic machining toolpath deviations
After the experimental tests, the different test pieces were measured using a MITUTOYO coordinate measuring machine, model EUROC-APEX.
Figure 6 shows a piece of Al and another of PUR300 obtained in the experimental phase of this study corresponding to tests E2 and E18 respectively. The profiles of both sides of the groove were extracted, and the maximum path deviation values were measured. The results of measurements are summarized in
Table 3 and
Table 4.
For a better understanding of results, the original groove and the measurements performed, corresponding to tests E2 (Blue) and E18 (Pink), are shown in
Figure 7,
Figure 8 and
Figure 9. The measurements of the E2 test groove (blue) have been plotted overlap on the designed probe. The programmed path of the cutting tool TCP tool is also shown (Black). The measurements representation of test E18 (pink) have been moved from their natural position to be able to visualize them properly and it avoid overlap with the representation of test E2 (blue). The lateral profiles of the E2 test have been raised 0.2 mm and the low plane of the groove has been lowered 0.2 mm.
In the front view measurements in
Figure 8, the path deviations can be better appreciated.
Finally, in the top view measurements of tests E2 and E18,
Figure 9, it is shown that the profiles of one of the sides is enlarged to visualize the evident difference in paths described by the cutting tool for the two materials tested.
Evaluation and comparison of different structural configurations
The different robot structural configurations were evaluated and compared based on the maximum experimental path deviation values. The structural configuration with the best experimental cutting tool path deviation result was then selected, and the most influential factors in robotic machining were identified. The machining conditions with the best experimental results are those corresponding to test E18 for PUR 300 at 0.352 mm, and E2 for Al at 0.607 mm.
4. Results through the Application of the Factorial Procedure
The simulated and experimental maximum cutting tool path deviation (SEMPAD) results are shown in
Table 4 and
Table 5, along with the predictive error percentages.
The following figures show the percentages of predictive error committed for machining the groove in Al (
Figure 10) and in PUR 300 (
Figure 11).
The values of the robotic machining variables and parameters that provide lower cutting tool path deviation outputs are shown in the following
Table 6.
Therefore, the factorial procedure has been validated through evaluating the results obtained, stating that:
The achieved precision depends fundamentally on the working material, becoming worse as its hardness increases. The most unfavorable results appear when machining tests are performed on Al.
The workpiece location is an important variable to control because it directly influences the stiffness available for the robot to counter the cutting forces. Considering the same robot wrist configuration and the same cutting force vector for positions A and B, different trajectory deviation values are obtained due to the change in structural rigidity of the robotic arm.
The milling head orientation with respect to the working direction (or the configuration of the robot’s axes) also modifies the robot’s stiffness and therefore influences the obtained precision.
The cutting conditions, such as cutting speed (Vc) or plunging depth (ap), influence the result and must be adequate.
Acting on the previous conditions, the precision has been improved from an experimental deviation error of 0.685 mm to 0.352 mm for PUR 300 and from 0.982 mm to 0.607 mm for Al.
Analyzing the results of maximum cutting tool path deviation obtained through the factorial procedure shows that the most influential factors on the obtained precision or manufacturing tolerances for the study performed, in order of highest to lowest importance, are as follows:
The differences between the predicted and the experimental cutting tool path deviations are below 12%, an acceptable level of error, which validates this factorial procedure for preliminary study of critical factors in robotic machining as a novel tool in the analyze of the most influential factors in robotic manufacturing systems.
5. Discussion
It should be noted that the factorial design of two levels is often used because of the high cost in terms of time and money that takes experimentation as a result of the large number of experiments that would be needed to assess many factors using many levels, as it is in the case of robotic machining. On the other hand, the reliability of PREMET to determine the TCP path deviation has already been evaluated in previous works as an acceptable method. For both reasons, it has been considered to establish a two-level factorial study as a suitable condition to evaluate the trend of each factor.
The evaluation of the machining path deviation results obtained after applying the factorial procedure, get a reduction of the error of 36.39% for Al and 17.11% for PUR 300. the precision has been improved from an experimental deviation error of 0.685 mm to 0.352 mm for PUR 300 and from 0.982 mm to 0.607 mm for Al, acting only on the conditions of the process studied and without turning to path compensation methods. Once the IRB 6660-205/1.9 robot datasheet is also evaluated, we can determine that its repeatability value is +/− 0.1 mm, which means that there is a systematic error between the values obtained from the test measurements and the programmed path with a maximum error of 0.1 mm, so the precision error results can be improved if they are corrected using corrective coefficients. Experimental improvements achieved in this study cannot be directly compared with similar works of other authors. It is not possible to establish direct quantitative relationships between the results of each study because neither the industrial robots nor the machining conditions allow it, but it is possible to position this document qualitatively with regard to other published methods of compensation and prediction of the path accuracy.
The circularity indices range obtained by Klimchik, A. et al. [
28] in circular groove milling with 100 mm diameter, under the cutting conditions described in the document with KUKA KR270, has been between 1.36 and 0.84 mm. Applying the error compensation method proposed it is possible to improve the robot accuracy around 80–95%, with the circularity error made in 0.29 mm. In the study by Janez, G. et al. [
29] the application of a predictive model of robotic machining precision allows for adjusting the position of the robot, improving the circularity precision of the hole in diameter from 1.86 to 0.23 mm and in cylindricity from 0.87 to 0.16 mm.
The scientific advance provided by the factorial procedure does not achieve as much improvement (in terms of precision of the machining path) as the aforementioned works. Obviously the two paths evaluated are very different, one goes straight and the other goes circular. In addition, both methods proposed path compensation techniques to improve robot accuracy while the experimental phase of this work seeks to identify the critical factors among the studied conditions to achieve the highest performance in terms of precision in a robotic machining cell, so the results obtained by this novel factorial procedure are considered satisfactory.
The evaluation of the obtained results provides a solution to the problem posed by the use of articulated industrial robots in machining operations, where the trajectory deviations and vibrations obtained condition the quality of the result.
The study has been limited to addressing the machining of two types of soft materials, with a wide variety of materials with relatively low hardness, which may be the object of study in future research. It is not ruled out that the factorial procedure can be applied to the study of the behavior of robotic machining systems in metallic or plastic materials with a hardness greater than 110 HB, but it has not been evaluated in this document.
Similarly, a flat cutting tool has been considered for the modeling of the cutting forces, but the factorial study procedure can be extended to the evaluation of cutting tools with other geometries, f.e. the ball end milling. The machining operation used to solve determines the type of tool to use significantly. In this sense we must highlight the interest in evaluating the behavior of industrial robots to perform complex machining operations, especially those that incorporate 3D trajectories in space, such as large-area contouring operations, where robotic systems have great advantages compared to expensive NC machining centers. However, we must emphasize that the current trend of programmed path robot machining using software tools allows linearization-curved paths by selecting smoothing parameters and tolerance, which is without the cycles regular programming, such as circular interpolations, whose use in robotic systems is either not allowed or not recommended. Therefore, the programming of cutting paths in robotized machining complex operations as a set of rectilinear movements from point to point with a close enough is the most common. This is the reason why this novel factorial procedure has been designed for an analysis of rectilinear machining paths, since the analysis of these rectilinear movements from point to point are the basic element of study to advance in this field of research. Even so, the main challenge for this procedure is identified as addressing the evaluation of more complex machining paths in order to rule out possible performance deficiencies in other stages.
6. Conclusions
The results obtained experimentally allow the validation of this factorial procedure, which represents a novel advance in the development of preliminary tools for the design. Implementation and optimization of flexible manufacturing robot systems can be applied to sectors such as automation, aeronautics, naval application, etc.
The factorial procedure for preliminary study of critical factors in robotic machining has enabled the analysis of the milling conditions of the groove in soft materials and the identification of those that improve the precision of the cutting tool path in robotic machining, obtaining an improvement in the experimental deviation error of 36.39% for Al, and 17.11% for PUR 300.
PREMET has been applied to obtain values of estimation of robot trajectory deviation with error less than 12%. Therefore, the use of PREMET, in the production of parts, has been validated for the machining of the groove in soft materials, which allows the prediction of deviation of the cutting tool concerning the programmed path and simplifying the study of the main factors that determine the result of robotic machining. The use of this prediction tool helps to assess what causes certain parameters to affect the precision of the robotic machining operation.
Consequently, the obtained results show that the factorial procedure serves to characterize the experimental robotic system, predicting the attainable manufacturing tolerances, and allowing the study of the main constraints in the machining of relatively soft materials, with an acceptable level of precision, around tenths of a millimeter.
The test results show that the conditioning factor in order of relevance are that material hardness, followed by the work piece location, and the milling head orientation with respect to the working direction or robot’s axes configuration and cutting conditions.
In addition, the factorial procedure also facilitates the analysis of more effective robotic system machining strategies. Such tool path deviation prediction provides guidelines for the attainable manufacturing tolerances. The prognosis of the manufacturing quality facilitates the selection of the optimal machining strategy and anticipates whether a certain machining operation is feasible in a robotic cell; thus, it ensures the appropriate use of the robot’s stiffness and safeguards the life of mechanical elements such as the drill head and the robot itself.
This novel factorial procedure can also help to establish design criteria in machining robotic cells by facilitating the robot’s selection, coherent location of the external axes and proper design of the machining head or the method used for workpiece clamping.
Finally, this factorial procedure opens an opportunity in the field of Industry 4.0, through the possibility of developing digital tools that integrate and automate the factorial design phases, calculation of the path deviations and evaluation of results.