Stability Analysis of Multi-Agent Tracking Systems with Quasi-Cyclic Switching Topologies
Abstract
1. Introduction
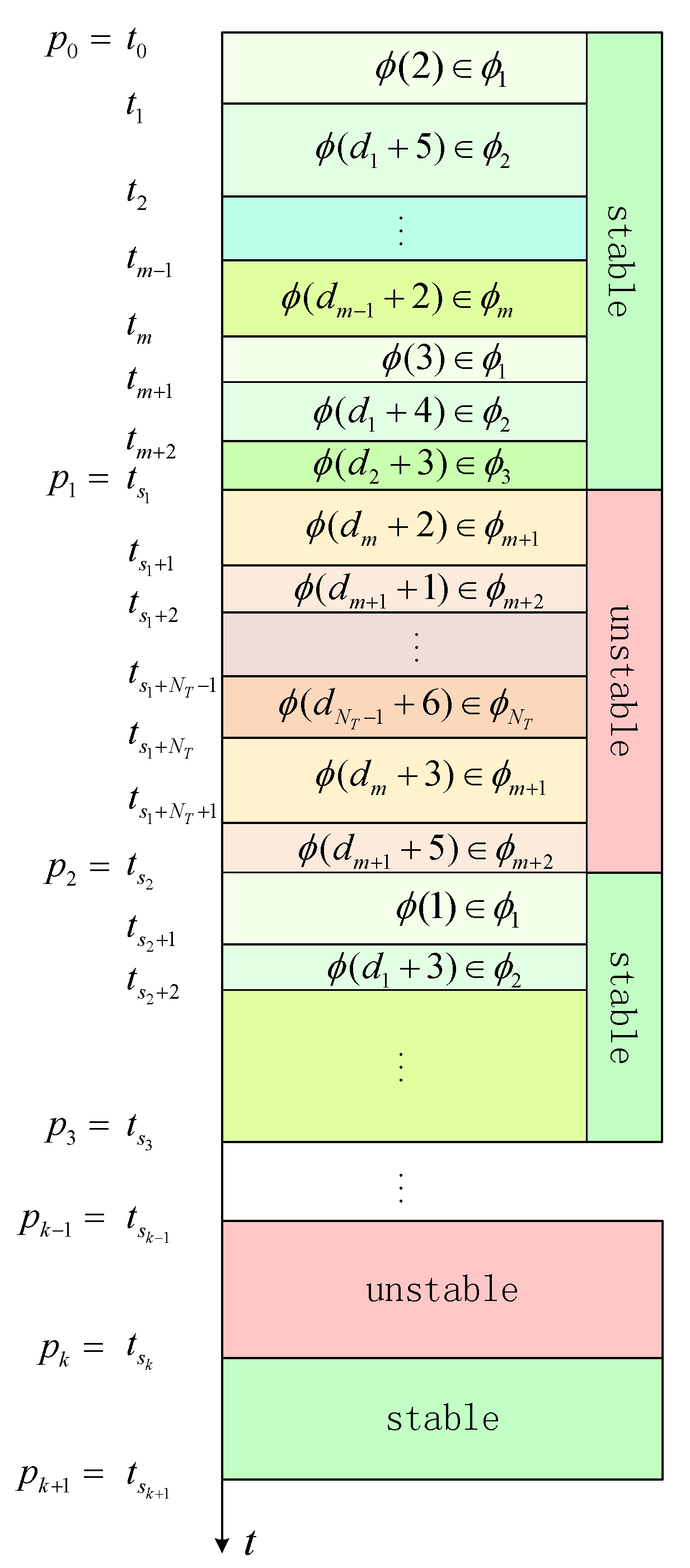
2. Preliminaries and Problem Formulation
2.1. Notations
2.2. Graph Theory
2.3. Problem Formulation
- If , ;
- If , ;
- If , ;
- If , .
3. Controller Design and Stability Analysis
3.1. Controller Design
3.2. Stability Analysis
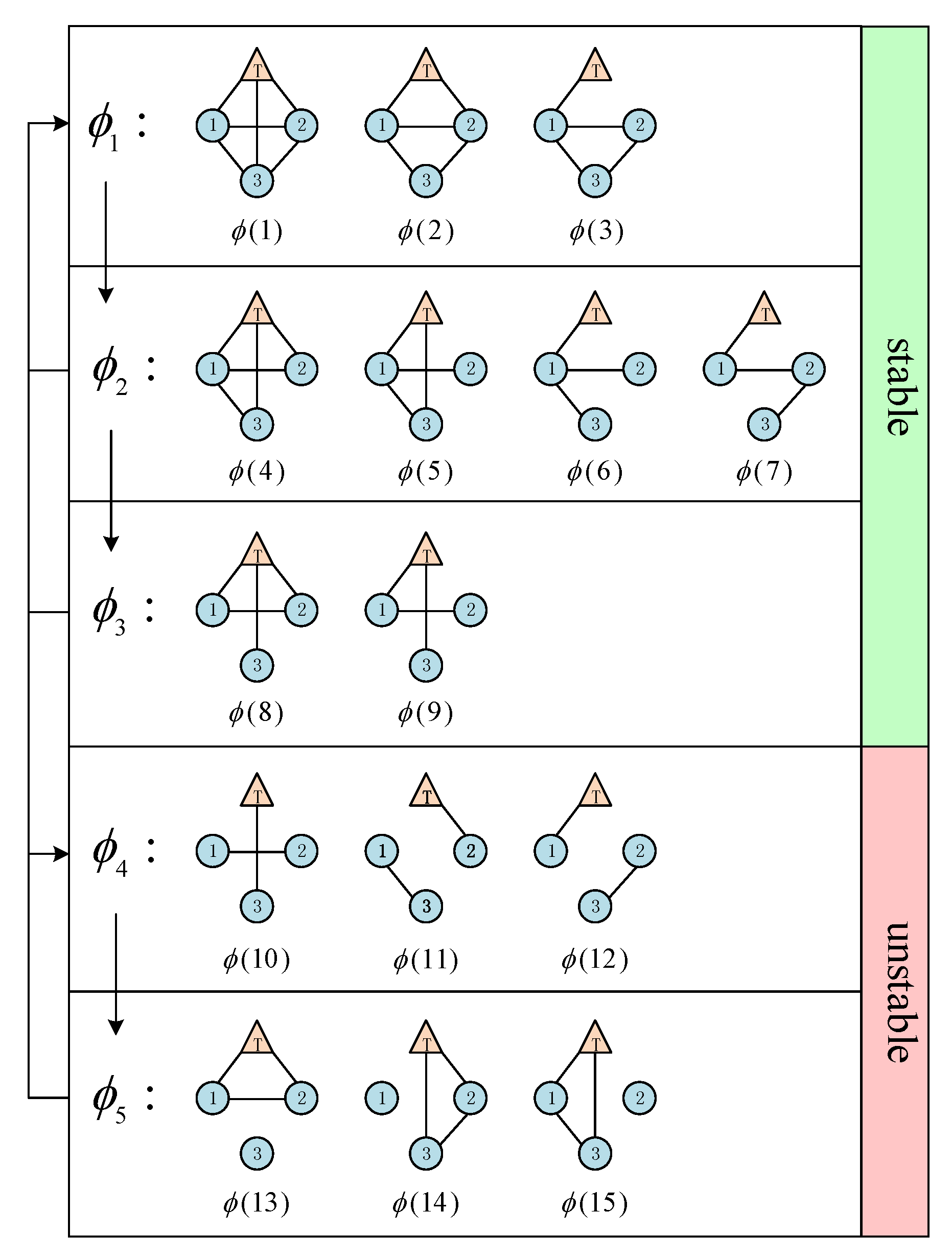
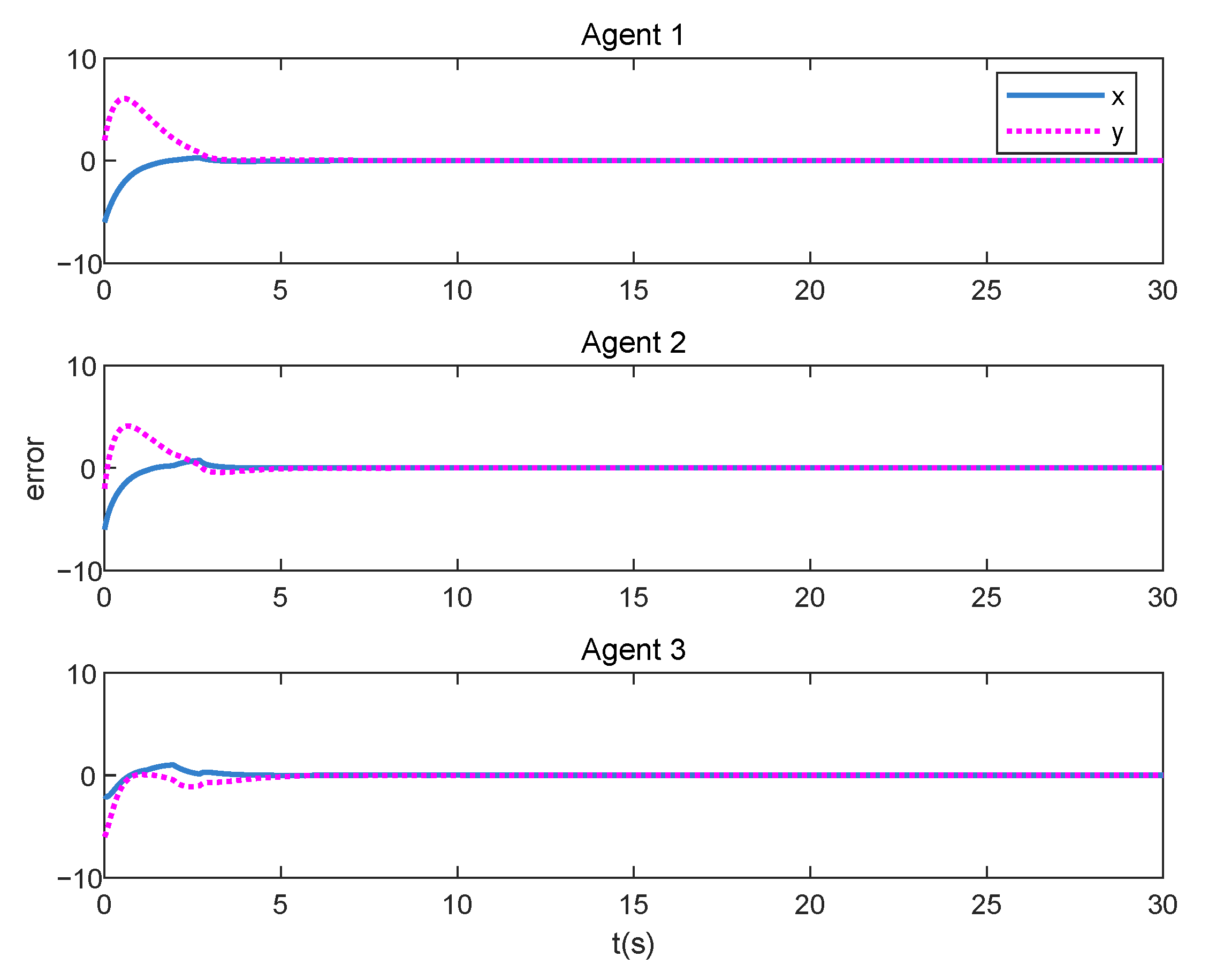
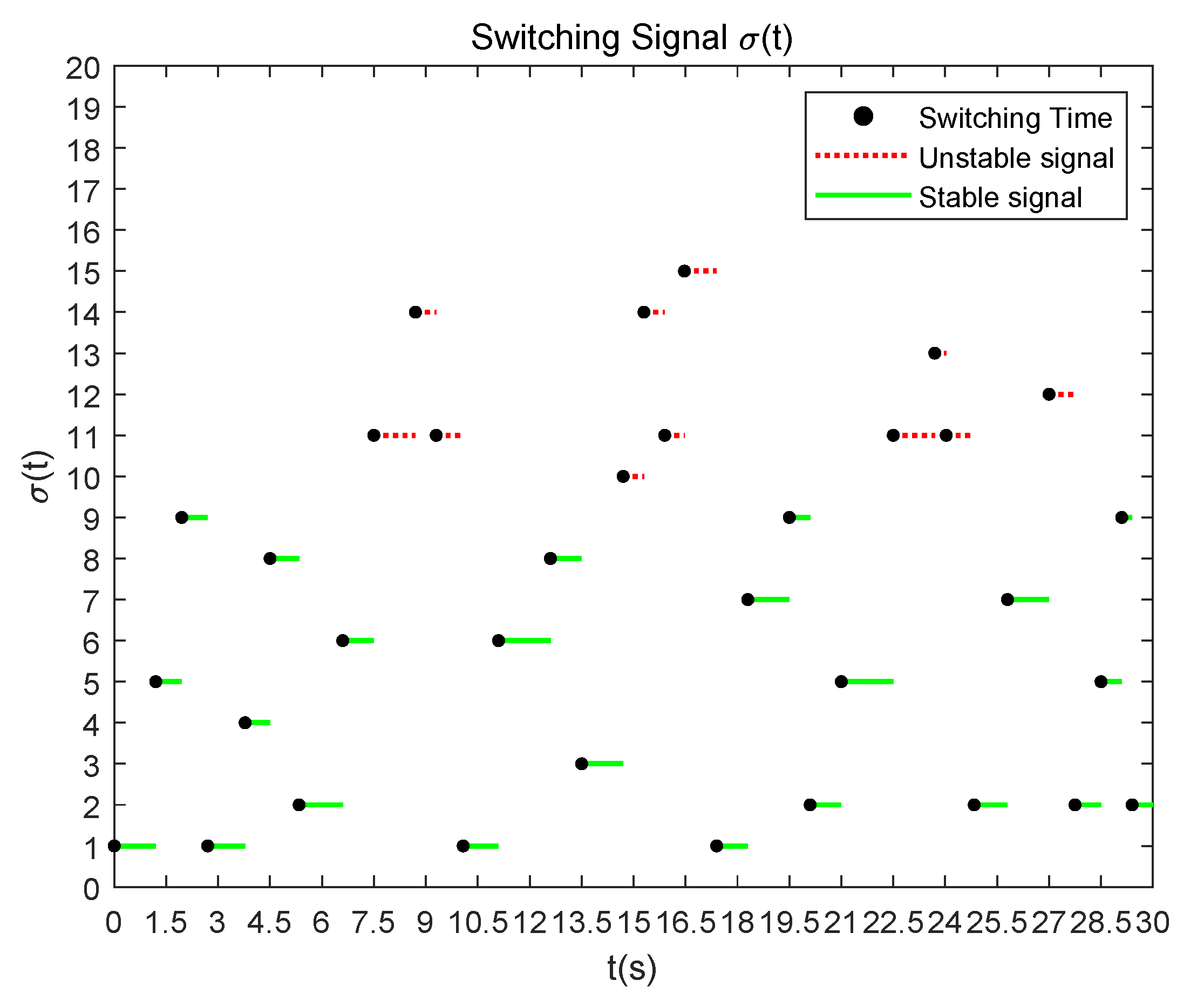
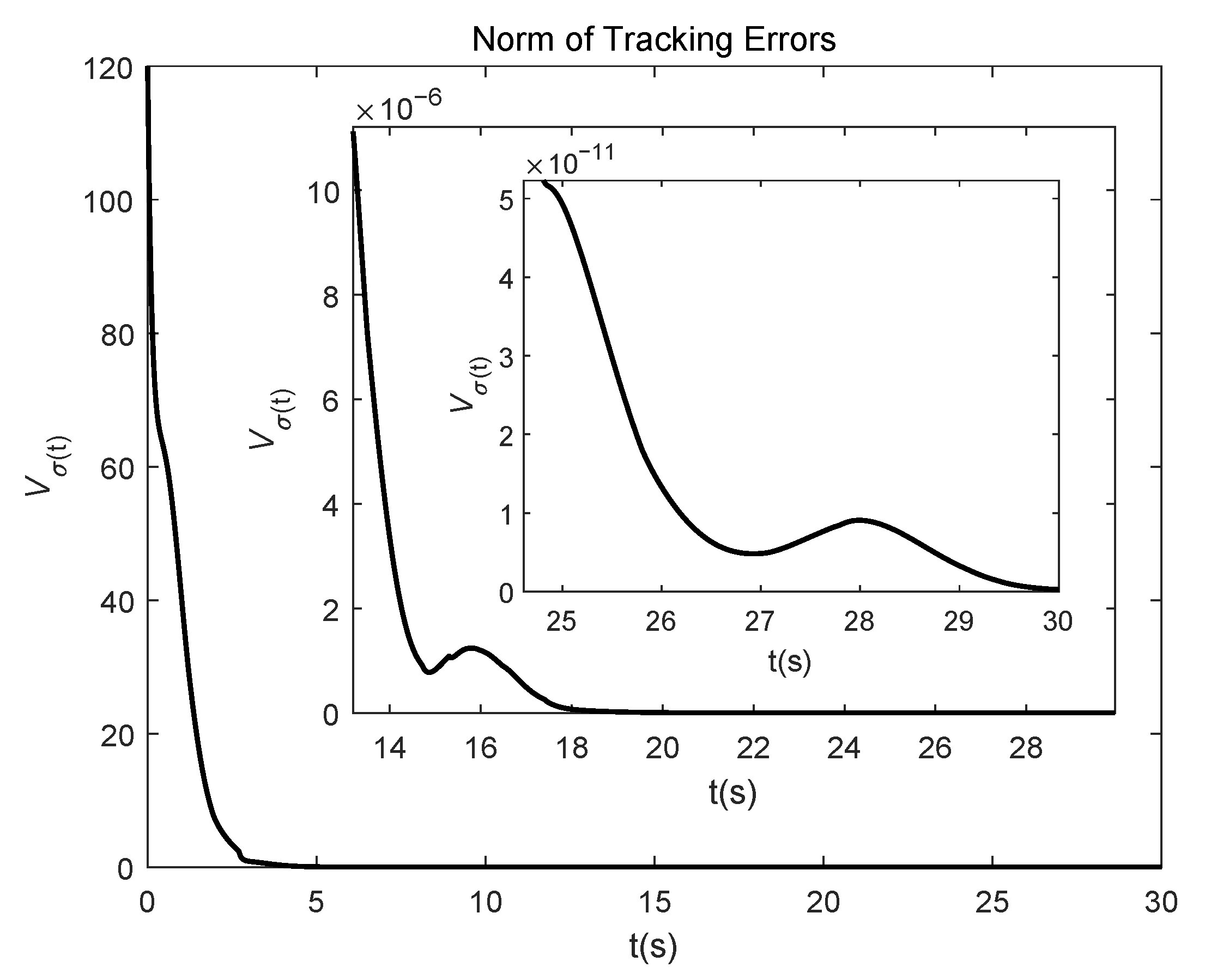
4. A Numerical Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MASs | Multi-agent Systems |
| QCSS | Quasi-cyclic Switching Signals |
| QCST | Quasi-cyclic Switching Topologies |
References
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep Reinforcement Learning for Multiagent Systems: A Review of Challenges, Solutions, and Applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef] [PubMed]
- Dorri, A.; Kanhere, S.S.; Jurdak, R. Multi-Agent Systems: A Survey. IEEE Access 2018, 6, 28573–28593. [Google Scholar] [CrossRef]
- Kamdar, R.; Paliwal, P.; Kumar, Y. A State of Art Review on Various Aspects of Multi-Agent System. J. Circuits Syst. Comput. 2018, 27, 1830006. [Google Scholar] [CrossRef]
- Qin, J.; Ma, Q.; Yang, S.; Long, W. Recent Advances in Consensus of Multi-Agent Systems: A Brief Survey. IEEE Trans. Ind. Electron. 2017, 64, 4972–4983. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, J.; Zhang, D.; Shao, X. Fault-tolerant Adaptive Finite-time Attitude Synchronization and Tracking Control for Multi-spacecraft Formation. Aerosp. Sci. Technol. 2018, 73, 197–209. [Google Scholar] [CrossRef]
- Cardona, G.A.; Calderon, J.M. Robot Swarm Navigation and Victim Detection Using Rendezvous Consensus in Search and Rescue Operations. Appl. Sci. 2019, 9, 1702. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Kim, H.; Shin, J.U.; Myung, H. An Extended Any-angle Path Planning Algorithm for Maintaining Formation of Multi-agent Jellyfish Elimination Robot System. Int. J. Control Autom. Syst. 2016, 14, 598–607. [Google Scholar] [CrossRef]
- Kim, J. Cooperative Localization and Unknown Currents Estimation Using Multiple Autonomous Underwater Vehicles. IEEE Robot. Autom. Lett. 2020, 5, 2365–2371. [Google Scholar] [CrossRef]
- Pantelimon, G.; Tepe, K.; Carriveau, R.; Ahmed, S. Survey of Multi-agent Communication Strategies for Information Exchange and Mission Control of Drone Deployments. J. Intell. Robot. Syst. 2019, 95, 779–788. [Google Scholar] [CrossRef]
- Adamey, E.; Oguz, A.E.; Ozguner, U. Collaborative Multi-MSA Multi-Target Tracking and Surveillance: A Divide & Conquer Method Using Region Allocation Trees. J. Intell. Robot. Syst. 2017, 87, 471–485. [Google Scholar]
- Polyakov, I.; Shvets, E. Algorithm for Covert Convoy of a Moving Target Using a Group of Autonomous Robots. In Proceedings of the Tenth International Conference on Machine Vision (ICMV), Vienna, Austria, 13–15 November 2017; pp. 119–127. [Google Scholar]
- Hasan, Y.A.; Garg, A.; Sugaya, S.; Tapia, L. Defensive Escort Teams for Navigation in Crowds via Multi-Agent Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 5645–5652. [Google Scholar] [CrossRef]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An Overview of Recent Progress in the Study of Distributed Multi-Agent Coordination. IEEE Trans. Ind. Inf. 2013, 9, 427–438. [Google Scholar] [CrossRef]
- Dong, X.; Yan, Z.; Zhang, R.; Zhong, Y. Time-varying Formation Tracking for Second-order Multi-agent Systems Subjected to Switching Topologies with Application to Quadrotor Formation Flying. IEEE Trans. Ind. Electron. 2017, 64, 5014–5024. [Google Scholar] [CrossRef]
- Wang, Y.; Long, C.; Wei, R.; Hou, Z.G.; Min, T. Seeking Consensus in Networks of Linear Agents: Communication Noises and Markovian Switching Topologies. IEEE Trans. Autom. Control 2015, 60, 1374–1379. [Google Scholar] [CrossRef]
- Chen, M.Z.Q.; Su, H. Multi-agent Containment Control with Input Saturation on Switching Topologies. IET Control Theory Appl. 2015, 9, 399–409. [Google Scholar]
- Mu, C.; Zhao, Q.; Sun, C. Optimal Model-Free Output Synchronization of Heterogeneous Multiagent Systems Under Switching Topologies. IEEE Trans. Ind. Electron. 2020, 67, 10951–10964. [Google Scholar] [CrossRef]
- Zhu, J.W.; Yang, Y.P.; Zhang, W.A.; Yu, L.; Wang, X. Cooperative Attack Tolerant Tracking Control for Multi-agent System with a Resilient Switching Scheme. Neurocomputing 2020, 409, 372–380. [Google Scholar] [CrossRef]
- Luo, Z.; Xiong, W.; He, W. Observer-based State Tracking for Discrete Linear Multi-agent Systems with Switching Topologies via Learning Control Strategies. IET Control Theory Appl. 2020, 14, 1639–1647. [Google Scholar] [CrossRef]
- Tanner, H.G.; Jadbabaie, A. Flocking in Fixed and Switching Networks. IEEE Trans. Autom. Control 2007, 52, 863–868. [Google Scholar] [CrossRef]
- Yu, D.; Chen, C.L.P. Automatic Leader–Follower Persistent Formation Generation with Minimum Agent-Movement in Various Switching Topologies. IEEE Trans. Cybern. 2020, 50, 1569–1581. [Google Scholar] [CrossRef]
- Xie, D.; Xu, S.; Chu, Y.; Zou, Y. Event-triggered Average Consensus for Multi-agent Systems with Nonlinear Dynamics and Switching topology. J. Frankl. Inst. 2014, 352, 1080–1098. [Google Scholar] [CrossRef]
- Wu, X.; Tang, Y.; Cao, J.; Zhang, W. Distributed Consensus of Stochastic Delayed Multi-agent Systems under Asynchronous Switching. IEEE Trans. Cybern. 2016, 46, 1817–1827. [Google Scholar] [CrossRef]
- Liu, K.; Ji, Z.; Xie, G.; Long, W. Consensus for Heterogeneous Multi-agent Systems under Fixed and Switching Topologies. J. Frankl. Inst. 2015, 352, 3670–3683. [Google Scholar] [CrossRef]
- Xi, J.; Fan, Z.; Hao, L.; Tang, Z. Guaranteed-cost Consensus for Multiagent Networks with Lipschitz Nonlinear Dynamics and Switching Topologies. Int. J. Robust Nonlinear Control 2018, 28, 2841–2852. [Google Scholar] [CrossRef]
- Hao, Z.; Yang, R.; Yan, H.; Yang, F. H∞ Consensus of Event-based Multi-agent Systems with Switching Topology. Inf. Sci. 2016, 370, 623–635. [Google Scholar]
- Meng, D.; Jia, Y.; Du, J. Robust Consensus Tracking Control for Multiagent Systems with Initial State Shifts, Disturbances, and Switching Topologies. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 809–824. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Chen, G. Consensus Tracking of Multi-Agent Systems with Lipschitz-type Node Dynamics and Switching Topologies. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 499–511. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Zhang, K.; Liang, Y. Distributed Leader-following Consensus of Heterogeneous Second-order Time-varying Nonlinear Multi-agent Systems under Directed Switching Topology. Neurocomputing 2019, 325, 31–47. [Google Scholar] [CrossRef]
- Meng, D.; Moore, K.L. Learning to Cooperate: Networks of Formation Agents with Switching Topologies. Automatica 2016, 64, 278–293. [Google Scholar] [CrossRef]
- Liu, B.; Su, H.; Li, R.; Sun, D.; Hu, W. Switching Controllability of Discrete-time Multi-agent Systems with Multiple Leaders and Time-delays. Appl. Math. Comput. 2014, 228, 571–588. [Google Scholar] [CrossRef]
- Han, F.; Gao, L.; Yang, H. Sampling Control on Collaborative Flocking Motion of Discrete-time System with Time-delays. Neurocomputing 2016, 216, 242–249. [Google Scholar]
- Yan, Y.; Huang, J. Cooperative Output Regulation of Discrete-time Linear Time-delay Multi-agent Systems under Switching Network. Neurocomputing 2017, 241, 108–114. [Google Scholar] [CrossRef]
- Dong, L.; Chai, S.; Zhang, B.; Nguang, S.K.; Savvaris, A. Stability of a Class of Multiagent Tracking Systems with Unstable Subsystems. IEEE Trans. Cybern. 2017, 47, 2193–2202. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, B.; Zhao, J. On Finite-Time Stability of Cyclic Switched Nonlinear Systems. IEEE Trans. Autom. Control 2015, 60, 2201–2206. [Google Scholar] [CrossRef]
- Wu, Z.G.; Yong, X.; Lu, R.; Wu, Y.; Huang, T. Event-Triggered Control for Consensus of Multiagent Systems with Fixed/Switching Topologies. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1736–1746. [Google Scholar] [CrossRef]
- Dong, L. A Class of Cooperative Relay Analysis of Multi-agent Systems with Tracking Number Switching and Time Delays. ISA Trans. 2019, 90, 138–146. [Google Scholar] [CrossRef]
- Yu, Q.; Wu, B. Robust Stability Analysis of Uncertain Switched Linear Systems with Unstable Subsystems. Int. J. Syst. Sci. 2015, 46, 1278–1287. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.P. Distributed Formation Control of Nonholonomic Mobile Robots without Global Position Measurements. Automatica 2013, 49, 592–600. [Google Scholar] [CrossRef]
- Zhang, X.; Han, W.; Liu, X. Bipartite Tracking Consensus of Linear Multi-agent Systems with a Dynamic Leader under Signed Digraph. IET Control Theory Appl. 2020, 14, 2127–2133. [Google Scholar] [CrossRef]
- Zhang, J.; Lyu, M.; Shen, T.; Liu, L.; Bo, Y. Sliding Mode Control for a Class of Nonlinear Multi-agent System with Time Delay and Uncertainties. IEEE Trans. Ind. Electron. 2018, 65, 865–875. [Google Scholar] [CrossRef]

| Symbol | Description |
|---|---|
| state vector of the i-th agent | |
| control input of the i-th tracking agent | |
| switching signal | |
| period length of stable subsystems | |
| period length of unstable subsystems | |
| tracking error between the i-th and the j-th tracking agent | |
| tracking error between the i-th tracking agent and the target agent | |
| the set of stable subsystems in the quasi-cyclic switching process | |
| the set of unstable subsystems in the quasi-cyclic switching process |
| Stable Subsystems | Unstable Subsystems | |||||
|---|---|---|---|---|---|---|
| ... | ... | |||||
| ⋮ | ⋮ | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, D.; Shen, H.; Dong, L. Stability Analysis of Multi-Agent Tracking Systems with Quasi-Cyclic Switching Topologies. Appl. Sci. 2020, 10, 8889. https://doi.org/10.3390/app10248889
Fan D, Shen H, Dong L. Stability Analysis of Multi-Agent Tracking Systems with Quasi-Cyclic Switching Topologies. Applied Sciences. 2020; 10(24):8889. https://doi.org/10.3390/app10248889
Chicago/Turabian StyleFan, Dongyu, Haikuo Shen, and Lijing Dong. 2020. "Stability Analysis of Multi-Agent Tracking Systems with Quasi-Cyclic Switching Topologies" Applied Sciences 10, no. 24: 8889. https://doi.org/10.3390/app10248889
APA StyleFan, D., Shen, H., & Dong, L. (2020). Stability Analysis of Multi-Agent Tracking Systems with Quasi-Cyclic Switching Topologies. Applied Sciences, 10(24), 8889. https://doi.org/10.3390/app10248889





