Solving Order Planning Problem Using a Heuristic Approach: The Case in a Building Material Distributor
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Response Surface Methodology (RSM)
3.2. A Computational Framework
4. A Case Study
4.1. Problem Description
4.2. Numerical Example
5. Empirical Results
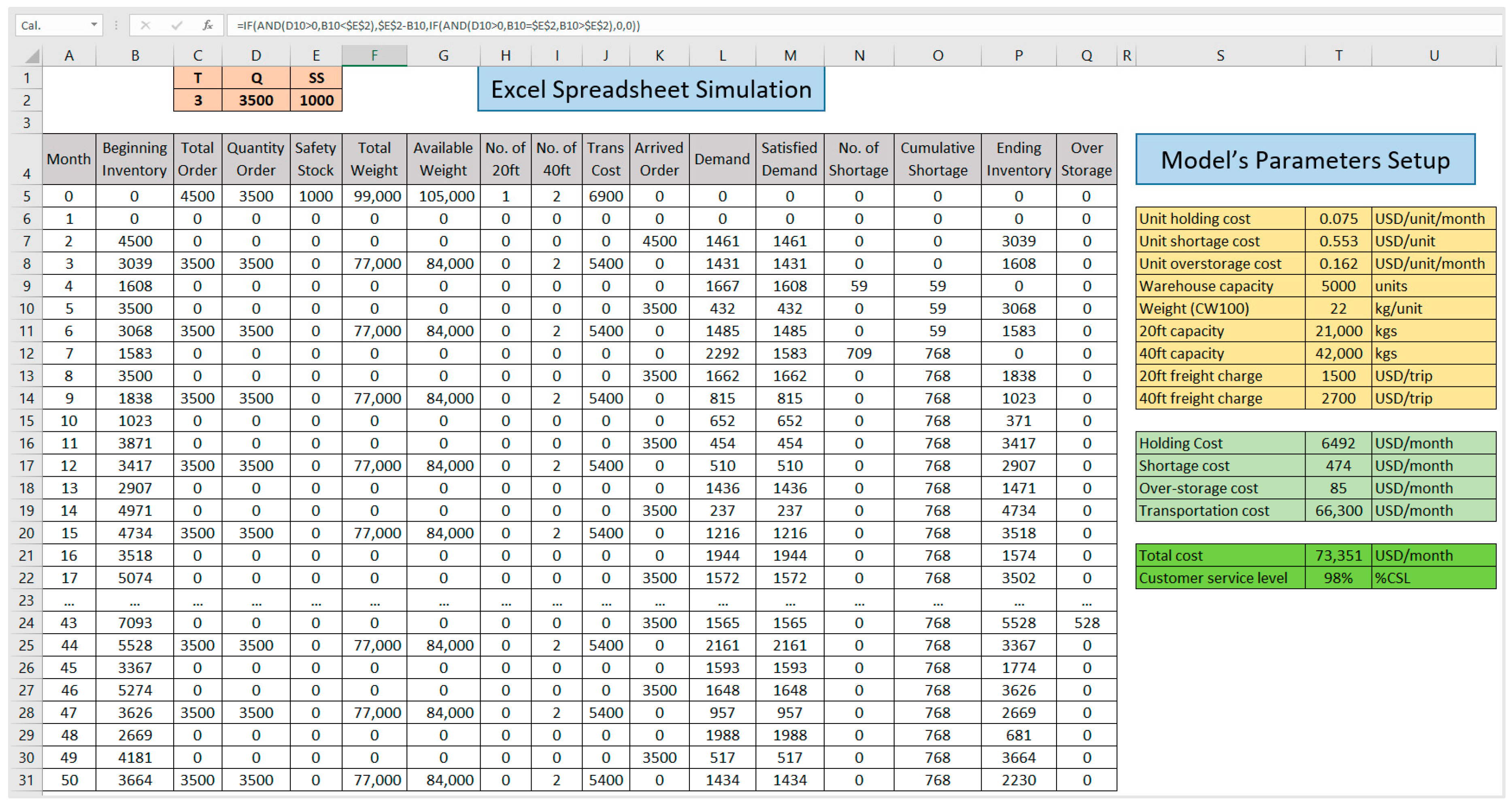
5.1. Excel Spreadsheet Simulation
- Unit holding cost, Ch = 0.075 USD/unit/month;
- Unit shortage cost, Cs = 0.553 USD/unit;
- Unit over-storage cost, Co = 0.162 USD/unit/month;
- Warehouse capacity = 5000 units;
- Weight (CW100) = 22 kg/unit;
- Maximum capacity of container type 20 ft = 21,000 kg;
- Maximum capacity of container type 40 ft = 42,000 kg;
- Freight charge of container type 2 0ft = 1500 USD/trip;
- Freight charge of container type 40 ft = 2700 USD/trip.
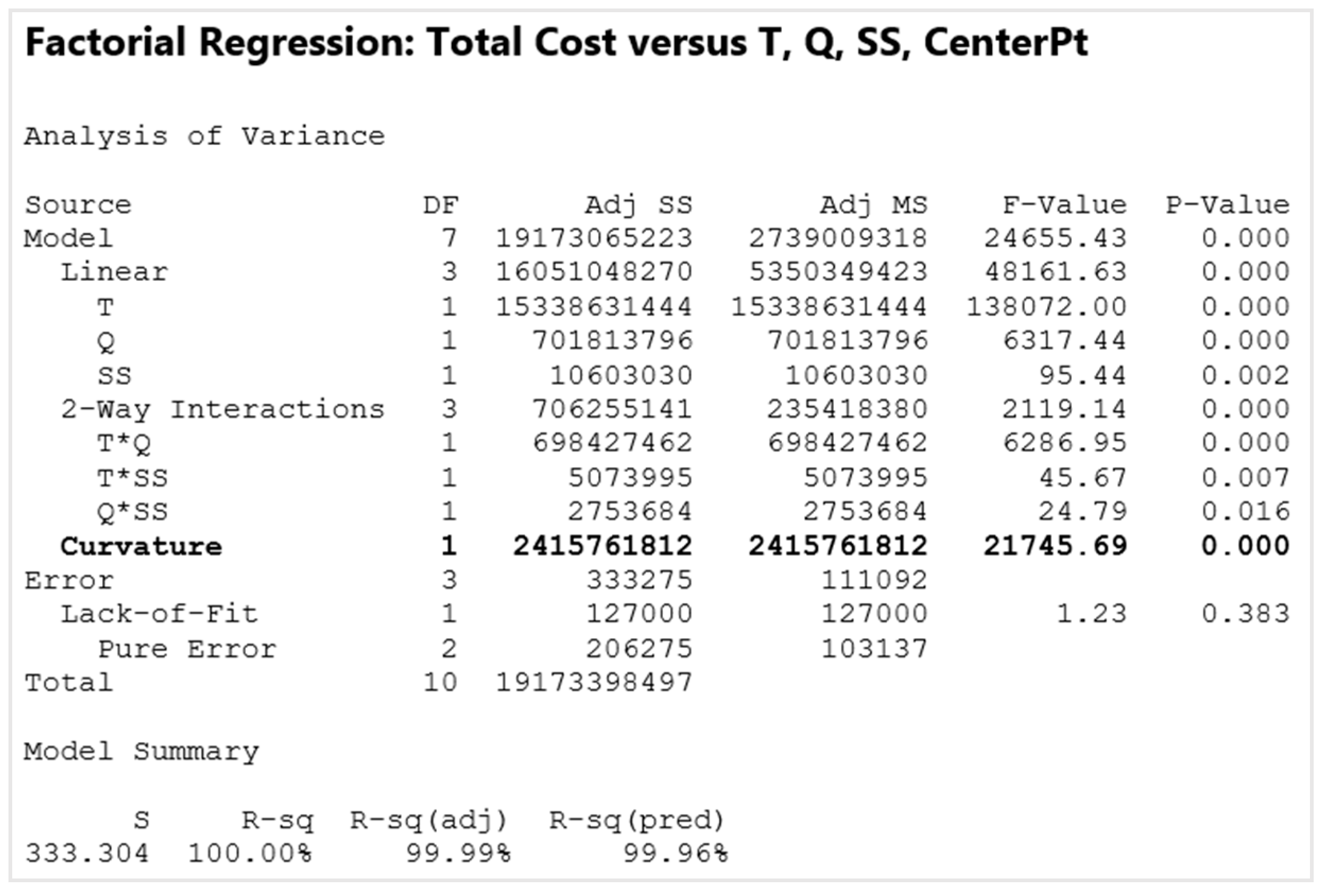
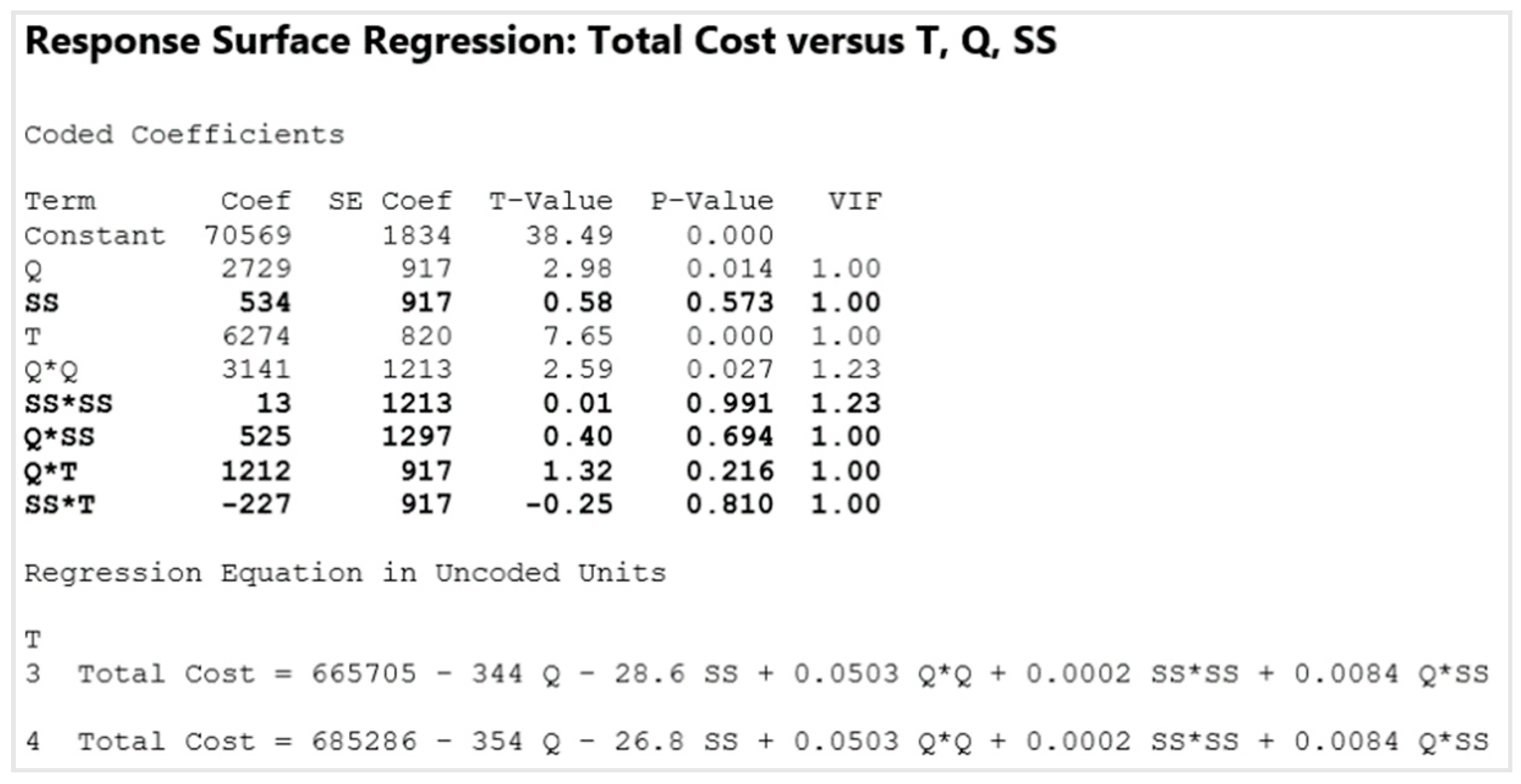
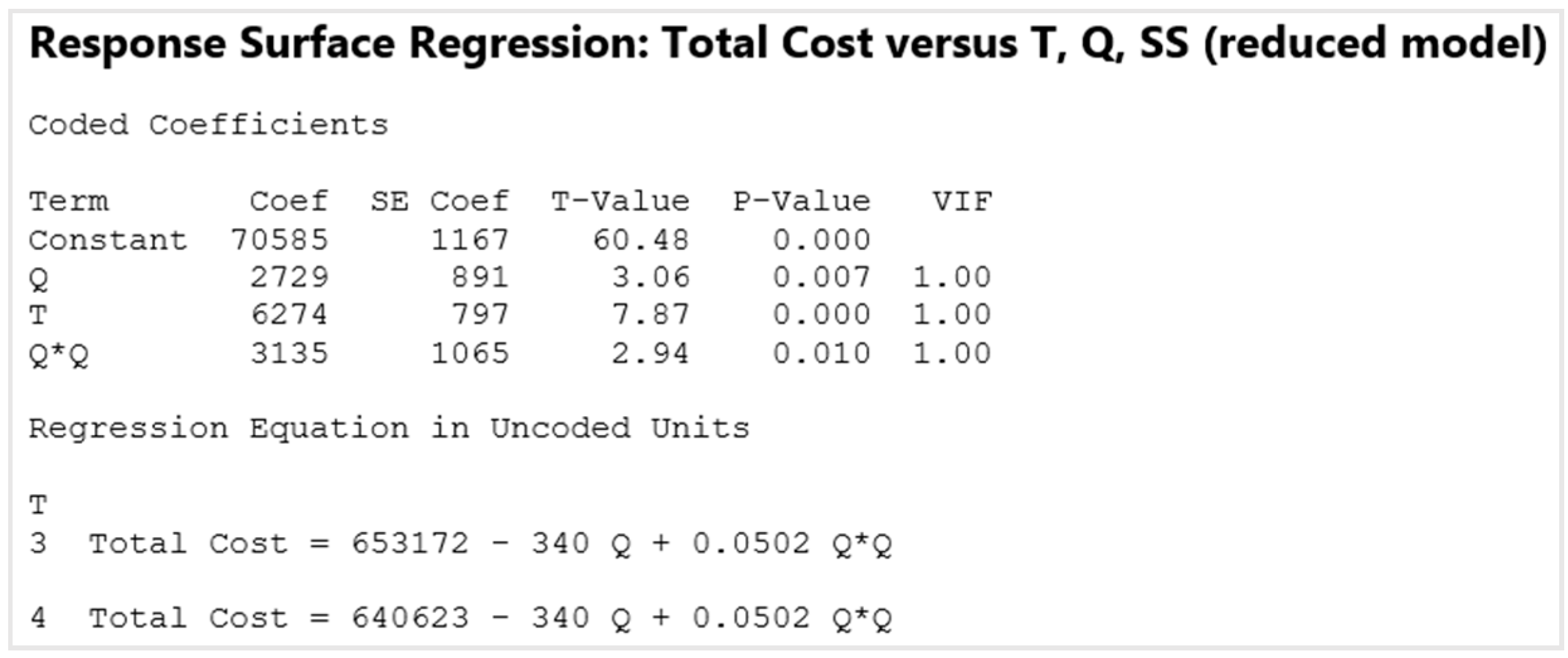
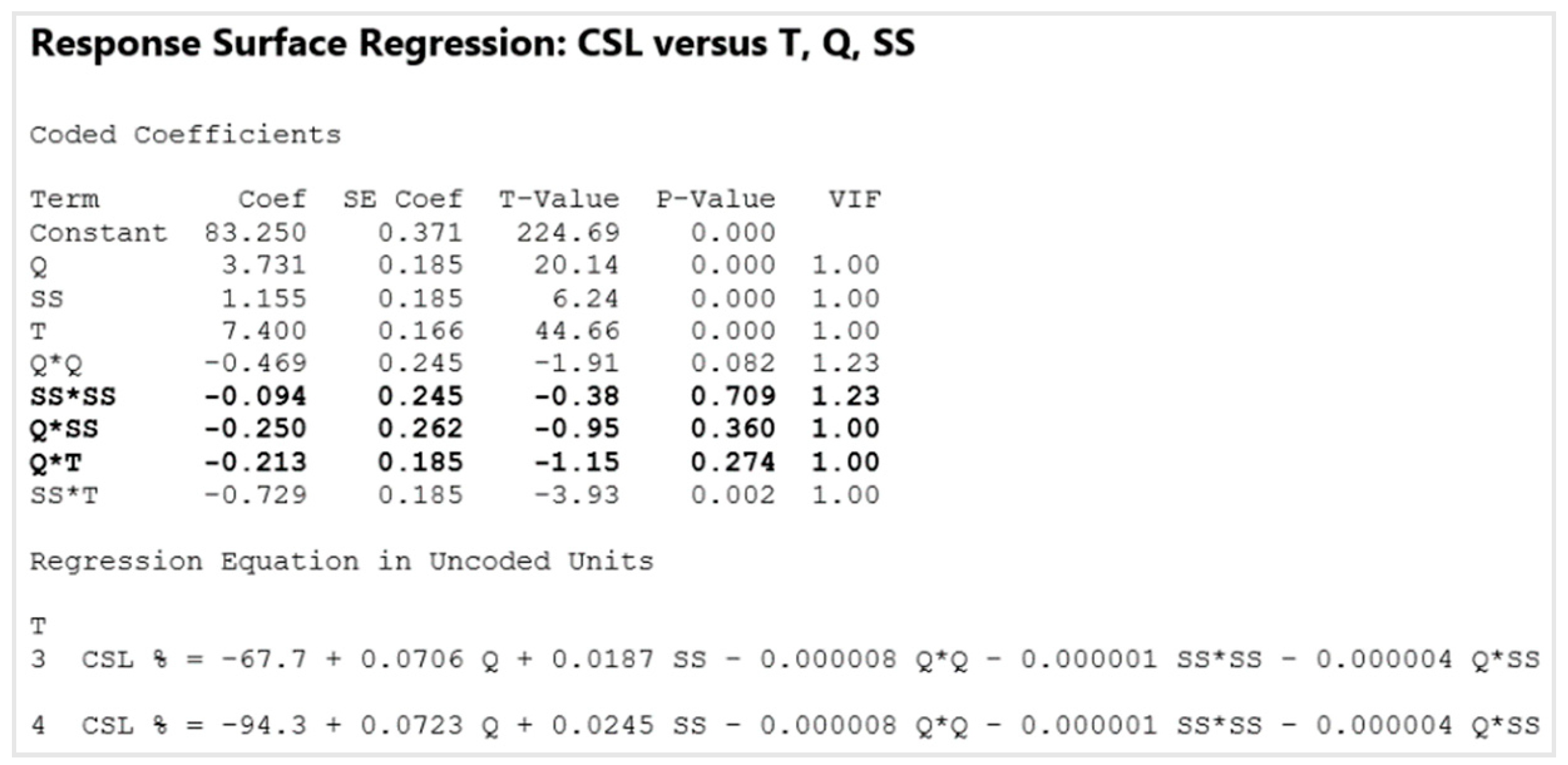
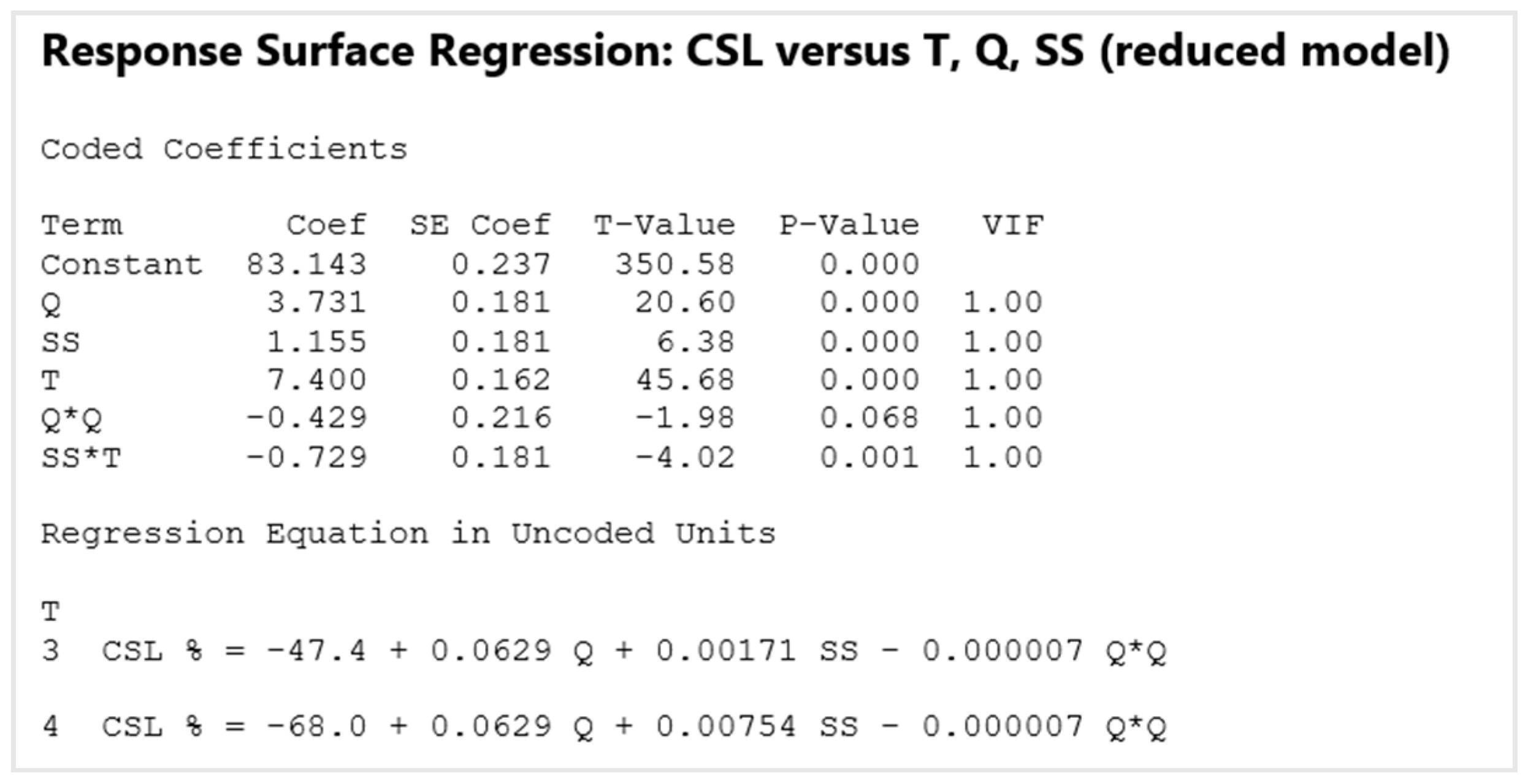
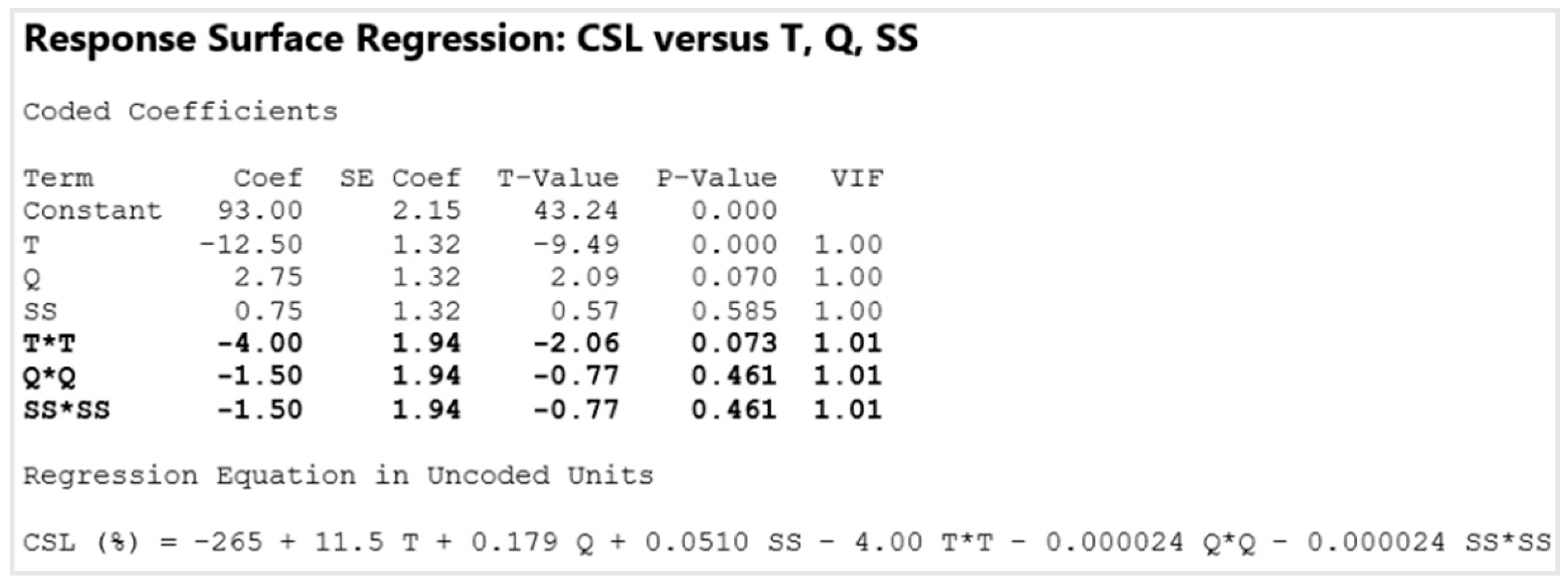
5.2. Statistical Analysis
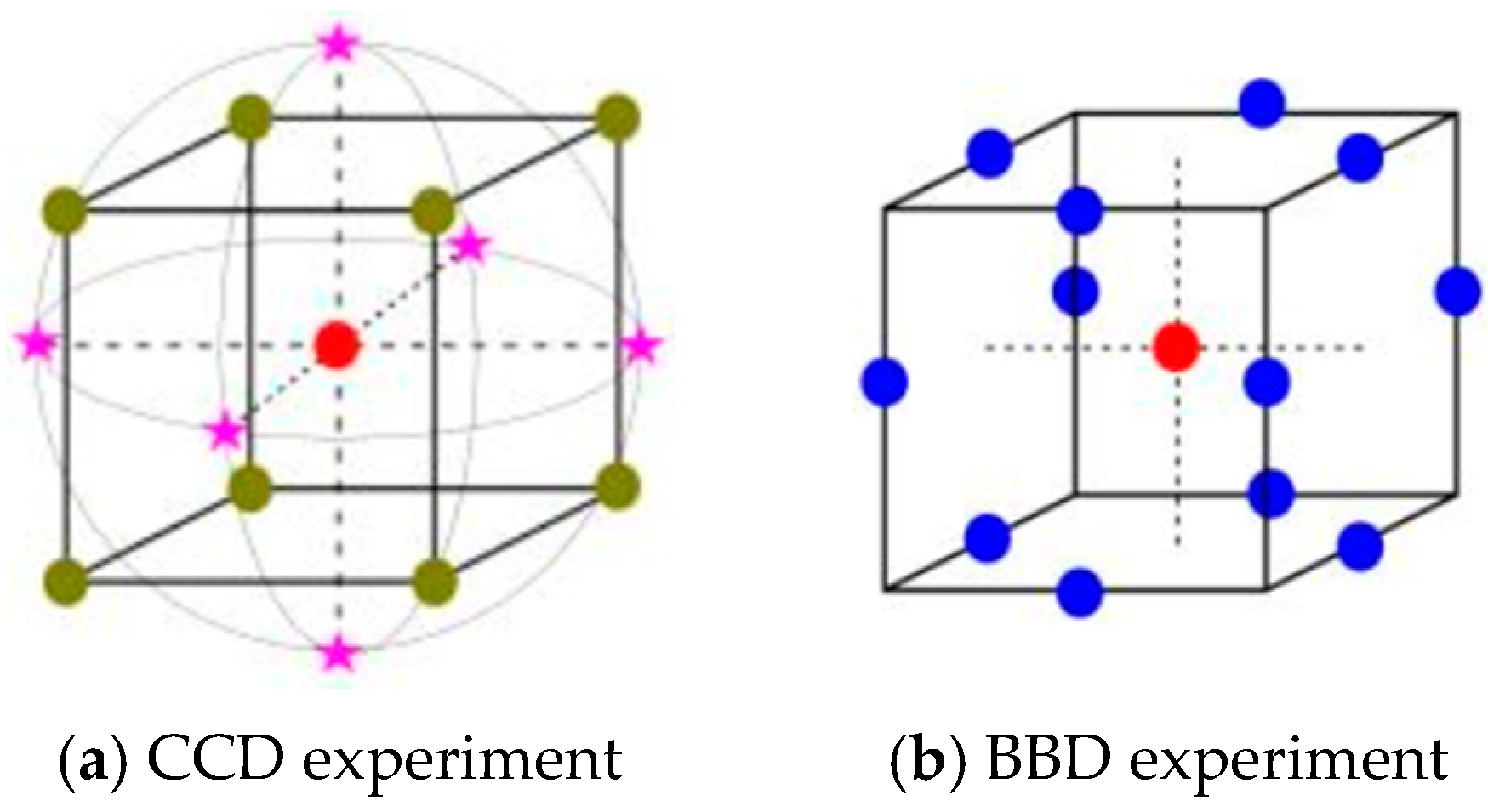
5.3. Central Composite Design (CCD)
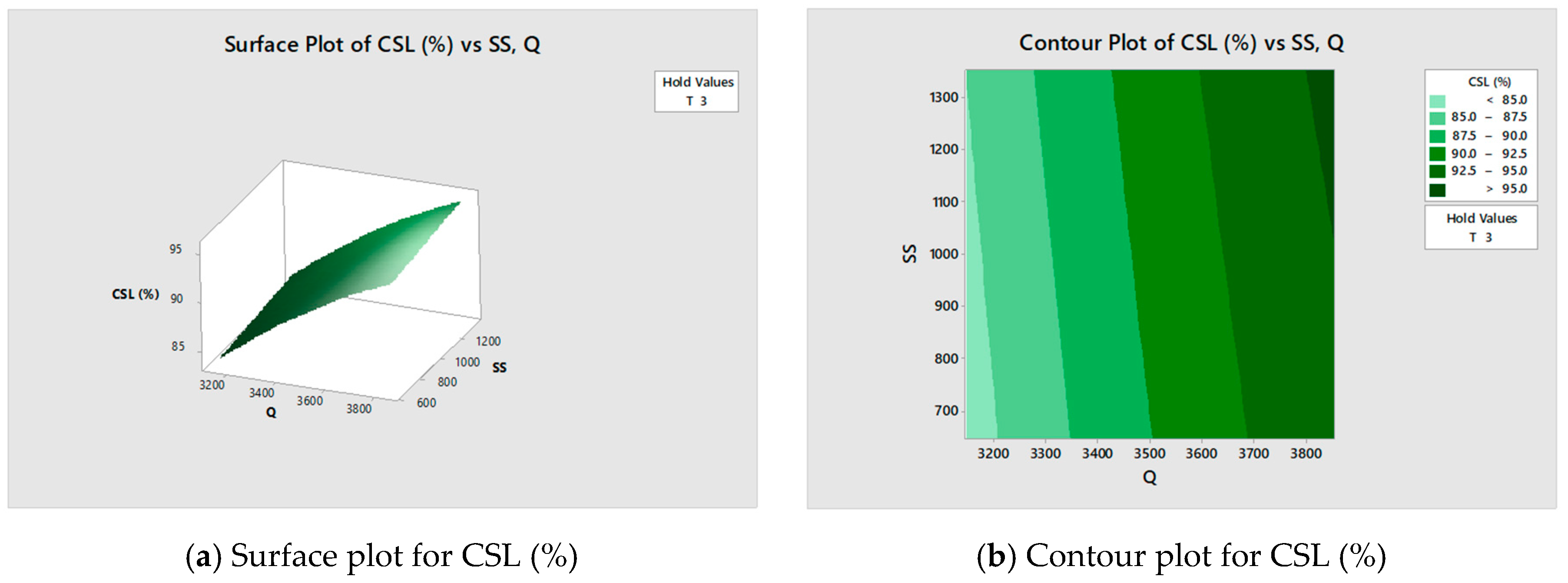
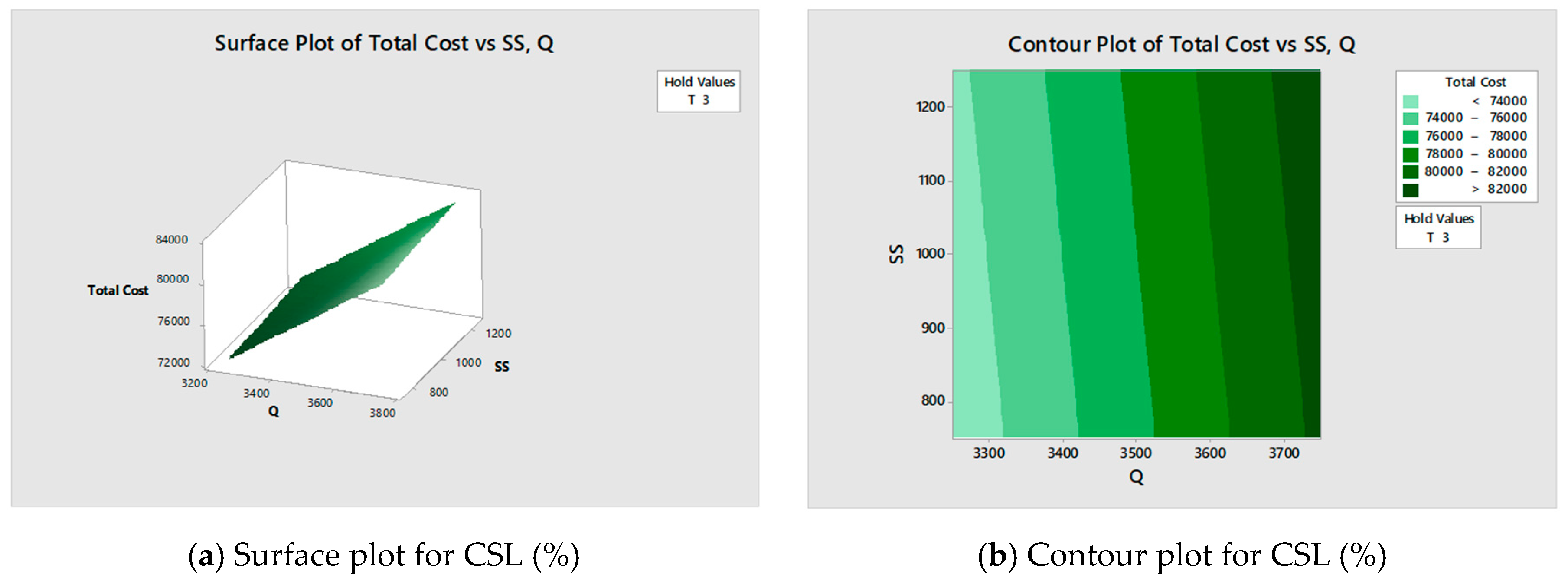
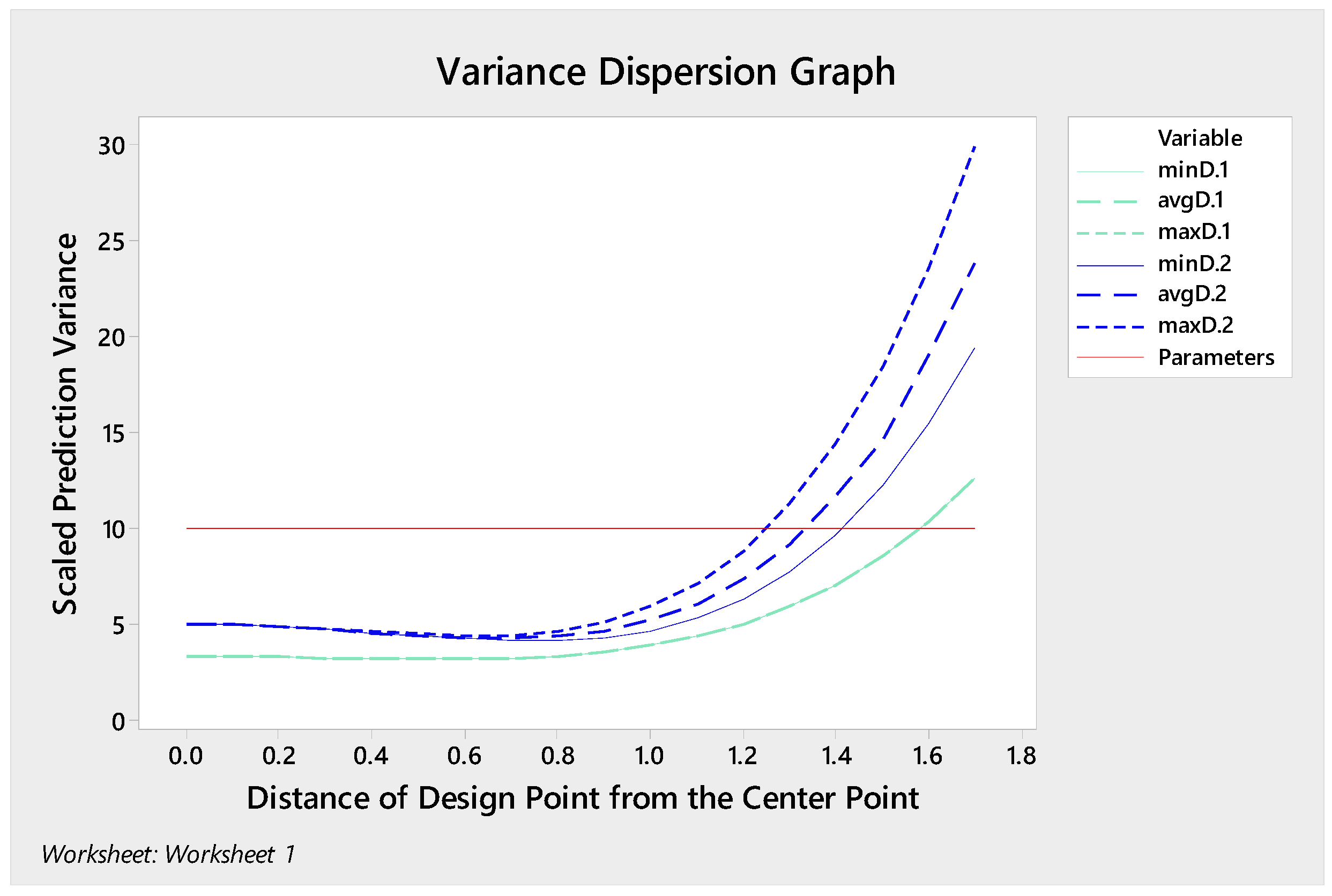
5.4. Box–Behnken Design (BBD)
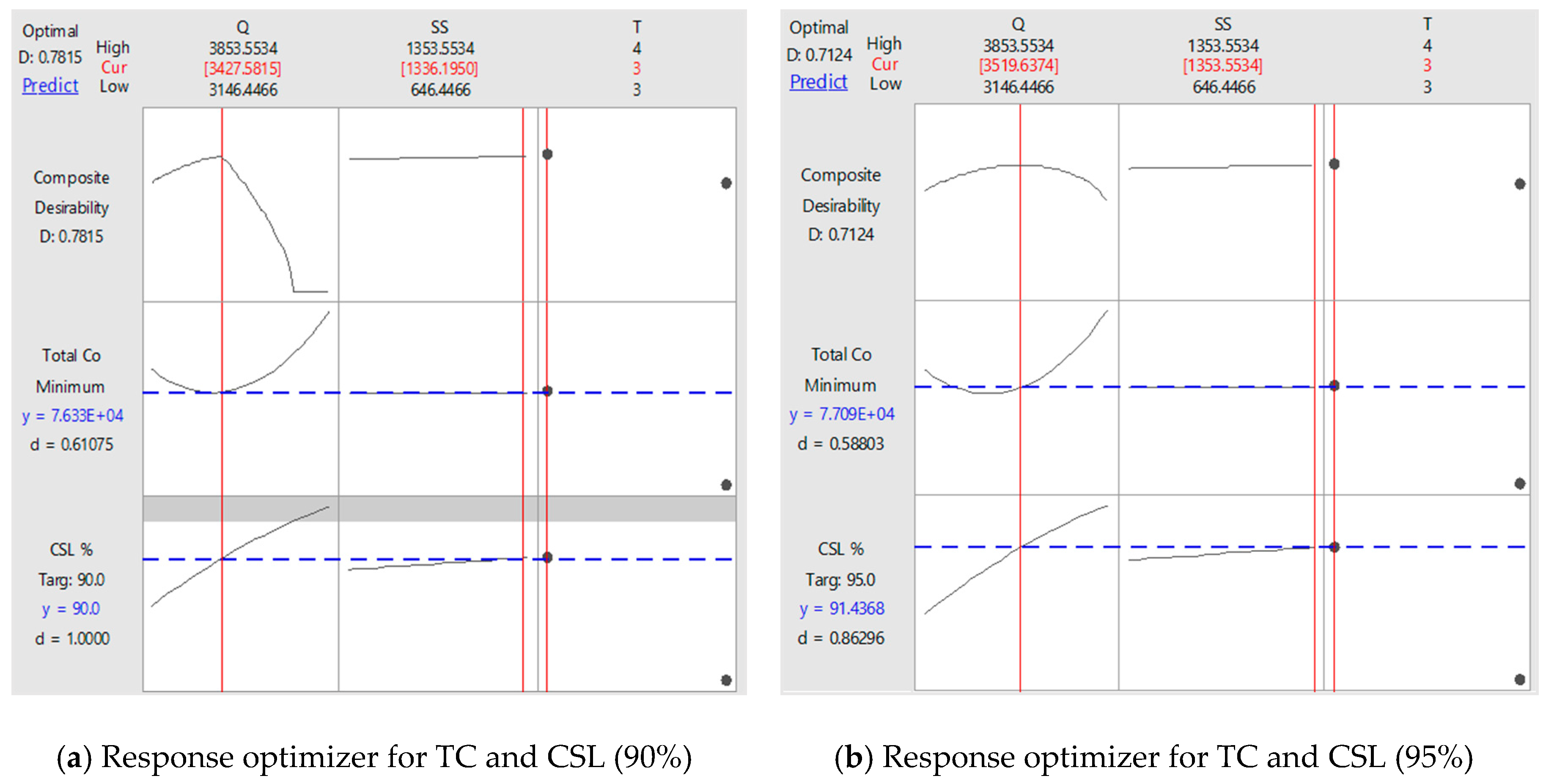
5.5. The Comparision of the CCD and BBD Experiment
6. Discussions and Conclusions
- Central composite design (CCD), customer service level CSL was at 90%, the minimum total cost was 76,330 with the possible optimal settings were the time period (T) = 3, order quantity (Q) = 3428, safety stock (SS) = 1336; (2) customer service level CSL was at 95%, the minimum total cost was 77,090 with the possible optimal settings were T = 3, Q = 3520, and SS = 1354.
- Box–Behnken design (BBD), customer service level CSL was at 90%, the minimum total cost was 70,870 with the possible optimal settings were the time period (T) = 3, order quantity (Q) = 3603, and safety stock (SS) = 1250; (2) customer service level CSL was at 95%, the minimum total cost was 85,920 with the possible optimal settings were T = 3, Q = 3690, and SS = 1250.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Designing Building Wiki. Supply Chain Management in Construction. Available online: https://www.designingbuildings.co.uk/wiki/Supply_chain_management_in_construction#The_need_for_SCM_in_construction (accessed on 31 November 2020).
- Right Place, Right Time: The Importance of Order-Slotting Solutions. Available online: https://blog.flexis.com/right-place-right-time-the-importance-of-order-slotting-solutions (accessed on 31 November 2020).
- Cavalcante, C.A. Order planning policies for business-to-consumer e-tail stores. Comput. Ind. Eng. 2019, 136, 106–116. [Google Scholar]
- Chien, C.F.; Lin, Y.S.; Lin, S.K. Deep reinforcement learning for selecting demand forecast models to empower Industry 3.5 and an empirical study for a semiconductor component distributor. Int. J. Prod. Res. 2020, 58, 2784–2804. [Google Scholar] [CrossRef]
- Geunes, J.; Akçali, E.; Pardalos, P.M.; Romeijn, H.E.; Shen, Z.J.M. (Eds.) Applications of Supply Chain Management and e-Commerce Research; Springer Science & Business Media: Berlin, Germany, 2006; Volume 92. [Google Scholar]
- Partovi, F.Y.; Anandarajan, M. Classifying inventory using an artificial neural network approach. Comput. Ind. Eng. 2002, 41, 389–404. [Google Scholar] [CrossRef]
- Yao, X.; Huang, R.; Song, M.; Mishra, N. Pre-positioning inventory and service outsourcing of relief material supply chain. Int. J. Prod. Res. 2018, 56, 6859–6871. [Google Scholar] [CrossRef]
- Diabat, A.; Abdallah, T.; Le, T. A hybrid tabu search based heuristic for the periodic distribution inventory problem with perishable goods. Ann. Oper. Res. 2016, 242, 373–398. [Google Scholar] [CrossRef]
- Diabat, A.; Deskoores, R. A hybrid genetic algorithm based heuristic for an integrated supply chain problem. J. Manuf. Syst. 2016, 38, 172–180. [Google Scholar] [CrossRef]
- Clark, A.J.; Scarf, H. Optimal policies for a multi-echelon inventory problem. Manag. Sci. 1960, 6, 475–490. [Google Scholar] [CrossRef]
- Gharaei, A.; Pasandideh, S.H.R.; Khamseh, A.A. Inventory model in a four-echelon integrated supply chain: Modeling and optimization. J. Model. Manag. 2017, 12, 739–762. [Google Scholar] [CrossRef]
- Hoseini Shekarabi, S.A.; Gharaei, A.; Karimi, M. Modelling and optimal lot-sizing of integrated multi-level multi-wholesaler supply chains under the shortage and limited warehouse space: Generalised outer approximation. Int. J. Syst. Sci. Oper. Logist. 2019, 6, 237–257. [Google Scholar] [CrossRef]
- Ben-Daya, M.; Hariga, M. Integrated single vendor single buyer model with stochastic demand and variable lead time. Int. J. Prod. Econ. 2004, 92, 75–80. [Google Scholar] [CrossRef]
- Jauhari, W.A.; Laksono, P.W. A joint economic lot-sizing problem with fuzzy demand, defective items and environmental impacts. Mater. Sci. Eng. 2017, 273, 12–18. [Google Scholar] [CrossRef]
- Kao, C.; Hsu, W.K. A single-period inventory model with fuzzy demand. Comput. Math. Appl. 2002, 43, 841–848. [Google Scholar] [CrossRef] [Green Version]
- Kim, G.; Wu, K.; Huang, E. Optimal inventory control in a multi-period newsvendor problem with non-stationary demand. Adv. Eng. Inform. 2015, 29, 139–145. [Google Scholar] [CrossRef]
- Modak, N.M.; Panda, S.; Sana, S.S.; Basu, M. Corporate social responsibility, coordination and profit distribution in a dual-channel supply chain. Pac. Sci. Rev. 2014, 16, 235–249. [Google Scholar] [CrossRef] [Green Version]
- Modak, N.M.; Panda, S.; Sana, S.S. Pricing policy and coordination for a two-layer supply chain of duopolistic retailers and socially responsible manufacturer. Int. J. Logist. Res. Appl. 2016, 19, 487–508. [Google Scholar] [CrossRef]
- Modak, N.M.; Panda, S.; Sana, S.S. Pricing policy and coordination for a distribution channel with manufacturer suggested retail price. Int. J. Syst. Sci. Oper. Logist. 2016, 3, 92–101. [Google Scholar] [CrossRef]
- Modak, N.M.; Panda, S.; Sana, S.S. Three-echelon supply chain coordination considering duopolistic retailers with perfect quality products. Int. J. Prod. Econ. 2016, 182, 564–578. [Google Scholar] [CrossRef]
- Modak, N.M.; Panda, S.; Sana, S.S. Two-echelon supply chain coordination among manufacturer and duopolies retailers with recycling facility. Int. J. Adv. Manuf. Technol. 2016, 87, 1531–1546. [Google Scholar] [CrossRef]
- Modak, N.M.; Modak, N.; Panda, S.; Sana, S.S. Analyzing structure of two-echelon closed-loop supply chain for pricing, quality and recycling management. J. Clean. Prod. 2018, 171, 512–528. [Google Scholar] [CrossRef]
- Wang, C.-N.; Dang, T.-T.; Le, T.Q.; Kewcharoenwong, P. Transportation Optimization Models for Intermodal Networks with Fuzzy Node Capacity, Detour Factor, and Vehicle Utilization Constraints. Mathematics 2020, 8, 2109. [Google Scholar] [CrossRef]
- Chilmon, B.; Tipi, N.S. Modelling and simulation considerations for an end-to-end supply chain system. Comput. Ind. Eng. 2020, 150, 106870. [Google Scholar] [CrossRef]
- Tordecilla, R.D.; Juan, A.A.; Montoya-Torres, J.R.; Quintero-Araujo, C.L.; Panadero, J. Simulation-optimization methods for designing and assessing resilient supply chain networks under uncertainty scenarios: A review. Simul. Model. Pract. Theory 2020, 106, 102166. [Google Scholar] [CrossRef]
- Shaban, A.; Shalaby, M.A. Modeling and optimizing of variance amplification in supply chain using response surface methodology. Comput. Ind. Eng. 2018, 120, 392–400. [Google Scholar] [CrossRef]
- Giddings, A.P.; Bailey, T.G.; Moore, J.T. Optimality analysis of facility location problems using response surface methodology. Int. J. Phys. Distrib. Logist. Manag. 2001, 31, 38–52. [Google Scholar] [CrossRef]
- Shang, J.S.; Li, S.; Tadikamalla, P. Operational design of a supply chain system using the Taguchi method, response surface methodology, simulation, and optimization. Int. J. Prod. Res. 2004, 42, 3823–3849. [Google Scholar] [CrossRef]
- Buchholz, P.; Müller, D.; Thümmler, A. Optimization of process chain models with response surface methodology and the ProC/B toolset. In Supply Chain Management und Logistik; Physica-Verlag HD: Heidelberg, Germany, 2005; pp. 553–575. [Google Scholar]
- Hassanzadeh, A.; Jafarian, A.; Amiri, M. Modeling and analysis of the causes of bullwhip effect in centralized and decentralized supply chain using response surface method. Appl. Math. Model. 2014, 38, 2353–2365. [Google Scholar] [CrossRef]
- Devika, K.; Jafarian, A.; Hassanzadeh, A.; Khodaverdi, R. Optimizing of bullwhip effect and net stock amplification in three-echelon supply chains using evolutionary multi-objective metaheuristics. Ann. Oper. Res. 2016, 242, 457–487. [Google Scholar] [CrossRef]
- Tang, L.; Yang, T.; Ma, Y.; Wang, J. Analysis of bullwhip effect and the robustness of supply chain using a hybrid Taguchi and dual response surface method. In Proceedings of the 2017 International Conference on Service Systems and Service Management, Dalian, China, 16–18 June 2017; pp. 1–6. [Google Scholar]
- Zhang, T.; Zheng, Q.P.; Fang, Y.; Zhang, Y. Multi-level inventory matching and order planning under the hybrid Make-To-Order/Make-To-Stock production environment for steel plants via Particle Swarm Optimization. Comput. Ind. Eng. 2015, 87, 238–249. [Google Scholar] [CrossRef]
- Guo, Z.X.; Yang, C.; Wang, W.; Yang, J. Harmony search-based multi-objective optimization model for multi-site order planning with multiple uncertainties and learning effects. Comput. Ind. Eng. 2015, 83, 74–90. [Google Scholar] [CrossRef]
- Lim, L.L.; Alpan, G.; Penz, B. A simulation-optimization approach for sales and operations planning in build-to-order industries with distant sourcing: Focus on the automotive industry. Comput. Ind. Eng. 2017, 112, 469–482. [Google Scholar] [CrossRef]
- Singha, K.; Buddhakulsomsiri, J.; Parthanadee, P. Mathematical model of inventory policy under limited storage space for continuous and periodic review policies with backlog and lost sales. Math. Probl. Eng. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Jansen, S.; Atan, Z.; Adan, I.; de Kok, T. Setting optimal planned leadtimes in configure-to-order assembly systems. Eur. J. Oper. Res. 2019, 273, 585–595. [Google Scholar] [CrossRef]
- Kokuryo, D.; Yamashita, K.; Kaihara, T.; Fujii, N.; Umeda, T.; Izutsu, R. A proposed production decision method for order planning considering decision criteria of multiple organizations. Procedia CIRP 2020, 93, 933–937. [Google Scholar] [CrossRef]
- Thinakaran, N.; Jayaprakas, J.; Elanchezhian, C. Survey on inventory model of EOQ & EPQ with partial backorder problems. Mater. Today Proc. 2019, 16, 629–635. [Google Scholar]
- Tai, P.; Huyen, P.; Buddhakulsomsiri, J. A novel modeling approach for a capacitated (S,T) inventory system with backlog under stochastic discrete demand and lead time. Int. J. Ind. Eng. Comput. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- Hunsucker, J.L.; Shah, J.R. Performance of priority rules in a due date flow shop. Omega 1992, 20, 73–89. [Google Scholar] [CrossRef]
- Wang, C.-N.; Dang, T.-T.; Nguyen, N.-A.-T. A computational model for determining levels of factors in inventory management using response surface methodology. Mathematics 2020, 8, 1210. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Cook, C.M.A. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 39. [Google Scholar]
- Khuri, A.I. Response surface methodology and its applications in agricultural and food sciences. Int. J. Biom. Biostat. 2017, 5, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Goh, T.N. The role of statistical design of experiments in six sigma: Perspectives of a practitioner. Qual. Eng. 2002, 14, 659–671. [Google Scholar] [CrossRef]
- Shi, W.; Shang, J.; Liu, Z.; Zuo, X. Optimal design of the auto parts supply chain for JIT operations: Sequential bifurcation factor screening and multi-response surface methodology. Eur. J. Oper. Res. 2014, 236, 664–676. [Google Scholar] [CrossRef]
- Widodo, E. A review of response surface methodology approach in supply chain management. In Proceedings of the 3rd Asia Pacific Conference on Research in Industrial and Systems Engineering, Depok, Indonesia, 16–17 June 2020; pp. 322–327. [Google Scholar]
- Radasanu, A.C. Inventory management, service level and safety stock. J. Public Adm. Financ. Law 2016, 9, 145–153. [Google Scholar]
- Coleman, B.J. Determining the correct service level target. Prod. Inventory Manag. J. 2000, 41, 19. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]










| Authors | Independent Variables | Response Variables | Methods/Techniques |
|---|---|---|---|
| Zhang et al. [33], 2015 | Number of orders Planning horizon Production capacity | Penalty for delivery Penalty for order Inventory cost Production cost | NLP PSO algorithm |
| Guo et al. [34], 2015 | Due date of order Production workload Capacity efficiency | Completion time Production capacity Processing time | MOLP DOE |
| Lim et al. [35], 2017 | Demand variability Lead time | Holding cost Supply cost Safety stock | Simulation modeling MOLP |
| Singha et al. [36], 2017 | Reorder point Order quantity Inventory policies | Ordering cost Shortage cost Holding cost Over-ordering cost | EOQ (R, Q) model Mathematical model |
| Jansen et al. [37], 2019 | Planned lead time Production plan | Holding cost Penalty cost | Mathematical model |
| Thinakaran et al. [40], 2019 | Time-varying Stock demand Lot size | Backorder Lost sales | EOQ EPQ |
| Wang et al. [42], 2020 | Ordering quantity Reorder point Target stock Inventory policies | Holding cost Penalty cost | Simulation modeling DOE |
| Kokuryo et al. [38], 2020 | Order quantity Production schedule Order period | Delivery time Profit | Mathematical model |
| Tai et al. [39], 2020 | Order quantity Lead time Inventory policies | Over-storage amount Inventory cost | EOQ (S, T) model Mathematical model |
| This paper, 2020 | Review period Order quantity Safety stock | Holding cost Shortage cost Over-storage cost Transportation cost | Simulation modeling RSM |
| 2017 | Spectite CW100 | Spectite WS | Spectite HP600 | Speccoat PE145 |
| Max | 1663 | 131 | 224 | 40 |
| Min | 215 | 0 | 0 | 1 |
| Avg | 1044.58 | 45 | 36.33 | 5.83 |
| SD | 470.18 | 47.13 | 63.58 | 11.81 |
| 2018 | Spectite CW100 | Spectite WS | Spectite HP600 | Speccoat PE145 |
| Max | 2140 | 965 | 100 | 114 |
| Min | 411 | 0 | 0 | 2 |
| Avg | 1093.50 | 198.17 | 21.42 | 31.83 |
| SD | 538.73 | 265.93 | 35.64 | 34.91 |
| 2019 | Spectite CW100 | Spectite WS | Spectite HP600 | Speccoat PE145 |
| Max | 2290 | 359 | 75 | 83 |
| Min | 219 | 0 | 0 | 0 |
| Avg | 1387.75 | 142.42 | 32.67 | 30.17 |
| SD | 649.19 | 124.85 | 30.79 | 24.88 |
| Materials | Spectite CW100 | Spectite WS | Spectite HP600 | Speccoat PE145 | Unit |
|---|---|---|---|---|---|
| Packing size | 22 kg/set | 25 kg/bag | 20 L/pail | 15 L/pail | - |
| Wholesale price | 11 | 20 | 78 | 49.5 | USD/unit |
| Receipt cost | 12.93 | 22.12 | 84.73 | 54.70 | USD/unit |
| Selling price | 18.42 | 32.89 | 116.22 | 87.72 | USD/unit |
| Holding cost | 0.075 | 0.129 | 0.494 | 0.319 | USD/unit/month |
| Shortage cost | 0.553 | 0.987 | 3.487 | 2.632 | USD/unit |
| Over-storage cost | 0.162 | 0.277 | 1.059 | 0.684 | USD/unit/month |
| No. | Variables | Notation | Interval Range | Unit |
|---|---|---|---|---|
| 1 | Review period (categorical factor) | T | (3, 4) | Month |
| 2 | Order quantity (continuous factor) | Q | (3500, 4000) | Unit |
| 3 | Safety stock (continuous factor) | SS | (1000, 1300) | Unit |
| 4 | Total cost (response) | TC | TC (Ch, Cs, Co, Ct) | USD |
| 5 | Customer service level (response) | CSL | CSL (90% and 95%) | % |
| StdOrder | RunOrder | PtType | Blocks | T | Q | SS | TC | CSL |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | −1 | −1 | 76,990.53 | 86 |
| 2 | 2 | 1 | 1 | 1 | 1 | −1 | 78,115.85 | 93 |
| 3 | 3 | 1 | 1 | 1 | −1 | 1 | 76,789.66 | 87 |
| 4 | 4 | 1 | 1 | 1 | 1 | 1 | 79,264.98 | 94 |
| 5 | 5 | 0 | 1 | 1 | 0 | 0 | 76,829.35 | 91 |
| 6 | 6 | 1 | 1 | 2 | −1 | −1 | 66,298.47 | 69 |
| 7 | 7 | 1 | 1 | 2 | 1 | −1 | 64,918.34 | 78 |
| 8 | 8 | 1 | 1 | 2 | −1 | 1 | 65,582.80 | 74 |
| 9 | 9 | 1 | 1 | 2 | 1 | 1 | 67,053.43 | 81 |
| 10 | 10 | 0 | 1 | 2 | 0 | 0 | 65,334.14 | 75 |
| 11 | 11 | −1 | 2 | 1 | −1.41 | 0 | 77,047.57 | 84 |
| 12 | 12 | −1 | 2 | 1 | 1.41 | 0 | 96,797.76 | 94 |
| 13 | 13 | −1 | 2 | 1 | 0 | −1.41 | 76,971.17 | 90 |
| 14 | 14 | −1 | 2 | 1 | 0 | 1.41 | 78,037.13 | 91 |
| 15 | 15 | 0 | 2 | 1 | 0 | 0 | 76,826.26 | 92 |
| 16 | 16 | −1 | 2 | 2 | −1.41 | 0 | 66,215.61 | 70 |
| 17 | 17 | −1 | 2 | 2 | 1.41 | 0 | 74,732.52 | 81 |
| 18 | 18 | −1 | 2 | 2 | 0 | −1.41 | 65,732.97 | 73 |
| 19 | 19 | −1 | 2 | 2 | 0 | 1.41 | 69,031.07 | 78 |
| 20 | 20 | 0 | 2 | 2 | 0 | 0 | 63,287.22 | 75 |
| StdOrder | RunOrder | PtType | Blocks | T | Q | SS | TC | CSL |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 2 | 3250 | 1000 | 134,828.00 | 100 |
| 2 | 2 | 2 | 1 | 4 | 3250 | 1000 | 65,946.84 | 71 |
| 3 | 3 | 2 | 1 | 2 | 3750 | 1000 | 171,568.82 | 100 |
| 4 | 4 | 2 | 1 | 4 | 3750 | 1000 | 64,635.88 | 79 |
| 5 | 5 | 2 | 1 | 2 | 3500 | 750 | 151,097.12 | 100 |
| 6 | 6 | 2 | 1 | 4 | 3500 | 750 | 65,616.60 | 73 |
| 7 | 7 | 2 | 1 | 2 | 3500 | 1250 | 154,401.55 | 100 |
| 8 | 8 | 2 | 1 | 4 | 3500 | 1250 | 64,982.51 | 77 |
| 9 | 9 | 2 | 1 | 3 | 3250 | 750 | 76,990.53 | 86 |
| 10 | 10 | 2 | 1 | 3 | 3750 | 750 | 78,115.85 | 93 |
| 11 | 11 | 2 | 1 | 3 | 3250 | 1250 | 76,789.66 | 87 |
| 12 | 12 | 2 | 1 | 3 | 3750 | 1250 | 79,264.98 | 94 |
| 13 | 13 | 0 | 1 | 3 | 3500 | 1000 | 76,826.26 | 92 |
| 14 | 14 | 0 | 1 | 3 | 3500 | 1000 | 80,511.79 | 100 |
| 15 | 15 | 0 | 1 | 3 | 3500 | 1000 | 77,198.46 | 87 |
| Central Composite Design (CCD) | Box-Behnken Design (BBD) | |||
|---|---|---|---|---|
| CSL (90%) | CSL (95%) | CSL (90%) | CSL (95%) | |
| T | 3 | 3 | 3 | 3 |
| Q | 3428 | 3520 | 3603 | 3690 |
| SS | 1336 | 1354 | 1250 | 1250 |
| TC | 76,330 | 77,090 | 70,870 | 85,920 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-N.; Nguyen, N.-A.-T.; Dang, T.-T. Solving Order Planning Problem Using a Heuristic Approach: The Case in a Building Material Distributor. Appl. Sci. 2020, 10, 8959. https://doi.org/10.3390/app10248959
Wang C-N, Nguyen N-A-T, Dang T-T. Solving Order Planning Problem Using a Heuristic Approach: The Case in a Building Material Distributor. Applied Sciences. 2020; 10(24):8959. https://doi.org/10.3390/app10248959
Chicago/Turabian StyleWang, Chia-Nan, Ngoc-Ai-Thy Nguyen, and Thanh-Tuan Dang. 2020. "Solving Order Planning Problem Using a Heuristic Approach: The Case in a Building Material Distributor" Applied Sciences 10, no. 24: 8959. https://doi.org/10.3390/app10248959
APA StyleWang, C.-N., Nguyen, N.-A.-T., & Dang, T.-T. (2020). Solving Order Planning Problem Using a Heuristic Approach: The Case in a Building Material Distributor. Applied Sciences, 10(24), 8959. https://doi.org/10.3390/app10248959







