A Parametric Study of a Deep Reinforcement Learning Control System Applied to the Swing-Up Problem of the Cart-Pole
Abstract
:1. Introduction
1.1. Background and Significance of the Research
1.2. Formulation of the Specific Problem of Interest for This Investigation
1.3. Literature Review
1.4. Scope and Contributions of This Paper
1.5. Organization of the Manuscript
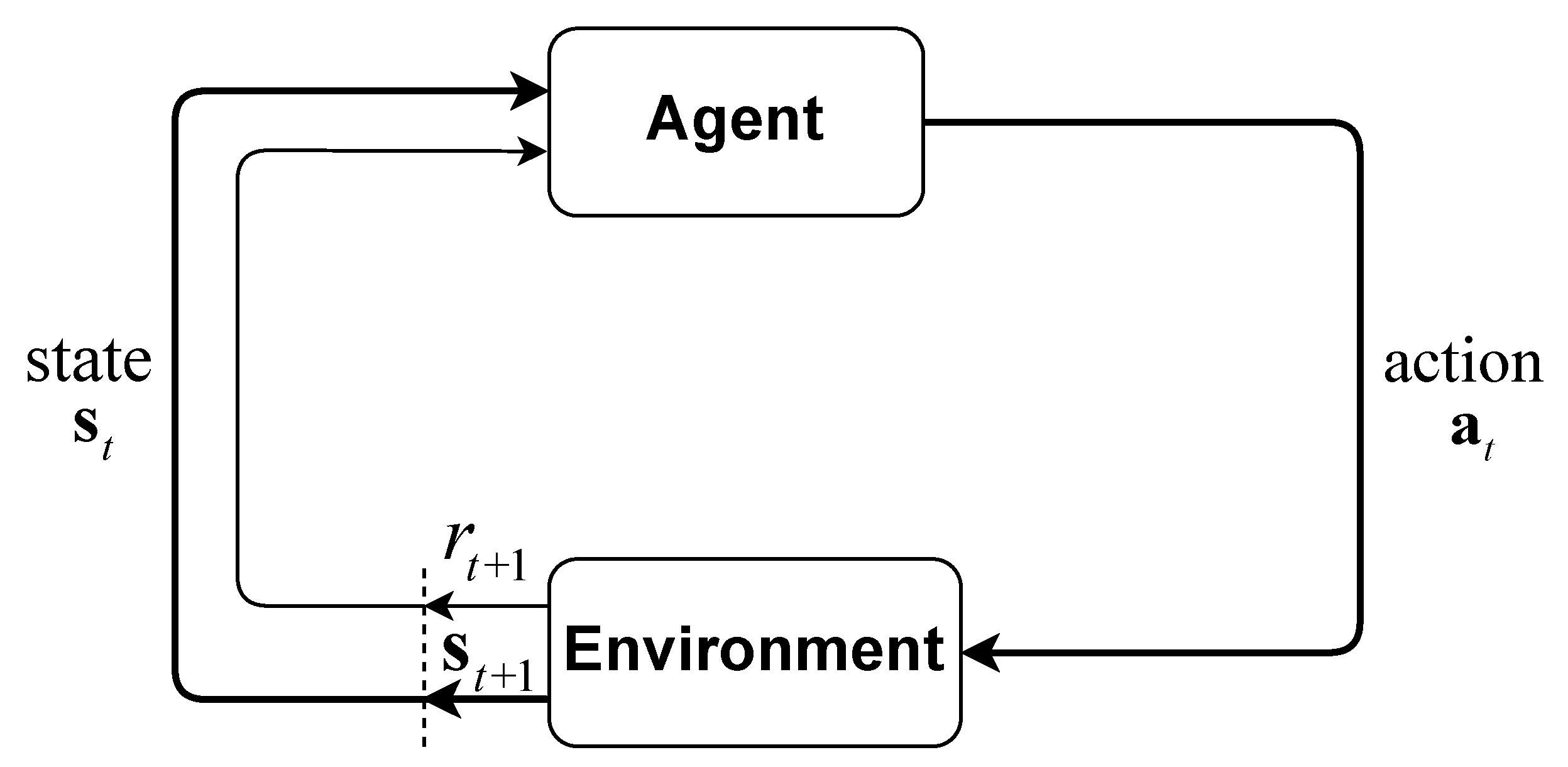
2. Research Methodology
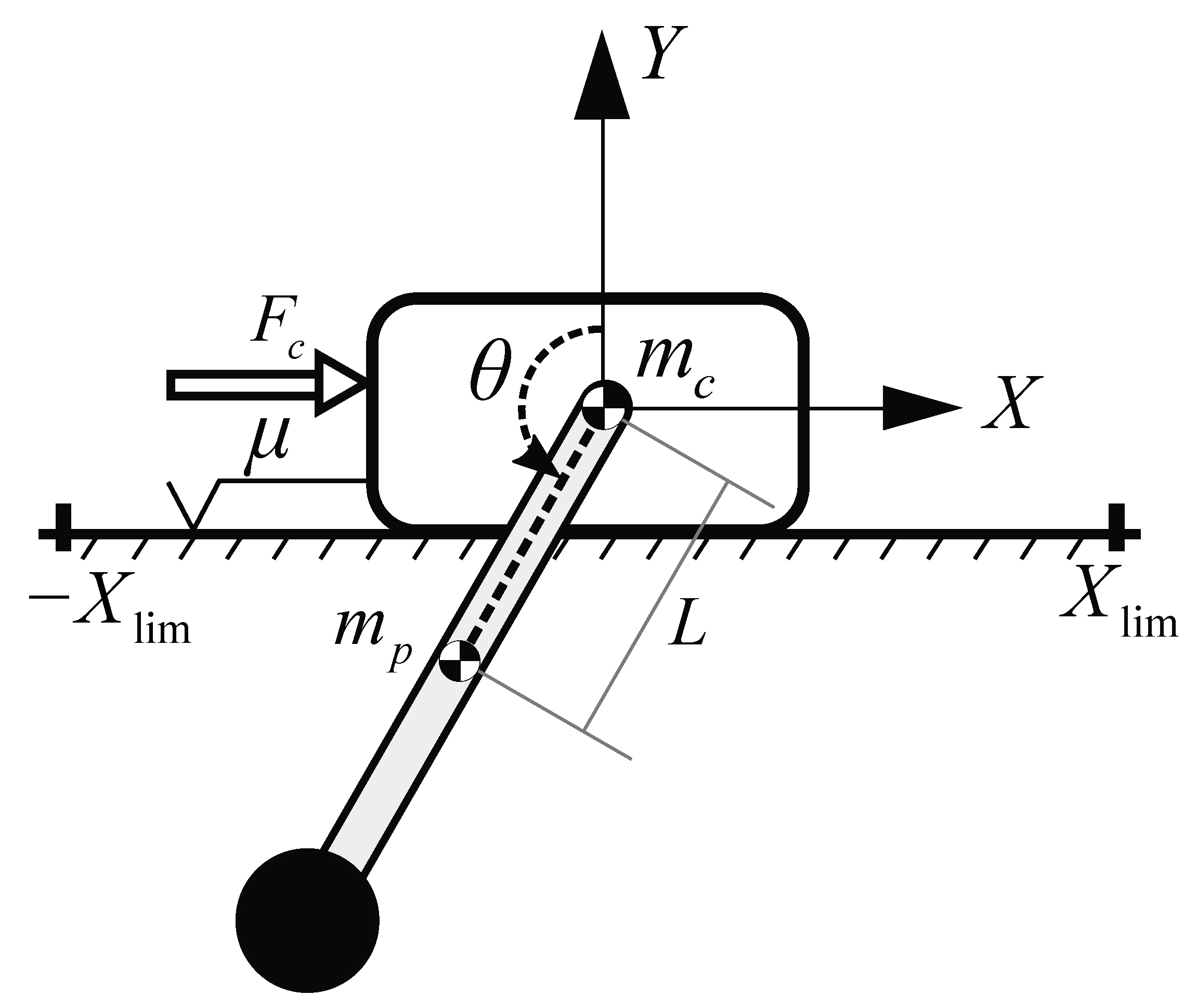
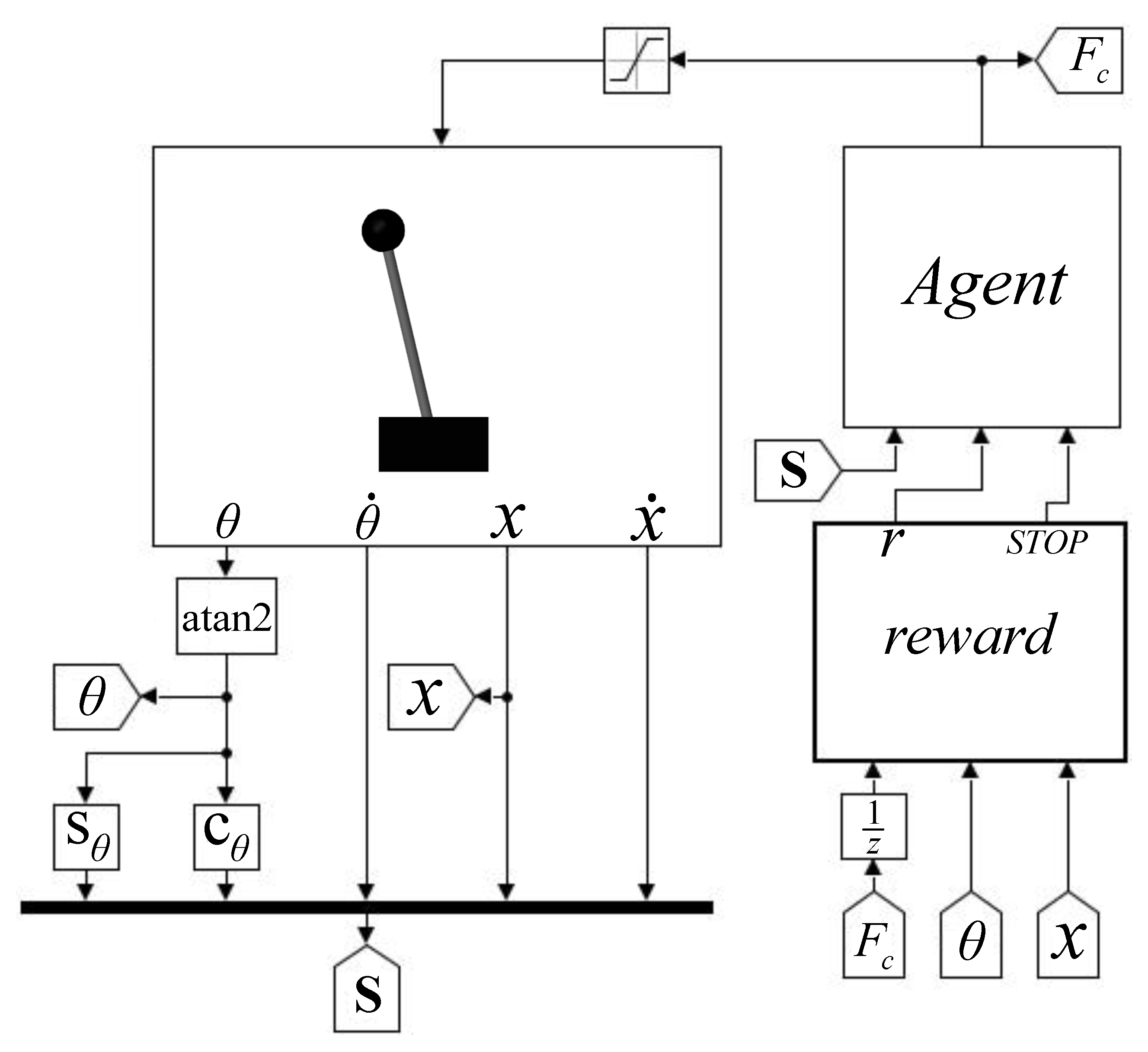
3. Dynamic Model Description and Numerical Experiments’ Setup
4. Numerical Results and Discussion
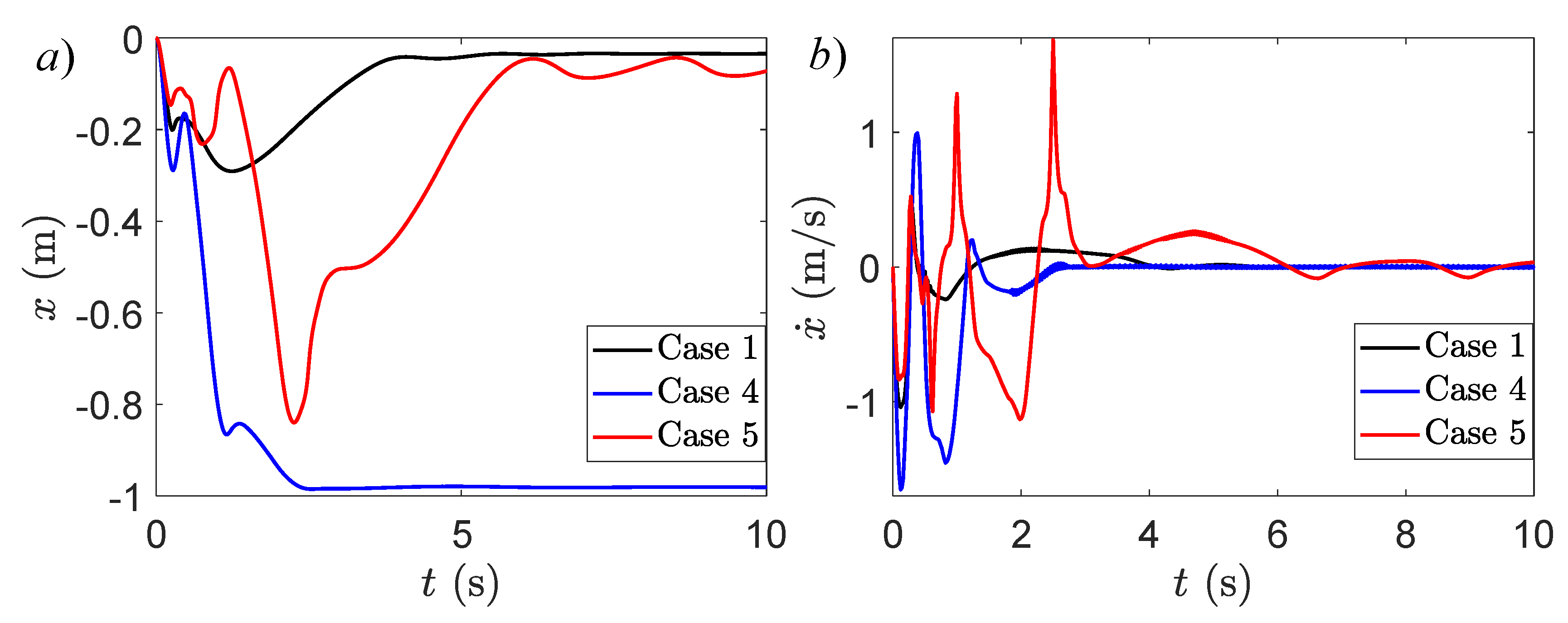
4.1. Physical Properties’ Parameter Study
4.2. Dry Friction Parameter Study
4.3. Discussion and Final Remarks
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hesse, M.; Timmermann, J.; Hüllermeier, E.; Trächtler, A. A Reinforcement Learning Strategy for the Swing-Up of the Double Pendulum on a Cart. Procedia Manuf. 2018, 24, 15. [Google Scholar] [CrossRef]
- Manrique, C.; Pappalardo, C.M.; Guida, D. A Model Validating Technique for the Kinematic Study of Two-Wheeled Vehicles. Lect. Notes Mech. Eng. 2019, 549–558. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; De Simone, M.C.; Guida, D. Multibody modeling and nonlinear control of the pantograph/catenary system. Arch. Appl. Mech. 2019, 89, 1589–1626. [Google Scholar] [CrossRef]
- Pappalardo, C.; Guida, D. Forward and Inverse Dynamics of a Unicycle-Like Mobile Robot. Machines 2019, 7, 5. [Google Scholar] [CrossRef] [Green Version]
- Villecco, F.; Pellegrino, A. Evaluation of Uncertainties in the Design Process of Complex Mechanical Systems. Entropy 2017, 19, 475. [Google Scholar] [CrossRef] [Green Version]
- Villecco, F.; Pellegrino, A. Entropic Measure of Epistemic Uncertainties in Multibody System Models by Axiomatic Design. Entropy 2017, 19, 291. [Google Scholar] [CrossRef] [Green Version]
- Hu, D.; Pei, Z.; Tang, Z. Single-Parameter-Tuned Attitude Control for Quadrotor with Unknown Disturbance. Appl. Sci. 2020, 10, 5564. [Google Scholar] [CrossRef]
- Talamini, J.; Bartoli, A.; De Lorenzo, A.D.; Medvet, E. On the Impact of the Rules on Autonomous Drive Learning. Appl. Sci. 2020, 10, 2394. [Google Scholar] [CrossRef] [Green Version]
- Sharifzadeh, S.; Chiotellis, I.; Triebel, R.; Cremers, D. Learning to drive using inverse reinforcement learning and deep q-networks. arXiv 2016, arXiv:1612.03653. [Google Scholar]
- Cho, N.J.; Lee, S.H.; Kim, J.B.; Suh, I.H. Learning, Improving, and Generalizing Motor Skills for the Peg-in-Hole Tasks Based on Imitation Learning and Self-Learning. Appl. Sci. 2020, 10, 2719. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Qu, C.; Zhang, J.; Li, J. Self-Adaptive Priority Correction for Prioritized Experience Replay. Appl. Sci. 2020, 10, 6925. [Google Scholar] [CrossRef]
- Hong, D.; Kim, M.; Park, S. Study on Reinforcement Learning-Based Missile Guidance Law. Appl. Sci. 2020, 10, 6567. [Google Scholar] [CrossRef]
- Rivera, Z.B.; De Simone, M.C.; Guida, D. Unmanned Ground Vehicle Modelling in Gazebo/ROS-Based Environments. Machines 2019, 7, 42. [Google Scholar] [CrossRef] [Green Version]
- De Simone, M.C.; Guida, D. Control design for an under-actuated UAV model. FME Trans. 2018, 46, 443–452. [Google Scholar] [CrossRef]
- Murray, R.; Palladino, M. A model for system uncertainty in reinforcement learning. Syst. Control Lett. 2018, 122, 24–31. [Google Scholar] [CrossRef] [Green Version]
- Sutton, R.S.; Barto, A.G.; Williams, R.J. Reinforcement learning is direct adaptive optimal control. IEEE Control Syst. 1992, 12, 19–22. [Google Scholar] [CrossRef]
- Cheng, Q.; Wang, X.; Niu, Y.; Shen, L. Reusing Source Task Knowledge via Transfer Approximator in Reinforcement Transfer Learning. Symmetry 2018, 11, 25. [Google Scholar] [CrossRef] [Green Version]
- Nichols, B.D. Continuous Action-Space Reinforcement Learning Methods Applied to the Minimum-Time Swing-Up of the Acrobot. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 2084–2089. [Google Scholar]
- Lesort, T.; Díaz-Rodríguez, N.; Goudou, J.-F.; Filliat, D. State representation learning for control: An overview. Neural Netw. 2018, 108, 379–392. [Google Scholar] [CrossRef] [Green Version]
- Oh, E. Reinforcement-Learning-Based Virtual Energy Storage System Operation Strategy for Wind Power Forecast Uncertainty Management. Appl. Sci. 2020, 10, 6420. [Google Scholar] [CrossRef]
- Phan, B.C.; Lai, Y.-C. Control Strategy of a Hybrid Renewable Energy System Based on Reinforcement Learning Approach for an Isolated Microgrid. Appl. Sci. 2019, 9, 4001. [Google Scholar] [CrossRef] [Green Version]
- Kővári, B.; Hegedüs, F.; Bécsi, T. Design of a Reinforcement Learning-Based Lane Keeping Planning Agent for Automated Vehicles. Appl. Sci. 2020, 10, 7171. [Google Scholar] [CrossRef]
- Tran, D.Q.; Bae, S.-H. Proximal Policy Optimization Through a Deep Reinforcement Learning Framework for Multiple Autonomous Vehicles at a Non-Signalized Intersection. Appl. Sci. 2020, 10, 5722. [Google Scholar] [CrossRef]
- Sattarov, O.; Muminov, A.; Lee, C.W.; Kang, H.K.; Oh, R.; Ahn, J.; Oh, H.J.; Jeon, H.S. Recommending Cryptocurrency Trading Points with Deep Reinforcement Learning Approach. Appl. Sci. 2020, 10, 1506. [Google Scholar] [CrossRef] [Green Version]
- Rundo, F. Deep LSTM with Reinforcement Learning Layer for Financial Trend Prediction in FX High Frequency Trading Systems. Appl. Sci. 2019, 9, 4460. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Liu, Y.; Zhou, Z.; Zhang, M. A2C: Attention-Augmented Contrastive Learning for State Representation Extraction. Appl. Sci. 2020, 10, 5902. [Google Scholar] [CrossRef]
- Xiang, G.; Su, J. Task-Oriented Deep Reinforcement Learning for Robotic Skill Acquisition and Control. IEEE Trans. Cybern. 2019, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Wawrzyński, P. Control Policy with Autocorrelated Noise in Reinforcement Learning for Robotics. Int. J. Mach. Learn. Comput. 2015, 5, 91–95. [Google Scholar] [CrossRef] [Green Version]
- Beltran-Hernandez, C.C.; Petit, D.; Ramirez-Alpizar, I.G.; Harada, K. Variable Compliance Control for Robotic Peg-in-Hole Assembly: A Deep-Reinforcement-Learning Approach. Appl. Sci. 2020, 10, 6923. [Google Scholar] [CrossRef]
- Moreira, I.; Rivas, J.; Cruz, F.; Dazeley, R.; Ayala, A.; Fernandes, B. Deep Reinforcement Learning with Interactive Feedback in a Human–Robot Environment. Appl. Sci. 2020, 10, 5574. [Google Scholar] [CrossRef]
- Williams, G.; Wagener, N.; Goldfain, B.; Drews, P.; Rehg, J.M.; Boots, B.; Theodorou, E.A. Information theoretic MPC for model-based reinforcement learning. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1714–1721. [Google Scholar]
- Anderson, C.W.; Lee, M.; Elliott, D.L. Faster reinforcement learning after pretraining deep networks to predict state dynamics. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–16 July 2015; Volume 2015, pp. 1–7. [Google Scholar]
- Lee, M.; Anderson, C.W. Convergent reinforcement learning control with neural networks and continuous action search. In Proceedings of the 2014 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning (ADPRL), Orlando, FL, USA, 9–12 December 2014; pp. 1–8. [Google Scholar]
- Maei, H.R.; Szepesvari, C.; Bhatnagar, S.; Precup, D.; Silver, D.; Sutton, R.S. Convergent temporal-difference learning with arbitrary smooth function approximation. In Proceedings of the 22nd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 1204–1212. [Google Scholar]
- Morimoto, J.; Doya, K. Robust Reinforcement Learning. Neural Comput. 2005, 17, 335–359. [Google Scholar] [CrossRef] [PubMed]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An Introduction to Deep Reinforcement Learning. Found. Trends Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Li, X.; Zhang, L. Task-specific pre-learning to improve the convergence of reinforcement learning based on a deep neural network. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; Volume 2016, pp. 2209–2214. [Google Scholar]
- Zagal, J.C.; Ruiz-del-Solar, J.; Vallejos, P. Back to reality: Crossing the reality gap in evolutionary robotics. IFAC Proc. Vol. 2004, 37, 834–839. [Google Scholar] [CrossRef]
- Bekar, C.; Yuksek, B.; Inalhan, G. High Fidelity Progressive Reinforcement Learning for Agile Maneuvering UAVs. In Proceedings of the AIAA Scitech 2020 Forum; American Institute of Aeronautics and Astronautics, Orlando, FL, USA, 6–10 January 2020; pp. 1–12. [Google Scholar]
- Boubaker, O.; Iriarte, R. (Eds.) The Inverted Pendulum in Control Theory and Robotics: From Theory to New Innovations; IET: London, UK, 2017; Volume 111, ISBN 978-1-78561-321-0. [Google Scholar]
- Gonzalez, O.; Rossiter, A. Fast hybrid dual mode NMPC for a parallel double inverted pendulum with experimental validation. IET Control Theory Appl. 2020, 14, 2329–2338. [Google Scholar] [CrossRef]
- Nekoo, S.R. Digital implementation of a continuous-time nonlinear optimal controller: An experimental study with real-time computations. ISA Trans. 2020, 101, 346–357. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, L.; Li, H. Robust Control for Switched Systems with Unmatched Uncertainties Based on Switched Robust Integral Sliding Mode. IEEE Access 2020, 8, 138396–138405. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, Q.; Mehmood, A.; Bhatti, A.I. Robust Backstepping Sliding Mode Control Design for a Class of Underactuated Electro–Mechanical Nonlinear Systems. J. Electr. Eng. Technol. 2020, 15, 1821–1828. [Google Scholar] [CrossRef]
- Khan, Q.; Akmeliawati, R.; Bhatti, A.I.; Khan, M.A. Robust stabilization of underactuated nonlinear systems: A fast terminal sliding mode approach. ISA Trans. 2017, 66, 241–248. [Google Scholar] [CrossRef]
- Al-Araji, A.S. An adaptive swing-up sliding mode controller design for a real inverted pendulum system based on Culture-Bees algorithm. Eur. J. Control 2019, 45, 45–56. [Google Scholar] [CrossRef]
- Su, T.-J.; Wang, S.-M.; Li, T.-Y.; Shih, S.-T.; Hoang, V.-M. Design of hybrid sliding mode controller based on fireworks algorithm for nonlinear inverted pendulum systems. Adv. Mech. Eng. 2017, 9, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Mansoor, H.; Bhutta, H.A. Genetic algorithm based optimal back stepping controller design for stabilizing inverted pendulum. In Proceedings of the 2016 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 11–12 April 2016; pp. 6–9. [Google Scholar]
- Singla, A.; Singh, G. Real-Time Swing-up and Stabilization Control of a Cart-Pendulum System with Constrained Cart Movement. Int. J. Nonlinear Sci. Numer. Simul. 2017, 18, 525–539. [Google Scholar] [CrossRef]
- Dındış, G.; Karamancıoğlu, A. A Self-learning Robust Swing-up algorithm. Trans. Inst. Meas. Control 2016, 38, 395–401. [Google Scholar] [CrossRef]
- Al-Janan, D.H.; Chang, H.-C.; Chen, Y.-P.; Liu, T.-K. Optimizing the double inverted pendulum’s performance via the uniform neuro multiobjective genetic algorithm. Int. J. Autom. Comput. 2017, 14, 686–695. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, X.; Xu, L. Balance Control for the First-order Inverted Pendulum Based on the Advantage Actor-critic Algorithm. Int. J. Control. Autom. Syst. 2020. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. arXiv 2016, arXiv:1602.01783. [Google Scholar]
- Kim, J.-B.; Lim, H.-K.; Kim, C.-M.; Kim, M.-S.; Hong, Y.-G.; Han, Y.-H. Imitation Reinforcement Learning-Based Remote Rotary Inverted Pendulum Control in OpenFlow Network. IEEE Access 2019, 7, 36682–36690. [Google Scholar] [CrossRef]
- Dao, P.N.; Liu, Y.-C. Adaptive Reinforcement Learning Strategy with Sliding Mode Control for Unknown and Disturbed Wheeled Inverted Pendulum. Int. J. Control. Autom. Syst. 2020. [Google Scholar] [CrossRef]
- Kukker, A.; Sharma, R. Genetic Algorithm-Optimized Fuzzy Lyapunov Reinforcement Learning for Nonlinear Systems. Arab. J. Sci. Eng. 2020, 45, 1629–1638. [Google Scholar] [CrossRef]
- Koryakovskiy, I.; Kudruss, M.; Babuška, R.; Caarls, W.; Kirches, C.; Mombaur, K.; Schlöder, J.P.; Vallery, H. Benchmarking model-free and model-based optimal control. Rob. Auton. Syst. 2017, 92, 81–90. [Google Scholar] [CrossRef] [Green Version]
- Grondman, I.; Vaandrager, M.; Busoniu, L.; Babuska, R.; Schuitema, E. Efficient Model Learning Methods for Actor—Critic Control. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 591–602. [Google Scholar] [CrossRef]
- Maity, S.; Luecke, G.R. Stabilization and Optimization of Design Parameters for Control of Inverted Pendulum. J. Dyn. Syst. Meas. Control 2019, 141. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018; ISBN 9780262039246. [Google Scholar]
- Szepesvári, C. Algorithms for Reinforcement Learning, 1st ed.; Brachman, R.J., Dietterich, T., Eds.; Morgan & Claypool Publishers: Alberta, MN, USA, 2010; Volume 4, ISBN 9781608454921. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.P.; Heess, N.H.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971v6. [Google Scholar]
- Bellemare, M.G.; Naddaf, Y.; Veness, J.; Bowling, M. The Arcade Learning Environment: An Evaluation Platform for General Agents. J. Artif. Intell. Res. 2013, 47, 253–279. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Boubaker, O. The inverted pendulum: A fundamental benchmark in control theory and robotics. In Proceedings of the International Conference on Education and e-Learning Innovations, Sousse, Tunisia, 1–3 July 2012; pp. 1–6. [Google Scholar]
- Nagendra, S.; Podila, N.; Ugarakhod, R.; George, K. Comparison of reinforcement learning algorithms applied to the cart-pole problem. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; Volume 2017, pp. 26–32. [Google Scholar]
- Wawrzynski, P. Learning to Control a 6-Degree-of-Freedom Walking Robot. In Proceedings of the EUROCON 2007—The International Conference on “Computer as a Tool”, Warsaw, Poland, 9–12 September 2007; pp. 698–705. [Google Scholar]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Riedmiller, M.; Peters, J.; Schaal, S. Evaluation of Policy Gradient Methods and Variants on the Cart-Pole Benchmark. In Proceedings of the 2007 IEEE International Symposium on Approximate Dynamic Programming and Reinforcement Learning, Honolulu, HI, USA, 1–5 April 2007; pp. 254–261. [Google Scholar]
- Pennestrì, E.; Valentini, P.P.; Vita, L. Multibody dynamics simulation of planar linkages with Dahl friction. Multibody Syst. Dyn. 2007, 17, 321–347. [Google Scholar] [CrossRef]
- Pennestrì, E.; Rossi, V.; Salvini, P.; Valentini, P.P. Review and comparison of dry friction force models. Nonlinear Dyn. 2016, 83, 1785–1801. [Google Scholar] [CrossRef]
- Kikuuwe, R.; Takesue, N.; Sano, A.; Mochiyama, H.; Fujimoto, H. Fixed-step friction simulation: From classical Coulomb model to modern continuous models. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 1009–1016. [Google Scholar]
- De Simone, M.C.; Guida, D. Experimental investigation on structural vibrations by a new shaking table. Lect. Notes Mech. Eng. 2020, 819–831. [Google Scholar] [CrossRef]
- Pappalardo, C.; Lettieri, A.; Guida, D. Stability analysis of rigid multibody mechanical systems with holonomic and nonholonomic constraints. Arch. Appl. Mech. 2020, 90, 1961–2005. [Google Scholar] [CrossRef]









| Symbol | Meaning | Value |
|---|---|---|
| Actor learning rate | ||
| Critic learning rate | ||
| Gradient threshold | ||
| D | Experience buffer length | |
| d | Replay buffer size | |
| Polyak averaging factor | ||
| Value function discount factor | ||
| Sampling time | s |
| Case | (kg) | (kg) | L (m) | (s) | |
|---|---|---|---|---|---|
| 1 | 1.00 | 1.00 | 0.10 | 0.98 | −71.55 |
| 2 | 0.06 | 1.00 | 0.10 | 1.54 | −233.93 |
| 3 | 2.00 | 1.00 | 0.10 | 5.1 | −269.89 |
| 4 | 1.00 | 0.10 | 0.10 | 1.70 | −204.93 |
| 5 | 1.00 | 1.90 | 0.1 | 3.30 | −205.93 |
| 6 | 1.00 | 1.00 | 0.07 | 1.70 | −262.46 |
| 7 | 1.00 | 1.00 | 0.19 | 3.42 | −197.49 |
| 8 | 0.65 | 0.65 | 0.06 | 1.44 | −226.57 |
| 9 | 1.25 | 1.25 | 0.12 | 1.28 | −201.23 |
| Case | Agent | (kg) | (kg) | L (kg) | (s) | ||
|---|---|---|---|---|---|---|---|
| 10 | A | 0.30 | 1.00 | 1.00 | 0.10 | - | −341.48 |
| 11 | B | 0.30 | 1.00 | 1.00 | 0.10 | 2.00 | −74.71 |
| 12 | B | 0 | 1.00 | 1.00 | 0.10 | 2.74 | −81.51 |
| 13 | B | 0.80 | 1.00 | 1.00 | 0.10 | 0.80 | −78.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manrique Escobar, C.A.; Pappalardo, C.M.; Guida, D. A Parametric Study of a Deep Reinforcement Learning Control System Applied to the Swing-Up Problem of the Cart-Pole. Appl. Sci. 2020, 10, 9013. https://doi.org/10.3390/app10249013
Manrique Escobar CA, Pappalardo CM, Guida D. A Parametric Study of a Deep Reinforcement Learning Control System Applied to the Swing-Up Problem of the Cart-Pole. Applied Sciences. 2020; 10(24):9013. https://doi.org/10.3390/app10249013
Chicago/Turabian StyleManrique Escobar, Camilo Andrés, Carmine Maria Pappalardo, and Domenico Guida. 2020. "A Parametric Study of a Deep Reinforcement Learning Control System Applied to the Swing-Up Problem of the Cart-Pole" Applied Sciences 10, no. 24: 9013. https://doi.org/10.3390/app10249013





