A Large-Deformation Gradient Damage Model for Single Crystals Based on Microdamage Theory
Abstract
:1. Introduction
2. Microdamage Model for Single Crystals
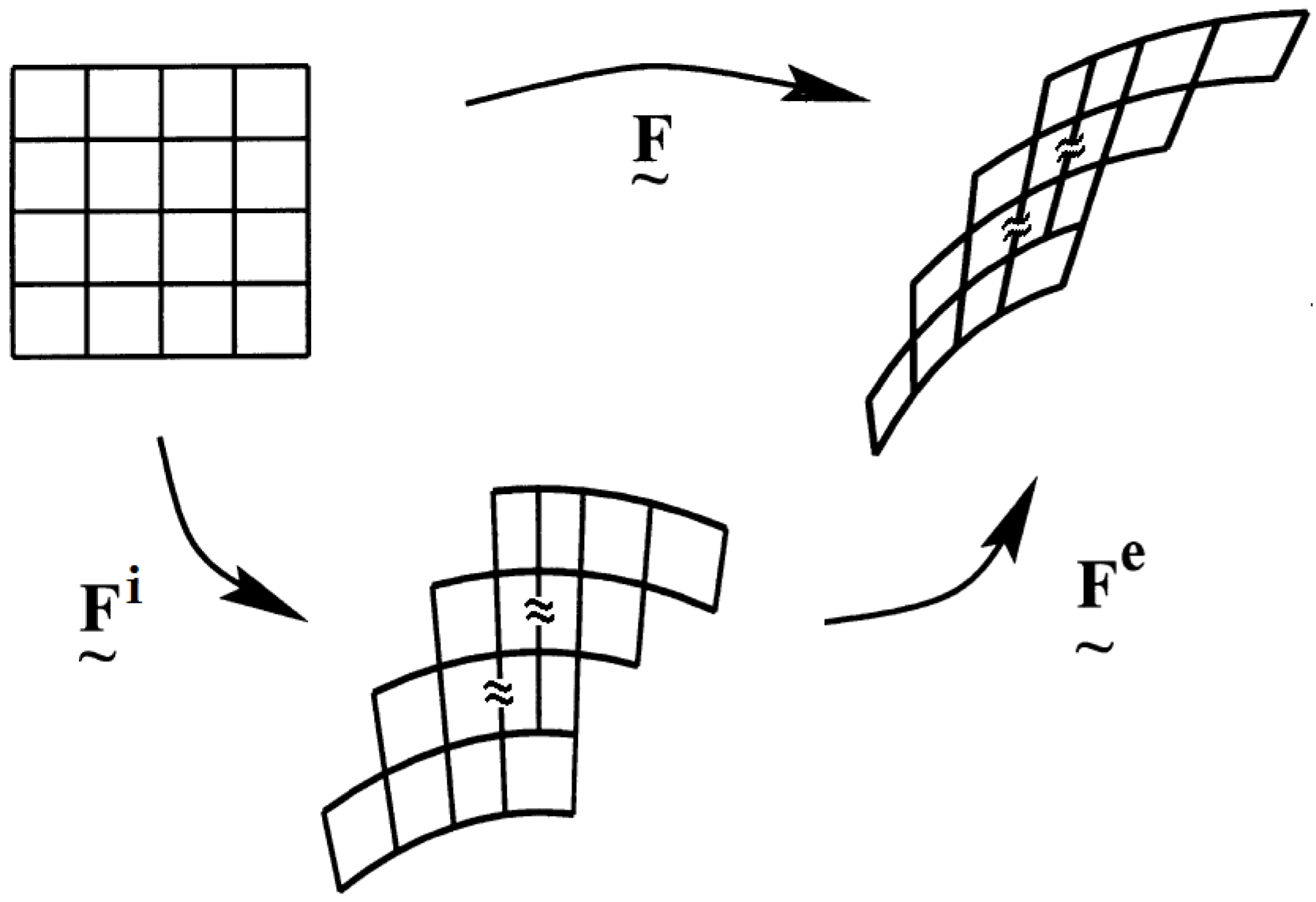
2.1. Basic Kinematics
2.2. Micromorphic Variable χd
The power over is expended by the microscopic stress π, is expended by the scalar microscopic stress , is expended by the microscopic stress vector , and is expended by the microscopic traction at the boundary.
3. Principle of Virtual Power
4. Constitutive Equations
5. Specialization of the Constitutive Equations
6. Numerical Results and Discussion
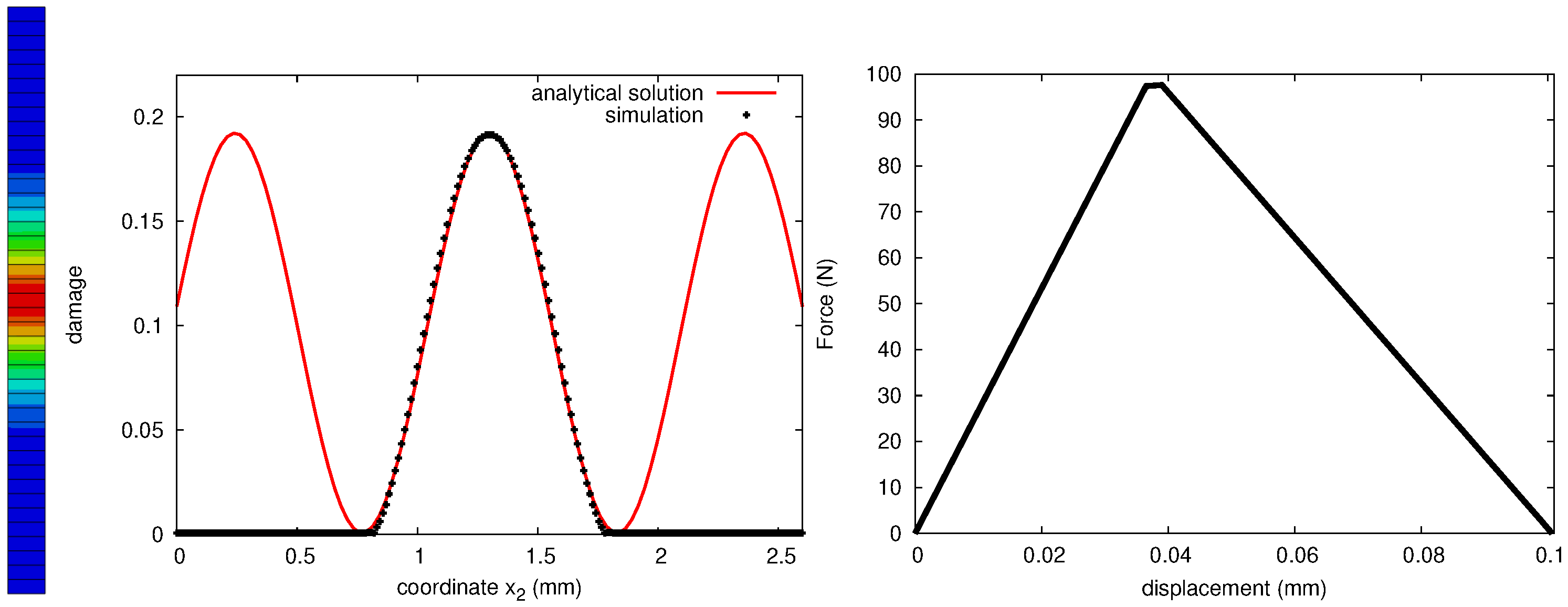
6.1. Analysis of a 1D Bar
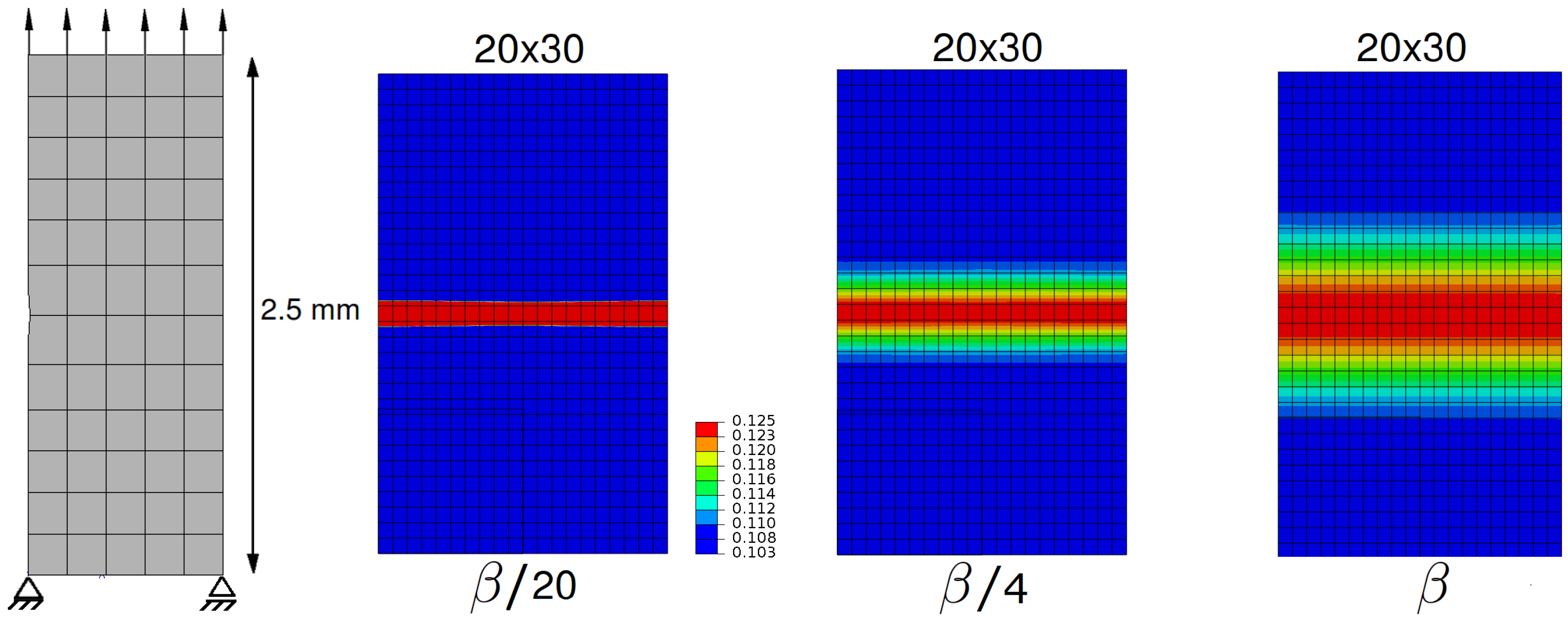
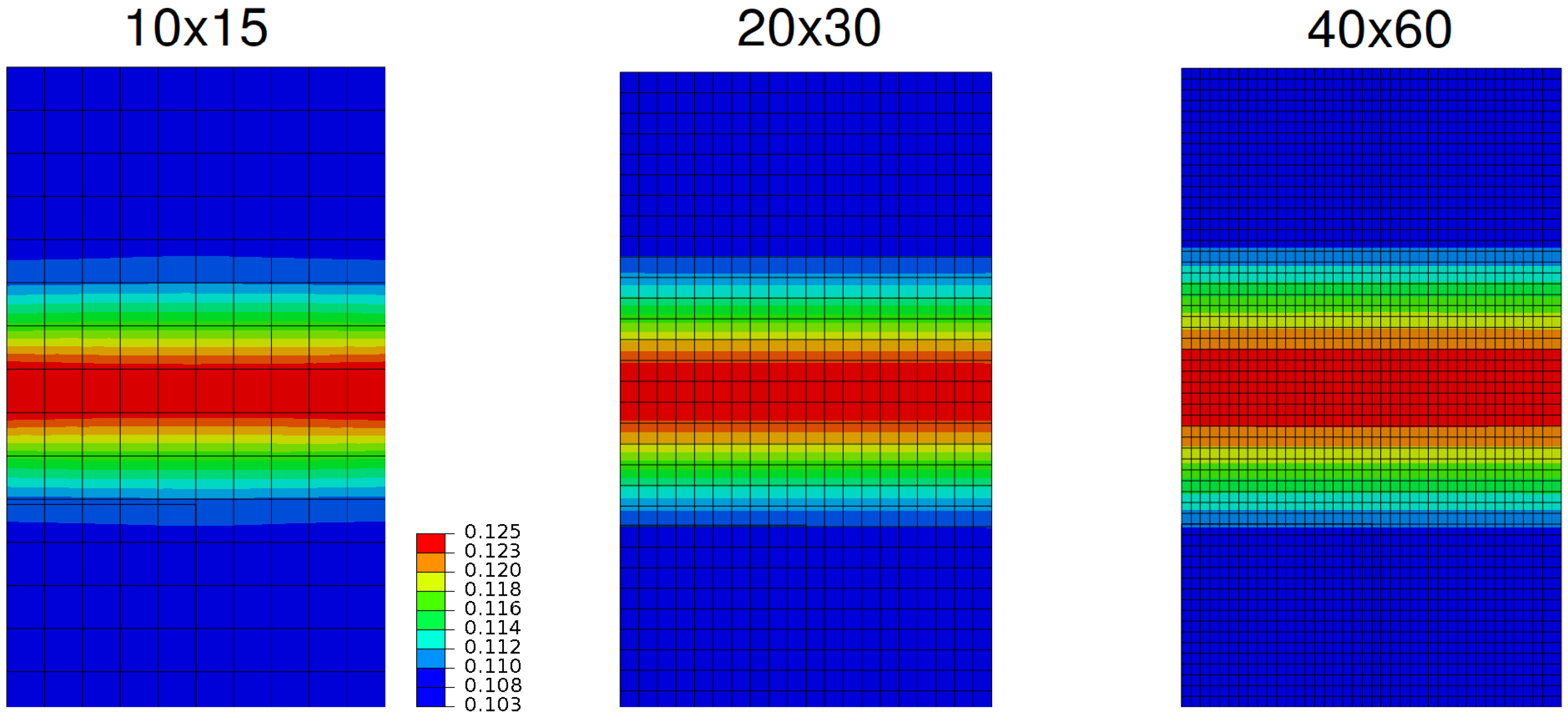
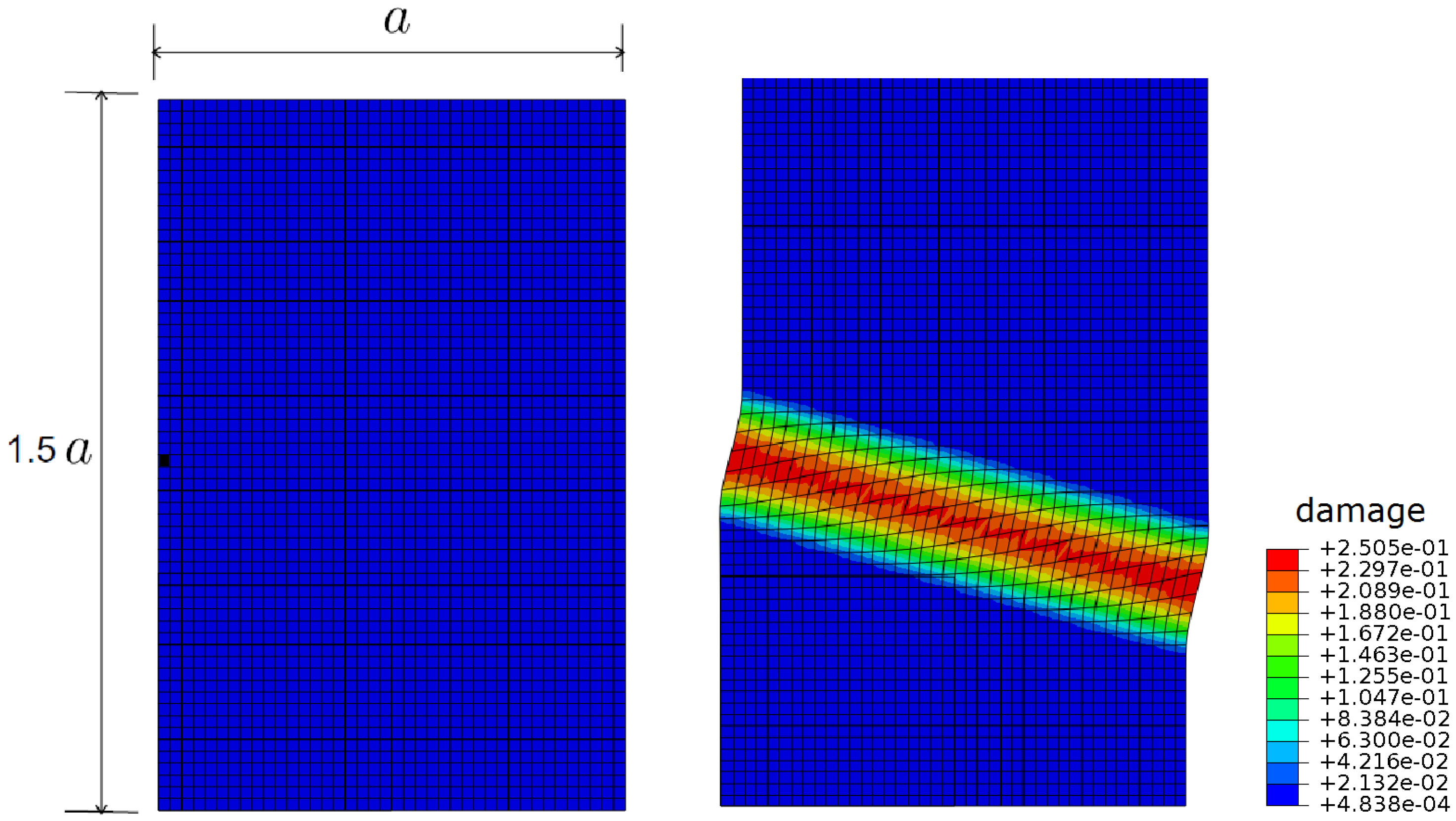
6.2. Analysis of a 2D Single Crystal Block
7. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Aslan, O.; Quilici, S.; Forest, S. Numerical modeling of fatigue crack growth in single crystals based on microdamage theory. Int. J. Damage Mech. 2011, 5, 681–705. [Google Scholar] [CrossRef]
- Sait, F.; Gurses, E.; Aslan, O. Modeling and simulation of coupled phase transformation and stress evolution in thermal barrier coatings. Int. J. Plast. 2020, 134, 102790. [Google Scholar] [CrossRef]
- Flouriot, S.; Forest, S.; Cailletaud, G.; Köster, A.; Rémy, L.; Burgardt, B.; Gros, V.; Mosset, S.; Delautre, J. Strain localization at the crack tip in single crystal CT specimens under monotonous loading: 3D finite element analyses and application to nickel-base superalloys. Int. J. Fract. 2003, 124, 43–77. [Google Scholar] [CrossRef]
- Parisot, R.; Forest, S.; Pineau, A.; Nguyen, F.; Démonet, X.; Mataigne, J.-M. Deformation and damage mechanisms of zinc coatings on galvanized steel sheets, Part II: Damage modes. Metall. Mater. Trans. 2003, 35A, 813–823. [Google Scholar] [CrossRef]
- Musienko, A.; Cailletaud, G. Simulation of inter and transgranular crack propagation in polycrystalline aggregates due to stress corrosion cracking. Acta Mater. 2009, 57, 3840–3855. [Google Scholar] [CrossRef] [Green Version]
- Aifantis, E.C. On the microstructural origin of certain inelastic models. J. Eng. Mat. Technol. 1984, 106, 106. [Google Scholar] [CrossRef]
- Aifantis, E.C. The physics of plastic deformation. Int. J. Plast. 1987, 3, 211–247. [Google Scholar] [CrossRef]
- De Borst, R.; Muhlhaus, H.B. Gradient dependent plasticity: Formulation and algorithmic aspects. Int. J. Numer. Meth. Eng. 1992, 35, 521–539. [Google Scholar] [CrossRef] [Green Version]
- De Borst, R.; Sluys, L.J.; Muhlhaus, H.B.; Pamin, J. Fundamental issues in finite element analysis of localization of deformation. Eng. Comput. 1993, 10, 99–121. [Google Scholar] [CrossRef] [Green Version]
- De Borst, R.; Pamin, J. Some novel developments in finite element procedures for gradient-dependent plasticity. Int. J. Numer. Meth. Eng. 1996, 39, 2477–2505. [Google Scholar] [CrossRef]
- Engelen, R.A.B.; Geers, M.G.D.; Baaijens, F.P.T. Nonlocal implicit gradient enhanced elasto-plasticity for the modelling of softening behaviour. Int. J. Numer. Meth. Eng. 1996, 19, 403–433. [Google Scholar] [CrossRef]
- Geers, M.G.D. Finite strain logarithmic hyperelasto-plasticity with softening: A strongly non-local implicit gradient framework. Comput. Methods Appl. Mech. Eng. 1996, 193, 3377–3401. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; Geers, M.G.D.; de Borst, R.; Brekelmans, W.A.M. A critical comparison of nonlocal and gradient-enhanced softening continua. Int. J. Solids. Struct. 2001, 38, 7723–7746. [Google Scholar] [CrossRef]
- Geers, M.G.D. On the role of moving elastic-plastic boundaries in strain gradient plasticity. Model. Simul. Mater. Sci. Eng. 2007, 15, 7723–7746. [Google Scholar]
- Forest, S. Micromorphic approach for gradient elasticity, viscoplasticity, and damage. J. Eng. Mech. 2009, 135, 117–131. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Anand, L. Thermodynamics applied to gradient theories involving the accumulated plastic strain: The theories of Aifantis and Fleck and Hutchinson and their generalization. J. Mech. Phys. Solids. 2009, 57, 405–421. [Google Scholar] [CrossRef]
- Anand, L.; Aslan, O.; Chester, S.A. A large-deformation gradient theory for elasticplastic materials: Strain softening and regularization of shear bands. Int. J. Plasticity 2012, 30–31, 116–143. [Google Scholar] [CrossRef]
- Aslan, O.; Forest, S. Crack growth modelling in single crystals based on higher order continua. Comp. Mater. Sci. 2009, 3, 756–761. [Google Scholar] [CrossRef]
- Aslan, O.; Cordero, N.M.; Gaubert, A.; Forest, S. Micromorphic approach to single crystal plasticity and damage. Int. J. Eng. Sci. 2011, 49, 1311–1325. [Google Scholar] [CrossRef]
- Kröner, E. Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Arch. Ration. Mech. Anal. 1959, 4, 273–334. [Google Scholar] [CrossRef]
- Hencky, H. The elastic behavior of vulcanized rubber. Rubber Chem. Technol. 1933, 2, 217–224. [Google Scholar] [CrossRef]
- Anand, L. Moderate deformations in extension-torsion of incompressible isotropic elastic materials. J. Mech. Phys. Solids 1986, 34, 293–304. [Google Scholar] [CrossRef]
- Anand, L. On, H. Hencky’s approximate strain-energy function for moderate deformations. J. Appl. Mech. 2011, 46, 78–82. [Google Scholar] [CrossRef]
| B | H | |||||
|---|---|---|---|---|---|---|
| 7.0 × | 1.5 × | 3.0 × | 1.0 × | 2.0 × | −1.0 × | 6.0 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aslan, O.; Bayraktar, E. A Large-Deformation Gradient Damage Model for Single Crystals Based on Microdamage Theory. Appl. Sci. 2020, 10, 9142. https://doi.org/10.3390/app10249142
Aslan O, Bayraktar E. A Large-Deformation Gradient Damage Model for Single Crystals Based on Microdamage Theory. Applied Sciences. 2020; 10(24):9142. https://doi.org/10.3390/app10249142
Chicago/Turabian StyleAslan, Ozgur, and Emin Bayraktar. 2020. "A Large-Deformation Gradient Damage Model for Single Crystals Based on Microdamage Theory" Applied Sciences 10, no. 24: 9142. https://doi.org/10.3390/app10249142
APA StyleAslan, O., & Bayraktar, E. (2020). A Large-Deformation Gradient Damage Model for Single Crystals Based on Microdamage Theory. Applied Sciences, 10(24), 9142. https://doi.org/10.3390/app10249142






