Next Article in Journal
Machine Learning-Based Prediction of Air Quality
Previous Article in Journal
Systematic Quantification of Cell Confluence in Human Normal Oral Fibroblasts
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 10
Issue 24
10.3390/app10249149
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Building Reliable Massive Capacity SSDs through a Flash Aware RAID-Like Protection †

by
Jaeho Kim
1 and
Jung Kyu Park
2,*
1
Department of Aerospace and Software Engineering & Engineering Research Institute, Gyeongsang National University, Jinju 52828, Korea
2
Department of Computer Software Engineering, Changshin University, Changwon 51352, Korea
*
Author to whom correspondence should be addressed.
†
This Paper Is an Extended Version of Paper Published in the IEEE International Conference on Consumer Electronics (ICCE) 2020, Las Vegas, NV, USA, 4–6 January 2020.
Appl. Sci. 2020, 10(24), 9149; https://doi.org/10.3390/app10249149
Submission received: 14 November 2020 / Revised: 16 December 2020 / Accepted: 16 December 2020 / Published: 21 December 2020
(This article belongs to the Section Computing and Artificial Intelligence)
Browse Figures
Versions Notes

Abstract

:
The demand for mass storage devices has become an inevitable consequence of the explosive increase in data volume. The three-dimensional (3D) vertical NAND (V-NAND) and quad-level cell (QLC) technologies rapidly accelerate the capacity increase of flash memory based storage system, such as SSDs (Solid State Drives). Massive capacity SSDs adopt dozens or hundreds of flash memory chips in order to implement large capacity storage. However, employing such a large number of flash chips increases the error rate in SSDs. A RAID-like technique inside an SSD has been used in a variety of commercial products, along with various studies, in order to protect user data. With the advent of new types of massive storage devices, studies on the design of RAID-like protection techniques for such huge capacity SSDs are important and essential. In this paper, we propose a massive SSD-Aware Parity Logging (mSAPL) scheme that protects against n-failures at the same time in a stripe, where n is protection strength that is specified by the user. The proposed technique allows for us to choose the strength of protection for user data. We implemented mSAPL on a trace-based simulator and evaluated it with real-world I/O workload traces. In addition, we quantitatively analyze the error rates of a flash based SSD for different RAID-like configurations with analytic models. We show that mSAPL outperforms the state-of-the-art RAID-like technique in the performance and reliability.

1. Introduction

The amount of data has exploded in recent years due to the rapid development of big data and AI technologies. Therefore, the demand for mass storage devices inevitably follows [1]. The three-dimensional (3D) vertical NAND (V-NAND) and quad-level cell (QLC) flash memories enable the implementation of massive capacity of Solid State Drives (SSDs) [2], which features a capacity of tens or hundred of TB on the market [3,4,5,6,7,8]. Furthermore, the capacity is increasing rapidly with the developments of semiconductor process and firmware controller technologies. Such massive capacity SSDs adopt tens or hundreds of flash memory chips in order to implement large capacity storage. For example, a 15 TB capacity SSD employs 512 256 Gb V-NAND flash chips [8]. However, employing such a large number of flash chips increases the error rate in SSDs. A technique that can cope with errors other than Error Correction Code (ECC) is necessary due to the increase in the number of flash memories and the complexity of SSD configuration. In order to supplement ECC, Redundant Array of Independent Disks (RAID)-like configurations are typically used to protect data [9,10,11,12,13]. However, existing RAID-like techniques with fixed data protection strength that tolerate a single failure has limitations in introducing it to massive capacity of SSDs [11,12,14]. It is necessary to maintain two or more parities per RAID stripe like RAID6 in order to cope with two or more simultaneous failures [15]. However, increasing the parity write, which is redundant data, adversely affects the space, lifespan, and performance of the storage device. In particular, it is more efficient and practical to apply differentiated data protection for each type of data [16], rather than having the fixed strength of protection for all data in massive capacity SSDs.
In order to reflect this strategy, we proposed a massive SSD-Aware Parity Logging (mSAPL) scheme that protects against n-failures in a stripe, where n is protection strength that is specified by the user [17]. The design of mSAPL considers the following three elements. (1) It is necessary to cope with more than one failure per stripe due to employing a large number of flash memories in a massive capacity storage. (2) A parity update policy should be designed to minimize a GC overhead in SSDs in order to minimize the overhead caused by parity management. (3) Applying the same protection strength to all data in a massive flash based storage is not suitable for both performance and reliability aspects. Different protection strengths are needed for different kinds of data type or a user criterion among a massive volume of data. For reliability analysis, it is important to derive the quantitative error rates of a flash-based SSD. Therefore, we analyzed the error rates of various flash memory error recovery techniques.
We implement mSAPL on a trace-based SSD simulator [18] and then compare it with the state-of-the-art RAID-like scheme, showing improvements of performance by lowering parity management overhead inside the SSD. In addition, we observe that the mSAPL can significantly improve the reliability and extend the lifetime of the SSD by 16% when compared to the state-of-the-art RAID-like technology.
The remainder of this paper is organized, as follows. In the next section, we present an overview of flash based SSD and reliability of SSDs. In Section 3, we introduce the motivation of our work with analyzing the error rates of an SSD. Subsequently, in Section 4, we present the design of the mSAPL scheme. Afterwards, we describe the experimental environment results with various workloads in Section 5. After that, we analyze the reliability and lifetime of an SSD by deriving equations for RAID-like techniques. Finally, we conclude the paper with a summary and conclusions in Section 7.

2. Background and Related Work

In this section, we briefly explain the basics of flash memory and SSDs, and introduce the reliability of SSDs.

2.1. Basics of Flash Memory and SSDs

Most of thee SSDs in the market today provide high performance and large capacity by connecting a large number of NAND flash memories to channels and parallelizing them with a SSD controller [19,20,21,22,23].
NAND flash memory chips are composed of multiple dies and planes, which has a large number of blocks, and each block has a fixed number of pages [19,21]. Read and write operations, which are basic operations of flash memory, are performed in units of pages. IO requests that are issued from the host are interleaved at the multiple channel, die, and plane levels [19,21,22,24].
One of the unique characteristics of flash memory is that, once data have been written, pages cannot be overwritten [25]. In order to write data to the page, the block containing the page must be erased first. This erase operation is another order of magnitude slower than a page write operation. Furthermore, the number of erasures after writing, generally termed the Program/Erasure (P/E) cycle, is limited, depending on the manufacturing technology. Today, four types of technologies, namely, single-level cell (SLC), multi-level cell (MLC), triple-level cell (TLC), and qual-level cell (QLC), are widely used [2].
Empty pages in flash memory are eventually exhausted due to the continuous service of write requests. To get rid of invalid pages, which hold old data that were logically overwritten, and turn them back to clean pages, a process that is called garbage collection (GC) is performed. Because the erase operation is only performed in block units, GC starts by finding the target block (also called victim block) to be erased [19,20,21,26]. However, in many cases, the victim block may hold a mixture of valid and invalid pages, so, before the erase operation is done on this block, valid data that are contained in the block must be transferred to a page of another block that has already been erased [20,21,27]. This movement of valid page data is called write amplification (WA), which is the main overhead of GC [19,21,26,27].

2.2. Write Amplification in Flash Memory

Flash memory entails GCs to service write requests due to out-of-place update nature. In other words, a larger amount of write is performed internally than the amount of writes requested from the file system. We describe this as a write amplification. Therefore, as the write amplification increases, the performance of flash-based SSDs decreases [19,21,26,27]. From another point of view, as the amount of writing increases on flash memories, SSDs wear out and its lifespan decreases [28]. In addition, when a RAID-like protection technology is employed inside an SSD, the amount of writing increases, due to parity writing [11,12,14]. Additional writes other than write requests from the file system occur due to GC, parity write, and metadata. The Write Amplification Factor (WAF) is used to represent additional write amounts to the storage [26,27].

2.3. Reliability of Flash Memory

Although SSDs are widely used in various fields, errors including hardware and firmware are still being reported including enterprise area [29,30,31,32,33]. The occurrence of such errors is mostly due to the characteristics of the flash memory introduced below.
The flash memory has a limited number of allowed P/E times, depending on the process technology (e.g., SLC, MLC, TLC, or QLC). The increased density by storing multiple bits per cell provides larger storage capacity. However, it sacrifices reliability as the number of allowable P/E cycles is drastically reduced [28,34]. The permitted P/E cycles for SLC is around 100,000, whereas the P/E cycles for MLC, TLC, and QLC are 35,000–10,000, 5000, and 1000, respectively [28,35,36]. The technique of storing multiple bits per cell not only reduces P/E cycles, but it also increases the bit errors [37]. The bit error rate (BER) of the flash memory increases in proportion to the cumulative P/E count. The bit error rate is a representative measure of the reliability of the flash memory due to these characteristics. Mielke et al. and Sun et al. measure the bit error rates of flash chips of various manufacturer and reports relationship between bit error rate (BER) and P/E cycles [38,39].
Recently, V-NAND or 3D NAND has been introduced on the market by major manufacturers. The technology allows for stackings memory cells vertically in order to increase capacity without reducing cell size. Although the cell stack structure of 3D and planar (i.e., 2D) NAND are different, the bit error characteristics of two types of flash memories are similar [40,41]. The BER of 3D NAND is generally lower than that of 2D NAND. Particularly, the relationship between the number of P/E cycles and increase of BER is the same for both [40,42,43,44]. In this paper, we use BER as the reliability criterion for flash memory storage. Therefore, our proposal aiming to lower BER is universally applicable, regardless of the NAND flash memory type. For 2D and 3D NAND flash memories, the absolute values of BER of these two types of memory are different, but this does not affect the design of our proposed scheme.
The Error Correction Code (ECC), which is stored in out of band (OOB) area in each page, is a basic method for detecting and correcting errors in flash memory [45,46,47,48]. ECC has the capability to detect and correct a fixed number of bit errors, regardless of the error rate of flash memory since the ECC code size is fixed. Therefore, ECC cannot cope with bit errors exceeding the detectable range [45,46,48]. Studies for addressing the limitation of ECC have been proposed, but they require additional hardware and complex management overhead [49,50].
RAID-like protection architectures have been introduced in order to complement the limitation of the ECC [11,12,14,51]. The RAID-like architectures significantly reduce BER of flash memory. However, it requires redundant data for the protection [9,14,28], and this overhead could be more prominent in a large capacity of SSD. Several studies present how the data protection of RAID affects BER reduction through numerical analysis models [9,14,51,52,53,54]. In this paper, we also analyze the reliability of RAID configuration inside SSD through the same BER analysis model [14,52,53].
In this work, we address this redundant overhead of RAID architecture while improving the reliability of flash memory for a massive capacity of SSD.

3. Motivation

In this section, we introduce the motive of this study by showing the bit error rate according to the increase in the number of P/E cycles when RAID-like technology is built in an SSD.
Figure 1 show the error rate of an SSD device with RAID protections. The x-axis shows the number of P/E cycles and the y-axis shows the page error rate. The horizontal red bar indicates the industry standard error rate, which refers to the error rate of the HDD [55].
The error rate is calculated under the following assumptions. Three different RAID configurations are applied to the SSD simulator that is presented in Table 1. We ran the Financial workload in Table 2 and measured WAF of the SSD by simulating each RAID (i.e., RAID0, RAID5, and RAID6) configuration. The three configurations provide different levels of reliability by maintaining different numbers of parity data per stripe. That is, RAID0, RAID5, and RAID6 maintain zero, one, and two parities per stripe, respectively. We adopt the state-of-the-art RAID-like technique, which was proposed for flash memory friendly policy, in order to minimize the parity management overhead of RAID configurations in the SSD [14]. Recall that ECC is used by default and RAID-like configurations are introduced in order to supplement reliability. The ECC is capable of correcting eight-bit errors per 1 KB code word with BCH code [45] and a stripe consists of 16 pages for the RAID configurations. The raw bit error rate (RBER) of flash memory is based on 3x nm MLC products [38].The WAF of flash memory increases due to the parity write cost of RAIDs, which increases the number of P/E and bit error rate. Through the simulation, we observed that RAID5 and RAID6 increase WAF by 20 and 50%, respectively, as compared to RAID0 configuration, due to parity overhead.
Figure 1a assumes that the WAFs of RAID0, RAID5, and RAID6 are all the same in order to find out the reduction in error rate that can be obtained with pure RAID protection. On the other hand, Figure 1b reflects the increase in WAF due to parity overhead. As a result of observation in the simulation using Financial workload, the WAF ratio of RAID0, RAID5, and RAID6 is 1:1.2:1.5, respectively. Recall that, as WAF increases, the number of P/E increases. We derive the uncorrectable page error rate (UPER) of each RAID configuration through Equations (1)–(5), as in Section 6. The procedure for deriving the UPER in Figure 1 is as follows.
(1)
We first obtain the P/E cycles from the SSD simulator for Financial workload.
(2)
Subsequently, the RBER can be converted from the obtained P/E number through Equation (1) or [38].
(3)
With the given ECC parameter in Table 3, we calculate the UPER through Equation (2). This probability is the error rate when the ECC is applied, and it is the same for RAID0. This is because RAID0 has no error recovery function other than ECC.
(4)
RAID5 reduces the error rate by providing enhanced data protection through ECC and RAID parity. Therefor, the UPER for RAID5 is derived by Equations (3) and (4).
(5)
Because RAID6 maintains two parities per stripe, the error rate can be further reduced and it is calculated by Equation (5).
We observe that the UPER of RAID5 and RAID6 exceed the UPER of RAID0 at 16K and 19K P/E cycles, respectively, in Figure 1b. The relationship and derivation of the corresponding models [14,53] are described in detail in Section 6. Through this, we observe that protecting the data with RAID-like technologies greatly reduces the error rate, but the increase in WAF due to parity management overhead adversely affects the reliability of the SSD. Therefore, reducing the parity cost of RAID-like technologies is a major issue in terms of reliability. In addition, the cost of parity not only affects reliability, but also the performance and lifetime of SSDs [14,28,51].

4. Design of mSAPL

In this section, we describe the design of mSAPL proposed to improve the reliability of massive flash based SSDs.

4.1. Design Goal and Approach

The design goal of mSAPL is to improve the reliability and performance of a massive capacity flash based SSD. mSAPL takes a design approach that considers the following three aspects.
  • It is necessary to cope with more than one failure per stripe due to employing a large number of flash memories in a massive capacity SSD.
  • In order to minimize the overhead caused by parity management, a parity update policy should be designed in order to minimize a GC overhead in SSDs.
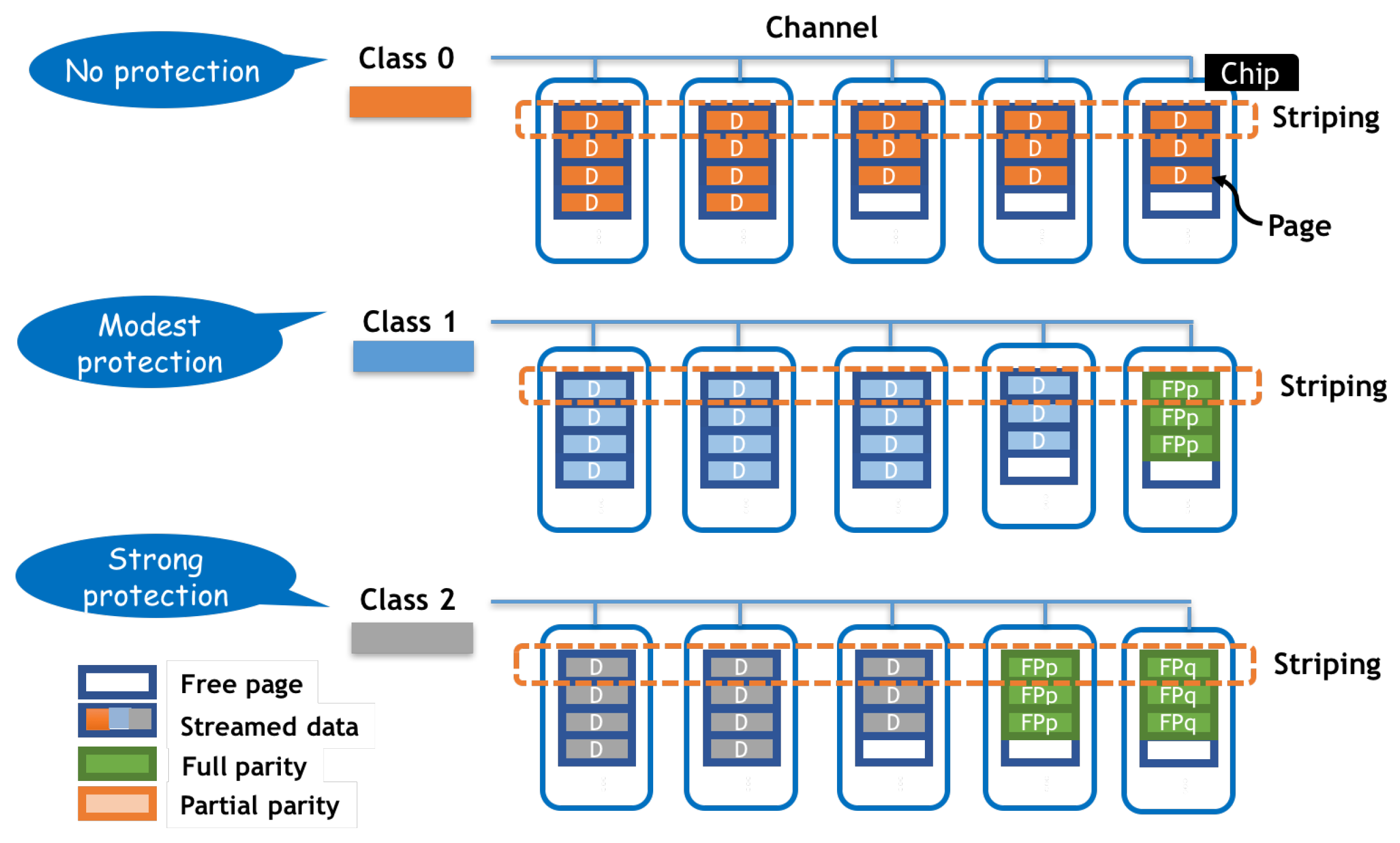
  • Applying the same protection strength to all data in a massive flash based storage is not suitable for both performance and reliability aspects. Different protection strengths are needed for different kinds of data type or a user specification among massive volume of data.

4.2. Differentiate Protection Strength through Classification

A massive capacity SSD can store various kinds of data according to the purpose of usage. The mSAPL differentiates protection strengths for each data by classifying the data according to the type of data or the user’s request. Figure 2 shows that data are deployed in the SSD with different data protection policies applied per class. In order to improve reliability, generating parity of the same level for all data has negative effects in terms of space, performance, and lifetime of massive flash memory based SSDs. Therefore, the data protection strengths are differentiated according to the type of data and the classification from the users to alleviate the negative effects.
In this work, user data are classified into multiple types according to the strength of data protection. As shown in Figure 3, the data are categorized into three types that are based on a user selection, such as importance of data. Class 0 is data that do not require data protection and is striped and stored on n flash chips without parity protection like RAID-0. Class 1 is medium-weighted data with RAID-5 (one parity) protection and Class 2 is striped with RAID-6 (two parity) protection as important data.
Classification studies that are based on the type of user data are widely used in previous studies to differentiate services and improve system performance [16,56,57]. The use of the context information from the host in the storage device has been widely used in recent studies and the interface standard has also been recently established [57,58].

4.3. Data Placement in a Stripe

mSAPL adopts the latest flash memory friendly stripe construction policy, called eSAP [14], to minimize parity update overhead for all user data, regardless of the protection strength. Conventional RAID approaches impose excessive parity update overhead of flash memory storage, due to out-of-place characteristics. eSAP reduces the parity overhead through dynamically constructing a stripe in the order of write requests, regardless of the logical number of user data. In this way, a stripe is formed with only newly written data, so there is no need to read in order to generate new parity. However, a partial stripe is constructed according to the size of the data write request and the stripe may not be completed. The data of the partial stripe must be protected with a parity, called Partial-stripe Parity (PP), before the full stripe is completed. The PP write consumes more user space, which increases the GC cost and reduces the performance and lifetime due to additional writes. For large-capacity SSDs with a large number of flash chips, the cost of such parity management is higher. mSAPL proposes a new way to deal with partial stripe parity. The method reduces the GC overhead of the flash memory storage and it is described in the following section.

4.4. Partial-Stripe Parity Space of mSAPL

We introduce a method for reducing parity management overhead through Partial-stripe Parity (PP). If the user request does not arrive while filling the stripe or if the flush command comes in, the stripe may not be completely filled. That is, the data that are not protected by the parity become unprotected for a certain period of time in the stripe. In order to protect such data, PP is written in the current write stripe. mSAPL provides a way to minimize this parity management overhead.
Figure 4 shows how mSAPL performs parity writing. It is assumed that the SSD has six flash memory chips and it has two blocks per chip and four pages per block. One stripe is composed of pages that correspond to the same page offset of each chip. In the figure, stripe 0 consists of user data LBN D0~D3 and full stripe parities FPp and FPq. Subsequently, D4 to D7 are written to the 2nd pages of the block 0 across all the chips and stripe 1 is constructed with two full stripe parities (FPp and FPq). The remaining D8 and D9 of the write request are written to the third pages of block 0 on the chip 0 and 1, respectively. After a certain period of time (in our evaluation, 50 ms is specified), the PPs are written PP block (block 1) in order to protect the partial stripe. mSAPL maintains logical to physical (L2P) and PP map table on SDRAM. In the map, LPN, CN, PBN, and PPN denote the logical page number, chip number, physical block number, and physical page number, respectively. The map contents is periodically flushed to flash memory in order to keep consistency of the map tables [59].
By doing this, the cost of copying valid pages during GC is greatly reduced, since adjacent PPs, which belong to the same block, are invalidated at a similar period. If the PPs in one block, which are erase units, are invalidated at the same time, then the GC cost decreases [57,60].

5. Performance Evaluation

We implemented mSAPL on the DiskSim simulator with SSD Extension [18] in order to evaluate performance. Table 1 shows the parameter of the SSD simulator that is used in our evaluation. Inside the SSD, the RAID configuration is done at the flash memory chip level, and one stripe is composed of eight pages (one page per chip). The real application I/O traces are used as the workloads for evaluation, and Table 2 shows the characteristics.
A comparison target of the evaluation is eSAP, which is the most typical and the state-of-the-art RAID technique considering flash memory [14]. The performance evaluation shows the WAF and I/O response time, which are representative criteria for measuring SSD’s internal data management efficiency.

5.1. Write Amplification Factor

WAF represents the ratio of the amount written to flash memory to the user request. Figure 5 shows the measured WAF of eSAP and mSAPL for each workload. We observe the mSAPL decrease 13.3%, 14.8%, and 19.1% of WAFs for Financial, Exchange, and MSN workloads, respectively, as compared to eSAP. The reasons of the results are that mSAPL employs multi-level protection and our new policy for handling PPs. Multi-level protection protects only selected data. Selected data are classified by similar characteristics, which results in hot-cold classification effects and reducing GC costs. The designated Partial-stripe Parity (PP) blocks reduce GC costs, since PP in a block is invalidated at the same time or at a similar time.

5.2. Response Time

Figure 6 shows the average response time for mSAPL and eSAP. We observe that mSAPL reduces the average response time for all three workloads. mSAPL reduces 18.6%, 20.2%, and 26.2% of average response time for Financial, Exchange, and MSN workloads, respectively. mSAPL could reduce the response time through multi-level protection and PP blocks.

6. Analysis of Reliability and Lifetime of SSDs

In this section, we analyze the reliability and lifetime of the SSD through deriving equations of the error rates for mSAPL and the state-of-the-art flash aware RAID technology, called eSAP [14]. The raw bit error rate (RBER) of the flash memory increases exponentially with respect to the P/E cycle, as follows. In this equation, x denotes the P/E cycle of a block, and A and B are constant values according to the type of flash memory and process [38].
R B E R ( x ) = A · e B x
In order to reduce the error of a page, the flash memory records the ECC in the spare area whenever the page is written [45,48]. The ECC code is capable of correcting up to k bit errors per specific code word (n). Correctable page error rate (CPER) and uncorrectable page error rate (UPER) can be calculated as binary distributions, as follows [10,51].
C P E R ( n , k , x ) = ∑ i = 0 k n i R B E R ( x ) i ( 1 − R B E R ( x ) ) n − i U P E R ( n k , x ) = 1 − C P E R ( n , k , x )
However, the ECC has a limitation, in that, if the number of error bits exceeds k, then the error can not be corrected by the ECC. To solve this problem, a method for correcting page errors through RAID-like technologies have been introduced [11,14]. A RAID stripe consist of a certain number of multiple pages, including a fixed number of parity pages for recovering errors. Therefore, errors that cannot be corrected by ECC are recovered through RAID parity. However, in order to perform error recovery through RAID parity, errors must first be detected through ECC. ECC can correct errors up to k bits and detect errors up to 2k bits. Therefore, the detectable page error rate (DPER), which can not be corrected, but detected by ECC, is defined, as follows.
D P E R ( n , k , x ) = ∑ i = k + 1 2 k n i R B E R ( x ) i · ( 1 − R B E R ( x ) ) n − i
In case of one parity per stripe (i.e., a RAID5 type configuration), failures can be recovered for the following two cases: (1) pages in a stripe have correctable error bits by ECC. (2) detectable errors by the ECC occur in one page in a stripe and correctable errors by the ECC occur in the remaining pages. Therefore, the uncorrectable page error rate with the ECC and RAID5 configuration are derived is as follows.
U P E R R 5 ( n , k , x ) = 1 N ( 1 − N 0 C P E R ( n , k , x ) N − N 1 C P E R ( n , k , x ) N − 1 · D P E R ( n , k , k ) )
Let us consider a case where two parities per stripe are maintained (i.e., a RAID6 configuration). In case of the RAID6 configuration, two pages can be recovered when errors in two pages that can be detected by ECC occur simultaneously. Therefore, the uncorrectable page error rate is calculated, as follows.
U P E R R 6 ( n , k , x ) = 1 N ( 1 − N 0 C P E R ( n , k , x ) N − N 1 C P E R ( n , k , x ) N − 1 · D P E R ( n , k , k ) − N 2 C P E R ( n , k , x ) N − 2 · D P E R ( n , k , k ) 2 )
mSAPL has lower WAF than that of eSAP for all three workloads, as shown in Figure 5. Figure 7 compares the page error rates of mSAPL and eSAP when running the Financial workload on the SSD simulator. The uncorrectable page error rates in the figure are derived from Equation (5), which means that mSAPL and eSAP maintain two parities per stripe (i.e., employing RAID6 configuration). Table 3 presents the parameters of the equations for calculating the UPER. mSAPL shows lower UPER than that of eSAP until about 19,000 P/E cycles. The reason of the lower UPER of mSAPL is that mSAPL reduces WAF as compared to the state-of-the-art RAID technology, called eSAP. Assuming that the acceptable error rate is the error rate of hard disk (1.0 × 10−15), the lifespan of the SSD while using mSAPL technique is increased by 1.16 times when compared to eSAP.

7. Conclusions

We propose a RAID-like protection scheme, called mSAPL, for massive capacity of flash based SSDs. mSAPL supports differentiated data protection strengths according to user’s decision to improves reliability and performance of flash based SSDs. Design of mSAPL considers the following three elements. (1) It is necessary to cope with more than one failure per stripe due to employing a large number of flash memories in a massive capacity storage. (2) In order to minimize the overhead that is caused by parity management, a parity update policy should be designed to minimize a GC overhead in SSDs. (3) Different protection strengths are required for different kinds of data type or a user criterion among massive volume of data.
Our evaluation study shows the effectiveness of mSAPL with multiple workloads in terms of reliability, WAF, and average response time. Furthermore, we analyze the error rates of a flash based SSD for different RAID-like configurations through deriving error rate equations. We observe that mSAPL outperforms the state-of-the-art RAID-like technique regarding the reliability and lifetime of an SSD.

Author Contributions

Both authors contributed to this work by collaboration. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (No. 2018R1C1B5046282). This work was supported by Changshin University Research Fund of 2020-010.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Siddiqa, A.; Karim, A.; Gani, A. Big data storage technologies: A survey. Front. Inf. Technol. Electron. Eng. 2017, 18, 1040–1070. [Google Scholar] [CrossRef] [Green Version]
  2. Wikipedia. Flash Memory. 2019. Available online: https://en.wikipedia.org/wiki/Flash_memory (accessed on 20 November 2020).
  3. Samsung. Enterprise SSDs. 2019. Available online: http://www.samsung.com/semiconductor/ssd/enterprise-ssd/ (accessed on 20 November 2020).
  4. Kingsley-Hughes, A. World’s lArgest SSD Hits 100TB. 2018. Available online: https://www.zdnet.com/article/worlds-largest-ssd-hits-100tb/ (accessed on 20 November 2020).
  5. Tung, L. ‘World’s Largest’ SSD Revealed as Seagate Unveils 60TB Monster. 2016. Available online: https://www.zdnet.com/article/worlds-largest-ssd-revealed-as-seagate-unveils-60tb-monster/ (accessed on 20 November 2020).
  6. Nimbus Data World’s Highest Capacity and Most Efficient SSDs. 2020. Available online: https://nimbusdata.com/products/exadrive/ (accessed on 20 November 2020).
  7. Samsung. Samsung Electronics Begins Mass Production of Industry’s Largest Capacity SSD-30.72TB-for Next-Generation Enterprise Systems. 2018. Available online: https://news.samsung.com/global/samsung-electronics-begins-mass-production-of-industrys-largest-capacity-ssd-30-72tb-for-next-generation-enterprise-systems (accessed on 20 November 2020).
  8. Mearian, L. Samsung’s Massive 15TB SSD Can Be Yours. 2016. Available online: https://www.computerworld.com/article/3101165/samsungs-massive-15tb-ssd-can-be-yours-for-about-10k.html (accessed on 20 November 2020).
  9. Moon, S.; Reddy, A.L.N. Don’t Let RAID Raid the Lifetime of Your SSD Array. In Proceedings of the 5th USENIX Conference on Hot Topics in Storage and File Systems, San Jose, CA, USA, 27–28 June 2013. [Google Scholar]
  10. Kim, J.; Lee, J.; Choi, J.; Lee, D.; Noh, S.H. Improving SSD Reliability with RAID via Elastic Striping and Anywhere Parity. In Proceedings of the 43rd Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Budapest, Hungary, 24–27 June 2013. [Google Scholar]
  11. Im, S.; Shin, D. Flash-Aware RAID Techniques for Dependable and High-Performance Flash Memory SSD. IEEE Trans. Comput. 2011, 60, 80–92. [Google Scholar] [CrossRef]
  12. Lee, Y.; Jung, S.; Song, Y.H. FRA: A flash-aware redundancy array of flash storage devices. In Proceedings of the CODES+ISSS ’09, Grenoble, France, 11–16 October 2009; pp. 163–172. [Google Scholar]
  13. Micron. NAND Flash Media Management Through RAIN. 2011. Available online: https://www.micron.com/~/media/documents/products/technical-marketing-brief/brief-ssd-rain.pdf (accessed on 20 November 2020).
  14. Kim, J.; Lee, E.; Choi, J.; Lee, D.; Noh, S.H. Chip-Level RAID with Flexible Stripe Size and Parity Placement for Enhanced SSD Reliability. IEEE Trans. Comput. 2016, 65, 1116–1130. [Google Scholar] [CrossRef]
  15. Wikipedia. Standard RAID Levels. 2019. Available online: https://en.wikipedia.org/wiki/Standard_RAID_levels (accessed on 20 November 2020).
  16. Mesnier, M.P.; Akers, J.B. Differentiated Storage Services. SIGOPS Oper. Syst. Rev. 2011, 45, 45–53. [Google Scholar] [CrossRef]
  17. Kim, J.; Lee, E.; Park, J.K. Flash based SSD Aware Parity Logging for Building Reliable Massive Capacity SSDs. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 4–6 January 2020; pp. 1–4. [Google Scholar]
  18. Prabhakaran, V.; Wobber, T. SSD Extension for DiskSim Simulation Environment. 2008. Available online: http://research.microsoft.com/en-us/downloads/b41019e2-1d2b-44d8-b512-ba35ab814cd4 (accessed on 20 November 2020).
  19. Agrawal, N.; Prabhakaran, V.; Wobber, T.; Davis, J.D.; Manasse, M.; Panigrahy, R. Design tradeoffs for SSD performance. In 2008 USENIX ATC; USENIX Association: Berkeley, CA, USA, 2008; pp. 57–70. [Google Scholar]
  20. Seong, Y.J.; Nam, E.H.; Yoon, J.H.; Kim, H.; yong Choi, J.; Lee, S.; Bae, Y.H.; Lee, J.; Cho, Y.; Min, S.L. Hydra: A Block-Mapped Parallel Flash Memory Solid-State Disk Architecture. IEEE Trans. Comput. 2010, 59, 905–921. [Google Scholar] [CrossRef]
  21. Chen, F.; Koufaty, D.A.; Zhang, X. Understanding Intrinsic Characteristics and System Implications of Flash Memory Based Solid State Drives. In Proceedings of the Eleventh International Joint Conference on Measurement and Modeling of Computer Systems, Seattle, WA, USA, 15–19 June 2009; pp. 181–192. [Google Scholar]
  22. Jung, M.; Kandemir, M. An Evaluation of Different Page Allocation Strategies on High-speed SSDs. In Proceedings of the USENIX Workshop on Hot Topics in Storage and File Systems (HotStorage), Boston, MA, USA, 13–14 June 2012. [Google Scholar]
  23. Lee, J.; Byun, E.; Park, H.; Choi, J.; Lee, D.; Noh, S.H. CPS-SIM: Configurable and accurate clock precision solid state drive simulator. In Proceedings of the 2009 ACM Symposium on Applied Computing, Honolulu, HI, USA, 15–19 March 2009; pp. 318–325. [Google Scholar]
  24. Hu, Y.; Jiang, H.; Feng, D.; Tian, L.; Luo, H.; Zhang, S. Performance Impact and Interplay of SSD Parallelism Through Advanced Commands, Allocation Strategy and Data Granularity. In Proceedings of the International Conference on Supercomputing (ICS), Tucson, AZ, USA, 31 May–4 June 2011; pp. 96–107. [Google Scholar]
  25. Kim, J.; Kim, J.M.; Noh, S.; Min, S.L.; Cho, Y. A space-efficient flash translation layer for CompactFlash systems. IEEE Trans. Consum. Electron. 2002, 48, 366–375. [Google Scholar]
  26. Desnoyers, P. Analytic Models of SSD Write Performance. ACM Trans. Storage 2014, 10, 8:1–8:25. [Google Scholar] [CrossRef]
  27. Kwon, H.; Kim, E.; Choi, J.; Lee, D.; Noh, S.H. Janus-FTL: Finding the Optimal Point on the Spectrum between Page and Block Mapping Schemes. In Proceedings of the International Conference on Embedded Software (EMSOFT), Scottsdale, AZ, USA, 24–29 October 2010; pp. 169–178. [Google Scholar]
  28. Kim, B.S.; Choi, J.; Min, S.L. Design Tradeoffs for SSD Reliability. In Proceedings of the 17th USENIX Conference on File and Storage Technologies (FAST 19), Boston, MA, USA, 25–28 February 2019; pp. 281–294. [Google Scholar]
  29. Gunawi, H.S.; Suminto, R.O.; Sears, R.; Golliher, C.; Sundararaman, S.; Lin, X.; Emami, T.; Sheng, W.; Bidokhti, N.; McCaffrey, C.; et al. Fail-Slow at Scale: Evidence of Hardware Performance Faults in Large Production Systems. ACM Trans. Storage 2018, 14, 1–26. [Google Scholar] [CrossRef]
  30. Maneas, S.; Mahdaviani, K.; Emami, T.; Schroeder, B. A Study of SSD Reliability in Large Scale Enterprise Storage Deployments. In Proceedings of the 18th USENIX Conference on File and Storage Technologies (FAST 20), Santa Clara, CA, USA, 25–27 February 2020; pp. 137–149. [Google Scholar]
  31. Xu, E.; Zheng, M.; Qin, F.; Xu, Y.; Wu, J. Lessons and Actions: What We Learned from 10 K SSD-Related Storage System Failures. In Proceedings of the 2019 USENIX Conference on Usenix Annual Technical (ATC) Conference, Renton, WA, USA, 10–12 July 2019. [Google Scholar]
  32. Tai, A.; Kryczka, A.; Kanaujia, S.O.; Jamieson, K.; Freedman, M.J.; Cidon, A. Who’s Afraid of Uncorrectable Bit Errors? Online Recovery of Flash Errors with Distributed Redundancy. In Proceedings of the 2019 USENIX Conference on Usenix Annual Technical (ATC) Conference, Renton, WA, USA, 10–12 July 2019; pp. 977–991. [Google Scholar]
  33. Narayanan, I.; Wang, D.; Jeon, M.; Sharma, B.; Caulfield, L.; Sivasubramaniam, A.; Cutler, B.; Liu, J.; Khessib, B.; Vaid, K. SSD Failures in Datacenters: What? When? And Why? In Proceedings of the 9th ACM International on Systems and Storage Conference (SYSTOR), Haifa, Israel, 6–8 June 2016. [Google Scholar]
  34. Grupp, L.M.; Caulfield, A.M.; Coburn, J.; Swanson, S.; Yaakobi, E.; Siegel, P.H.; Wolf, J.K. Characterizing Flash Memory: Anomalies, Observations, and Applications. In Proceedings of the MICRO 42, New York, NY, USA, 12–16 December 2009. [Google Scholar]
  35. Grupp, L.M.; Davis, J.D.; Swanson, S. The Bleak Future of NAND Flash Memory. In Proceedings of the FAST’12; USENIX Association: San Jose, CA, USA, 2012; pp. 17–24. [Google Scholar]
  36. What Is QLC Flash and What Workloads It Is Good for? 2019. Available online: https://www.computerweekly.com/feature/What-is-QLC-flash-and-what-workloads-it-is-good-for (accessed on 20 November 2020).
  37. Cai, Y.; Haratsch, E.F.; Mutlu, O.; Mai, K. Error Patterns in MLC NAND Flash Memory: Measurement, Characterization, and Analysis. In Proceedings of the Design, Automation and Test in Europe Conference and Exhibition (DATE), Dresden, Germany, 12–16 March 2012; pp. 521–526. [Google Scholar]
  38. Mielke, N.; Marquar, T.; Wu, N.; Kessenich, J.; Belgal, H.; Schares, E.; Trivedi, F.; Goodness, E.; Nevill, L. Bit Error Rate in NAND Flash Memories. In Proceedings of the IEEE International Reliability Physics Symposium, Phoenix, AZ, USA, 27 April–1 May 2008; pp. 9–19. [Google Scholar]
  39. Sun, H.; Grayson, P.; Wood, B. Quantifying Reliability of Solid-State Storage from Multiple Aspects. In Proceedings of the IEEE International Workshop on Storage Network Architecture and Parallel I/O (SNAPI ’11), Denver, CO, USA, 25 May 2011. [Google Scholar]
  40. Breen, P.; Griffin, T.; Papandreou, N.; Parnell, T.; Tressler, G. 3D NAND Assessment for Next Generation Flash Applications; Santa Clara, CA, USA, 9–11 August 2016. Available online: https://www.flashmemorysummit.com/English/Collaterals/Proceedings/2016/20160810_FM22_Tressler.pdf (accessed on 20 November 2020).
  41. Kim, H.; Ahn, S.; Shin, Y.G.; Lee, K.; Jung, E. Evolution of NAND Flash Memory: From 2D to 3D as a Storage Market Leader. In Proceedings of the 2017 IEEE International Memory Workshop (IMW), Monterey, CA, USA, 14–17 May 2017; pp. 1–4. [Google Scholar]
  42. Papandreou, N.; Pozidis, H.; Parnell, T.; Ioannou, N.; Pletka, R.; Tomic, S.; Breen, P.; Tressler, G.; Fry, A.; Fisher, T. Characterization and Analysis of Bit Errors in 3D TLC NAND Flash Memory. In Proceedings of the 2019 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 31 March–4 April 2019; pp. 1–6. [Google Scholar]
  43. Luo, Y.; Ghose, S.; Cai, Y.; Haratsch, E.F.; Mutlu, O. Improving 3D NAND Flash Memory Lifetime by Tolerating Early Retention Loss and Process Variation. In Proceedings of the 2018 ACM International Conference on Measurement and Modeling of Computer Systems, Irvine, CA, USA, 18–22 June 2018; pp. 1–48. [Google Scholar]
  44. Mizoguchi, K.; Takahashi, T.; Aritome, S.; Takeuchi, K. Data-Retention Characteristics Comparison of 2D and 3D TLC NAND Flash Memories. In Proceedings of the 2017 IEEE International Memory Workshop (IMW), Monterey, CA, USA, 14–17 May 2017; pp. 1–4. [Google Scholar]
  45. Chen, S. What Types of ECC Should Be Used on Flash Memory? 2007. Available online: http://www.spansion.com/Support/AppNotes/ (accessed on 20 November 2020).
  46. Sommer, N. Signal Processing and the Evolution of NAND Flash Memory. 2010. Available online: https://www.embedded-computing.com/embedded-computing-design/signal-processing-and-the-evolution-of-nand-flash-memory (accessed on 20 November 2020).
  47. Deal, E. Trends in NAND Flash Memory Error Correction. Cyclic Design, White Paper. June 2009. Available online: http://www.cyclicdesign.com/whitepapers/Cyclic_Design_NAND_ECC.pdf (accessed on 1 October 2020).
  48. Mariano, M. ECC Options for Improving NAND Flash Memory Reliability. Micron. 2012. Available online: http://www.micron.com/support/software/~/media/Documents/Products/Software%20Article/SWNL_implementing_ecc.ashx (accessed on 20 November 2020).
  49. Lee, H.; Jung, S.; Song, Y.H. PCRAM-assisted ECC management for enhanced data reliability in flash storage systems. IEEE Trans. Consum. Electron. 2012, 58, 849–856. [Google Scholar] [CrossRef]
  50. Hu, Y.; Xiao, N.; Liu, X. An elastic error correction code technique for NAND flash-based consumer electronic devices. IEEE Trans. Consum. Electron. 2013, 59, 1–8. [Google Scholar] [CrossRef]
  51. Lee, S.; Lee, B.; Koh, K.; Bahn, H. A Lifespan-Aware Reliability Scheme for RAID-based Flash Storage. In Proceedings of the SAC’11, TaiChung, Taiwan, 21–24 March 2011; pp. 374–379. [Google Scholar]
  52. Zambelli, C.; Marelli, A.; Micheloni, R.; Olivo, P. Modeling the Endurance Reliability of Intradisk RAID Solutions for Mid-1X TLC NAND Flash Solid-State Drives. IEEE Trans. Device Mater. Reliab. 2017, 17, 713–721. [Google Scholar] [CrossRef]
  53. Park, H.; Kim, J.; Choi, J.; Lee, D.; Noh, S.H. Incremental redundancy to reduce data retention errors in flash-based SSDs. In Proceedings of the 2015 31st Symposium on Mass Storage Systems and Technologies (MSST), Santa Clara, CA, USA, 30 May–5 June 2015; pp. 1–13. [Google Scholar]
  54. Pan, W.; Xie, T. A Mirroring-Assisted Channel-RAID5 SSD for Mobile Applications. ACM Trans. Embed. Comput. Syst. 2018, 17, 1–27. [Google Scholar] [CrossRef]
  55. Gary, J.; van Ingen, C. Empirical Measurements of Disk Failure Rates and Error Rates; Technical Report MSR-TR-2005-166; Microsoft: Redmond, WA, USA, December 2005. [Google Scholar]
  56. Thereska, E.; Ballani, H.; O’Shea, G.; Karagiannis, T.; Rowstron, A.; Talpey, T.; Black, R.; Zhu, T. IOFlow: A Software-defined Storage Architecture. In Proceedings of the ACM Symposium on Operating Systems Principles (SOSP), Farmington, PA USA, 3–6 November 2013; pp. 182–196. [Google Scholar]
  57. Kang, J.U.; Hyun, J.; Maeng, H.; Cho, S. The Multi-streamed Solid-State Drive. In Proceedings of the USENIX Workshop on Hot Topics in Storage and File Systems (HotStorage), Philadelphia, PA, USA, 17–18 June 2014. [Google Scholar]
  58. JEDEC. Data Tag Mechanism of eMMC. “Standard Specification No. JESD84-B45”. Available online: http://www.jedec.org/sites/default/files/docs/jesd84-B45.pdf (accessed on 20 November 2020).
  59. Gupta, A.; Kim, Y.; Urgaonkar, B. DFTL: A flash translation layer employing demand-based selective caching of page-level address mappings. In Proceedings of the 14th International Conference on Architectural Support for Programming Languages and Operating Systems, Washington, DC, USA, 7–11 March 2009; pp. 229–240. [Google Scholar]
  60. Rho, E.; Joshi, K.; Shin, S.U.; Shetty, N.J.; Hwang, J.; Cho, S.; Lee, D.D.; Jeong, J. FStream: Managing Flash Streams in the File System. In Proceedings of the 16th USENIX Conference on File and Storage Technologies (FAST 18), Renton, WA, USA, 9–11 April 2018; USENIX Association: Oakland, CA, USA, 2018; pp. 257–264. [Google Scholar]
Applsci 10 09149 g001 550
Figure 1. Comparison of the error rate according to the parity write cost in an SSD.
Figure 1. Comparison of the error rate according to the parity write cost in an SSD.
Applsci 10 09149 g001
Applsci 10 09149 g002 550
Figure 2. Overall architecture of mSAPL.
Figure 2. Overall architecture of mSAPL.
Applsci 10 09149 g002
Applsci 10 09149 g003 550
Figure 3. Example of multi-level protection with mSAPL.
Figure 3. Example of multi-level protection with mSAPL.
Applsci 10 09149 g003
Applsci 10 09149 g004 550
Figure 4. Example of writing partial stripe parity of mSAPL.
Figure 4. Example of writing partial stripe parity of mSAPL.
Applsci 10 09149 g004
Applsci 10 09149 g005 550
Figure 5. Comparison of Write Amplification Factors (WAFs).
Figure 5. Comparison of Write Amplification Factors (WAFs).
Applsci 10 09149 g005
Applsci 10 09149 g006 550
Figure 6. Comparison of average response time.
Figure 6. Comparison of average response time.
Applsci 10 09149 g006
Applsci 10 09149 g007 550
Figure 7. Comparison of UPER for mSAPL and eSAP.
Figure 7. Comparison of UPER for mSAPL and eSAP.
Applsci 10 09149 g007
Table
Table 1. Parameters of Solid State Drives (SSD) Simulator.
Table 1. Parameters of Solid State Drives (SSD) Simulator.
ParameterValueParameterValue
Total capacity128 GBNo. of chips8
Planes per chip8Blocks per plane2048
Pages per block128Page size8 KB
Over-provisioning4%GC policyGreedy
Write time800 usRead time60 us
Erase time1.5 msPage Xfer time30 ns
Parities per stripe2Stripe size8 × 4 KB
Table
Table 2. Characteristics of I/O workloads.
Table 2. Characteristics of I/O workloads.
WorkloadRequestWriteAverage
TotalRatioReq. Size
Financial14.1 GB0.7614 KB
MSN28.2 GB0.9627 KB
Exchange19.2 GB0.6717 KB
Table
Table 3. Parameters of UPER equations.
Table 3. Parameters of UPER equations.
ParameterDescriptionValue
AConstant [38]1.09 × 10 − 7
BConstant [38]3.01 × 10 − 4
nNo. of bits of an ECC code word64 Kb
kCorrectable bits of ECC8
NNo. of pages for a stripe8
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Kim, J.; Park, J.K. Building Reliable Massive Capacity SSDs through a Flash Aware RAID-Like Protection. Appl. Sci. 2020, 10, 9149. https://doi.org/10.3390/app10249149

AMA Style

Kim J, Park JK. Building Reliable Massive Capacity SSDs through a Flash Aware RAID-Like Protection. Applied Sciences. 2020; 10(24):9149. https://doi.org/10.3390/app10249149

Chicago/Turabian Style

Kim, Jaeho, and Jung Kyu Park. 2020. "Building Reliable Massive Capacity SSDs through a Flash Aware RAID-Like Protection" Applied Sciences 10, no. 24: 9149. https://doi.org/10.3390/app10249149

APA Style

Kim, J., & Park, J. K. (2020). Building Reliable Massive Capacity SSDs through a Flash Aware RAID-Like Protection. Applied Sciences, 10(24), 9149. https://doi.org/10.3390/app10249149

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop