Abstract
Consumer depth cameras bring about cheap and fast acquisition of 3D models. However, the precision and resolution of these consumer depth cameras cannot satisfy the requirements of some 3D face applications. In this paper, we present a super-resolution method for reconstructing a high resolution 3D face model from a low resolution 3D face model acquired from a consumer depth camera. We used a group of radial curves to represent a 3D face. For a given low resolution 3D face model, we first extracted radial curves on it, and then estimated their corresponding high resolution ones by radial curve matching, for which Dynamic Time Warping (DTW) was used. Finally, a reference high resolution 3D face model was deformed to generate a high resolution face model by using the radial curves as the constraining feature. We evaluated our method both qualitatively and quantitatively, and the experimental results validated our method.
1. Introduction
In recent years, 3D face modeling has received extensive attention due to its widespread applications in face recognition, animation and 3D video games. The usual way to obtain 3D face models is 3D scanning by some high resolution 3D scanners, such as Artec Eva and Minolta Vivid. However, these professional 3D scanners are expensive and have a high computational cost. For this reason, some consumer depth cameras, such as Microsoft Kinect and Intel RealSense, have drawn wide attention because of their low cost and easy integration. A depth camera is able to acquire the depth information of objects in a scene; i.e., the distances between the camera and the surfaces of objects. Depth information can be transformed into 3D information; i.e., corresponding 3D models of objects can be constructed from depth images. The emergence of consumer depth cameras makes a cheap and fast acquisition of 3D face model possible. However, the precision and resolution of these consumer depth cameras cannot satisfy the requirements of some 3D face applications. How to acquire high precision and high resolution face models fast and cheaply still is a challenging task. Much research about 3D reconstruction based on depth cameras has been done [1,2,3], but the resolution is not high enough when involving the human face. Improving the precision and resolution of 3D face models acquired by consumer cameras, i.e., 3D face model super-resolution, is a valuable study.
In this work, we built a database including 111 sets of 3D face models, where each set contains a low resolution 3D face model and the corresponding high resolution one of the same participant. The low resolution model was acquired by Kinect with the Kinect Fusion method [2], while the high resolution one was acquired by Artec Eva. With this database, we propose a 3D face model super-resolution method based on radial curves. In the method, we estimate the radial curves of the high resolution 3D face model from the corresponding low resolution one, and generate the high resolution 3D face model by deforming a high resolution face reference with the landmarks on the radial curves being control points. Experiments validated the proposed method.
2. Related Work
Formerly, super-resolution [4] was introduced for 2D images, and its aim was to obtain a high-resolution image from one or more possibly contaminated low resolution observations. Super-resolution methods in the 3D space can be divided into two categories: methods based on multi-view fusion [2,5,6,7,8] and methods based on learning [9,10,11].
Methods based on multi-view fusion obtain a high-resolution depth map or 3D model by fusing depth scans from multiple viewpoints. In order to solve the problem of low resolution and high noise, Sebastian et al. [5] proposed a depth image super-resolution method named Lidar Boost to deal with depth images acquired by ToF cameras. Its main idea is to minimize an energy function, which consists of a data fidelity term and a geometry prior regularization term. The data fidelity term is to ensure the similarity between the super-resolution image and the low-resolution image. The regularization term is to ensure the smoothness of super-resolution image edges, and it is defined as the sum of L2 norm of the gradient in each pixel. Based on the Lidar Boost method, Cui et al. [12] proposed a shape scanning algorithm. They tried three non-linear regularization terms to replace the linear regularization term in Lidar Boost for improving the super-resolution accuracy, and fused the high resolution depth data to generate a high resolution 3D model by a probabilistic scan alignment approach. Methods in [2,6,7,8] reduce the noise in depth data by aligning multiple scans to construct a high resolution 3D model, where Kinect Fusion [2] is a classical real-time 3D reconstruction method designed for general objects using Microsoft Kinect, while the methods in [6,7,8] are designed for 3D face models. These methods intend to approach the noise problem in depth data by fusing multiple scans using geometry priors, and still cannot well solve the low accuracy problem of the depth sensors.
Learning based methods [10] obtain high resolution models by teaching the mapping from the low resolution models to high resolution models. Methods in [9,10] use mesh simplification and down-sampling to high-resolution 3D face models to produce low-resolution models. The super-resolution is realized by building the mapping in the regular representation domain. However, the way they generate the low resolution models cannot well simulate the imaging conditions of the sensors so that the methods are not necessarily applicable for the observed real low resolution models. Liang et al. [11] proposed a super-resolution method for 3D face models from a single depth frame. They divide the input depth frame into several regions, eyes, nose, etc., and search the best matching shape per region from a database they built, which includes 3D face models from 1204 distinct individuals. Then the matched database shapes are combined with the input depth frame to generate a high resolution face model. This method relies on the similarity measure between the low resolution face regions and the corresponding high-resolution regions. But this similarity measure between the heterogeneous data is unreliable. Unlike the methods mentioned above, our method is to estimate a high resolution 3D face model from a low resolution face model based on radial curve estimation. We use radial curves to represent 3D face models, and estimate the radial curves on the high resolution model through the radial curve matching of the low resolution models. The high resolution 3D face model is recovered using the estimated radial curves.
3. Method
In this section, we introduce the proposed 3D face model super-resolution method, where radial curves are used to represent the face model. For a low resolution face model, we first extract a set of radial curves from it, and then estimate the radial curves on its corresponding high resolution face model. Finally, we recover the high resolution face model using the estimated radial curves.
3.1. The Radial Curves’ Extraction
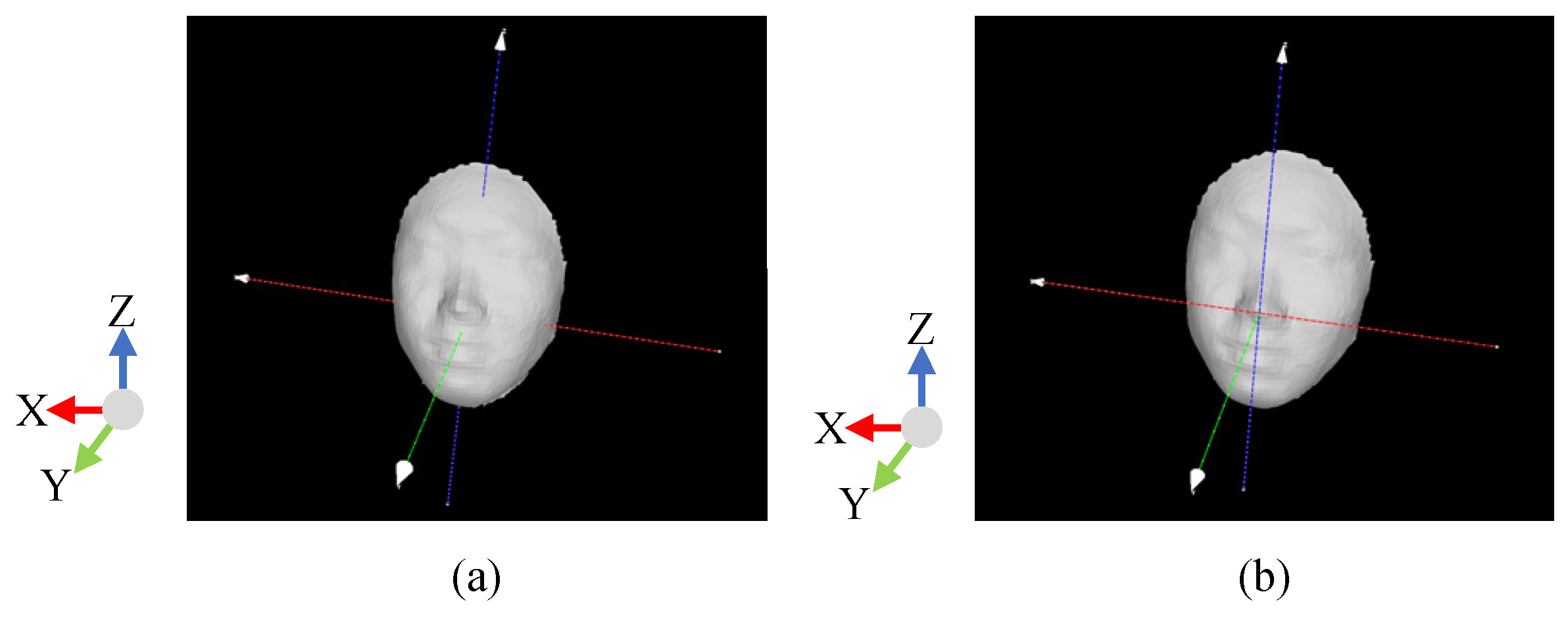
As shown in Figure 1, radial curves on a face model are a set of curves passing the nose tip, and they can be defined by the intersections between the face model and a set of planes obtained by rotating the facial symmetrical plane around the normal direction of the nose tip. Thus, we have to locate the nose tip point and the symmetrical plane of a 3D face model for radial curve extraction. Assuming 3D face models are triangle mesh models, we first perform principal component analysis for the vertices of the face model to establish an initial coordinate system, i.e., three principal orientations as the coordinate axes with Y axis throughout the front and back of the face, and then fit a cylinder to the 3D face model [13] and adjust the Z axis to be parallel to the cylinder’s axis. The nose tip is the most protruding point on the face’s surface, so the point of the maximal value in Y direction is chosen as the nose tip. In order to establish a uniform coordinate system, we adjust the Y axis to be parallel to the normal vector of the nose tip with the nose tip being the coordinate center (see Figure 2). In order to get rid of the influence caused by the head size on the following radial curve estimation, we normalize all high resolution face models in size by a scale transform determined by several landmarks, such as nose tip and the corner points of the eyes and mouth, which can be labeled manually. With the nose tip, we estimate the symmetrical plane of the 3D face model using the method proposed in [14].

Figure 1.
(a) Symmetrical plane (shown in green). (b) Radial curves (shown in red) on 3D face model.
Figure 2.
(a) Initial coordinate system. (b) Standard face model coordinate system. X, Y and Z axes are shown in red, green and blue respectively.
As illustrated in Figure 1, we get the first radial curve by calculating the intersection curve of the symmetrical plane and face mesh, and then rotate the symmetrical plane around the normal direction of the nose tip by a fixed angle gradually to extract the other radial curves. A radial curve is initially represented in a group of intersection points of the plane and edges of the triangle patches in the face mesh. For the following radial curve registration, we uniformly sample the radial curves with a fixed sampling internal (here, 0.01 by experience). Then each radial curve is represented in a point sequence.
3.2. Radial Curves Database
As radial curves are used as the main feature of face models, we establish a radial curve database for the subsequent processing. As described in Section 1, the face database we used contains 111 sets of face models. Each set consists of a low resolution 3D face model and a high resolution 3D face model. Considering N sets of low resolution and high resolution face models in face database D, for low resolution face models, we extract K curves from each model as described in Section 3.1 using as rotation angle. Then we can get the low resolution face model radial curve database , where represents the set of the i-th radial curve from all the low resolution face models. Similarly, for high resolution face models, we extract corresponding radial curves using the same . These curves form the high resolution face model radial curve database . Figure 3 shows radial curves and numbering when °; i.e., .

Figure 3.
The correspondence of radial curves from (a) the low-resolution model and (b) the high-resolution model.
3.3. Face Model Super-Resolution
3.3.1. Registration of Radial Curves
Registration of radial curves is to establish a point correspondence between two radial curves. Dynamic Time Warping (DTW) [15] is one method for finding an optimal match and measuring similarity between two temporal sequences in time series analysis. It has been applied to analyze any data that can be transferred into a linear sequence, such as temporal sequences of video, audio and graphics data. Here radial curve registration and radial curve match are realized by using DTW of two point sequences of two radial curves. In order to keep the central feature area of human faces for radial curve match, we eliminate the boundary area by cropping all the radial curves in the following way: keep 40 points in both directions centered on the nose tip point. After cropping, each radial curve has 81 sampling points at equal intervals. The point number 40 is set by the distribution of face features. Of course, it can vary in a wide range; for example, 38 or 42 are also good selections, since they will have little influence on the radial curve match as long as the sampling points cover the central face feature area.
For point sequences of two radial curves, DTW is used to align them and measure their similarity. In order to eliminate the pose effect, we use the curvature difference of the two curve points to calculate their local match cost in DTW. For example, the curvature of the point can be calculated as follows:
where is radius of curvature; i.e., is radius of circle determined by . Assume the matching point pair of two curves X and Y is ; then the match cost of the two curves is:
3.3.2. Radial Curve Estimation
For a given low resolution model , we want to estimate radial curves of its unknown high resolution model . Here we assume that if two radial curves from two low resolution models are similar, the corresponding curves from their high resolution models are similar too. The assumption is rational since the data acquisition conditions (and thus noise models) are consistent for low resolution models. Thus, for a low resolution 3D face model, we first extract its radial curves . Then, for each radial curve , we search for the best matching curve in the radial curve database by the match cost defined in Equation (2); i.e., the curve with the least match cost. Finally, the radial curve in the database corresponding to the best matching curve is considered as the estimated high resolution radial curve . Then, . Considering the symmetry of the human face, the i-th and -th radial curve should be symmetric about the symmetry plane of the human face with a even number K (see Figure 3). Thus, assume the i-th radial curve comes from the high resolution face model labeled ; that is,
Correspondingly, the -th radial curve should come from the same face model; that is,
3.3.3. High Resolution Face Model Estimation
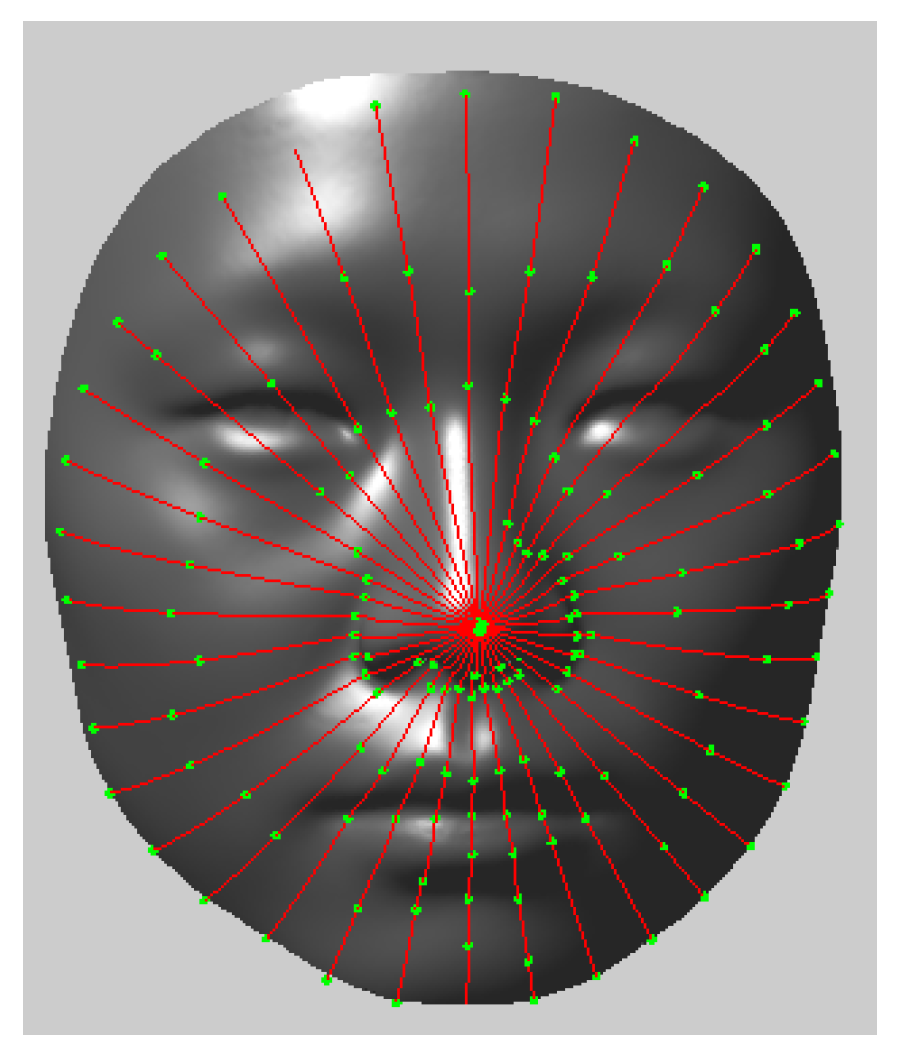
At this point, although we obtained a radial curve representation of the estimated high resolution face model, its mesh model was not yet constructed. For constructing the mesh model, the mean high resolution face model was taken as the reference and radial curves were extracted from it. Some landmarks were labeled on each radial curve manually (see Figure 4). Then, the corresponding landmarks on each radial curve we estimated by DTW registration of corresponding radial curves could be obtained. Therefore, we obtained a group of landmark correspondences between the estimated high resolution face model and the reference face model. Using these landmark correspondences as control points, we deformed the reference face to obtain the high resolution face models by using Thin Plate Splines (TPS) deformation [13].
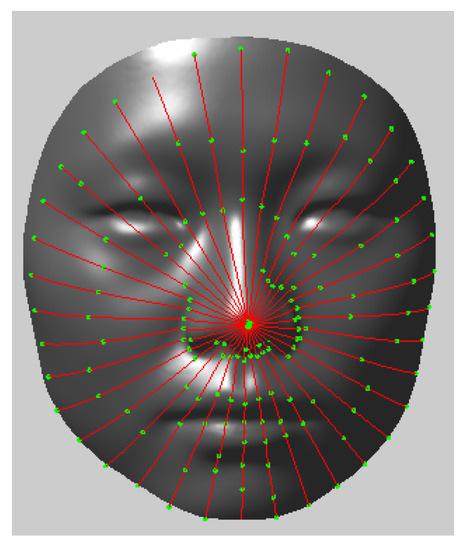
Figure 4.
Landmarks (green) on reference model.
4. Experiment
4.1. Experiment Setting
4.1.1. Dataset
In this research, we used face models from 111 people. For each person, one low resolution face model was acquired using Kinect and one high resolution face model was acquired using Artec Eva, with a neutral expression. The high resolution face model was considered ground truth. In the experiment, we performed leave-one-out cross validation; i.e., one low resolution face model from the face database was chosen as a probe; meanwhile, we removed its corresponding high resolution face model from the face database. The remaining 110 sets of face models formed the training database D. We chose a high resolution model from D randomly as the reference model. When labeling landmarks on the reference model, it is better to choose inflection points or points that have large curvature. On the reference model, 158 landmarks are labeled.
4.1.2. Error Metric
To evaluate experimental results quantitatively, we used the attribute deviation metric [16] to measure geometric error between the high resolution estimation model and the ground truth model. Given a 3D surface S and a 3D point p, the distance between p and S based on attribute i is defined as:
where is the nearest point from point p to surface S, attribute deviation distance is the difference between p and by attribute i, and denotes the attribute i of the point p. Here we use two attributes; i.e., the point coordinate and the normal vector [17]. We calculate mean error for all vertexes of the estimation model to the ground truth model.
4.2. Results and Analysis
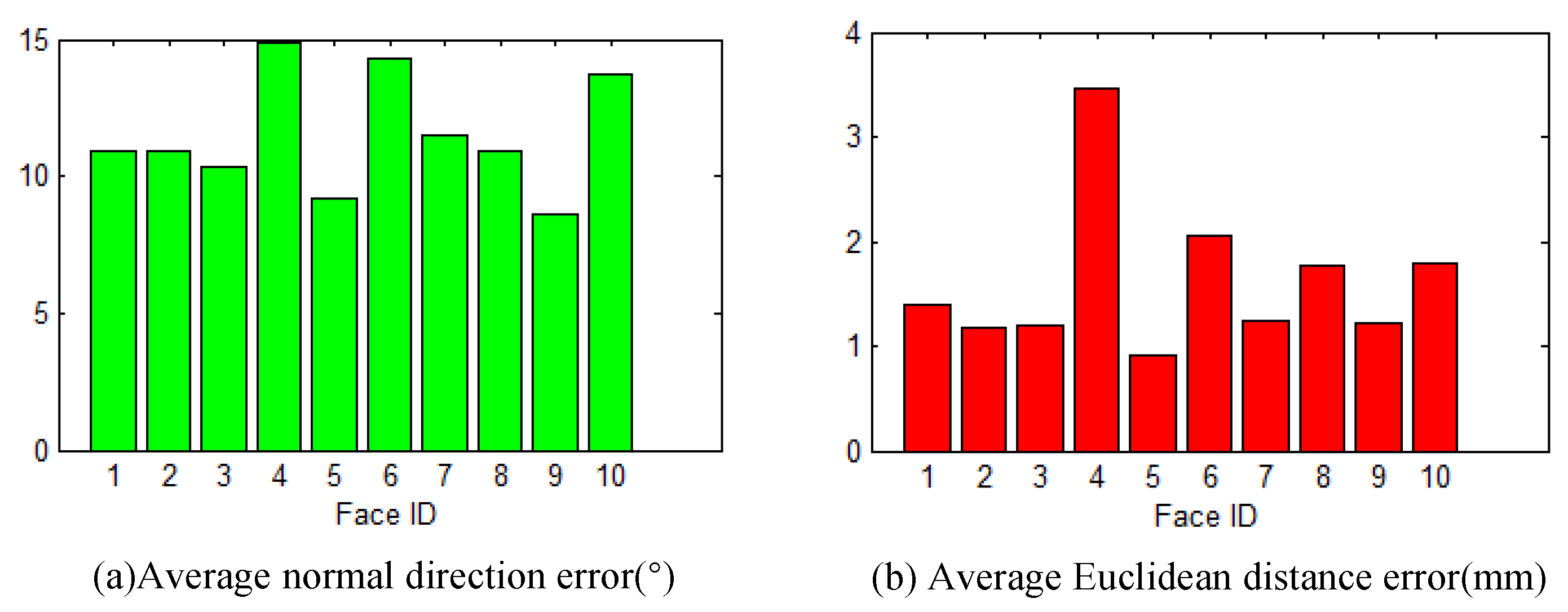
Figure 5 shows 10 super-resolution results we randomly chose, and their error metrics are shown in Figure 6. In Figure 5, low resolution models are shown in the first column; the high resolution models estimated using our method are shown in the second column; the ground truth models are shown in the third column; and the comparison diagrams of the estimation models and the ground truths by normal vector are shown in the fourth column. We can see from Figure 5 that each estimation model and its ground truth are similar overall; the error in most regions of the human face is small (i.e., under 15 degrees); and higher error mainly concentrates on boundaries. That is because the calculation of the normal vector is not stable in boundary region. From Figure 6 we can see that the average error in normal direction for each model is less than 15 degrees, and the average error in Euclidean distance is less than 4 mm, but is less than 2 mm for eight models of the total 10 models. By comparing the Figure 5 and Figure 6, we can see that the error metrics of the models of higher error metrics, such as model 4, 7 and 10, are mainly affected by the higher errors in the boundary region. That is, the overall similarity is high for each estimation model. The experiment demonstrates the proposed method is effective.

Figure 5.
Experimental results of 10 face models. For each model, we show the low resolution model, made by the Kinect Fusion [2] method, the high resolution model derived by our method, the ground truth model (short for GT) and the normal direction error displayed with color map from left to right. The color scale of error map is shown in the right.
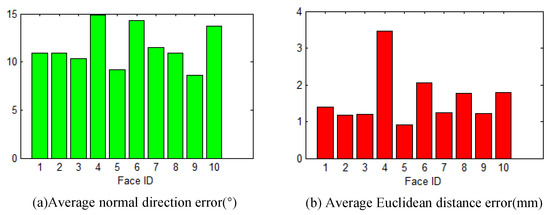
Figure 6.
Errors of the estimated models are shown in histograms.
4.3. Discussion
In the proposed method, radial curves are used to represent the face model. The advantage is that we can estimate the radial curves on the high resolution face models by curve matching among low resolution face models, and then use the estimated radial curves to construct the high resolution face model. In fact, if the point correspondence among 3D face models is established, we also can teach the mapping from low resolution models to high resolution models such as the learning based methods [9,10]. However, it is difficult to establish point correspondence among low resolution 3D face models acquired form a consumer depth camera due to the high noise. The methods in [9,10] use mesh simplification and down-sampling of high-resolution 3D face models to produce low-resolution models. They only need to perform data registration among high-resolution 3D face models, which can be realized easily by many existing methods [13]. We also tried to use the registration method [13] to establish the point correspondence among low resolution 3D face models. As a result, the registration accuracy was very bad. This is the reason why we do not use a learning based method like [9,10]. On the other hand, a larger training dataset is necessary for learning based methods. Our dataset only contains 111 samples; it is not enough in a statistical sense for machine learning. In our work, to improve the statistical sense, we performed leave-one-out validation in the testing phase. The visual results show high similarity against the ground truth. This validates the effectiveness of our proposed method.
5. Conclusions
In this paper, we presented a super-resolution method for 3D face models, aiming to improve the resolution and resolution of 3D face model acquired by consumer depth cameras. We established a face model database which contains low resolution and high resolution face models of 111 participants acquired respectively using Kinect and Artec Eva. Based on this database, we estimated a radial curve database which includes low resolution radial curves and their corresponding high resolution ones. For a given high resolution 3D face model, we first extracted a set of radial curves on it, and then estimated their corresponding high resolution ones by utilizing the radial curve database. Finally, we deformed a reference high resolution 3D face model to generate a high-resolution face model by using radial curves as the main feature. We evaluated the method both quantitatively and qualitatively. The evaluation results show that the proposed method is effective. Our method has practical implications for improving the quality of 3D face models and promoting applications such as 3D face recognition and 3D games. However, our assumption in the radial curve estimation phase, i.e., if two radial curves from two low resolution models are similar, the corresponding curves from their high resolution models are similar too, is too strict. In the future, we will improve the radial curve estimation method to relax this assumption.
Author Contributions
Conceptualization, J.Z. and F.D.; methodology, F.Z., J.Z. and L.W.; software, F.Z.; validation, F.Z.; data curation, F.Z.; writing—original draft preparation, J.Z., L.W. and F.Z.; writing—review and editing, F.Z., J.Z., L.W. and F.D.; visualization, F.Z. and J.Z.; supervision, F.D.; project administration, F.D.; funding acquisition, F.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Natural Science Foundation of China, grant numbers 61572078, 61702293 and 61772050, and the Chinese Postdoctoral Science Foundation, 2017M622137.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berretti, S.; Del Bimbo, A.; Pala, P. Superfaces: A super-resolution model for 3D faces. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 73–82. [Google Scholar]
- Newcombe, R.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.J.; Kohli, P.; Shotton, J.; Hodges, S.; Fitzgibbon, A.W. Kinectfusion: Real-time dense surface mapping and tracking. In Proceedings of the 2011 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; Volume 11, pp. 127–136. [Google Scholar]
- Drira, H.; Amor, B.B.; Daoudi, M.; Srivastava, A. Pose and expression-invariant 3d face recognition using elastic radial curves. In Proceedings of the British Machine Vision Conference, Aberystwyth, UK, 31 August–3 September 2010; pp. 1–11. [Google Scholar]
- Nasrollahi, K.; Moeslund, T.B. Super-resolution: A comprehensive survey. Mach. Vis. Appl. 2014, 25, 1423–1468. [Google Scholar] [CrossRef]
- Schuon, S.; Theobalt, C.; Davis, J.; Thrun, S. Lidarboost: Depth superresolution for tof 3d shape scanning. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 343–350. [Google Scholar]
- Berretti, S.; Pala, P.; Del Bimbo, A. Face recognition by super-resolved 3D models from consumer depth cameras. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1436–1449. [Google Scholar] [CrossRef]
- Hernandez, M.; Choi, J.; Medioni, G. Laser scan quality 3-d face modeling using a low-cost depth camera. In Proceedings of the 2012 Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 1995–1999. [Google Scholar]
- Bondi, E.; Pala, P.; Berretti, S.; Del Bimbo, A. Reconstructing high-resolution face models from kinect depth sequences. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2843–2853. [Google Scholar] [CrossRef]
- Pan, G.; Han, S.; Wu, Z.; Wang, Y. Super-resolution of 3d face. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 389–401. [Google Scholar]
- Peng, S.; Pan, G.; Wu, Z. Learning-based super-resolution of 3D face model. In Proceedings of the IEEE International Conference on Image Processing, Genoa, Italy, 1–14 September 2005; Volume 2, p. II-382. [Google Scholar]
- Liang, S.; Kemelmacher-Shlizerman, I.; Shapiro, L.G. 3d face hallucination from a single depth frame. In Proceedings of the 2014 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014; Volume 1, pp. 31–38. [Google Scholar]
- Cui, Y.; Schuon, S.; Thrun, S.; Stricker, D.; Theobalt, C. Algorithms for 3d shape scanning with a depth camera. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1039–1050. [Google Scholar]
- Chen, Y.; Zhao, J.; Deng, Q.; Duan, F. 3D craniofacial registration using thin-plate spline transform and cylindrical surface projection. PLoS ONE 2017, 12, e0185567. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liu, J.; Tang, X. Robust 3D face recognition by local shape difference boosting. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1858–1870. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Itti, L. Shapedtw: Shape dynamic time warping. Pattern Recognit. 2018, 74, 171–184. [Google Scholar] [CrossRef]
- Roy, M.; Foufou, S.; Truchetet, F. Mesh comparison using attribute deviation metric. Int. J. Image Graph. 2004, 4, 127–140. [Google Scholar] [CrossRef]
- Fouhey, D.F.; Gupta, A.; Hebert, M. Data-driven 3D primitives for single image understanding. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 3392–3399. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).