Next Article in Journal
Uncertainty Analysis of 3D Line Reconstruction in a New Minimal Spatial Line Representation
Previous Article in Journal
Whole-Body Dynamic Analysis of Challenging Slackline Jumping
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 10
Issue 3
10.3390/app10031095
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Density Clustering Algorithm for Simultaneous Modulation Format Identification and OSNR Estimation

by
Zhao Zhao
,
Aiying Yang
*,
Peng Guo
and
Qingzhao Tan
Beijing Institute of Technology, School of Optics and Photonics, 5 South Zhongguancun Street, Haidian District, Beijing 100081, China
*
Author to whom correspondence should be addressed.
Appl. Sci. 2020, 10(3), 1095; https://doi.org/10.3390/app10031095
Submission received: 23 November 2019 / Revised: 18 January 2020 / Accepted: 4 February 2020 / Published: 6 February 2020
(This article belongs to the Section Optics and Lasers)
Browse Figures
Versions Notes

Abstract

:
In this work, we propose a combined method to implement both modulation format identification (MFI) and optical signal-to-noise ratio (OSNR) estimation, a method based on density-based spatial clustering of applications with a noise (DBSCAN) algorithm. The proposed method can automatically extract the cluster number and density information of samples. The cluster number can be used for MFI and the density information combined with a fourth-order polynomial fitting can correctly estimate OSNR. We verify the feasibility of the method through simulation and conceptual proof experiments. The results show that the MFI can achieve 100% accuracy when the OSNR values are higher than the 7% forward error correction (FEC) thresholds for five commonly used modulation formats (MFs) like polarization division multiplexing (PDM)-QPSK, PDM-8PSK, PDM-16QAM, PDM-32QAM, and PDM-64QAM. Mean absolute OSNR estimation errors are not higher than 1 dB for different signals. There is no additional hardware required, so the proposed method has the ability to be integrated into existing optical performance monitoring systems without burden. Furthermore, the proposed method has the potential to be used in bit-error ratio (BER) calculation, linear, or nonlinear impairments monitoring. We believe that our multifunctional and simple method would be favorable to a future elastic optical network (EON).

1. Introduction

In the past 10 years, considerable attention has been given to optical network technology. Traditional wavelength division multiplexing (WDM) optical networks with fixed wavelength and a single modulation format are facing challenges. To satisfy the exponential growth of global communication, optical fiber communication systems are envisioned to be flexible, large capacity, long transmission distance, and high spectral utilization. O. Gerstel et al. proposed the concept of spectrum sliced elastic optical network (EON) with a large capacity, high flexibility, strong scalability, and adaption to various network service forms [1]. In particular, EON based on orthogonal frequency division multiplexing (OFDM) provides an important idea for solving the spectrum flexibility problem of optical networks and has attracted extensive interest.
In EONs, the unit of spectral resources is no longer fixed wavelength, but the smaller frequency gap. According to network operating demands, the EONs will be capable of dynamically implementing signal of different modulation formats (MFs), data rates, and error correction protocols to maximize the bandwidth and energy efficiency of the network [2]. Dynamic variation of transmission parameters in EONs poses an important challenge to digital signal processing (DSP) algorithms employed in the optical receivers. Under the condition of modulation format switching, it is preferred to make the receivers have the ability of automatically identifying the signal modulation format, hence DSP algorithms can be deployed to achieve the optimum detection performance accordingly. Modulation format identification (MFI) technique is indispensable for re-configurable digital coherent receivers used in EONs.
It is imperative to have appropriate monitoring mechanisms across the networks to acquire precise and real-time information about the quality of transmission links and health of optical signals [3,4]. Benefiting from the rapid advancement of DSP technology, the digital coherent receiver can compensate almost all linear impairments, resulting in the transmission performance being mainly determined by optical signal-to-noise ratio (OSNR) [5]. OSNR is one of the most noteworthy parameters in coherent optical networks because of its direct relation with BER. OSNR information is also vital for automatic fault detection and diagnosis, as well as for in-service characterization of signal quality [6].
In recent years, researchers have utilized various technologies to achieve MFI such as signal cumulant and signal power distribution-based method [7,8], peak-to-average-power ratio of received data samples-based methods [9,10], Stokes space-based methods [11,12,13,14,15], and machine learning-based methods [16,17,18,19]. Various OSNR estimation techniques for coherent detection systems have been proposed recently including statistical moments [20], error vector magnitude [21], delay-line interferometer [22,23], Stokes parameters [24], Golay sequences [25], offset filtering, and optical power measurement [26], radio frequency (RF) spectrum [27], and amplitude noise correlation [28] based methods.
The above techniques have a single function and can only implement MFI or OSNR estimation. A cost-effective multi-parameter estimation in next-generation EONs is attractive. F. N. Khan et al. propose a method combining optical signal-to-noise ratio (OSNR) monitoring and MFI based on signals’ amplitude histograms with the use of deep neural networks [29]. The method utilizes amplitude information of the received signals and is insensitive to phase noises. However, the method cannot distinguish MFs with same amplitude distribution such as QPSK and 8PSK. D. Wang et al. propose an intelligent constellation diagram analysis algorithm using convolutional neural network to implement both MFI and OSNR estimation [30]. Based on the characteristics of neural networks and supervised-learning, these two methods both need a large number of signal samples as training data.
The density-based clustering algorithm assumes that the clustering structure can be determined by the tightness of the sample distribution. In general, the density-based clustering algorithm examines the connectivity between samples and gives the connectable samples an expanding cluster until obtain the final clustering results. Several density-based clustering have been put forward, like DBSCAN, ordering points to identify the clustering structure (OPTICS), and clustering by fast search and find of density peaks (DP).
With prior information of the cluster number, the DP method generates a decision map containing the density information of each sample point and the minimum distance between the sample point and any other point with higher density. The cluster centers are recognized as points for which the value of decision map is anomalously large [31,32,33]. The DP algorithm needs prior information of the cluster number in advance, and limits the application of MFI.
The OPTICS method performs clustering by computing an augmented cluster-ordering of the database objects [34,35,36,37]. It can perform clustering of different-densities clusters. In principle, the OPTICS clustering method can be used to perform MFI. However, it cannot extract change of cluster density in different OSNR and cannot be used to estimate OSNR.
DBSCAN is a well-known clustering algorithm that maps the density of samples [38,39,40,41,42]. With the ability of unsupervised-learning, DBSCAN can directly extract clustering information of data which can be utilized in identifying some widely used MFs such as PDM-QPSK, PDM-8PSK, PDM-16QAM, PDM-32QAM, and PDM-64QAM without training data. Moreover, by fitting the proportion of core points in the sample set, the DBSCAN-based method can realize OSNR estimation for five MFs mentioned above with low mean absolute error even when the testing data is not trained. Thus, we propose a joint algorithm for MFI and OSNR estimation based on DBSCAN in this work. The experimental results demonstrate successful identification of QPSK & 16QAM signals and low OSNR estimation error.
In Section 2, we introduce how DBSCAN is applied to the MFI and OSNR estimation. In Section 3, we verify the correctness of the proposed method by numerical simulation and proof experiments. In Section 4, we conclude that the proposed method in this article is feasible in numerical simulated and practical optical fiber communication systems and has the potential to be used in BER calculation, linear or nonlinear impairments monitoring. In Abbreviations, we present an acronym list for conveniently searching the acronym. In Appendix A, we present the basic notion, pseudocode, and framework of DBSCAN algorithm.

2. Proposed Algorithm: DBSCAN-Based MFI and OSNR Estimation

The basic notion, pseudocode, and framework of DBSCAN algorithm are shown in Appendix A. We define R to represent the proportion of core points in the sample set, shown as
R = Ω / D
where Ω represents the set of all core points in D; D represents the set of whole points of data; || means the number of elements in the data set.

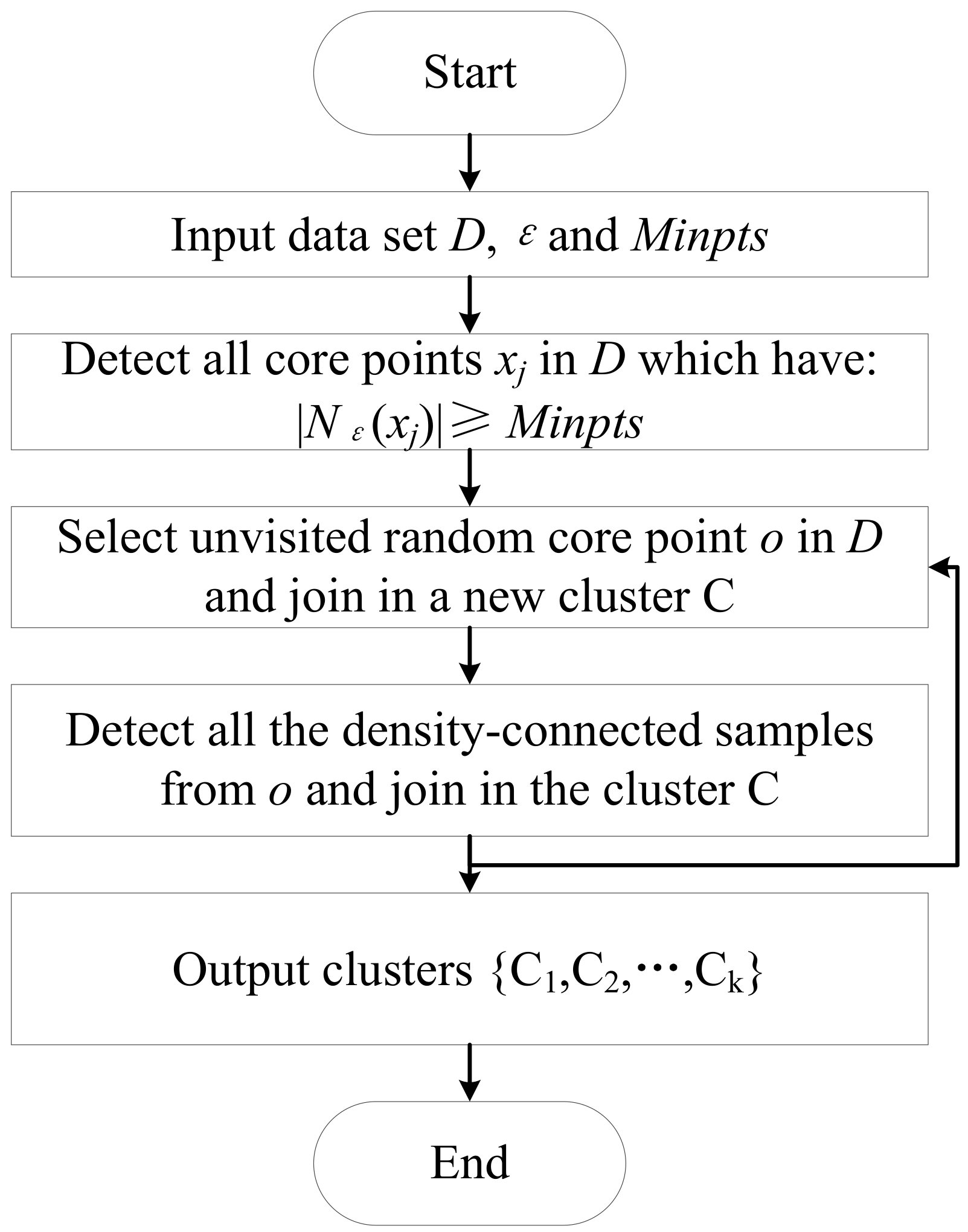
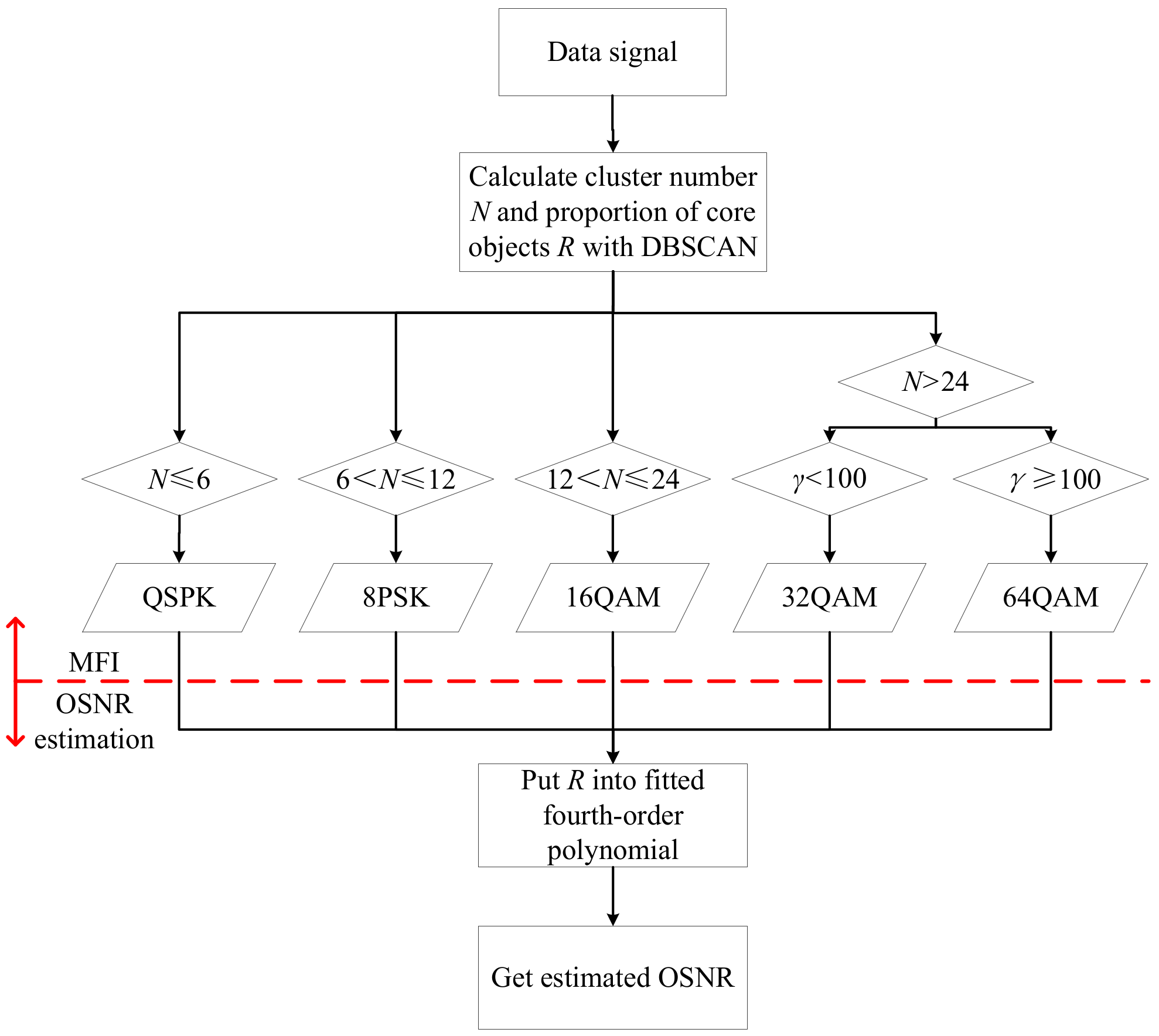
2.1. Model of MFI and OSNR Estimation Based on DBSCAN Algorithm

The DSP configuration of the proposed joint algorithm is shown in Figure 1. After chromatic dispersion (CD) compensation, timing recovery, normalization, constant modulus algorithm (CMA)-based equalization, and frequency-offset (FO) compensation for compensating nearly all linear transmission impairments, signals are mainly affected by amplified spontaneous emission (ASE) noise [29,43,44]. The proposed DBSCAN-based joint algorithm can extract MF and OSNR information which are used in subsequent DSP blocks such as symbol decision, decoding and signal quality characterization.
Constellation diagrams of different MFs have their own unique distribution characteristics; thus, commonly used signal types can be distinguished by countering the number of clusters. The DBSCAN does not need to know the number of clusters in advance and has an unparalleled advantage for identifying non-convex sample sets, making the DBSCAN algorithm more suitable for processing the non-spherical constellation points and irregular noise distribution due to the influence of the laser linewidth than other clustering algorithms.
Figure 2 shows the clustering results for five simulated MFs using DBSCAN algorithm ( ε = 0.09 and M i n P t s = 25) when the OSNR values equal to their respective 7% FEC thresholds (QPSK: 12 dB, 8PSK: 15 dB, 16QAM: 18 dB, 32QAM: 22 dB, 64QAM: 24 dB). The laser linewidth is 100 kHz. The clustering results are 4, 8, 16, 32 and 36 for QPSK, 8PSK, 16QAM, 32QAM and 64QAM signals respectively. We can see that for QPSK, 8PSK, and 16QAM signals, the DBSCAN algorithm can correctly obtain the number of clusters. Due to the small Euclidean distance and vulnerability to noise, the cluster number of 32QAM and 64QAM is approximate. For these two signals, we use the MF index to distinguish two MFs which defined as γ = N R , where N is cluster number and R is defined by Equation (1).
As OSNR increases, the effect of ASE noise on the signal decreases, leading to the constellation points better concentrated than lower OSNR conditions. According to the introduction of DBSCAN algorithm, the neighborhood parameters (ε and MinPts) set a density threshold on symbols. The core points are the symbols which are reaching the density threshold. If the symbols are getting better concentrated, the number of core points apparently increases leading the R value increases. So parameter R defined by Equation (1) is positively correlated to OSNR for five MFs and is showed in Figure 3.
In our proposed method, the DBSCAN algorithm calculates the R values corresponding to different OSNR. In order to make the fitting polynomial have the generalization ability to the multi-pattern signals without overfitting, we choose fourth-order polynomial. After fitting the fourth-order polynomial of R values and referenced OSNR values, we can estimate the corresponding OSNR from a known R with the fitted polynomial. The fitted fourth-order polynomial can be expressed as:
f 4 ( x , w ) = w 0 + w 1 x + w 2 x 2 + w 3 x 3 + w 4 x 4 = ∑ j = 0 4 w j x j
Figure 4 shows fitted curve and R value of five other different QPSK signal patterns by changing the pseudo-random binary sequence (PRBS) random seed in arbitrary waveform generator (AWG), proving that the R value does not depend on the randomness of the signal patterns and the fitted polynomial can accurately estimate the real OSNR.

2.2. Flowchart of MFI and OSNR Estimation Based on DBSCAN Algorithm

Figure 5 is the flowchart of MFI and OSNR estimation joint algorithm based on DBSCAN. First, the DBSCAN algorithm calculates the cluster number N and proportion of core objects R of input signal with two neighborhood parameters being set the same values for five MFs. The respective decision zone for cluster number is set to identify different MFs with considering that the noise (phase noise due to laser linewidth and ASE noise from optical amplifiers used in optical transmission link) may cause the cluster number to decrease. The 32QAM and 64QAM signals are identified with extra steps combining cluster number N and R value.
After identifying the MF of input signal, the DBSCAN-based OSNR estimation algorithm is performed by using different neighborhood parameters on five MFs, respectively, with consideration of different Euclidean distances. In this stage, the R value is calculated and OSNR is estimated by the fitted fourth-order polynomial expressed by Equation (2).
In our proposed joint method, the most computation intensive process is the DBSCAN block. So the total time complexity of our proposed method is on the order of O(n*log n) [38]. Considering the proposed method does not need training large number of signal samples before performing MFI and OSNR estimation, we believe our method taking less time than the other two joint algorithms for MFI and OSNR estimation using deep neural network [29] and convolutional neural network [30].

3. Simulation and Experiment Results

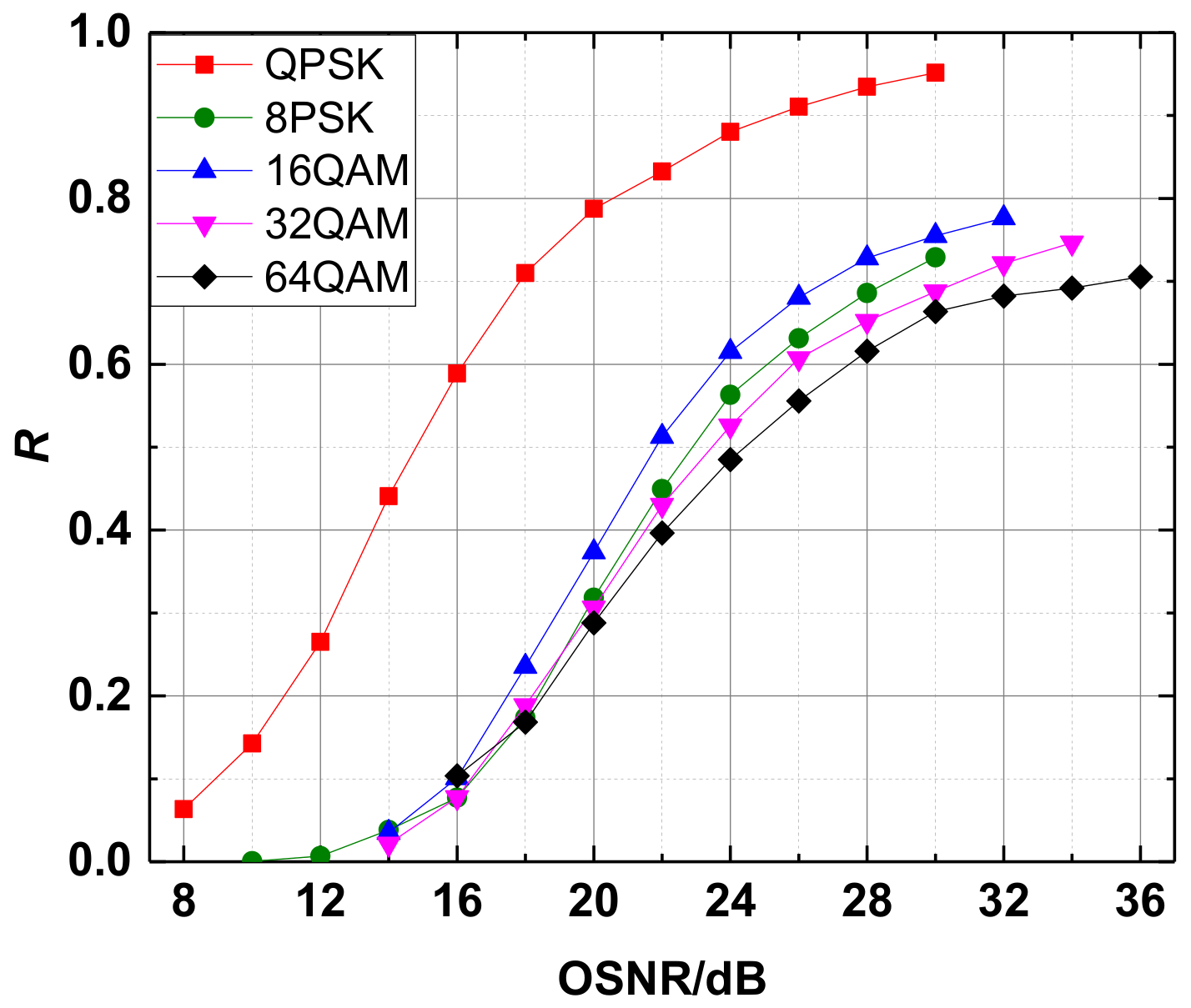
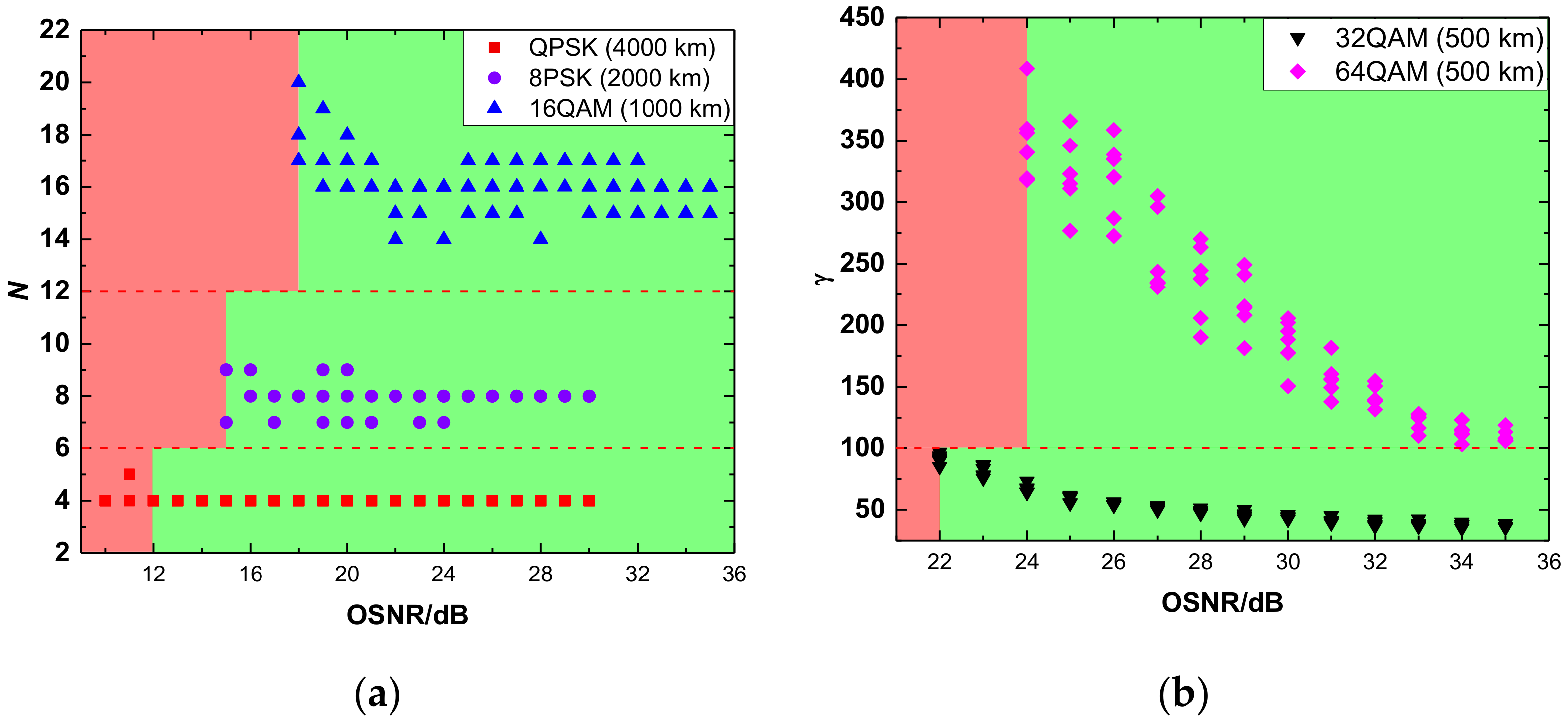
3.1. Simulation Results

As shown in Figure 6, we set up the simulation system using the commercial software Virtual Photonics Inc (Norwood, MA, USA). and the DBSCAN-based joint algorithm is used at the receiver end to identify the MF and estimate OSNR. The wavelength of the laser at transmitter is 1553.6 nm with 100 kHz linewidth. After modulated by an IQ modulator which I and Q branches independently driven by two 30-order PRBS produced by AWG, five widely used MFs are generated. By changing the random seed of PRBS, we can get five different signal patterns. The symbol rate is set to 28 GBaud and the launched optical power to standard single-mode fiber (SSMF) is 0 dBm. The modulated signal light is amplified by an Erbium Doped Fiber Amplifier (EDFA) and transmitted in 100 km SSMF with CD parameter is 16 p s / ( n m . k m ) every span. The polarization mode dispersion (PMD) parameter is set as 0.1 p s / k m . The transmission fiber length is set to 4000 km, 2000 km, 1000 km, 500 km and 500 km for PDM-QPSK, PDM-8PSK, PDM-16QAM, PDM-32QAM, and PDM-64QAM signals, respectively. A variable optical attenuator (VOA) and an EDFA are used to vary OSNR with transmitted signal light in 3 dB coupler. The linewidth of local oscillator laser is 100 kHz. After analog-to-digital converter (ADC), the DSP blocks described in Section 2.1 are followed.
Figure 7a shows the cluster number N varies with different OSNR after using the DBSCAN-based algorithm for QPSK, 8PSK, and 16QAM signals with the same neighborhood parameters ε = 0.09 and M i n P t s = 25. The cluster numbers of three different MFs are represented by different color symbols. There are five different signal patterns for every OSNR condition. With the decision thresholds proposed in Section 2.2, modulation formats of different signal patterns are correctly identified with 100% accuracy. Figure 7b shows the γ value of 32QAM and 64QAM signals and these two MFs can be divided with the decision thresholds proposed in Section 2.2. The red/green area in Figure 7a,b represents the OSNR range below/upon the 7% FEC threshold of different MFs.
Figure 8 shows the estimated OSNR and mean absolute error of five different signal patterns for five MFs signals. Signal patterns used for fitting fourth-order polynomial are not the same as five different signal patterns above. The estimated OSNR values are represented by different solid points while the mean absolute errors of five different signal patterns for every OSNR condition are represented by different hollow points. It can be seen that the mean absolute errors of all reference OSNR conditions for five MFs are all less than 1 dB. The mean estimated error is 0.3 dB, 0.2 dB, 0.3 dB, 0.5 dB, and 0.6 dB for QPSK, 8PSK, 16QAM, 32QAM, and 64QAM, respectively. It notes that the OSNR estimation error increases with greater reference OSNR. It can be explained that the ASE noise power is too low and the algorithm cannot extract the change of density information of clusters. As a result, OSNR estimation will have more deviation [45]. Table 1 shows the neighborhood parameters of five different MFs.

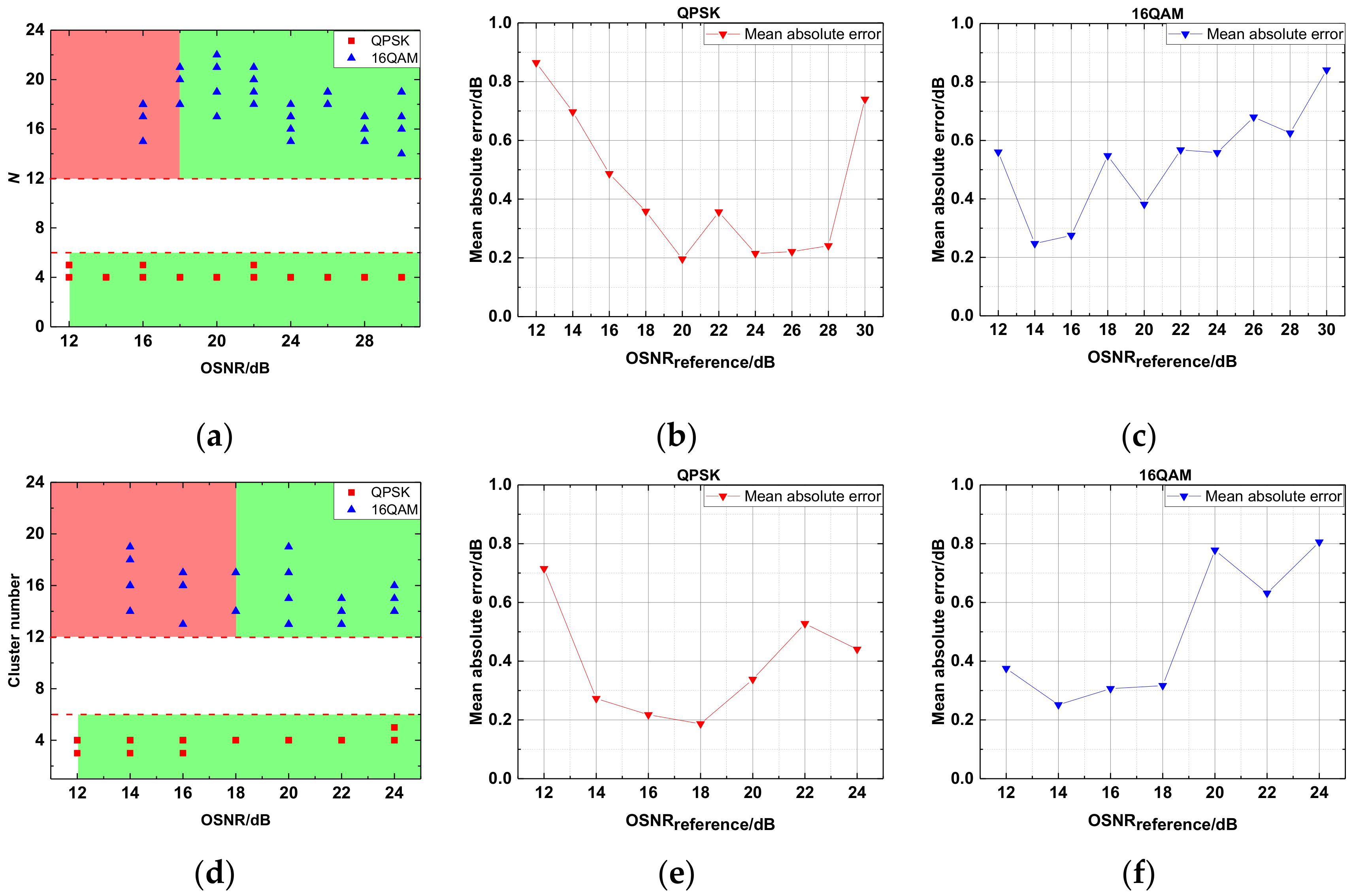
3.2. Results of Proof Experiments

We build an experimental system according to Figure 6. The experimental configuration is as the following: at the transmitter, the wavelength and the linewidth of the laser are 1550 nm and 5 kHz. An AWG produces two independent PRBS which drive I and Q branches of the IQ modulator. Then the modulated QPSK and 16QAM signals are generated. The symbol rate is set to 20 GBaud and launched optical power to SSMF is 0 dBm. The generated optical signal is amplified by EDFA and then transmitted to a fiber link which transmission distance is 100 km. The CD index and PMD parameter of SSMF are 16 p s / ( n m . k m ) and 0.1 p s / k m . At the end of the fiber link, an EDFA is used to add ASE noise to the transmitted optical signal. The reference OSNR for QPSK and 16QAM is varied in the range of 12~30 dB and 12~24 dB with fixed step of 2 dB for back to back system and 100 km fiber transmission systems respectively. We can obtain the reference OSNR from the optical spectrum analyzer by using out-of-band noise measurement. At the receiver end, the linewidth of local oscillator laser is 5 kHz. We use a real-time scope with 50 GSa/s sampling rate works as ADC to sample the coherent detected signals with following offline DSP blocks including proposed joint algorithm.
As shown in Figure 9a,c, with the OSNR range not lower than 7% threshold of QPSK and 16QAM signals, the MFI decision threshold proposed in Section 2.2 can correctly divide two MF signals. In addition, the mean estimated error for QPSK signal is 0.4 dB (back to back system) and 0.4 dB (100 km fiber transmission system) and for 16QAM is 0.5 dB (back to back system) and 0.5 dB (100 km fiber transmission system). The above results indicate that the proposed method is feasible in practical optical fiber communication systems.

4. Discussion and Conclusions

In this work, we propose a joint algorithm for MFI and OSNR estimation based on the DBSCAN clustering method. The cluster number and the proportion of core points are extracted by the DBSCAN algorithm to achieve MFI and OSNR estimation. The numerical simulation results show that for five widely used signal types (PDM-QPSK, PDM-8PSK, PDM-16QAM, PDM-32QAM, and PDM-64QAM), the MFI can achieve 100% accuracy when the incoming OSNR values are higher than their respective 7% FEC thresholds. The mean estimated error is 0.3 dB, 0.2 dB, 0.3 dB, 0.5 dB, and 0.6 dB for five MFs, respectively. The experimental results demonstrate that, with the OSNR range not lower than 7% threshold of QPSK and 16QAM signals, the MFI decision threshold proposed in Section 2.2 can correctly divide two MF signals. In addition, the mean estimated error for QPSK signal is 0.4 dB (back to back system) and 0.4 dB (100 km fiber transmission system) and for 16QAM is 0.5 dB (back to back system) and 0.5 dB (100 km fiber transmission system). The experimental results prove that the proposed method is feasible in practical optical fiber communication systems. There is no additional hardware required, so the proposed method has the ability to be integrated into existing optical performance monitoring systems without burden. Furthermore, the proposed method has the potential to be used in BER calculation, and linear or nonlinear impairments monitoring. We believe that our multifunctional and simple method would be more favorable in comparison to future EON.

Author Contributions

Conceptualization, Z.Z. and A.Y.; methodology, Z.Z. and A.Y.; software, Z.Z.; validation, Z.Z., and A.Y.; formal analysis, Z.Z. and P.G.; investigation, Z.Z.; resources, Z.Z. and Q.T.; data curation, Z.Z. and Q.T.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z., A.Y. and P.G.; visualization, Z.Z.; supervision, A.Y. and P.G.; project administration, A.Y.; funding acquisition, A.Y. All authors have read and agree to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China, grant number 61427813 and Open Fund of IPOC (BUPT), grant number IPOC2018B003.

Acknowledgments

This work is supported by State Key Laboratory of Advanced Optical Communication Systems and Networks, China and Key Laboratory of Photonics Information Technology, Ministry of Industry and Information Technology, Beijing Institute of Technology, Beijing, China.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

Acronym List
ADCanalog-to-digital converter
ASEamplified spontaneous emission
AWGarbitrary waveform generator
BERbit-error ratio
CDchromatic dispersion
CMAconstant modulus algorithm
DBSCANdensity-based spatial clustering of applications with noise
DPdensity peaks
DSPdigital signal processing
EDFAerbium doped fiber amplifier
EONelastic optical network
FECforward error correction
FOfrequency-offset
MFmodulation format
MFImodulation format identification
OFDMorthogonal frequency division multiplexing
OPTICSordering points to identify the clustering structure
OSNRoptical signal-to-noise ratio
PDMpolarization division multiplexing
PRBSpseudo-random binary sequence
QAMquadrature amplitude modulation
QPSKquadrature phase shift keying
RF radio frequency
SSMFstandard single-mode fiber
VOAvariable optical attenuator
WDMwavelength division multiplexing

Appendix A

A. Basic Notion of DBSCAN
DBSCAN algorithm characterizes the closeness of the samples based on two neighborhood parameters, ε and M i n P t s . For a given data set D = { x 1 , x 2 , … , x n } , there defines some notions as following:
  • ε -neighborhood
To x j ∈ D , the ε -neighborhood of x j is defined as the samples in D and the Euclidean distance from x j is not greater than ε , can be expressed as:
N ε ( x j ) = { x i ∈ D | d i s t ( x i , x j ) ≤ ε }
  • Core point
If the ε -neighborhood of x j contains at least M i n P t s samples, which is N ε ( x j ) ≥ M i n P t s (|| means the number of elements in the data set), then x j is a core point.
  • Directly density-reachable
If x j is in the ε -neighborhood of x i , and x i is a core point, then x j is directly density-reachable from x i .
  • Density-reachable
Assuming a sample sequence { p 1 , p 2 , … , p n } , p 1 = x i , p n = x j and p k + 1 is directly density-reachable from p k , then x j is density-reachable from x i .
  • Density-connected
If x i and x j are density-reachable with x k respectively, then x i and x j are density-connected.
Figure A1 visually shows the above notions.
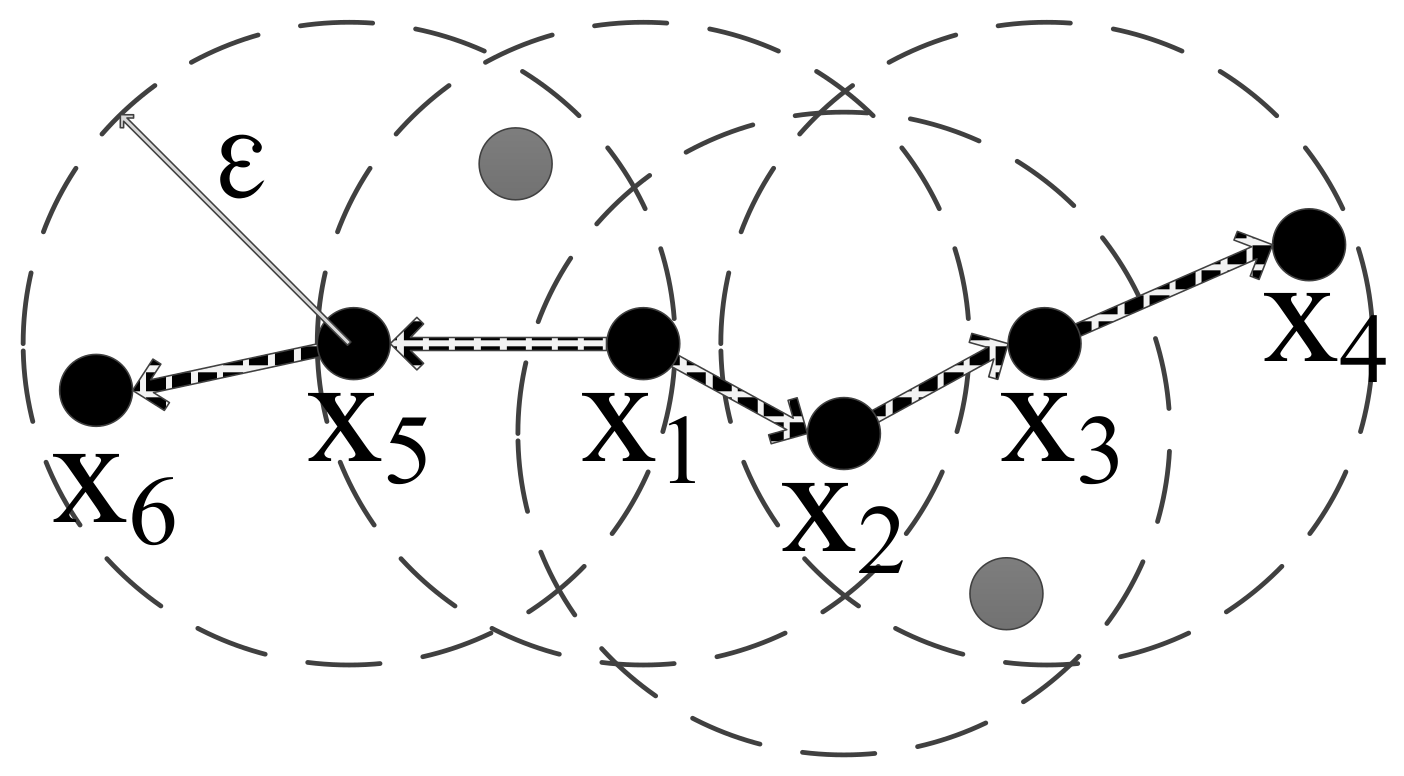
Applsci 10 01095 g0a1 550
Figure A1. Basic notions of DBSCAN.
Figure A1. Basic notions of DBSCAN.
Applsci 10 01095 g0a1
As shown in Figure A1, when M i n P t s = 3 and dotted circle represent ε -neighborhood of each points; { x 1 , x 2 , x 3 , x 5 } are core points; x 4 and x 6 are both density-reachable from x 1 ; x 4 and x 6 are density-connected.
Based on the notions defined above, DBSCAN defines clusters as: a set of largest density-connected samples. For given parameters ε and M i n P t s , cluster C ⊆ D is a non-empty sample subset which satisfies the following properties:
  • connectivity: x i ∈ C , x j ∈ C ⇒ x i and x j are density-connected.
  • maximality: x i ∈ C , x i and x j are density-connected ⇒ x j ∈ C .
B. DBSCAN Algorithm and Framework
The DBSCAN algorithm is shown as Figure A2. The input to the algorithm are data set D and the parameters ( ε and M i n P t s ). From line 1 to line 7, the algorithm finds all core points based on the given parameters ( ε and M i n P t s ). After that, starting from any core point, the algorithm finds all the density-connected samples to generate clusters until all core points are visited. Then the clustering result ℂ = { C 1 , C 2 , … , C k } and number of core points Ω are output from the DBSCAN algorithm.
Figure A3 shows the basic framework of DBSCAN algorithm. It shows the DBSCAN clustering algorithm intuitively and concisely.
Applsci 10 01095 g0a2 550
Figure A2. DBSCAN algorithm.
Figure A2. DBSCAN algorithm.
Applsci 10 01095 g0a2
Applsci 10 01095 g0a3 550
Figure A3. Framework of DBSCAN algorithm.
Figure A3. Framework of DBSCAN algorithm.
Applsci 10 01095 g0a3

References

  1. Gerstel, O.; Jinno, M.; Lord, A.; Ben Yoo, S.J. Elastic Optical Networking: A New Dawn for the Optical Layer? IEEE Commun. Mag. 2012, 50, S12–S20. [Google Scholar]
  2. Zhao, Z.; Yang, A.Y.; Guo, P. A Modulation Format Identification Method Based on Information Entropy Analysis of Received Optical Communication Signal. IEEE Access 2019, 7, 41492–41497. [Google Scholar]
  3. Dong, Z.H.; Khan, F.N.; Sui, Q.; Zhong, K.P.; Lu, C.; Lau, A.P.T. Optical Performance Monitoring: A Review of Current and Future Technologies. J. Lightwave Technol. 2016, 34, 525–543. [Google Scholar]
  4. Khan, F.N.; Lu, C.; Lau, A.P. Optical performance monitoring for fiber-optic communication networks. In Enabling Technologies for High Spectral-Efficiency Coherent Optical Communication Networks; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
  5. Savory, S.J. Digital Coherent Optical Receivers: Algorithms and Subsystems. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1164–1179. [Google Scholar]
  6. Willner, A.E.; Pan, Z.; Yu, C. Optical performance monitoring. In Optical Fiber Telecommunications VB; Academic Press: Cambridge, MA, USA, 2008; pp. 233–292. [Google Scholar]
  7. Swami, A.; Sadler, B.M. Hierarchical digital modulation classification using cumulants. IEEE Trans. Commun. 2000, 48, 416–429. [Google Scholar]
  8. Liu, J.; Dong, Z.H.; Zhong, K.P.; Lau, A.P.T.; Lu, C.; Lu, Y.Z. Modulation Format Identification Based on Received Signal Power Distributions for Digital Coherent Receivers. In Proceedings of the 2014 Optical Fiber Communications Conference and Exhibition (Ofc), San Francisco, CA, USA, 9–13 March 2014. [Google Scholar]
  9. Liu, G.C.; Proietti, R.; Zhang, K.Q.; Lu, H.B.; Ben Yoo, S.J. Blind modulation format identification using nonlinear power transformation. Opt. Express 2017, 25, 30895–30904. [Google Scholar]
  10. Bilal, S.M.; Bosco, G.; Dong, Z.H.; Lau, A.P.T.; Lu, C. Blind modulation format identification for digital coherent receivers. Opt. Express 2015, 23, 26769–26778. [Google Scholar]
  11. Bo, T.W.; Tang, J.; Chan, C.K. Modulation Format Recognition for Optical Signals Using Connected Component Analysis. IEEE Photonics Technol. Lett. 2017, 29, 11–14. [Google Scholar]
  12. Mai, X.F.; Liu, J.; Wu, X.; Zhang, Q.; Guo, C.J.; Yang, Y.F.; Li, Z.H. Stokes space modulation format classification based on non-iterative clustering algorithm for coherent optical receivers. Opt. Express 2017, 25, 2038–2050. [Google Scholar]
  13. Jiang, L.; Yan, L.S.; Yi, A.L.; Pan, Y.; Bo, T.W.; Hao, M.; Pan, W.; Luo, B. Blind Density-Peak-Based Modulation Format Identification for Elastic Optical Networks. J. Lightwave Technol. 2018, 36, 2850–2858. [Google Scholar]
  14. Chen, P.Y.; Liu, J.; Wu, X.; Zhong, K.P.; Mai, X.F. Subtraction-Clustering-Based Modulation Format Identification in Stokes Space. IEEE Photonics Technol. Lett. 2017, 29, 1439–1442. [Google Scholar]
  15. Boada, R.; Borkowski, R.; Monroy, I.T. Clustering algorithms for Stokes space modulation format recognition. Opt. Express 2015, 23, 15521–15531. [Google Scholar]
  16. Wang, D.S.; Zhang, M.; Fu, M.X.; Cai, Z.L.; Li, Z.; Han, H.H.; Cui, Y.; Luo, B. Nonlinearity Mitigation Using a Machine Learning Detector Based on k-Nearest Neighbors. IEEE Photonics Technol. Lett. 2016, 28, 2102–2105. [Google Scholar]
  17. Guesmi, L.; Ragheb, A.M.; Fathallah, H.; Menif, M. Experimental Demonstration of Simultaneous Modulation Format/Symbol Rate Identification and Optical Performance Monitoring for Coherent Optical Systems. J. Lightwave Technol. 2018, 36, 2230–2239. [Google Scholar]
  18. Zhang, S.T.; Peng, Y.Q.; Sui, Q.; Li, J.P.; Li, Z.H. Modulation format identification in heterogeneous fiber-optic networks using artificial neural networks and genetic algorithms. Photonic Netw. Commun. 2016, 32, 246–252. [Google Scholar]
  19. Khan, F.N.; Zhong, K.P.; Al-Arashi, W.H.; Yu, C.Y.; Lu, C.; Lau, A.P.T. Modulation Format Identification in Coherent Receivers Using Deep Machine Learning. IEEE Photonics Technol. Lett. 2016, 28, 1886–1889. [Google Scholar]
  20. Faruk, M.S.; Mori, Y.; Kikuchi, K. In-Band Estimation of Optical Signal-to-Noise Ratio from Equalized Signals in Digital Coherent Receivers. IEEE Photonics J. 2014, 6, 7800109. [Google Scholar]
  21. Schmogrow, R.; Nebendahl, B.; Winter, M.; Josten, A.; Hillerkuss, D.; Koenig, S.; Meyer, J.; Dreschmann, M.; Huebner, M.; Koos, C.; et al. Error Vector Magnitude as a Performance Measure for Advanced Modulation Formats. IEEE Photonics Technol. Lett. 2012, 24, 61–63. [Google Scholar]
  22. Chitgarha, M.R.; Khaleghi, S.; Daab, W.; Almaiman, A.; Ziyadi, M.; Mohajerin-Ariaei, A.; Rogawski, D.; Tur, M.; Touch, J.D.; Vusirikala, V.; et al. Demonstration of in-service wavelength division multiplexing optical-signal-to-noise ratio performance monitoring and operating guidelines for coherent data channels with different modulation formats and various baud rates. Opt. Lett. 2014, 39, 1605–1608. [Google Scholar]
  23. Ahsan, A.S.; Wang, M.S.; Chitgarha, M.R. Autonomous OSNR monitoring and cross-layer control in a mixed bit-rate and modulation format system using pilot tones. In Photonic Networks and Devices; Optical Society of America: Washington, DC, USA, 2014; p. NT4C. 3. [Google Scholar]
  24. Lundberg, L.; Sunnerud, H.; Johannisson, P. In-Band OSNR Monitoring of PM-QPSK Using the Stokes Parameters. In Proceedings of the 2015 Optical Fiber Communications Conference and Exhibition (Ofc), Los Angeles, CA, USA, 22–26 March 2015. [Google Scholar]
  25. Do, C.; Tran, A.V.; Zhu, C.; Hewitt, D.; Skafidas, E. Data-Aided OSNR Estimation for QPSK and 16-QAM Coherent Optical System. IEEE Photonics J. 2013, 5, 6601609. [Google Scholar]
  26. Oda, S.; Yang, J.Y.; Akasaka, Y. In-band OSNR monitor using an optical bandpass filter and optical power measurements for super channel signals. In Proceedings of the 39th European Conference and Exhibition on Optical Communication (ECOC 2013), London, UK, 22–26 September 2013. [Google Scholar]
  27. Shen, T.S.R.; Sui, Q.; Lau, A.P.T. OSNR Monitoring for PM-QPSK Systems With Large Inline Chromatic Dispersion Using Artificial Neural Network Technique. IEEE Photonics Technol. Lett. 2012, 24, 1564–1567. [Google Scholar]
  28. Dong, Z.H.; Lau, A.P.T.; Lu, C. OSNR monitoring for QPSK and 16-QAM systems in presence of fiber nonlinearities for digital coherent receivers. Opt. Express 2012, 20, 19520–19534. [Google Scholar]
  29. Khan, F.N.; Zhong, K.P.; Zhou, X.; Al-Arashi, W.H.; Yu, C.Y.; Lu, C.; Lau, A.P.T. Joint OSNR monitoring and modulation format identification in digital coherent receivers using deep neural networks. Opt. Express 2017, 25, 17767–17776. [Google Scholar]
  30. Wang, D.S.; Zhang, M.; Li, J.; Li, Z.; Li, J.Q.; Song, C.; Chen, X. Intelligent constellation diagram analyzer using convolutional neural network-based deep learning. Opt. Express 2017, 25, 17150–17166. [Google Scholar]
  31. Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar]
  32. Mehmood, R.; Zhang, G.Z.; Bie, R.F.; Dawood, H.; Ahmad, H. Clustering by fast search and find of density peaks via heat diffusion. Neurocomputing 2016, 208, 210–217. [Google Scholar]
  33. Wang, S.L.; Wang, D.K.; Li, C.Y.; Li, Y.; Ding, G.Y. Clustering by Fast Search and Find of Density Peaks with Data Field. Chin. J. Electron. 2016, 25, 397–402. [Google Scholar]
  34. Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod Rec. 1999, 28, 49–60. [Google Scholar]
  35. Jajoo, G.; Kumar, Y.; Yadav, S.K.; Adhikari, B.; Kumar, A. Blind signal modulation recognition through clustering analysis of constellation signature. Expert Syst. Appl. 2017, 90, 13–22. [Google Scholar]
  36. Agrawal, K.P.; Garg, S.; Sharma, S.; Patel, P. Development and validation of OPTICS based spatio-temporal clustering technique. Inf. Sci. 2016, 369, 388–401. [Google Scholar]
  37. Gungor, E.; Ozmen, A. Distance and density based clustering algorithm using Gaussian kernel. Expert Syst. Appl. 2017, 69, 10–20. [Google Scholar]
  38. Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X.A. Density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 1996, 96, 226–231. [Google Scholar]
  39. Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X.W. DBSCAN Revisited, Revisited: Why and How You Should (Still) Use DBSCAN. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar]
  40. Kumar, K.M.; Reddy, A.R.M. A fast DBSCAN clustering algorithm by accelerating neighbor searching using Groups method. Pattern Recognit. 2016, 58, 39–48. [Google Scholar]
  41. Shen, J.; Hao, X.; Liang, Z.; Liu, Y.; Wang, W.; Shao, L. Real-time superpixel segmentation by DBSCAN clustering algorithm. IEEE Trans. Image Process. 2016, 25, 5933–5942. [Google Scholar]
  42. Czerniawski, T.; Sankaran, B.; Nahangi, M.; Haas, C.; Leite, F. 6D DBSCAN-based segmentation of building point clouds for planar object classification. Autom. Constr. 2018, 88, 44–58. [Google Scholar]
  43. Tan, Q.Z.; Yang, A.Y.; Guo, P. Blind Modulation Format Identification Using Differential Phase and Amplitude Ratio. IEEE Photonics J. 2019, 11, 7201312. [Google Scholar]
  44. Tan, Q.Z.; Yang, A.Y.; Guo, P. Blind Modulation Format Identification Using the DC Component. IEEE Photonics J. 2019, 11, 7902910. [Google Scholar]
  45. Wang, Z.Y.; Yang, A.Y.; Guo, P.; He, P.J. OSNR and nonlinear noise power estimation for optical fiber communication systems using LSTM based deep learning technique. Opt. Express 2018, 26, 21346–21357. [Google Scholar]
Applsci 10 01095 g001 550
Figure 1. DSP model of MFI and OSNR estimation based on DBSCAN algorithm.
Figure 1. DSP model of MFI and OSNR estimation based on DBSCAN algorithm.
Applsci 10 01095 g001
Applsci 10 01095 g002 550
Figure 2. Clustering results for five MFs. (a) QPSK; (b) 8PSK; (c) 16QAM; (d) 32QAM; (e) 64QAM.
Figure 2. Clustering results for five MFs. (a) QPSK; (b) 8PSK; (c) 16QAM; (d) 32QAM; (e) 64QAM.
Applsci 10 01095 g002
Applsci 10 01095 g003 550
Figure 3. The value of R varies with different OSNR under five MFs.
Figure 3. The value of R varies with different OSNR under five MFs.
Applsci 10 01095 g003
Applsci 10 01095 g004 550
Figure 4. The value of R varies with different patterns of QPSK signal.
Figure 4. The value of R varies with different patterns of QPSK signal.
Applsci 10 01095 g004
Applsci 10 01095 g005 550
Figure 5. The flowchart of DBSCAN based MFI and OSNR estimation joint algorithm.
Figure 5. The flowchart of DBSCAN based MFI and OSNR estimation joint algorithm.
Applsci 10 01095 g005
Applsci 10 01095 g006 550
Figure 6. Simulation setup to utilize the DBSCAN-based joint algorithm.
Figure 6. Simulation setup to utilize the DBSCAN-based joint algorithm.
Applsci 10 01095 g006
Applsci 10 01095 g007 550
Figure 7. MFI results using the DBSCAN-based algorithm. (a) cluster number N of QPSK, 8PSK and 16QAM varies with different OSNR; (b) γ value of 32QAM and 64QAM varies with different OSNR.
Figure 7. MFI results using the DBSCAN-based algorithm. (a) cluster number N of QPSK, 8PSK and 16QAM varies with different OSNR; (b) γ value of 32QAM and 64QAM varies with different OSNR.
Applsci 10 01095 g007
Applsci 10 01095 g008 550
Figure 8. The estimated OSNR and mean absolute error for five MFs. (a) QPSK; (b) 8PSK; (c) 16QAM; (d) 32QAM; (e) 64QAM.
Figure 8. The estimated OSNR and mean absolute error for five MFs. (a) QPSK; (b) 8PSK; (c) 16QAM; (d) 32QAM; (e) 64QAM.
Applsci 10 01095 g008
Applsci 10 01095 g009 550
Figure 9. Experimental results of MFI and OSNR estimation for 20 GBaud QPSK and 16QAM optical communication system. (a) MFI results for back to back systems; (b) Mean absolute error of estimated OSNR for back to back QPSK signal; (c) Mean absolute error of estimated OSNR for back to back 16QAM signal; (d) MFI results for 100 km transmission systems; (e) Mean absolute error of estimated OSNR for 100 km transmitted QPSK signal; (f) Mean absolute error of estimated OSNR for 100 km transmitted 16QAM signal.
Figure 9. Experimental results of MFI and OSNR estimation for 20 GBaud QPSK and 16QAM optical communication system. (a) MFI results for back to back systems; (b) Mean absolute error of estimated OSNR for back to back QPSK signal; (c) Mean absolute error of estimated OSNR for back to back 16QAM signal; (d) MFI results for 100 km transmission systems; (e) Mean absolute error of estimated OSNR for 100 km transmitted QPSK signal; (f) Mean absolute error of estimated OSNR for 100 km transmitted 16QAM signal.
Applsci 10 01095 g009
Table
Table 1. Neighborhood parameters of five different MFs.
Table 1. Neighborhood parameters of five different MFs.
Modulation Format ε M i n p t s  
QPSK0.0523
8PSK0.0925
16QAM0.0722
32QAM0.126
64QAM0.0524

Share and Cite

MDPI and ACS Style

Zhao, Z.; Yang, A.; Guo, P.; Tan, Q. A Density Clustering Algorithm for Simultaneous Modulation Format Identification and OSNR Estimation. Appl. Sci. 2020, 10, 1095. https://doi.org/10.3390/app10031095

AMA Style

Zhao Z, Yang A, Guo P, Tan Q. A Density Clustering Algorithm for Simultaneous Modulation Format Identification and OSNR Estimation. Applied Sciences. 2020; 10(3):1095. https://doi.org/10.3390/app10031095

Chicago/Turabian Style

Zhao, Zhao, Aiying Yang, Peng Guo, and Qingzhao Tan. 2020. "A Density Clustering Algorithm for Simultaneous Modulation Format Identification and OSNR Estimation" Applied Sciences 10, no. 3: 1095. https://doi.org/10.3390/app10031095

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop