Wind Pressure Coefficient on a Multi-Storey Building with External Shading Louvers

Abstract

Wind characteristics on building surfaces are used to evaluate natural ventilation of a building. As a type of building component, external shading louvers are applied in hot climatic regions to block solar radiation and provide better visual environments. The structure of external louvers can affect wind-induced characteristics, such as convective heat transfer coefficient, wind pressure and pollutant dispersion around building envelopes. This paper aims to analyze the potential ventilation capacity of a multi-storey building with shading louvers, based on wind pressure coefficient by the numerical method. A reference case was established and a previous study was applied to validate the numerical results. The rotation angle of horizontal louvers is taken from 0° to 75° in the simulation cases. The results show that average wind pressure has the greatest reduction for all floors when rotation angle turns from 60° to 75°. Ventilation openings on the stagnation zone contribute to higher ventilation rates for the windward facade with louvers. The analysis, based on multi-floor and multi-row buildings under shaded conditions, will provide a greater perspective for engineers to make optimal natural ventilation routes in multi-storey buildings with external shading louvers.

1. Introduction

Building energy use accounts for a great part of energy consumption [1]. Ventilating and shading are two effective methods to reduce building energy use of air-conditioning systems. In hot climatic regions, shading devices are widely used as they can block solar radiation and reduce heat gain, especially for glazed facades, on which the cooling loads account for much higher energy consumption in summer [2]. Several types of shading devices, such as shading louvers, can disperse solar beams and create homogenous daylight distribution in all seasons. Therefore, shading louvers are also applied in other climate regions to provide a better visual environment [3]. The previous research in shading devices mainly focused on the potentialities of energy saving [4], environmental influences [5], optical and thermal performances [5,6,7], as well as visual and thermal comfort for buildings under shaded conditions [5,8]. However, the performance of natural ventilation in a building is also significantly related to components on building surfaces [9,10,11,12]. As the blocking effect of building components influence airflow routes and pollutant dispersion, evaluation of the impact of external shading devices on airflow field is significant in building design to control both ventilation and air-conditioning system efficiently.

Natural ventilation comprises two mechanisms: Wind-driven ventilation and buoyancy-driven ventilation. In wind-driven ventilation, when a building undergoes the approaching airflow, wind pressure difference between two facades can drive natural ventilation and air penetration to supply fresh air to indoor environment from the outside [13,14,15]. In coastal areas and hot climatic regions with sufficient wind energy, natural ventilation between openings of building surfaces has become a common method of cooling. Wind environment is sensible to many factors, such as wind direction, building structures and surrounding conditions [16,17]. As a common type of building component, external shading louvers can affect airflow patterns around buildings. Figure 1 shows an array of shading louvers and the control system to rotate louvers. When the rotation angle of louvers changes, it can affect the wind speed and incident angle, resulting in fluctuations in natural ventilation around the shaded building. The presence of shading louvers must be considered in wind pressure investigation.

Wind-induced physical fields are investigated based on four methods, including theoretical analysis, in-situ field measurement, wind tunnel experiment and computational fluid dynamics (CFD) technology. In-situ field measurement of full-scale buildings investigates wind fields under real conditions, where all building surroundings are taken into account [18,19,20,21,22,23]. Wind tunnel experiments, with reduced-scale models, can provide data under controlled laboratory conditions. In addition, wind tunnels have advantages for investigating specific parameters, such as wind direction and turbulent intensity [24,25,26,27]. Theoretical analysis methods, based on fluid mechanisms, aim to develop analytical solutions with mathematical formulations [25,28,29,30]. Numerical simulation methods, based on CFD, are used to simulate both full-scale and reduced-scale wind environment to obtain a wider range of data [31,32].

To evaluate the nature ventilation around buildings, various parameters related to wind environments were investigated [24,26,28,33,34,35,36,37]. As a dimension-less parameter, the wind pressure coefficient is almost unaffected by wind speed [24,37]. In the orifice equation, based on the sealed body assumption, the difference of wind pressure coefficient is an input to calculate the cross-ventilation capacity of the building with openings like windows and doors [13,14,15]. Generally speaking, the potential cross-ventilation capacity becomes higher with the larger difference of wind pressure coefficient between two outside surfaces. When openings are installed on outside surfaces of a sealed building, the pressure difference can be applied to forecast wind-induced distributions, design airflow routes and evaluate natural ventilation patterns in different wind environments. For these reasons, analyzing the distribution of wind pressure coefficient on shaded building facades is critical to exploring their potential ventilation capacity. The distribution of wind pressure coefficient is sensitive to building structure and envelopes. A parametrical model of calculating wind pressure coefficient was developed to investigate wind profile on building envelope by Grosso [28]. Gomes et al. [26] compared the pressure distributions on cube, U-shaped and L-shaped building models, which demonstrated the shading effect by building geometry. Guan et al. [24] investigated the wind pressure coefficients around enclosed and open-window buildings. Cóstola et al. [33] compared wind pressure coefficient data from different sources and concluded that the degree of exposure/sheltering was one of the most significant parameters causing the differences in wind pressure coefficients.

Many studies evaluated the mean and local wind pressure coefficients on building surfaces [23,25,28,30,31,33,37,38,39,40,41,42]. For airflow calculation models, the average values of wind pressure coefficients on each whole building surface are not sufficient, because local values at many positions have obvious deviations compared with averaged value of a whole facade [33,43]. Some research focused on local values along specific lines to investigate the impacts of different factors on wind pressure coefficient [42,44]. This method provides comparisons between different cases intuitively, but local values along lines are also not sufficient for calculating airflow rate, as natural ventilation occurs on opening areas instead of lines. For these reasons, the average wind pressure coefficient for each room surface is more feasible for evaluating natural ventilation capacity in multi-storey buildings [17]. Some studies focused on wind pressure distribution on surfaces of buildings with shading louvers. Jiang et al. [44] experimentally measured airflow fields around a sealed cubic building and investigated wind pressure by simulation. The results show that rotation angle and louver width had an influence on airflow fields, and the fluctuation of wind pressure coefficient was primarily on the windward surface and roof. Zheng et al. [45] numerically investigated distribution of wind pressure coefficient on a building with shutter louvers. The solution was significantly dependent on wind direction. However, these studies focused on the shaded buildings mainly treat one building facade as a whole surface, rather than considering building surfaces as multi-storey zones. Some parameters, like the range of wind pressure coefficient in a specific room surface, were not investigated in shaded buildings. So these studies are not sufficient for the ventilation design of shaded buildings.

In the present study, wind pressure coefficient on building surfaces of a cube building were investigated numerically under various shaded conditions. A reference case is established to perform validation based on velocity data and wind pressure coefficient data from the previous study. The airflow pattern of approaching flow is investigated, and the impact of various rotation angles of single-sided shading lovers, on local wind pressure coefficient, is analyzed. Then, the average wind pressure coefficient is evaluated in different rows and floors. Afterwards, several conclusions of the present study are provided. The results will be helpful to natural ventilation design of multi-storey buildings with external shading louvers.

2. Wind Tunnel Experiment

The airflow field around the cube building was experimentally measured at a scale of 1:30 with or without shading louvers by Jiang et al. [44]. The wind tunnel test section was 12 m × 1.8 m × 1.8 m, and the blocking ratio is below 8%. The scales of the test building were 0.5 m for all building edges, and 26 rows of single-sided sunshade louvers were installed near the windward surface. There were five blinds in each row. The slat size was 93 mm (length) × 17.5 mm (width) × 1.0 mm (thickness), and the spacing between adjacent rows was 18.3 mm. The rotation angle of the shading louvers was 45°, and the windward surface was normal to the approaching airflow. The geometric model of the single-shaded building is shown in Figure 2. All louvers have the same rotation angle θ. In Figure 2, W is taken as 0.025 m, and B is taken as 0.0175 m.

The wind velocity was measured on the mid-surface of the wind tunnel for validation, as shown in Figure 3. Some solid elements were set on the ground to establish the atmospheric boundary layer near the inlet of the wind tunnel. The turbulent intensity I and the wind velocity U profiles for the approaching airflow were measured in the wind tunnel. The power law of velocity profile on the inlet is described in Equation (1),

$$U(z)=U_{\mathrm{ref}}{(\frac{z}{h_0})}^{\mathsf{\alpha }}$$

(1)

where U(z) is the wind velocity at height z. The reference velocity U_ref and the reference height h₀ are equal to those experimental parameters, set by Jiang et al. [44] to establish the wind environment in the computational domain. The reference velocity U_ref was 3.41 m/s at h₀ from the measurement result. The reference height h₀ is the building height. α is the coefficient for power-law profile to describe the characteristics of surface roughness considering terrain category and was set as 0.27 for suburban terrain. Figure 4 shows the turbulent intensity I and the wind velocity U profiles of airflow on the inlet of experiments and simulation.

3. CFD Simulation

To evaluate the influence of rotation angle θ of shading louvers on the distribution of wind pressure coefficient in a wider range, six simulation cases with θ = 0°, 15°, 30°, 45°, 60° and 75° were established. The reference case with θ = 45° was applied to validate the simulation results. Figure 5 summaries the numerical process to investigating airflow fields of the shaded building in this study.

3.1. Reference Case

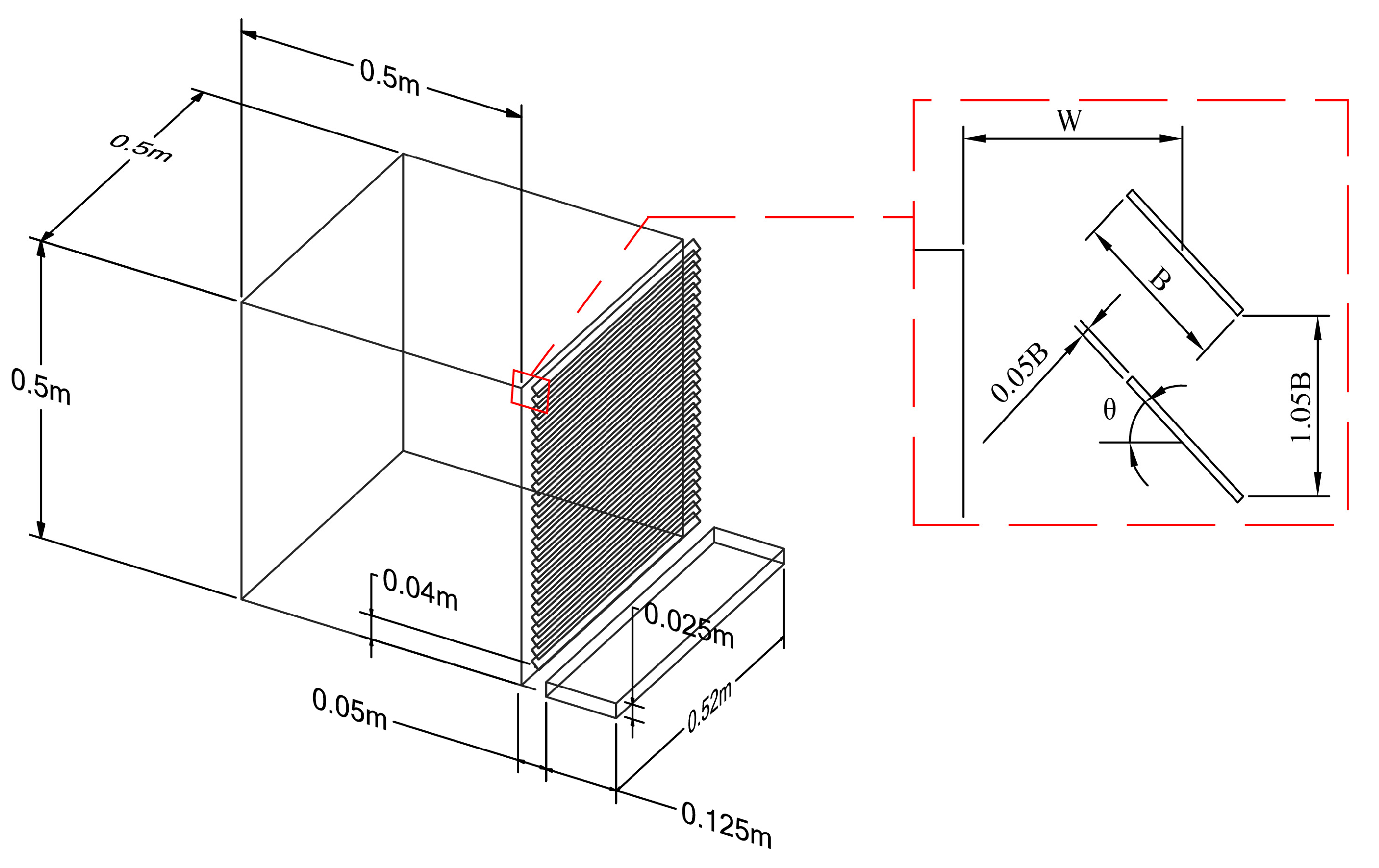
3.1.1. Geometric Model

All scales of the cubic building and single-shaded louvers are the same as those of the building geometry in the wind tunnel experiment, as shown in Figure 2. The geometric settings for two adjacent louvers are described.

3.1.2. Turbulence Model

To investigate the airflow fields around buildings through CFD technology, the two-equation Reynolds-averaged Navier-Stokes models (RANS) were frequently applied as these models have a good balance between accuracy and computational consumption [46,47]. The most widely validated RANS model in urban environment is k-ε turbulence model [48]. For k-ε models, it is not necessary to investigate the turbulent fluctuations thoroughly when simulation is performed for wind characteristics [17,44]. The Reynolds-averaged and time-averaged properties of airflow have sufficient accuracy to perform the simulation around shaded buildings. One of the most commonly used RANS models for urban climates is the standard k-ε model [49]. In addition, some modified k-ε models, like RNG k-ε model and realizable k-ε model, can provide more accurate data for some situations because of their better reproduction of swirling flows [44]. The realizable k-ε model was used in the reference case according to the simulation performed by Jiang et al. [44]. Some other CFD studies of wind pressure coefficient on building surfaces show that k-ε models, especially realizable k-ε model, have good performances at various angles of attack on buildings. For example, Montazeri and Blocken investigated the wind pressure coefficient on a building with balconies by using five turbulence models [17]. The results show that the wind pressure coefficient, obtained from the realizable k-ε model, has good agreement with experimental data. Meng et al. [50] investigated wind pressure coefficient on a high-rise building at different angles of attack and by using five turbulence models. The results show that realizable k-ε model has good performances at angle of attack from 0° to 90°.

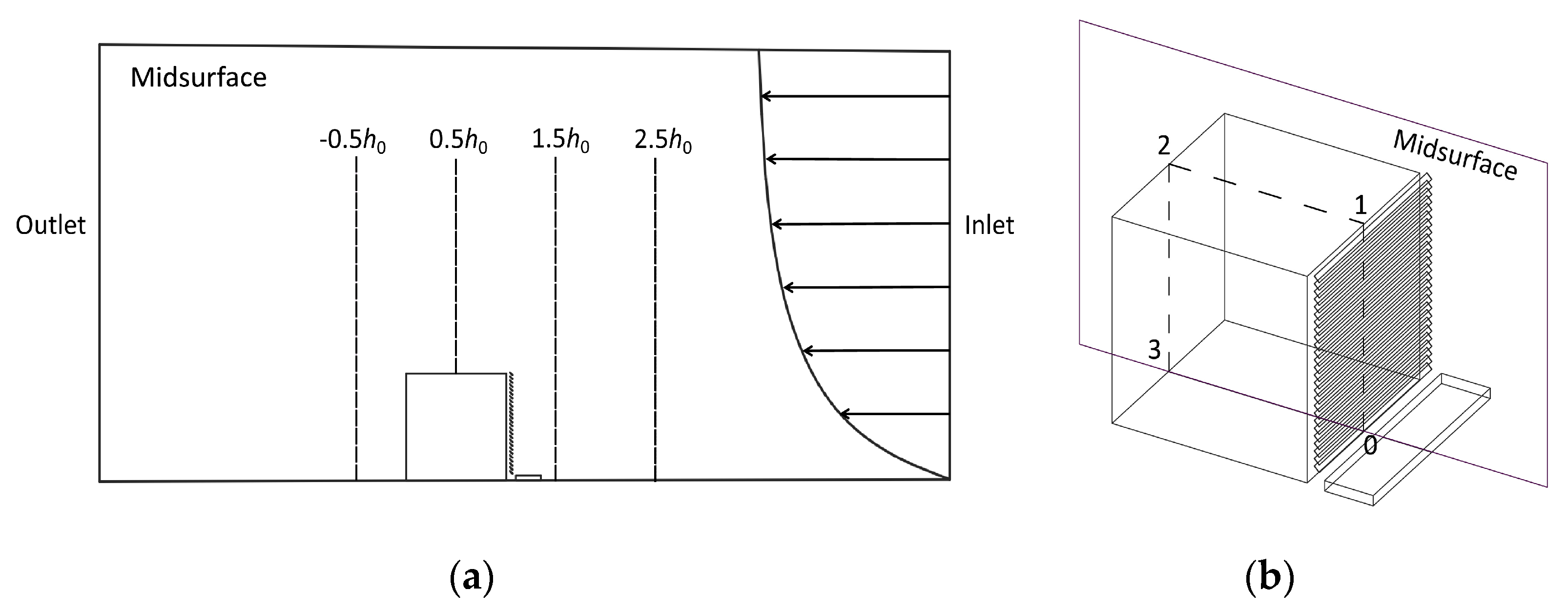
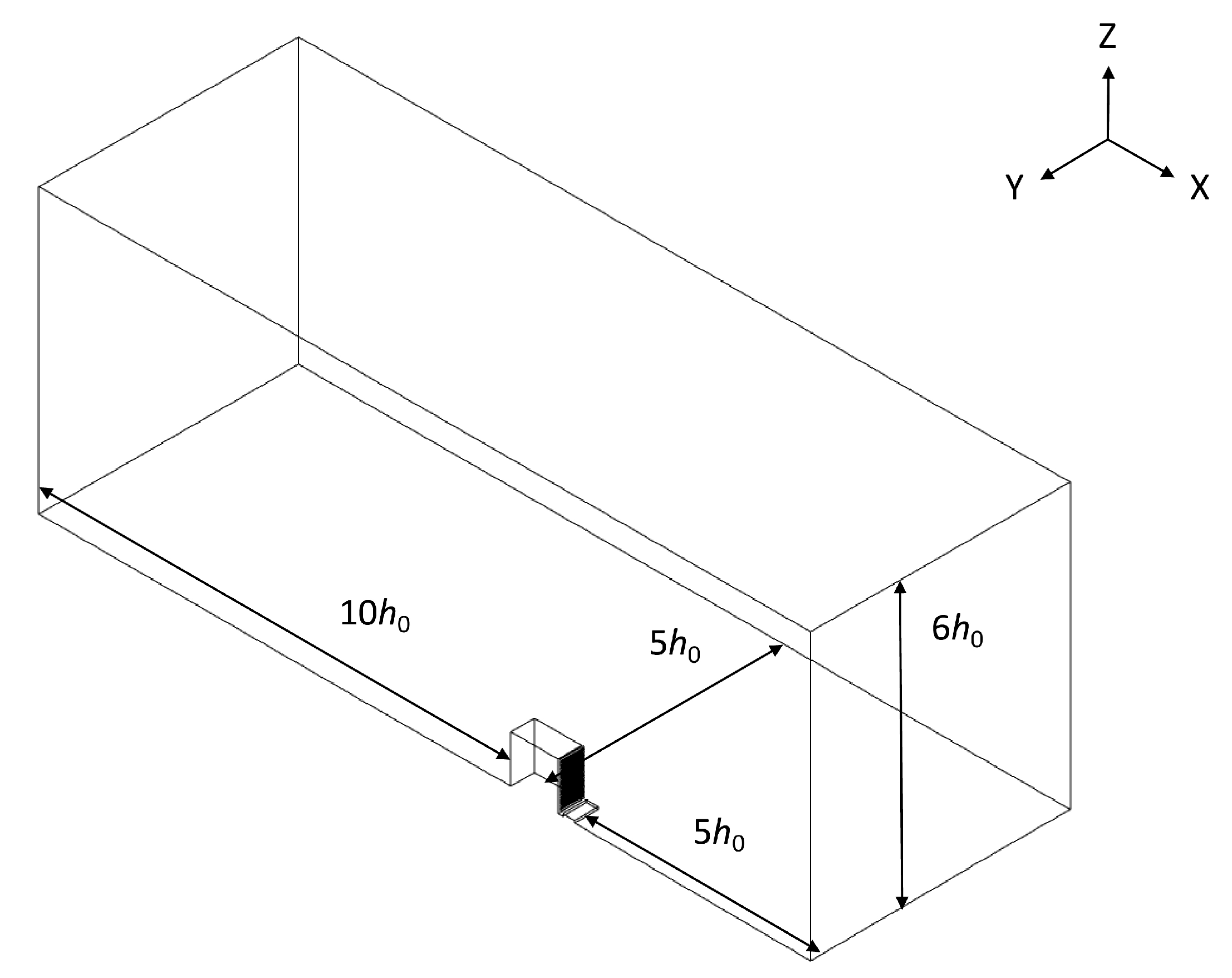
3.1.3. Computational Domain and Grid Resolution

The computational domain around the studied building is demonstrated in Figure 6. Two standards were used to define the scales of the computational domain [46,47], and the blockage ratio is below 3%. The minimum heights of the near-wall grids on the ground, building walls and shading louvers were 0.0003 m (0.0006h₀). Note that the near-wall grids are just the wall-adjacent grids closed to the solids, rather than all grids between two adjacent louvers. In near-wall boundary layers on these surfaces, enhanced wall treatment is applied for y+ < 5 and y+ ≈ 1 [51]. Figure 7 shows the grid resolution in computational domain and around the cubic building. Compared with published research of a building with louvered windows [12], we had much higher grid density along louver length but lower grid density along louver width, because in our pre-simulation, it was found that in the study of wind pressure coefficient, the deviations were mainly caused by the grid density along louver length, rather than that along louver width. Based on the grid resolution, a coarser mesh and a finer mesh were created to ensure grid accuracy. The Grid Convergence Index (GCI) [52,53] was calculated to show the deviation between different mesh sizes. For the reference case, GCI of normalized velocity and wind pressure coefficient are 0.37% and 1.8%, which are small enough to ensure grid accuracy, as recommended by Vinchurkar and Longest [54].

3.1.4. Boundary Conditions

In the reference case, the airflow inlet in front of the louvers was defined as velocity inlet. The turbulent intensity I and wind velocity U of the approaching airflow given by Equation (2) and Equation (1) are measured in the wind tunnel experiment by Jiang et al. [44] and applied, in order to calculate the turbulent kinetic energy k and turbulence dissipation rate ε by using Equations (3) and (4):

$$I(z)=0.1{(\frac{z}{h_0})}^{-a-0.05}$$

(2)

$$k(z)={[U(z)I(z)]}^2$$

(3)

$$\mathsf{\epsilon }(z)={\mathrm{C}}_{\mathsf{\mu }}{}^{0.5}k(z)\frac{U(z)}{h_0}\alpha {(\frac{z}{h_0})}^{\alpha -1}$$

(4)

The measurement results of velocity U and turbulent intensity I on the inlet obtained from the experiments and their fitting profiles for CFD simulations are shown in Figure 4. The constant value C_μ is set as 0.09 [47].

On the louvers, ground and building surfaces, the boundary conditions were defined as no-slip wall, on which the fluid sticks to the solid plane. For all these wall boundaries, enhanced wall treatment was used to simulate the near-wall airflow with y+ < 5. The top and the lateral boundaries were defined as symmetry, which means that the normal velocity and normal gradients of all variables are taken as zero at this boundary. The outlet was defined as outflow, on which the diffusion fluxes are zero for all flow variables [51].

3.1.5. Solver Settings

The discretized governing equations were solved by the finite volume method (FVM) in the steady state. The SIMPLEC algorithm was applied to couple the pressure and momentum equations. The second-order upwind difference scheme was applied for discretizing turbulent kinetic energy, momentum and turbulent dissipation rate. When the scaled residuals were below 10⁻⁶ for x, y, z momentum and 10⁻⁴ for continuity, k and ε, the convergence of the simulation was considered to be achieved. The monitors were also set at some points in the measurement lines in the simulation to verify the convergence. Oscillatory convergence was observed for the scaled residuals. As recommended by Ref [34] and [55], the results were monitored for more than 10,000 iterations. There were no significant oscillations in measurement lines of velocity and pressure, the average values over the last iterations were unnecessary and not calculated.

3.1.6. Calculation of Wind Pressure Coefficient

Wind pressure coefficient C_p is calculated from the pressure difference between static pressure P on the building surfaces and static pressure P_ref at the reference point, as provided in Equation (5):

$$C_{\mathrm{p}}=\frac{P-P_{\mathrm{ref}}}{\frac{1}{2}\rho U_{\mathrm{ref}}{}^2}$$

(5)

The reference point was set on the lateral boundary at the reference height h₀ and had the same distance from the inlet to the windward facade. ρ is the air density and taken as 1.225 kg/m³.

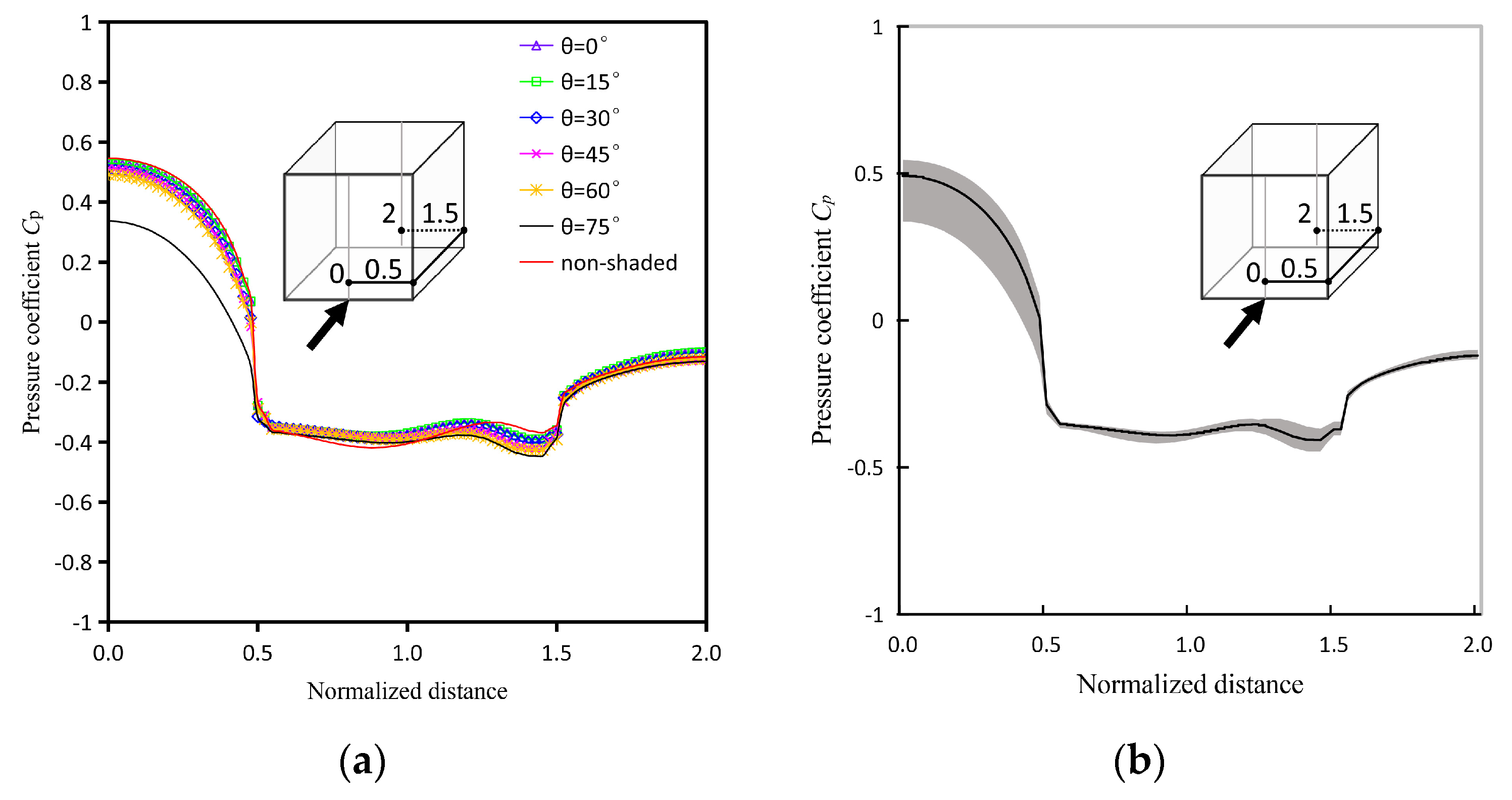
3.2. Result Validation

Validation was performed by comparing the deviation between the numerical results of the reference case and the experimental data from Jiang et al. [44]. In that reference, research with experimental and numerical results, allowed the velocity value to be measured at some points along several lines, which was on the mid-surface of the cubic building and perpendicular to the ground in the wind tunnel, while wind pressure coefficients were investigated along three lines on the intersection between building surfaces and the mid-surface in CFD simulations. The normalized velocity U_n as shown in Equation (6) is to demonstrate the airflow velocity distribution:

$$U_n(z)=\frac{U(z)}{U_{\mathrm{ref}}}$$

(6)

Figure 2 demonstrates the measurement locations to validate the numerical results. Figure 8 shows the normalized velocity U/U_ref distribution of the simulation data and the experimental results on vertical measurement locations. The average absolute deviation is 0.068 between simulation data and experimental data. Figure 9 shows C_p distribution for comparison of the data from the reference case and the data from Jiang et al. [44] along measurement lines on the windward, roof and leeward surfaces. The average absolute deviation is 0.046 between the two cases for wind pressure coefficient. The average values of U/U_ref and C_p, as long as their deviation on each line, are shown in

Table 1. Comparison of average value of normalized velocity U/U_ref and wind pressure coefficient C_p on measurement lines.

Value Type	U/Uref				Cp
	−0.5h0	0.5h0	1.5h0	2.5h0	Windward	Roof	Leeward
Average value (reference case)	1.21	0.94	1.03	0.72	0.62	−0.45	−0.19
Average value (Jiang et al.)	1.22	0.97	1.05	0.74	0.6	−0.45	−0.18
Absolute deviation	0.08	0.05	0.04	0.1	0.03	0.09	0.02

. The comparison results show that U and C_p in the reference case are in good agreement with results from the previous study. The U and C_p tendencies on these locations can be reproduced well by CFD technology. The maximum deviations occur beyond the roof for both, U and C_p distributions. This phenomenon seems to be that the realizable k-ε model with default parameters may provide airflow characteristics with overestimated reattachment lengths on the roof, and in the recirculating region at the corner between the ground and the leeward facade [32,56,57]. This over-estimation leads to the U near the roof and leeward facade and the smaller gradient for C_p along the roof line. Although, there are higher distortions in the reattachment region for the realizable k-ε model, the simulation accuracy is considered to be suitable enough to perform CFD simulations.

4. Results and Discussion

When openings are installed on outside surfaces of a sealed building, the pressure distribution on the envelope can be applied to forecast air leakage, design indoor airflow routes and evaluate natural ventilation patterns in different wind environments [17]. Analyzing the distribution of wind pressure coefficient C_p on shaded building surfaces is critical for exploring the potential ventilation capacity. For a sealed building, orifice equation assumes that the pressure distribution is independent to the presence of openings [13]. In orifice equation, C_p is applied to calculate wind-induced airflow rate Q of natural ventilation in buildings [14,15], as shown in Equations (7) and (8),

$$Q=C_{\mathrm{d}}A\sqrt{\frac{2\Delta P}{\rho }}$$

(7)

$$\Delta P=\frac{1}{2}\rho U_{\mathrm{ref}}{}^2{C}_{\mathrm{p}}-P_i$$

(8)

where A is the area of an opening in the sealed building assumption. C_d is the discharge coefficient. P_i is the pressure inside the building.

4.1. General Features of Airflow Pattern

Figure 10 shows airflow streamlines around the building and wind pressure distribution on the building surfaces under the shaded condition with θ = 45°. In Figure 10a, the approaching flow towards the central rows was separated into three regions: Stagnation zone on the windward facade at about 0.7h₀, the upward flow near the roof and the downward vortex near the ground. The streamlines were smooth above the small reverse flow on the roof. The larger reverse flow and the recirculating zone were generated on the lateral façade, and the leeward facade, respectively. In Figure 10b, the airflow streamlines towards the side rows were smoother than that towards the central rows, which demonstrates that the airflow pattern was almost not affected by the detailed geometry of the shaded building.

4.2. Features of Local Wind Pressure Coefficient along Measurement Lines

The windward, lateral and leeward facades are divided into seven equal rows and five equal floors to ensure that the outside surfaces of rooms have the same area in the same direction. The rows are marked from R1 to R7, and the floors are marked from F1 to F5, as shown in Figure 11a. Note that the area for calculation is half of the real area for R1 and R7, considering the usage of the symmetry building model and symmetry domain in simulations. The distribution of wind pressure coefficient are investigated on two W-R-L lines, five W-S-L lines and three R-S lines. All these lines are located on the center of their rows or floors, which are also shown in Figure 11b–d. The impact of shading louvers with various rotation angle θ on C_p at a specific point is evaluated by the range R as shown in Equation (9).

$$R=C_{\text{p-max}}-C_{\text{p-min}}$$

(9)

where R is the range of wind pressure coefficient C_p at a specific point on a measurement line for different shaded conditions. C_p-max and C_p-min are the maximum and minimum C_p at that point in these shaded conditions. Note that C_p-max and C_p-min only represent the local values of a special point on a line in all shaded cases, which are different from the maximum and minimum C_p on a whole line.

4.2.1. Local Wind Pressure Coefficient on W-R-L Lines

Figure 12a,b present the local range R, local and average value of wind pressure coefficient C_p on the central lines of R1 and R7 along the windward, roof and leeward surfaces under different shaded conditions. Generally speaking, the roof suffers the largest fluctuation of C_p, while the leeward surface has the smallest difference of the local C_p and R along the lines. The maximum and minimum value of C_p are 0.86 and −1.08, respectively. The C_p-max line and C_p-min line have the similar shape and tendency except near the edge of the roof for around 1–1.4h₀ where has a flow separation. On the line of the windward facade, the maximum R is at about 0.8–0.9h₀ on the stagnation zone and the minimum R is near the edge between the windward and the roof surfaces. The R along these lines increases along 0–0.1h₀, but the local C_p decreases. From 0.1h₀ to 0.7h₀, the local C_p and the R both increase. After 0.7h₀, the local C_p in some cases begins to decrease but the R still grows up until around 0.9h₀. These results indicate that near the maximum positive C_p on the stagnation zone, the C_p is strongly sensitive to the rotation angle θ of shading louvers. For the area near the vortex at the corner of the windward facade and the ground, the C_p is not sensitive to different shaded conditions. On the lines of the roof, the C_p suffers a sharp decrease near the edge, which is the continuation of the windward surface. Then the R increases to the widest at 1.05h₀. In this area, the blocking effect of shading louvers makes the C_p tendency smoother along the roof line. On the leeward line, the local C_p just changes slightly at different points due to the leeward recirculation.

Figure 12c,d present the local range R, local and average value of wind pressure coefficient C_p on the central lines of R2 and R6 along the windward, roof and leeward surfaces. Generally speaking, the tendencies of the C_p-max line and the C_p-min line along the lines in Figure 12d are similar to those in Figure 12b. The R along the central lines of R2 and R6 is smaller than that along the central lines of R1 and R7. However, there are also some significant differences between the two locations. On the windward surface, the R along the central lines of R2 is always larger. Even if the maximum C_p on two locations are almost the same, the local C_p-min near the ground is obviously different between two locations. the C_p-max along the central lines of R1 is over 0.5 within 0–0.9h₀, but the C_p-max along the central lines of R2 is below 0.5 within 0–0.3h₀. The shape difference on the C_p-min line is not as obvious as that on the C_p-max line. The C_p-min along the central lines of R2 is about 0.2 smaller. These differences mean that on the lines of R2, the windward surface tends to suffer a larger fluctuation of positive wind pressure. On the roof, the shape and tendency of the C_p-max and C_p-min on the central lines of R2 and R6 are almost the same as those on the central lines of R1 and R7, and only the R is a little smaller for most locations than the central line. On the leeward, the gradient and the maximum value of C_p along the central lines of R6 are slightly lower than those along the central lines of R7.

4.2.2. Local Wind Pressure Coefficient on W-S-L Lines

Figure 13a,b present the local range R, local and average value of wind pressure coefficient C_p on the central lines of the first floor along the windward, the lateral and the leeward surfaces. The windward surface suffers the largest fluctuation of C_p, while the lateral wall has the smallest fluctuation of C_p. Generally speaking, the windward surface has the widest R and the largest difference of the local C_p along the central line. The leeward surface has the smallest R along the central lines. The C_p-max line and the C_p-min line have the similar shape and tendency. The maximum value and the C_p-min are 0.55, and −0.44, respectively. On the windward surface, the largest R locates at 0.38h₀ and the smaller R locates on the edge between the windward and the lateral surfaces. On the lateral surface, the R increases slightly along 0.5–0.8h₀, then within 0.8–1.2h₀ the R are almost the same. From 1.2h₀ to 1.4h₀, the R increases obviously, then it decreases again near the edge between the lateral surface and the leeward surface. On the leeward surface, the local C_p increases obviously but the R just increases slightly.

Figure 13c–j present the local range R, local and average value of wind pressure coefficient C_p on the central lines of the F2–F5 along the windward, the lateral and the leeward surfaces. Generally speaking, the tendencies of the C_p-max and C_p-min along the central lines on different floors are similar to those on F1. The maximum value on the C_p-max line is larger when the floor is higher, except for F5, on which the maximum value on the C_p-max line is a little smaller than those on F4. The minimum value on the C_p-min line is lower when the floor is higher. The locations of the minimum value on the C_p-min lines are on the lateral surface for all floors. However, for F1 and F2, the locations are near edge of the windward surface at around 1.4h₀, while for the higher floors, C_p near the edge of the leeward surface at around 0.55h₀ is the minimum value on the C_p-min lines. On the windward surface, the R along the central lines is wider for the higher floors. The absolute gradient of the C_p-max line becomes lower near the central vertical lines but becomes higher near the edge of the lateral surface. On the lateral surface, the R becomes wider at around 0.55h₀ for the higher floors because of the lower C_p-min. Along the lines on the lateral surface, the location of the minimum R becomes closer to the windward surface, as the floor becomes higher. The fluctuation of R near the edge of the leeward surface becomes smooth. This phenomenon means that as the floor gets higher, the wind suction effect of reverse flow becomes greater than the effect of the backward recirculation, but the negative pressure area, caused by the reverse flow, seems to be smaller than the negative pressure area caused by recirculation. On the leeward surface, the R along the central lines are similar for F1, F2 and F3, while the R are a little wider for F4 and F5. The absolute gradient of C_p becomes lower for the higher floors, which means that higher floors are prone to have smoother C_p distribution along these lines.

4.2.3. Local Wind Pressure Coefficient on R-S Lines

Figure 14a–f presents the local range R, local and average value of wind pressure coefficient C_p, on the central lines of R3–R5, along the roof and leeward surfaces. The C_p distributions along R-S lines are obviously smoother than C_p along W-R-L and W-S-L lines, because only the windward surface undergoes positive wind pressure. Generally, The R has the largest value on the central lines of R3, while R has the smallest value on the central lines of R4. The result indicates that R4 on the lateral surface seems to be the transitional zone, where the impact of reverse flow becomes weaker, so the presence of shading louvers cannot change C_p greatly. On the three lines, most local R on the roof is larger than those on the lateral surface. The maximum C_p locates on the lateral surface near the ground for the central lines of R3 but on the roof for the central lines of R4 and R5. The minimum C_p locates on the roof for the central lines of R3 and R4 and on the lateral surface for the central lines of R5. The largest R locates at 0h₀ for the central lines of R3 and R5 and at around 0.48h₀ near the edge between the roof and lateral surfaces for the central lines of R4. The R changes strongly along the central lines of R3 but more slightly along other two lines. The result of R3 means that the reverse flow near the roof and the lateral surface are both sensitive to the shaded conditions.

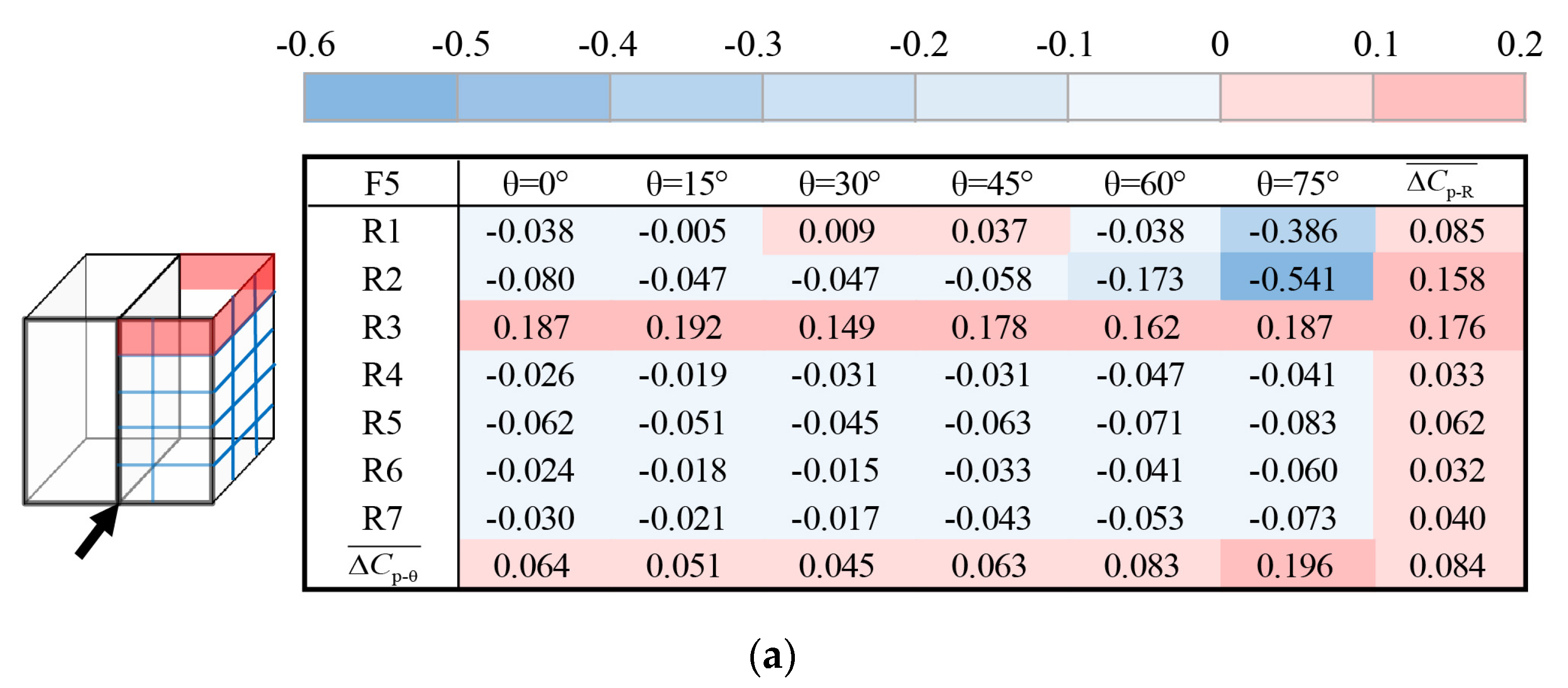
4.3. Impact of Shading Louvers on Average Wind Pressure Coefficient

Some parameters are introduced to describe the characteristics of average C_p on outside surfaces of rooms. $\overline{C_{\mathrm{p}}}$ is the average C_p on outside surface of a room belongs to the intersection of one floor and one row, as given by Equation (10). $\Delta \overline{C_{\mathrm{p}}}$ is the difference of $\overline{C_{\mathrm{p}}}$ between a shaded condition and the non-shaded condition, as given by Equation (11). $\overline{\Delta C_{\mathrm{p}\text{-}\mathrm{R}}}$ is the average difference of $\overline{C_{\mathrm{p}}}$ for all shaded conditions, compared with the non-shaded condition in a special row, as given by Equation (12). $\overline{\Delta C_{\mathrm{p}\text{-}\mathsf{\theta }}}$ is the average difference of $\overline{C_{\mathrm{p}}}$ between a specific shaded condition and the non-shaded condition in a whole row, as given by Equation (13),

$$\overline{C_{\mathrm{p}}}=\frac{1}{A_{\mathrm{R}}}{\displaystyle \sum _{A_{\mathrm{R}}}{C}_{\mathrm{p}}\Delta S_{\mathrm{R}}}$$

(10)

$$\Delta \overline{C_{\mathrm{p}}}=\overline{C_{\mathrm{p}}}-\overline{C_{\mathrm{p}\text{-}\mathrm{n}}}$$

(11)

$$\overline{\Delta C_{\mathrm{p}\text{-}\mathrm{R}}}={\displaystyle \sum _{i=1}^6{\left|\overline{C_{\mathrm{p}\text{-}\mathsf{\theta }\text{-}i}}-\overline{C_{\mathrm{p}\text{-}\mathrm{n}}}\right|}_{}}$$

(12)

$$\overline{\Delta C_{\mathrm{p}\text{-}\mathsf{\theta }}}={\displaystyle \sum _{j=1}^7\left|\overline{C_{\mathrm{p}\text{-}\mathrm{R}\text{-}j}}-\overline{C_{\mathrm{p}\text{-}\mathrm{n}}}\right|}$$

(13)

where A_R is the area of the outside surface of a room. In all simulation cases, the rooms in different floors and rows are assumed to have the same A_R. Considering the usage of the symmetry model and symmetry domain in simulations, A_R in R1 and R7 are set as the half value of the real area. ∆S_R is the area of a grid on the outside surface. $\overline{C_{\mathrm{p}\text{-}\mathsf{\theta }\text{-}i}}$ is the $\overline{C_{\mathrm{p}}}$ for the shaded condition with a specific rotation angle θ, and i is set as 1–6 to represent θ = 0°, 15°, 30°, 45°, 60° and 75°. $\overline{C_{\mathrm{p}\text{-}\mathrm{n}}}$ is the $\overline{C_{\mathrm{p}}}$ in the non-shaded condition. $\overline{C_{\mathrm{p}\text{-}\mathrm{R}\text{-}j}}$ is the $\overline{C_{\mathrm{p}}}$ in a specific row, and j is set as 1–7 to represent R1–R7.

Figure 15 presents $\overline{C_{\mathrm{p}}}$ on five different floors along R1–R7. Figure 16 presents $\Delta \overline{C_{\mathrm{p}}}$ between the non-shaded condition and other shaded conditions. In Figure 15, the $\overline{C_{\mathrm{p}}}$ results of R1 and R2 show that the windward surface has the largest difference of $\overline{C_{\mathrm{p}}}$ on different floors for most shaded conditions. On the windward R1 and R2, F4 has the highest $\overline{C_{\mathrm{p}}}$ and F1 has the lowest $\overline{C_{\mathrm{p}}}$ for most shaded conditions. $\overline{C_{\mathrm{p}}}$ has the greatest reduction for all floors when θ turns from 60° to 75°. For most floors, $\overline{C_{\mathrm{p}}}$ decreases with a higher θ, except for F5. On the lateral R3, the greatest difference occurs between the non-shaded condition and the shaded condition for any θ, but $\overline{C_{\mathrm{p}}}$ does not have much fluctuation when θ changes. The $\overline{C_{\mathrm{p}}}$ results of R4, R5 and R6 show that the smallest difference of $\overline{C_{\mathrm{p}}}$ for different floors occurs near the edge between the lateral and leeward surfaces. The results of R4, R5, R6 and R7 show that the impact of shading louvers on $\overline{C_{\mathrm{p}}}$ can be neglected in some non-shaded facades. In Figure 16, the impact of shading louvers on $\overline{C_{\mathrm{p}}}$, which is described as $\Delta \overline{C_{\mathrm{p}}}$, becomes higher for the higher floors in general. Considering the different rows, R2 and R3 have the largest and the second largest $\overline{\Delta C_{\mathrm{p}\text{-}\mathrm{R}}}$ for most floors with the presence of shading louvers. And the impact of shading louvers on $\overline{C_{\mathrm{p}}}$ is obviously smaller for R4, R6 and R7. With shading louvers, $\overline{C_{\mathrm{p}}}$ on R3 are larger than those without shading louvers for all floors. And the situation are almost the same on R4 except for F5. But on the most parts of other rows, $\overline{C_{\mathrm{p}}}$ decreases when shading louvers are installed. For F1, the largest and the second largest $\overline{\Delta C_{\mathrm{p}\text{-}\mathrm{R}}}$ occur on R1 and R2. The largest absolute value of $\Delta \overline{C_{\mathrm{p}}}$ occurs on R4 for just θ = 0° and on R2 for the other θ. For F2 to F5, the largest and the second largest $\overline{\Delta C_{\mathrm{p}\text{-}\mathrm{R}}}$ occur on R2 and R3. The presence of shading louvers has the largest influence on $\Delta \overline{C_{\mathrm{p}}}$ of R3 for θ = 0°–45° but on $\Delta \overline{C_{\mathrm{p}}}$ of R2 for higher θ.

5. Conclusions

Taking into account rotation angle of shading louvers, this study investigated the distribution of wind pressure coefficient of a multi-storey building, with single-shaded louvers, through CFD simulation, in order to analyse the potential ventilation capacity of the shaded building. A comparison for validation was performed between the numerical results and data from the previous study. To investigate the wind pressure distribution in detail, the studied outside surfaces were divided into seven rows and five floors to obtain the average wind pressure coefficients of different rooms. The local wind pressure coefficients were also measured along central lines of different rows and floors. The rotation angle of louvers was taken as 0°, 15°, 30°, 45°, 60° and 75°. Through the analysis of the impact of shading louvers, some conclusions are provided as follows:

• The validation of the studied building shows a small deviation between the numerical data and the data from the previous study. The average absolute deviation is 0.046 for wind pressure coefficient C_p and 0.068 for normalized velocity U/U_ref. The Grid Convergence Index of U/U_ref and C_p for the reference case is 0.37%, and 1.8%, respectively. Therefore, the parameters of the simulation cases are feasible for the shaded building, and the computational settings is useful for further case studies of shaded buildings.
• In general, the fluctuations of C_p on the windward and roof surfaces are mostly stronger than those on the lateral and leeward surfaces along the measurement lines. These results indicate that when the ventilation openings located on the roof and windward facade with louvers, the ventilation routes can lead to larger fluctuations of ventilation rate. In building design, it is important to diagnose the risks of inadequate ventilation for shaded buildings, especially those with roof ventilation systems.
• The stagnation zone of the windward surface has the highest average wind pressure coefficient $\overline{C_{\mathrm{p}}}$. For most floors and rows, $\overline{C_{\mathrm{p}}}$ decreases with a higher rotation angle θ. And $\overline{C_{\mathrm{p}}}$ has the greatest reduction for all floors when θ turns from 60° to 75°. These results indicate that ventilation openings on the stagnation zone contribute to higher ventilation rate for the windward facade with louvers. When the rotation angle is taken for more than 60°, it is essential to avoid bad indoor wind environment for rooms with ventilation openings located on the shaded facade.

Overall, several parameters of wind pressure coefficient distribution were investigated in this study to gain a greater understanding of fluctuations in wind characteristics caused by the presence of external shading louvers. These kinds of data provide a wider perspective for building engineers and designers to understand the wind-induced fields around shaded buildings and improve the indoor environment in buildings with external shading louvers.