Optimal Design of the Vertical Earthing with Electrodes Arranged in Line
Abstract
:1. Introduction
- Defining five optimal criteria as follows: the footprint area (noted AP), the EG total volume (VP), the total dispersion surface (AD), the conducting materials mass (MP), and the investment costs (IP).
- From the eight characteristic variables of the earthing system with vertical electrodes (VEG), the length and number of electrodes are considered independent variables, and the distance between adjacent electrodes is considered as an intrinsic variable, determined by the condition of the design value resistance.
- Creating an Excel program, which allows determining the distance between adjacent electrodes for all combinations of lengths and numbers of electrodes, achieving the design value resistance.
- Within the same program, the five optimal criteria are applied to the same combinations of lengths–numbers–distances between electrodes to highlight the optimal (minimal) solutions.
- The use of optimal criteria, mentioned above, in the VEG dimensioning with electrodes arranged in a rectangle (VEGR) favored the improvement of the calculation methodology, the achievement of the variables importance hierarchy, and emphasized distinct areas of minimum values.
2. Methodological Aspects
2.1. Basic Sizes
- In all practical cases, the variables {ρp, q, RPn} have determined or imposed values. Thus, the resistivity of the soil ρp is experimentally determined by measurements on the soil where the VEGL is to be made. The burial depth, q, is imposed by the maximum freezing depth, according to the geographical position of the objective, q ∈ {0.8–0.9} m (in Romania and other European countries); RPn ∈ {1, 4, 5, 10} Ω, depending on the VEGL’s concrete destination [1,3,4,5] when there is no natural earthing system. When there is a natural earthing system, the design value resistance will be calculated so that the resistance to earth of combined systems has one of the above values.
- The wall thickness, g, of the pipe electrode has a reduced influence on the VEGL resistance to earth, with a recommended value of g ≥ 3.5 mm for a longer lifetime of the earthing system.
- The electrode’s number, which can only be a natural number, ne ∈ {1, 2, 3, ...}.
- The sizes ℓ and ne are considered as independent variables, with the ranges of interest values ℓ ∈ [0.5–4] m and ne ∈ {1, 2, 3, ...}, increasing the electrodes’ numbers up to the limits of the technical solution.
- The variable a is considered an intrinsic one because its value is determined by the mathematical model based on the other sizes. The lower technical limit is a ≈ 0.2 m.
- The sizes {d, ρp, q, g, RPn} are considered as parameters that justifiably change from one case to another.
2.2. Calculation Methodology for VEG with Linearly Placed Electrodes
2.3. Optimal Criteria
2.3.1. The Footprint Area
2.3.2. The VEGL Total Volume
2.3.3. The VEGL Dispersion Surface Area
2.3.4. The VEGL Metal Mass
2.3.5. Total Investment
- The cost per length unit of the electrode material is dependent on the diameter d and the thickness g of the pipe wall, as indicated below in the manner adopted in [16]:
- The percentage cost m% of the small materials were identified based on the norms data as a linear dependence on the electrode length ℓ, according to the relation:
- The other costs are estimated as follows:
3. Results
3.1. The Data Set
- 167.8/1.99 = 84.3 at the AP criterion;
- 370.3/4.08 = 90.8 at the VP criterion;
- 170/16.8 = 10.1 at MP criterion;
- 6.1/1.7 = 3.59 at AD criterion;
- 9.412/875.5 = 10.8 at IP criterion.
3.2. The Characteristic Curves a(ℓ,ne)
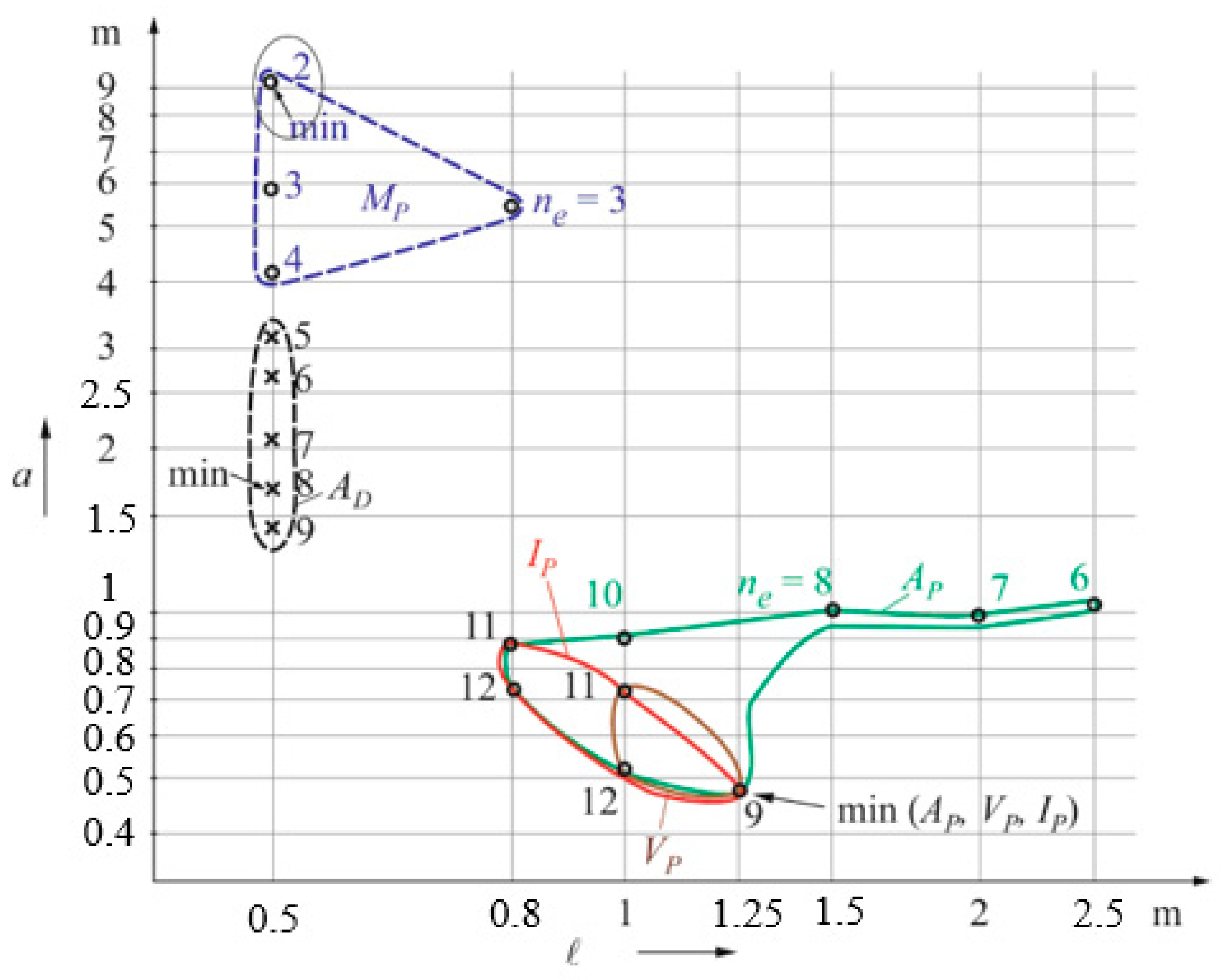
3.3. Minimum Zones
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- BS Code of Practice for Earthing; BS 7430; BS: Geneva, Switzerland, 1998.
- BS (IEC). Glossary of Electrotechnical, Power, Telecommunication, Electronics, Lighting and Color Terms; BS 4727-1: Group 09:1991 (IEC 60050-161:1990); BS: Geneva, Switzerland, 1990. [Google Scholar]
- IEC. Low-Voltage Electrical Installations-Selection and Erection of Electrical Equipment-Earthing Arrangements and Protective Conductors; IEC 60364-5-54:2011; IEC: Geneva, Switzerland, 2011. [Google Scholar]
- IEC. Earthing of Power Installations Exceeding 1 kV a.c.; IEC EN Standard 50522/Jul. 2011; IEC: Brussels, Belgium, 2011. [Google Scholar]
- Normative for the Design, Execution and Operation of Electrical Installations Related to Buildings, I7-2011; MATRIX ROM: Bucharest, Romania, 2011; Volume 1–2.
- Good Practice Guide for Designing Lighting/Protection Installations in Buildings; Gex 12-2015; MATRIX ROM: Bucharest, Romania, 2016.
- Sufrim, M. Design and Construction Guide for Earthing Systems; 1 RE-Ip 30/2004; SIER Ed.: Bucharest, Romania, 2004. [Google Scholar]
- STAS. Electrical Installations of 1,000 V and More than 1,000 V. Installations for Protective Earthing; STAS 7334-83; ASRO: Bucharest, Romania, 1983. [Google Scholar]
- Comşa, D.; Darie, S.; Maier, V.; Chindriş, M. Design of the Industrial Electrical Installations, 2nd ed.; Editura Didactică şi Pedagogică: Bucharest, Romania, 1983. [Google Scholar]
- Lucache, D.D. Low-voltage Electrical Installations, Theoretical Basics and Designing Elements; Editura PIM: Iași, Romania, 2009. [Google Scholar]
- Markievicz, H.; Klajn, A. Earthing and EMC, Earthing Systems–Basical Constructive Aspects, Application Guide-Power Quality; SIER Ed.: Bucharest, Romania, 2004. [Google Scholar]
- Seidman, A.; Beaty, H.W.; Mahrous, H. Handbook of Electric Power Calculations, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Sufrim, M.; Goia, M.L.; și Petran, M. Earthing Installations; Editura Tehnică: Bucharest, Romania, 1987. [Google Scholar]
- Maier, V.; Pavel, S.G.; Beleiu, H.G.; Birou, I.; Fărcaș, V. Nomograms for sizing the vertical earth grounding. In Proceedings of the EPE, Bucharest, Romania, 20–22 October 2016; pp. 483–486. [Google Scholar]
- Maier, V.; Pavel, S.G.; Beleiu, H.G.; Pică, C.S. Vertical Earth Grounding Design Using Optimal Criteria. In Proceedings of the ATEE, Bucharest, Romania, 23–25 March 2017; pp. 539–544. [Google Scholar]
- Ciorca, C.; Maier, V.; Pavel, S.G.; Birou, I.; Beleiu, H.G. Dimensioning of the Vertical Earth Grounding with Rectangular Contour through Minimizing the Investments Costs. In Proceedings of the EPE 2018, Bucharest, Romania, 17–21 September 2018; pp. 154–158. [Google Scholar]
- Maier, V.; Pavel, S.G.; Ciorca, C.; Birou, I.; Beleiu, H.G. Dissipation Surface Minimization of Vertical Earth Grounding, with Rectangular Contour. In Proceedings of the ATEE, Bath, UK, 14–16 August 2019. [Google Scholar]
- He, J.; Gao, Y.; Zeng, R.; Sun, W.; Zou, J.; Guan, Z. Optimal Design of Grounding System Considering the Influence of Seasonal Frozen Soil Layer. IEEE Trans. Power Deliv. 2005, 20, 107–115. [Google Scholar]
- Wang, S. Optimal Arrangement of Long Vertical Rods to Reduce Ground Resistance considering Their Shielding Effect. In Proceedings of the IEEE ICHVE 2018, Athens, Greece, 10–13 September 2018. [Google Scholar]


| ℓ, m | ne, pcs. | a, m | RPe, Ω | RPc, Ω | AP, m2 | VP, m3 | AD, m2 | MP, kg | IP, u.m. |
|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 2 | 9.16 | 54.35 | 4.32 | 167.81 | 218.15 | 1.74 | 14.96 | 9412.99 |
| 3 | 2 | 6.98 | 15.75 | 5.36 | 97.44 | 370.28 | 1.98 | 29.88 | 5729.04 |
| 0.5 | 3 | 5.82 | 36.71 | 4.49 | 101.62 | 132.10 | 1.72 | 19.82 | 5803.98 |
| 0.8 | 3 | 5.50 | 26.14 | 4.69 | 90.75 | 145.20 | 1.75 | 22.20 | 5259.34 |
| 0.5 | 4 | 4.16 | 27.92 | 4.66 | 69.22 | 89.99 | 1.72 | 22.63 | 4054.17 |
| 0.5 | 6 | 2.51 | 22.67 | 4.86 | 37.80 | 49.14 | 1.70 | 26.25 | 2390.14 |
| 2.5 | 6 | 1.03 | 6.64 | 10.00 | 6.37 | 21.01 | 2.43 | 59.36 | 1180.37 |
| 0.5 | 7 | 2.05 | 16.71 | 5.24 | 29.42 | 38.24 | 1.70 | 27.70 | 1961.64 |
| 0.5 | 8 | 1.70 | 14.87 | 5.47 | 23.12 | 30.06 | 1.70 | 28.97 | 1647.60 |
| 1.25 | 9 | 0.47 | 5.56 | 13.19 | 1.99 | 4.08 | 1.79 | 44.39 | 875.53 |
| 1.25 | 10 | 0.69 | 7.04 | 9.21 | 4.76 | 9.76 | 2.18 | 51.86 | 1126.34 |
| 0.8 | 11 | 0.85 | 8.82 | 7.32 | 7.95 | 12.72 | 1.93 | 41.66 | 1113.71 |
| 1 | 11 | 0.72 | 7.68 | 8.30 | 5.70 | 10.26 | 2.08 | 47.80 | 1113.98 |
| 0.5 | 12 | 0.93 | 10.63 | 6.38 | 6.22 | 9.95 | 1.97 | 43.76 | 1070.90 |
| 0.8 | 12 | 0.72 | 8.22 | 7.77 | 3.24 | 5.84 | 2.06 | 49.48 | 1037.20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavel, S.G.; Maier, V.; Ciorca, C.; Beleiu, H.G.; Birou, I. Optimal Design of the Vertical Earthing with Electrodes Arranged in Line. Appl. Sci. 2020, 10, 1177. https://doi.org/10.3390/app10031177
Pavel SG, Maier V, Ciorca C, Beleiu HG, Birou I. Optimal Design of the Vertical Earthing with Electrodes Arranged in Line. Applied Sciences. 2020; 10(3):1177. https://doi.org/10.3390/app10031177
Chicago/Turabian StylePavel, Sorin Gheorghe, Virgil Maier, Claudiu Ciorca, Horia Gheorghe Beleiu, and Iulian Birou. 2020. "Optimal Design of the Vertical Earthing with Electrodes Arranged in Line" Applied Sciences 10, no. 3: 1177. https://doi.org/10.3390/app10031177
APA StylePavel, S. G., Maier, V., Ciorca, C., Beleiu, H. G., & Birou, I. (2020). Optimal Design of the Vertical Earthing with Electrodes Arranged in Line. Applied Sciences, 10(3), 1177. https://doi.org/10.3390/app10031177





