Complete Evaluation of Cell Mixing and Hydrodynamic Performance of Thin-Layer Cascade Reactor
Abstract
:1. Introduction
2. TLC Description and Mathematical Modeling
2.1. Hydrodynamic Modeling
2.2. Algae Cell Modeling
3. Numerical Details
4. Results and Discussion
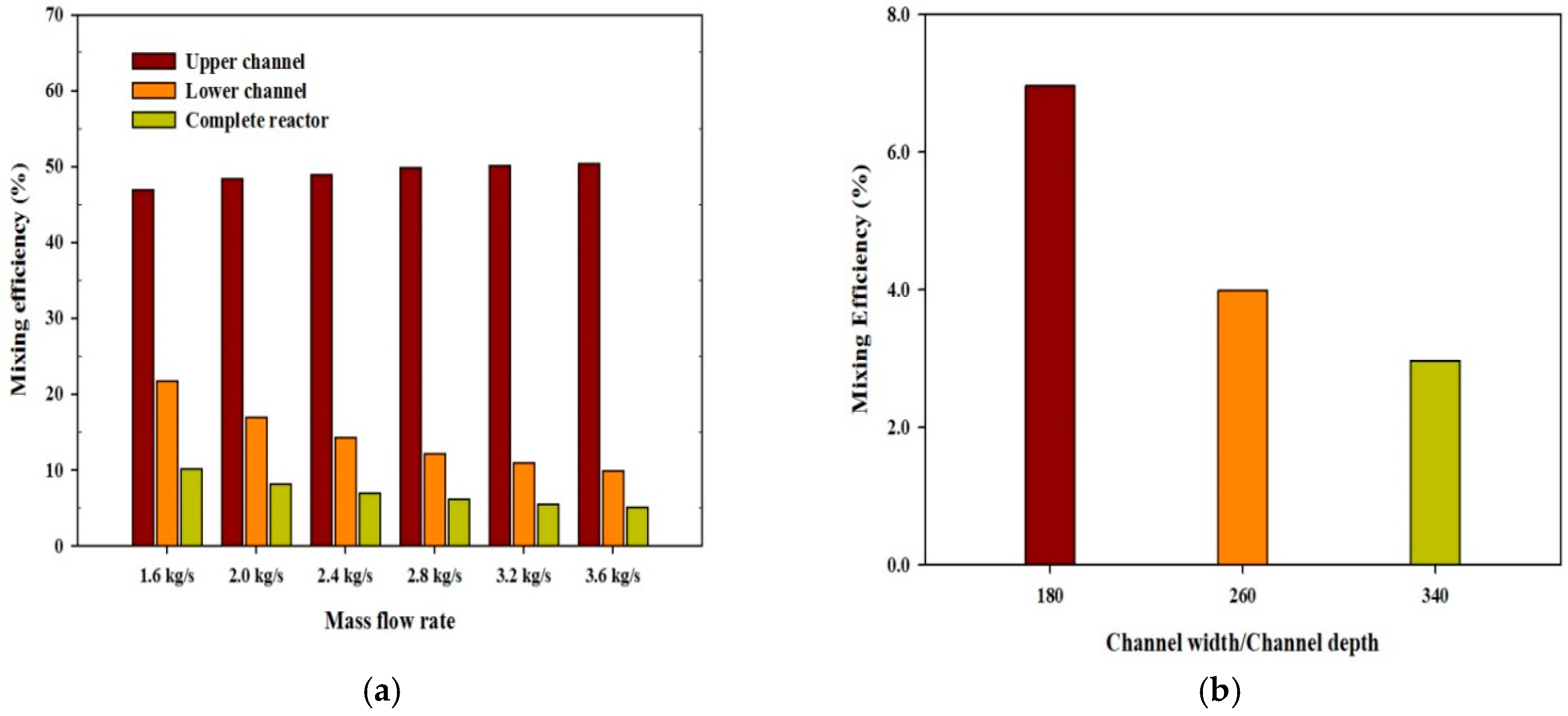
4.1. Mixing Performance of TLC Reactor
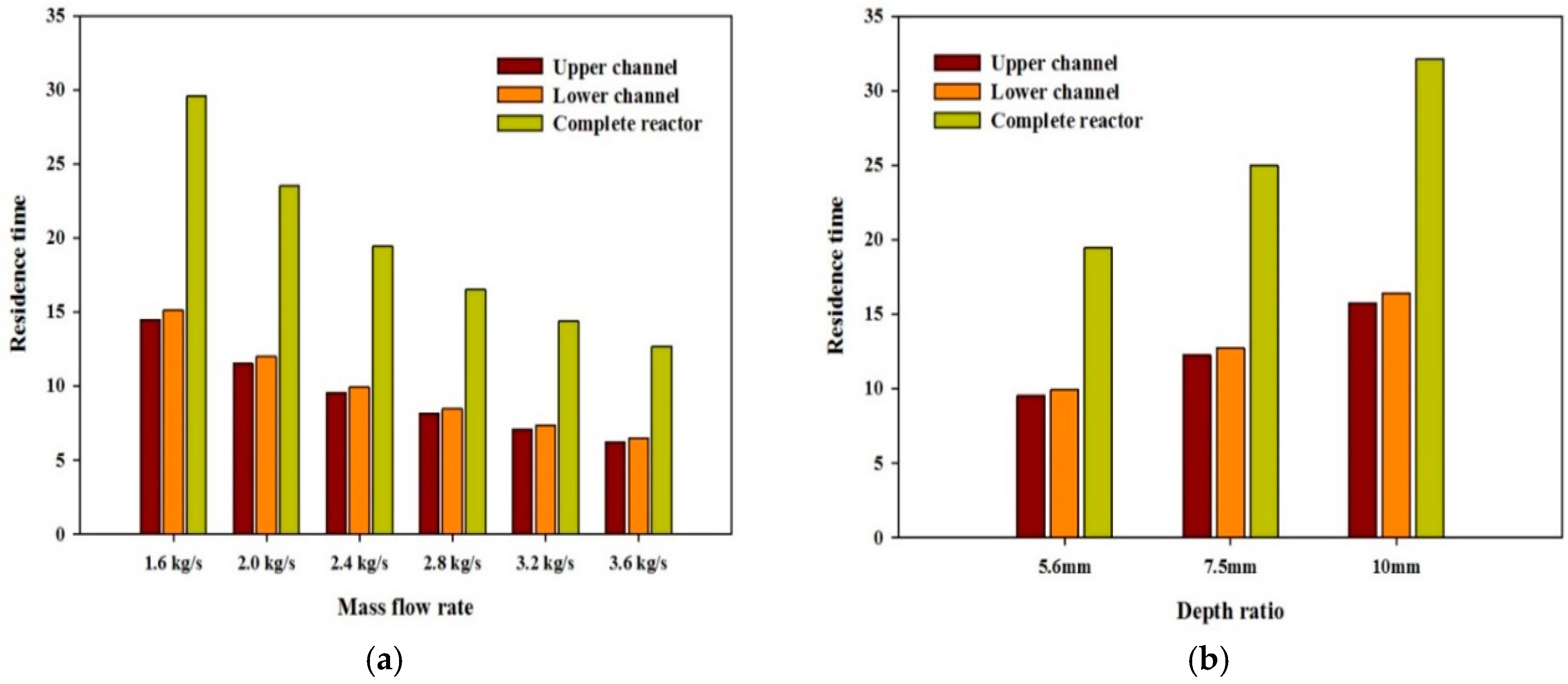
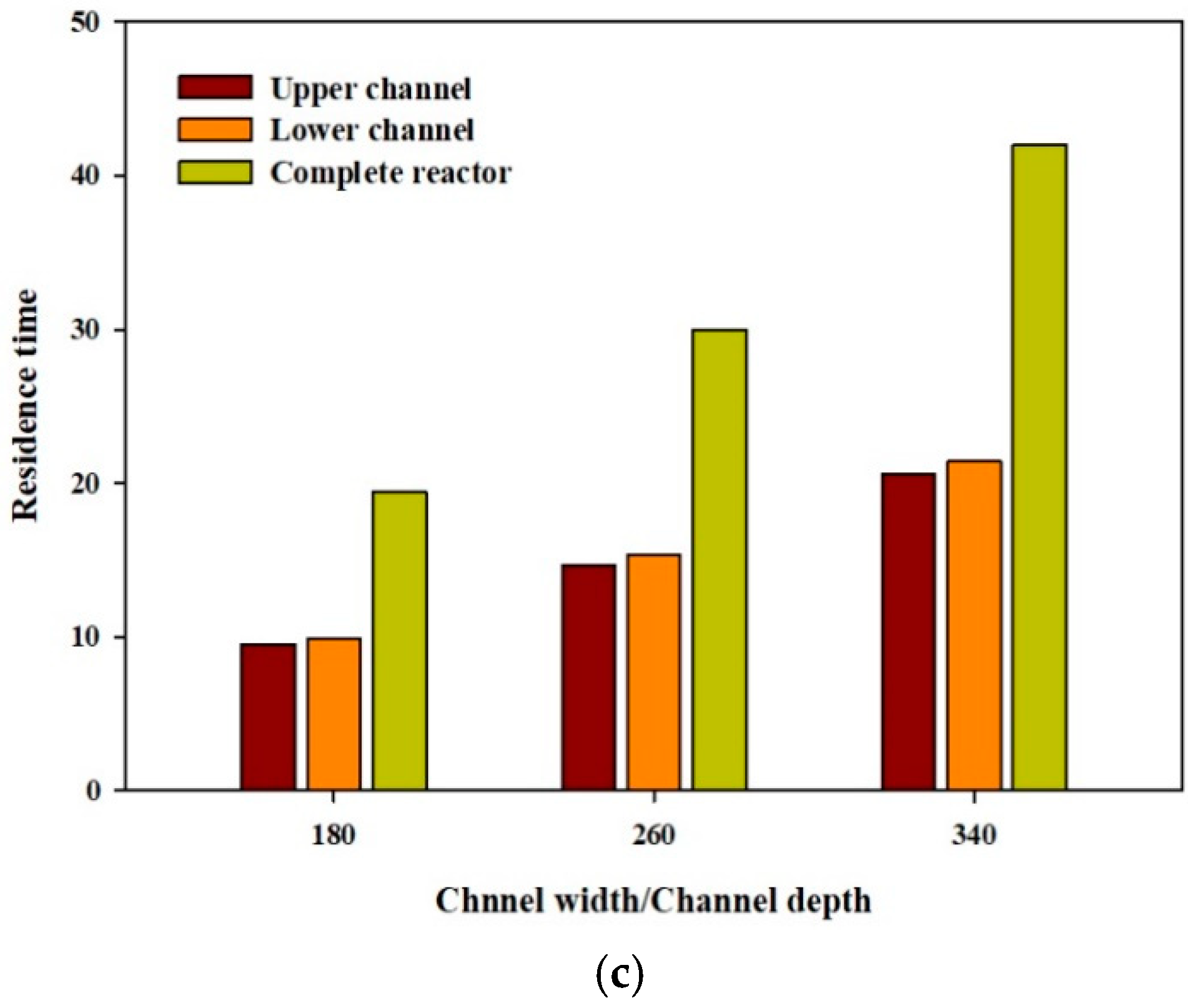
Residence Time
4.2. Hydrodynamic Performance of TLC Reactor
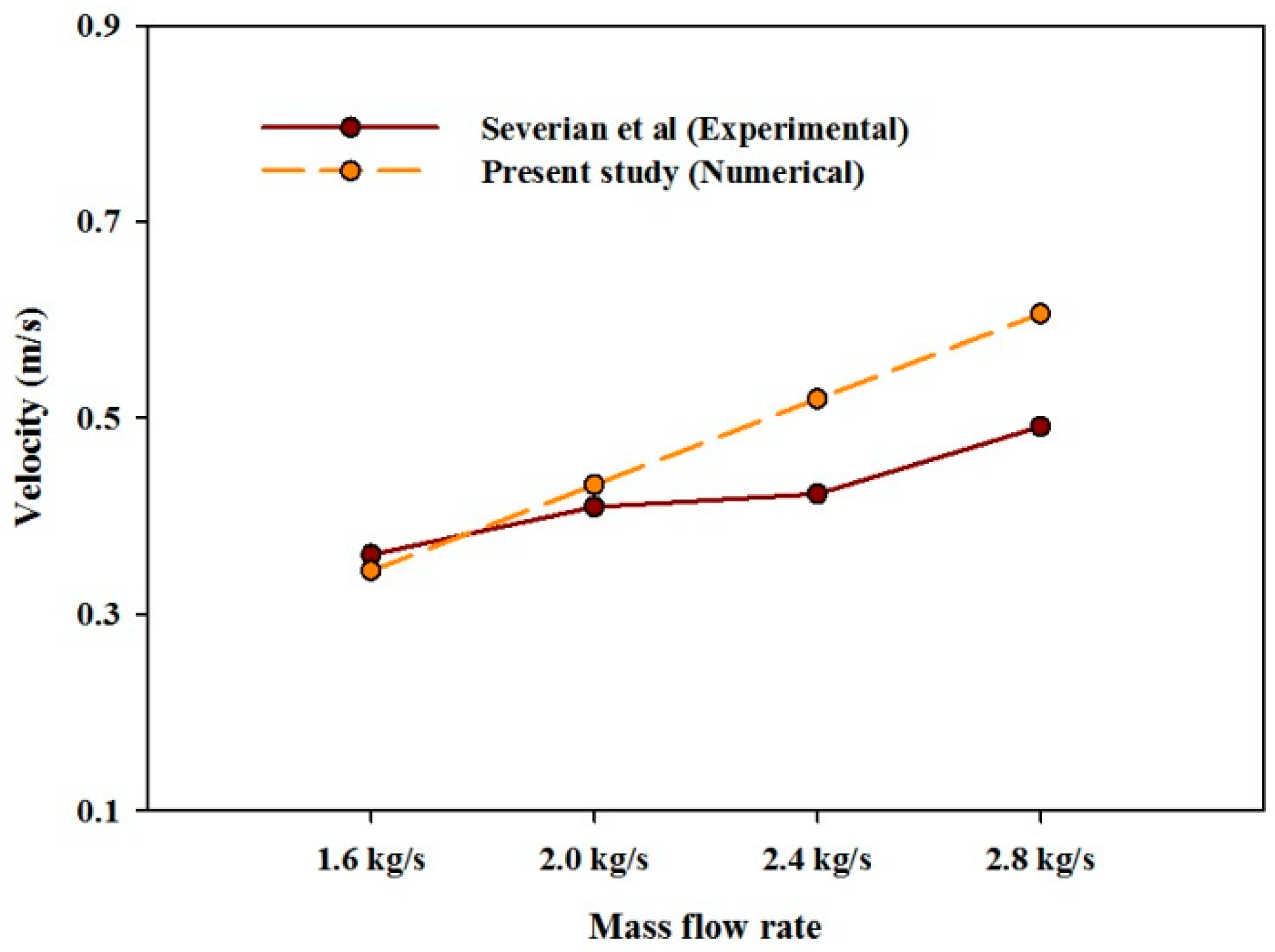
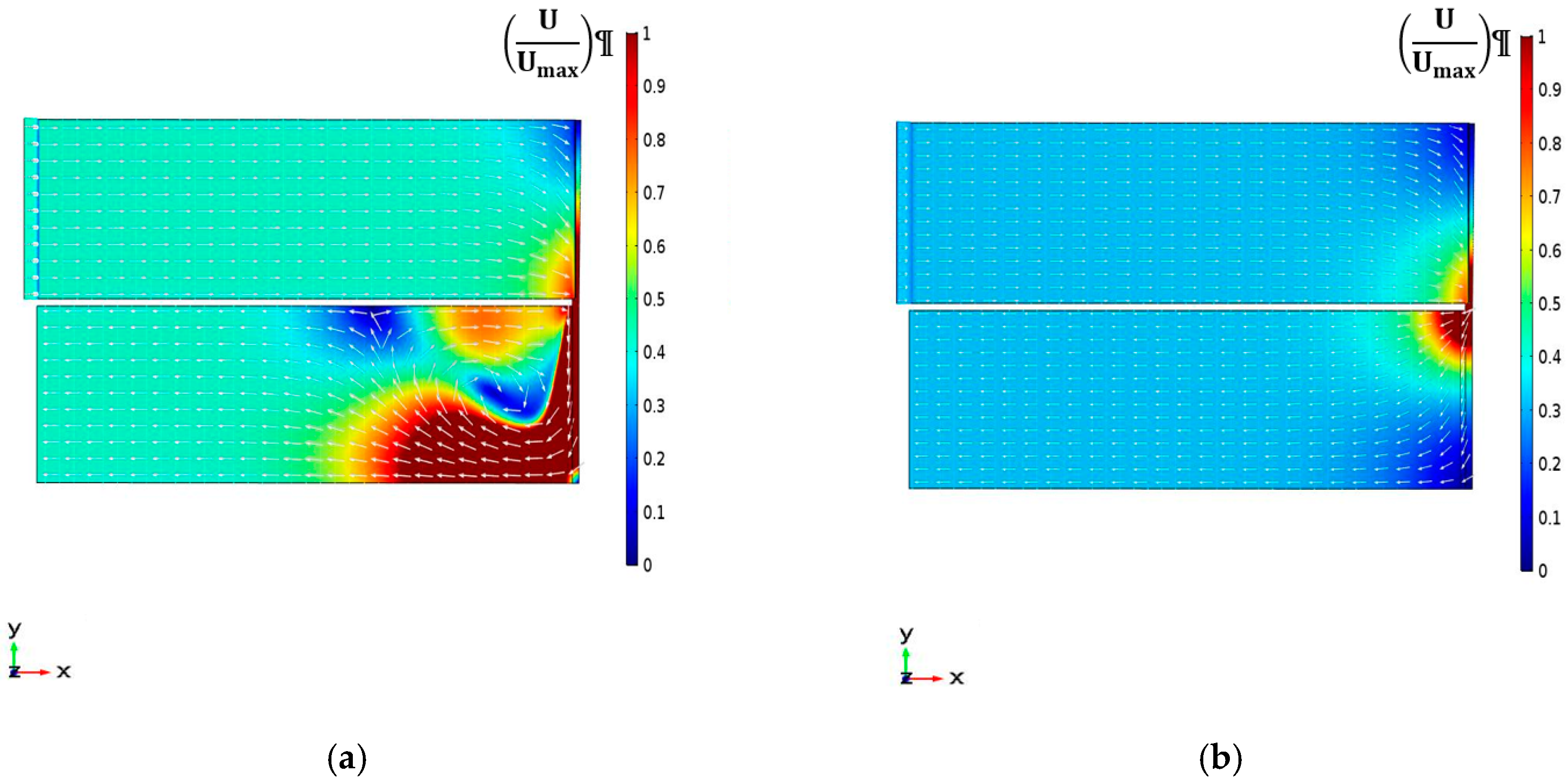
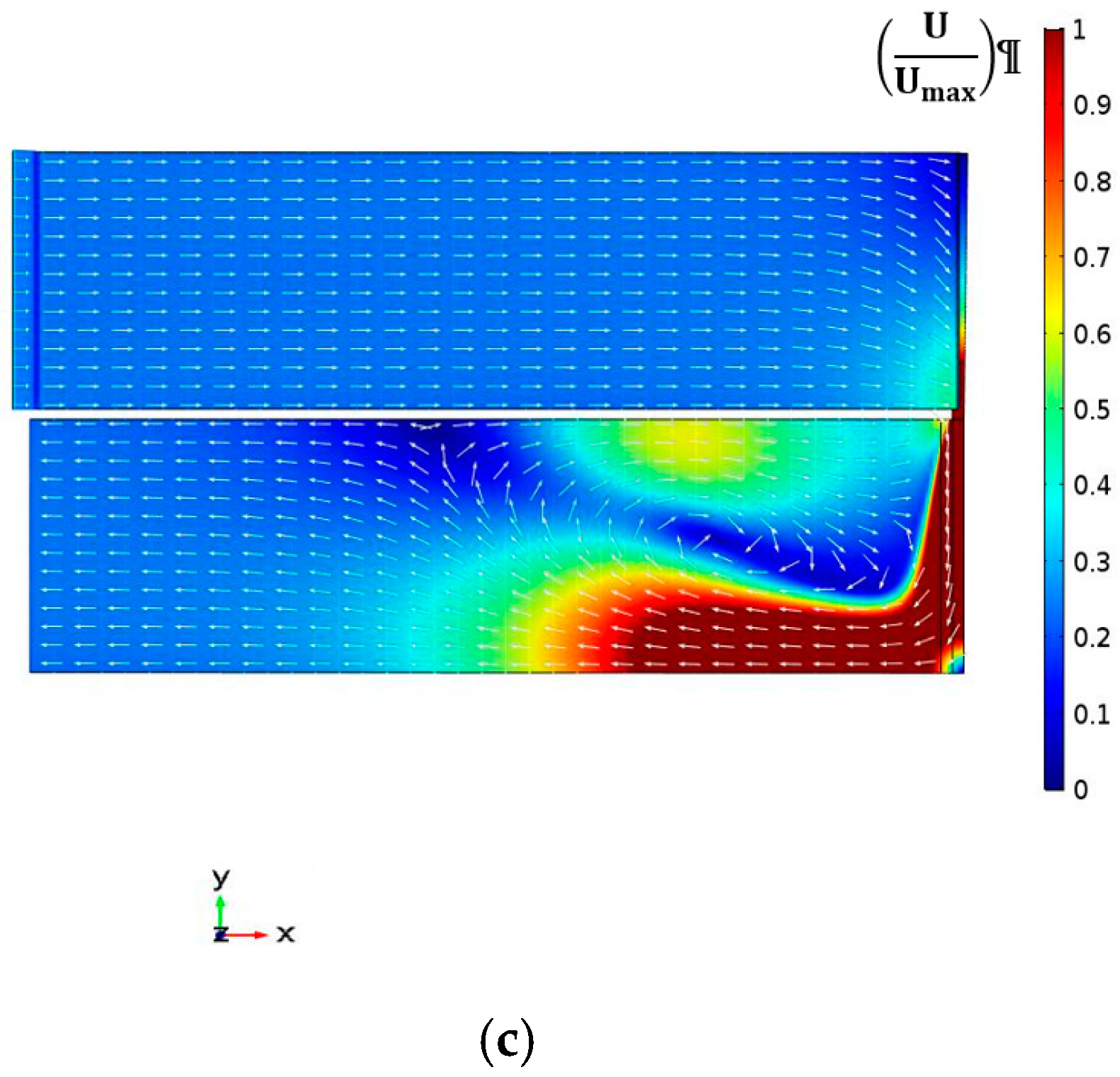
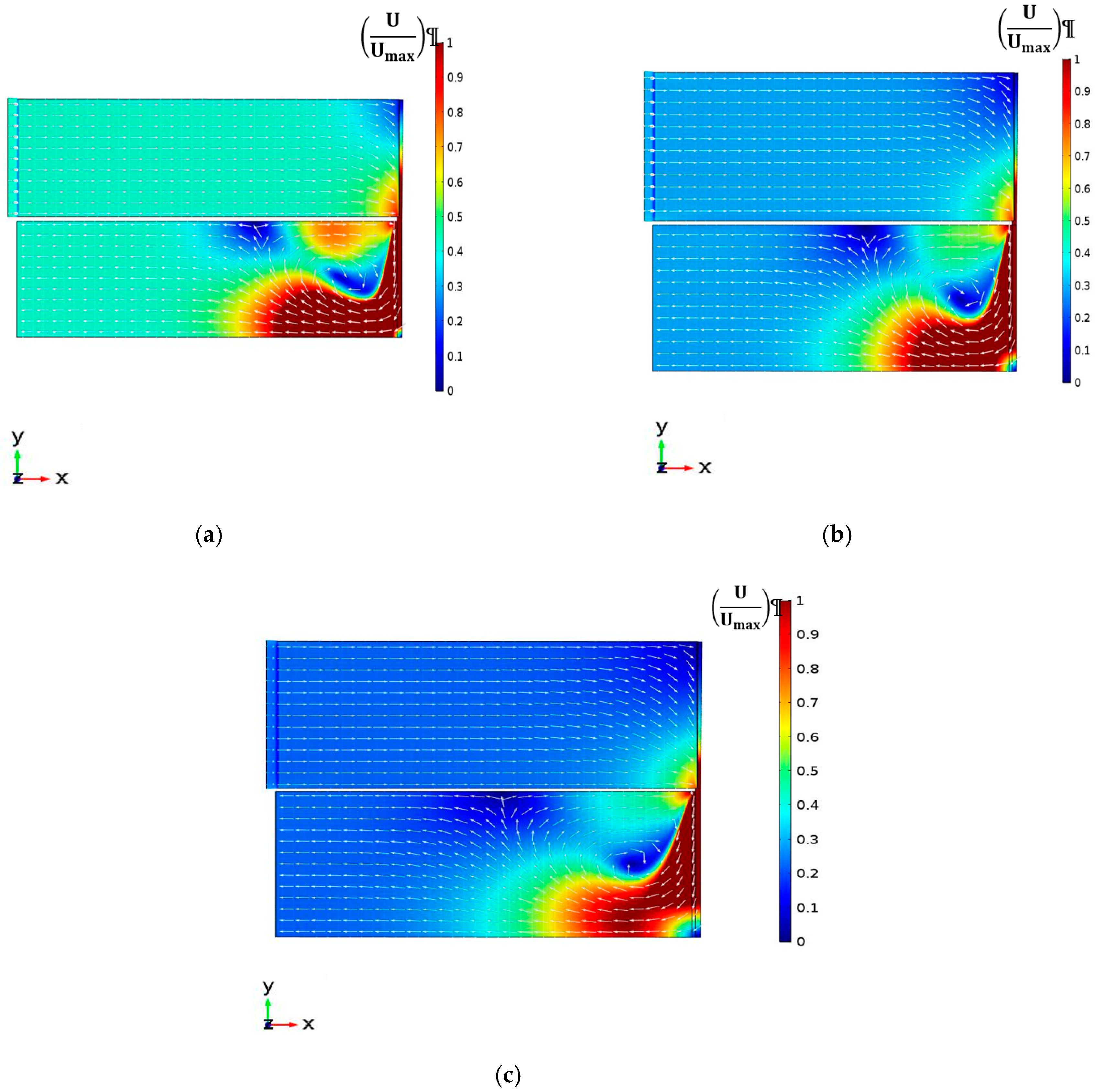
4.2.1. Velocity Magnitude
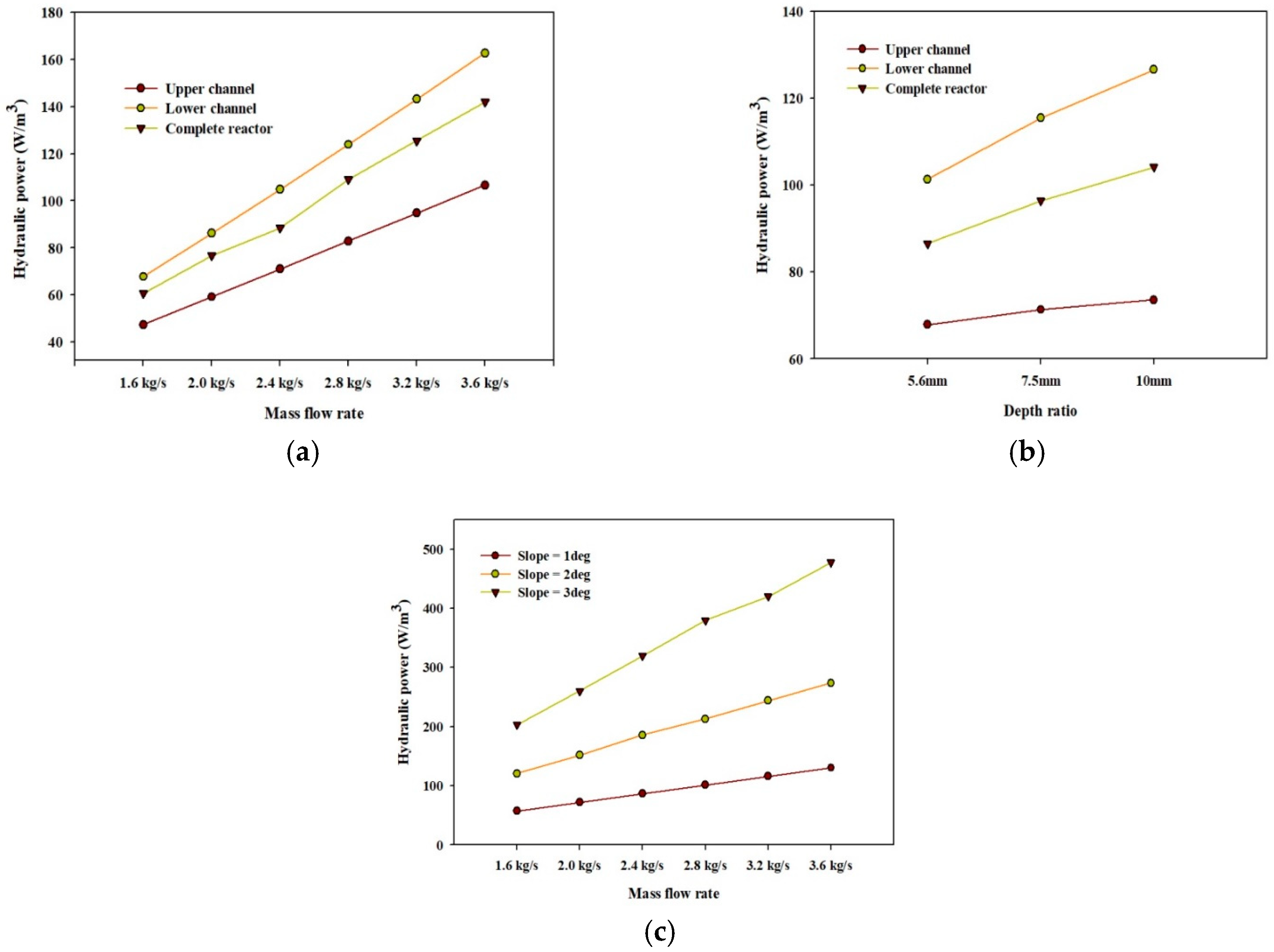
4.2.2. Power Consumption
5. Conclusions
- The mixing process is more effective when the reactor has narrow geometry and operates at high mass flow rates.
- The residence time of algae cells increases with the increase in water depth and aspect ratio.
- The increases in liquid volume with the increase in channel width and water depth causes a substantial reduction in the velocity magnitude.
- The hydraulic power consumption required to move the liquid along the channel increases with the increase in mass flow rate, slope angle, and water depth.
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| cross sectional area, m2 | inclination of surface (-) | ||
| hydraulic diameter, m | aspect ratio, (-) | ||
| Reynolds number, (-) | volumetric flow rate, m3/s | ||
| velocity vector, m/s | Stokes number (-) | ||
| identity matrix | hydraulic power, W/m2 | ||
| time-averaged velocity, m/s | Greek symbols | ||
| length, m | water density, kg/m3 | ||
| mass flow rate, kg/s | water viscosity, Pa. s | ||
| channel width, m | turbulent viscosity, Pa·s | ||
| mixing length, m | algae cell density, kg/m3 | ||
| residence time, s | turbulent dissipation rate, 1/s | ||
| drag force, N | chlorella cell velocity, m/s | ||
| algae cell diameter, m | relaxation time, s | ||
| channel depth, m | Prandtl number for dissipation rate | ||
| turbulent kinetic energy, m2/s2 | Prandtl number for kinetic energy | ||
References
- Mata, T.M.; Martins, A.A.; Caetano, N.S. Microalgae for Biodiesel Production and Other Applications: A Review. Renew. Sustain. Energy Rev. 2010, 14, 217–232. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.A.; Hussain, M.Z.; Prasad, S.; Banerjee, U.C. Prospects of Biodiesel Production from Microalgae in India. Renew. Sustain. Energy Rev. 2009, 13, 2361–2372. [Google Scholar] [CrossRef]
- Suh, I.S.; Lee, C.G. Photobioreactor Engineering: Design and Performance. Biotechnol. Bioprocess Eng. 2003, 8, 313–321. [Google Scholar] [CrossRef]
- Pulz, O. Photobioreactors: Production Systems for Phototrophic Microorganisms. Appl. Microbiol. Biotechnol. 2001, 57, 287–293. [Google Scholar] [CrossRef] [PubMed]
- Fon Sing, S.; Isdepsky, A.; Borowitzka, M.A.; Moheimani, N.R. Production of Biofuels from Microalgae. Mitig. Adapt. Strateg. Glob. Chang. 2013, 18, 47–72. [Google Scholar] [CrossRef]
- Šetlík, I.; Šust, V.; Málek, I. Dual Purpose Open Circulation Units for Large Scale Culture of Algae in Temperate Zones. I. Basic Design Considerations and Scheme of a Pilot Plant. Algol. Stud. Hydrobiol. Suppl. Vol. 1970, 1, 111–164. [Google Scholar]
- Doucha, J.; Lívanský, K. Novel Outdoor Thin-Iayer High Density Microalgal Culture System: Productivity and Operational Parameters. Arch. Hydrobiol. Suppl. Algol. Stud. 1995, 76, 129–147. [Google Scholar]
- Masojídek, J.; Kopecký, J.; Giannelli, L.; Torzillo, G. Productivity Correlated to Photobiochemical Performance of Chlorella Mass Cultures Grown Outdoors in Thin-Layer Cascades. J. Ind. Microbiol. Biotechnol. 2011, 38, 307–317. [Google Scholar] [CrossRef]
- Grobbelaar, J.U. Factors Governing Algal Growth in Photobioreactors: The “Open” versus “Closed” Debate. J. Appl. Phycol. 2009, 21, 489–492. [Google Scholar] [CrossRef]
- Severin, T.S.; Apel, A.C.; Brück, T.; Weuster-Botz, D. Investigation of Vertical Mixing in Thin-Layer Cascade Reactors Using Computational Fluid Dynamics. Chem. Eng. Res. Des. 2018, 132, 436–444. [Google Scholar] [CrossRef]
- Apel, A.C.; Pfaffinger, C.E.; Basedahl, N.; Mittwollen, N.; Göbel, J.; Sauter, J.; Brück, T.; Weuster-Botz, D. Open Thin-Layer Cascade Reactors for Saline Microalgae Production Evaluated in a Physically Simulated Mediterranean Summer Climate. Algal Res. 2017, 25, 381–390. [Google Scholar] [CrossRef]
- Jerez, C.G.; Navarro, E.; Malpartida, I.; Rico, R.M.; Masojídek, J.; Abdala, R.; Figueroa, F.L. Hydrodynamics and Photosynthesis Performance of Chlorella Fusca (Chlorophyta) Grown in a Thin-Layer Cascade (TLC) System. Aquat. Biol. 2014, 22, 111–122. [Google Scholar] [CrossRef] [Green Version]
- De Marchin, T.; Erpicum, M.; Franck, F. Photosynthesis of Scenedesmus Obliquus in Outdoor Open Thin-Layer Cascade System in High and Low CO2 in Belgium. J. Biotechnol. 2015, 215, 2–12. [Google Scholar] [CrossRef] [PubMed]
- Doucha, J.; Lívanský, K. Productivity, CO2/O2 exchange and Hydraulics in Outdoor Open High Density Microalgal (Chlorella Sp.) Photobioreactors Operated in a Middle and Southern European Climate. J. Appl. Phycol. 2006, 18, 811–826. [Google Scholar] [CrossRef]
- Kristiansen, T.; Pedersen, I.L. Sociolingvistik. Nydanske Sprogstudier (NyS) 2006, 2, 217–267. [Google Scholar] [CrossRef]
- Doucha, J.; Lívanský, K. Outdoor Open Thin-Layer Microalgal Photobioreactor: Potential Productivity. J. Appl. Phycol. 2009, 21, 111–117. [Google Scholar] [CrossRef]
- Silva Benavides, A.M.; Ranglová, K.; Malapascua, J.R.; Masojídek, J.; Torzillo, G. Diurnal Changes of Photosynthesis and Growth of Arthrospira Platensis Cultured in a Thin-Layer Cascade and an Open Pond. Algal Res. 2017, 28, 48–56. [Google Scholar] [CrossRef]
- Doucha, J.; Lívanský, K. High Density Outdoor Microalgal Culture. In Algal Biorefineries: Volume 1: Cultivation of Cells and Products; Bajpai, R., Prokop, A., Zappi, M., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 147–173. [Google Scholar] [CrossRef]
- Masojídek, J.; Sergejevová, M.; Malapascua, J.R.; Kopecký, J. Thin-Layer Systems for Mass Cultivation of Microalgae: Flat Panels and Sloping Cascades. In Algal Biorefineries: Volume 2: Products and Refinery Design; Prokop, A., Bajpai, R.K., Zappi, M.E., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 237–261. [Google Scholar] [CrossRef]
- Republiky, C.; Examiner, P.; Beisner, W.H.; Michalos, P.C. United States Patent (19) 11 Patent Number: 11. U.S. Patent 1999. No. 19. [Google Scholar]
- Doucha, J. Additional CO2 Saturation of Thin-Layer Outdoor Microalgal Cultures: CO2 Mass Transfer and Absorption Efficiency. Arch. Hydrobiol. Suppl. 1997, 122, 145–154. [Google Scholar]
- Bitog, J.P.; Lee, I.-B.; Lee, C.-G.; Kim, K.-S.; Hwang, H.-S.; Hong, S.-W.; Seo, I.-H.; Kwon, K.-S.; Mostafa, E. Application of Computational Fluid Dynamics for Modeling and Designing Photobioreactors for Microalgae Production: A Review. Comput. Electron. Agric. 2011, 76, 131–147. [Google Scholar] [CrossRef]
- Savat, J. The Hydraulics of Sheet Flow on a Smooth Surface and the Effect of Simulated Rainfall. Earth Surf. Process. 1977, 2, 125–140. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics. In Open-channel hydraulics; McGraw-Hill: New Yourk, NY, USA, 1959. [Google Scholar]
- Buhr, H.O.; Miller, S.B. A Dynamic Model of the High-Rate Algal-Bacterial Wastewater Treatment Pond. Water Res. 1983, 17, 29–37. [Google Scholar] [CrossRef]
- Weissman, J.C.; Goebel, R.P.; Benemann, J.R. Photobioreactor Design: Mixing, Carbon Utilization, and Oxygen Accumulation. Biotechnol. Bioeng. 1988, 31, 336–344. [Google Scholar] [CrossRef] [PubMed]
- Ali, H.; Cheema, T.A.; Yoon, H.S.; Do, Y.; Park, C.W. Numerical Prediction of Algae Cell Mixing Feature in Raceway Ponds Using Particle Tracing Methods. Biotechnol. Bioeng. 2015, 112, 297–307. [Google Scholar] [CrossRef]
- Brennen, C.E. Fundamentals of Multiphase Flow; Cambridge University Press: Cambridge, UK, 2013; Volume 9780521848. [Google Scholar] [CrossRef] [Green Version]
- Tropea, C.; Yarin, A.L. Springer Handbook of Experimental Fluid Mechanics; Springer Science & Business Media: Berlin, Germany, 2007; Volume 1. [Google Scholar]
- Thomas, W.H.; Gibson, C.H. Effects of Small-Scale Turbulence on Microalgae. J. Appl. Phycol. 1990, 2, 71–77. [Google Scholar] [CrossRef]
- Wilcox, D.C. Summary for Policymakers. Clim. Chang. 2013 Phys. Sci. Basis 1995, 289, 1–30. [Google Scholar] [CrossRef]
- Valigore, J.M.; Gostomski, P.A.; Wareham, D.G.; O’Sullivan, A.D. Effects of Hydraulic and Solids Retention Times on Productivity and Settleability of Microbial (Microalgal-Bacterial) Biomass Grown on Primary Treated Wastewater as a Biofuel Feedstock. Water Res. 2012, 46, 2957–2964. [Google Scholar] [CrossRef] [PubMed]
- Ugwu, C.U.; Aoyagi, H.; Uchiyama, H. Photobioreactors for Mass Cultivation of Algae. Bioresour. Technol. 2008, 99, 4021–4028. [Google Scholar] [CrossRef]
- Pruvost, J.; Pottier, L.; Legrand, J. Numerical Investigation of Hydrodynamic and Mixing Conditions in a Torus Photobioreactor. Chem. Eng. Sci. 2006, 61, 4476–4489. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Slope angle | 1°; 2°; 3° |
| Depth ratio | 5.6 mm; 7.5 mm; 10 mm |
| Aspect ratio | 180; 260; 340 |
| Mass flow rate | 1.6–3.6 kg/s |
| No of Mesh Elements | U (m/s) |
|---|---|
| (523,359) | 0.5165 |
| (134,191) | 0.5128 |
| (60,175) | 0.5110 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhtar, S.; Ali, H.; Park, C.W. Complete Evaluation of Cell Mixing and Hydrodynamic Performance of Thin-Layer Cascade Reactor. Appl. Sci. 2020, 10, 746. https://doi.org/10.3390/app10030746
Akhtar S, Ali H, Park CW. Complete Evaluation of Cell Mixing and Hydrodynamic Performance of Thin-Layer Cascade Reactor. Applied Sciences. 2020; 10(3):746. https://doi.org/10.3390/app10030746
Chicago/Turabian StyleAkhtar, Shehnaz, Haider Ali, and Cheol Woo Park. 2020. "Complete Evaluation of Cell Mixing and Hydrodynamic Performance of Thin-Layer Cascade Reactor" Applied Sciences 10, no. 3: 746. https://doi.org/10.3390/app10030746
APA StyleAkhtar, S., Ali, H., & Park, C. W. (2020). Complete Evaluation of Cell Mixing and Hydrodynamic Performance of Thin-Layer Cascade Reactor. Applied Sciences, 10(3), 746. https://doi.org/10.3390/app10030746






