Effect of Landing Posture on Jump Height Calculated from Flight Time
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Instrumentation
2.3. Procedures
2.4. Data Reduction
2.5. Statistical Analysis
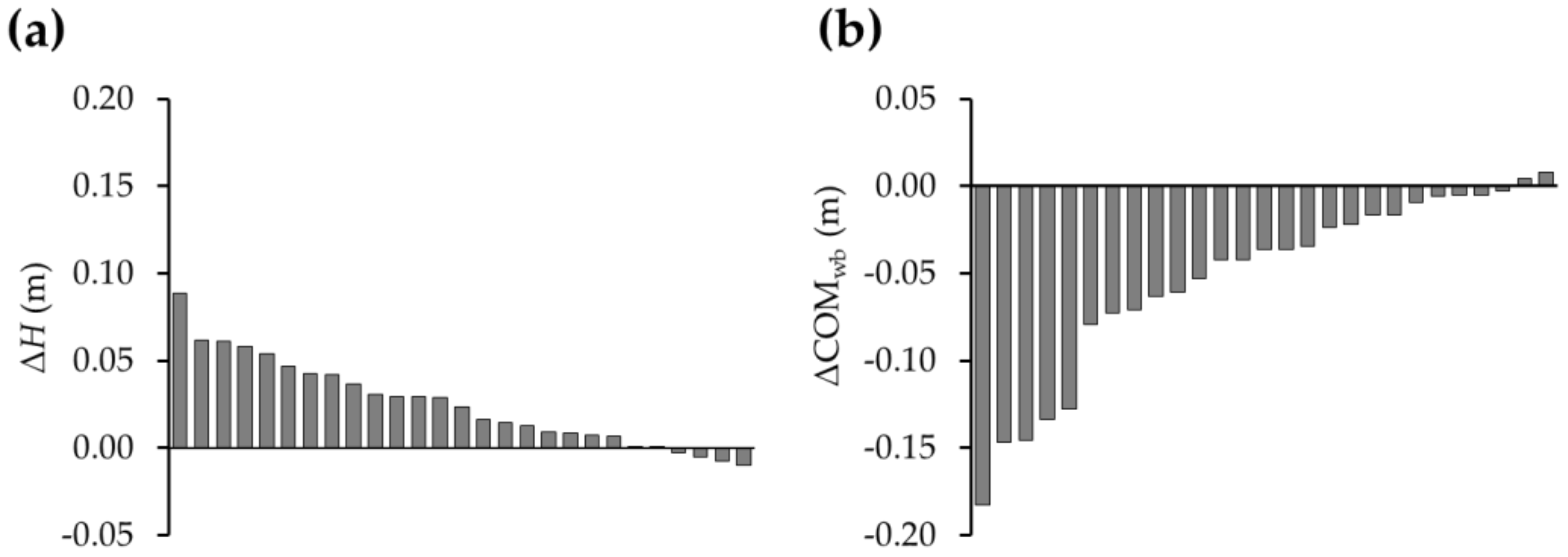
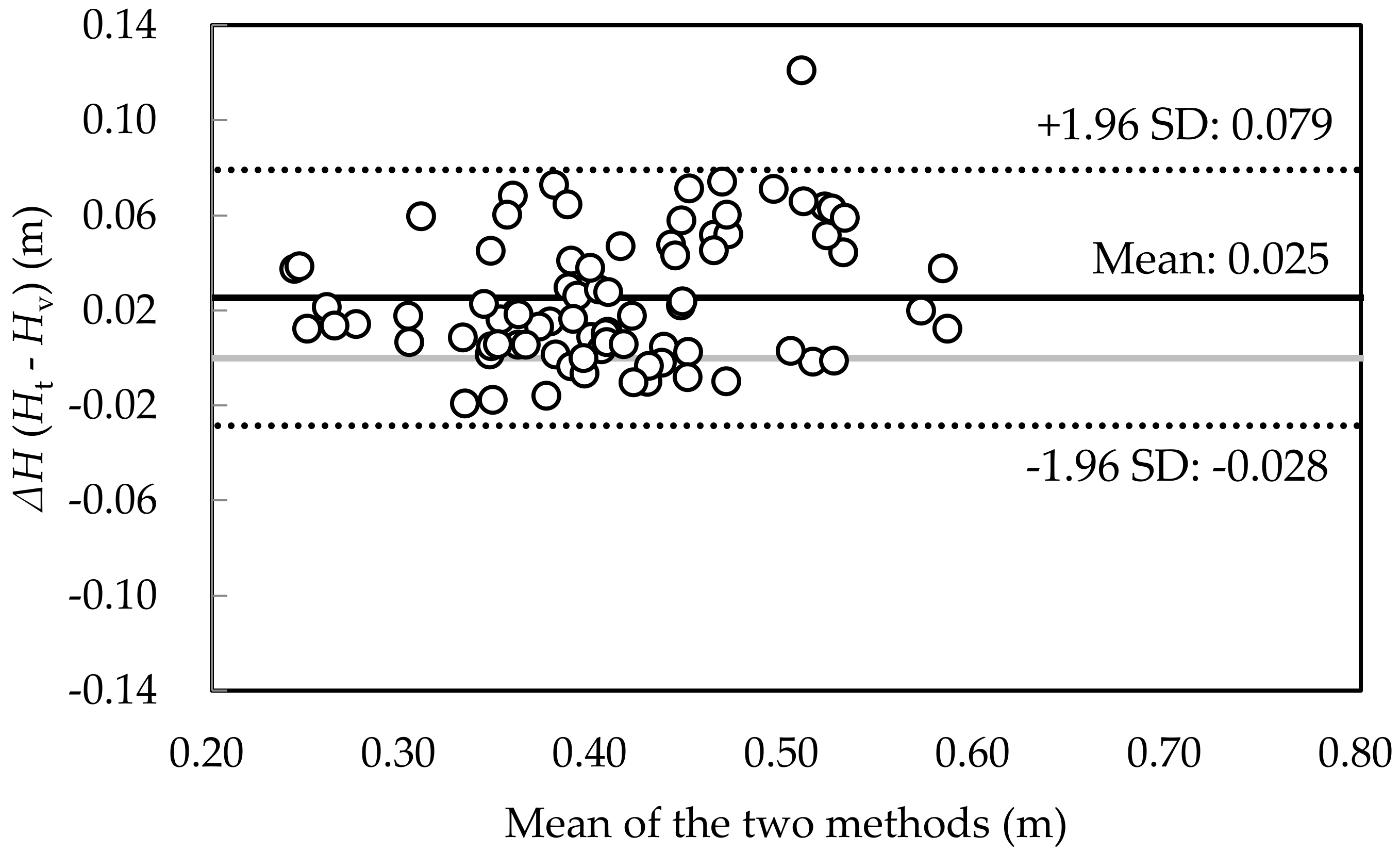
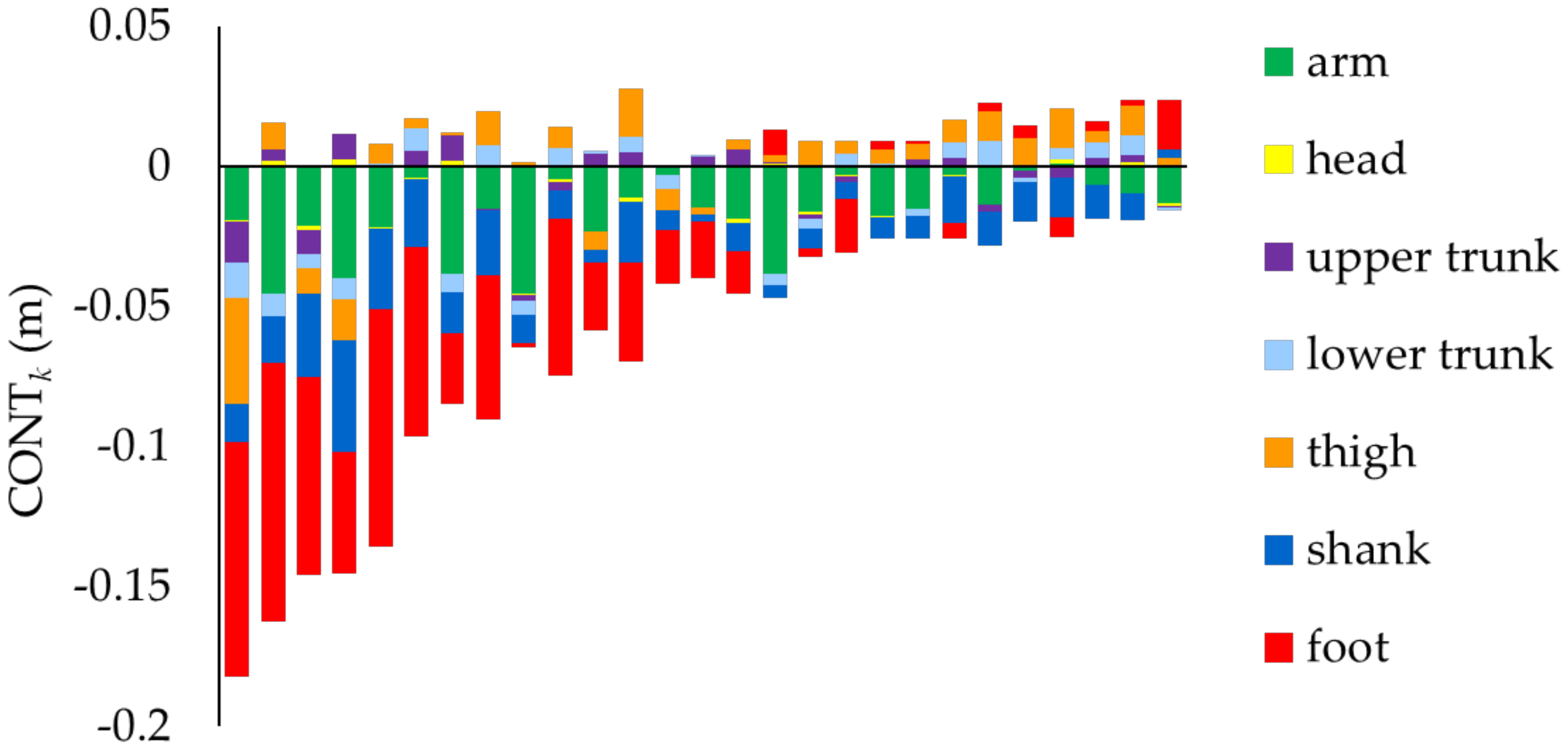
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Calculation of Jump Height from Flight Time
Appendix B. Calculation of the Flight Time from the Vertical Displacement of the COMwb
References
- Ache-Dias, J.; Dal Pupo, J.; Gheller, R.G.; Kulkamp, W.; Moro, A.R. Power Output Prediction From Jump Height and Body Mass Does Not Appropriately Categorize or Rank Athletes. J. Strength Cond. Res. 2016, 30, 818–824. [Google Scholar] [CrossRef]
- Young, W.B.; Bilby, G.E. The Effect of Voluntary Effort to Influence Speed of Contraction on Strength, Muscular Power, and Hypertrophy Development. J. Strength Cond. Res. 1993, 7, 172–178. [Google Scholar] [CrossRef]
- Claudino, J.G.; Cronin, J.; Mezencio, B.; McMaster, D.T.; McGuigan, M.; Tricoli, V.; Amadio, A.C.; Serrao, J.C. The countermovement jump to monitor neuromuscular status: A meta-analysis. J. Sci. Med. Sport 2016, 20, 397–402. [Google Scholar] [CrossRef]
- Sierer, S.P.; Battaglini, C.L.; Mihalik, J.P.; Shields, E.W.; Tomasini, N.T. The National Football League Combine: Performance differences between drafted and nondrafted players entering the 2004 and 2005 drafts. J. Strength Cond. Res. 2008, 22, 6–12. [Google Scholar] [CrossRef]
- Teramoto, M.; Cross, C.L.; Rieger, R.H.; Maak, T.G.; Willick, S.E. Predictive Validity of National Basketball Association Draft Combine on Future Performance. J. Strength Cond. Res. 2017. [Google Scholar] [CrossRef]
- Lake, J.; Mundy, P.; Comfort, P.; McMahon, J.J.; Suchomel, T.J.; Carden, P. Concurrent Validity of a Portable Force Plate Using Vertical Jump Force-Time Characteristics. J. Appl. Biomech. 2018, 34, 410–413. [Google Scholar] [CrossRef]
- Kibele, A. Possibilities and Limitations in the Biomechanical Analysis of Countermovement Jumps: A Methodological Study. J. Appl. Biomech. 1998, 14, 105. [Google Scholar] [CrossRef]
- Moir, G.L. Three Different Methods of Calculating Vertical Jump Height from Force Platform Data in Men and Women. Meas. Phys. Educ. Exerc. Sci. 2008, 12, 207–218. [Google Scholar] [CrossRef]
- Aragón, L.F. Evaluation of four vertical jump tests: Methodology, reliability, validity, and accuracy. Meas. Phys. Educ. Exerc. Sci. 2000, 4, 215–228. [Google Scholar] [CrossRef]
- Dowling, J.J.; Vamos, L. Identification of kinetic and temporal factors related to vertical jump performance. J. Appl. Biomech. 1993, 9, 95–110. [Google Scholar] [CrossRef] [Green Version]
- Lees, A.; Vanrenterghem, J.; De Clercq, D. Understanding how an arm swing enhances performance in the vertical jump. J. Biomech. 2004, 37, 1929–1940. [Google Scholar] [CrossRef]
- Hara, M.; Shibayama, A.; Takeshita, D.; Fukashiro, S. The effect of arm swing on lower extremities in vertical jumping. J. Biomech. 2006, 39, 2503–2511. [Google Scholar] [CrossRef]
- Suzuki, Y.; Ae, M.; Takenaka, S.; Fujii, N. Comparison of support leg kinetics between side-step and cross-step cutting techniques. Sport. Biomech. 2014, 13, 144–153. [Google Scholar] [CrossRef]
- Woltring, H.J. A Fortran package for generalized, cross-validatory spline smoothing and differentiation. Adv. Eng. Softw. 1986, 8, 104–113. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 4th ed.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2009. [Google Scholar]
- Street, G.; McMillan, S.; Board, W.; Rasmussen, M.; Heneghan, J.M. Sources of error in determining countermovement jump height with the impulse method. J. Appl. Biomech. 2001, 17, 43–54. [Google Scholar] [CrossRef]
- Ae, M.; Tang, H.; Yokoi, T. Estimation of inertia properties of the body segments in Japanese athletes. Biomechanisms 1992, 11, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: Abington, UK, 2013. [Google Scholar]
- Baumgartner, T.A.; Chung, H. Confidence Limits for Intraclass Reliability Coefficients. Meas. Phys. Educ. Exerc. Sci. 2001, 5, 179–188. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- García-Ramos, A.; Pérez-Castilla, A.; Martín, F. Reliability and concurrent validity of the Velowin optoelectronic system to measure movement velocity during the free-weight back squat. Int. J. Sports Sci. Coach. 2018, 13, 737–742. [Google Scholar] [CrossRef]
- Rogers, S.A.; Hassmén, P.; Hunter, A.; Alcock, A.; Crewe, S.T.; Strauts, J.A.; Gilleard, W.L.; Weissensteiner, J.R. The Validity and Reliability of the MyJump2 Application to Assess Vertical Jumps in Trained Junior Athletes. Meas. Phys. Educ. Exerc. Sci. 2018, 1–9. [Google Scholar] [CrossRef]
- Rodriguez-Rosell, D.; Mora-Custodio, R.; Franco-Marquez, F.; Yanez-Garcia, J.M.; Gonzalez-Badillo, J.J. Traditional vs. Sport-Specific Vertical Jump Tests: Reliability, Validity, and Relationship With the Legs Strength and Sprint Performance in Adult and Teen Soccer and Basketball Players. J. Strength Cond. Res. 2017, 31, 196–206. [Google Scholar] [CrossRef]
- Casartelli, N.; Müller, R.; Maffiuletti, N.A. Validity and reliability of the Myotest accelerometric system for the assessment of vertical jump height. J. Strength Cond. Res. 2010, 24, 3186–3193. [Google Scholar] [CrossRef]
- Glatthorn, J.F.; Gouge, S.; Nussbaumer, S.; Stauffacher, S.; Impellizzeri, F.M.; Maffiuletti, N.A. Validity and reliability of Optojump photoelectric cells for estimating vertical jump height. J. Strength Cond. Res. 2011, 25, 556–560. [Google Scholar] [CrossRef]
- Kenny, I.C.; Cairealláin, A.Ó.; Comyns, T.M. Validation of an electronic jump mat to assess stretch-shortening cycle function. J. Strength Cond. Res. 2012, 26, 1601–1608. [Google Scholar] [CrossRef] [Green Version]
- McKay, G.D.; Goldie, P.A.; Payne, W.R.; Oakes, B.W. Ankle injuries in basketball: Injury rate and risk factors. Br. J. Sports Med. 2001, 35, 103–108. [Google Scholar] [CrossRef]
- Iida, Y.; Kanehisa, H.; Inaba, Y.; Nakazawa, K. Activity modulations of trunk and lower limb muscles during impact-absorbing landing. J. Electromyogr. Kinesiol. 2011, 21, 602–609. [Google Scholar] [CrossRef]
- Shinya, M.; Wada, O.; Yamada, M.; Ichihashi, N.; Oda, S. The effect of choice reaction task on impact of single-leg landing. Gait Posture 2011, 34, 55–59. [Google Scholar] [CrossRef]
- Young, W.B.; MacDonald, C.; Flowers, M.A. Validity of double-and single-leg vertical jumps as tests of leg extensor muscle function. J. Strength Cond. Res. 2001, 15, 6–11. [Google Scholar]
- Lesinski, M.; Muehlbauer, T.; Granacher, U. Concurrent validity of the Gyko inertial sensor system for the assessment of vertical jump height in female sub-elite youth soccer players. BMC Sports Sci. Med. Rehabil. 2016, 8, 35. [Google Scholar] [CrossRef] [Green Version]
- McMahon, J.J.; Jones, P.A.; Comfort, P. A Correction Equation for Jump Height Measured Using the Just Jump System. Int. J. Sports Physiol. Perform. 2016, 11, 555–557. [Google Scholar] [CrossRef] [Green Version]
- Balsalobre-Fernandez, C.; Glaister, M.; Lockey, R.A. The validity and reliability of an iPhone app for measuring vertical jump performance. J. Sports Sci. 2015, 33, 1574–1579. [Google Scholar] [CrossRef]
- O’Donnell, S.; Tavares, F.; McMaster, D.; Chambers, S.; Driller, M. The validity and reliability of the GymAware linear position transducer for measuring counter-movement jump performance in female athletes. Meas. Phys. Educ. Exerc. Sci. 2018, 22, 101–107. [Google Scholar] [CrossRef] [Green Version]


| Segment | Takeoff (m) | Landing (m) | Difference (m) | Effect Size (d) |
|---|---|---|---|---|
| Whole body | 1.140 ± 0.071 | 1.087 ± 0.100 * | –0.053 | 1.17 |
| Head | 0.143 ± 0.024 | 0.143 ± 0.028 | 0.000 | 0.02 |
| Arm | 0.109 ± 0.133 | –0.067 ± 0.187 * | –0.175 | 1.33 |
| Upper Trunk | 0.183 ± 0.021 | 0.184 ± 0.019 | 0.001 | 0.13 |
| Lower Trunk | 0.086 ± 0.010 | 0.086 ± 0.010 | 0.000 | 0.00 |
| Thigh | 0.225 ± 0.013 | 0.227 ± 0.015 | 0.002 | 0.25 |
| Shank | 0.237 ± 0.018 | 0.229 ± 0.021 * | –0.009 | 1.64 |
| Foot | 0.129 ± 0.009 | 0.108 ± 0.031 * | –0.021 | 0.97 |
| Segment | Takeoff (m) | Landing (m) | Difference (m) | Effect Size (d) |
|---|---|---|---|---|
| Upper Trunk | 0.321 ± 0.035 | 0.323 ± 0.032 | 0.002 | 0.13 |
| Lower Trunk | 0.220 ± 0.026 | 0.220 ± 0.028 | 0.000 | 0.00 |
| Thigh | 0.427 ± 0.026 | 0.430 ± 0.003 | 0.003 | 0.25 |
| Shank | 0.400 ± 0.032 | 0.385 ± 0.035 * | –0.015 | 1.64 |
| Foot | 0.199 ± 0.011 | 0.173 ± 0.037 * | –0.025 | 0.99 |
| Segment | Contribution (m) | Effect Size (d) |
|---|---|---|
| Head | 0.000 ± 0.001 | 0.023 |
| Arm | –0.017 ± 0.013 * | 1.259 |
| Upper Trunk | –0.001 ± 0.005 | 0.119 |
| Lower Trunk | 0.000 ± 0.006 | 0.009 |
| Thigh | 0.003 ± 0.011 | 0.244 |
| Shank | –0.014 ± 0.009 * | 1.446 |
| Foot | −0.025 ± 0.032 * | 0.781 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamashita, D.; Murata, M.; Inaba, Y. Effect of Landing Posture on Jump Height Calculated from Flight Time. Appl. Sci. 2020, 10, 776. https://doi.org/10.3390/app10030776
Yamashita D, Murata M, Inaba Y. Effect of Landing Posture on Jump Height Calculated from Flight Time. Applied Sciences. 2020; 10(3):776. https://doi.org/10.3390/app10030776
Chicago/Turabian StyleYamashita, Daichi, Munenori Murata, and Yuki Inaba. 2020. "Effect of Landing Posture on Jump Height Calculated from Flight Time" Applied Sciences 10, no. 3: 776. https://doi.org/10.3390/app10030776
APA StyleYamashita, D., Murata, M., & Inaba, Y. (2020). Effect of Landing Posture on Jump Height Calculated from Flight Time. Applied Sciences, 10(3), 776. https://doi.org/10.3390/app10030776






