Exceptional Points in Non-Hermitian Photonic Crystals Incorporated With a Defect
Abstract
:1. Introduction
2. Non-Hermitian Photonic Crystals
3. Exceptional Points and Sharp Change in Phase
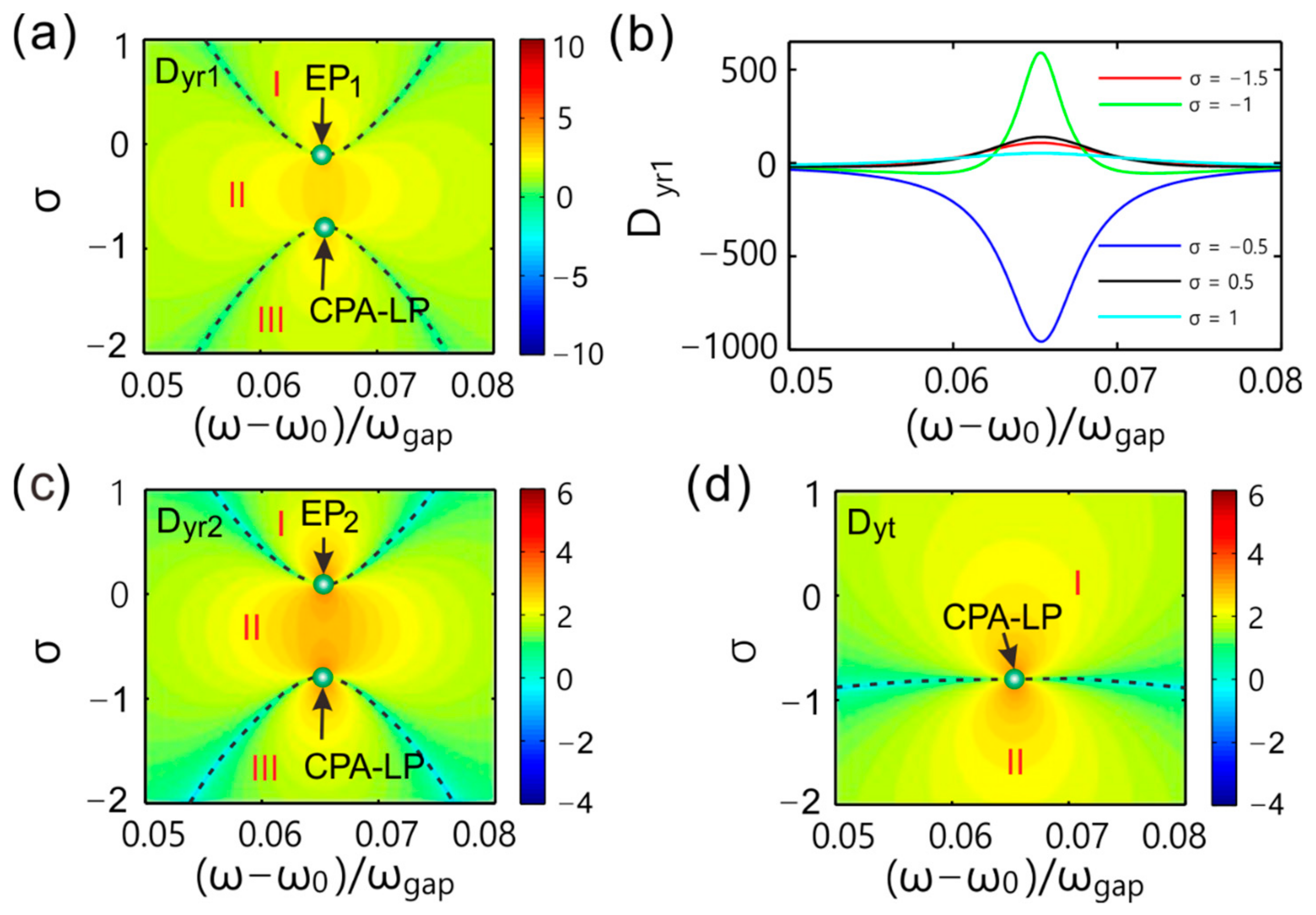
4. Applications and Giant GH Shift
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.L.; Petrovi, N.; Belić, M.R.; Deng, W. Exact solutions for the quintic nonlinear Schrödinger equation with time and space. Nonlinear Dyn. 2017, 84, 251–259. [Google Scholar] [CrossRef]
- Xu, S.L.; Petrović, N.; Belić, M.R. Exact solutions of the (2 + 1)-dimensional quintic nonlinear Schrödinger equation with variable coefficients. Nonlinear Dyn. 2015, 80, 583–589. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, Q.; Wu, S.; Wang, B.; Lu, P. Optical imaginary directional couplers. J. Lightwave Technol. 2018, 36, 2510–2515. [Google Scholar] [CrossRef]
- Wang, H.; Kong, W.; Zhang, P.; Li, Z.; Zhong, D. Coherent perfect absorption laser points in one-dimensional anti-parity–time-symmetric photonic crystals. Appl. Sci. 2019, 9, 2738. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Ramezani, H.; Shi, C.; Zhu, J.; Zhang, X. PT-symmetric acoustics. Phys. Rev. X 2014, 4, 031042. [Google Scholar] [CrossRef] [Green Version]
- Ezawa, M. Electric circuits for non-Hermitian Chern insulators. Phys. Rev. B 2019, 100, 081401. [Google Scholar] [CrossRef] [Green Version]
- Ke, S.; Wang, B.; Qin, C.; Long, H.; Wang, K.; Lu, P. Exceptional points and asymmetric mode switching in plasmonic waveguides. J. Lightwave Technol. 2016, 34, 5258–5262. [Google Scholar] [CrossRef] [Green Version]
- He, J.R.; Xu, S.; Xue, L. Generation of high-power parabolic pulses in quantum dot waveguide amplifiers. Optik 2019, 182, 1106–1112. [Google Scholar] [CrossRef]
- He, J.R.; Xu, S.; Xue, L. Snakelike similaritons in tapered grating dual-core waveguide amplifiers. Phys. Scr. 2019, 94, 105216. [Google Scholar] [CrossRef]
- Ke, S.; Liu, Q.; Zhao, D.; Liu, W. Spectral discrete diffraction with non-Hermitian coupling. J. Opt. Soc. Am. B 2018, 35, 2387–2393. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, Q.; Liu, W. Adiabatic transfer of surface plasmons in non-Hermitian graphene waveguides. Opt. Quantum Electron. 2018, 50, 393. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, B.; Ke, S.; Long, H.; Wang, K.; Lu, P. Exceptional points in Fano-resonant graphene metamaterials. Opt. Express 2017, 25, 7203–7212. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.L.; Belić, M.R. Three-dimensional Hermite-Bessel solitons in strongly nonlocal media with variable potential coefficients. Opt. Commun. 2014, 313, 62–69. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Qu, X.; Wang, S.; Peng, J. Pattern transfer of hexagonal packed structure via ultrathin metal nanomesh masks for formation of Si nanopore arrays. J. Alloys Compd. 2017, 695, 458–461. [Google Scholar] [CrossRef]
- Xu, S.L.; Zhao, Y.; Petrović, N.Z.; Belić, M.R. Spatiotemporal soliton supported by parity-time symmetric potential with competing nonlinearities. EPL 2016, 115, 14006. [Google Scholar] [CrossRef]
- Xu, S.L.; Petrović, N.; Belić, M.R.; Hu, Z.L. Light bullet supported by parity-time symmetric potential with power-law nonlinearity. Nonlinear Dyn. 2016, 84, 1877–1882. [Google Scholar] [CrossRef]
- Zhao, D.; Ke, S.; Liu, Q.; Wang, B.; Lu, P. Giant Goos-Hänchen shifts in non-Hermitian dielectric multilayers incorporated with graphene. Opt. Express 2018, 26, 2817–2828. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Ramezani, H.; Eichelkraut, T.; Kottos, T.; Cao, H.; Christodoulides, D.N. Unidirectional invisibility induced by PT-symmetric periodic structures. Phys. Rev. Lett. 2011, 106, 213901. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Zhao, D.; Fang, M.; Guo, H.; Hu, Y.; Liu, F.; Zhong, D.; Xiong, H. Unidirectional invisibility induced by complex anti-parity–time symmetric periodic lattices. Appl. Sci. 2019, 9, 3808. [Google Scholar] [CrossRef] [Green Version]
- Ke, S.; Zhao, D.; Liu, J.; Liu, Q.; Liao, Q.; Wang, B.; Lu, P. Topological bound modes in anti-PT-symmetric optical waveguide arrays. Opt. Express 2019, 27, 13858–13870. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Xu, S.L.; Belić, M.R.; Cheng, J.X. Three-dimensional solitons in Bose-Einstein condensates with spin-orbit coupling and Bessel optical lattices. Phys. Rev. A 2018, 98, 033827. [Google Scholar] [CrossRef]
- Xu, S.L.; Zhao, G.P.; Belić, M.R.; He, J.R.; Xue, L. Light bullets in coupled nonlinear Schrödinger equations with variable coefficients and a trapping potential. Opt. Express 2017, 25, 9094–9104. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Xu, B.; Guo, H.; Xu, W.; Zhong, D. Low threshold optical bistability in aperiodic PT-symmetric lattices composited with Fibonacci sequence dielectrics and graphene. Appl. Sci. 2019, 9, 5125. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Zhang, P.; Zhao, D.; Guo, H.; Huang, M.; Ke, S. Plasmonic Jackiw-Rebbi modes in graphene waveguide arrays. Appl. Sci. 2019, 9, 4152. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Wang, J.; Zhu, X.; Liu, X. Thermodynamic modeling and experimental verification of a NaNO3–KNO3–LiNO3–Ca (NO3)2 system for solar thermal energy storage. New J. Chem. 2017, 41, 10376–10382. [Google Scholar] [CrossRef]
- Hu, Y.; Shu, T.; Mao, C.; Xue, L.; Yan, Z.; Wu, Y. Arsenene and antimonene doped by group-VA atoms: First-principles studies of the geometric structures, electronic properties and STM images. Physica B 2019, 553, 195–201. [Google Scholar] [CrossRef]
- Xu, S.L.; Xue, L.; Belić, M.R.; He, J.R. Spatiotemporal soliton clusters in strongly nonlocal media with variable potential coefficients. Nonlinear Dyn. 2017, 87, 827–834. [Google Scholar] [CrossRef]
- Chen, S.; Guo, Q.; Xu, S.; Belic, M.R.; Zhao, Y.; Zhao, D.; He, J. Vortex solitons in Bose-Einstein condensates with spin-orbit coupling and gaussian optical lattices. Appl. Math. Lett. 2019, 92, 15–21. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, B.; Long, H.; Wang, K.; Lu, P. Surface plasmonic lattice solitons in semi-infinite graphene sheet arrays. J. Lightwave Technol. 2017, 35, 2960–2965. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J.X.; Xu, S.L.; Belić, M.R.; Li, H.; Zhao, Y.; Deng, W.W.; Sun, Y.Z. Multipole solitons in a cold atomic gas with a parity-time symmetric potential. Nonlinear Dyn. 2019, 95, 2325–2332. [Google Scholar] [CrossRef]
- Liang, H.; Xu, S.L.; Deng, W.W.; Dai, Y.; Li, H.; Belić, M.R.; Zhao, Y.; Ai, Y. Solitons in the two-dimensional fractional Schrödinger equation with radially symmetric PT potential. Optik 2020, 202, 163652. [Google Scholar] [CrossRef]
- Deng, W.W.; Chen, S.F.; Guo, Y.W.; Li, H.; Xu, S.L.; Guo, Q.; Belić, M.J.; Zhao, Y. Two-dimensional vector solitons in a cold atomic gas via electromagnetically induced transparency. Phys. Lett. A 2019, 383, 3025–3029. [Google Scholar] [CrossRef]
- Meng, P.; Zhao, D.; Zhong, D.; Liu, W. Topological plasmonic modes in graphene-coated nanowire arrays. Opt. Quantum Electron. 2019, 51, 156. [Google Scholar] [CrossRef]
- Barik, S.; Miyake, H.; DeGottardi, W.; Waks, E.; Hafezi, M. Two-dimensionally confined topological edge states in photonic crystals. New J. Phys. 2016, 18, 113013. [Google Scholar] [CrossRef]
- Ke, S.; Liu, J.; Liu, Q.; Zhao, D.; Liu, W. Strong absorption near exceptional points in plasmonic wave guide arrays. Opt. Quantum Electron. 2018, 50, 318. [Google Scholar] [CrossRef]
- Artoni, M.; La Rocca, G.; Bassani, F. Resonantly absorbing one-dimensional photonic crystals. Phys. Rev. E 2005, 72, 046604. [Google Scholar] [CrossRef]
- Bai, F.; Hu, Y.; Hu, Y.; Qiu, T.; Miao, X.; Zhang, S. Lead-free, air-stable ultrathin Cs3Bi2I9 perovskite nanosheets for solar cells. Sol. Energy Mater. Sol. Cells 2018, 184, 15–21. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, Y.; Hu, Z.; Cai, B.; Zeng, H. Hydrogenated arsenenes as planar magnet and Dirac material. Appl. Phys. Lett. 2015, 107, 022102. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Z.Q.; Long, H.; Wang, K.; Wang, B.; Lu, P.X. Optical bistability in defective photonic multilayers doped by graphene. Opt. Quantum Electron. 2017, 49, 163. [Google Scholar] [CrossRef]
- Zhao, D.; Ke, S.; Hu, Y.; Wang, B.; Lu, P. Optical bistability in parity-time-symmetric dielectric multilayers incorporated with graphene. J. Opt. Soc. Am. B 2019, 36, 1731–1737. [Google Scholar] [CrossRef]
- Felbacq, D.; Moreau, A.; Smaâli, R. Goos-Hänchen effect in the gaps of photonic crystals. Opt. Lett. 2003, 28, 1633–1635. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Zhong, D.; Hu, Y.; Ke, S.; Liu, W. Imaginary modulation inducing giant spatial Goos-Hänchen shifts in one-dimensional defective photonic lattices. Opt. Quantum Electron. 2019, 51, 113. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, W.W.; Ke, S.L.; Liu, Q.J. Large lateral shift in complex dielectric multilayers with nearly parity–time symmetry. Opt. Quantum Electron. 2018, 50, 323. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, F.; Meng, P.; Wen, J.; Xu, S.; Li, Z.; Zhong, D. Reflection enhancement and giant lateral shift in defective photonic crystals with graphene. Appl. Sci. 2019, 9, 2141. [Google Scholar] [CrossRef] [Green Version]
- Ma, P.; Gao, L. Large and tunable lateral shifts in one-dimensional PT-symmetric layered structures. Opt. Express 2017, 25, 9676. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity–time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Xu, Y.L.; Fegadolli, W.S.; Lu, M.; Oliveira, J.E.B.; Almeida, V.R.; Chen, Y.; Scherer, A. Experimental demonstration of a unidirectional refectionless parity-time metamaterial at optical frequencies. Nat. Mater. 2013, 12, 108–113. [Google Scholar] [CrossRef]
- Regensburger, A.; Bersch, C.; Miri, M.A.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Parity-time synthetic photonic lattices. Nature 2012, 488, 167–171. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Photonics: Optical Electronics in Modern Communications, 6th ed.; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Longhi, S.; Della Valle, G.; Staliunas, K. Goos-Hänchen shift in complex crystals. Phys. Rev. A 2011, 84, 042119. [Google Scholar] [CrossRef]
- Zhu, X.F. Defect states and exceptional point splitting in the band gaps of one-dimensional parity-time lattices. Opt. Express 2015, 23, 22274–22284. [Google Scholar] [CrossRef]
- Monfared, Y.E.; Liang, C.; Khosravi, R.; Kacerovská, B.; Yang, S. Selectively toluene-filled photonic crystal fiber Sagnac interferometer with high sensitivity for temperature sensing applications. Results Phys. 2019, 13, 102297. [Google Scholar] [CrossRef]
- Monfared, Y.E.; Hajati, M.; Liang, C.; Yang, S.; Qasymeh, M. Quasi-d-shaped fiber optic plasmonic biosensor for high-index analyte detection. IEEE Sens. J. 2019. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Bliokh, Y.P. Conservation of angular momentum, transverse shift, and spin Hall effect in reflection and refraction of an electromagnetic wave packet. Phys. Rev. Lett. 2006, 96, 073903. [Google Scholar] [CrossRef] [PubMed] [Green Version]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Zhao, D.; Cao, H.; Xu, B.; Xu, W.; Ke, S. Exceptional Points in Non-Hermitian Photonic Crystals Incorporated With a Defect. Appl. Sci. 2020, 10, 823. https://doi.org/10.3390/app10030823
Liu F, Zhao D, Cao H, Xu B, Xu W, Ke S. Exceptional Points in Non-Hermitian Photonic Crystals Incorporated With a Defect. Applied Sciences. 2020; 10(3):823. https://doi.org/10.3390/app10030823
Chicago/Turabian StyleLiu, Fangmei, Dong Zhao, Hui Cao, Bin Xu, Wuxiong Xu, and Shaolin Ke. 2020. "Exceptional Points in Non-Hermitian Photonic Crystals Incorporated With a Defect" Applied Sciences 10, no. 3: 823. https://doi.org/10.3390/app10030823
APA StyleLiu, F., Zhao, D., Cao, H., Xu, B., Xu, W., & Ke, S. (2020). Exceptional Points in Non-Hermitian Photonic Crystals Incorporated With a Defect. Applied Sciences, 10(3), 823. https://doi.org/10.3390/app10030823




