Numerical Investigation of the Combustion Characteristics of an Internal Combustion Engine with Subcritical and Supercritical Fuel

Featured Application

Supercritical fuel can be fully mixed with air to reduce the local concentration area in the cylinder, improve the combustion performance of the engine, and greatly reduce pollutant emissions.

Abstract

The similarities and differences in the combustion and emission characteristics of supercritical- and subcritical-state fuel injection conditions of an internal combustion engine was clarified. The effects of fuel state on temperature, pressure, turbulent kinetic energy, heat release rate, NO, and soot in the cylinder during the operation of the internal combustion engine were simulated. Ignition occurred faster, and the peak temperature in the cylinder was achieved in shorter time under the supercritical-state fuel injection condition than under the subcritical condition. The cylinder pressures in both states peaked at the same time, but the value of pressure in the supercritical fuel state was larger than that in the subcritical state. Furthermore, the turbulence in the supercritical fuel state was more intense than that in the subcritical state. The intense turbulence was beneficial to fuel and air mixing. NO emission increased, and soot emission decreased in the supercritical fuel state. The results show that supercritical fuel can be fully mixed with air to reduce the local concentration area in the cylinder, improve the combustion performance of the engine, and greatly reduce pollutant emissions.

1. Introduction

The global automotive industry has undergone a period of rapid growth due to social development. Data provided by the Automobile Industry Association [1] show that car ownership in China will increase to 500 million by 2030. Although the rapid development of the automobile industry has made people’s lives convenient, it has caused energy and environmental problems. Automobile exhaust has become the main source of atmospheric pollution in cities and continues to threaten the health of urban residents. The main pollutants in vehicle exhaust are HC, NO_X, CO, and particulate matter (PM) [2]. PM contains many harmful substances that stay permanently in the atmosphere. Therefore, its impact on human health and atmospheric quality has elicited much concern [3].

Means to improve the fuel economy, combustion, and emission performance of internal combustion engines have consistently been a key issue. Gasoline engine energy utilization is approximately 30% lower than the energy utilization of diesel engines. To improve the thermal efficiency of gasoline engines, scholars have extensively investigated gasoline direct injection (GDI) technology in the field of internal combustion engines [4,5,6]. Although GDI technology can improve the thermal efficiency of gasoline engines, the time of fuel and air mixing is shortened, leading to partial uneven mixing and serious PM emission problems [7]. Therefore, the main problem is improving the thermal efficiency and reducing the PM emissions of GDI engines [8,9]. Traditional diesel engines use high-pressure injection to form a non-uniform mixture of fuel and air for diffusion combustion. The heat release rate is determined by the mixing rate of fuel and air in the diffusion combustion stage. Fuel and air are mixed unevenly due to the short mixing time and low fuel diffusion rate in air. This situation results in the production of large amounts of soot in the high-temperature anoxic zone and increased soot emissions during combustion. Soot emission reduction is thus a major problem in diesel engines. Given the low thermal efficiency of GDI engines and high soot emission of diesel engines, scholars established a method to achieve high temperature and pressure in the combustion chamber during engine operation; this high-temperature and high-pressure environment is called the supercritical environment of fuel [10].

Fuel can rapidly form a homogeneous mixture with air for combustion and heat release due to the low surface tension, low viscosity, and large diffusion coefficient of supercritical fuel. This feature helps reduce the uneven distribution of concentration in the cylinder so that fuel can be completely burned and thermal efficiency can be improved. Supercritical-state fuel can evaporate directly without phase change. As a result, the formation of the mixture within the cylinder is accelerated, and fuel and air are uniformly mixed before combustion. Supercritical-state fuel is conducive for premixed combustion and improves combustion efficiency. In addition, in the diffusion combustion stage, supercritical fuel can be quickly mixed with air because of the large diffusion coefficient of this fuel. Thus, the reactant concentration becomes uniform, and the heat release rate is improved. Supercritical-state fuel can be combined with the latest injection technology to further control the combustion process, thereby reducing the emissions of pollutants and optimizing the combustion performance of engines.

The development of supercritical fuel combustion technology requires reliable data on fuel properties. Surrogate models are commonly used to estimate the chemical and physical properties of real fuels because the composition of fuels is highly complicated and lacks corresponding experimental data. In their study on dieseline, Anitescu et al. [11] found that phase behavior is substantially improved when the transition of dieseline (10% volume gasoline) from liquid to liquid−vapor and then to the supercritical fluid state and gasoline also prevents diesel coking. Lin et al. [12] presented a methodology for effectively evaluating the performance of diesel fuel surrogates in representing real diesel fuel thermophysical properties. The researchers estimated the critical temperature of diesel fuel to be 717–745 K. This result is important for the design of supercritical fuel delivery and injection systems. Kumar [13,14] explored the thermophysical properties of diesel fuel surrogates in supercritical state and proposed the use of statistical parameters, such as absolute average of relative error and sum of average residues, to evaluate the accuracy of the surrogates. In our previous study, we estimated the critical temperature and pressure of gasoline by using the values 550.4 K and 3.092 MPa, respectively [15].

Thus far, most of the research on supercritical fuels is based on the rocket engine, whereas investigations of supercritical fuels in internal combustion engine applications are rare. Zheng et al. [16] proposed a modifying mechanism for simulating supercritical gasoline, this mechanism contains 103 species and 201 reactions and is obtained by modifying the pre-exponential factors of key reactions and adding key reactions on the basis of the original mechanism proposed by our research program. Anitescu claimed that the delivery of a diesel fuel–diluent mixture in supercritical state increases engine efficiency and reduces NO_X and PM by avoiding two-phase reactions in fuel-rich regions [17,18,19]. De Boer et al. [20,21] studied the combustion and emission performance of supercritical fuel via experiments. They found that the emission of soot particles and NO is improved in the supercritical fuel condition of a single cylinder and obtained the trend of NO and soot emission with the change in fuel temperature. Zoldak et al. [22] discovered that supercritical gasoline combustion combined with exhaust gas recirculation results in low emissions and high thermal efficiency of single-cylinder engines under all operating conditions, and the maximum indicated thermal efficiency is 45%. Canter [23] explored the combustion effect of supercritical-state diesel and concluded that combustion efficiency is improved, and fuel economy is increased to 20%. Fan et al. [24,25,26], through their aviation kerosene Jet-A research, established a supercritical calculation model and a calculation method for the physical parameters of supercritical-state fuel. This study provides an effective theoretical basis and guidance for follow-up studies.

Diesel and gasoline (diesel mass fraction 10%) was selected as the research object in the current study due to the combined advantages of easy diffusion, small viscosity coefficient, good flow capability, and short combustion time of supercritical fuel. On the basis of the special physical properties of supercritical fuel and supercritical injection technology, a simulation of supercritical fuel combustion was conducted under a high compression–ignition ratio in an internal combustion engine. To our knowledge, no study has been conducted on the combustion of supercritical fuel in internal combustion engines. In this work, we explored flow and temperature fields and the quality score distribution of supercritical and subcritical fuels in the cylinder. Thus, different combustion and diffusion characteristics of supercritical and subcritical fuels were revealed.

2. Numerical Simulation Method

2.1. Fuel Injection and Turbulent Combustion Models

Prior to this simulation, we have established and verified the supercritical fuel injection model and chose the modified standard k-ε two equation model as the turbulence model to study the supercritical injection process; and to validate the model accuracy of the spray model, the supercritical nitrogen environment was studied by numerical simulation, the results shows relative error of the jet length is less than 5%, whereas that of the divergence angle is less than 8%. Both values meet the requirements for the accuracy of the calculation simulation [27].

The combustion of fuel in the operation of an internal combustion engine is turbulent. Turbulent combustion involves not only the complex flow of fuel and air but also the chemical reaction of fuel and air in the flow process. This complex process occurs when fuel combustion interacts with turbulence. Combustion can affect the turbulent flow in the cylinder through various means. For example, the heat released by combustion causes a change in fluid temperature in the flow field, which in turn results in partial fluid expansion and a change in the density gradient. This change in the cylinder leads to a highly complex turbulent flow and increases the difficulty of performing a numerical simulation. Meanwhile, the released heat changes the temperature, physical properties, and transport characteristics of the fluid, resulting in flow randomness. Turbulent flow also affects combustion, which in turn influences the chemical reaction rate, mixed condition of fuel and air, heat and mass transfer, and the combustion rate. Notably, the turbulence combustion reaction is primarily affected by turbulence disturbances, molecular diffusion, and chemical kinetics. The interaction of these influencing factors must be considered when selecting a combustion model.

In this study, the extended coherent flamelet model (ECFM) was used. ECFM is an extension of the coherent flamelet model. To determine the flame surface density, the ECFM uses the fuel/air equivalence ratio in fresh gases, the composition (including residual gases), and the temperature near the flame. The resulting flame surface density is used to describe large scale burned/unburned stratification. This model is fully coupled to the spray model and enables stratified combustion modeling including EGR effects and NO formation.

2.2. Emission Model

The main purpose of emission simulation is to predict the chemical composition and concentration distribution of pollutants generated during combustion. However, research on HC and CO has not achieved remarkable progress because combustion theory lags behind. Scholars have focused on simulations and theoretical analyses of NO_X and soot. In this work, NO_X and soot simulation was explored.

The NO_X generated by the operation of an internal combustion engine includes NO and NO₂. NO plays the leading role, so the generation mechanism and model of NO were the focus of this work. NO is also generated by the conversion of N₂O, which produces a negligible amount of NO that does not need to be considered in the calculation of NO generation [28,29]. We used the Zeldovich model, which is a widely used generation model of NO, and the mechanism of the model is

$$\begin{gathered} {\mathrm{N}}_2+\mathrm{O}\stackrel{{\mathrm{k}}_{1\mathrm{f}}{\mathrm{k}}_{1\mathrm{b}}}{\leftrightarrow }\mathrm{NO}+\mathrm{N} \\ \mathrm{N}+{\mathrm{O}}_2\stackrel{{\mathrm{k}}_{2\mathrm{f}}{\mathrm{k}}_{2\mathrm{b}}}{\leftrightarrow }\mathrm{NO}+\mathrm{O} \\ \mathrm{N}+\mathrm{OH}\stackrel{{\mathrm{k}}_{3\mathrm{f}}{\mathrm{k}}_{3\mathrm{b}}}{\leftrightarrow }\mathrm{NO}+\mathrm{H} \end{gathered}$$

Meanwhile, the Kennedy/Hiroyasu/Magnussen model was selected as the calculation model for soot emission. The model is based on the two-step empirical model proposed by Hiroshima et al. [30].

3. Establishment and Verification of the Engine Model

3.1. Establishment of the Engine Model

This research was based on the operating conditions of an engine with direct fuel injection and supercritical injection and combustion technology. We assumed that the mixture of gasoline and diesel would burn in the cylinder of the gasoline engine. The parameters of in-cylinder air cannot easily exceed the critical value of fuel at fuel injection time and cannot make fuel enter the supercritical state because the in-cylinder pressure is too low at the top dead center. Therefore, the diesel engine model and boundary condition used in [31] was utilized to simulate the operation of the engine under supercritical conditions by jetting a supercritical state mixture of gasoline and diesel into the cylinder in supercritical state [32]. The main structural parameters of the engine used are shown in

Table 1. Engine structural parameters

Parameters	Values
Cylinder diameter × cylinder stroke, mm	115 × 115
Compression ratio	16:1
Connecting rod length, mm	210
Displacement, L	1.2
Combustion chamber shape	ω
Rotating speed, r·min−1	1800

.

An engine model needs to be meshed in a numerical simulation. What we used in this simulation is unstructured grid. An unstructured grid easily adopts the boundary region and the calculation of stress concentration on the fluid surface. According to the symmetry of the selected engine, one-eighth of the entire combustion chamber was used as the calculation area. Figure 1 shows the shape of the combustion chamber at TDC and the grid used for calculation.

Owing to the transient characteristics of parameters during engine operation, the relaxation time of turbulence and time-averaged movement are short, which reduces the influence of the initial conditions on the results. Therefore, the time-averaged parameters were selected as the initial condition in the numerical simulation.

Grid size affects the accuracy of the calculation. As shown in Figure 2, in accordance with the geometrical structure of the model, the maximum grid size was set to 1, 2, and 4 mm, and a grid independent test was implemented. The maximum grid size was then determined to be 2 mm.

3.2. Verification of the Engine Model

In the verification of the accuracy of the model under subcritical state fuel injection conditions, the initial parameters of the engine were set to 10 according to [10]. The change curve of the average in-cylinder pressure was calculated under the operating condition of the engine with an initial temperature of 362 K, initial pressure of 0.15 MPa, rotation speed of 1400 r/min, and fuel injection quantity of 70 mg/cyc. According to experience, temperature of the top of the piston, cylinder head wall and cylinder liner wall were set as 570.15, 570.15, and 470.15 K, respectively. A comparison of the simulation and experimental curves is shown in Figure 3. The calculated average pressure curve and heat release rate are in good agreement with the experimental average pressure curve. Therefore, the initial parameters and the calculation method adopted are effective for the simulation of subcritical conditions. The initial boundary conditions in the simulation under supercritical conditions are similar to those under subcritical conditions due to the lack of research on the change in in-cylinder pressure. The model was then selected for simulation.

4. Results

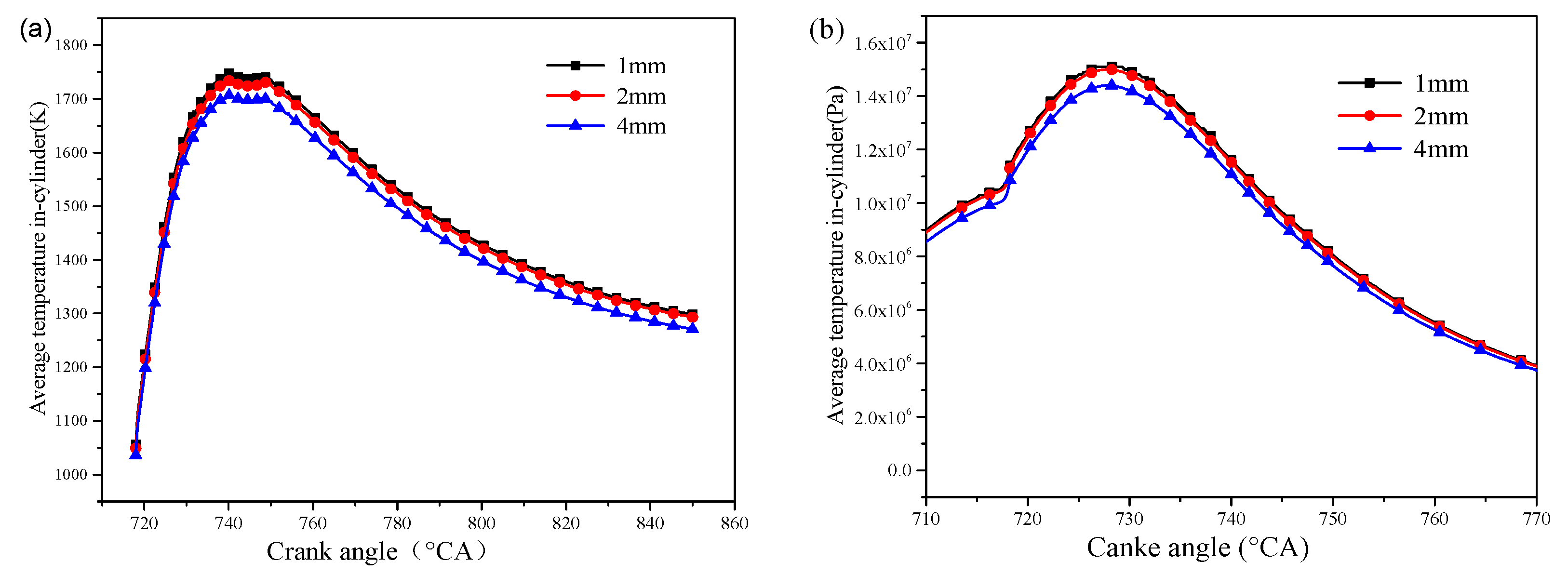
4.1. Comparison of In-Cylinder Temperature and Pressure

We measured the critical parameters, namely, temperature and pressure, of gasoline and found them to be 550 K and 3.092 MPa, respectively [15]. In this simulation, the alternative fuel for gasoline is isooctane. Many researchers use n-heptane instead of diesel in their numerical simulations when the diesel supercritical parameters are unknown. The temperature and pressure of n-heptane are 540.3 K and 2.74 MPa [33]. The heat of combustion per unit of isooctane and n-heptane are −537.9705 KJ/Kg and −1536.5545 KJ/Kg, respectively.

In this study, the initial temperature of fuel was set to 350 K/400 K to simulate the subcritical fuel injection condition. The initial fuel temperature was set to 600–650 K/700 K for the supercritical fuel injector condition.

As shown in Figure 4a, the times of temperature mutation and temperature peak appearance in the supercritical condition are shorter than those in the subcritical condition. Compared with the situation in the subcritical condition, the rise rate of temperature in the supercritical condition is higher, and the peak temperature is slightly increased. This phenomenon is caused by the supercritical fuel’s low density, high flow velocity, and high diffusion rate when the fuel flows into the cylinder, resulting in rapid mixing of fuel and air and fast fuel ignition. As shown in Figure 4b, compared with the situation in the subcritical condition, the pressure rise rate and average pressure in the supercritical fuel injection condition increase significantly. The pressure peak appears at 730° crank angle (CA), at which the piston has passed through the top dead center and is moving toward the bottom of the cylinder. According to the perfect gas equation, the pressure is proportional to the temperature in the enclosed volume. At 730° CA, the average temperature in the supercritical fuel injection condition is higher than that in the subcritical condition. Hence, pressure is higher in the supercritical condition than that in the subcritical condition. Moreover, the supercritical state fuel is close to the gaseous phase. According to the relationship between mass and density, the same mass of fuel flows into the cylinder. Supercritical fuel accounts for a large volume, and liquid fuel has a small volume only, resulting in an increase in in-cylinder density and pressure.

Figure 5a shows the distribution of fuel at 350, 400, 600, 650, and 700 K in the cylinder when the fuel begins to catch fire. The distribution of fuel in supercritical and subcritical fuel injection conditions was compared at 718° and 720° CA. At 718° CA, the fuel is evenly distributed in the cylinder under three supercritical conditions. Then, the fuel is sprayed to the wall of the combustion chamber. The jet flow remains relatively small in the two cases of subcritical conditions, and the subcritical fuel lacks sufficient contact with air and is mixed. At this point, the supercritical state fuel begins to burn, which makes the combustion time of the supercritical condition shorter than that of the subcritical condition. At 720° CA, the subcritical state fuel begins to burn, but the supercritical fuel has been burned already. As shown in Figure 3a, the in-cylinder peak temperature was immediately reached in the supercritical condition.

Figure 5b shows that the diffusion rate of the fuel in the supercritical fuel injection condition is higher than that in the subcritical condition, which is beneficial to the mixing of fuel and air, increases the mixing speed of fuel and air, and makes the mixture uniform. The combustion reaction is rapid in the supercritical condition. Hence, the average in-cylinder temperature increases faster, and the temperature reaches the peak earlier than in the subcritical conditions.

Figure 6 shows the change in the rate of heat release. The trend of the rate of heat release is consistent with the trends of in-cylinder temperature and pressure, and the exothermic start time in the supercritical fuel injection condition is ahead of that in the subcritical condition. The fuel is in the subcritical or supercritical state, the heat release rate decreases with the increase in fuel temperature in the premixed combustion stage. The area under the heat release rate curve in the supercritical condition is larger than that in the subcritical condition, indicating that the fuel releases a large quantity of heat, and fuel combustion is efficient.

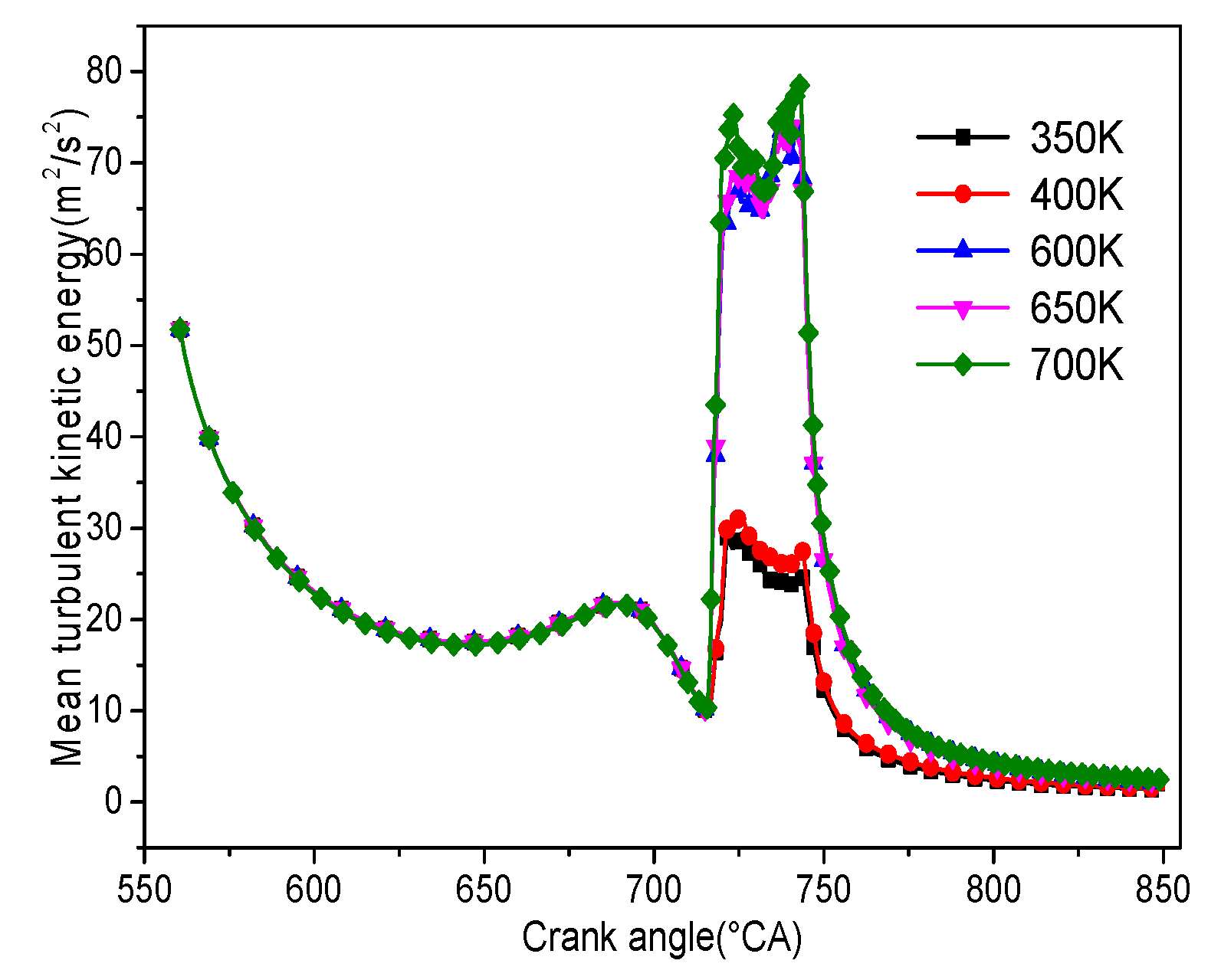
4.2. Comparison of In-Cylinder Turbulent Kinetic Energy under Engine Operation

Turbulent kinetic energy is an important parameter to describe the turbulence intensity in the cylinder, and it reflects the fluid flow strength in the cylinder. Turbulent kinetic energy exerts a significant impact during the mixing of fuel and air and fuel combustion. Figure 7 shows the change curve of the average turbulent kinetic energy in the cylinder under supercritical and subcritical fuel injection conditions.

Figure 7 shows that fuel temperature exerts a minimal effect on the change process of the average turbulent kinetic energy in the cylinder under supercritical and subcritical fuel conditions. With the change in CA, the change in turbulent kinetic energy is enhanced in the supercritical condition compared with that in the subcritical condition. This phenomenon occurs possibly because the supercritical fuel density is smaller and the average flow velocity of the fuel is higher than those in the subcritical fuel. The fuel and air relative movement is obvious and forms a strong local eddy in the cylinder; thus, the turbulent flow of fluid is enhanced.

Figure 8 shows the flow behavior of fluid at 350, 400, 600, 650, and 700 K in the cylinder at 720, 735, and 750° CA. With the increase in CA, the average flow rate and turbulent region in the cylinder are gradually increased. At 720° CA, in the subcritical fuel injection condition, the average velocity of the fluid is low, and the turbulence near the oil beam is weak. In the supercritical fluid injection condition, the average velocity of the fluid is high. Moreover, a vortex is formed around the oil beam and is distributed at the bottom of the combustion chamber, facilitating the uniform distribution of fuel in the cylinder. At 735° CA, the difference between supercritical and subcritical conditions becomes more pronounced. Under the supercritical fuel injection condition, the area with high flow velocity is widely distributed, and the eddy intensifies. At 750° CA, the flow of fluid is rapid, and the fuel is evenly distributed in the combustion chamber under the supercritical fuel injection condition. In the supercritical condition, an additional vortex is formed near the nozzle. This analysis shows that the flow of the fluid is intense under the supercritical condition, which is beneficial to the rapid mixing of fuel and air and makes the mixture of fuel and air in the cylinder highly uniform. The fuel has a high heat release rate in the premixed combustion stage, which is consistent with the law of heat release rate.

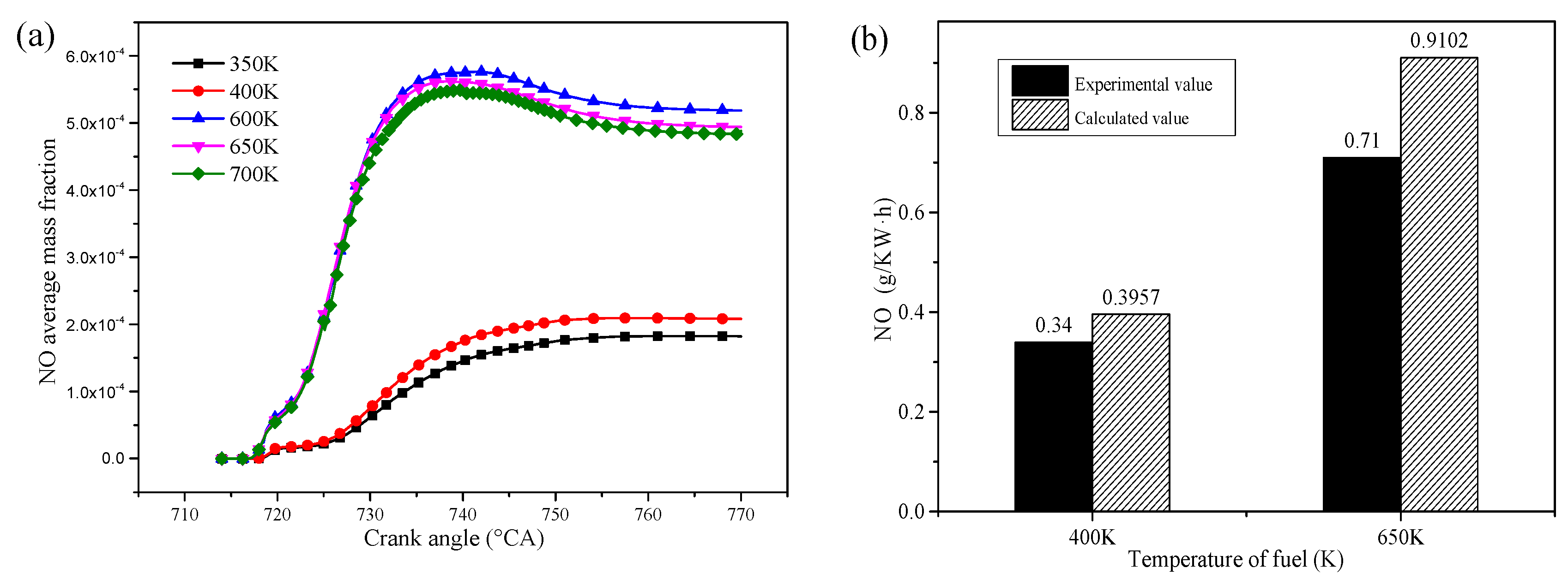
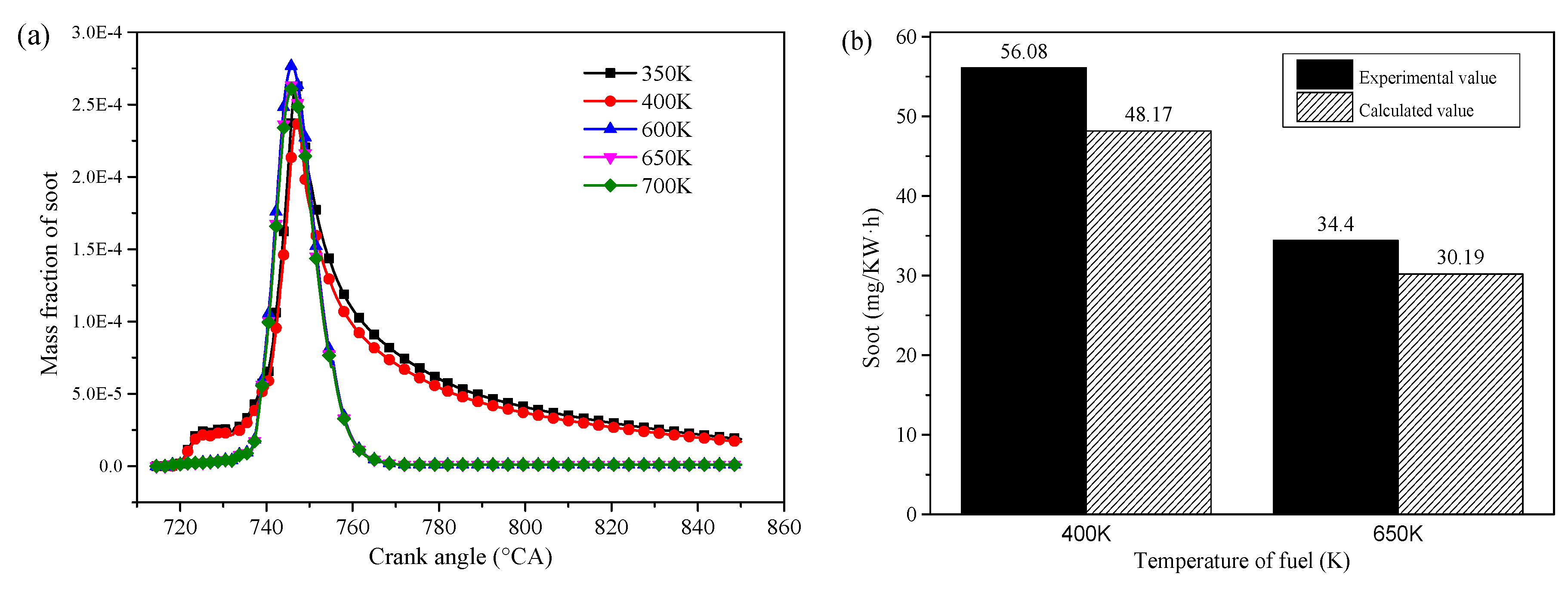
4.3. Emission Performance Analysis

Figure 9a shows the change curve of the average NO mass fraction in the cylinder under supercritical fuel injection and subcritical conditions. The calculation results for the initial fuel temperature of 650 and 400 K shows that the mass fraction of NO at a fuel temperature of 650 K is 2.3 times the fuel temperature of 400 K in the steady state. As shown in Figure 9b, compared with the experimental data of Chris De Boer [21], the NO emissions of the engine are 0.34 g/kW·h and 0.71 g/h at the initial fuel temperature of 650 and 400 K, respectively. The numerical simulation results are close to the experimental results. Thus, the computational model is reliable under subcritical fuel injection conditions, and the emission performance under subcritical conditions can be compared with that under supercritical conditions. The mass fraction of NO under the supercritical fuel injection condition is higher than that under the subcritical condition. At 720–735° CA, the combustion is premixed. The average temperature of the fluid under the supercritical condition is higher than that under the subcritical condition. Therefore, the generation rate of NO is rapid under the supercritical condition.

In Figure 10a, the NO generation rate under the supercritical injection condition is faster than that under the subcritical condition. Furthermore, the region where NO is generated corresponds to the high-temperature region of the temperature distribution cloud diagram at 730° CA in Figure 10b, indicating that the formation of NO is closely related to the temperature distribution in the cylinder. Similar to thermal efficiency, NO plays a dominant role in NO_X products.

Figure 11 shows the changes in the average mass fraction of soot in the cylinder with CA under supercritical fuel injection and subcritical conditions. According to the results of Chris De Boer [21], when the fuel temperature is 400 and 650 K, the quality of soot emissions is 56.08 and 34.4 mg/KW·h, respectively. The quality of soot emissions obtained from the calculated results is shown in Figure 10b. The results are close to the experimental ones. Thus, the numerical simulation of soot emission is reliable.

As shown in Figure 11a, under subcritical and supercritical conditions, the fuel temperature exerts no significant effect on the average mass fraction of soot. When CA increases, the average weight of soot increases to the maximum then gradually decreases because soot formation is the result of the interaction between the formation and oxidation of inert products [34].

Figure 11a shows that the average mass fraction of soot before 750° CA is gradually increased. After 750° CA, the average mass fraction of soot begins to decrease. However, during the increase in the mass fraction of soot, the mass fraction change ratio of soot under the subcritical fuel injection condition is faster than that under the supercritical condition in the early stages of combustion. Under the subcritical state fuel injection condition, fuel and air mixing is not sufficient to form a number of high-temperature and lean oxygen areas. Therefore, part of the fuel cracking produces hydrocarbons or gas-phase precursors of carbon particles in the combustion process. In addition, soot is also formed by further condensation and polymerization of hydrocarbons or gas-phase precursors of carbon particles. Under the supercritical condition, the phenomenon in which soot is significantly increased does not occur in the early stages of combustion because supercritical state fuel has a large diffusion coefficient. Hence, forming a uniform mixture is easy, and the fuel can be burned well in the premixed combustion stage.

As the combustion reaction progresses, the combustion mode of the fuel in the cylinder begins to change into diffusion. In this process, fuel and air are not effectively mixed, resulting in soot generation. In the supercritical condition, the mass fraction of soot declines rapidly, and the final mass fraction is lower than that in the subcritical condition. At the end of soot generation, the oxidation process of soot becomes the main influencing factor. In the supercritical state fuel injection conditions, supercritical fluids have their own unique physical and chemical properties, so chemical reactions are likely to occur in the supercritical environment [35]. The supercritical environment affects the physical and chemical properties of oxygen and soot. Thus, the oxidation rate of soot in the cylinder is rapid, resulting in a rapid decrease in the mass fraction of soot.

5. Conclusions

The temperature, pressure, and turbulent kinetic energy in the cylinder were investigated with the change in the crank angle under supercritical and subcritical fuel injection conditions. The numerical simulation method was used. The flow characteristics of fuel and the combustion and emission performance (e.g., heat release rate, NO mass fraction, and soot quality fraction) were studied. The operating characteristics of the engine under supercritical and subcritical conditions were analyzed, and the following conclusions were obtained.

(1)

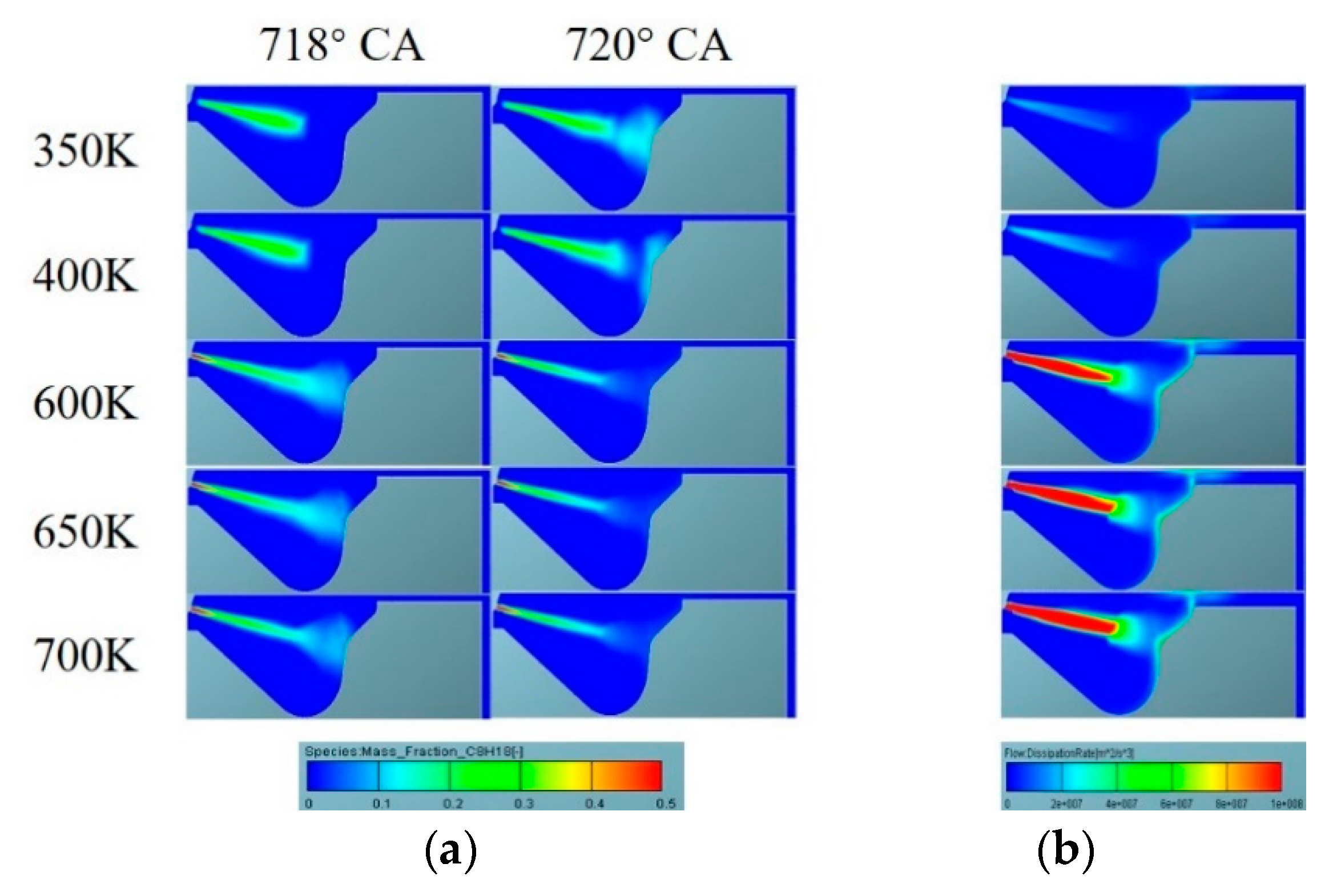
The ignition time is shorter and the peak temperature in the cylinder is achieved earlier in the supercritical fuel injection condition compared with the subcritical fuel injection condition. The rate of pressure increase and the peak value of the average pressure of the supercritical state fuel are significantly higher than those of the subcritical fuel.

(2)

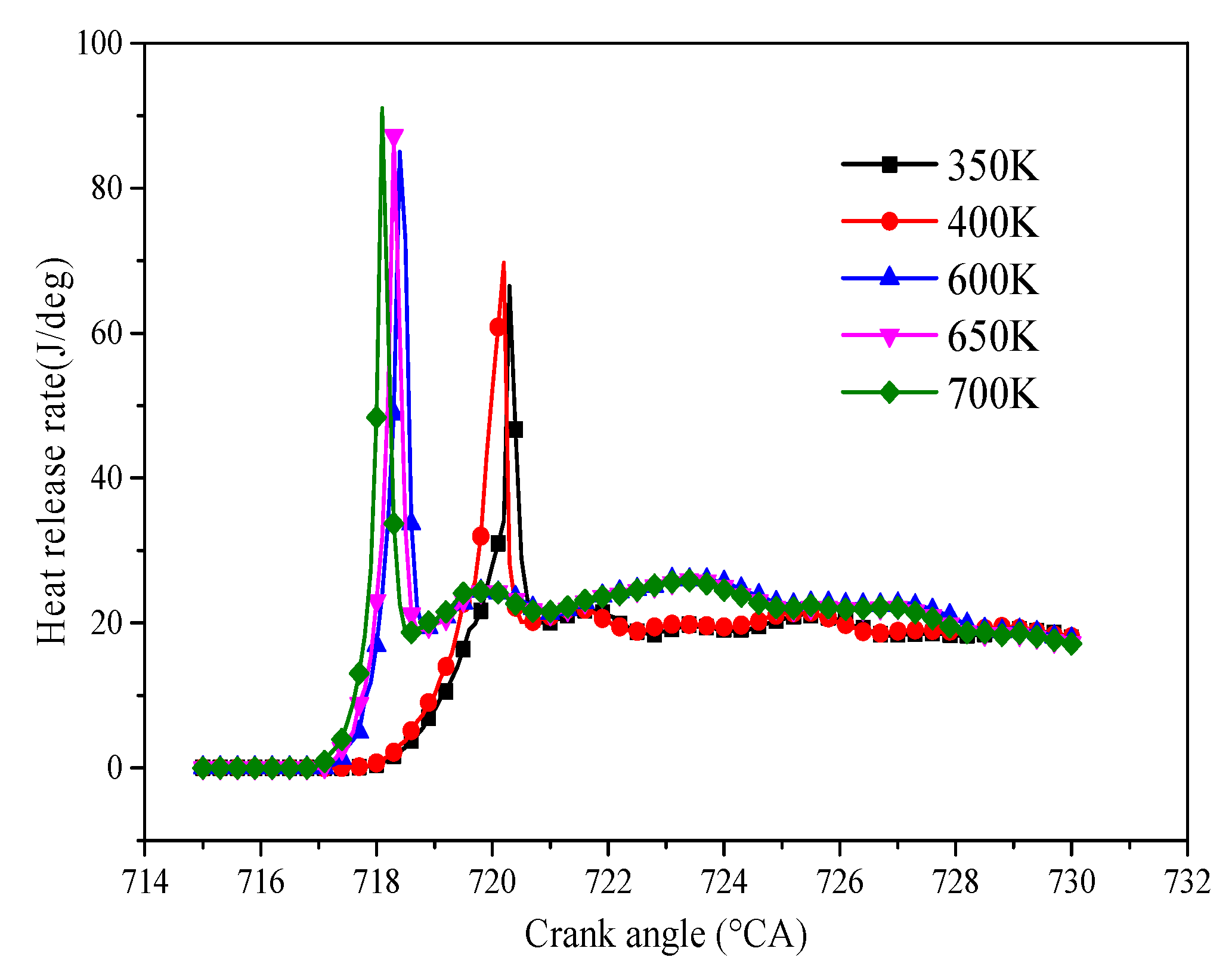
The time to release heat in the supercritical fuel injection condition is shorter than that in the subcritical condition. The rate of heat release in the premixed combustion stage decreases, whereas that in the diffusion combustion stage increases with the increase in the fuel temperature in both conditions.

(3)

The velocity of the fluid is high in the supercritical state fuel injection condition. Hence, the eddy current of high-velocity flow is formed in the local area of the cylinder, resulting in a significant increase in turbulent energy after the fuel is injected into the cylinder.

(4)

NO emission increases and soot emission decreases under the supercritical condition compared with the subcritical condition.