Planetary-Gearbox Fault Classification by Convolutional Neural Network and Recurrence Plot
Abstract
:1. Introduction
2. Materials and Methods
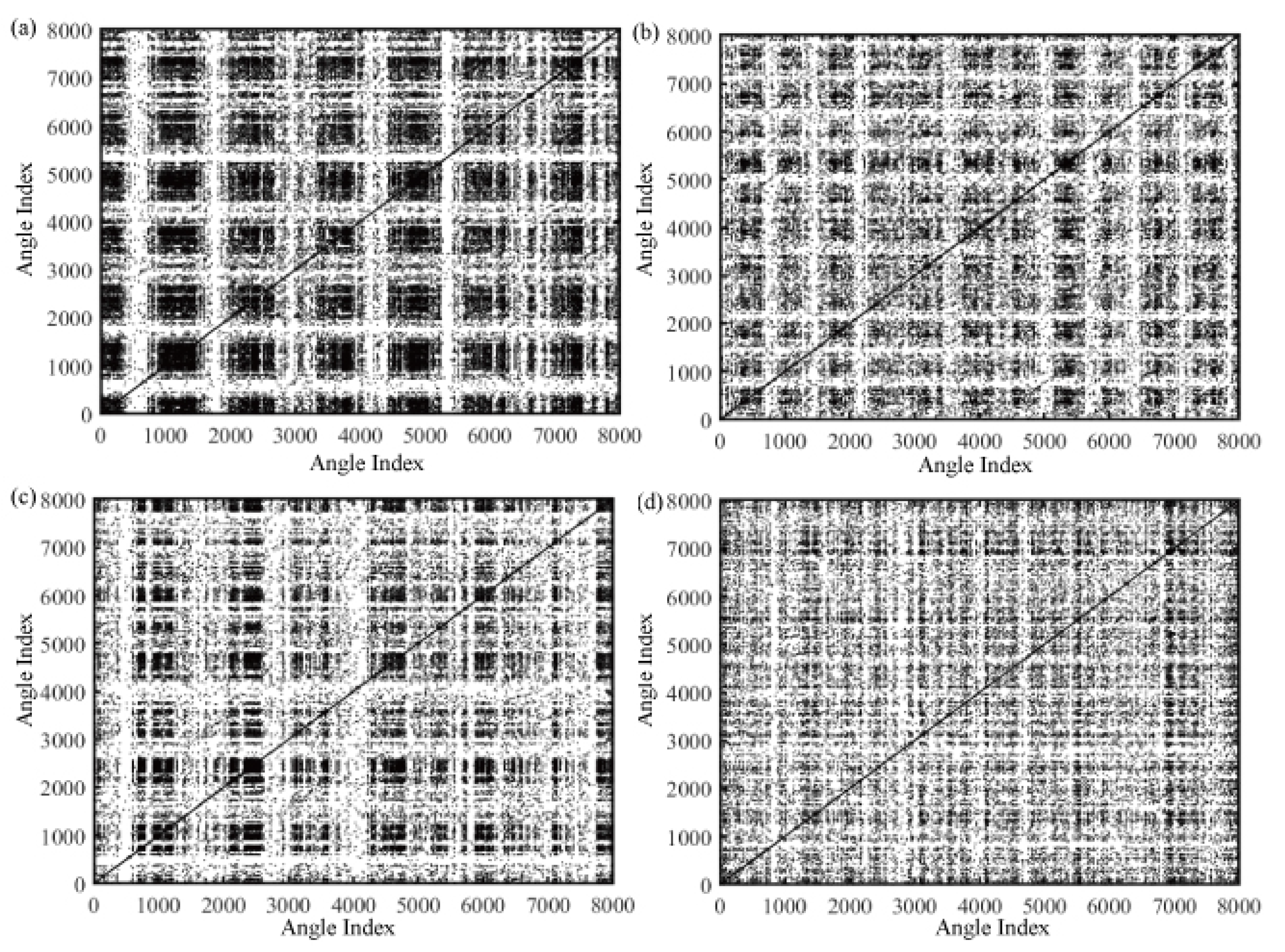
2.1. Angular-Domain Recurrence-Plot Analysis
2.1.1. Phase-Space Reconstruction in Angular Domain
2.1.2. Determination of Embedding Dimension
2.1.3. Determination of Angle Delay
2.2. Briefs on Recurrence Plot
3. Briefs on Convolutional Neural Network
3.1. Typical Configuration of Convolutional Neural Network
3.2. Evaluation Indicators of CNN Model
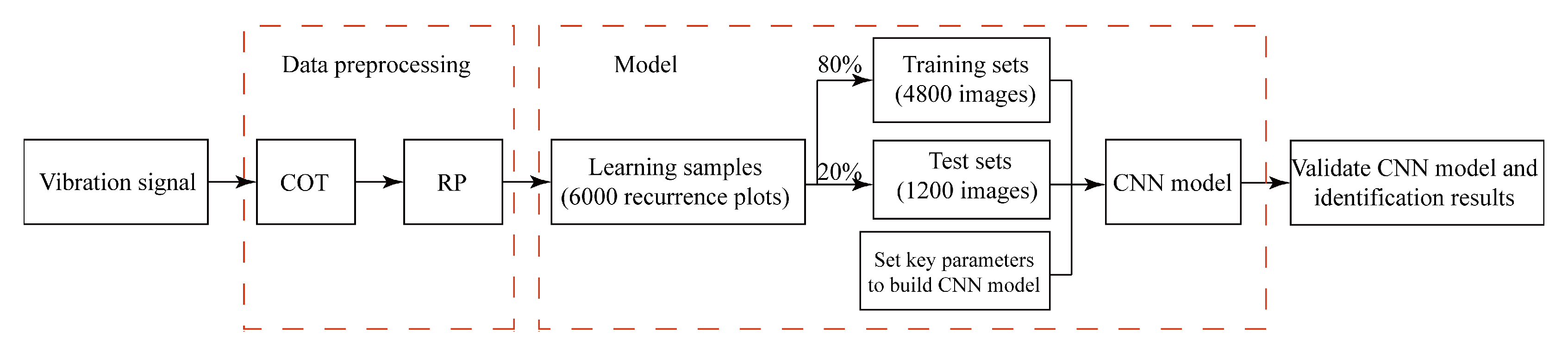
4. CNN Combined with Angular-Domain RP for Fault Classification of Planetary Gearboxes
- Vibration-signal acquisition and processing. Raw vibration of the planetary gearbox is picked up synchronously with the tacho plus trains of the reference shaft. Then, equiangle resampling is performed to convert the data series into those in the angular domain.
- Construction of training dataset. Vibration data series are first divided into segments. For a planetary gearbox with a fixed annulus gear, the transmission ratio of the planet carrier and sun gear can be expressed bywhere , are the tooth numbers of the sun and ring gear, respectively. For the minimal common complete integral period of the sun gear and planet carrier, the sun gear needs to rotate circles, and the carrier rotates circles. Therefore, to ensure each segment covering the meshing vibration of all teeth, the corresponding rotating circles of the sun gear should not be less than .We assumed that the rotating speed of the sun gear was , and the total time of the observed signal was T. To save computation time, the resampled length data in the angular domain can be expressed by:where is resampling points per revolution. Thus, the points of each segment equal to . Then, to a condition with three operating speeds, each segment was randomly selected to constitute the training sample.
- Build CNN model and set parameters. The configuration of a 2D CNN was used. Several key parameters, such as learning rate, the size of convolutional kernels, number of iterations, and nodes of fully connected layers were set and are discussed in the next section.
- Identification results and evaluation of CNN model.
5. Experiments and Discussion
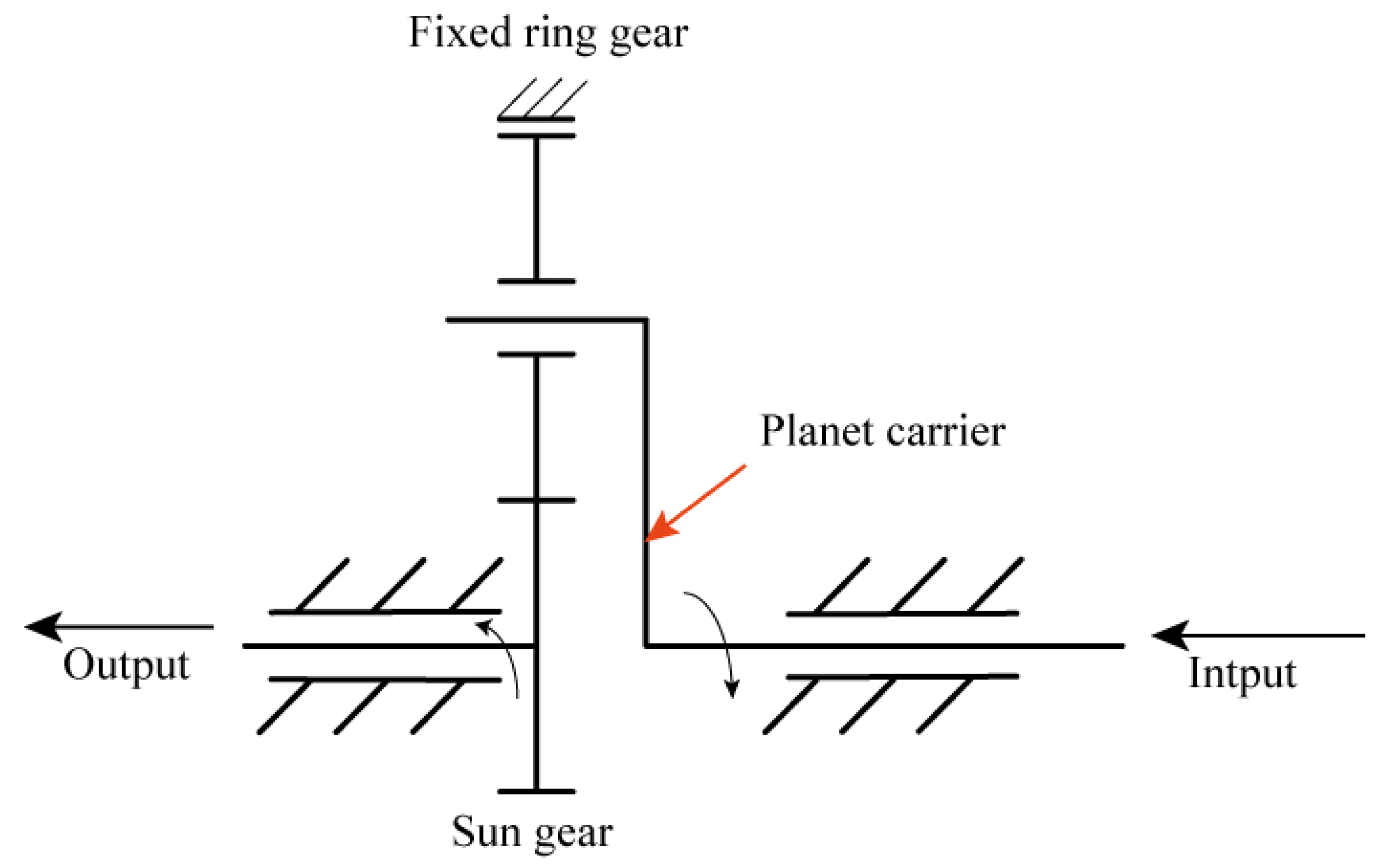
5.1. Planetary-Gearbox Test Rig
5.2. Data Preprocessing and Model Design
5.2.1. Data Preprocessing
5.2.2. Model Design
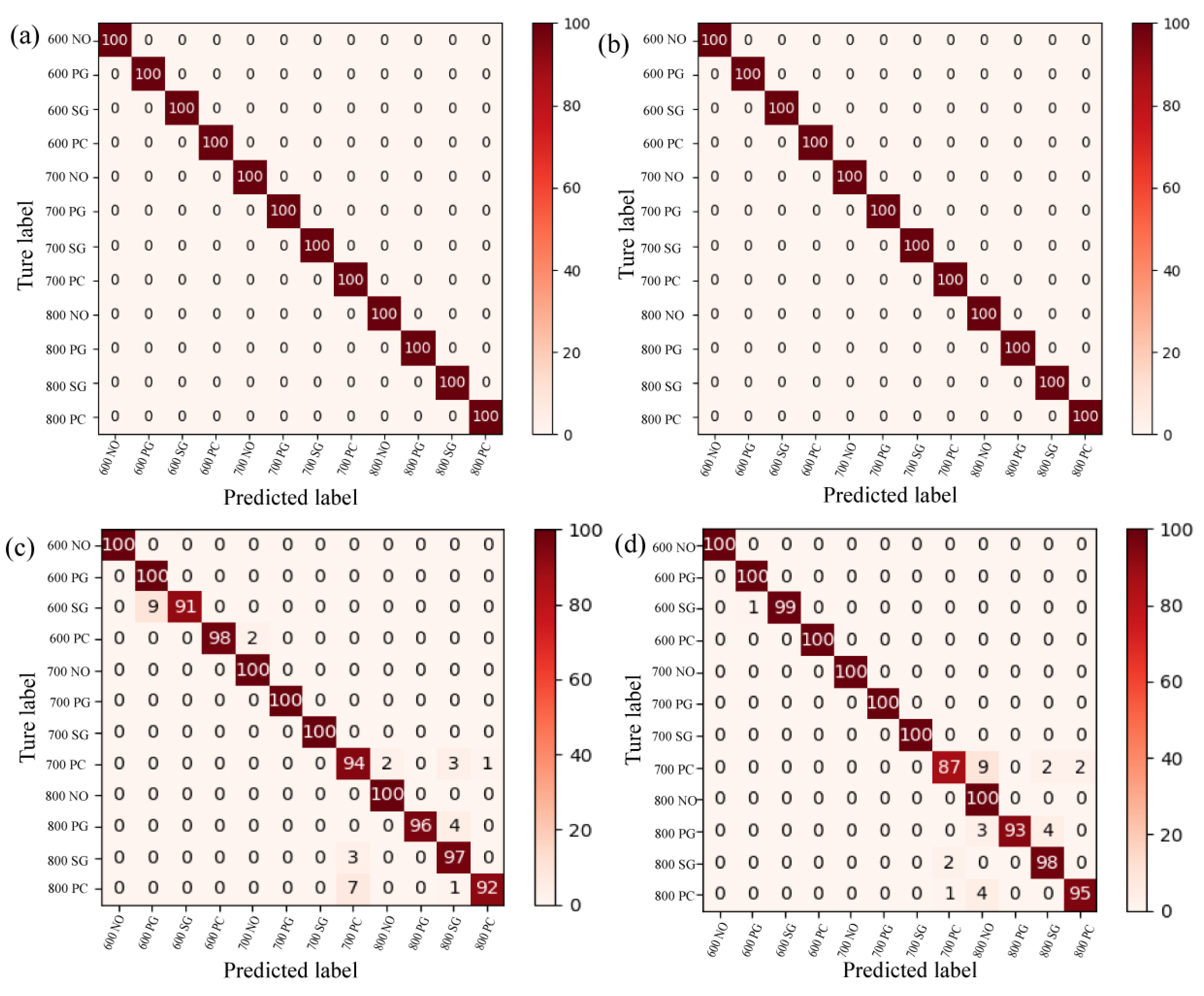
5.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RP | Recurrence plot |
| CNN | Convolutional neural network |
| COT | Computed order tracking |
| AI | Artificial intelligent |
| FFT | Fast Fourier transform |
| CWT | Continuous wavelet transform |
| STFT | Short-time Fourier transform |
| FT | Fourier transform |
| FNN | False nearest neighbors |
| SNR | Signal-to-noise ratio |
| ReLU | Rectified linear unit |
| ADAM | Adaptive moment estimation |
| IMF | Intrinsic mode function |
| EMD | Empirical mode decomposition |
References
- Guo, Y.; Zhao, L.; Wu, X.; Na, J. Vibration separation technique based localized tooth fault detection of planetary gear sets: A tutorial. Mech. Syst. Signal Process. 2019, 129, 130–147. [Google Scholar] [CrossRef]
- Feng, Z.P.; Ma, H.Q.; Zuo, M.J. Amplitude and frequency demodulation analysis for fault diagnosis of planet bearings. J. Sound Vib. 2016, 382, 395–412. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, Q.N.; Wu, X.; Na, J. Gear fault diagnosis based on narrowband demodulation with frequency shift and spectrum edit. Int. J. Eng. Technol. Innov. 2016, 4, 243–254. [Google Scholar]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; de Walle, R.V.; van Hoecke, S. Convolutional neural network based fault detection for rotating machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Li, C.; Sanchez, R.V. Gearbox fault identification and classification with convolutional neural networks. Shock Vib. 2015, 2015, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Wang, H.L.; Li, S.B.; Liu, Z.H.; Gui, G.; Dan, Y.B.; Hu, J.J. End-to-end convolutional neural network model for gear fault diagnosis based on sound signals. Appl. Sci. 2018, 9, 1584. [Google Scholar] [CrossRef] [Green Version]
- Lv, Y.; Pan, B.Q.; Yi, C.C.; Ma, Y.B. A Novel Fault Feature Recognition Method for Time-Varying Signals and Its Application to Planetary Gearbox Fault Diagnosis under Variable Speed Conditions. Sensors 2019, 14, 3154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jing, L.Y.; Zhao, M.; Li, P.; Xu, X.Q. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Syta, A.; Jonak, J.; Jedliński, Ł.; Litak, G. Failure diagnosis of a gear box by recurrences. J. Vib. Acoust. 2012, 4, 041006–041014. [Google Scholar] [CrossRef]
- Ambrożkiewicz, B.; Guo, Y.; Litak, G.; Wolszczak, P. Dynamical Response of a Planetary Gear System with Faults Using Recurrence Statistics. In Topics in Nonlinear Mechanics and Physics; Springer: Singapore, 2019; pp. 177–185. [Google Scholar]
- Guo, Y.; Wu, X.; Na, J.; Fung, R.F. Envelope synchronous average scheme for multi-axis gear faults detection. J. Sound Vib. 2016, 365, 276–286. [Google Scholar] [CrossRef]
- Fyfe, K.R.; Munck, E.D.S. Analysis of computed order tracking. Mech. Syst. Signal Process. 1997, 11, 187–205. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.Y. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. D Nonlinear Phenom. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.; Gore, J.C.; Peterson, B.S. Mutual information analysis of the EEG in patients with Alzheimer’s disease. Clin. Neurophysiol. 2001, 112, 827–835. [Google Scholar] [CrossRef]
- Thiel, M.; Romano, M.C.; Kurths, J.; Meucci, R.; Allaria, E.; Arecchi, F.T. Influence of observational noise on the recurrence quantification analysis. Phys. D Nonlinear Phenom. 2002, 171, 138–152. [Google Scholar] [CrossRef] [Green Version]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.X..; Wang, G.; Cai, J.F.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. J. Intell. Learn. Syst. Appl. 2014, 10, 121–134. [Google Scholar]
- Sen, A.K.; Longwic, R.; Litak, G.; Górskid, K. Analysis of cycle-to-cycle pressure oscillations in a diesel engine. Mech. Syst. Signal Process. 2008, 2, 362–373. [Google Scholar] [CrossRef]
- Hu, N.Q.; Chen, H.P.; Cheng, Z.; Zhang, L.; Zhang, Y. Fault diagnosis for planetary gearbox based on EMD and deep convolutional neural networks. J. Mech. Eng. 2019, 7, 9–18. [Google Scholar] [CrossRef] [Green Version]


| Layer | Variable and Dimension | Training Parameters |
|---|---|---|
| Convolutional layer 1 | CW = 5; CH = 5; CN = 32 | Padding = ‘same’ |
| Pooling layer 1 | S = 2 | MaxPooling |
| Convolutional layer 2 | CW = 5; CH = 5; CN = 64 | Drop out = 0.5 |
| Poling layer 2 | S = 2 | MaxPooling |
| Fully connected layer 1 | Nodes = 1024 | Training sample rate = 80% |
| Fully connected layer 2 | Nodes = 512 | Max epoch = 60 |
| Fully connected layer 3 | Nodes = 64 | Learning rate = 0.0001 |
| softmax regression layer | Nodes = 4 | active function = ReLU |
| Evaluation Indicators | Accuracy | Precision | Recall | -Score |
|---|---|---|---|---|
| Time domain RP | 97.2431 ( = 0.838) | 97.4874 ( = 0.603) | 97 ( = 0.84) | 97 ( = 0.863) |
| Angular domain RP | 100 ( = 0) | 100 ( = 0) | 100 ( = 0) | 100 ( = 0) |
| CWT (cmor4-4) | 100 ( = 0) | 100 ( = 0) | 100 ( = 0) | 100 ( = 0) |
| Artificially selected IMF | 97.3266 ( = 3.237) | 97.5712 ( = 2.993) | 97.0833 ( = 3.845) | 97.0833 ( = 3.485) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.-F.; Guo, Y.; Wu, X.; Na, J.; Litak, G. Planetary-Gearbox Fault Classification by Convolutional Neural Network and Recurrence Plot. Appl. Sci. 2020, 10, 932. https://doi.org/10.3390/app10030932
Wang D-F, Guo Y, Wu X, Na J, Litak G. Planetary-Gearbox Fault Classification by Convolutional Neural Network and Recurrence Plot. Applied Sciences. 2020; 10(3):932. https://doi.org/10.3390/app10030932
Chicago/Turabian StyleWang, Dan-Feng, Yu Guo, Xing Wu, Jing Na, and Grzegorz Litak. 2020. "Planetary-Gearbox Fault Classification by Convolutional Neural Network and Recurrence Plot" Applied Sciences 10, no. 3: 932. https://doi.org/10.3390/app10030932
APA StyleWang, D.-F., Guo, Y., Wu, X., Na, J., & Litak, G. (2020). Planetary-Gearbox Fault Classification by Convolutional Neural Network and Recurrence Plot. Applied Sciences, 10(3), 932. https://doi.org/10.3390/app10030932






