Segmented Composite Optical Parametric Amplification
Abstract
1. Introduction
2. Theory
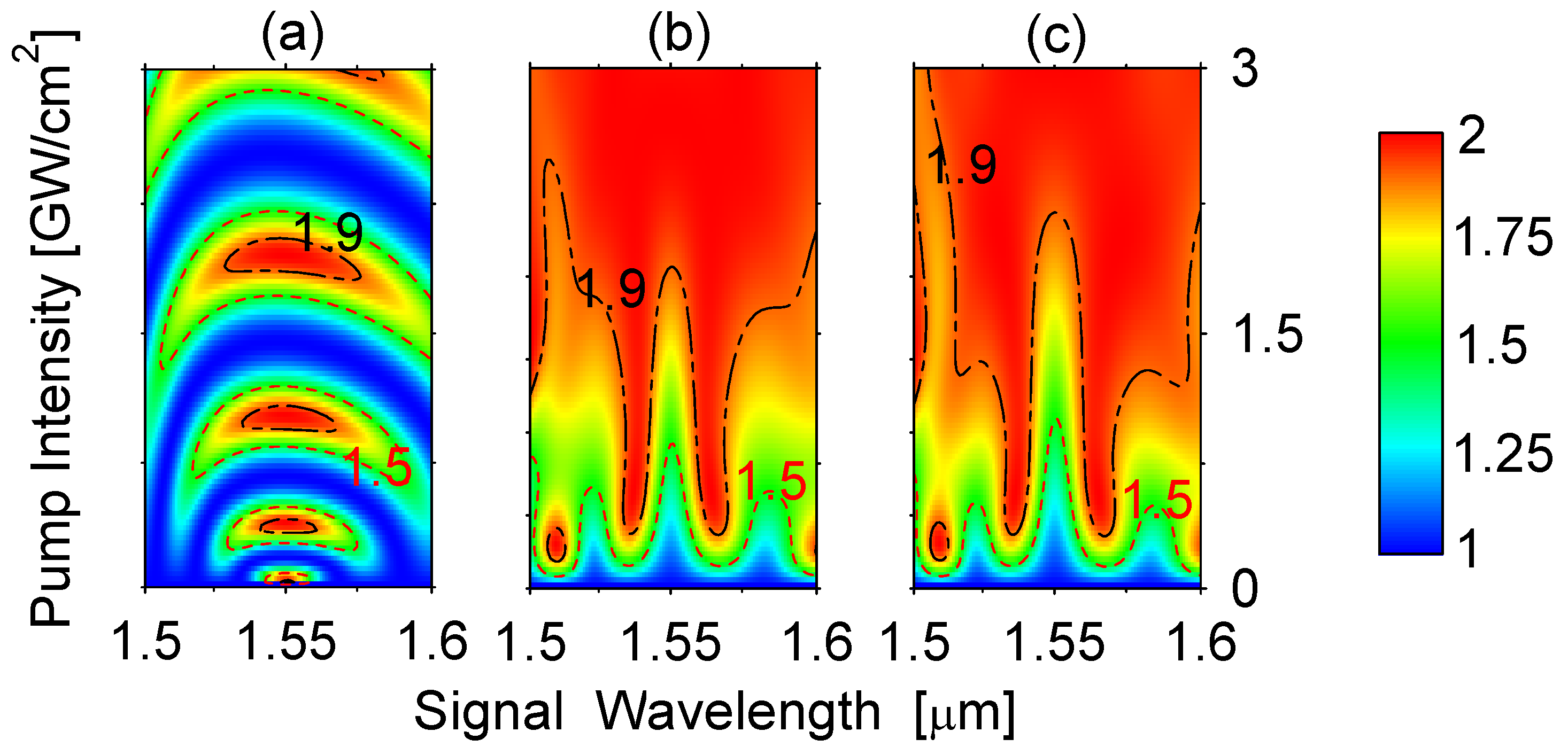
3. General Numerical Approach and LiNbO Crystal Simulations
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| OPA | Optical Parametric Amplifier |
| QPM | Quasi-phase-matching |
| NMR | Nuclear Magnetic Resonance |
| SFG | Sum Frequency Generation |
| DFG | Difference Frequency Generation |
| SHG | Second Harmonic Generation |
Appendix A. Mapping between Two State Quantum System and SFG in Case of Undepleted Pump Approximation
References
- Joosen, W.; Agostini, P.; Petite, G.; Chambaret, J.P.; Antonetti, A. Broadband femtosecond infrared parametric amplification in β-BaB2O4. Opt. Lett. 1992, 17, 133–135. [Google Scholar] [CrossRef] [PubMed]
- Gale, G.M.; Cavallari, M.; Driscoll, T.J.; Hache, F. Sub-20-fs tunable pulses in the visible from an 82-MHz optical parametric oscillator. Opt. Lett. 1995, 20, 1562–1564. [Google Scholar] [CrossRef] [PubMed]
- Gale, G.M.; Hache, F.; Cavallari, M. Broad-bandwidth parametric amplification in the visible: Femtosecond experiments and simulations. IEEE J. Sel. Top. Quantum Electron. 1998, 4, 224–229. [Google Scholar] [CrossRef]
- Schmidt, B.E.; Thiré, N.; Boivin, M.; Laramée, A.; Poitras, F.; Lebrun, G.; Ozaki, T.; Ibrahim, H.; Légaré, F. Frequency domain optical parametric amplification. Nat. Commun. 2014, 5, 3643. [Google Scholar] [CrossRef] [PubMed]
- Harris, S.E. Chirp and compress: Toward single-cycle biphotons. Phys. Rev. Lett. 2007, 98, 063602. [Google Scholar] [CrossRef] [PubMed]
- Charbonneau-Lefort, M.; Afeyan, B.; Fejer, M.M. Optical parametric amplifiers using chirped quasi-phase-matching gratings. I: Practical design formulas. J. Opt. Soc. Am. B 2008, 25, 463–480. [Google Scholar] [CrossRef]
- Charbonneau-Lefort, M.; Afeyan, B.; Fejer, M.M. Optical parametric amplifiers using nonuniform quasi-phase-matched gratings. II: Space-time evolution of light pulses. J. Opt. Soc. Am. B 2008, 25, 680–697. [Google Scholar] [CrossRef]
- Phillips, C.R.; Fejer, M.M. Adiabatic optical parametric oscillators: Steady-state and dynamical behavior. Opt. Express 2012, 20, 2466–2482. [Google Scholar] [CrossRef]
- Phillips, C.R.; Langrock, C.; Chang, D.; Lin, Y.W.; Gallmann, L.; Fejer, M.M. Apodization of chirped quasi-phasematching devices. J. Opt. Soc. Am. B 2013, 30, 1551–1568. [Google Scholar] [CrossRef]
- Suchowski, H.; Krogen, P.R.; Huang, S.W.; Kärtner, F.X.; Moses, J. Octave-spanning coherent mid-IR generation via adiabatic difference frequency conversion. Opt. Express 2013, 21, 28892–28901. [Google Scholar] [CrossRef]
- Levitt, M.H.; Freeman, R. NMR population inversion using a composite pulse. J. Magn. Reson. 1979, 33, 473–476. [Google Scholar] [CrossRef]
- Shaka, A. Composite pulses for ultra-broadband spin inversion. Chem. Phys. Lett. 1985, 120, 201–205. [Google Scholar] [CrossRef]
- Shaka, A.; Pines, A. Symmetric phase-alternating composite pulses. J. Magn. Reson. 1987, 71, 495–503. [Google Scholar] [CrossRef][Green Version]
- Dubietis, A.; Jonusauskas, G.; Piskarskas, A. Powerful femtosecond pulse generation by chirped and stretched pulse parametric amplification in BBO. Opt. Commun. 1992, 88, 4437–4440. [Google Scholar] [CrossRef]
- Dubietis, A.; Butkus, R.; Piskarskas, A.P. Trends in chirped pulse optical parametric amplification. IEEE J. Sel. Topics Quantum Electr. 2006, 12, 163–172. [Google Scholar] [CrossRef]
- Deng, Y.; Schwartz, A.; Fattahi, H.; Ueffing, M.; Gu, X.; Ossiander, M.; Metzger, T.; Pervak, V.; Ishizuki, H.; Taira, T.; et al. Carrier-envelope-phase-stable 1.2 mJ, 1.5 cycle laser pulses at 2.1 μm. Opt. Lett. 2012, 37, 4973–4975. [Google Scholar] [CrossRef]
- Toth, G.; Palfalvi, L.; Tokodi, L.; Hebling, J.; Fülöp, J.A. Scalable broadband OPCPA in Lithium Niobate with signal angular dispersion. Opt. Commun. 2016, 370, 250–255. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Yariv, A.; Yeh, P. Photonics: Optical Electronics in Modern Communications, 6th ed.; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Shen, Y.R. The Principles of Nonlinear Optics; John Wiley and Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- Baumgartner, R.; Byer, R. Optical parametric amplification. IEEE J. Quantum Electron. 1979, 15, 432–444. [Google Scholar] [CrossRef]
- Jacobi Elliptic Functions. Available online: http://mathworld.wolfram.com/JacobiEllipticFunctions.html (accessed on 28 December 2019).
- Levitt, M.H. Composite pulses. Prog. Nucl. Magn. Reson. Spectrosc. 1986, 18, 61–122. [Google Scholar] [CrossRef]
- Freeman, R. Spin Choreography; Spektrum: Oxford, UK, 1997. [Google Scholar]
- Schmidt-Kaler, F.; Häffner, H.; Riebe, M.; Gulde, S.; Lancaster, G.P.T.; Deuschle, T.; Becher, C.; Roos, C.F.; Eschner, J.; Blatt, R. Realization of the Cirac–Zoller controlled-NOT quantum gate. Nature (Lond.) 2003, 422, 408–411. [Google Scholar] [CrossRef]
- Timoney, N.; Elman, V.; Glaser, S.; Weiss, C.; Johanning, M.; Neuhauser, W.; Wunderlich, C. Error-resistant single-qubit gates with trapped ions. Phys. Rev. A 2008, 77, 052334. [Google Scholar] [CrossRef]
- Torosov, B.T.; Guerin, S.; Vitanov, N.V. High-Fidelity Adiabatic Passage by Composite Sequences of Chirped Pulses. Phys. Rev. Lett. 2011, 106, 233001. [Google Scholar] [CrossRef] [PubMed]
- Schraft, D.; Halfmann, T.; Genov, G.T.; Vitanov, N.V. Experimental demonstration of composite adiabatic passage. Phys. Rev. A 2013, 88, 063406. [Google Scholar] [CrossRef]
- Genov, G.T.; Rangelov, A.A.; Vitanov, N.V. Efficient broadband frequency generation in composite crystals. J. Opt. 2014, 16, 062001. [Google Scholar] [CrossRef]
- Rangelov, A.A.; Vitanov, N.V.; Montemezzani, G. Robust and broadband frequency conversion in composite crystals with tailored segment widths and χ(2) nonlinearities of alternating signs. Opt. Lett. 2014, 39, 2959–2962. [Google Scholar] [CrossRef]
- Erlich, Y.; Rangelov, A.A.; Montemezzani, G.; Suchowski, H. Robust, efficient, and broadband SHG of ultrashort pulses in composite crystals. Opt. Lett. 2019, 44, 3837–3840. [Google Scholar] [CrossRef]
- Suchowski, H.; Porat, G.; Arie, A. Adiabatic processes in frequency conversion. Laser Photonics Rev. 2014, 8, 333–367. [Google Scholar] [CrossRef]
- Suchowski, H.; Oron, D.; Arie, A.; Silberberg, Y. Geometrical representation of sum frequency generation and adiabatic frequency conversion. Phys. Rev. A 2008, 78, 063821. [Google Scholar] [CrossRef]
- Nikogosyan, D.N. Nonlinar Optical Crystals; Springer: New York, NY, USA, 2005. [Google Scholar]
- Bach, F.; Mero, M.; Chou, M.-H.; Petrov, V. Laser induced damage studies of LiNbO3 using 1030-nm, ultrashort pulses at 10-1000 kHz. Opt. Mater. Express 2017, 7, 240–252. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, B.; Zhong, S.; Zhu, L. Damage threshold of lithium niobate crystal under single and multiple femtosecond laser pulses: Theoretical and experimental study. Appl. Phys. A 2016, 122, 582. [Google Scholar] [CrossRef]
- Allen, L.; Eberly, J.H. Optical Resonance and Two-Level Atoms; Dover: New York, NY, USA, 1987. [Google Scholar]
- Shore, B.W. The Theory of Coherent Atomic Excitation; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Vitanov, N.V.; Halfmann, T.; Shore, B.W.; Bergmann, K. Laser-induced population transfer by adiabatic passage techniques. Annu. Rev. Phys. Chem. 2001, 52, 763–809. [Google Scholar] [CrossRef] [PubMed]
- Vitanov, N.V.; Fleischhauer, M.; Shore, B.W.; Bergmann, K. Coherent manipulation of atoms and molecules by sequential laser pulses. Adv. At. Mol. Opt. Phys. 2001, 46, 55–190. [Google Scholar]
- Suchowski, H.; Prabhudesai, V.; Oron, D.; Arie, A.; Silberberg, Y. Robust efficient sum frequency conversion. Opt. Express 2009, 17, 12731–12740. [Google Scholar] [CrossRef] [PubMed]
- Suchowski, H.; Bruner, B.D.; Ganany-Padowicz, A.; Juwiler, I.; Arie, A.; Silberberg, Y. Adiabatic frequency conversion of ultrafast pulses. Appl. Phys. B 2011, 105, 697–702. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Slichter, C.P. Principles of Magnetic Resonance; Springer: Berlin, Germany, 1990. [Google Scholar]
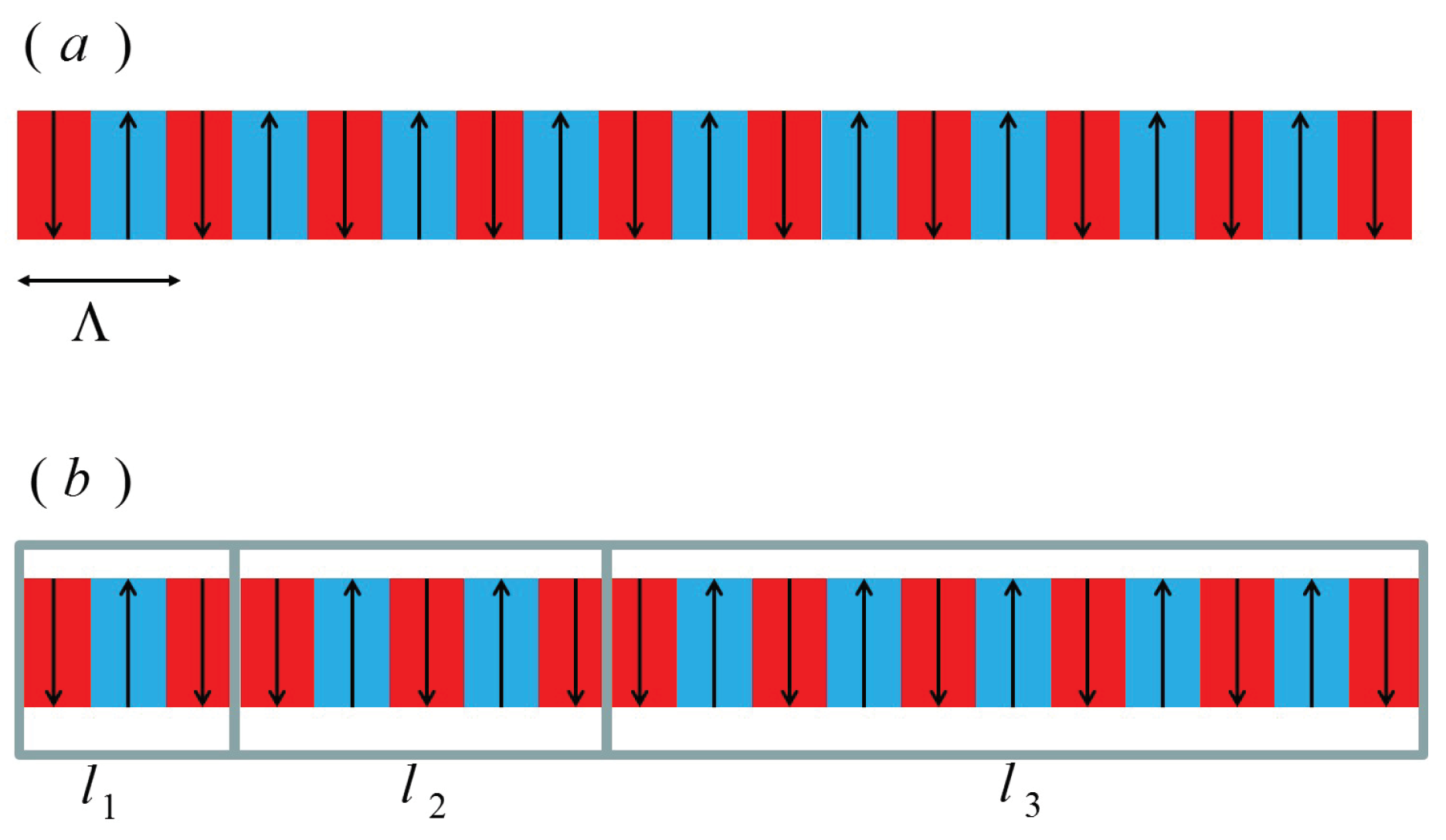
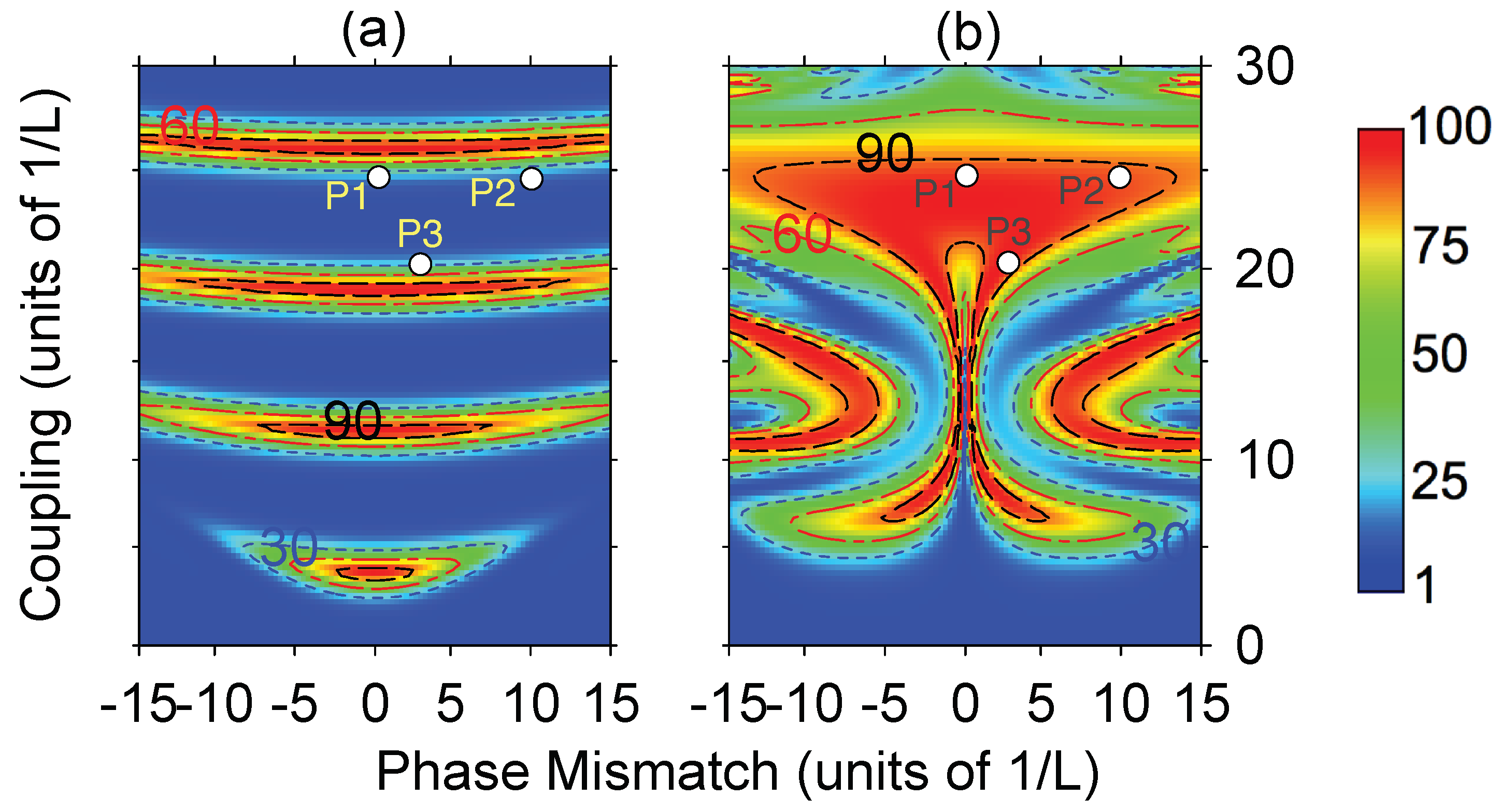
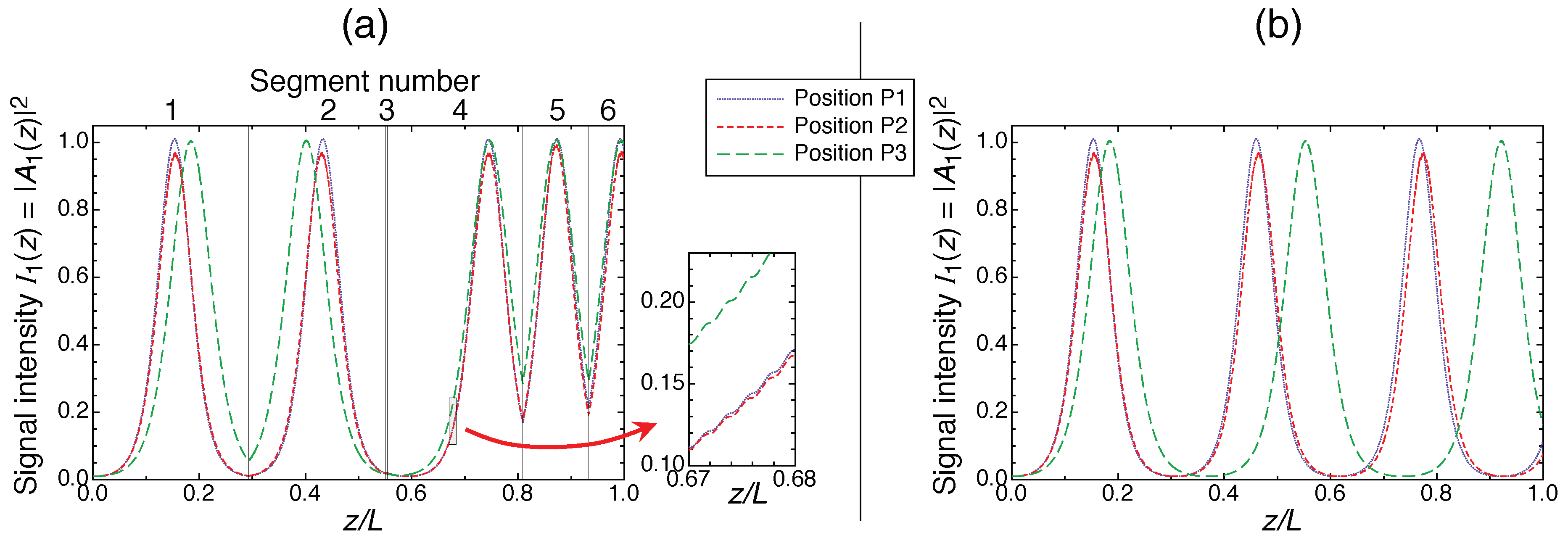
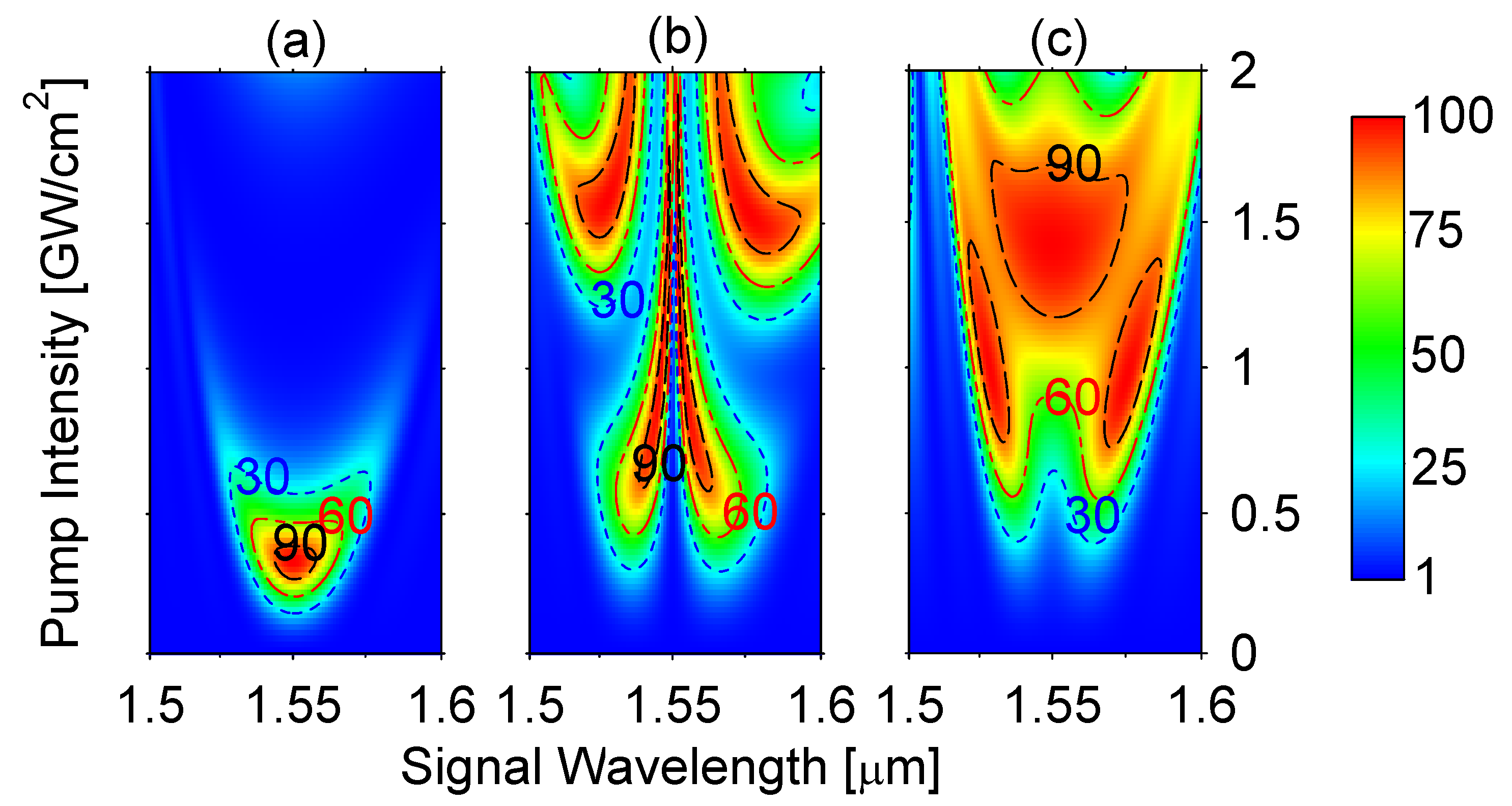

| N | Name | Segment Lengths in Units of L |
|---|---|---|
| 3 | 3 | 0.373; 0.594; 0.033 |
| 4 | 4 | 0.303; 0.522; 0.124; 0.051 |
| 6 | 6a | 0.293; 0.258; 0.003; 0.255; 0.124; 0.067 |
| 6 | 6b | 0.168; 0.035; 0.345; 0.023; 0.222; 0.207 |
| 6 | 6c | 0.223; 0.005; 0.404; 0.175; 0.113; 0.080 |
| 8 | 8 | 0.022; 0.064; 0.046; 0.205; 0.270; 0.096; 0.222; 0.075 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Mahmoud, M.; Rangelov, A.A.; Coda, V.; Montemezzani, G. Segmented Composite Optical Parametric Amplification. Appl. Sci. 2020, 10, 1220. https://doi.org/10.3390/app10041220
Al-Mahmoud M, Rangelov AA, Coda V, Montemezzani G. Segmented Composite Optical Parametric Amplification. Applied Sciences. 2020; 10(4):1220. https://doi.org/10.3390/app10041220
Chicago/Turabian StyleAl-Mahmoud, Mouhamad, Andon A. Rangelov, Virginie Coda, and Germano Montemezzani. 2020. "Segmented Composite Optical Parametric Amplification" Applied Sciences 10, no. 4: 1220. https://doi.org/10.3390/app10041220
APA StyleAl-Mahmoud, M., Rangelov, A. A., Coda, V., & Montemezzani, G. (2020). Segmented Composite Optical Parametric Amplification. Applied Sciences, 10(4), 1220. https://doi.org/10.3390/app10041220






