Dynamic Analysis and Security Characteristics of Carrier-Based Aircraft Arresting in Yaw Condition
Abstract
:1. Introduction
2. Arresting Dynamics Model of Carrier Aircraft
2.1. Research Object
2.2. Drag Force Model of Carrier Aircraft
- The runway is a plane, and the aircraft’s head is parallel to the runway plane;
- In the process of arresting, the vibration after the engagement of the hook and cable is not considered, and the sum of forces in the cable (TL and TR) are shown in the exact opposite direction of aircraft movement;
- The influence of the vertical height of the carrier aircraft on the arresting resistance is not considered.
2.3. Calculation Model of Arresting Device
3. Calculation Model of Kink-Wave Propagation
3.1. Model Assumptions
- There is no relative sliding between the arresting hook and the arresting cable;
- The component force of the arresting hook in the vertical direction is not considered;
- At any time, the tension of the arresting cable on one side of the arresting hook is the same everywhere;
- It is assumed that the arresting cable is the same cable with the same material;
- The arresting cable is in the linear elastic range during the arresting process.
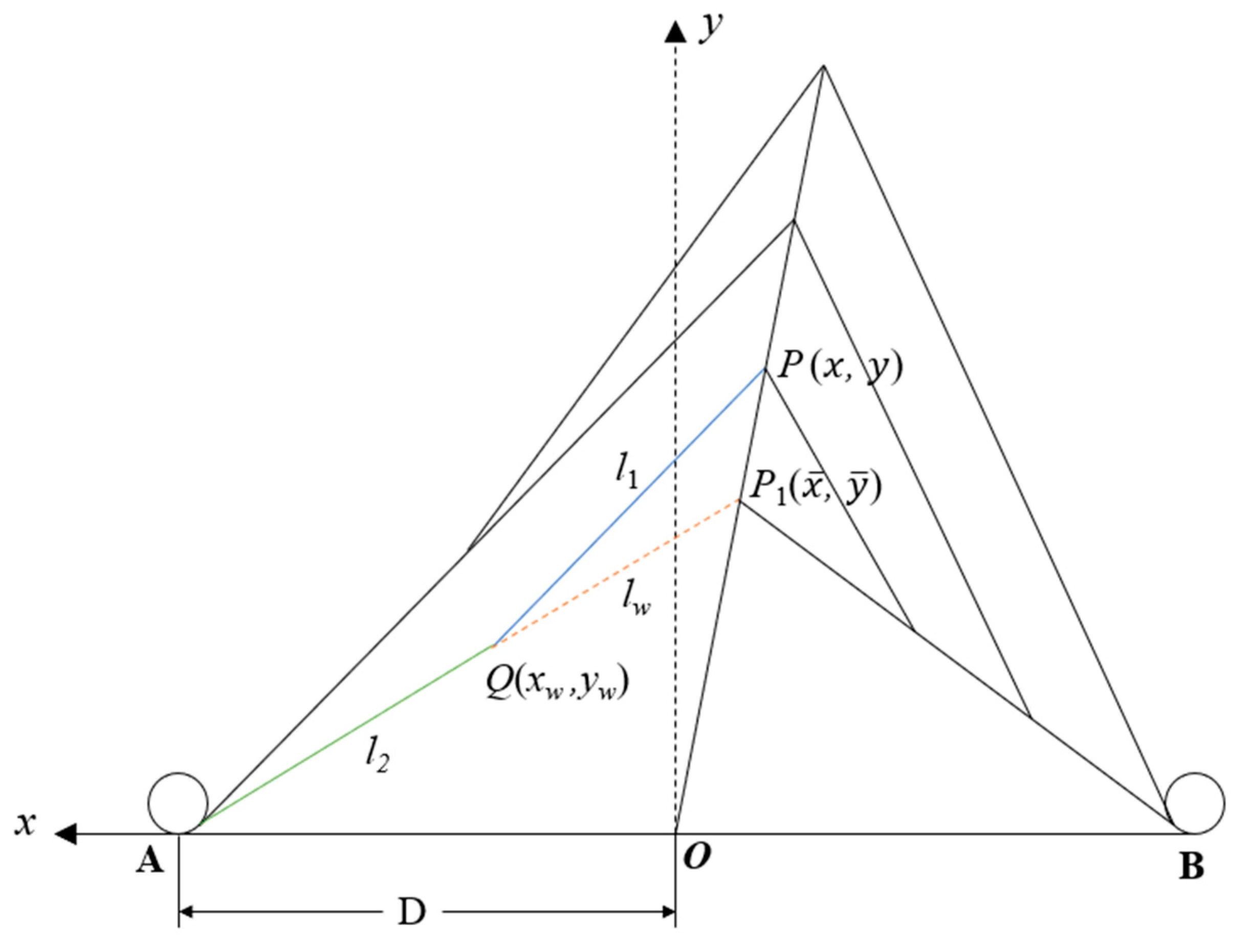
3.2. Model Comparison of Centering and Yaw Arrest
3.3. Calculation Method of Kink-Wave
4. Model Checking
4.1. Model Solving Process
4.2. Model Validation
5. Calculation and Analysis
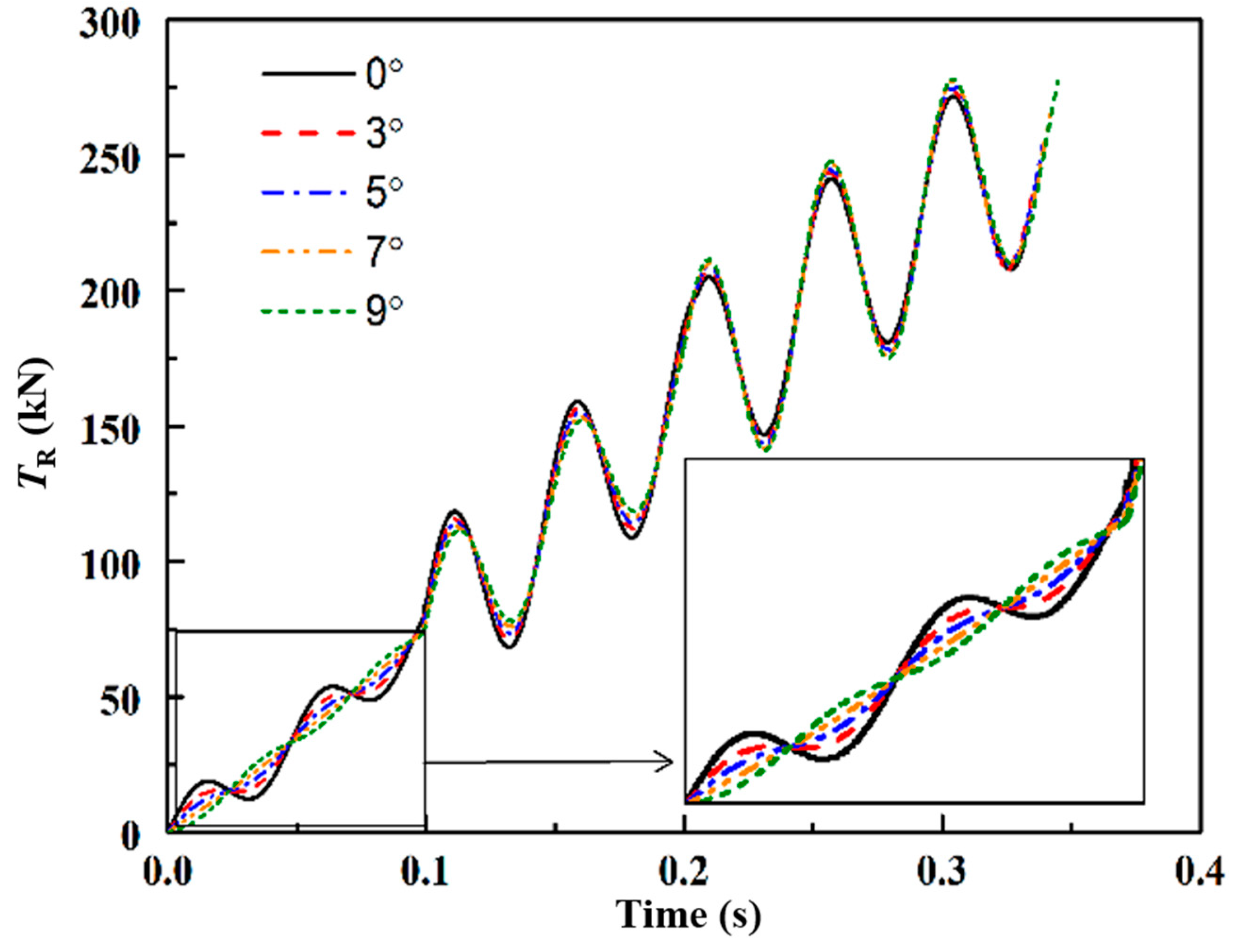
5.1. The Influence of Yaw Angle on Kink-Wave
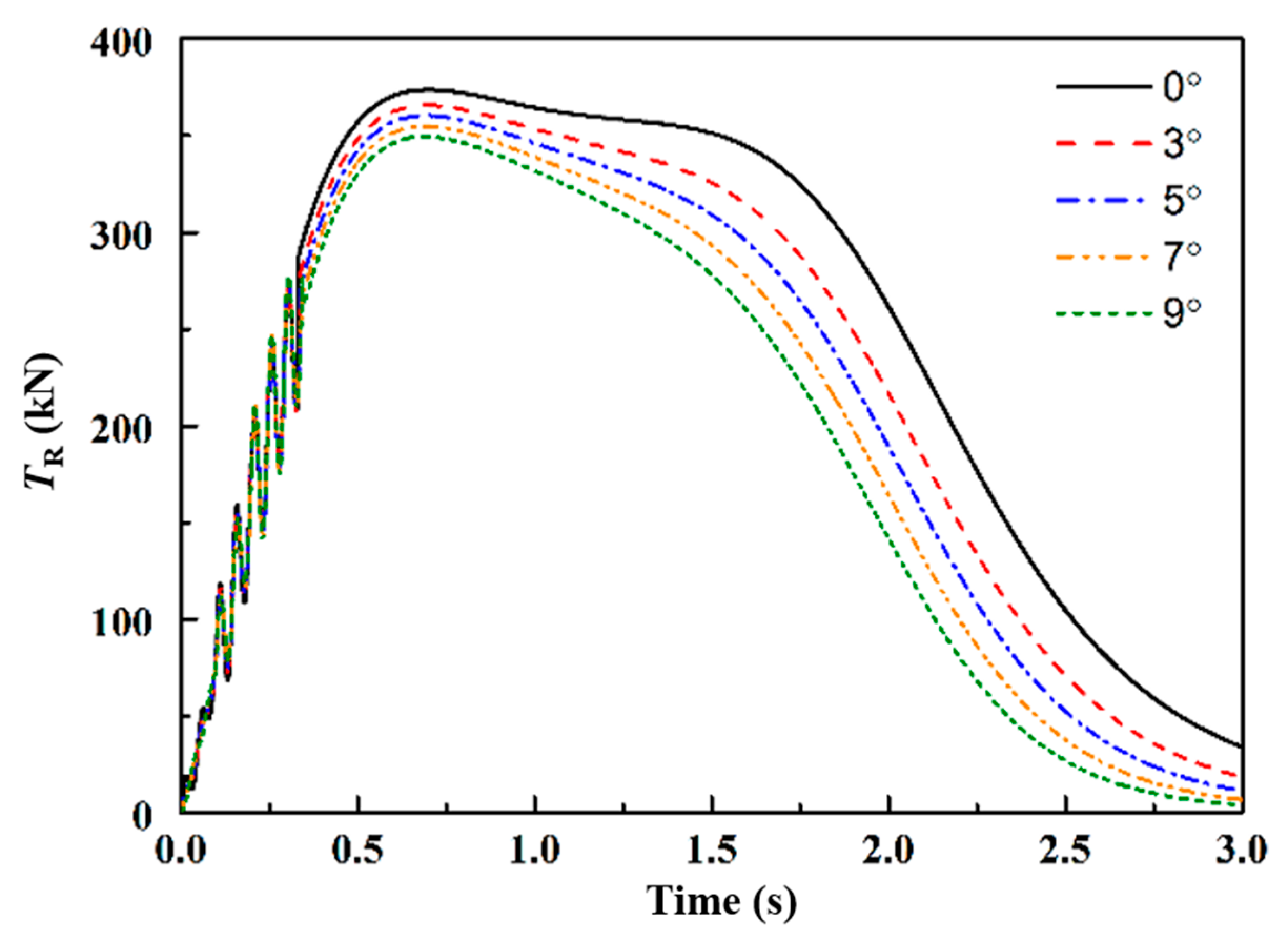
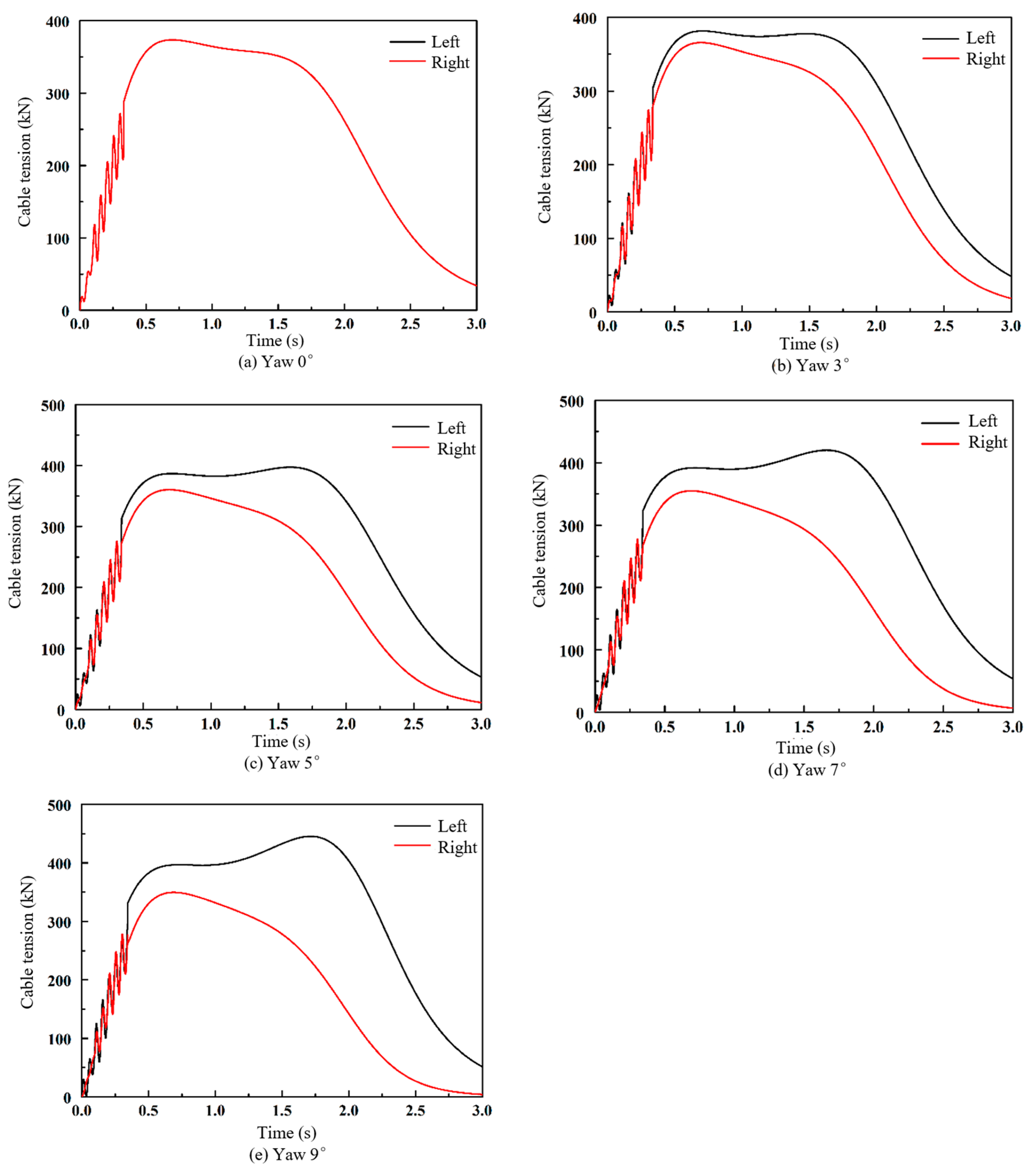
5.2. The Influence of Yaw Angle on the Tension of Arresting Cable
5.3. The Influence of Yaw Angle on the Performance of the Arresting System
5.4. The Influence of Yaw Angle on Arresting Safety
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, Y.D. Review of the Carrier Approach Criteria; National Defense Industry Press: Beijing, China, 2006. [Google Scholar]
- Neves, M.A.S.; Rodríguez, C.A. On un-stable ship motions resulting from strong non-linear coupling. Ocean Eng. 2006, 33, 1853–1883. [Google Scholar] [CrossRef]
- Thomas, R.; Stephen, C.; Marshell, H. Review of the Carrier Approach Criteria for Carrier-Based Aircraft Phase I; Naval Air Warfare Center Aircraft Division Patuxent River: Saint Mary’s County, MD, USA, 2002. [Google Scholar]
- Lawrence, J.T. Milestones and developments in US naval carrier aviation-part II: AIAA-2005-6120. In Reston: AIAA. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar]
- Jones, L.W. Development of Curves for Estimating Aircraft Arresting Hook Loads: ADA119551; Air Force Flight Test Center, Edwards Air Force Base: Edwards AFB, CA, USA, 1982; pp. 15–42. [Google Scholar]
- Naval Air Engineering Center. MIL-STD-2066(AS) Military Standard: Catapulting and Arresting Gear Forcing Functions for Aircraft Structural Design; Naval Air Systems Command, Department of the Navy: Manchester Township, NJ, USA, 1981. [Google Scholar]
- Department of the Air Force. Guide to Mobile Aircraft Arresting System Installation: Air Force Handbook 10–222; Secretary of the Air Force Washington: Washington, DC, USA, 2000; Volume 8, pp. 19–174. [Google Scholar]
- Thomlinson, J. A Study of the Aircraft Arresting Hook Bounce Problem. The Principal Director of Scientific Research (Air); Her majesty’s Stationery Office: London, UK, 1954. [Google Scholar]
- Taylor, R.T. An Experimental Investigation to Determine the Effect of Speed-Brake Position on the Longitudinal Stability and Trim of a Swept-Wing Fighter Airplane, 19980235623; Langley Re-search Center: Hampton, VA, USA, 1959. [Google Scholar]
- Anderson, S.B.; Cooper, G.E.; Faye, A.E., Jr. Flight Measurements of the Effect of a Controllable Thrust Reverser on the Flight Characteristics of a Single-Engine Jet Airplane, 19980228232; Ames Research Center: Mountain View, CA, USA, 1959. [Google Scholar]
- Hsin, C. Arrested Landing Studies for STOL aircraft, A73-17627 (AH); American Institute of Aeronautics and Astronautics, Annual Meeting and Technical Display: Washington, DC, USA, 1973. [Google Scholar]
- Engineered Arresting Systems Corporation. Safety Bulletin; Engineering Arresting System Corporation: Plasisir Credex, France, 2004. [Google Scholar]
- Zhang, S.S.; Jin, D.P. Nonlinear optimal control of aircraft arresting process. Acta Aeronaut. Astronaut. Sinica 2009, 30, 849–854. [Google Scholar]
- Zhang, Z.K.; Nie, H.; Yu, H. Dynamics Analysis for Aircraft Arresting with Yawing and Off-center. Adv. Aeronaut. Sci. Eng. 2010, 1, 327–332. [Google Scholar]
- Peng, Y.M.; Nie, H.; Zhang, M.; Wei, X.H. Dynamics analysis of arresting hook following engagement of an arresting cable in yaw condition. Acta Aeronaut. Astronaut. Sinica 2015, 36, 1876–1884. [Google Scholar]
- Zhang, X.X.; Zhang, Y.X.; Liu, Y. Method of Arresting Cable Tension Control. J. Natl. Univ. Def. Technol. 2016. [Google Scholar] [CrossRef]
- Zhu, Q.D.; Wen, Z.X.; Zhang, Z. Kinetic Modeling and Simulation of Shipboard Arresting System. Acta Aero-Naut. Astronaut. Sinica 2012, 33, 520–529. [Google Scholar]
- Liu, G.; Nie, H. Dynamics analysis for aircraft ar-resting based on absorbing aircraft kinetic energy. China Mech. Eng. 2009, 20, 450–454. [Google Scholar]
- George, M.L. Development of Mathematical Performance Prediction Model for Rotary–Hydraulic-Type Arresting Gears. AD893157; Navy Air Test Facility, Naval Air Station Lakehurst: Manchester Township, NJ, USA, 1972; pp. 5–27. [Google Scholar]
- Zhang, P.; Jin, D.P. Control of Arresting Process for Carrier Aircraft Considering Kink-wave. Acta Aero-Naut. Astronaut. Sinica 2011, 32, 2008–2015. [Google Scholar]
- Theriault, L.M.; Swienciski, H.J. Aircraft Compatibility and Evaluation of the Mark 7 Mod 3 Arresting Gear; Navil Air Test Facility Lakehursut N J: Saint Mary’s County, MD, USA, 1968; pp. 23–65. [Google Scholar]
- Naval Air Systems Command. NAVAIR 00-80T-105CV NATOPS Manual; Naval Air System Command: Patuxent River, MD, USA, 2009. [Google Scholar]















| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Mass of aircraft (kg) | 22,680 | Accumulator air bag volume (m3) | 2 |
| Landing speed (m·s−1) | 63 | Initial pressure of accumulator (MPa) | 3 |
| Maximum stopping distance (m) | 104 | Accumulator piston mass (kg) | 10 |
| Piston area of energy absorber (m2) | 0.28 | Accumulator piston area (m2) | 1 |
| Piston stroke of energy absorber (m) | 5 | Distance between pulleys on deck (m) | 34 |
| Yaw Angle | First Kink-Wave (s) | Second Kink-Wave (s) | Third Kink-Wave (s) | |
|---|---|---|---|---|
| 0° | Port | 0.0994 | 0.2055 | 0.3320 |
| Starboard | 0.0994 | 0.2055 | 0.3320 | |
| 3° | Port | 0.0993 | 0.2071 | 0.3360 |
| Starboard | 0.0992 | 0.2035 | 0.3264 | |
| 5° | Port | 0.0993 | 0.2083 | 0.3390 |
| Starboard | 0.0992 | 0.2023 | 0.3227 | |
| 7° | Port | 0.0993 | 0.2094 | 0.3419 |
| Starboard | 0.0992 | 0.2010 | 0.3189 | |
| 9° | Port | 0.0993 | 0.2106 | 0.3450 |
| Starboard | 0.0992 | 0.1998 | 0.3152 | |
| Parameters | Centering | Yaw 3° | Yaw 5° | Yaw 7° | Yaw 9° |
|---|---|---|---|---|---|
| Port maximum belt tension (kN) | 373.76 | 381.63 | 397.25 | 420.06 | 445.31 |
| Starboard maximum belt tension (kN) | 373.76 | 365.74 | 360.35 | 354.93 | 349.50 |
| Parameters | Centering | Yaw 3° | Yaw 5° | Yaw 7° | Yaw 9° |
|---|---|---|---|---|---|
| Maximum arresting force (kN) | 698.78 | 698.76 | 698.72 | 698.68 | 698.61 |
| Maximum acceleration (m·s−2) | 30.81 | 30.81 | 30.81 | 30.80 | 30.80 |
| Arresting distance (m) | 86.76 | 86.62 | 86.39 | 86.06 | 85.38 |
| Parameters | Centering | Yaw 3° | Yaw 5° | Yaw 7° | Yaw 9° |
|---|---|---|---|---|---|
| Arresting offset distance (m) | 0 | 4.53 | 7.53 | 10.49 | 13.36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Xie, P.; Wei, X.; Nie, H. Dynamic Analysis and Security Characteristics of Carrier-Based Aircraft Arresting in Yaw Condition. Appl. Sci. 2020, 10, 1253. https://doi.org/10.3390/app10041253
Peng Y, Xie P, Wei X, Nie H. Dynamic Analysis and Security Characteristics of Carrier-Based Aircraft Arresting in Yaw Condition. Applied Sciences. 2020; 10(4):1253. https://doi.org/10.3390/app10041253
Chicago/Turabian StylePeng, Yiming, Pengpeng Xie, Xiaohui Wei, and Hong Nie. 2020. "Dynamic Analysis and Security Characteristics of Carrier-Based Aircraft Arresting in Yaw Condition" Applied Sciences 10, no. 4: 1253. https://doi.org/10.3390/app10041253
APA StylePeng, Y., Xie, P., Wei, X., & Nie, H. (2020). Dynamic Analysis and Security Characteristics of Carrier-Based Aircraft Arresting in Yaw Condition. Applied Sciences, 10(4), 1253. https://doi.org/10.3390/app10041253






