Simplified Theoretical Model for Temperature Evaluation in Tissue–Implant–Bone Systems during Ultrasound Diathermy
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Evaluation of Pressure Fields
2.2. Evaluation of Temperature Fields
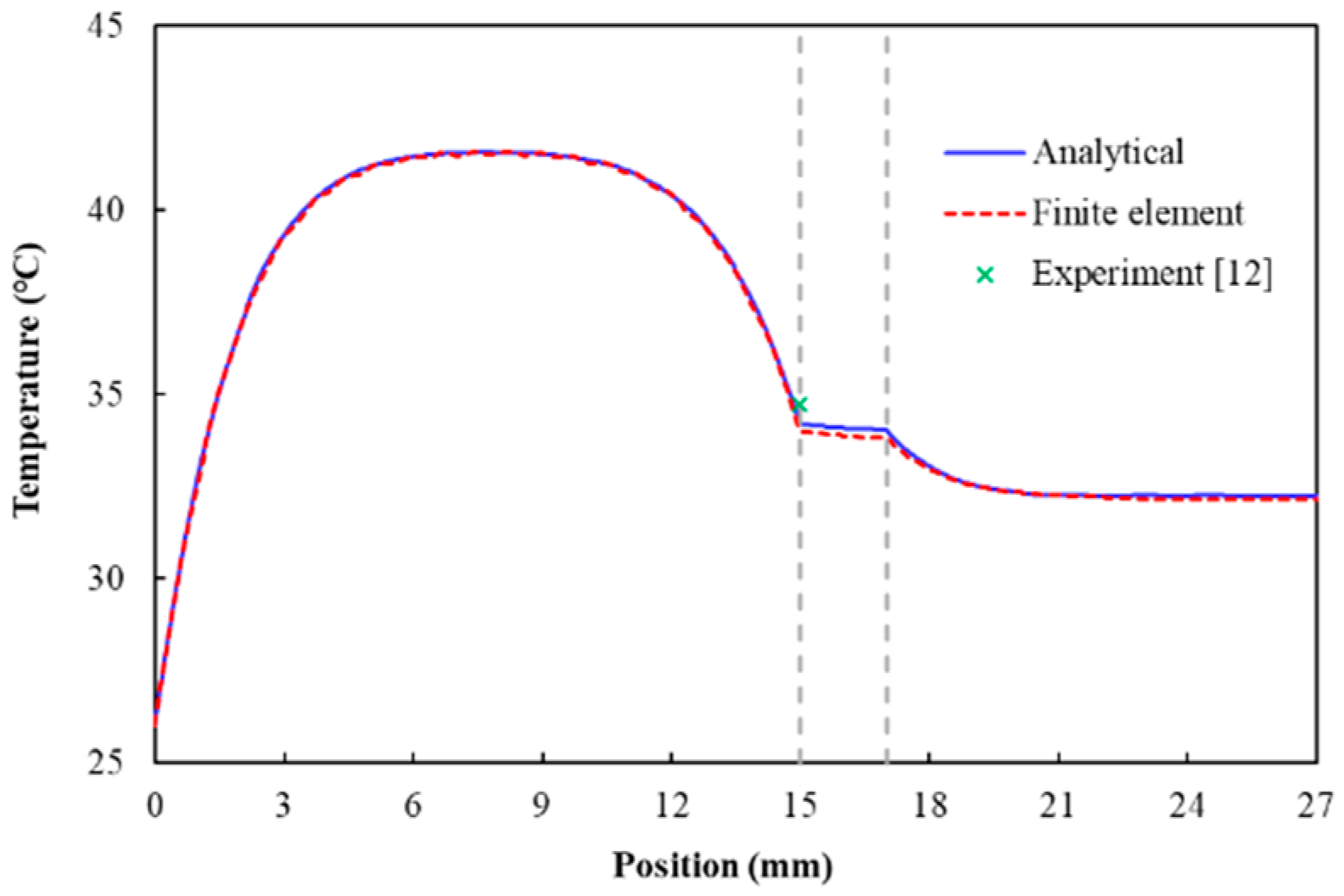
3. Results and Discussions
3.1. Ultrasound Operation Frequency
3.2. Tissue Thickness
3.3. Implant Materials
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Cameron, M.H. Physical Agents in Rehabilitation: From Research to Practice, 4th ed.; Elsevier Health Sciences: USA, 2012; pp. 185–214. [Google Scholar]
- Lehmann, J.F.; Lane, K.E.; Bell, J.W.; Brunner, G.D. Influence of surgical metal implants on the distribution of the intensity in the ultrasonic field. Arch. Phys. Med. Rehabil. 1958, 39, 756–760. [Google Scholar] [CrossRef]
- Rose, S.; Draper, D.O.; Schulthies, S.S.; Durrant, E. The stretching window part two: Rate of thermal decay in deep muscle following 1-MHz ultrasound. J. Athl. Train. 1996, 31, 139–143. [Google Scholar] [CrossRef]
- Denegar, C.R.; Saliba, E.; Saliba, S. Therapeutic Modalities for Musculoskeletal Injuries, 4th ed.; Human Kinetics: Champaign, IL, USA, 2015; pp. 1–42. [Google Scholar]
- Morishita, K.; Karasuno, H.; Yokoi, Y.; Morozumi, K.; Ogihara, H.; Ito, T.; Hanaoka, M.; Fujiwara, T.; Fujimoto, T.; Abe, K. Effects of therapeutic ultrasound on range of motion and stretch pain. J. Phys. Ther. Sci. 2014, 26, 711–715. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Analan, P.D.; Leblebici, B.; Adam, M. Effects of therapeutic ultrasound and exercise on pain, function, and isokinetic shoulder rotator strength of patients with rotator cuff disease. J. Phys. Ther. Sci. 2015, 27, 3113–3117. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Xie, Y.; Luo, X.; Ji, Q.; Lu, C.; He, C.; Wang, P. Effects of therapeutic ultrasound on pain, physical functions and safety outcomes in patients with knee osteoarthritis: A systematic review and meta-analysis. Clin. Rehabil 2016, 30, 960–971. [Google Scholar] [CrossRef] [PubMed]
- Baker, K.G.; Robertson, V.J.; Duck, F.A. A review of therapeutic ultrasound: Biophysical effects. J. Womens Health Phys. Ther. 2010, 34, 111–118. [Google Scholar] [CrossRef]
- Gersten, J.W. Effect of metallic objects on temperature rises produced in tissue by ultrasound. Am. J. Phys. Med. Rehabil. 1958, 37, 75–82. [Google Scholar] [CrossRef]
- Lehmann, J.F.; Brunner, G.D.; McMillan, J.A. Influence of surgical metal implants on the temperature distribution in thigh specimens exposed to ultrasound. Arch. Phys. Med. Rehabil. 1958, 39, 692–695. [Google Scholar] [CrossRef]
- Lehmann, J.F.; Brunne, G.D.; Martinis, A.J.; McMillan, J.A. Ultrasonic effects as demonstrated in live pigs with surgical metallic implants. Arch. Phys. Med. Rehabil. 1659, 40, 483–488. [Google Scholar] [CrossRef]
- Sun, M.K.; Shieh, J.; Chen, C.S.; Chiang, H.G.; Huang, C.W.; Chen, W.S. Effects of an implant on temperature distribution in tissue during ultrasound diathermy. Ultrason. Sonochem. 2016, 32, 44–53. [Google Scholar] [CrossRef]
- Andrades, A.O.; Mazzanti, A.; Beckmann, D.V.; Aiello, G.; Chaves, R.O.; Santos, R.P. Heating produced by therapeutic ultrasound in the presence of a metal plate in the femur of canine cadavers. Arq. Bras. Med. Vet. Zootec. 2014, 66, 1343–1350. [Google Scholar] [CrossRef]
- Hsu, S.K.; Huang, W.T.; Liu, B.S.; Li, S.M.; Chen, H.T.; Chang, C.J. Effects of near-field ultrasound stimulation on new bone formation and osseointegration of dental titanium implants in vitro and in vivo. Ultrasound Med. Biol. 2011, 37, 403–416. [Google Scholar] [CrossRef] [PubMed]
- Schröder, C.; Steinbrück, A.; Müller, T.; Woiczinski, M.; Chevalier, Y.; Weber, P.; Müller, P.E.; Jansson, V. Rapid prototyping for in vitro knee rig investigations of prosthetized knee biomechanics: Comparison with cobalt-chromium alloy implant material. BioMed Res. Int. 2015, 2015, 185142. [Google Scholar] [CrossRef] [Green Version]
- Öztürk, S.; Sengezer, M.; Zor, F. Reconstruction of acquired partial auricular defects by porous polyethylene implant and superficial temporoparietal fascia flap in adult patients. Plast. Reconstr. Surg. 2006, 118, 1349–1357. [Google Scholar] [CrossRef]
- Vainionpää, S.; Rokkanen, P.; Törmälä, P. Surgical applications of biodegradable polymers in human tissues. Prog. Polym. Sci. 1989, 14, 679–716. [Google Scholar] [CrossRef]
- Kienapfel, H.; Sprey, C.; Wilke, A.; Griss, P. Implant fixation by bone ingrowth. J. Arthroplast. 1999, 14, 355–368. [Google Scholar] [CrossRef]
- Iwai, T.; Harada, Y.; Imura, K.; Iwabuchi, S.; Murai, J.; Hiramatsu, K.; Myoui, A.; Yoshikawa, H.; Tsumaki, N. Low-intensity pulsed ultrasound increases bone ingrowth into porous hydroxyapatite ceramic. J. Bone Miner. Metab. 2007, 25, 392–399. [Google Scholar] [CrossRef]
- Adams, T.S.; Crook, T.; Cadier, M.A. A late complication following the insertion of hydrogel breast implants. J. Plast. Reconstr. Aesthet. Surg. 2007, 60, 210–212. [Google Scholar] [CrossRef]
- Lints, M. Optimised Signal Processing for Nonlinear Ultrasonic Nondestructive Testing of Complex Materials and Biological Tissues. Ph.D. Thesis, Tallinn University of Technology, Tallinn, Estonia, 2017. [Google Scholar]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 4th ed.; John Wiley & Sons: New York, NY, USA, 1999; pp. 171–203. [Google Scholar]
- Zhou, Y. Principles and Applications of Therapeutic Ultrasound in Healthcare; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Oxfordshire, UK, 2016; p. 129. [Google Scholar]
- Shaw, A.; Hodnett, M. Calibration and measurement issues for therapeutic ultrasound. Ultrasonics 2008, 48, 234–252. [Google Scholar] [CrossRef]
- Blackstock, D.T. Fundamentals of Physical Acoustics; John Wiley & Sons: New York, NY, USA, 2000; pp. 163–172. [Google Scholar]
- Meaney, P.M.; Clarke, R.L.; Ter Haar, G.R.; Rivens, I.H. A 3-D finite-element model for computation of temperature profiles and regions of thermal damage during focused ultrasound surgery exposures. Ultrasound Med. Biol. 1998, 24, 1489–1499. [Google Scholar] [CrossRef]
- Schimmel, W.P.; Beck, J.V.; Donaldson, A.B. Effective thermal diffusivity for a multimaterial composite laminate. J. Heat Transfer 1977, 99, 466–470. [Google Scholar] [CrossRef]
- Hahn, D.W.; Özisik, M.N. Heat Conduction, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2012; pp. 393–430. [Google Scholar]
- SIMULIA-Abaqus 2017 User’s Manual; Dassault Systemes Simulia: Providence, RI, USA, 2017.
- Xi, F.; Jin, K.; Cai, L.; Geng, H.; Tan, Y.; Li, J. Sound velocity of tantalum under shock compression in the 18–142 GPa range. J. Appl. Phys. 2015, 117, 185901. [Google Scholar] [CrossRef]
- Veiga, C.; Davim, J.P.; Loureiro, A.J.R. Properties and applications of titanium alloys: A brief review. Rev. Adv. Mater. Sci. 2012, 32, 133–148. [Google Scholar] [CrossRef]
- Baron, S.; Desmond, D.; Ahearne, E. The fundamental mechanisms of wear of cemented carbide in continuous cutting of medical grade cobalt chromium alloy (ASTM F75). Wear 2019, 424, 89–96. [Google Scholar] [CrossRef]
- Grill, R.; Gnadenberger, A. Niobium as mint metal: Production–properties–processing. Int. J. Refract. Metals Hard Mater. 2006, 24, 275–282. [Google Scholar] [CrossRef]
- Guo, S.Q. Densification of ZrB2-based composites and their mechanical and physical properties: A review. J. Eur. Ceram. Soc. 2009, 29, 995–1011. [Google Scholar] [CrossRef]
- Zhang, Y.; Malzbender, J.; Mack, D.E.; Jarligo, M.O.; Cao, X.; Li, Q.; Vaßen, R.; Stöver, D. Mechanical properties of zirconia composite ceramics. Ceram. Int. 2013, 39, 7595–7603. [Google Scholar] [CrossRef]












| Hydrogel Phantom | 316 Stainless Steel | Bone | |
|---|---|---|---|
| Density (kg/m3) | 1190 | 8000 | 1975 |
| Specific heat (J/kg°C) | 3431 | 502 | 1313 |
| Sound velocity (m/s) | 1512 | 5600 | 3476 |
| Thermal conductivity (W/m°C) | 0.6 | 16.27 | 0.32 |
| Attenuation coefficient (dB/m) | 54 | 110 | 690 |
| Polyethylene (POL) [12] | Tantalum (TAN) [30] | Titanium Alloys (TIT) [31] | |
|---|---|---|---|
| Density (kg/m3) | 960 | 16,650 | 4470 |
| Specific heat (J/kg°C) | 2300 | 141.8 | 561 |
| Sound velocity (m/s) | 2460 | 5374 | 6132 |
| Thermal conductivity (W/m°C) | 0.442 | 57 | 7.2 |
| Attenuation coefficient (dB/m) | 66 | 144 | 150 |
| Co-Cr-Mo Alloy (CCM) [32] | Niobium (NIO) [33] | Zirconia Oxide (ZO) [34,35] | |
|---|---|---|---|
| Density (kg/m3) | 8768 | 8570 | 6050 |
| Specific heat (J/kg°C) | 452 | 265 | 418 |
| Sound velocity (m/s) | 4750 | 3480 | 7040 |
| Thermal conductivity (W/m°C) | 14.8 | 53.70 | 2.7 |
| Attenuation coefficient (dB/m) | 230 | 347 | 120 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-W. Simplified Theoretical Model for Temperature Evaluation in Tissue–Implant–Bone Systems during Ultrasound Diathermy. Appl. Sci. 2020, 10, 1306. https://doi.org/10.3390/app10041306
Huang C-W. Simplified Theoretical Model for Temperature Evaluation in Tissue–Implant–Bone Systems during Ultrasound Diathermy. Applied Sciences. 2020; 10(4):1306. https://doi.org/10.3390/app10041306
Chicago/Turabian StyleHuang, Chang-Wei. 2020. "Simplified Theoretical Model for Temperature Evaluation in Tissue–Implant–Bone Systems during Ultrasound Diathermy" Applied Sciences 10, no. 4: 1306. https://doi.org/10.3390/app10041306
APA StyleHuang, C.-W. (2020). Simplified Theoretical Model for Temperature Evaluation in Tissue–Implant–Bone Systems during Ultrasound Diathermy. Applied Sciences, 10(4), 1306. https://doi.org/10.3390/app10041306




