Adaptive Neural Fault-Tolerant Control for the Yaw Control of UAV Helicopters with Input Saturation and Full-State Constraints
Abstract
1. Introduction
2. Main Results
2.1. UAV Yaw-Channel Model
2.2. Normal Model
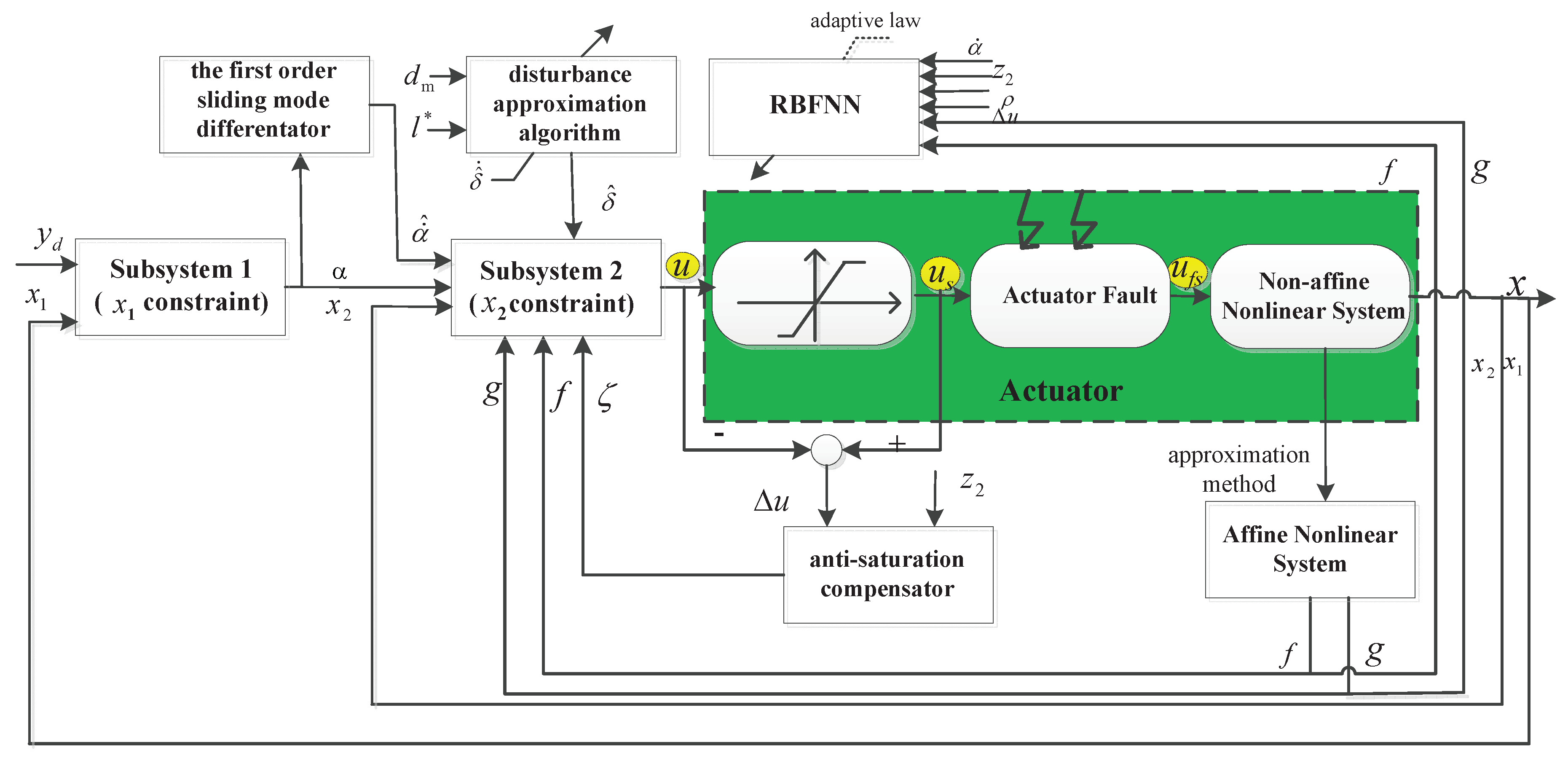
2.3. Controller Design and Stability Analysis
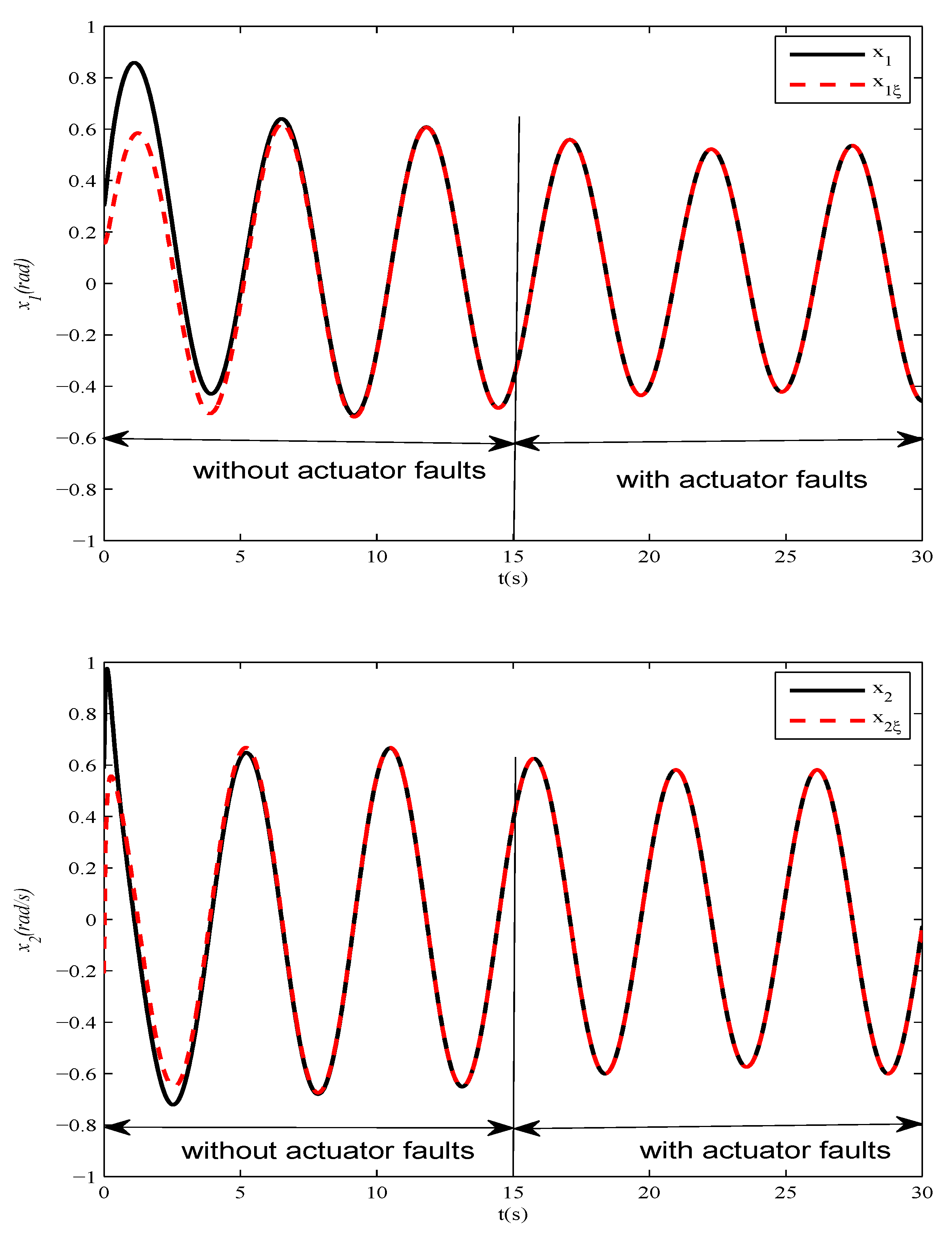
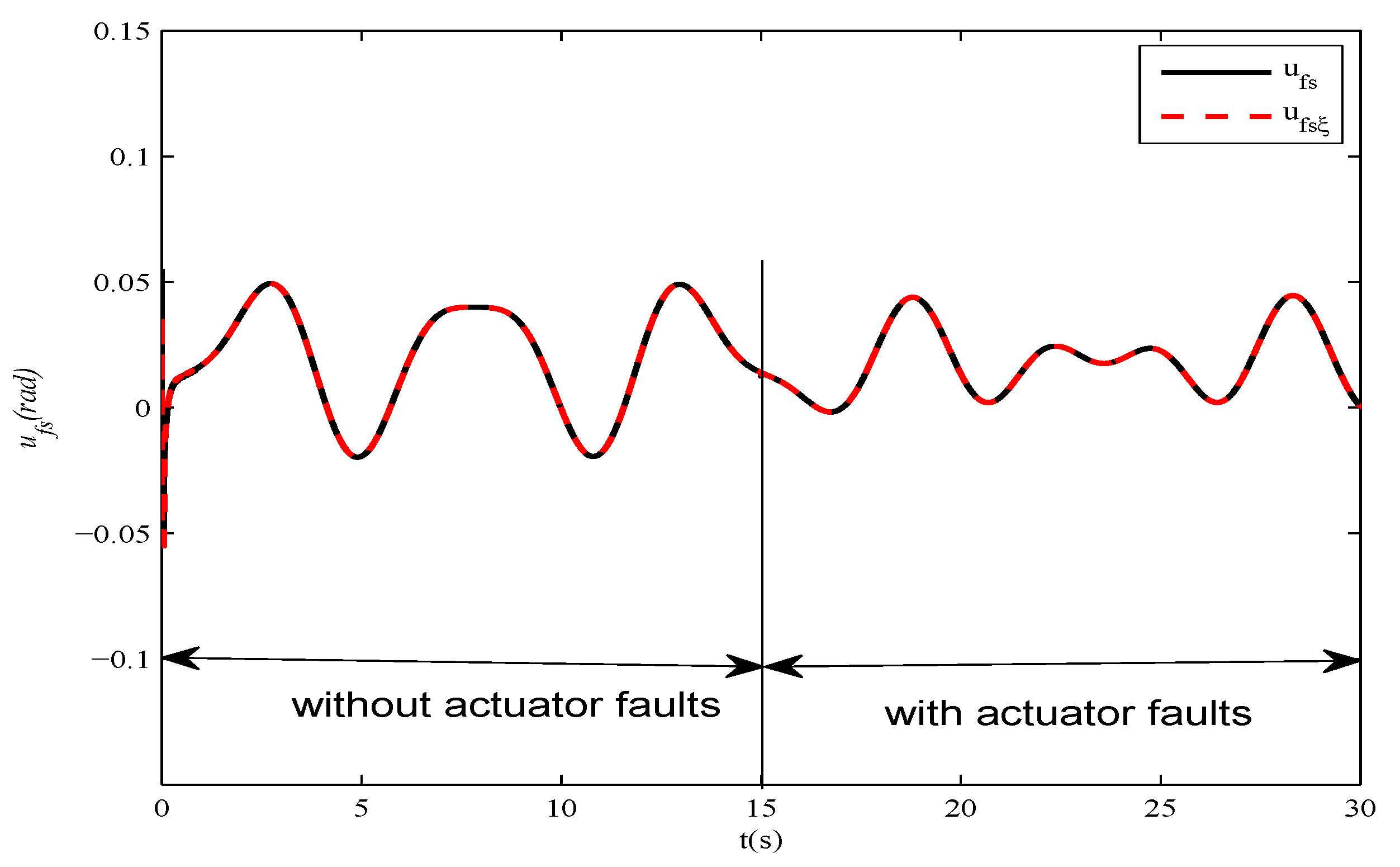
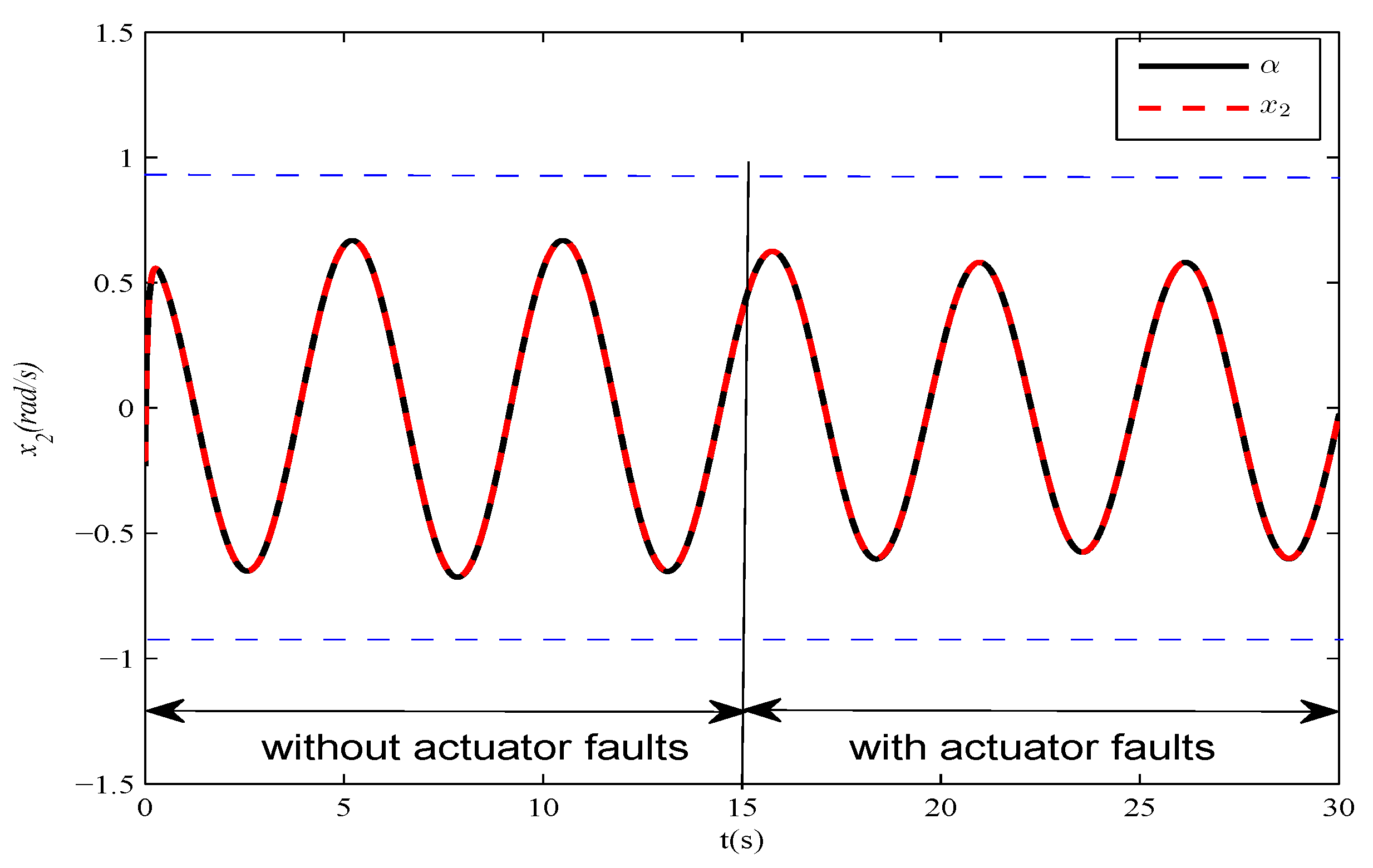
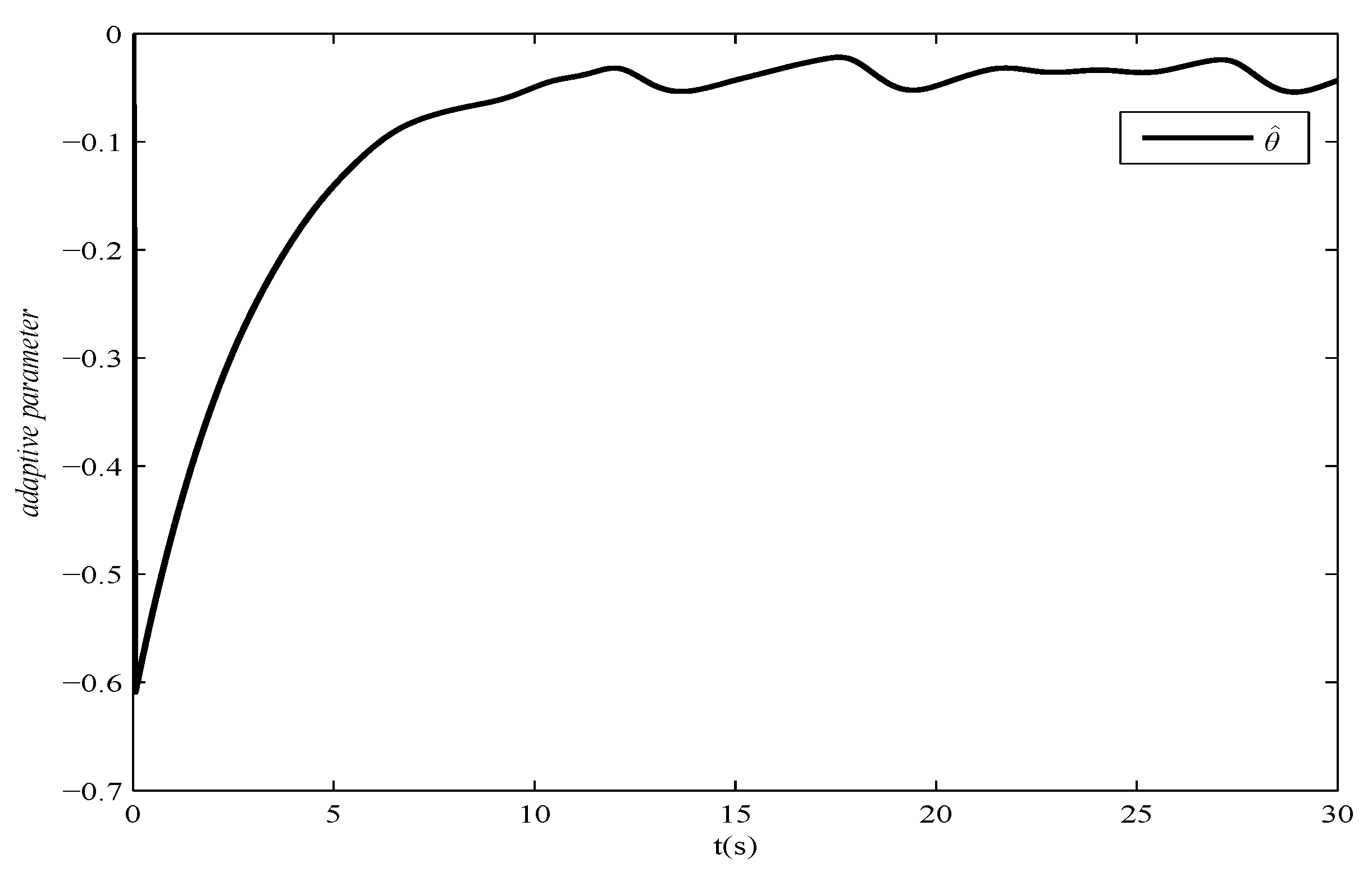
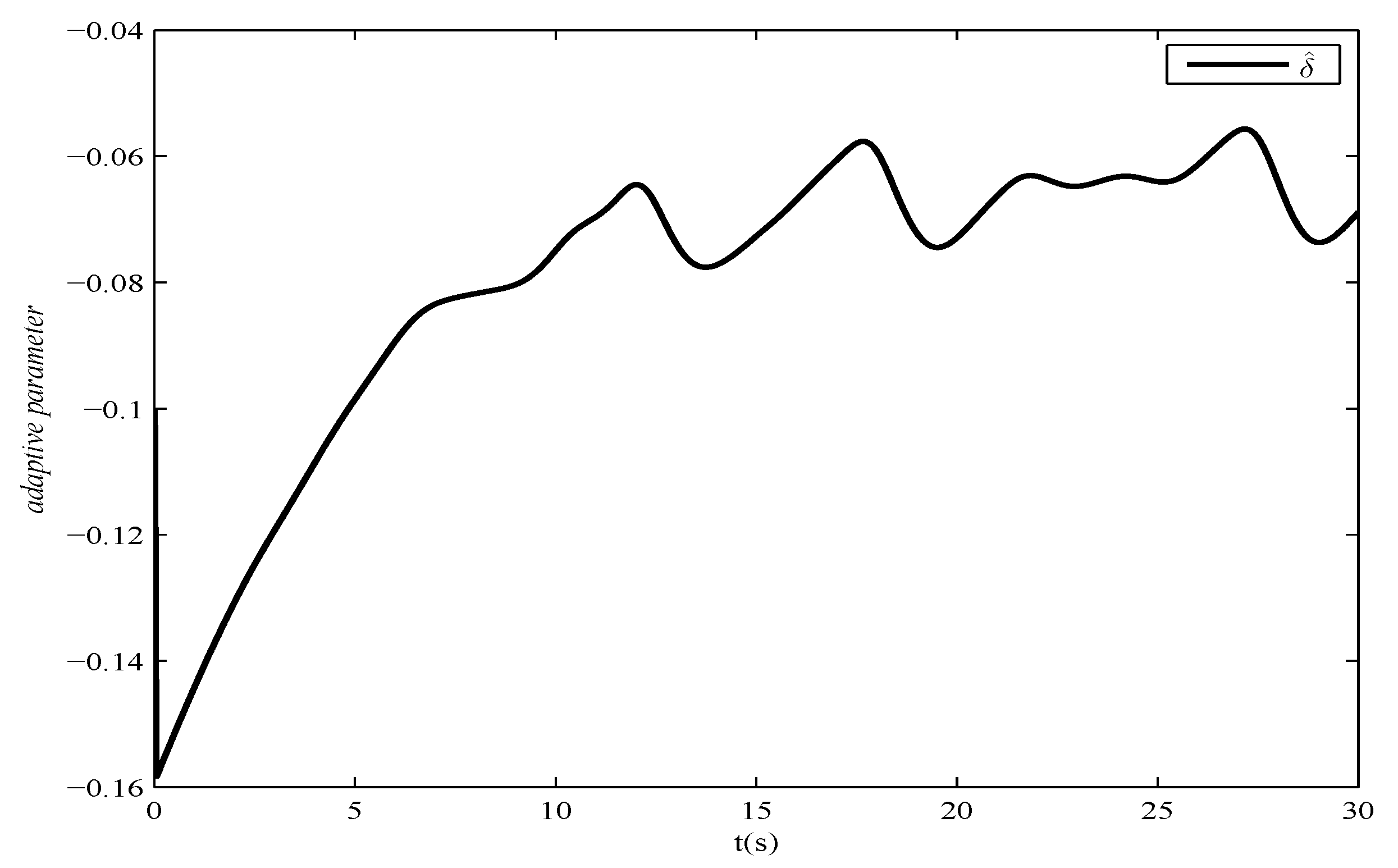
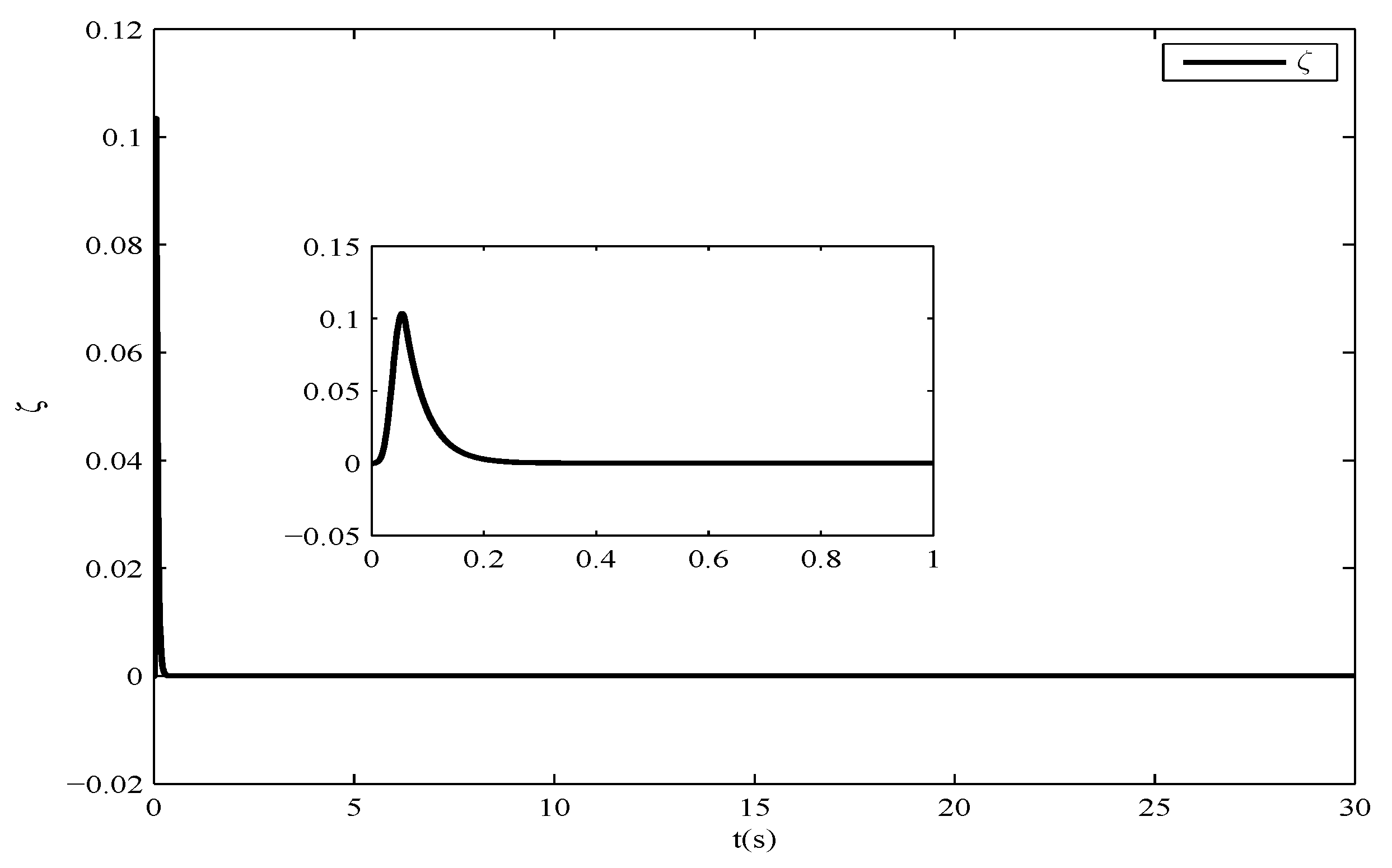
2.4. Simulation Results
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Detailed Dynamic Equations of Helicopter Yaw-Channel Model
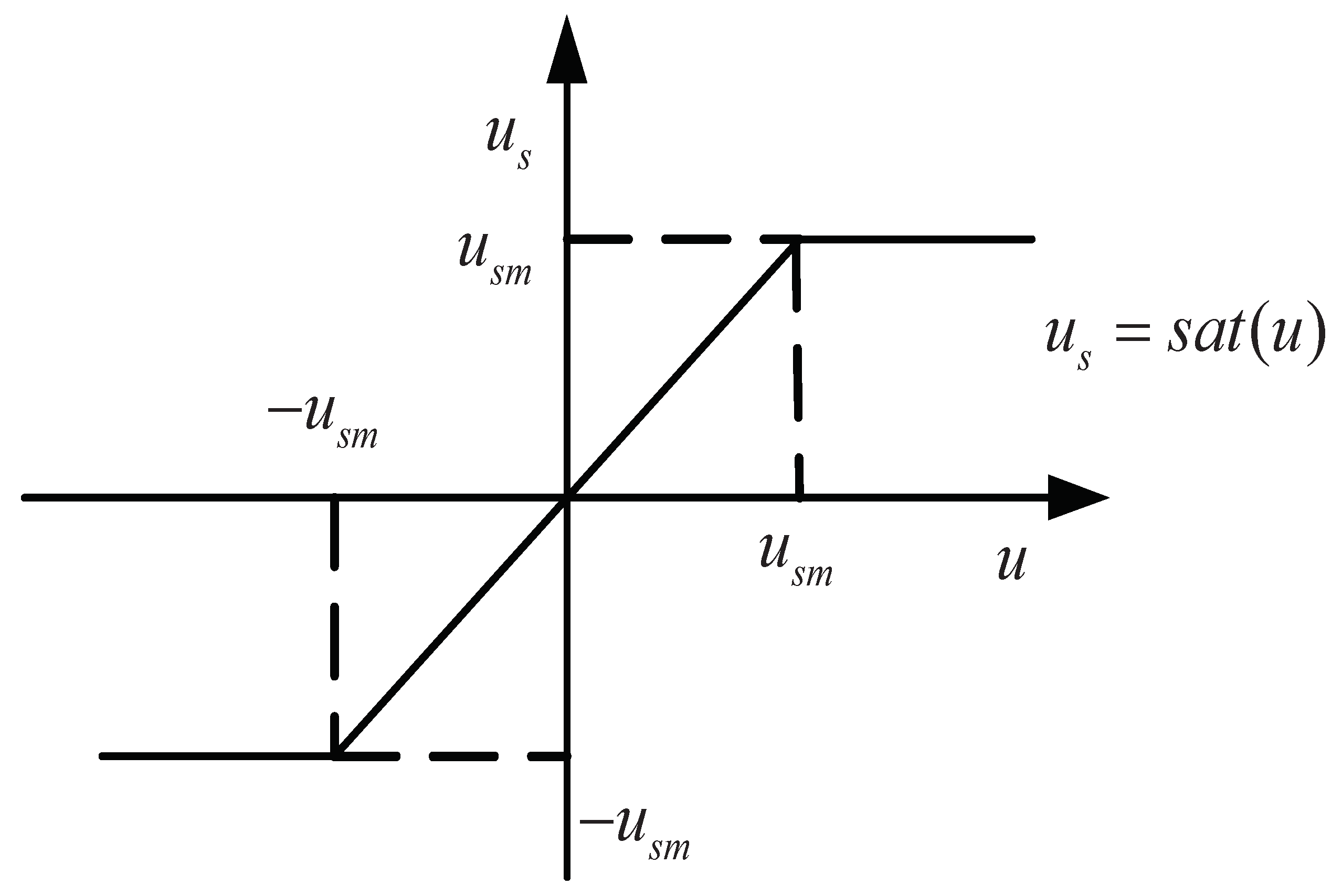
Appendix B. The Expression of Saturation Function us
References
- Raptis, I.A.; Valavanis, K.P. Linear and Nonlinear Control of Small-Scale Unmanned Helicopters; Springer: Amsterdam, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Srikanthakumar, S.; Liu, C.; Chen, W.H. Optimization-based safety analysis of obstacle avoidance systems for unmanned aerial vehicles. J. Int. Robot Syst. 2013, 65, 219–231. [Google Scholar] [CrossRef]
- Paul, T.; Krogstad, T.R.; Gravdahl, J.T. UAV formation flight using 3D potential field. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 1240–1245. [Google Scholar]
- Zhang, Q. Robust Adaptive Control for Nonlinear Flight Control Systems of Near Space Vehicle; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2013; pp. 17–21. [Google Scholar]
- Teo, J.; How, J.P.; Lavretsky, E. Proportional-Integral Controllers for Minimum-Phase Nonaffine-in-Control Systems. IEEE Trans. Autom. Control. 2010, 55, 1477–1483. [Google Scholar] [CrossRef]
- Wen, J.; Jiang, C.S. Adaptive fuzzy control for a class of chaotic systems with nonaffine inputs. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 475–492. [Google Scholar] [CrossRef]
- Arefi, M.M.; Zarei, J.; Karimi, H.R. Adaptive output feedback neural network control of uncertain non-affine systems with unknown control direction. J. Frankl. Inst. 2014, 351, 4302–4316. [Google Scholar] [CrossRef]
- Esfandiari, K.; Abdollahi, F.; Talebi, H.A. Adaptive Control of Uncertain Nonaffine Nonlinear Systems With Input Saturation Using Neural Networks. IEEE Trans. Neural Networks Learn. Syst. 2015, 26, 2311–2322. [Google Scholar] [CrossRef]
- Ramezani, Z.; Aref, M.M.; Zargarzadeh, H.; Jahedmotlagh, M.R. Neuro-adaptive backstepping control of SISO non-affne systems with unknown gain sign. ISA Trans. 2016, 65, 199–209. [Google Scholar] [CrossRef]
- Xu, D.Z.; Jiang, B.; Shi, P. Global robust tracking control of non-affine nonlinear systems with application to yaw control of UAV helicopter. Int. J. Control. Autom. Syst. 2013, 11, 957–965. [Google Scholar] [CrossRef]
- Wiktorowicz, K. Design of State Feedback Adaptive Fuzzy Controllers for Second-Order Systems Using a Frequency Stability Criterion. IEEE Trans. Fuzzy Syst. 2017, 25, 499–510. [Google Scholar] [CrossRef]
- Liu, J.; Wu, C.; Wang, Z.; Wu, L. Reliable filter design for sensor networks in the type-2 fuzzy framework. IEEE Trans. Ind. Inf. 2017, 13, 1742–1752. [Google Scholar] [CrossRef]
- Tong, S.; He, X.; Li, Y. Direct adaptive fuzzy backstepping robust control for single input and single output uncertain nonlinear systems using small-gain approach. Inf. Sci. 2010, 180, 1738–1758. [Google Scholar] [CrossRef]
- Li, Y.M.; Sui, S.; Tong, S.C. Adaptive fuzzy control design for stochastic nonlinear switched systems with arbitrary switchings and unmodeled dynamics. IEEE Trans. Cybern. 2017, 47, 403–414. [Google Scholar] [CrossRef] [PubMed]
- Li, M.M.; Verma, B. Nonlinear curve fitting to stopping power data using RBF neural networks. Expert Syst. Appl. 2016, 45, 161–171. [Google Scholar] [CrossRef]
- Fei, J.; Wang, T. Adaptive fuzzy-neural-network based on RBFNN control for active power filter. Int. J. Mach. Learn. Cybern. 2018, 12. [Google Scholar] [CrossRef]
- Ak, A.; Cansever, G. Three link robot control with fuzzy sliding mode controller based on RBF neural network. In Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design, Munich, Germany, 4–6 October 2006; pp. 2719–2724. [Google Scholar]
- Wang, A.M.; Wang, C.; Shi, P. Dynamic learning from neural control for strict-feedback systems with guaranteed predefined performance. IEEE Trans. Neural Networks Learn. Syst. 2017, 27, 2564–2576. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.G.; Ge, S.S.; Xiang, C.; Chai, T.; Lee, T.H. Output feedback NN control for two classes of discrete-time systems with unknown control directions in a unified approach. IEEE Trans. Neural Netw. 2008, 19, 873–886. [Google Scholar]
- Su, H.; Zhang, W. A Combined backstepping and dynamic surface control to adaptive fuzzy state-feedback control. Int. J. Adapt. Control. Signal Process. 2017, 31, 1666–1685. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Z.G.; Xu, D.Z. Second order dynamic terminal sliding mode control for a class of non-affine nonlinear systems with input constraint. Control Decis. 2017, 31, 1537–1545. [Google Scholar]
- Zou, A.M.; Kumar, K.D. Finite-time attitude control for rigid spacecraft subject to actuator saturation. Nonlinear Dyn. 2019, 20, 5919–5928. [Google Scholar] [CrossRef]
- Ling, S.; Wang, H. Adaptive fuzzy dynamic surface control of flexible-joint robot systems with input saturation. IEEE/CAA J. Autom. Sin. 2019, 6, 97–106. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Yang, X.G.; Mao, Z. Incipient voltage sensor fault isolation for rectifier in railway electrical traction systems. IEEE Trans. Ind. Electron. 2017, 64, 6763–6774. [Google Scholar] [CrossRef]
- Chen, M.; Tao, G. Adaptive fault-tolerant control of uncertain nonlinear large-scale systems with unknown dead zone. IEEE Trans. Cybern. 2016, 46, 1851–1862. [Google Scholar] [CrossRef] [PubMed]
- Van, M.; Ge, S.S.; Ren, H. Robust fault-tolerant control for a class of second-order nonlinear systems using an adaptive third-order sliding mode control. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 221–228. [Google Scholar] [CrossRef]
- Gong, J.Y.; Jiang, B.; Shen, Q.K. Adaptive fault-tolerant neural control for large-scale systems with actuator faults. Int. J. Control Autom. Syst. 2019, 17, 1421–1431. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Z.; Zhang, H. Adaptive NN fault-tolerant control for discrete-time systems in triangular forms with actuator fault. Neurocomputing 2015, 152, 209–221. [Google Scholar] [CrossRef]
- Zhang, H.; Cui, Y.; Wang, Y. Hybrid fuzzy adaptive fault-tolerant control for a class of uncertain nonlinear systems with unmeasured states. IEEE Trans. Fuzz Syst. 2017, 25, 1041–1050. [Google Scholar] [CrossRef]
- Wen, S.; Chen, M.Z.Q.; Zeng, Z. Adaptive neural-fuzzy sliding-mode fault-tolerant control for uncertain nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2268–2278. [Google Scholar] [CrossRef]
- Ren, B.; Ge, S.S.; Tee, K.P. Adaptive neural control for output feedback nonlinear systems using a barrier Lyapunov function. IEEE Trans. Neural Netw. 2010, 21, 1339–1345. [Google Scholar]
- He, W.; David, A.O.; Yin, Z. Neural network control of a robotic manipulator with input deadzone and output constraint. IEEE Trans. Syst. Man Cybern. 2016, 46, 759–770. [Google Scholar] [CrossRef]
- Chang, W.; Tong, S. Adaptive fuzzy tracking control design for permanent magnet synchronous motors with output constraint. Nonlinear Dyn. 2017, 87, 291–302. [Google Scholar] [CrossRef]
- Niu, B.; Zhao, J. Tracking control for output-constrained nonlinear switched systems with a barrier lyapunov function. Int. J. Syst. Sci. 2013, 44, 978–985. [Google Scholar] [CrossRef]
- He, W.; Ge, S.S. Cooperative control of a nonuniform gantry crane with constrained tension. Automatica 2016, 66, 146–154. [Google Scholar] [CrossRef]
- Si, W.J.; Dong, X.D.; Yang, F.F. Nussbaum gain adaptive neural control for stochastic pure-feedback nonlinear time-delay systems with full-state constraints. Neurocomputing 2018, 26, 130–141. [Google Scholar] [CrossRef]
- Li, D.J.; Lu, S.M.; Liu, Y.J. Adaptive fuzzy tracking control based Barrier Functions of uncertain nonlinear MIMO systems with full-state constraints and applications to chemical process. IEEE Trans. Fuzz Syst. 2018, 26, 2145–2159. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, C.; Xu, D.Z. Robust adaptive backstepping control for a class of non-affine nonlinear system with full states constraints and input saturation. Control Decis. 2018, 12, 1–12. [Google Scholar]
- Leishman, J.G. Principles of Helicopter Aerodynamics; Cambridge University Press: London/Britain, UK, 2002; pp. 277–310. [Google Scholar]
- Wang, H.; Chen, B.; Liu, X. Robust constrained control for MIMO nonlinear systems based on disturbance observer. IEEE Trans. Autom. Control 2015, 60, 3281–3286. [Google Scholar]
- Wang, H.; Chen, B.; Liu, X. Adaptive neural tracking control for stochastic nonlinear strict-feedback systems with unknown input saturation. Inf. Sci. 2014, 269, 300–315. [Google Scholar] [CrossRef]
- Wang, L.X.; Mendel, J.M. Fuzzy basis functions, universal approximation, and orthogonal least-squares learning. IEEE Trans. Neural Netw. 1992, 5, 807–814. [Google Scholar] [CrossRef]
- Na, J.; Ren, X.; Zheng, D. Adaptive control for nonlinear pure-feedback systems with high-order sliding mode observer. IEEE Trans. Neural Netw. 2013, 24, 370–382. [Google Scholar]
- Bechlioulis, C.P.; Rovithakis, G.A. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems. Automatica 1992, 45, 532–538. [Google Scholar] [CrossRef]
- Zhao, X.; Han, J. Robust tracking control for the yaw control of helicopter with time-varying uncertainty. Ind. Electron. Soc. 2007, 11, 816–821. [Google Scholar]
- Wang, H.; Peng, Y.; Wu, W.Q. Yaw-angle control channel of subminiature unmanned helicopter based on ADRC. Adv. Mater. Res. 2012, 503, 1527–1531. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Chen, X.; Xu, D. Adaptive Neural Fault-Tolerant Control for the Yaw Control of UAV Helicopters with Input Saturation and Full-State Constraints. Appl. Sci. 2020, 10, 1404. https://doi.org/10.3390/app10041404
Zhang Q, Chen X, Xu D. Adaptive Neural Fault-Tolerant Control for the Yaw Control of UAV Helicopters with Input Saturation and Full-State Constraints. Applied Sciences. 2020; 10(4):1404. https://doi.org/10.3390/app10041404
Chicago/Turabian StyleZhang, Qiang, Xia Chen, and Dezhi Xu. 2020. "Adaptive Neural Fault-Tolerant Control for the Yaw Control of UAV Helicopters with Input Saturation and Full-State Constraints" Applied Sciences 10, no. 4: 1404. https://doi.org/10.3390/app10041404
APA StyleZhang, Q., Chen, X., & Xu, D. (2020). Adaptive Neural Fault-Tolerant Control for the Yaw Control of UAV Helicopters with Input Saturation and Full-State Constraints. Applied Sciences, 10(4), 1404. https://doi.org/10.3390/app10041404



