A Hybrid Tolerance Design Method for the Active Phased-Array Antenna
Abstract
:Featured Application
Abstract
1. Introduction
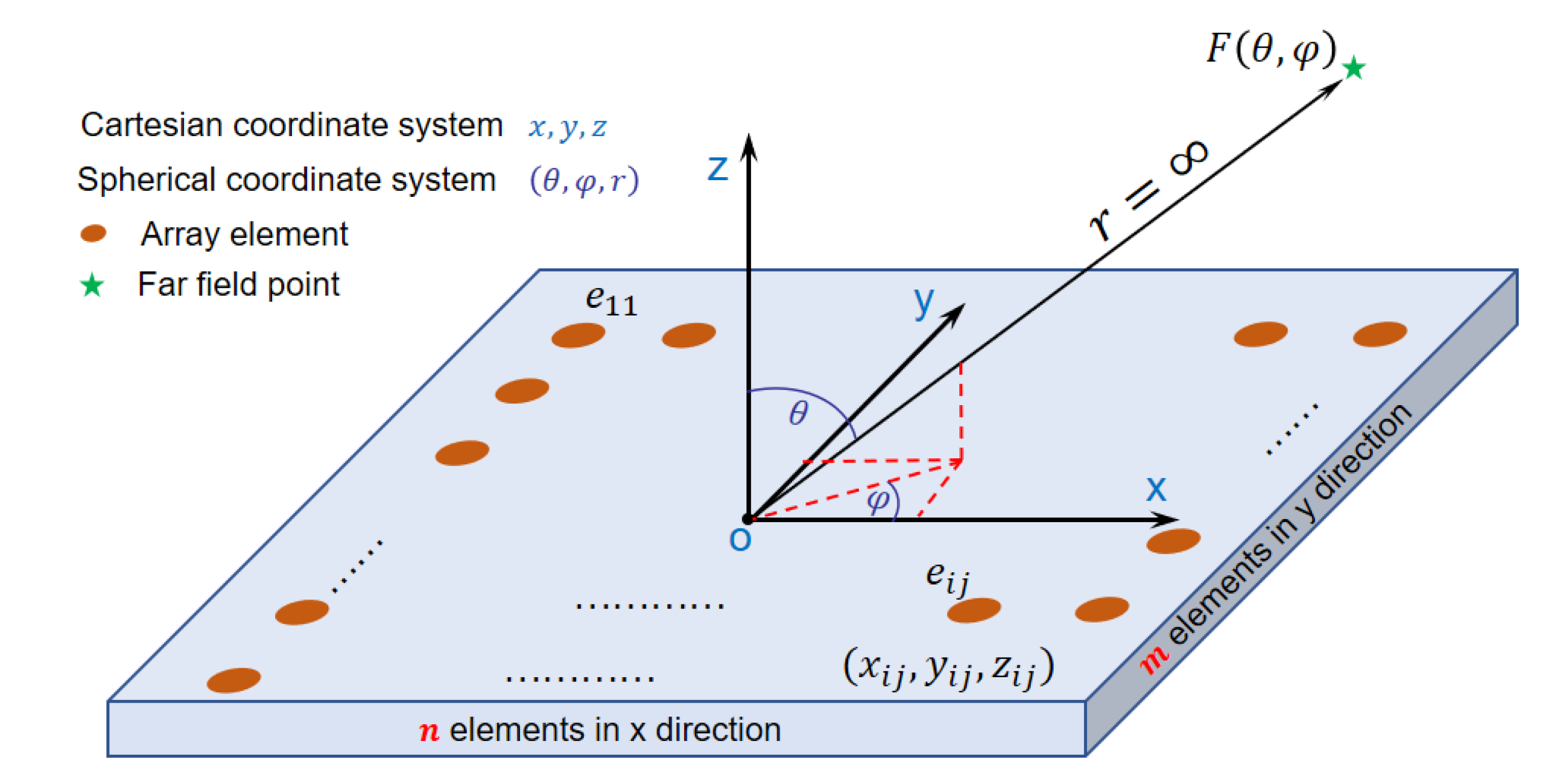
2. Surrogate Model of the Electrical Performance and Hybrid Geometric Errors
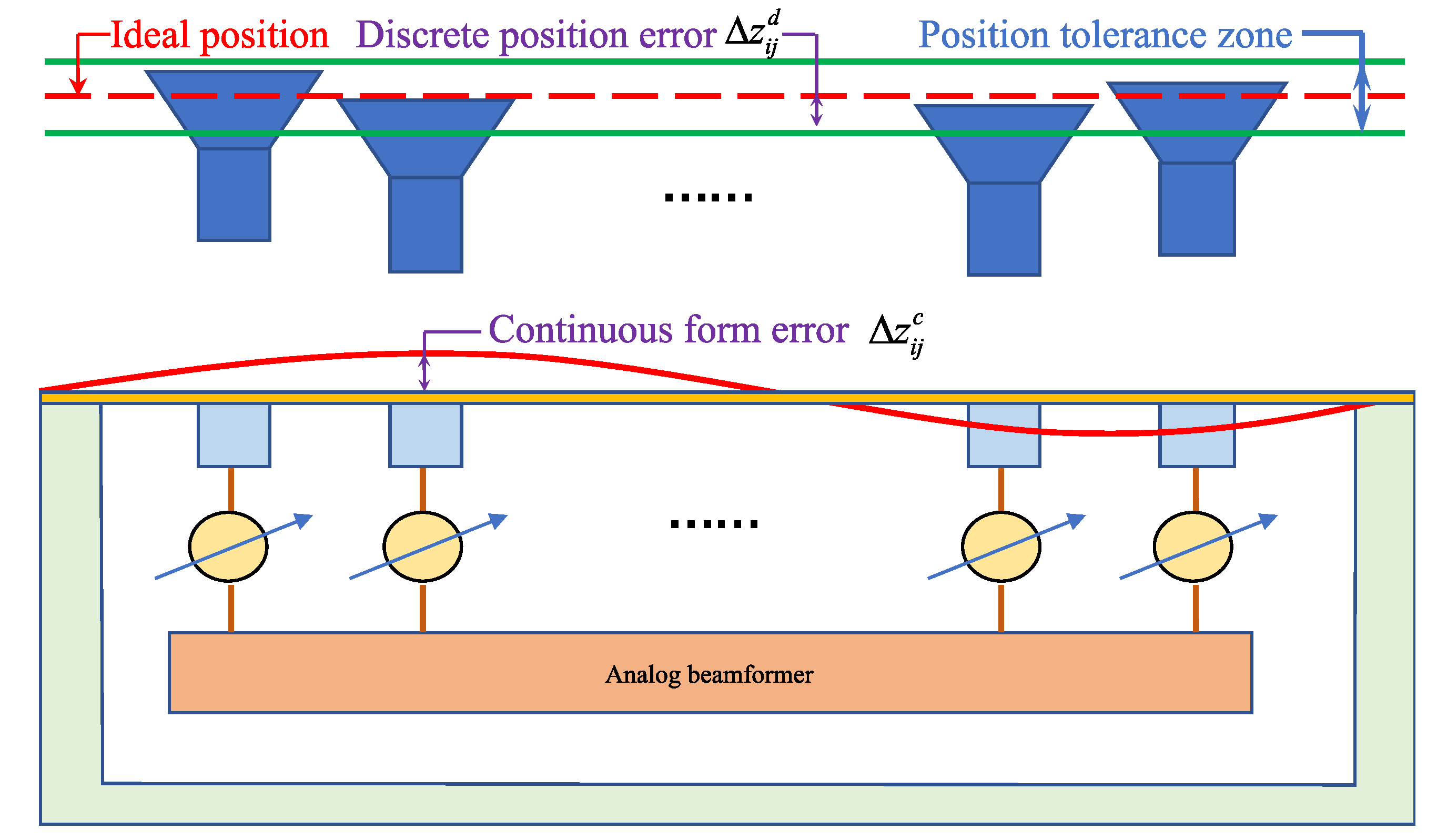
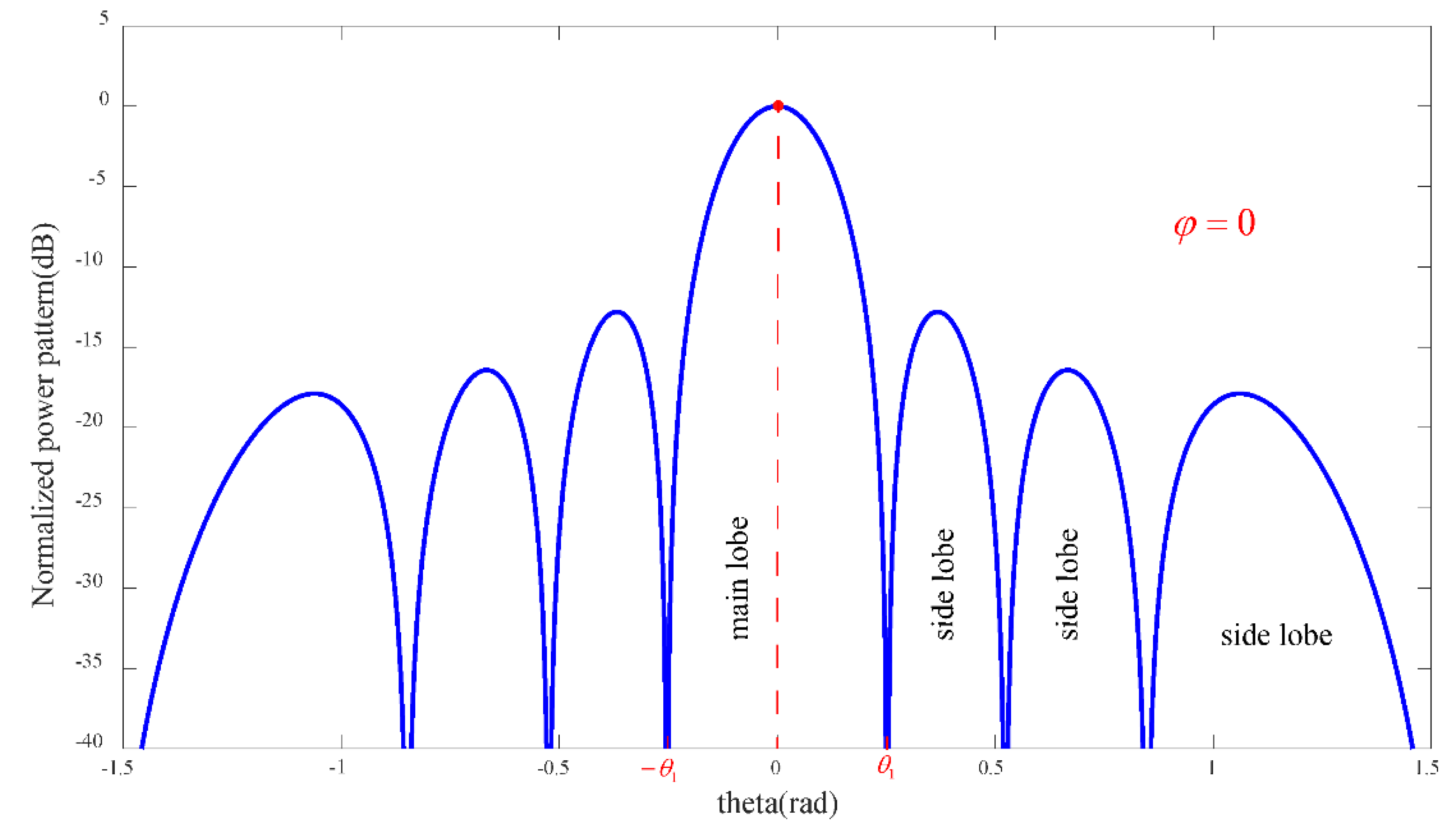
2.1. Hybrid Error Analysis
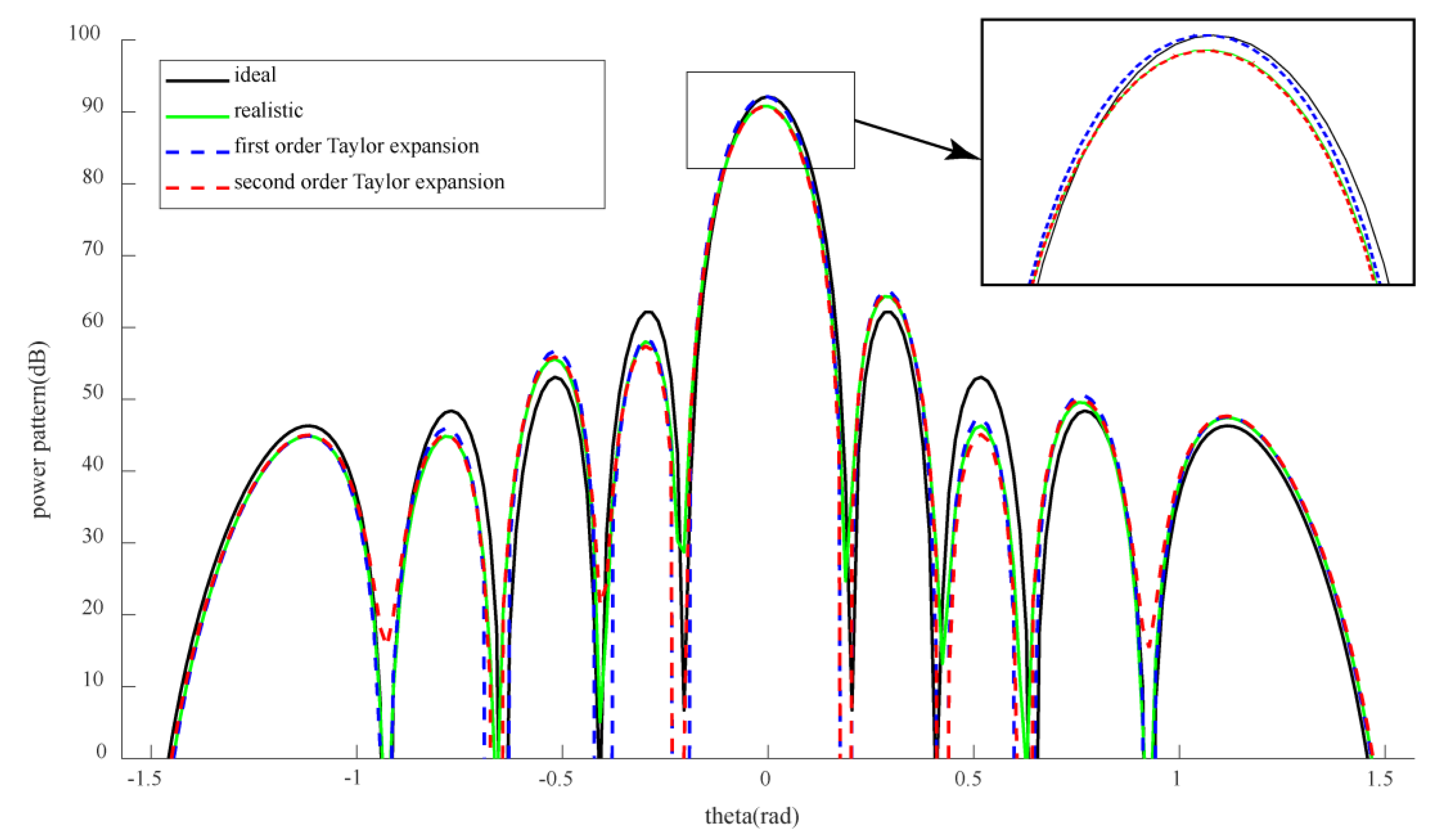
2.2. Second-Order Taylor Expansion
3. Statistical Analysis of the Performance of the Array Antenna
3.1. Expectation Derivation
3.2. Variance Derivation
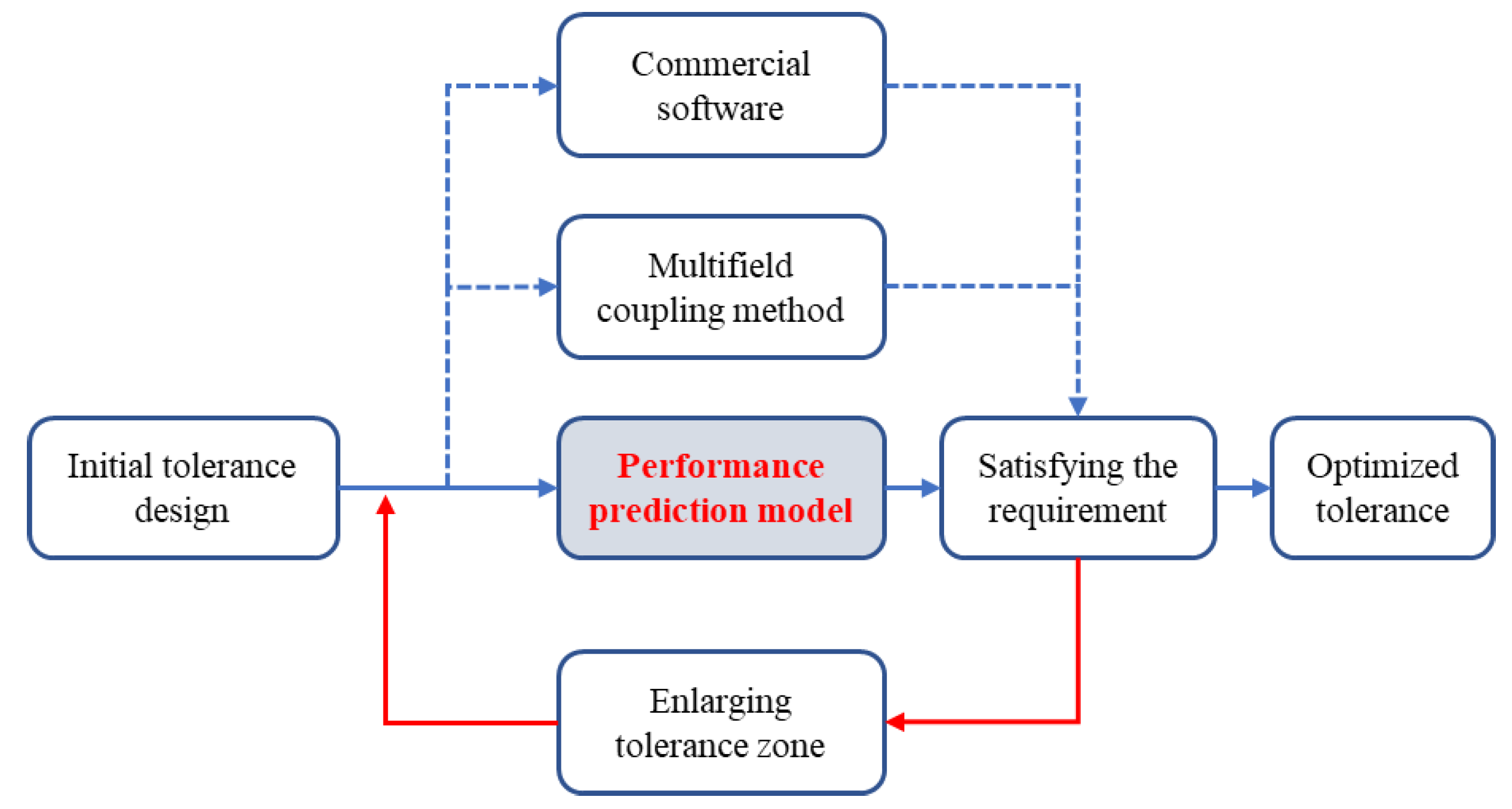
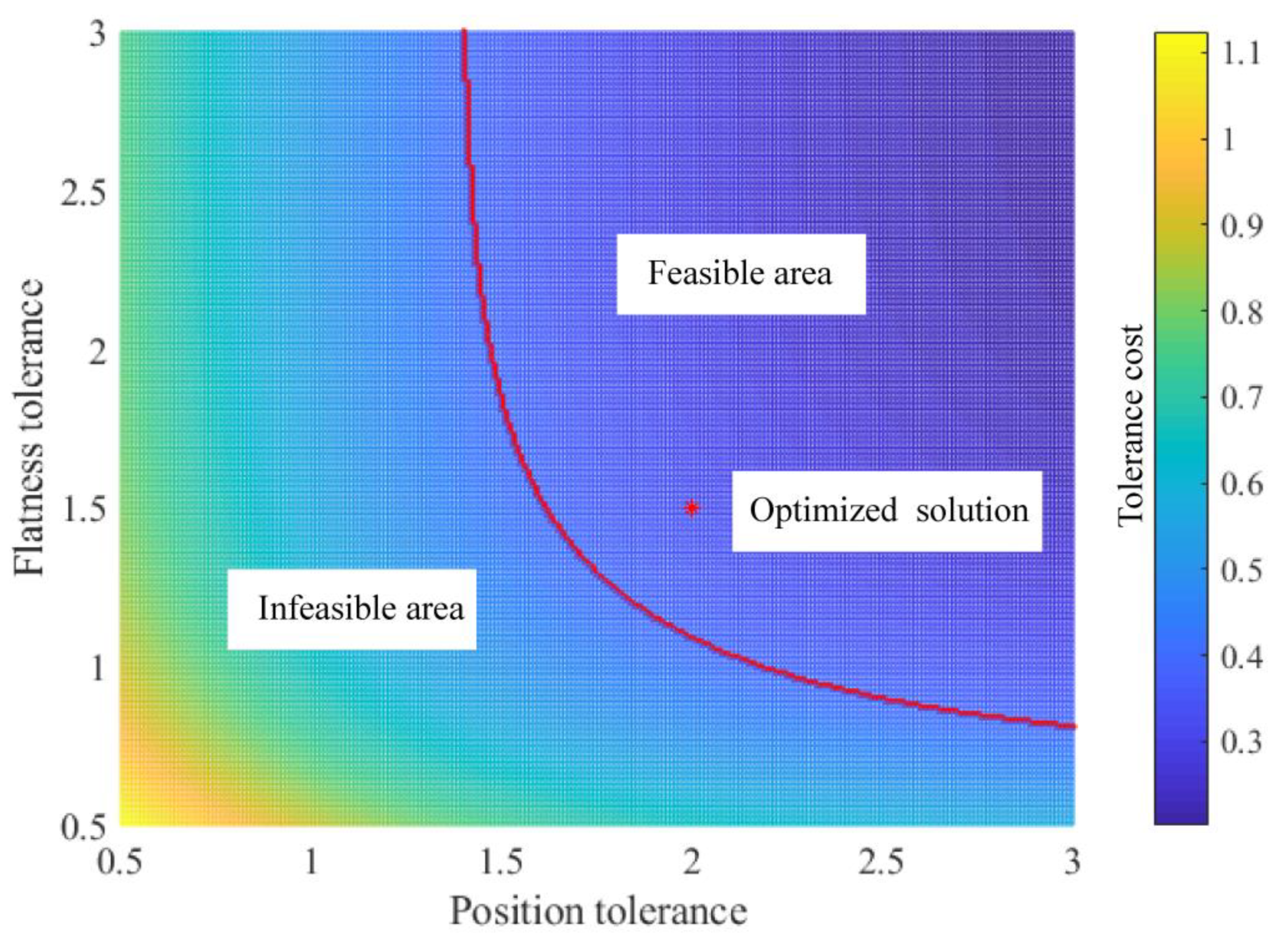
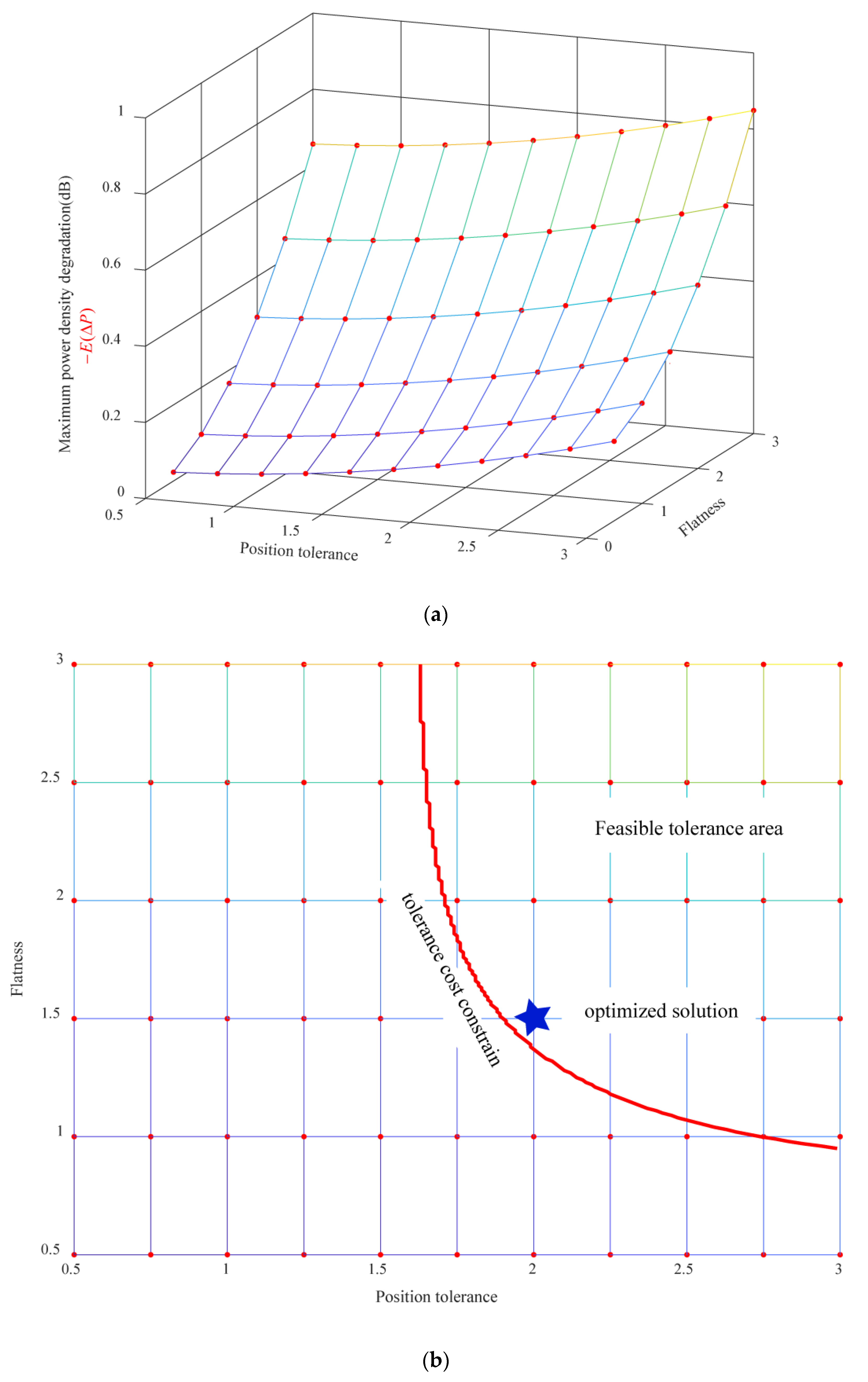
4. Tolerance Design Based on the Statistical Model
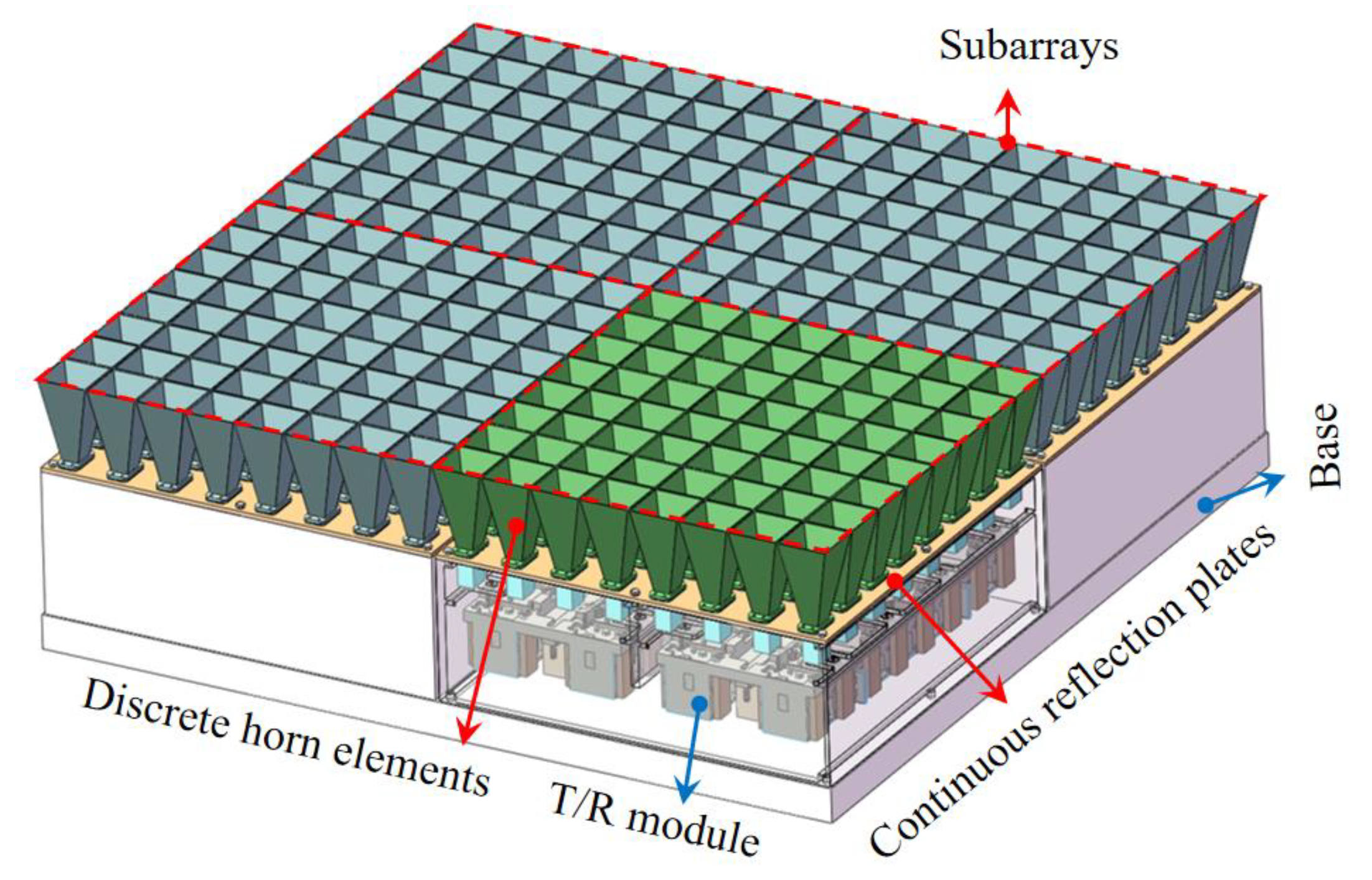
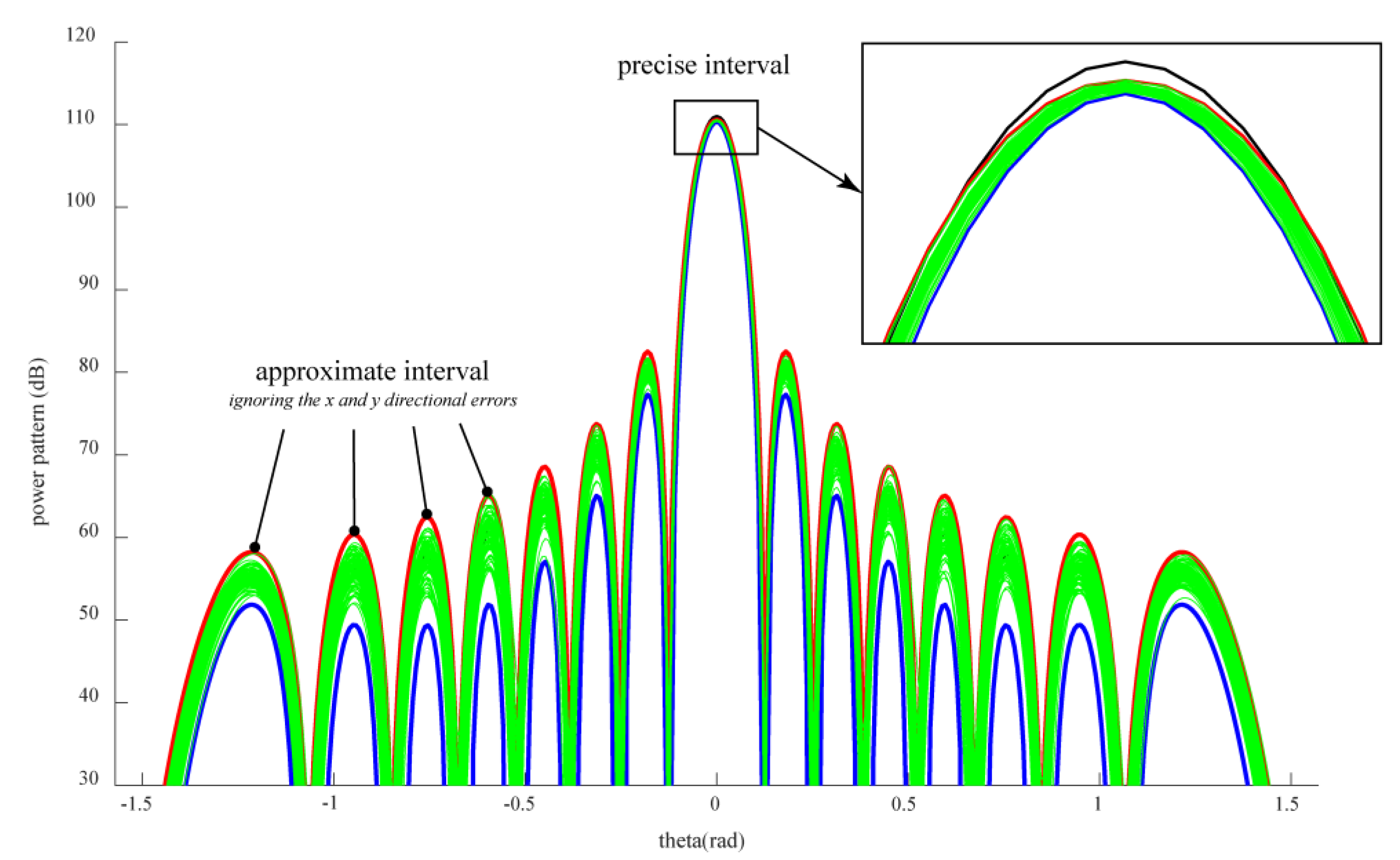
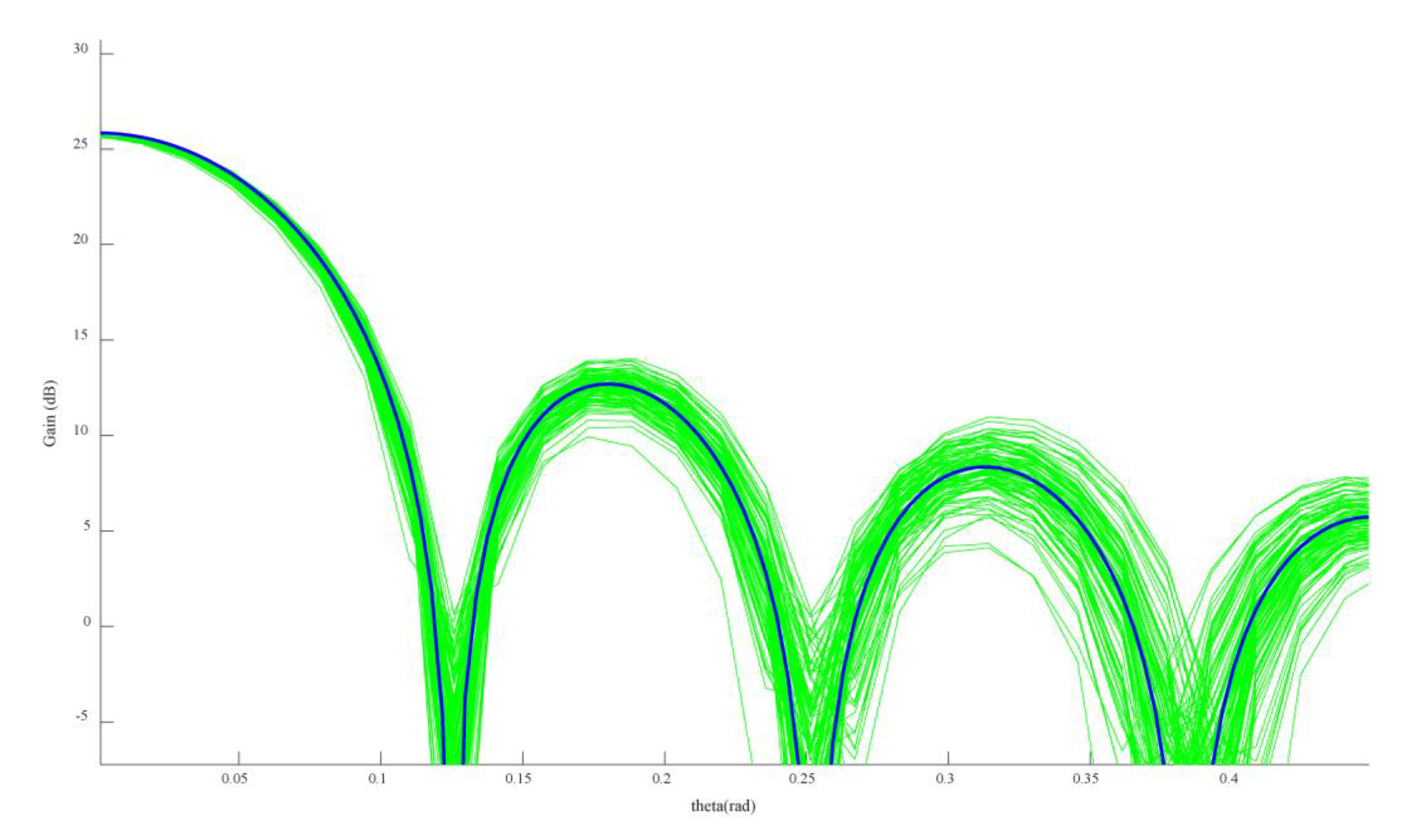
5. Results
6. Conclusions
- The hybrid geometric errors of the array antenna were analyzed, and the surrogate model of the electrical performance and hybrid geometric errors were established based on the second-order Taylor expansion.
- The expectation and the variance of the power pattern of the array antenna was derived, then the direct and explicit relationship between the performance and the hybrid tolerances was identified.
- The proposed method was applied on an active phased-array antenna, and the hybrid tolerances were optimized finally. Numerical simulation results prove the effectiveness of the method.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Elliott, R. Mechanical and Electrical Tolerances for Two-Dimensional Scanning Antenna Arrays. IRE Trans. Antennas Propag. 1958, 6, 114–120. [Google Scholar] [CrossRef]
- Wang, H.S.C. Performance of phased-array antennas with mechanical errors. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 535–545. [Google Scholar] [CrossRef]
- So, K.K.; Luk, K.M.; Chan, C.H.; Chan, K.F. 3D Printed High Gain Complementary Dipole/Slot Antenna Array. Appl. Sci. 2018, 8, 1410. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Kim, S.; Choi, J. A 28 GHz 5G Phased Array Antenna with Air-Hole Slots for Beam Width Enhancement. Appl. Sci. 2019, 9, 4204. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Yuan, S.; Yang, X.; Gao, W.; Zhu, C.; Wang, Z.; Wang, S.; Peng, X. Position Tolerance Design Method for Array Antenna in Internet of Things. Wirel. Commun. Mob. Comput. 2018, 2018, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Ruze, J. The Effect of Aperture Errors on the Antenna Radiation Pattern. Il Nuovo Cim. 1952, 9, 364–380. [Google Scholar] [CrossRef]
- Bao, V.T. Influence of correlation interval and illumination taper in antenna tolerance theory. Proc. Inst. Electr. Eng. 1969, 116, 195. [Google Scholar] [CrossRef]
- Rahmat-Samii, Y. An efficient computational method for characterizing the effects of random surface errors on the average power pattern of reflectors. IRE Trans. Antennas Propag. 1983, 31, 92–98. [Google Scholar] [CrossRef]
- Kim, J.W.; Kim, B.S.; Nam, S.; Lee, C.W. Computation of the Average Power Pattern of a Reflector Antenna with Random Surface Errors and Misalignment Errors. IRE Trans. Antennas Propag. 1996, 44, 996–999. [Google Scholar] [CrossRef]
- Lee, J.; Lee, Y.; Kim, H. Decision of error tolerance in array element by the Monte Carlo method. IRE Trans. Antennas Propag. 2005, 53, 1325–1331. [Google Scholar] [CrossRef]
- Wang, C.; Kang, M.; Wang, W.; Zhong, J.; Zhang, Y.; Jiang, C.; Duan, B. Electromechanical coupling based performance evaluation of distorted phased array antennas with random position errors. Int. J. Appl. Electromagn. Mech. 2016, 51, 285–295. [Google Scholar] [CrossRef]
- Schmid, C.M.; Schuster, S.; Feger, R.; Stelzer, A. On the effects of calibration errors and mutual coupling on the beam pattern of an antenna array. IRE Trans. Antennas Propag. 2013, 61, 4063–4072. [Google Scholar] [CrossRef]
- Anselmi, N.; Manica, L.; Rocca, P.; Massa, A. Tolerance analysis of antenna arrays through interval arithmetic. IRE Trans. Antennas Propag. 2013, 61, 5496–5507. [Google Scholar] [CrossRef]
- Anselmi, N.; Salucci, M.; Rocca, P.; Massa, A. Power pattern sensitivity to calibration errors and mutual coupling in linear arrays through circular interval arithmetics. Sensors 2016, 16, 791. [Google Scholar] [CrossRef]
- Guo, F.; Liu, Z.; Sa, G.; Tan, J. A Position Error Representation Method for Planar Arrays. IEEE Antennas Wirel. Propag. Lett. 2019, 1. [Google Scholar] [CrossRef]
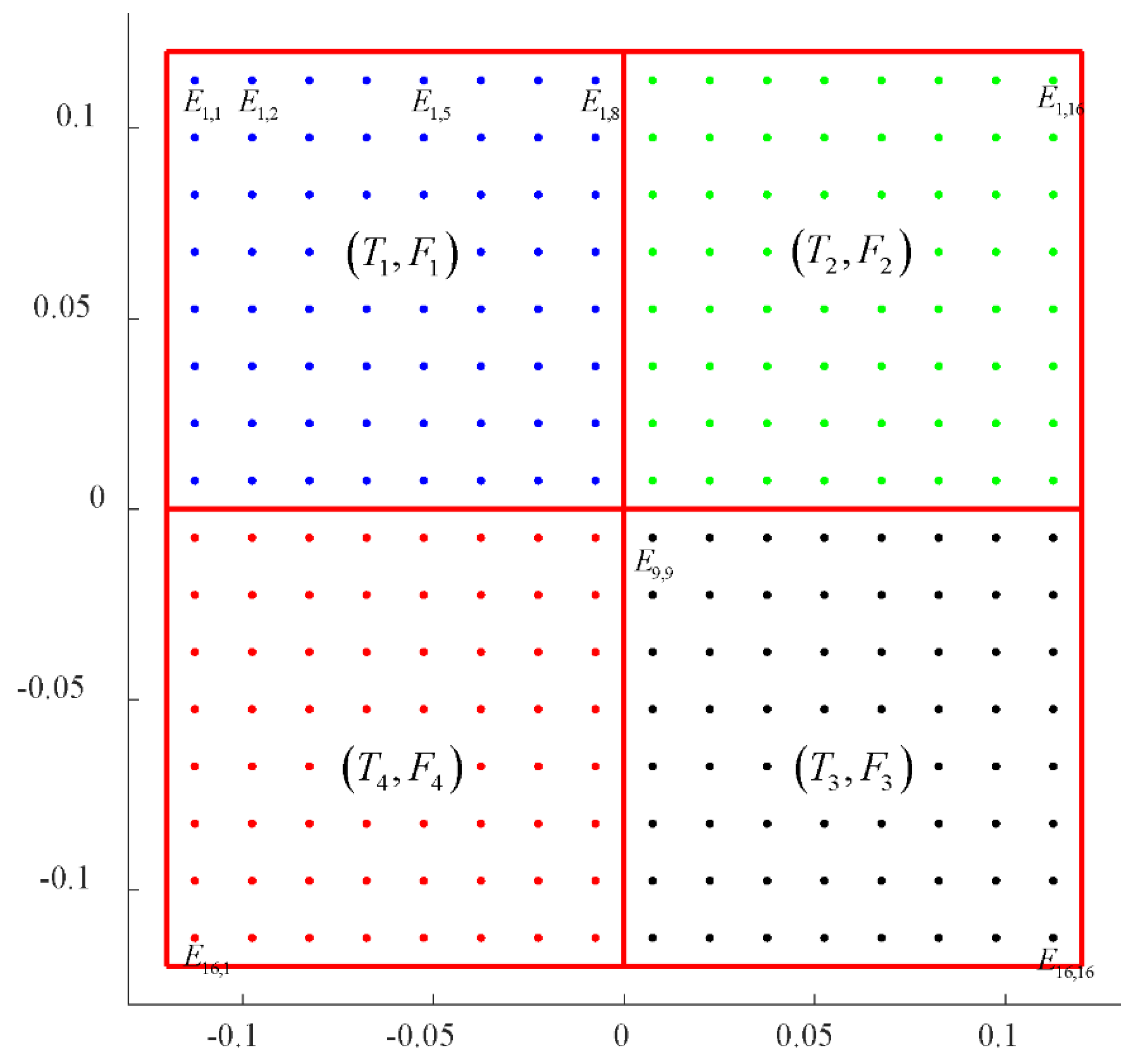
- Sa, G.; Liu, Z.; Qiu, C.; Tan, J. A Novel Region-Division-Based Tolerance Design Method for a Large Number of Discrete Elements Distributed on a Large Surface. ASME J. Mech. Des. 2019, 141, 041701. [Google Scholar] [CrossRef]
- Wang, C.; Duan, B.; Zhang, F.; Zhu, M. Analysis of performance of active phased array antennas with distorted plane error. Int. J. Electron. 2009, 96, 549–559. [Google Scholar] [CrossRef]
- Sa, G.; Liu, Z.; Qiu, C.; Peng, X.; Tan, J. A Tolerance Analysis Method Considering Form Defects Based on Variance Separation. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2019, in press. [Google Scholar]
- Winkler, D.F.; Webster, J.L. Searching the Skies: The Legacy of the United States Cold War Defense Radar Program (No. SR-97-78); Construction Engineering Research Lab (Army): Champaign, IL, USA, 1997. [Google Scholar]
- Liu, S.G.; Jin, Q.; Liu, C.; Xie, R.J. Analytical method for optimal component tolerances based on manufacturing cost and quality loss. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2013, 227, 1484–1491. [Google Scholar] [CrossRef]
- He, C.; Zhang, S.; Qiu, L.; Liu, X.; Wang, Z. Assembly Tolerance Design Based on Skin Model Shapes Considering Processing Feature Degradation. Appl. Sci. 2019, 9, 3216. [Google Scholar] [CrossRef] [Green Version]
- Mailloux, R.J. Phased Array Antenna Handbook, 2nd ed.; Artech House: Boston, UK, 2005; pp. 12–19. [Google Scholar]
- Kraus John, D.; Marhefka Ronald, J. Antennas: For all Applications, 3rd ed.; Mc Graw Hill: Boston, UK, 2008. [Google Scholar]



| Expectation (db) | Flatness of the Reflection Plate (mm) | ||||||
|---|---|---|---|---|---|---|---|
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | ||
| Position tolerance of the discrete elements (mm) | 0.50 | 0.0232 | 0.0768 | 0.1649 | 0.2930 | 0.4534 | 0.6562 |
| 0.75 | 0.0298 | 0.0834 | 0.1716 | 0.2997 | 0.4602 | 0.6630 | |
| 1.00 | 0.0390 | 0.0927 | 0.1809 | 0.3091 | 0.4696 | 0.6726 | |
| 1.25 | 0.0509 | 0.1046 | 0.1929 | 0.3212 | 0.4818 | 0.6850 | |
| 1.50 | 0.0655 | 0.1192 | 0.2076 | 0.3359 | 0.4967 | 0.7001 | |
| 1.75 | 0.0827 | 0.1364 | 0.2249 | 0.3534 | 0.5144 | 0.7179 | |
| 2.00 | 0.1025 | 0.1564 | 0.2449 | 0.3736 | 0.5347 | 0.7385 | |
| 2.25 | 0.1251 | 0.1790 | 0.2677 | 0.3965 | 0.5579 | 0.7619 | |
| 2.50 | 0.1503 | 0.2043 | 0.2931 | 0.4221 | 0.5837 | 0.7881 | |
| 2.75 | 0.1783 | 0.2323 | 0.3213 | 0.4505 | 0.6124 | 0.8171 | |
| 3.00 | 0.2089 | 0.2631 | 0.3522 | 0.4816 | 0.6438 | 0.8489 | |
| Standard Deviation | Flatness of the Reflection Plate (mm) | ||||||
|---|---|---|---|---|---|---|---|
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | ||
| Position tolerance of the discrete elements (mm) | 0.50 | 0.0030 | 0.0119 | 0.0268 | 0.0478 | 0.0727 | 0.1091 |
| 0.75 | 0.0031 | 0.0120 | 0.0268 | 0.0479 | 0.0728 | 0.1093 | |
| 1.00 | 0.0033 | 0.0121 | 0.0270 | 0.0480 | 0.0730 | 0.1094 | |
| 1.25 | 0.0036 | 0.0123 | 0.0272 | 0.0482 | 0.0732 | 0.1097 | |
| 1.50 | 0.0040 | 0.0126 | 0.0274 | 0.0485 | 0.0735 | 0.1100 | |
| 1.75 | 0.0046 | 0.0130 | 0.0277 | 0.0488 | 0.0738 | 0.1103 | |
| 2.00 | 0.0053 | 0.0134 | 0.0281 | 0.0491 | 0.0741 | 0.1107 | |
| 2.25 | 0.0062 | 0.0140 | 0.0285 | 0.0495 | 0.0746 | 0.1112 | |
| 2.50 | 0.0072 | 0.0146 | 0.0290 | 0.0500 | 0.0751 | 0.1117 | |
| 2.75 | 0.0084 | 0.0155 | 0.0297 | 0.0506 | 0.0757 | 0.1123 | |
| 3.00 | 0.0097 | 0.0164 | 0.0304 | 0.0512 | 0.0763 | 0.1130 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sa, G.; Liu, Z.; Qiu, C.; Tan, J. A Hybrid Tolerance Design Method for the Active Phased-Array Antenna. Appl. Sci. 2020, 10, 1435. https://doi.org/10.3390/app10041435
Sa G, Liu Z, Qiu C, Tan J. A Hybrid Tolerance Design Method for the Active Phased-Array Antenna. Applied Sciences. 2020; 10(4):1435. https://doi.org/10.3390/app10041435
Chicago/Turabian StyleSa, Guodong, Zhenyu Liu, Chan Qiu, and Jianrong Tan. 2020. "A Hybrid Tolerance Design Method for the Active Phased-Array Antenna" Applied Sciences 10, no. 4: 1435. https://doi.org/10.3390/app10041435





