Adaptive Graph Convolution Using Heat Kernel for Attributed Graph Clustering

Featured Application

We propose a novel model to perform attributed graph clustering, which exploits heat kernel to enhance the performance of graph convolution and adopts adaptive architecture to work on different graph datasets. The model proposed in this paper can be deployed to a product recommendation system, where users with specific preferences can be classified precisely and recommended satisfactory products. It can be applied to citation networks to analyze the categories of different articles without prior knowledge. It can be deployed into business forecasting, where the proposed model can identify the operating situation of enterprises significantly by analyzing their business data and investment relationships jointly.

Abstract

Attributed graphs contain a lot of node features and structural relationships, and how to utilize their inherent information sufficiently to improve graph clustering performance has attracted much attention. Although existing advanced methods exploit graph convolution to capture the global structure of an attributed graph and achieve obvious improvements for clustering results, they cannot determine the optimal neighborhood that reflects the relevant information of connected nodes in a graph. To address this limitation, we propose a novel adaptive graph convolution using a heat kernel model for attributed graph clustering (AGCHK), which exploits the similarity among nodes under heat diffusion to flexibly restrict the neighborhood of the center node and enforce the graph smoothness. Additionally, we take the Davies–Bouldin index (DBI) instead of the intra-cluster distance individually as the selection criterion to adaptively determine the order of graph convolution. The clustering results of AGCHK on three benchmark datasets—Cora, Citeseer, and Pubmed—are all more than 1% higher than the current advanced model AGC, and 12% on the Wiki dataset especially, which obtains a state-of-the-art result in the task of attributed graph clustering.

1. Introduction

With the rapid developments of social networks, communication networks, biological networks, and other applications in various fields, the scale of graph data grows sharply. Attributed graphs as the basic data representation contain a large number of node attributes and connection relationships, but it is difficult to perform node classification due to the massive nodes and complicated topology. How to mine the inherent information hidden in the attributed graph without the prior knowledge is a challenging task.

Attributed graph clustering aims to group nodes into different clusters by exploiting node attributes and graph structures sufficiently, where relevant nodes are assigned to the same cluster and the difference between clusters is maximized. By leveraging node attributes and structural information, attributed graph clustering is mainly summarized in three main categories as follows.

Attribute-based clustering such as spectral clustering only respects node attributes and performs clustering on the similarity matrix with node attributes directly. In comparison, structure-based clustering just explores vertex connectivity by manipulating the adjacency matrix of the attributed graph, e.g., random walk [1], Laplacian eigenmaps [2]. However, the above two kinds of graph clustering methods lack incorporated node features and a mining topological structure.

In recent years, generative models based on graph convolutional network (GCN [3]) has been widely studied for attributed graph clustering, where GCN [3] updates the node representation by incorporating neighbor node features to construct graph embedding. Classic generative models include variational graph auto-encoder (VGAE) [4], marginalized graph autoencoder (MGAE) [5], and adversarially regularized graph autoencoder (ARGE) [6]. These methods have been demonstrated as being very practical for performing clustering by unifying graph structures and attributing information. However, graph clustering via GCN [3], such as VGAE [4] or MGAE [5], simply employs shadow two-layer or three-layer graph convolution respectively, which only leverages two or three-hop neighborhood features, and it is hard to capture global structural information. On the contrast, stacking too many layers may lead to over-smoothing and complex computation.

Zhang et al. [7] adopt adaptive graph convolution (AGC) as a low-pass graph filter to make node features smoother. Nevertheless, AGC [7] might not determine the appropriate neighborhood that reflects the relevant information of connected nodes represented in graph structures.

To overcome the above difficulty, we propose an adaptive graph convolution model using heat kernel (AGCHK) to obtain an appropriate neighborhood of the center node and enhance the ability to capture graph smoothness. Our contributions can be summarized as follows:

• We replace the weak linear low-pass filter in standard AGC [7] by heat kernel to enhance the low-pass characteristics of the graph filter.
• We leverage the scaling parameter to restrict the neighborhood of the center node, which is flexible to exploit distant-distance nodes while excluding some irrelevant close-distance nodes.
• We choose the Davies–Bouldin index (DBI) as the criterion to evaluate the cluster quality, which can exactly determine the order of adaptive graph convolution.
• Experimental results show that AGCHK is obviously superior to other compared methods in the task of attribute graph clustering on benchmark datasets such as Cora, Citeseer, Pubmed, and Wiki.

2. Preliminary

2.1. Problem Formalization

2.1.1. Graph Definition

An undirected graph is represented as $G=\left\{V,E,X\right\}$, where $V={\left\{v_i\right\}}_{i=1}^N$ consists of a set of nodes with $\left|V\right|=N$. A graph signal $x:V\to ℝ$ is a real-valued function on the nodes regarded as a vector $x\in {ℝ}^N$, where $x_i$ is the value of $x$ at the $i^{th}$ node. $E$ is a set of edges, and $A=\left\{a_{i,j}\right\}\in {ℝ}^{N\times N}$ is the adjacency matrix with $a_{i,j}=a_{j,i}$ representing the connection relationships between node $v_i$ and node $v_j$. The graph Laplacian matrix is denoted as $ℒ=D-A$, where $D$ is the diagonal degree matrix with $D_{i,i}={{\displaystyle \sum }}_j{A}_{i,j}$, and the normalized graph Laplacian is defined as $L=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$. Since $L$ is a real symmetric positive semidefinite matrix, it can be eigendecomposed as $L=U\mathsf{\Lambda }{U}^T$ where $U=\left[u_1,u_2,\dots ,u_N\right]\in {ℝ}^{N\times N}$ is a complete set of orthonormal eigenvectors known as graph Fourier modes and $\mathsf{\Lambda }=\mathrm{diag}{\left\{{\lambda }_i\right\}}_{i=1}^N$ are ordered real nonnegative eigenvalues associated with ${\left\{u_i\right\}}_{i=1}^N$, which are identified as the frequencies of the graph.

2.1.2. Goal

Given an attributed graph $G$, graph clustering aims to partition nodes $V$ into $m$ disjoint clusters $C={\left\{c_i\right\}}_{i=1}^m$ so that nodes within the same cluster are more likely to have similar features and be close to each other, while nodes distributed in different clusters have dissimilar features and are distant to each other.

2.2. Graph Convolution

Here, we briefly review the notions and evolutions of graph convolution. The graph Fourier transform of a graph signal $x$ is defined as $\widehat{x}=U^{T}x$, and the inverse graph Fourier transform is $x=U\widehat{x}$ [8]. According to the convolution theorem [8], the graph convolution operator represented as ${\ast }_G$ is defined as

$$x{\ast }_{G}f=U\left(\left(U^{T}f\right)\odot \left(U^{T}x\right)\right),$$

(1)

where $f$ denotes the graph convolution kernel in the spatial domain and $\odot$ is the element-wise Hadamard product.

Spectral CNN [9] replaces $U^{T}f$ by a diagonal matrix $g_{\theta }$ so that the Hadamard product can be written as matrix multiplication,

$$y=x{\ast }_{G}f=U{g}_{\theta }{U}^{T}x,$$

(2)

where $L$ is the normalized graph Laplacian matrix and $g_{\theta }=\mathrm{diag}\left({\left\{{\theta }_i\right\}}_{i=1}^N\right)$ defined in the spectral domain denotes the frequency response function of the graph filter $g_{\theta }\left(L\right)$.

However, there are two limitations with the above convolution kernel: (i) it does not have the spatial localization and (ii) it is computationally expensive [10]. To circumvent these issues, $g_{\theta }$ is well-approximated by a Chebyshev polynomial in ChebyNet [10], which is defined as

$$g_{\theta }\left(\mathsf{\Lambda }\right)={\displaystyle \sum }_{p=0}^{P-1}{\theta }_p{\mathsf{\Lambda }}^p,$$

(3)

where $P$ is a hyper-parameter and ${\theta }_p\in {ℝ}^N$ is the vector of polynomial coefficients. Correspondingly, the graph convolution of ChebyNet [10] is defined as

$$y=U{g}_{\theta }{U}^{T}x=U\left({\displaystyle \sum }_{p=0}^{P-1}{\theta }_p{\mathsf{\Lambda }}^p\right)U^{T}x={\displaystyle \sum }_{p=0}^{P-1}{\theta }_p{L}^{p}x.$$

(4)

GCN [3] only considers the first-order polynomial by setting $P=2$ and $\theta ={\theta }_0=-{\theta }_1$; thus, the simplified graph convolution is defined as

$$y=U{g}_{\theta }{U}^{T}x=\theta U\left(I-\mathsf{\Lambda }\right)U^{T}x=\theta \left(I-L\right)x,$$

(5)

where GCN [3] constrains the number of parameters further to address overfitting and accelerate computation.

To strengthen the low-pass performance of the graph filter and improve graph smoothness, AGC [7] modifies the frequency response function of GCN [3] as

$$y=U{g}_{\theta }{U}^{T}x=\theta U\left(I-\frac{1}{2}\mathsf{\Lambda }\right)U^{T}x=\theta \left(I-\frac{1}{2}L\right)x.$$

(6)

3. Clustering via Adaptive Graph Convolution Using Heat Kernel

Our basic assumption is that connected nodes tend to have similar features or same labels i.e., the graph smoothness. Although previous graph convolution methods gain success by capturing the smoothness of connected nodes, we still need a new methodology to enhance the low-pass performance of graph filter. In this section, we prove that graph smoothness is associated with the eigenvalues of the normalized graph Laplacian matrix, this is, it is relevant to the frequency of graph signal. Next, we analyze previous graph filters from the perspective of signal frequency response and propose AGCHK to circumvent the existing problem of previous filters.

3.1. Motivation

A graph signal $x$ can be linearly represented by the bases of the spectral domain, which are denoted as $x={\alpha }_1{u}_1+{\alpha }_2{u}_2+\dots +{\alpha }_N{u}_N$, where ${\left\{{\alpha }_i\right\}}_{i=1}^N$ is the coefficient of the eigenvector. The smoothness of a basis vector $u_q$ corresponding to the graph smoothness is measured by the Laplacian–Beltrami operator $\mathsf{\Omega }(·)$ [11], i.e.,

$$\mathsf{\Omega }\left(u_q\right)=\frac{1}{2}{\displaystyle \sum }_{\left(v_i,v_j\right)\in E}{a}_{ij}\Vert \frac{u_q\left(i\right)}{\sqrt{d_i}}-{\frac{u_q\left(j\right)}{\sqrt{d_j}}}_2^2\Vert =u_q^{T}L{u}_q={\lambda }_q,$$

(7)

where $u_q\left(i\right)$ means the $i^{th}$ element of the basis signal $u_q$, $d_i$ denotes the degree of node $v_i$, and $a_{ij}$ represents the connected weight between nodes $v_i$ and $v_j$. Equation (7) verifies that the basis signals associated with smaller eigenvalues (lower frequencies) are smoother concerning graph structures. Hence, to make the graph signal smoother, graph filters should highlight low-frequency signals by assigning larger weights to low-frequency basis signals, acting as a low-pass filter.

Based on the above principle, we analyze the weakness of previous graph filters in Section 2.2. The frequency response function in ChebyNet [10] is $g\left({\lambda }_q\right)={{\displaystyle \sum }}_{p=0}^{P-1}{\lambda }_q^p$, which assigns weight ${\lambda }_i^p$ to $u_i{u}_i^T$. Since ${\lambda }_q$ is in ascending order, i.e., $0\le {\lambda }_1^p\le {\lambda }_2^p\le \dots \le {\lambda }_N^p$, ChebyNet [10] assigns higher importance to high-frequency basis signals and discounts graph smoothness. GCN [3] defines graph convolution based on the frequency function $g\left({\lambda }_q\right)=1-{\lambda }_q$ [12], which cannot perform better low-pass characteristics as $g\left({\lambda }_q\right)$ is negative for $1<{\lambda }_q\le 2$. The frequency response function in AGC [7] is $g\left({\lambda }_q\right)=1-\frac{1}{2}{\lambda }_q$, which exploits a linear low-pass filter to suppress the high-frequency signal; however, it might not highlight low-frequency signals adequately and cannot determine the appropriate neighborhood that reflects the relevant information of smoothness.

3.2. Adaptive Graph Convolution Using Heat Kernel

3.2.1. Graph Convolution Using Heat Kernel

We propose a novel graph convolution model based on heat kernel to enhance low-frequency signals and suppress high-frequency signals, which can capture the smoothness of node features or labels sufficiently [13]. The heat kernel is defined as

$$f\left({\lambda }_q\right)=e^{-s{\lambda }_q},$$

(8)

where the scaling parameter $s>0$ determines the range of heat diffusion. The frequency response function based on heat kernel is defined as $g_{\theta }={{\displaystyle \sum }}_{p=0}^{P-1}{\theta }_p{\mathsf{\Lambda }}_s^p$ [13], where ${\mathsf{\Lambda }}_s=diag{\left\{e^{-s{\lambda }_q}\right\}}_{q=1}^N$, and graph convolution via heat kernel denotes

$$y=U{g}_{\theta }{U}^{T}x=U({\displaystyle \sum }_{p=0}^{P-1}{\theta }_p{\mathsf{\Lambda }}_s^p)U^{T}x={\displaystyle \sum }_{p=0}^{P-1}{\theta }_p{e}^{-psL}x.$$

(9)

To preserve the locality of graph convolution based on heat kernel and keep the tradeoff between low-pass performance and computational complexity, the frequency response function $g\left({\lambda }_q\right)=1+e^{-s{\lambda }_q}$ is obtained by setting $P=2$, and the associated graph filter is

$$y=\left(I+e^{-sL}\right)x.$$

(10)

The above graph filter can preserve more low-frequency signals by assigning the weight $e^{-s{\lambda }_q}$ to the basis signal $u_i{u}_i^T$, and $e^{-s{\lambda }_q}$ decreases exponentially as ${\lambda }_q$ increases. Furthermore, for datasets with different node connection structures, we can dynamically regulate the allocation strategy of various basis signal weights by adjusting the scaling coefficient $s$ of the heat kernel.

From the perspective of heat diffusion, ${(e^{-sL})}_{ij}$ reflects the similarity metric, which captures the amount of energy from node $v_i$ to node $v_j$, and a target node $v_j$ can be regarded as the neighboring node of the center node $v_i$ when the similarity metric ${(e^{-sL})}_{ij}$ between nodes $v_i$ and $v_j$ is higher than the threshold $\mathsf{\epsilon }$, which offers us a more flexible approach to define neighboring nodes of the center node and accelerates the computation by setting the threshold $\mathsf{\epsilon }$. Figure 1 depicted by the Graph Signal Processing toolbox [14] illustrates that the range of heat diffusion controlled by the scaling parameter $s$ becomes larger as $s$ increases. Different from the graph convolution methods in Section 2.2, which constrain neighboring nodes via the shortest path distance, graph convolution based on heat kernel leverages a continuous manner to determine the neighborhood, which can utilize high-order neighbor nodes sufficiently and discard some irrelevant low-order neighbor nodes [13].

Compared with the linear frequency response function $g\left({\lambda }_q\right)=1-\frac{1}{2}{\lambda }_q$ proposed in AGC [7], we leverage the exponential frequency function $g\left({\lambda }_q\right)=1+e^{-s{\lambda }_q}$ based on heat kernel, which highlights low-frequency signals exponentially to make the graph smoother. Figure 2 illustrates $g\left({\lambda }_q\right)=1+e^{-s{\lambda }_q}$ assigns larger weights to low-frequency basis signals compared with $g\left({\lambda }_q\right)=1-\frac{1}{2}{\lambda }_q$ so that connected nodes have more similar features, which indicates that graph convolution based on heat kernel might perform graph clustering better.

3.2.2. K-Order Adaptive Graph Convolution

First-order graph convolution is not sufficient to capture graph smoothness, since it updates the center node through aggregating a 1-hop neighborhood only, which might not suitable for large and sparse graphs. To make full use of node features and global structural information, we exploit $k$-order graph convolution, which is defined as

$$\overline{X}={\left(I+e^{-sL}\right)}^k\mathrm{X},$$

(11)

where $k>0$ is the order of graph convolution. Figure 2 shows that $g\left({\lambda }_q\right)={\left(I+e^{-s{\lambda }_q}\right)}^k$ becomes more low-pass as $k$ increases; that is, the filtered graph will be smoother. In particular, we normalize the node features at each iteration ($l1$ or $l2$), which scales the input vector to the unit norm.

3.2.3. Cluster Evaluation Index

According to Equation (11), the representation of connected nodes will be more similar as $k$ increases, and we perform spectral clustering on node features $\overline{X}$ filtered by graph convolution in each iteration. In detail, the pairwise similarity between nodes is measured as $S=\frac{1}{2}\left(\left|K\right|+{\left|K\right|}^T\right)$ [15], where $K=\overline{X}{\overline{X}}^T$ denotes a linear kernel. Since $K$ is symmetric and nonnegative, learning the eigenvectors of $K$ is equivalent to computing the left singular vectors of $X$ via singular value decomposition (SVD). Thus, we perform $k$-means on the left singular vectors associated with the $m$ largest eigenvalues of $X$ directly to obtain cluster partitions. Moreover, we do multiple spectral clustering in each iteration to preserve stable cluster partitions.

As the iteration goes on, the features of connected nodes will become more and more similar; this is, the intra-cluster distance is getting smaller. Figure 3 illustrates that nodes with different labels are mixed together when iteration number $k$ is smaller, while node features will be over-smoothing when iteration number $k$ is larger. To determine an appropriate iteration number $k$ comprehensively, we adopt Davies–Bouldin index (DBI) [16] as the criterion to evaluate cluster quality, which is defined as

$$DBI\left(C^k\right)=\frac{1}{m}{\displaystyle \sum }_{i=1}^m\underset{i\ne j}{\max }\frac{d_i+d_j}{r_{ij}}.$$

(12)

Denote by $m$ the number of clustering partitions, $d_i$ the average distance between each point of a cluster and the cluster centroid $i$, and $r_{ij}$ the distance between cluster centroids $i$ and $j$. The score is defined as the average similarity measure of each cluster with its most similar cluster, and clusters that are farther apart and less dispersed will result in a better (smaller) score. To stop iterating in time, we choose $k$ corresponding to the first local minimum of $DBI\left(C^k\right)$ as the most appropriate iteration number. More intuitively, considering $d\_DBI\left(k\right)=DBI\left(C^{k+1}\right)-DBI\left(C^k\right)$, we stop iterating immediately once $d\_DBI\left(k\right)>0$ as the iteration number $k$ increases and obtain the final cluster partition $C^k$. By leveraging the above strategy, AGCHK is able to capture the representation of graphs with different structures adaptively and avoid over-smoothi

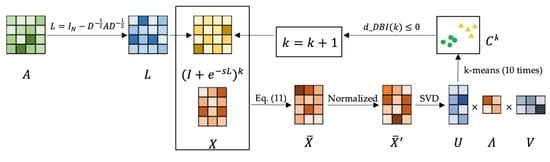
3.2.4. Architecture and Algorithm

Based on the design and analysis of the previous chapter, we summarize the proposed AGCHK algorithm as follows. Firstly, we construct a low-pass filter based on the heat kernel, which is defined as ${\left(I+e^{-sL}\right)}^k$, where $k=1$. Next, we exploit the low-pass filter to filter the original graph signals to obtain a smoother graph representation. Then, we can obtain the left singular vectors $U$ of ${\overline{X}}^k$ by the singular value decomposition and perform $k$-means on $U$ 10 times, getting the cluster partition $C^k$. Finally, we calculate the DBI of the cluster partition $C^k$; if the DBI decreases, we set $k=k+1$ and continue the above loop, else, we stop the loop, and the final cluster partition is $C^k$. Figure 4 is the architecture of the novel AGCHK model. Algorithm 1 describes in detail the algorithm of obtaining the better cluster partition by performing AGCHK. We utilize the low-pass filter based on heat kernel in the adaptive graph convolution architecture to enhance the smoothness of the graph representation, which can adaptively determine the order of graph convolution and does not require training parameters, unlike the other methods based on graph neural network [4,5,6].

Algorithm 1 AGCHK

Input: Node features $\mathit{X}$, adjacency matrix $\mathit{A}$, and maximum iteration number $\mathit{m}\mathit{a}\mathit{x}\_\mathit{i}\mathit{t}\mathit{e}\mathit{r}$. Output: Cluster partition $\mathit{C}$. 1. Initialize $\mathit{k}=0, \mathit{r}\mathit{e}\mathit{p}=0,\mathit{R}\mathit{E}\mathit{P}=10$, Compute the normalized graph Laplacian $L={\mathit{I}}_{\mathit{N}}-{\mathit{D}}^{-\frac{1}{2}}\mathit{A}{\mathit{D}}^{-\frac{1}{2}}$. 2. Compute graph filter $\mathit{I}+{\mathit{e}}^{-\mathit{s}\mathit{L}}$. 3. repeat 4.   Set $\mathit{k}=\mathit{k}+1$. 5.   Calculate $\mathit{k}$-order graph convolution by Equation (11) and obtain filtered features ${\overline{\mathit{X}}}^{\mathit{k}}$. 6.   ${\overline{\mathit{X}}}^{\mathit{k}}=\mathit{n}\mathit{o}\mathit{r}\mathit{m}\mathit{a}\mathit{l}\mathit{i}\mathit{z}\mathit{e}\left({\overline{\mathit{X}}}^{\mathit{k}}\right)$. 7.   Obtain the left singular vectors $\mathit{U}$$\mathit{of}{\overline{\mathit{X}}}^{\mathit{k}}$ by SVD. 8.   repeat 9.     Set $\mathit{r}\mathit{e}\mathit{p}=\mathit{r}\mathit{e}\mathit{p}+1$ 10.     Perform $\mathit{k}$-means on $\mathit{U}$ and obtain clustering partition ${\mathit{C}}^{\mathit{k}}$. 11.     Calculate $\mathit{D}\mathit{B}\mathit{I}\left({\mathit{C}}^{\mathit{k}}\right)\left[\mathit{r}\mathit{e}\mathit{p}\right]$ by Equation (12). 12.   $\mathbf{until}\mathit{r}\mathit{e}\mathit{p}= \mathit{R}\mathit{E}\mathit{P}$ 13.   Compute the mean of $\mathit{R}\mathit{E}\mathit{P}$ partition scores $\mathit{D}\mathit{B}\mathit{I}\left({\mathit{C}}^{\mathit{k}}\right)\left[0:\mathit{r}\mathit{e}\mathit{p}\right]$. 14. $\mathbf{until}\mathit{d}\_\mathit{D}\mathit{B}\mathit{I}\left(\mathit{k}\right)>0$ or $\mathit{t}>\mathit{m}\mathit{a}\mathit{x}\_\mathit{i}\mathit{t}\mathit{e}\mathit{r}$ 15. return final clustering partition ${\mathit{C}}^{\mathit{k}}$.

3.3. Algorithm Time Complexity

According to Algorithm 1, denote by $D$ the number of node features, $m$ the number of clusters, $N$ the number of nodes, and $rep$ the number of clustering in each iteration. The graph filter $I+e^{-sL}$ can be efficiently approximated by Chebyshev polynomials without requiring the eigendecomposition of the graph Laplacian matrix [17], and the computational complexity is $O\left(P\left|E\right|\right)$, where $P$ is the order of Chebyshev polynomial and $\left|E\right|$ is the number of edges. Such a linear complexity makes methods based on heat kernel applicable to large-scale networks [3]. After k iterations, the time complexity of calculating Equation (11) k times is $O\left(P\left|E\right|+NDk\right)$, performing spectral clustering on $X^k$ is $O\left(N^{2}Dk+N^{2}mk\right)$, and computing $DBI\left(C^k\right)$ is $O\left(\frac{1}{m}{N}^{2}Dk+m^{2}k\right)$. Note that for a spare A, $m\ll D, m\ll N^2$, the overall time complexity of AGCHK is $O\left(P\left|E\right|+NDk+N^{2}Dk\right)$. AGCHK is more time-efficient than the clustering methods based on graph neural networks, since AGCHK does not need to train parameters.

4. Experiments

4.1. Datasets

To verify the effectiveness and benefit of the proposed AGCHK for attributed graph clustering, we conduct experiments on four benchmark datasets. The dataset details are demonstrated in

Table 1. Statistics of datasets.

Dataset	Nodes	Edges	Features	Classes
Cora	2708	5429	1433	7
Citeseer	3327	4732	3703	6
Pubmed	19,717	44,338	500	3
Wiki	2405	17,981	4973	17

. Cora, Citeseer, and Pubmed [4] are citation networks whose nodes represent documents and edges are citation links. Wiki [17] is a webpage network, whose nodes are webpages and edges are link relations. The node features of Cora and Citeseer are binary word vectors, and the node features of Pubmed and Wiki are computed by the term frequency–inverse document frequency.

4.2. Baselines and Evaluation Metrics

To highlight the performance of AGCHK, we choose the same benchmark methods as AGC [7].

• Methods that only exploit node features: classic spectral clustering methods such as $k$-means and spectral-f, which perform clustering on the similarity matrix constructed by node features directly.
• Clustering methods that only handle graph structures: spectral-g clustering on the graph adjacency matrix simply, Deepwalk [2], and graph neural networks for graph representations (DNGR) [18].
• Attributed graph clustering methods utilize graph structures and graph node features jointly: AGC [7], which does not need to train graph neural network parameters, Graph neural network methods based on autoencoder such as graph autoencoder (GAE) and graph variational autoencoder (VGAE) [4], marginalized graph autoencoder (MGAE) [5], adversarially regularized graph autoencoder (ARGE), and variational graph autoencoder (ARVGE) [6].

To measure the ability of the model comprehensively, we adopt the following three cluster evaluation indexes [19]: graph clustering accuracy (Acc), normalized mutual information (NMI), and macro F1-score (F1).

4.3. Parameter Settings

For AGCHK, we set the maximum number of iterations $max\_iter$ to 20. According to Section 3.2.1, the range of heat diffusion becomes larger as the scaling parameter $s$ increases. Cora and Citeseer might have similar parameter settings since they have the close node and edge sizes, and the parameter $s$ might be smaller due to their lower quantity. Pubmed has more nodes and edges; thus, its parameter $s$ might be larger. Since Wiki has more edges and fewer nodes, we set $s$ very small so that AGCHK can leverage a fine structure. In view of the above analysis, for Cora, $s=3.3$ and $\epsilon ={10}^{-4}$, for Citeseer, $s=2$ and $\epsilon ={10}^{-5}$, for Pubmed, $s=8$ and $\epsilon ={10}^{-5}$, and for Wiki, $s=0.5$ and $\epsilon ={10}^{-5}$.

For other baseline methods, we keep the same parameter settings as the original papers. For AGC [7], we set $max\_iter$ to 60. For Deepwalk [2], denote by 10 the number of random walks, 128 the number of latent dimensions of each node, and 80 the path length of each random walk. For DNGR [18], the autoencoder is constructed by three layers, where the hidden layers are 512 neurons and 256 neurons respectively. For GAE and VGAE [4], we construct encoders with 32-neuron hidden and 16-neuron hidden layers respectively, and we use the Adam optimizer to train the encoders for 200 iterations with a learning rate 0.01. For MGAE [5], denote by 0.4 the degree of corruption level $p$, $3$ the number of layers, and ${10}^{-5}$ the coefficient $\lambda$. For ARGE and ARVGE [6], we build encoders with 32-neuron and 16-neuron hidden layers respectively, and their discriminators consist of two hidden layers, which are composed of 16 neurons and 64 neurons, respectively. On Cora, Citeseer, and Wiki, we use Adam optimizer to train ARGE and ARVGE [6] for 200 iterations, where their encoder and discriminator learning rate are both 0.001. On Pubmed, we train ARGE and ARVGE [6] for 2000 iterations, where the learning rates of the encoder and the discriminator are 0.001 and 0.008, respectively.

4.4. Result Analysis

To obtain stable clustering results, we repeat 10 experiments for each method, and the average clustering results are shown in

Table 2. Clustering performance. The best score is in bold, while the second best score is underlined. DNGR: graph neural networks for graph representations, GAE: graph autoencoder, VGAE: variational graph auto-encoder, MGAE: marginalized graph autoencoder, ARGE: adversarially regularized graph autoencoder, ARVGE: variational graph autoencoder, AGC: adaptive graph convolution.

Methods	Input	Cora			Citeseer			Pubmed			Wiki
		Acc%	NMI%	F1%	Acc%	NMI%	F1%	Acc%	NMI%	F1%	Acc%	NMI%	F1%
$k$-means	Feature	34.65	16.73	25.42	38.49	17.02	30.47	57.32	29.12	57.35	33.37	30.20	24.51
Spectral-f	Feature	36.26	15.09	25.64	46.23	21.19	33.70	59.91	32.55	58.61	41.28	43.99	25.20
Spectral-g	Graph	34.19	19.49	30.17	25.91	11.84	29.48	39.74	3.46	51.97	23.58	19.28	17.21
Deepwalk	Graph	46.74	31.75	38.06	36.15	9.66	26.70	61.86	16.71	47.06	38.46	32.38	25.38
DNGR	Graph	49.24	37.29	37.29	32.59	18.02	44.19	45.35	15.38	17.90	37.58	35.85	25.38
GAE	Both	53.25	40.69	41.97	41.26	18.34	29.13	64.08	22.97	49.26	17.33	11.93	15.35
VGAE	Both	55.95	38.45	41.50	44.38	22.71	31.88	65.48	25.09	50.95	28.67	30.28	20.49
MGAE	Both	63.43	45.57	38.01	63.56	39.75	39.49	43.88	8.16	41.98	50.14	47.97	39.20
ARGE	Both	64.00	44.90	61.90	57.30	35.00	54.60	59.12	23.17	58.41	41.40	39.50	38.27
ARVGE	Both	63.80	45.00	62.70	54.40	26.10	52.90	58.22	20.62	23.04	41.55	40.01	37.80
AGC	Both	68.92	53.68	65.61	67.00	41.13	62.48	69.78	31.59	68.72	47.65	45.28	40.36
AGCHK	Both	70.56$\pm$0.18	55.44$\pm 0.35$	67.09$\pm 0.24$	68.35$\pm 0.00$	42.25$\pm 0.00$	63.89$\pm 0.00$	70.82$\pm 0.01$	32.40 $\pm 0.01$	69.95$\pm 0.01$	60.13$\pm 0.05$	55.47$\pm 0.03$	46.27$\pm 0.02$

. Since autoencoder-based methods make use of node features and graph structures jointly, they perform better than classic spectral clustering methods that exploit node features or graph structures independently. Unfortunately, these autoencoder-based methods only utilize the 2-hop or 3-hop neighborhoods of the center node to update node representation, which is insufficient to capture global structures.

AGC [7] achieves better clustering results since it exploits adaptive graph convolution to select k-hop neighbors to aggregate information and update the central node representation. However, for Wiki that is more densely connected than other datasets, AGC [7] cannot perform well because of its weaker ability to capture smoothness.

As for our AGCHK model, it outperforms all the baseline methods, achieving state-of-the-art results on the four datasets, especially on Wiki. AGCHK implements such a smooth adaptive graph convolution by enhancing low-frequency basic filters and discounting high-frequency basic filters that it makes the representation of connected nodes smoother. Furthermore, the scaling parameter $s$ of the heat kernel is flexible to adjust the diffusion range to suit different applications and different networks. Especially for Wiki, AGCHK achieves its superiority significantly because it sets the scaling parameter $s$ smaller to leverage fine graph structure information.

To verify the reliability of the proposed cluster evaluation index $d\_DBI\left(k\right)>0$, we plot $d\_DBI\left(k\right)$ and the clustering performance w.r.t. $k$ on Cora and Wiki respectively in Figure 4. The intra-cluster distance decreases and the inter-cluster distance increases in the early iteration, which is corresponding to $d\_DBI\left(k\right)<0$. However, too many iterations will make node features over-smoothing, which leads to the inter-cluster distance rises. The cluster evaluation $d\_DBI\left(k\right)$ takes intra and inter-cluster distance comprehensively, and it can select the most appropriate $k$ to stop iterating, as shown in Figure 5. One can see that the Acc, NMI, and F1 scores evaluating clustering performance are the best or close to the best when $d\_DBI\left(k\right)$ is greater than zero the first time, which demonstrates the validity of the proposed selection evaluation index $d\_DBI\left(k\right)>0$. The selected iteration number $k$ for Cora, Citeseer, Pubmed, and Wiki is 9, 9, 13, and 8 respectively, which are all values that are lower than the respective $k$ values on these datasets in AGC [7]—12, 55, 60, and 8.

AGCHK performs very stable on benchmark datasets, and the standard deviations of Acc, NMI, and F1 are 0.18%, 0.35%, and 0.24% on Cora, 0.00%, 0.00%, and 0.00% on Citeseer, 0.01%, 0.01%, and 0.01% on Pubmed, and 0.05%, 0.03%, and 0.02% on Wiki, which are more stable than AGC [7].

We compare the time efficiency of several baseline methods as

Table 3. The running time of related methods performing on benchmark datasets. For other baselines, we follow the parameter settings in the original papers. Hardware configuration: Intel(R) Core(TM) i7-7700K CPU, 16.0 GB RAM and no GPU.

Methods	Cora	Citeseer	Pubmed	Wiki
GAE	38.72 s	57.95 s	2265.55 s	-
VGAE	41.66 s	61.34 s	2433.76 s	-
ARGE	48.49 s	68.59 s	2021.94 s	-
ARVGE	43.16 s	62.33 s	1850.21 s	-
AGC	17.46 s	111.04 s	151.71 s	22.09 s
AGCHK	8.23 s	22.92 s	854.55 s	23.64 s

, and the best score is in bold, while the second best score is underlined. We can see that the running time of AGCHK and AGC are comparable, while AGCHK is more than three times faster than the other methods. Since AGCHK does not need to train parameters, it is more efficient than the baselines based on graph neural networks.

4.5. Influence of Hyper-Parameters $s$ and $\epsilon$

To demonstrate the flexibility of the scaling parameter $s$ and the threshold $\epsilon$, we perform experiments on Cora as shown in Figure 6. For the fixed threshold $\epsilon$, Acc scores first increase and then decrease as the scaling parameter $s$ rises, i.e., sufficient neighborhood information cannot be employed when $s$ is small. On the contrast, the range of heat diffusion is large and different clusters cannot be well distinguished when $s$ is comparatively large.

For the fixed threshold $s$, good clustering results can be obtained with $s$ in a large range when $\epsilon$ is small, as many neighbors with weak relationships are excluded. However, as $\epsilon$ becomes larger, a large number of neighbor nodes with strong relationships are dropped, resulting in poor clustering. Briefly, by setting a smaller threshold $\epsilon$, noise nodes will be ignored and computation can be accelerated.

5. Conclusions

In this paper, we improve AGC [7] by utilizing heat kernel instead of the original weak linear kernel, which makes the low-pass performance of the graph filter better. The scaling parameter $s$ of heat kernel can adjust the range of heat diffusion effectively so that it is suitable for various datasets with different node and edge sizes. Besides, we redesign the clustering criterion to achieve the best clustering results in fewer $k$-order graph convolution. Our proposed method AGCHK has reached advanced levels in all four baseline datasets.