Time-Varying Dynamic Analysis of a Helical-Geared Rotor-Bearing System with Three-Dimensional Motion Due to Shaft Deformation
Abstract
:1. Introduction
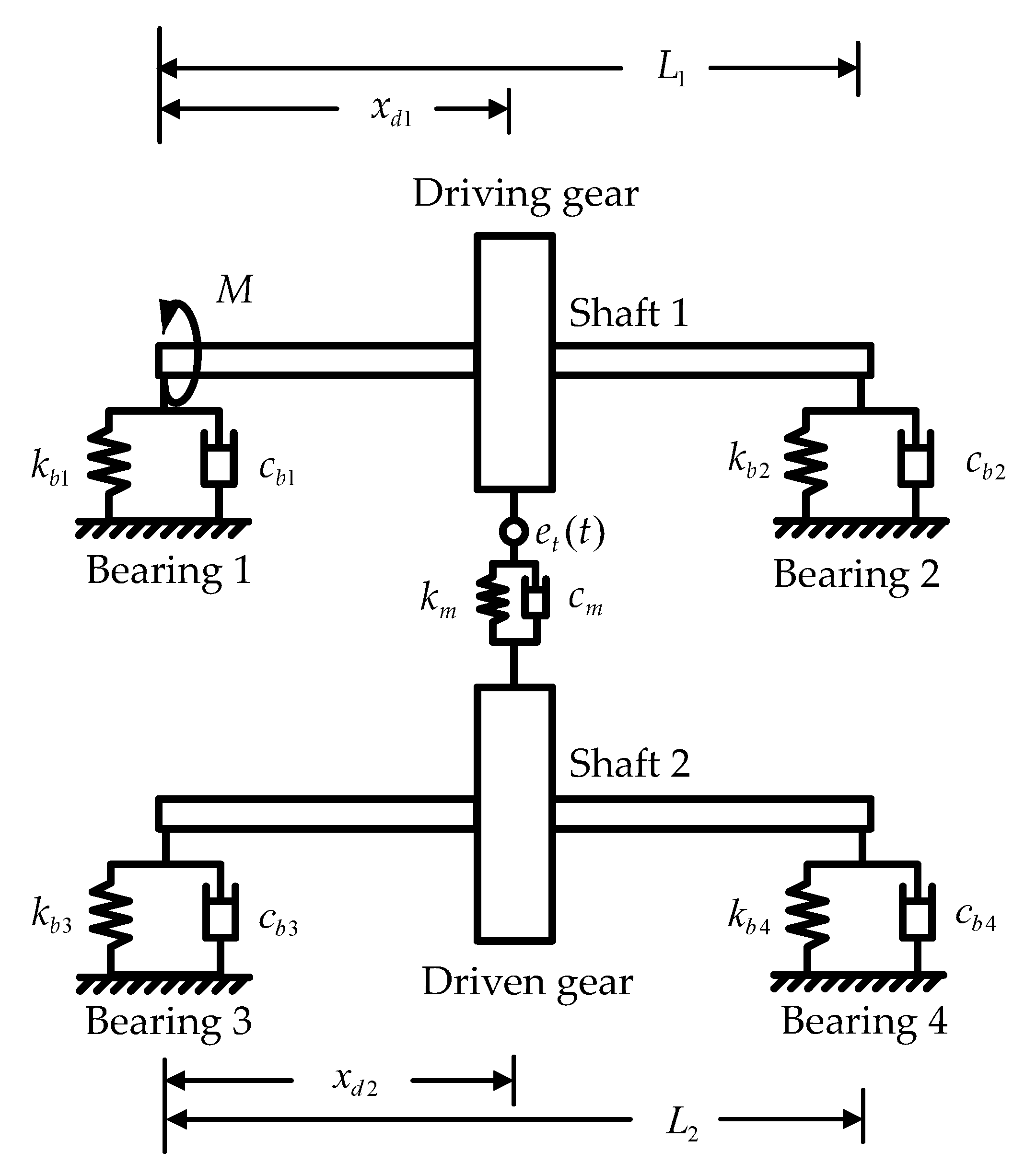
2. Dynamic Model of a Helical-Geared Rotor-Bearing System
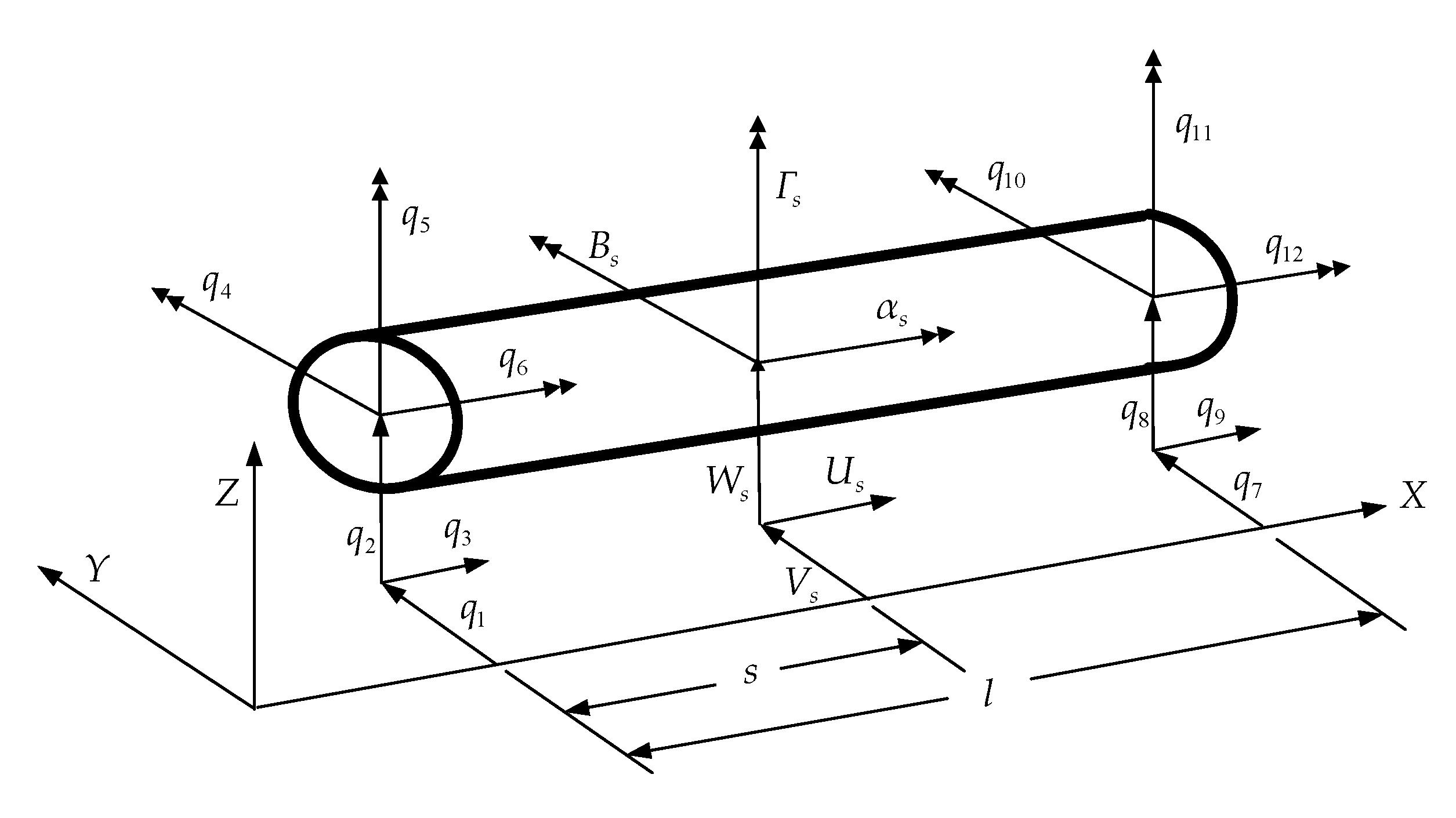
2.1. Shaft
2.2. Bearing Support
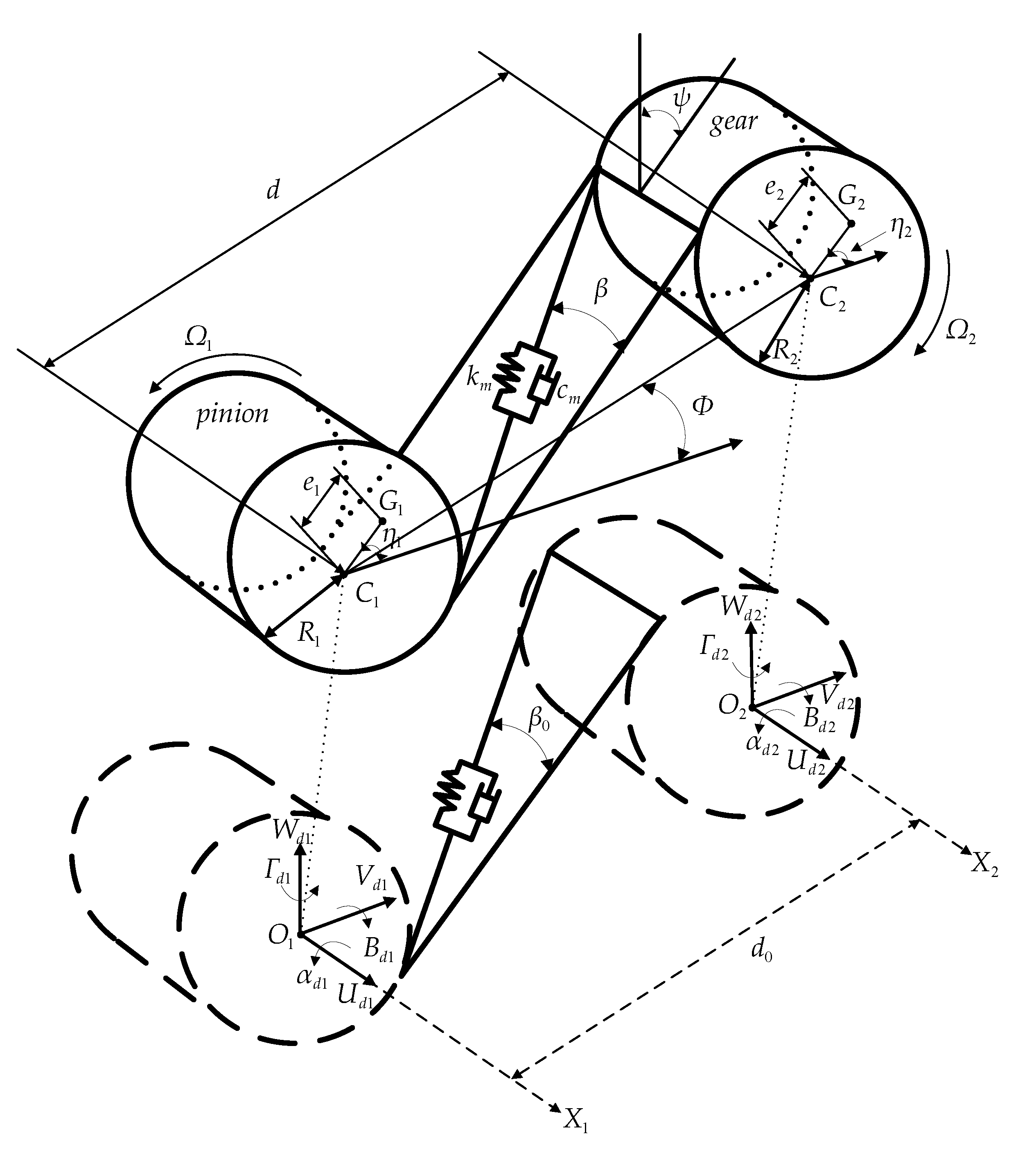
2.3. Disk and Helical Gear Pair
2.4. System Equation of Motion
3. Validation and Numerical Analysis
3.1. Dynamic Model Validation
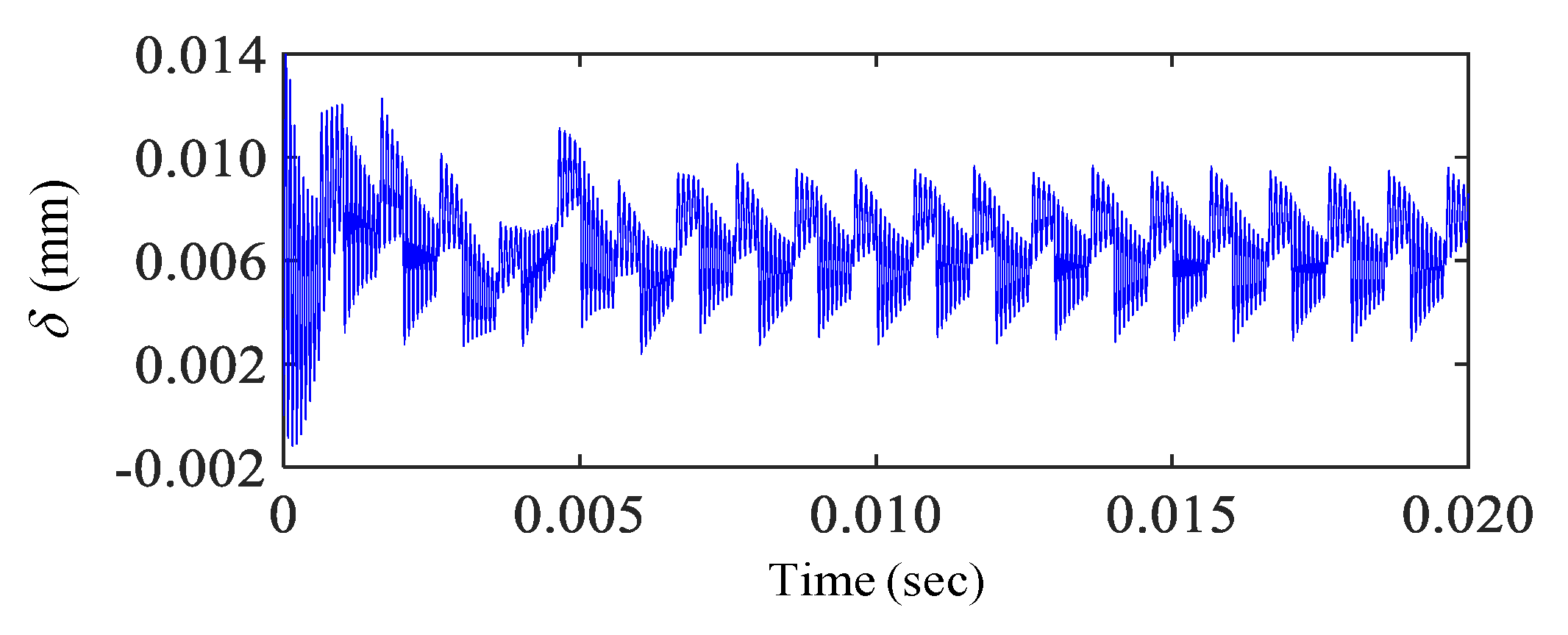
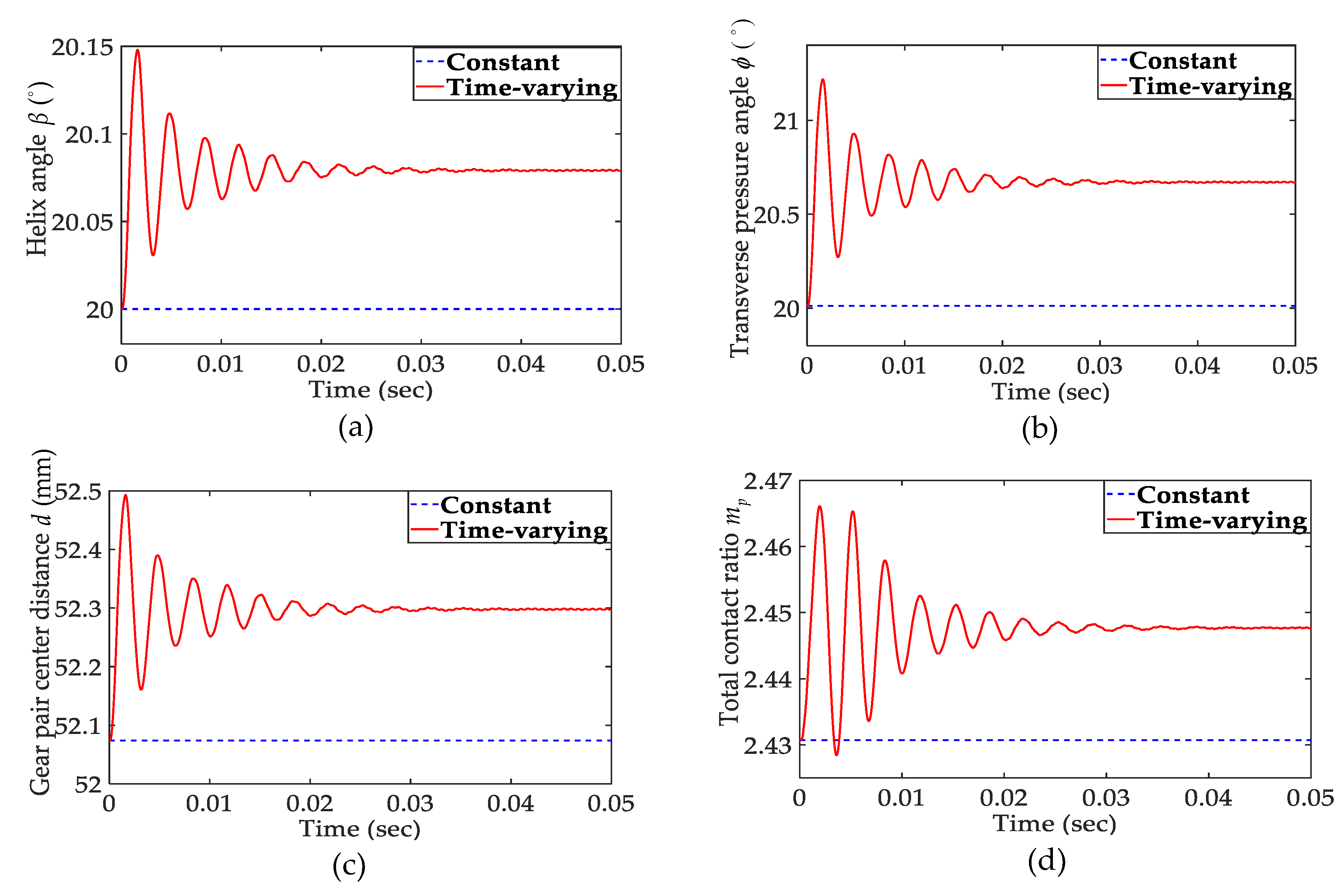
3.2. Time-Varying Effect of the Helical-Geared Rotor-Bearing System
3.3. Time-Varying Effect of the Original Helix Angle
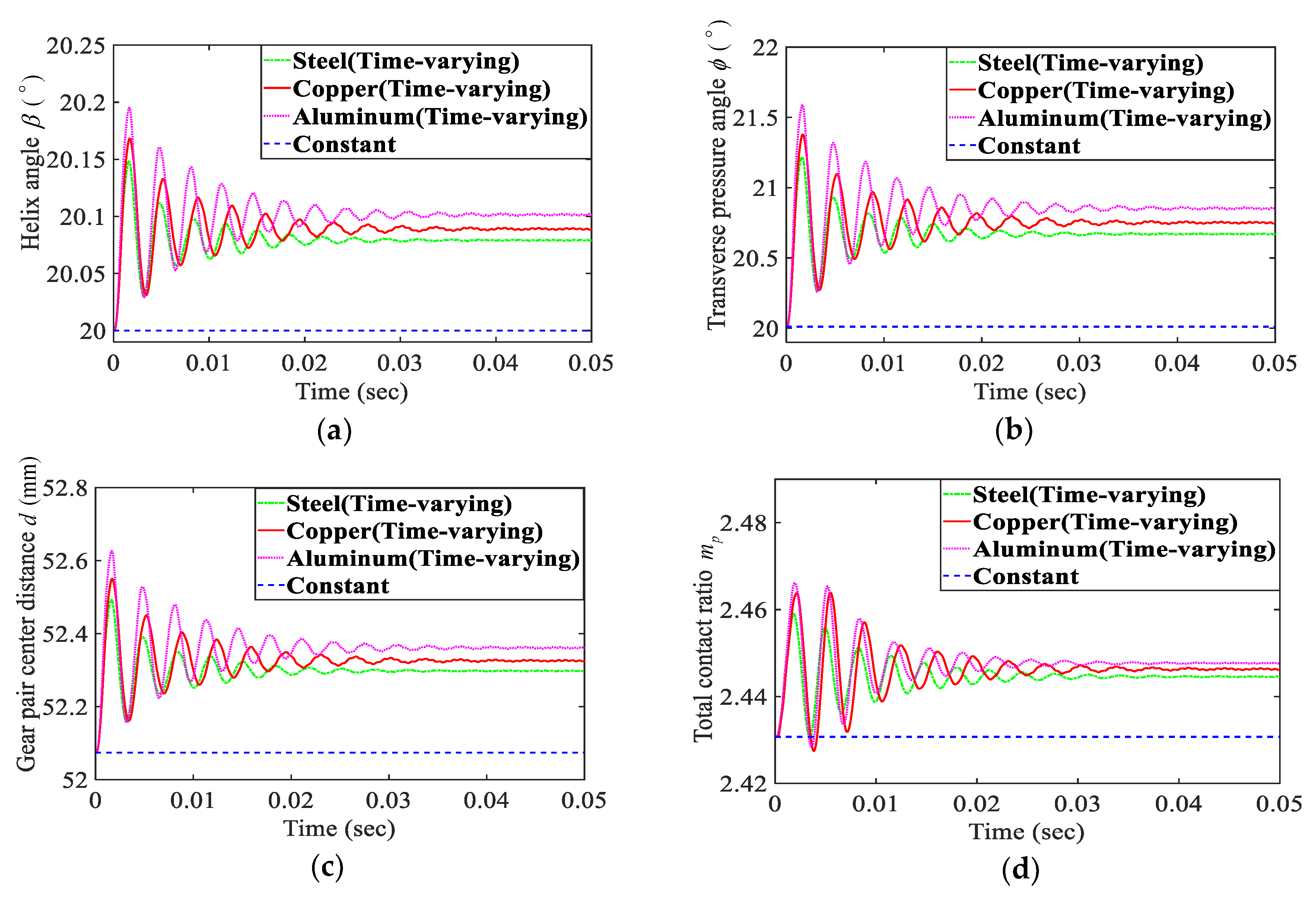
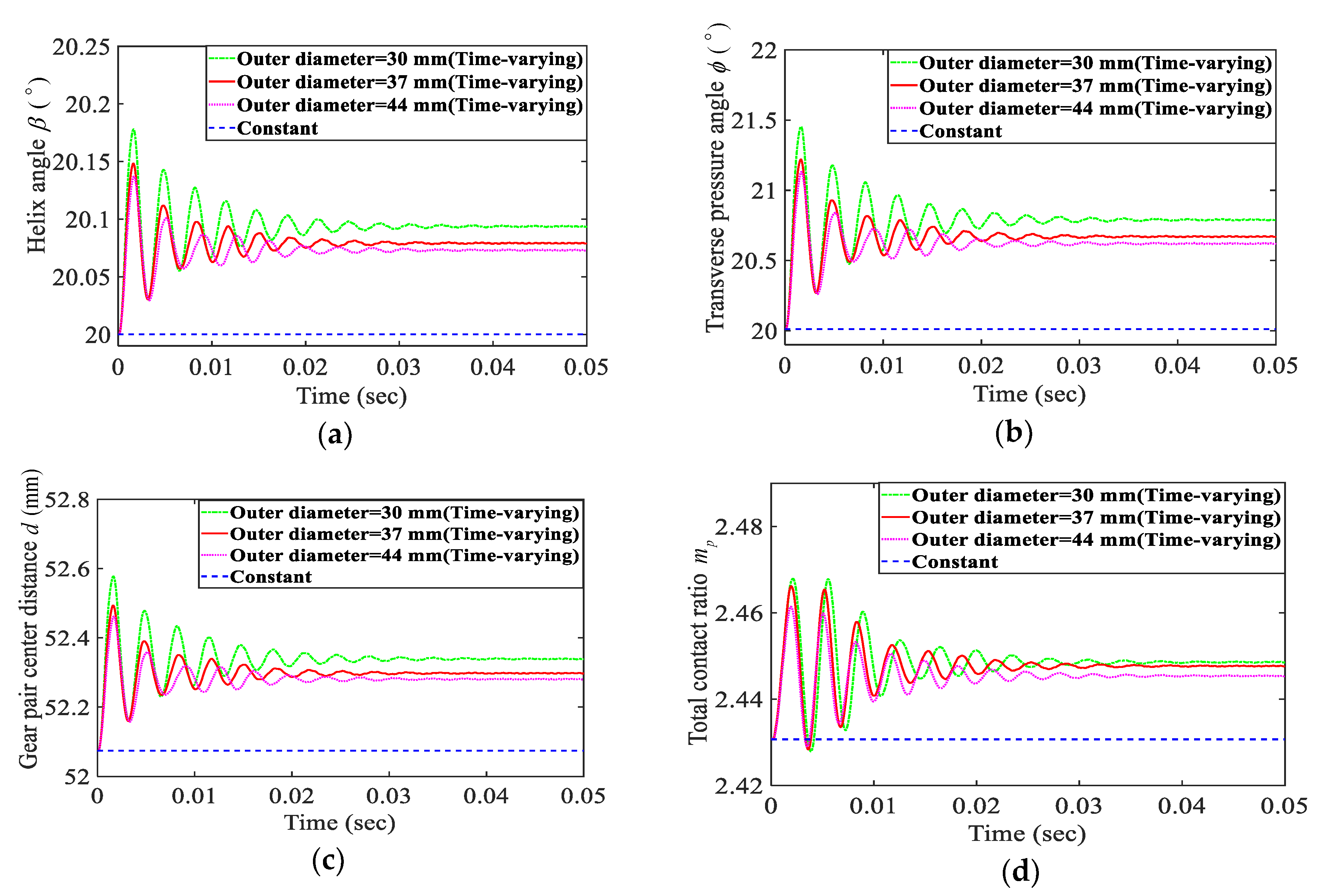
3.4. Time-Varying Effect of the Rotating Shaft Material and Outer Diameter
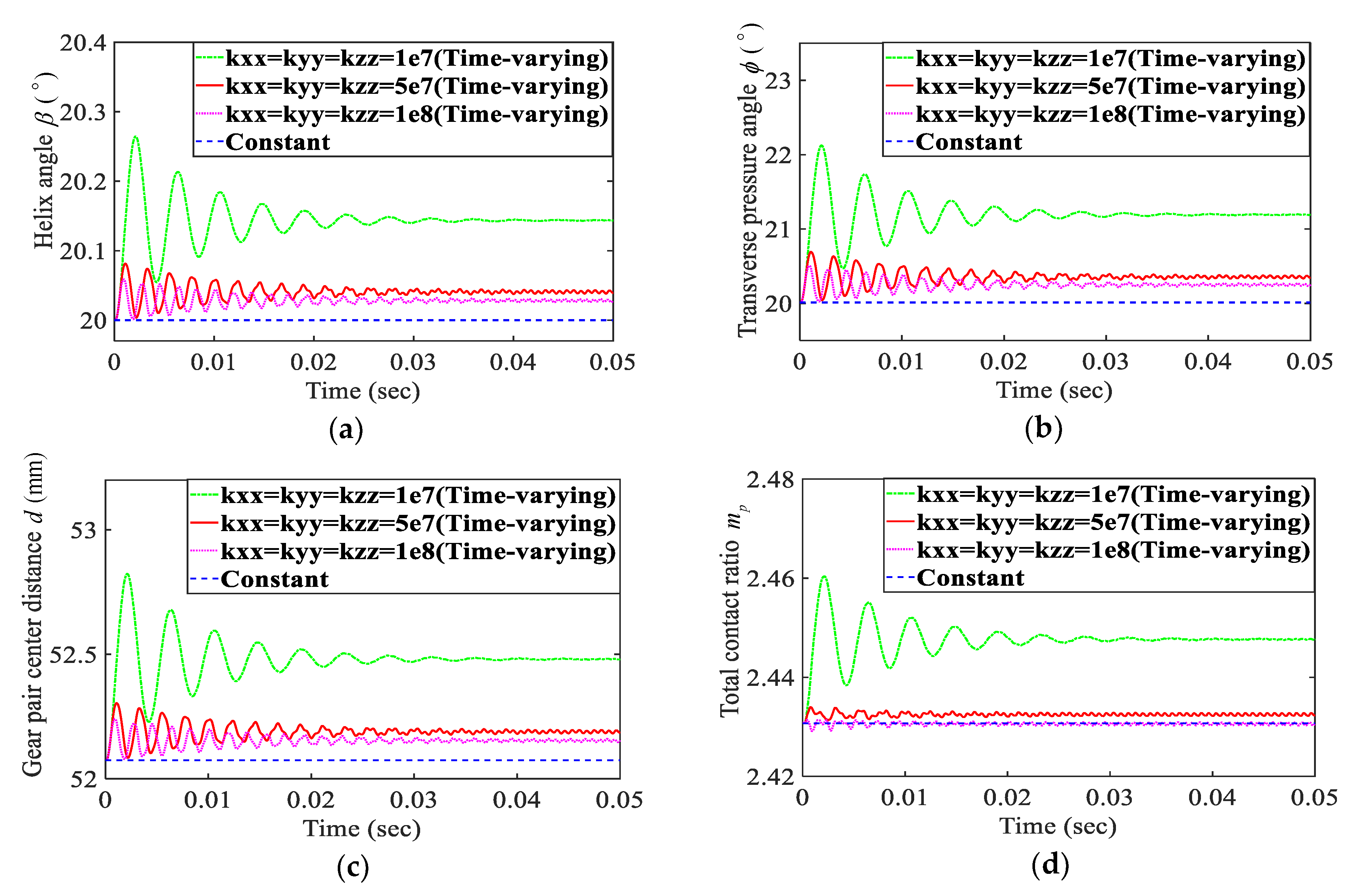
3.5. Time-Varying Effect of the Bearing Stiffness
4. Conclusions
- (1)
- This research proposed a new nonlinear dynamic model that has a time-varying helix angle, transverse pressure angle, gear pair center distance, and contact ratio. These time-varying variables provide more realistic numerical simulation values than previous models in which these aspects are considered as constant.
- (2)
- The time-varying variables for the higher initial helix angle are not negligible.
- (3)
- The time-varying variables have more influence on soft or thinner rotating shaft material and less influence on hard or thicker rotating shaft material. Similarly, the time-varying variables have a stronger influence on the common bearing stiffness and a weaker effect on the large bearing stiffness. Thus, it can be concluded that, in the case of a sufficiently soft rotating shaft or bearing, the numerical simulation results will be very different from the actual results when the time-varying effect is not considered.
- (4)
- The time-varying effect has a significant influence on the gear vibration analysis of the helical-geared rotor-bearing system and cannot be ignored. The results of this research present some useful information for gear vibration analysis.
Author Contributions
Funding
Conflicts of Interest
References
- Lalanne, M.; Ferraris, G. Rotordynamics Prediction in Engineering, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Umezawa, K.; Sato, T.; Ishikawa, J. Simulation of rotational vibration of spur gears. Bull. JSME 1984, 27, 102–109. [Google Scholar] [CrossRef] [Green Version]
- Kahraman, A.; Singh, R. Non-linear dynamics of a spur gear pair. J. Sound Vib. 1990, 142, 49–75. [Google Scholar] [CrossRef]
- Kahraman, A.; Singh, R. Non-linear dynamics of a geared rotor-bearing system with multiple clearances. J. Sound Vib. 1991, 144, 469–506. [Google Scholar] [CrossRef]
- Huang, K.J.; Liu, T.S. Dynamic analysis of a spur gear by the dynamic stiffness method. J. Sound Vib. 2000, 234, 311–329. [Google Scholar] [CrossRef] [Green Version]
- Kahraman, A. Effect of Axial Vibrations on the Dynamics of a Helical Gear Pair. J. Vib. Acoust. ASME 1993, 115, 33–39. [Google Scholar] [CrossRef]
- Kubur, M.; Kahraman, A.; Zini, D.M.; Kienzle, K. Dynamic analysis of a multi-shaft helical gear transmission by finite elements: Model and experiment. J. Vib. Acoust. ASME 2004, 126, 398–406. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Ma, H.; Huang, J. Dynamic analysis of three-dimensional helical geared rotor system with geometric eccentricity. J. Mech. Sci. Technol. 2013, 27, 3231–3242. [Google Scholar] [CrossRef]
- Bozca, M. Helix Angle Effect on the Helical Gear Load Carrying Capacity. World J. Eng. Technol. 2018, 6, 825–838. [Google Scholar] [CrossRef] [Green Version]
- Nelson, H.D. A Finite Rotating Shaft Element Using Timoshenko Beam Theory. J. Mech. Des. ASME 1980, 102, 793–803. [Google Scholar] [CrossRef]
- Kahraman, A.; Ozguven, H.N.; Houser, D.R.; Zakrajsek, J.J. Dynamics Analysis of Geared Rotors by Finite Elements. J. Mech. Des. ASME 1992, 114, 507–514. [Google Scholar] [CrossRef]
- Shiau, T.N.; Choi, S.T.; Chang, J.R. Theoretical Analysis of Lateral Response Due to Torsional Excitation of Geared Rotors. Mech. Mach. Theory 1998, 33, 761–783. [Google Scholar]
- Choi, S.T.; Mau, S.Y. Dynamic Analysis of Geared Rotor-Bearing Systems by the Transfer Matrix Method. J. Mech. Des. ASME 2001, 123, 562–568. [Google Scholar] [CrossRef]
- Chen, Y.C. Effect of residual shaft bow on the dynamic analysis of a double-stage geared rotor-bearing system with translational motion due to shaft deformation. Adv. Mech. Eng. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Prabel, B. Some Remarks on Time Integration of 3D Rotor-Stator Assembly. In Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016. [Google Scholar]
- Ozguven, H.N.; Houser, D.R. Dynamic analysis of high speed gears by using loaded static transmission error. J. Sound Vib. 1988, 125, 71–83. [Google Scholar] [CrossRef]
- Kim, W.; Yoo, J. Dynamic analysis for a pair of spur gears with translational motion due to bearing deformation. J. Sound Vib. 2010, 329, 4409–4421. [Google Scholar] [CrossRef]
- Saxena, A.; Parey, A.; Chouksey, M. Time varying mesh stiffness calculation of spur gear pair considering sliding friction and spalling defects. Eng. Fail. Anal. 2016, 70, 200–211. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, B.; Fu, Y.; Kong, X.; Ma, H. An improved time-varying mesh stiffness model for helical gear pairs considering axial mesh force component. Mech. Syst. Signal Process. 2018, 106, 413–429. [Google Scholar] [CrossRef]
- Yi, Y.; Huang, K.; Xiong, Y.; Sang, M.; Ma, H. Nonlinear dynamic modelling and analysis for a spur gear system with time-varying pressure angle and gear backlash. Mech. Syst. Signal Process. 2019, 132, 18–34. [Google Scholar] [CrossRef]
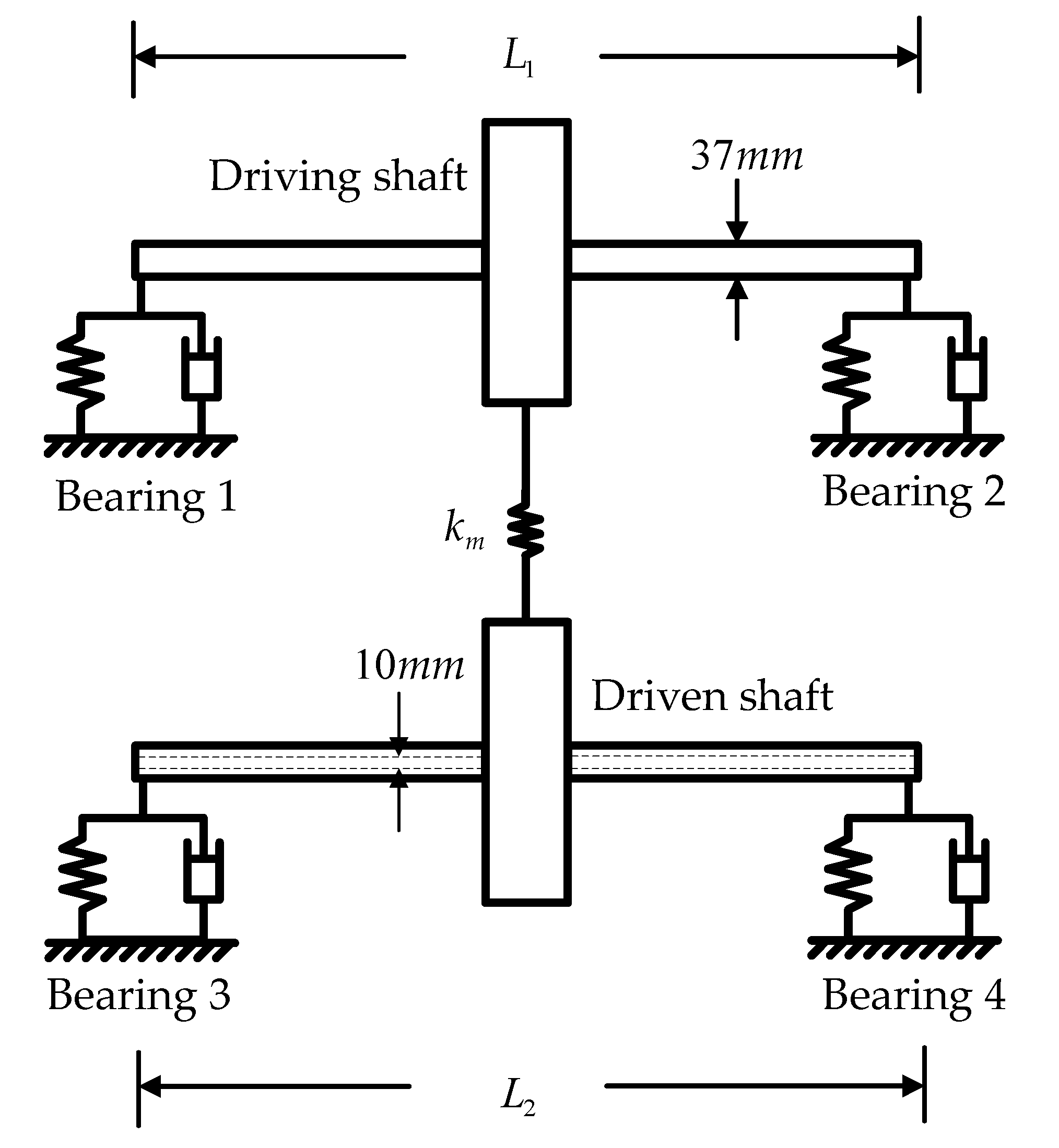
| Parameters | Pinion | Gear |
|---|---|---|
| Tooth number | 20 | 30 |
| Base circle radius (mm) | 18.8 | 28.2 |
| Addendum circle radius (mm) | 22 | 32 |
| Mass (kg) | 0.0784 | 0.1765 |
| Mass moment of inertia (kg-m2) | 1.39 × 10−5 | 7.01 × 10−5 |
| Radial damping coefficient (N-sec/m) | 5.6 | 8.4 |
| Mesh stiffness during one-pair contact (N/m) | 0.75 × 108 | |
| Mesh stiffness during two-pair contact (N/m) | 1.25 × 108 | |
| Shaft | ||
| Parameters | Driving Shaft | Driven Shaft |
| Shaft length (mm) | 254 | 254 |
| Outer diameter (mm) | 37 | 37 |
| Inner diameter (mm) | 0 | 10 |
| Modulus of elasticity (Gpa) | 207.8 | |
| Density of material (kg/m3) | 7806 | |
| Poisson’s ratio | 0.3 | |
| Gear | ||
| Parameters | Driving Gear | Driven Gear |
| Tooth number | 28 | 28 |
| Base circle radius (mm) | 44.5 | 44.5 |
| Mass (kg) | 1.84 | 1.84 |
| Mass moment of inertia (kg-m2) | 0.0009 | 0.0009 |
| Polar mass moment of inertia (kg-m2) | 0.0018 | 0.0018 |
| Gear mesh stiffness (N/m) | 1 × 108 | |
| Bearing Parameters | ||
| All radial bearing stiffness (N/m) | 1 × 109 | |
| Mode No. | Natural Frequency (rad/s) | Relative Errors (%) | Mode Description | |
|---|---|---|---|---|
| Present | Ref. [8] | |||
| 1 | 3574 | 3583 | −0.26 | coupled lateral-torsional |
| 2 | 4225 | 4237 | −0.29 | 1st lateral, Y-direction, driving shaft |
| 3 | 4237 | 4245 | −0.20 | coupled lateral-torsional |
| 4 | 4250 | 4246 | 0.09 | 1st lateral, Z-direction, driven shaft |
| 5 | 15,804 | 15,816 | −0.08 | coupled lateral-torsional |
| 6 | 20,643 | 20,796 | −0.74 | 2nd lateral, Y-direction, driving shaft |
| 7 | 20,643 | 20,796 | −0.74 | 2nd lateral, Z-direction, driving shaft |
| 8 | 20,978 | 21,084 | −0.50 | 2nd lateral, Y-direction, driven shaft |
| 9 | 20,978 | 21,084 | −0.50 | 2nd lateral, Z-direction, driven shaft |
| 10 | 38,093 | 38,336 | −0.64 | 3rd lateral, Y-direction, driving shaft |
| 11 | 38,143 | 38,374 | −0.60 | coupled lateral-torsional |
| 12 | 38,235 | 38,432 | −0.51 | 3rd lateral, Y-direction, driven shaft |
| 13 | 38,406 | 38,614 | −0.54 | coupled lateral-torsional |
| Shaft | ||
| Parameters | Driving Shaft | Driven Shaft |
| Shaft length (mm) | 254 | 254 |
| Outer diameter (mm) | 37 | 37 |
| Inner diameter (mm) | 0 | 0 |
| Modulus of elasticity (Gpa) | 207.8 | |
| Density of material (kg/m3) | 7806 | |
| Poisson’s ratio | 0.3 | |
| Gear | ||
| Parameters | Driving Gear | Driven Gear |
| Tooth number | 28 | 28 |
| Base circle radius (mm) | 24.4 | 24.4 |
| Addendum circle radius (mm) | 28.4 | 28.4 |
| Mass (kg) | 1.84 | 1.84 |
| Mass moment of inertia (kg-m2) | 0.0009 | 0.0009 |
| Polar mass moment of inertia (kg-m2) | 0.0018 | 0.0018 |
| Face width (mm) | 17.4 | 17.4 |
| Pitch diameter (mm) | 52.07 | 52.07 |
| Initial transverse pressure angle (degree) | 20 | |
| Initial helix angle (degree) | 20 | |
| Mesh stiffness during two teeth contact (N/m) | 1.9 × 108 | |
| Mesh stiffness during three teeth contact (N/m) | 2.4 × 108 | |
| Bearing Parameters | ||
| All radial bearing stiffness (N/m) | 2 × 107 | |
| All axial bearing stiffness (N/m) | 1 × 107 | |
| Initial Helix Angle (Degree) | 15 | 20 | 25 | 30 | 35 |
|---|---|---|---|---|---|
| The Difference Values between Time-Varying and Constant Conditions | |||||
| Helix angle | 0.061 | 0.0793 | 0.0954 | 0.1092 | 0.1203 |
| Transverse pressure angle | 0.666 | 0.671 | 0.675 | 0.681 | 0.686 |
| Gear pair center distance | 0.2218 | 0.2243 | 0.2265 | 0.2295 | 0.2332 |
| Total contact ratio | 0.0125 | 0.01696 | 0.02173 | 0.02689 | 0.03264 |
| Steel | Copper | Aluminum Alloys | |
|---|---|---|---|
| Modulus of elasticity (Gpa) | 207.8 | 115 | 73 |
| Density of material (kg/m3) | 7806 | 8900 | 2800 |
| Poisson’s ratio | 0.3 | 0.35 | 0.33 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-C. Time-Varying Dynamic Analysis of a Helical-Geared Rotor-Bearing System with Three-Dimensional Motion Due to Shaft Deformation. Appl. Sci. 2020, 10, 1542. https://doi.org/10.3390/app10041542
Chen Y-C. Time-Varying Dynamic Analysis of a Helical-Geared Rotor-Bearing System with Three-Dimensional Motion Due to Shaft Deformation. Applied Sciences. 2020; 10(4):1542. https://doi.org/10.3390/app10041542
Chicago/Turabian StyleChen, Ying-Chung. 2020. "Time-Varying Dynamic Analysis of a Helical-Geared Rotor-Bearing System with Three-Dimensional Motion Due to Shaft Deformation" Applied Sciences 10, no. 4: 1542. https://doi.org/10.3390/app10041542
APA StyleChen, Y.-C. (2020). Time-Varying Dynamic Analysis of a Helical-Geared Rotor-Bearing System with Three-Dimensional Motion Due to Shaft Deformation. Applied Sciences, 10(4), 1542. https://doi.org/10.3390/app10041542





