EEG-Based Emotion Recognition Using Logistic Regression with Gaussian Kernel and Laplacian Prior and Investigation of Critical Frequency Bands
Abstract
:1. Introduction
2. Materials and Methods
2.1. DEAP Dataset and Pre-Processing
2.2. Feature Extraction
2.3. Logistic Regression with Gaussian Kernel and Laplacian Prior
3. Experimental Results
3.1. Overall Classification Accuracy
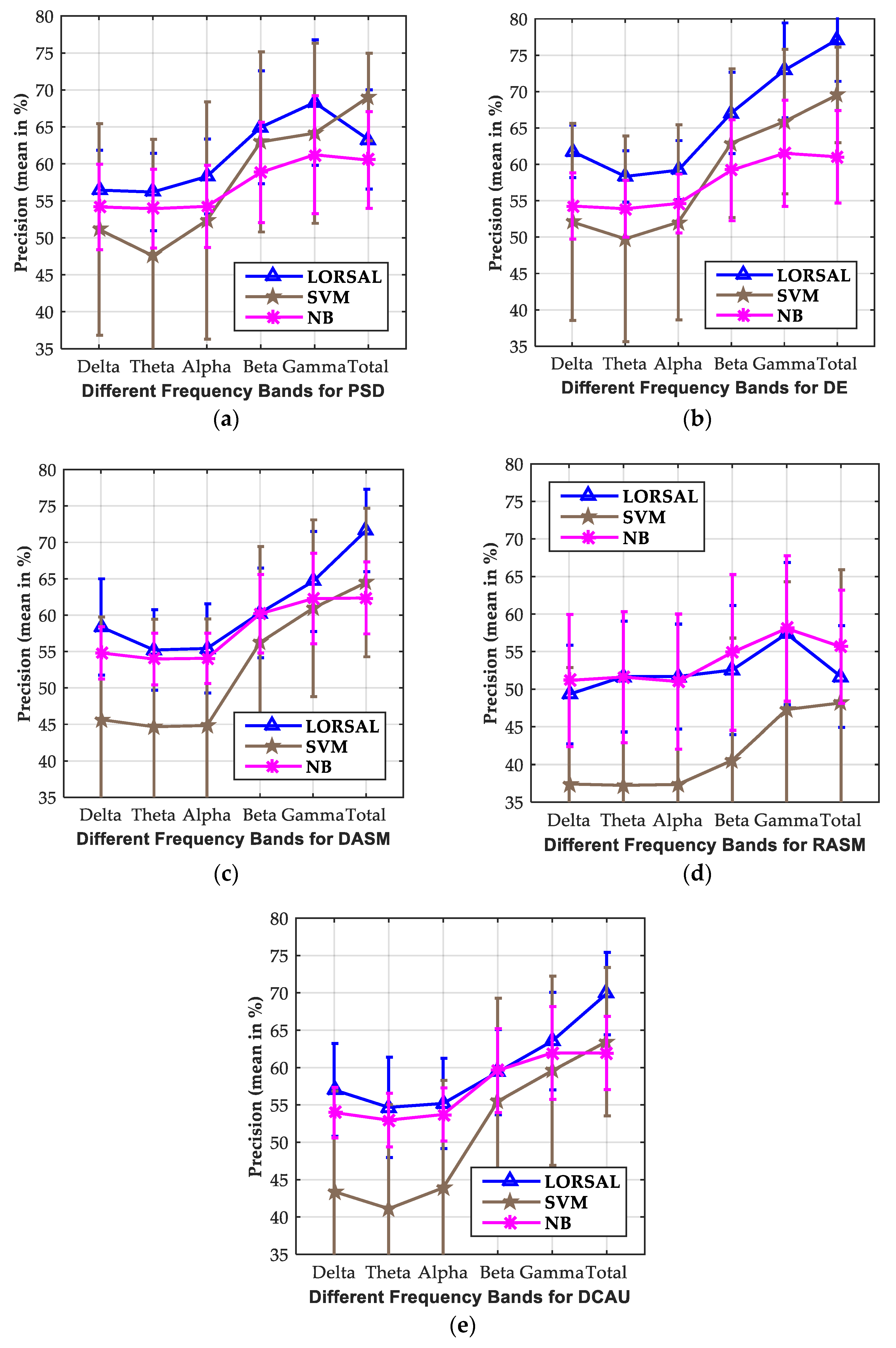
3.2. Investigation of Critical Frequency Bands
3.3. Effect of Extracted Features
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Picard, R.W. Affective Computing; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Levenson, R.W. The autonomic nervous system and emotion. Emotion Rev. 2014, 6, 100–112. [Google Scholar] [CrossRef]
- Bota, P.J.; Wang, C.; Fred, A.L.; Da Silva, H.P. A review, current challenges, and future possibilities on emotion recognition using machine learning and physiological signals. IEEE Access 2019, 7, 140990–141020. [Google Scholar] [CrossRef]
- Shu, L.; Xie, J.; Yang, M.; Li, Z.; Li, Z.; Liao, D.; Xu, X.; Yang, X. A review of emotion recognition using physiological signals. Sensors 2018, 8, 2074. [Google Scholar] [CrossRef] [Green Version]
- Cannon, W.B. The James-Lange theory of emotions: A critical examination and an alternative theory. Am. J. Psychol. 1927, 39, 106–124. [Google Scholar] [CrossRef]
- Ayaz, H.; Curtin, A.; Mark, J.; Kraft, A.; Ziegler, M. Predicting Future Performance based on Current Brain Activity: An fNIRS and EEG Study. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 3925–3930. [Google Scholar]
- Saadati, M.; Nelson, J.; Ayaz, H. Convolutional Neural Network for Hybrid fNIRS-EEG Mental Workload Classification. In Proceedings of the International Conference on Applied Human Factors and Ergonomics, Washington, DC, USA, 24–28 July 2019; pp. 221–232. [Google Scholar]
- Jiao, Z.; Gao, X.; Wang, Y.; Li, J.; Xu, H. Deep Convolutional Neural Networks for mental load classification based on EEG data. Pattern Recognit. 2018, 76, 582–595. [Google Scholar] [CrossRef]
- Sargent, A.; Heiman-Patterson, T.; Feldman, S.; Shewokis, P.A.; Ayaz, H. Mental Fatigue Assessment in Prolonged BCI Use Through EEG and fNIRS.-Neuroergonomics; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Abdul, A.; Chen, J.; Liao, H.Y.; Chang, S.H. An emotion-aware personalized music recommendation system using a convolutional neural networks approach. Appl. Sci. 2018, 8, 1103. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Z.; You, H.; Yang, F.; Li, X.; Zhang, H.; Shen, D. Decoding EEG by visual-guided deep neural networks. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 1387–1393. [Google Scholar]
- Ren, Z.; Li, J.; Xue, X.; Li, X.; Yang, F.; Jiao, Z.; Gao, X. Reconstructing Perceived Images from Brain Activity by Visually-guided Cognitive Representation and Adversarial Learning. arXiv 2019, arXiv:1906.12181. [Google Scholar]
- Lotte, F.; Congedo, M.; Lécuyer, A.; Lamarche, F.; Arnaldi, B. A review of classification algorithms for EEG-based brain–computer interfaces. J. Neural Eng. 2007, 4, R1–R13. [Google Scholar] [CrossRef] [PubMed]
- Lotte, F.; Bougrain, L.; Cichocki, A.; Clerc, M.; Congedo, M.; Rakotomamonjy, A.; Yger, F. A review of classification algorithms for EEG-based brain–computer interfaces: A 10 year update. J. Neural Eng. 2018, 15, 031005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Russell, J.A. A circumplex model of affect. J. Personal. Soc. Psychol. 1980, 39, 1161–1178. [Google Scholar] [CrossRef]
- Kim, M.-K.; Kim, M.; Oh, E.; Kim, S.-P. A review on the computational methods for emotional state estimation from the human EEG. Comput. Math. Methods Med. 2013, 2013, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cacioppo, J.T. Feelings and emotions: Roles for electrophysiological markers. Biol. Psychol. 2004, 67, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Sanei, S.; Chambers, J. EEG Signal Processing; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Al-Nafjan, A.; Hosny, M.; Al-Ohali, Y.; Al-Wabil, A. Review and classification of emotion recognition based on EEG brain-computer interface system research: A systematic review. Appl. Sci. 2017, 7, 1239. [Google Scholar] [CrossRef] [Green Version]
- Kroupi, E.; Vesin, J.M.; Ebrahimi, T. Subject-independent odor pleasantness classification using brain and peripheral signals. IEEE Trans. Affect. Comput. 2016, 7, 422–434. [Google Scholar] [CrossRef]
- Zhang, J.H.; Chen, M.; Zhao, S.K.; Hu, S.Q.; Shi, Z.G.; Cao, Y. Relieff-based EEG sensor selection methods for emotion recognition. Sensors 2016, 16, 1558. [Google Scholar] [CrossRef]
- Chew, L.H.; Teo, J.; Mountstephens, J. Aesthetic preference recognition of 3d shapes using EEG. Cogn. Neurodyn. 2016, 10, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Alelyani, S.; Liu, H. Feature Selection for Classification: A Review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; pp. 37–64. [Google Scholar]
- Chao, G.; Luo, Y.; Ding, W. Recent advances in supervised dimension reduction: A Survey. Mach. Learn. Knowl. Extr. 2019, 1, 20. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.-P.; Wang, C.-H.; Wu, T.-L.; Jeng, S.-K.; Chen, J.-H. EEG-based emotion recognition in music listening: A comparison of schemes for multiclass support vector machine. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 489–492. [Google Scholar]
- Horlings, R.; Datcu, D.; Rothkrantz, L.J.M. Emotion recognition using brain activity. In Proceedings of the 9th International Conference on Computer Systems and Technologies and Workshop for PhD students in Computing, Gabrovo, Bulgaria, 12–13 June 2008; ACM: New York, NY, USA, 2008. [Google Scholar]
- Koelstra, S.; Muhl, C.; Soleymani, M.; Lee, J.S.; Yazdani, A.; Ebrahimi, T.; Pun, T.; Nijholt, A.; Patras, I. DEAP: A database for emotion analysis; using physiological signals. IEEE Trans. Affect. Comput. 2012, 3, 18–31. [Google Scholar] [CrossRef] [Green Version]
- Craik, A.; He, Y.; Contreras-Vidal, J.L. Deep learning for electroencephalogram (EEG) classification tasks: A review. J. Neural Eng. 2019, 16, 031001. [Google Scholar] [CrossRef]
- Roy, Y.; Banville, H.; Albuquerque, I.; Gramfort, A.; Falk, T.H.; Faubert, J. Deep learning-based electroencephalography analysis: A systematic review. J. Neural Eng. 2019, 16, 051001. [Google Scholar] [CrossRef]
- Zheng, W.L.; Zhu, J.Y.; Peng, Y.; Lu, B.L. EEG-based emotion classification using deep belief networks. In Proceedings of the 2014 IEEE International Conference on Multimedia and Expo (ICME), Chengdu, China, 14–18 July 2014; pp. 1–6. [Google Scholar]
- Zheng, W.L.; Guo, H.T.; Lu, B.L. Revealing critical channels and frequency bands for emotion recognition from EEG with deep belief network. In Proceedings of the 2015 7th International IEEE/EMBS Conference on Neural Engineering (NER), Montpellier, France, 22–24 April 2015; pp. 154–157. [Google Scholar]
- Yang, Y.; Wu, Q.; Qiu, M.; Wang, Y.; Chen, X. Emotion recognition from multi-channel EEG through parallel convolutional recurrent neural network. In Proceedings of the International Joint Conference on Neural Networks, Rio, Brasil, 8–13 July 2018; pp. 1–7. [Google Scholar]
- Chen, J.X.; Zhang, P.W.; Mao, Z.J.; Huang, Y.F.; Jiang, D.M.; Zhang, Y.N. Accurate EEG-based emotion recognition on combined features using deep convolutional neural networks. IEEE Access 2019, 7, 44317–44328. [Google Scholar] [CrossRef]
- Chen, J.X.; Jiang, D.M.; Zhang, Y.N. A hierarchical bidirectional GRU model with attention for EEG-based emotion classification. IEEE Access 2019, 7, 118530–118540. [Google Scholar] [CrossRef]
- Martinez, H.P.; Bengio, Y.; Yannakakis, G.N. Learning deep physiological models of affect. IEEE Comput. Intell. Mag. 2013, 8, 20–33. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.X.; Mao, Z.J.; Yao, W.X.; Huang, Y.F. EEG-based biometric identification with convolutional neural network. Multimed. Tools Appl. 2019, 1–21. [Google Scholar] [CrossRef]
- Lee, J.; Yoo, S.K. Design of user-customized negative emotion classifier based on feature selection using physiological signal sensors. Sensors 2018, 18, 4253. [Google Scholar] [CrossRef] [Green Version]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Alkan, A.; Koklukaya, E.; Subasi, A. Automatic seizure detection in EEG using logistic regression and artificial neural network. J. Neurosci. Methods 2005, 148, 167–176. [Google Scholar] [CrossRef]
- Subasi, A.; Ercelebi, E. Classification of EEG signals using neural network and logistic regression. Comput. Methods Programs Biomed. 2005, 78, 87–99. [Google Scholar] [CrossRef]
- Tomioka, R.; Aihara, K.; Müller, K.R. Logistic regression for single trial EEG classification. In Advances in Neural Information Processing Systems 19, Proceedings of the Twentieth Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Ezzyat, Y.; Kragel, J.E.; Burke, J.F.; Levy, D.F.; Lyalenko, A.; Wanda, P.; O’Sullivan, L.; Hurley, K.B.; Busygin, S.; Pedisich, I.; et al. Direct brain stimulation modulates encoding states and memory performance in humans. Curr. Biol. 2017, 27, 1–8. [Google Scholar] [CrossRef]
- Arora, A.; Lin, J.J.; Gasperian, A.; Maldjian, J.; Stein, J.; Kahana, M.; Lega, B. Comparison of logistic regression, support vector machines, and deep learning classifiers for predicting memory encoding success using human intracranial EEG recordings. J. Neural Eng. 2018, 15, 066028. [Google Scholar] [CrossRef]
- Krishnapuram, B.; Carin, L.; Figueiredo, M.A.T.; Member, S. Sparse multinomial logistic regression: Fast algorithms and generalization bounds. IEEE Trans. Pat. Anal. Mach. Intell. 2005, 27, 957–968. [Google Scholar] [CrossRef] [Green Version]
- Bioucas-Dias, J.; Figueiredo, M. Logistic Regression via Variable Splitting and Augmented Lagrangian Tools; Instituto Superior Técnico: Lisboa, Portugal, 2009. [Google Scholar]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Hyperspectral image segmentation using a new Bayesian approach with active learning. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3947–3960. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.L.; Lu, B.L. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks. IEEE Trans. Auton. Ment. Dev. 2015, 7, 162–175. [Google Scholar] [CrossRef]
- Zheng, W.L.; Zhu, J.Y.; Lu, B.L. Identifying stable patterns over time for emotion recognition from EEG. IEEE Trans. Affect. Comput. 2019, 10, 417–429. [Google Scholar] [CrossRef] [Green Version]
- Bradley, M.M.; Lang, P.J. Measuring emotion: The self-assessment manikin and the semantic differential. J. Behav. Ther. Exp. Psychiatry 1994, 25, 49–59. [Google Scholar] [CrossRef]
- Jenke, R.; Peer, A.; Buss, M. Feature extraction and selection for emotion recognition from EEG. IEEE Trans. Affect. Comput. 2014, 5, 327–339. [Google Scholar] [CrossRef]
- Balconi, M.; Mazza, G. Brain oscillations and BIS/BAS (behavioral inhibition/activation system) effects on processing masked emotional cues: ERS/ERD and coherence measures of alpha band. Int. J. psychophysiol. 2009, 74, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Bos, D.O. EEG-based emotion recognition The Influence of Visual and Auditory Stimuli. Emotion 2006, 1359, 667–670. [Google Scholar]
- Chanel, G.; Karim, A.-A.; Thierry, P. Valence-arousal evaluation using physiological signals in an emotion recall paradigm. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007. [Google Scholar]
- Lin, Y.P.; Wang, C.H.; Jung, T.P.; Wu, T.L.; Jeng, S.K.; Duann, J.R.; Chen, J.H. EEG-based emotion recognition in music listening. IEEE Trans. Biomed. Eng. 2010, 57, 1798–1806. [Google Scholar]
- Shi, L.; Jiao, Y.; Lu, B. Differential entropy feature for EEG-based vigilance estimation. In Proceedings of the 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 6627–6630. [Google Scholar]
- Duan, R.; Zhu, J.; Lu, B. Differential entropy feature for EEG-based emotion classification. In Proceedings of the 6th International IEEE/EMBS Conference on Neural Engineering (NER), San Diego, CA, USA, 6–8 November 2013; pp. 81–84. [Google Scholar]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics—Developed with Especial Reference to the Rational Foundation of Thermodynamics; C. Scribner’s Sons: New York, NY, USA, 1902. [Google Scholar]
- Davidson, R.; Fox, N. Asymmetrical brain activity discriminates between positive and negative stimuli infants. Science 1982, 218, 1235–1237. [Google Scholar] [CrossRef]
- Lin, Y.P.; Yang, Y.H.; Jung, T.P. Fusion of electroencephalographic dynamics and musical contents for estimating emotional responses in music listening. Front. Neurosci. 2014, 8, 94. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Semi-supervised hyperspectral image segmentation using multinomial logistic regression with active learning. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4085–4098. [Google Scholar]
- Hunter, D.R.; Lange, K. A tutorial on MM algorithms. Amer. Statistician 2004, 58, 30–37. [Google Scholar] [CrossRef]
- Borges, J.S.; Bioucas-Dias, J.M.; Marçal, A.R.S. Fast Sparse Multinomial Regression Applied to Hyperspectral Data. In Proceedings of the Third International Conference on Image Analysis and Recognition—Volume Part II, Póvoa de Varzim, Portugal, 18–20 September 2006; Springer: Berlin, Germany, 2006. [Google Scholar]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. LIBLINEAR: A library for large linear classification. J. Mach Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Mao, K.Z. RBF neural network center selection based on Fisher ratio class separability measure. IEEE Trans. Neural Netw. 2002, 13, 1211–1217. [Google Scholar] [CrossRef] [PubMed]
- Wang, L. Feature selection with kernel class separability. IEEE Trans. Pat. Anal. Mach. Intell. 2008, 30, 1534–1546. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Gao, X.; Wang, Y.; Li, J. Markov random fields integrating adaptive interclass-pair penalty and spectral similarity for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2520–2534. [Google Scholar] [CrossRef]
- Ray, W.J.; Cole, H.W. EEG alpha activity reflects attentional demands, and beta activity reflects emotional and cognitive processes. Science 1985, 228, 750–752. [Google Scholar] [CrossRef]
- Klimesch, W.; Doppelmayr, M.; Russegger, H.; Pachinger, T.; Schwaiger, J. Induced alpha band power changes in the human EEG and attention. Neurosci. Lett. 1998, 244, 73–76. [Google Scholar] [CrossRef]
- Onton, J.; Makeig, S. High-frequency broadband modulations of electroencephalographic spectra. Front. Neurosci. 2009, 3, 61. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mu, L.; Lu, B.-L. Emotion classification based on gamma-band EEG. In Proceedings of the Annual International Conference of the IEEE, Minneapolis, MN, USA, 3–6 September 2009; pp. 1323–1326. [Google Scholar]
- Yoon, H.J.; Chung, S.Y. EEG-based emotion estimation using Bayesian weighted-log-posterior function and perceptron convergence algorithm. Comput. Biol. Med. 2013, 43, 2230–2237. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, J.; Campos, D. Improving BCI-based emotion recognition by combining EEG feature selection and kernel classifiers. Expert Syst. Appl. 2016, 47, 35–41. [Google Scholar] [CrossRef]
- Rozgic, V.; Vitaladevuni, S.N.; Prasad, R. Robust the EEG emotion classification using segment level decision fusion. In Proceedings of the IEEE Conference of Acoustics, Speech, and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 1286–1290. [Google Scholar]
- Li, X.; Song, D.; Zhang, P.; Yu, G.; Hu, B. Emotion recognition from multi-channel the EEG data through convolutional recurrent neural network. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Shenzhen, China, 15–18 December 2016; pp. 352–359. [Google Scholar]
- Tripathi, S.; Acharya, S.; Sharma, R.D.; Mittal, S.; Bhattacharya, S. Using deep and convolutional neural networks for accurate emotion classification on DEAP dataset. In Proceedings of the Twenty-Ninth AAAI Conference on Innovative Applications (IAAI-17), Austin, TX, USA, 25–30 January 2015; pp. 4746–4752. [Google Scholar]
- Alhagry, S.; Fahmy, A.A.; El-Khoribi, R.A. Emotion recognition based on EEG using LSTM recurrent neural network. Emotion 2017, 8, 355–358. [Google Scholar] [CrossRef] [Green Version]
- Salama, E.S.; El-Khoribi, R.A.; Shoman, M.E.; Shalaby, M.A.W. EEG-based emotion recognition using 3D convolutional neural networks. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 329–337. [Google Scholar] [CrossRef]
- Liu, Y.; Ayaz, H.; Shewokis, P.A. Multisubject “learning” for mental workload classification using concurrent EEG, fNIRS, and physiological measures. Front. Hum. Neurosci. 2017, 11, 389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saadati, M.; Nelson, J.; Ayaz, H. Multimodal fNIRS-EEG Classification Using Deep Learning Algorithms for Brain-Computer Interfaces Purposes. In Proceedings of the International Conference on Applied Human Factors and Ergonomics, Washington, DC, USA, 24–28 July 2019; pp. 209–220. [Google Scholar]









| Feature | Classifier | Delta | Theta | Alpha | Beta | Gamma | Total |
|---|---|---|---|---|---|---|---|
| PSD | NB | 54.18/5.39 | 53.94/5.24 | 54.25/5.08 | 58.85/7.63 | 61.23/8.48 | 60.51/6.71 |
| SVM | 51.14/14.31 | 47.57/15.75 | 52.35/16.04 | 62.97/12.18 | 64.15/12.19 | 69.04/5.91 | |
| LR_L1 | 44.80/4.63 | 45.23/4.72 | 44.00/5.51 | 38.41/8.75 | 36.18/9.67 | 34.43/9.52 | |
| LR_L2 | 44.57/4.88 | 45.11/4.92 | 44.14/5.49 | 38.47/8.63 | 36.38/9.58 | 34.38/9.57 | |
| LORSAL | 56.45/5.79 | 56.19/5.34 | 58.29/5.56 | 64.95/6.78 | 68.30/7.98 | 63.29/6.54 | |
| DE | NB | 54.27/3.62 | 53.90/3.53 | 54.62/4.07 | 59.19/5.59 | 61.52/6.51 | 61.04/5.76 |
| SVM | 52.08/13.54 | 49.76/14.14 | 52.04/13.41 | 62.91/10.23 | 65.88/9.93 | 69.55/6.58 | |
| LR_L1 | 44.04/4.80 | 44.67/4.73 | 43.16/5.34 | 38.22/8.67 | 36.08/9.52 | 33.69/9.88 | |
| LR_L2 | 43.86/4.88 | 44.44/4.69 | 43.15/5.41 | 38.15/8.64 | 36.06/9.52 | 33.81/9.59 | |
| LORSAL | 61.79/4.55 | 58.34/3.90 | 59.20/4.04 | 67.06/6.95 | 72.93/7.30 | 77.17/6.37 | |
| DASM | NB | 54.81/6.61 | 53.97/5.53 | 54.07/6.12 | 60.18/6.16 | 62.27/6.88 | 62.36/5.66 |
| SVM | 45.64/14.11 | 44.66/14.77 | 44.83/14.66 | 56.24/13.18 | 60.95/12.14 | 64.48/10.21 | |
| LR_L1 | 45.32/4.11 | 45.77/3.89 | 45.41/4.86 | 40.68/7.45 | 38.83/8.79 | 36.90/8.82 | |
| LR_L2 | 45.35/4.04 | 46.03/3.95 | 45.59/4.66 | 40.77/7.53 | 38.84/8.68 | 37.11/8.80 | |
| LORSAL | 58.38/3.58 | 55.21/3.55 | 55.42/3.46 | 60.31/5.39 | 64.63/6.22 | 71.63/4.94 | |
| RASM | NB | 51.17/6.55 | 51.61/7.37 | 51.02/6.98 | 54.90/8.57 | 58.08/9.47 | 55.65/6.77 |
| SVM | 37.41/15.45 | 37.23/14.33 | 37.35/13.87 | 40.56/16.24 | 47.29/17.02 | 48.17/17.72 | |
| LR_L1 | 49.39/6.07 | 48.19/5.55 | 48.17/6.24 | 45.29/6.11 | 42.39/7.44 | 42.71/6.64 | |
| LR_L2 | 49.45/4.75 | 47.92/4.30 | 47.95/4.73 | 45.44/5.87 | 42.53/6.97 | 42.69/6.37 | |
| LORSAL | 49.31/8.79 | 51.68/8.71 | 51.68/8.98 | 52.55/10.36 | 57.38/9.69 | 51.67/7.53 | |
| DCAU | NB | 53.98/6.22 | 52.97/6.73 | 53.72/6.03 | 59.61/5.70 | 61.97/6.52 | 61.95/5.52 |
| SVM | 43.40/13.46 | 41.11/13.93 | 43.91/14.39 | 55.47/13.83 | 59.57/12.67 | 63.48/9.93 | |
| LR_L1 | 45.94/4.24 | 46.26/4.11 | 45.82/4.41 | 41.38/7.32 | 39.19/8.29 | 37.41/8.21 | |
| LR_L2 | 46.03/4.23 | 46.45/4.11 | 45.74/4.38 | 41.33/7.24 | 39.21/8.35 | 37.45/8.22 | |
| LORSAL | 57.01/3.38 | 54.68/3.59 | 55.20/3.55 | 59.38/5.61 | 63.54/6.21 | 69.89/4.89 |
| Feature | Classifier | Delta | Theta | Alpha | Beta | Gamma | Total |
|---|---|---|---|---|---|---|---|
| PSD | NB | 54.22/5.37 | 53.08/5.66 | 53.82/5.30 | 55.39/8.03 | 58.44/8.94 | 57.54/6.15 |
| SVM | 50.83/15.93 | 48.07/15.6 | 49.95/15.65 | 58.05/15.31 | 58.82/15.08 | 68.60/8.07 | |
| LR_L1 | 47.74/6.07 | 47.96/5.66 | 47.46/6.49 | 45.34/9.97 | 44.11/11.67 | 43.55/14.04 | |
| LR_L2 | 47.66/6.31 | 47.94/5.78 | 47.42/6.41 | 45.47/9.96 | 44.03/11.64 | 43.58/14.23 | |
| LORSAL | 57.45/6.75 | 56.91/6.86 | 58.82/6.23 | 63.99/6.47 | 67.75/7.05 | 61.62/6.64 | |
| DE | NB | 54.13/3.76 | 53.43/3.68 | 54.08/3.76 | 56.97/4.81 | 58.75/5.33 | 58.46/5.00 |
| SVM | 46.90/14.53 | 45.03/14.93 | 47.51/14.57 | 55.88/13.34 | 63.33/12.79 | 69.92/7.94 | |
| LR_L1 | 47.29/6.52 | 47.69/5.93 | 46.96/6.81 | 45.26/10.88 | 44.16/12.99 | 43.10/15.21 | |
| LR_L2 | 47.38/6.40 | 47.81/5.89 | 46.91/6.88 | 45.29/11.03 | 44.12/13.03 | 43.25/15.00 | |
| LORSAL | 61.97/4.64 | 58.18/3.94 | 59.35/3.97 | 66.57/6.67 | 72.73/7.62 | 77.03/6.20 | |
| DASM | NB | 54.67/6.10 | 54.78/6.33 | 54.31/7.68 | 58.11/5.75 | 60.46/5.28 | 60.34/4.50 |
| SVM | 43.95/13.24 | 42.84/13.38 | 43.02/12.53 | 51.24/14.69 | 56.42/13.68 | 61.79/12.34 | |
| LR_L1 | 48.07/5.75 | 48.16/4.98 | 47.91/5.34 | 45.99/8.41 | 45.45/10.67 | 44.60/12.33 | |
| LR_L2 | 48.13/5.64 | 48.05/5.18 | 47.76/5.38 | 45.93/8.45 | 45.43/10.72 | 44.78/12.22 | |
| LORSAL | 58.13/3.75 | 55.14/3.62 | 55.18/3.37 | 59.70/4.94 | 64.54/5.87 | 71.20/4.96 | |
| RASM | NB | 51.31/7.57 | 51.92/7.12 | 51.01/6.47 | 54.25/6.52 | 55.26/6.84 | 53.57/4.25 |
| SVM | 36.59/13.04 | 35.31/11.31 | 36.18/12.49 | 37.79/14.05 | 42.61/17.12 | 43.46/15.61 | |
| LR_L1 | 49.45/6.07 | 49.07/4.97 | 50.18/4.32 | 49.14/5.75 | 47.83/7.35 | 47.94/7.39 | |
| LR_L2 | 49.44/5.08 | 49.16/4.41 | 50.19/4.22 | 49.05/5.73 | 47.92/7.21 | 48.10/7.31 | |
| LORSAL | 49.09/10.60 | 50.93/10.79 | 50.15/10.95 | 50.14/11.36 | 53.51/11.07 | 50.67/8.33 | |
| DCAU | NB | 55.09/7.10 | 53.86/6.91 | 53.98/7.42 | 56.98/7.23 | 60.14/5.99 | 59.98/4.50 |
| SVM | 42.34/13.47 | 41.56/13.26 | 43.19/13.26 | 50.64/13.76 | 55.06/14.99 | 60.04/12.79 | |
| LR_L1 | 48.19/5.42 | 48.36/4.90 | 48.01/5.18 | 46.34/8.24 | 45.29/10.05 | 44.47/11.45 | |
| LR_L2 | 48.21/5.31 | 48.38/5.04 | 47.86/5.14 | 46.29/8.13 | 45.33/9.93 | 44.61/11.51 | |
| LORSAL | 57.16/3.69 | 54.49/3.65 | 55.18/3.46 | 58.09/4.99 | 62.68/5.60 | 68.48/4.93 |
| Feature | Classifier | Valence | Arousal | ||||
|---|---|---|---|---|---|---|---|
| Precision | Recall | F1 | Precision | Recall | F1 | ||
| PSD | NB | 60.51/6.71 | 56.65/4.99 | 48.84/9.54 | 57.54/6.15 | 54.95/4.29 | 46.86/8.54 |
| SVM | 69.04/5.91 | 65.62/6.55 | 65.24/7.39 | 68.60/8.07 | 61.09/6.17 | 60.41/7.47 | |
| LORSAL | 63.29/6.54 | 62.15/6.65 | 61.84/7.27 | 61.62/6.64 | 59.02/5.53 | 58.46/6.54 | |
| DE | NB | 61.04/5.76 | 60.31/5.19 | 58.83/5.48 | 58.46/5.00 | 58.96/5.05 | 55.84/5.74 |
| SVM | 69.55/6.58 | 66.93/6.50 | 66.89/7.15 | 69.92/7.94 | 63.50/6.57 | 63.45/7.54 | |
| LORSAL | 77.17/6.37 | 76.79/6.21 | 76.90/6.27 | 77.03/6.20 | 76.15/6.14 | 76.47/6.14 | |
| DASM | NB | 62.36/5.66 | 62.18/5.54 | 61.73/5.57 | 60.34/4.50 | 60.79/4.90 | 59.76/4.77 |
| SVM | 64.48/10.21 | 63.01/7.15 | 62.01/9.11 | 61.79/12.34 | 59.06/6.36 | 57.49/8.46 | |
| LORSAL | 71.63/4.94 | 71.38/4.92 | 71.43/4.92 | 71.20/4.96 | 70.68/5.00 | 70.82/4.94 | |
| RASM | NB | 55.65/6.77 | 53.72/4.64 | 46.01/7.92 | 53.57/4.25 | 52.38/2.95 | 40.70/6.37 |
| SVM | 48.17/17.72 | 52.47/5.24 | 43.24/9.56 | 43.46/15.61 | 50.25/0.98 | 40.00/3.72 | |
| LORSAL | 51.67/7.53 | 51.35/2.98 | 46.69/5.49 | 50.67/8.33 | 50.60/2.11 | 45.32/3.94 | |
| DCAU | NB | 61.95/5.52 | 61.65/5.44 | 61.26/5.48 | 59.98/4.50 | 60.14/4.50 | 59.36/4.37 |
| SVM | 63.48/9.93 | 62.09/6.51 | 60.99/8.59 | 60.04/12.79 | 58.21/6.32 | 56.12/8.76 | |
| LORSAL | 69.89/4.89 | 69.68/4.77 | 69.71/4.81 | 68.48/4.93 | 68.11/4.90 | 68.19/4.88 | |
| Emotion | Valence | Arousal | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Frequency Bands | Delta | Theta | Alpha | Beta | Gamma | Delta | Theta | Alpha | Beta | Gamma |
| PSD | 0.046 | 0.005 | 0.014 | 0.155 | 0.414 | 0.045 | 0.005 | 0.013 | 0.124 | 0.418 |
| DE | 0.047 | 0.052 | 0.077 | 0.242 | 0.256 | 0.051 | 0.048 | 0.062 | 0.173 | 0.197 |
| DASM | 0.057 | 0.063 | 0.070 | 0.240 | 0.317 | 0.068 | 0.073 | 0.067 | 0.186 | 0.243 |
| RASM | 0.004 | 0.050 | 0.037 | 0.131 | 0.115 | 0.004 | 0.065 | 0.052 | 0.095 | 0.080 |
| DCAU | 0.059 | 0.062 | 0.064 | 0.224 | 0.307 | 0.062 | 0.064 | 0.067 | 0.195 | 0.244 |
| Classifier | Valence | Arousal | Description | ||
|---|---|---|---|---|---|
| NB | by Koelstra et al. [27] | 57.6 | 62.0 | 2-class classification for valence and arousal, and within-subject emotion recognition. | |
| Bayesian weighted-log-posterior | by Yoon et al. [72] | 70.9 | 70.1 | ||
| SVM+mRMR | by Atkinson et al. [73] | 73.41 | 73.06 | ||
| Segment level decision fusion | by Rozgić et al. [74] | 76.9 | 68.4 | ||
| CNN+RNN | by Li et al. [75] | 72.06 | 74.12 | ||
| DNN | by Tripathi et al. [76] | 75.78 | 73.12 | ||
| CNN | 81.41 | 73.36 | |||
| LSTM-RNN | by Alhagry et al. [77] | 85.65 | 85.45 | ||
| 3D-CNN | by Salama et al. [78] | 87.44 | 88.49 | ||
| GELM | by Zheng et al. [48] | 69.7 | 4-class classification in VA space. | ||
| SVM | +Raw | by Chen et al. [33] | 0.5590 | 0.7525 | 2-class classification for valence and arousal, and within-subject emotion recognition, and AUC (Area Under ROC Curve) used for evaluation. |
| +Norm | 0.5591 | 0.5590 | |||
| +PSD | 0.7596 | 0.5531 | |||
| +PSD+Raw | 0.9234 | 0.9462 | |||
| +PSD+Norm | 0.7460 | 0.7353 | |||
| CVCNN | +Raw | 0.6221 | 0.6012 | ||
| +Norm | 0.6551 | 0.6176 | |||
| +PSD | 0.9307 | 0.88.51 | |||
| +PSD+Raw | 0.9933 | 0.9988 | |||
| +PSD+Norm | 1.00 | 1.00 | |||
| GSCNN | +Raw | 0.6242 | 0.5902 | ||
| +Norm | 0.6394 | 0.5987 | |||
| +PSD | 0.8875 | 0.8802 | |||
| +PSD+Raw | 0.9933 | 0.9930 | |||
| +PSD+Norm | 1.00 | 1.00 | |||
| GSLTCNN | +Raw | 0.6717 | 0.6175 | ||
| +Norm | 0.6350 | 0.5670 | |||
| +PSD | 0.8523 | 0.8390 | |||
| +PSD+Raw | 0.9946 | 0.9958 | |||
| +PSD+Norm | 1.00 | 1.00 | |||
| CNN | +Raw | by Chen et al. [34] | 57.2 | 56.3 | 2-class classification for valence and arousal, and cross-subject emotion recognition |
| LSTM | 63.7 | 61.9 | |||
| H-ATT-BGRU | 67.9 | 66.5 | |||
| NB | +DE | in our study | 61.04 | 58.46 | 2-class classification for valence and arousal, and within-subject emotion recognition |
| SVM | 69.55 | 69.92 | |||
| MLR_L1 | 33.69 | 43.10 | |||
| MLR_L2 | 33.81 | 43.25 | |||
| LORSAL | 77.17 | 77.03 | |||
| Classifier | Valence | Arousal | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PSD | DE | DASM | RASM | DCAU | PSD | DE | DASM | RASM | DCAU | |
| NB | 4.37 | 4.36 | 1.91 | 1.92 | 1.51 | 4.42 | 4.41 | 1.93 | 1.93 | 3.44 |
| SVM | 4.53 | 4.37 | 2.34 | 2.47 | 2.04 | 4.26 | 4.16 | 2.26 | 2.34 | 3.45 |
| MLR_L1 | 0.14 | 0.13 | 0.04 | 0.04 | 0.03 | 0.17 | 0.15 | 0.04 | 0.04 | 0.08 |
| MLR_L2 | 0.12 | 0.11 | 0.04 | 0.04 | 0.03 | 0.13 | 0.11 | 0.04 | 0.04 | 0.07 |
| LORSAL | 3.75 | 3.89 | 3.87 | 3.69 | 3.85 | 3.74 | 3.86 | 3.86 | 3.69 | 3.87 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.; Shi, C.; Mu, H.; Li, J.; Gao, X. EEG-Based Emotion Recognition Using Logistic Regression with Gaussian Kernel and Laplacian Prior and Investigation of Critical Frequency Bands. Appl. Sci. 2020, 10, 1619. https://doi.org/10.3390/app10051619
Pan C, Shi C, Mu H, Li J, Gao X. EEG-Based Emotion Recognition Using Logistic Regression with Gaussian Kernel and Laplacian Prior and Investigation of Critical Frequency Bands. Applied Sciences. 2020; 10(5):1619. https://doi.org/10.3390/app10051619
Chicago/Turabian StylePan, Chao, Cheng Shi, Honglang Mu, Jie Li, and Xinbo Gao. 2020. "EEG-Based Emotion Recognition Using Logistic Regression with Gaussian Kernel and Laplacian Prior and Investigation of Critical Frequency Bands" Applied Sciences 10, no. 5: 1619. https://doi.org/10.3390/app10051619
APA StylePan, C., Shi, C., Mu, H., Li, J., & Gao, X. (2020). EEG-Based Emotion Recognition Using Logistic Regression with Gaussian Kernel and Laplacian Prior and Investigation of Critical Frequency Bands. Applied Sciences, 10(5), 1619. https://doi.org/10.3390/app10051619





