Relationship between Buchholz’s Apparent Power and Instantaneous Power in Three-Phase Systems
Abstract
:1. Introduction
- (1)
- Verification that instantaneous and Buchholz’s apparent powers are formally related quantities, as only Steinmetz could demonstrate for single-phase sinusoidal systems, 120 years ago;
- (2)
- Proposal of an original methodology to fast and directly obtain the expressions of Buchholz’s apparent power and its components in any three-phase system, sinusoidal or non-sinusoidal, balanced or unbalanced, star- or delta-configured systems, although the procedure is applied only to star-configured systems in this paper;
- (3)
- The methodology has been applied to obtain a novel quantity that we referred to as neutral-displacement power, which is able to determine the effects of the neutral path (real or virtual) in three-phase power systems.
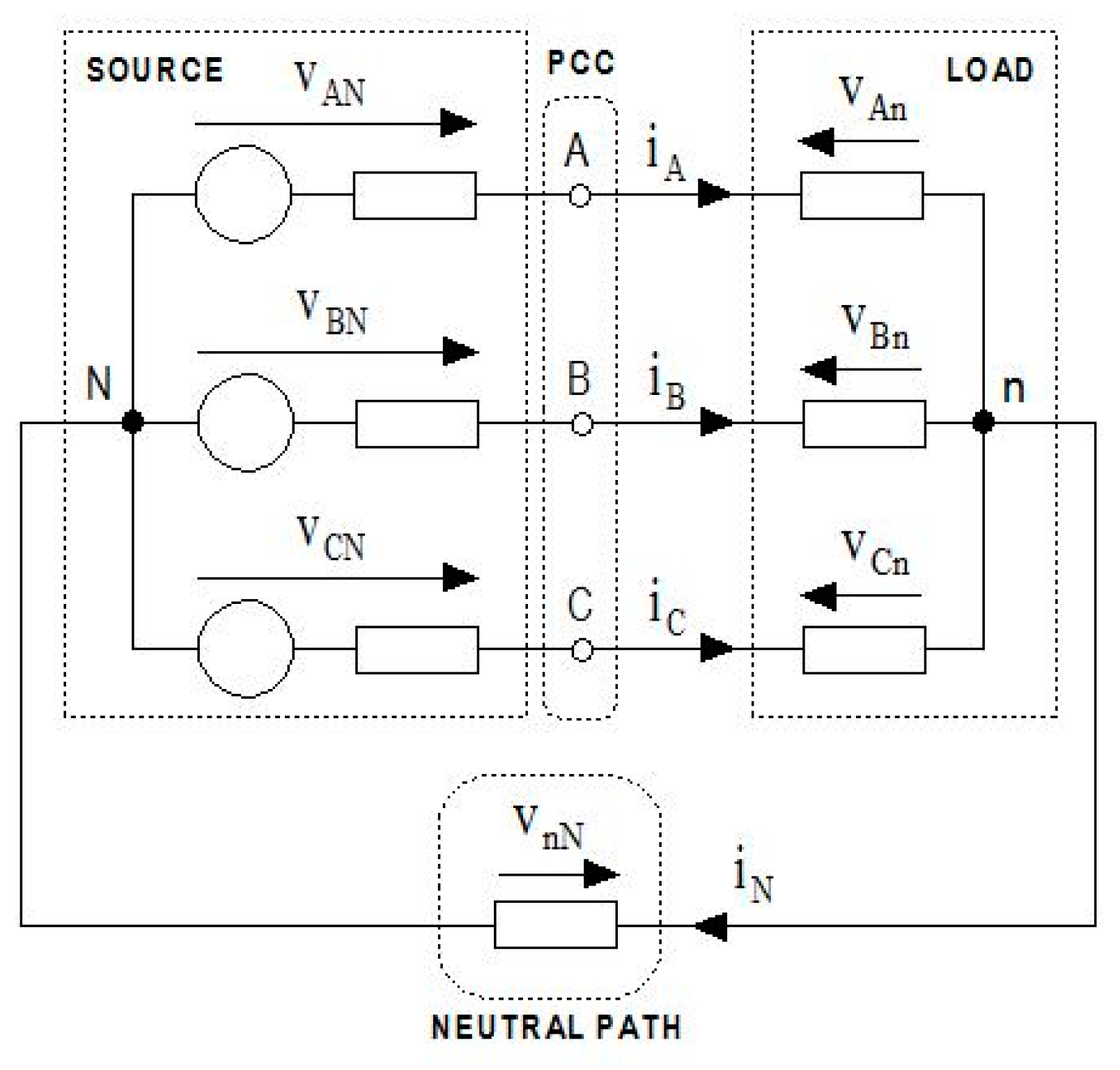
2. Formulations of Apparent and Instantaneous Power in Three-Phase Wye-Configured Systems
2.1. Instantaneous Power
2.2. Buchholz’s Apparent Power
2.3. Similarities between Formulations of Apparent Power and Instantaneous Power and their Components
- (a)
- The instantaneous power in each part or subsystem of a z-phase power system is defined by the inner products of the voltage () and current () vectors [22,23,24,25,26,27,28] formed by the instantaneous values of the voltages and currents in each phase of the subsystem (). Similarly, the instantaneous power components (active, reactive, unbalanced, non-fundamental, or distorted) are formed by the inner products of these voltage and current vector components.
- (b)
- The apparent power S in each part or subsystem of a z-phase power system is determined by the products of the norms (RMS values) of these voltage () and current () vectors in the subsystem (). Moreover, the apparent power components represent products between the norms (RMS values) of the components (active, reactive, unbalanced, non-fundamental, or distorted) of the voltage and current vectors.
- (c)
- The instantaneous and apparent types of power have the same components, which contain terms formed by the same voltages and currents in these components. The instantaneous power components are arithmetically added and identify each power phenomenon present in any part of the system. In contrast, the squares of the apparent power components are added, as they are orthogonal quantities that quantify the effects of each phenomenon identified by the instantaneous power components.
3. Proposed Methodology to Obtain Formulations of Buchholz’s Apparent Power and a Possible Set of its Components
- (1)
- The instantaneous power, , was expressed as a function of either of the following elements:
- (1-a)
- Its possible components (fundamental active () and reactive () of the positive-sequence, unbalanced (), non-fundamental () system), i.e.,
- (1-b)
- The instantaneous voltages and currents () in each phase (), i.e.,
- (1-c)
- The instantaneous voltage and current components () in each phase (), resulting in the application of Fortescue’s theorem and/or Fourier series to the part of the power system where the apparent power must be obtained, i.e.,
- (2)
- The expressions were set for the square of the Buchholz’s apparent power using the following method:
- (2-a)
- If the instantaneous power was expressed according to (29), the square of the apparent power () and the square of its possible components () were expressed by applying the changes , , , , and in order to obtain the general equation
- (2-b)
- If the instantaneous power was expressed by (30), the square of the apparent power was expressed as the product of the squares of the norms of the voltage () and current () vectors, which were determined as the product of the squares of RMS voltages () and currents (), i.e.,where the vertical bars () represent the norm of a voltage or current vector;
- (2-c)
- If the instantaneous power was expressed according to (31) as a function of the components () of the voltage and current vectors in each phase (), the square of the apparent power was expressed as the products of the squares of the RMS voltages and currents, which were obtained as functions of the RMS voltage components () and RMS current components () in each phase (), as follows:
- (3)
- A square root was applied to Expressions (32), (33), and (34) to formulate the apparent power or its components.
4. Formulation of the Neutral Conductor Effects According to the Proposed Methodology
- (1)
- In Expression (36), not only the active and reactive power in the neutral conductor are included, but also the power due to imbalances and distortions in the loads and sources;
- (2)
- The neutral-displacement power does not directly depend on the value of the neutral current () and can also be applied to three-phase systems with no neutral conductor.
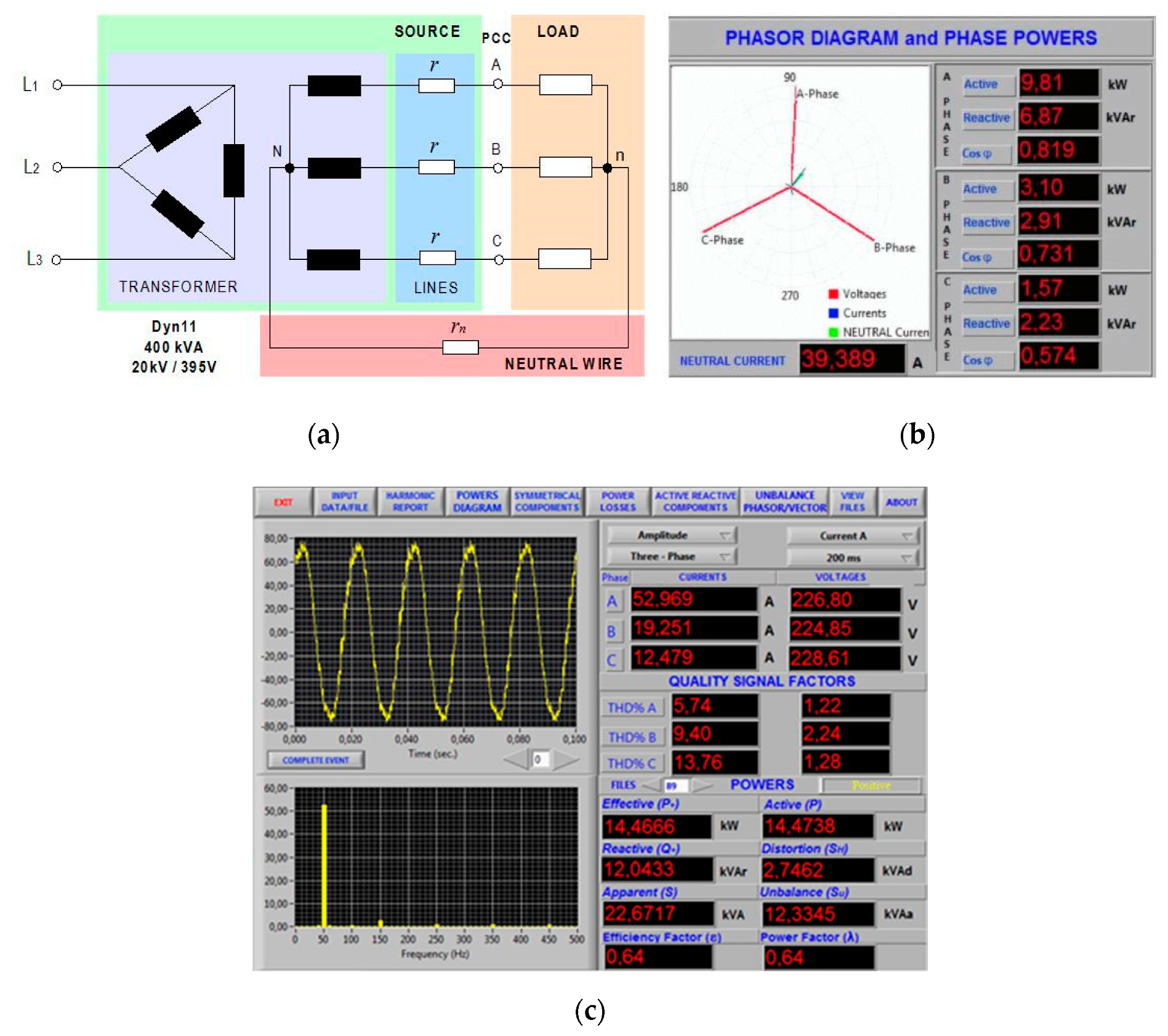
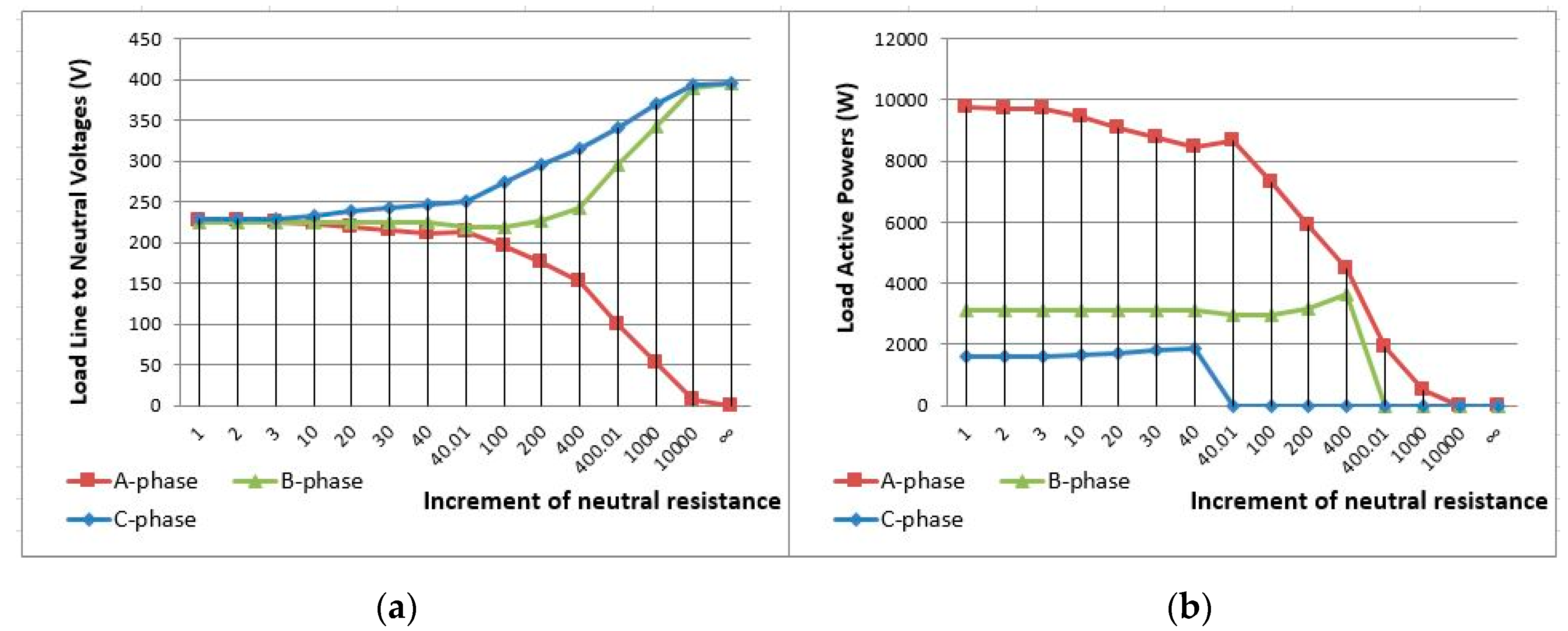
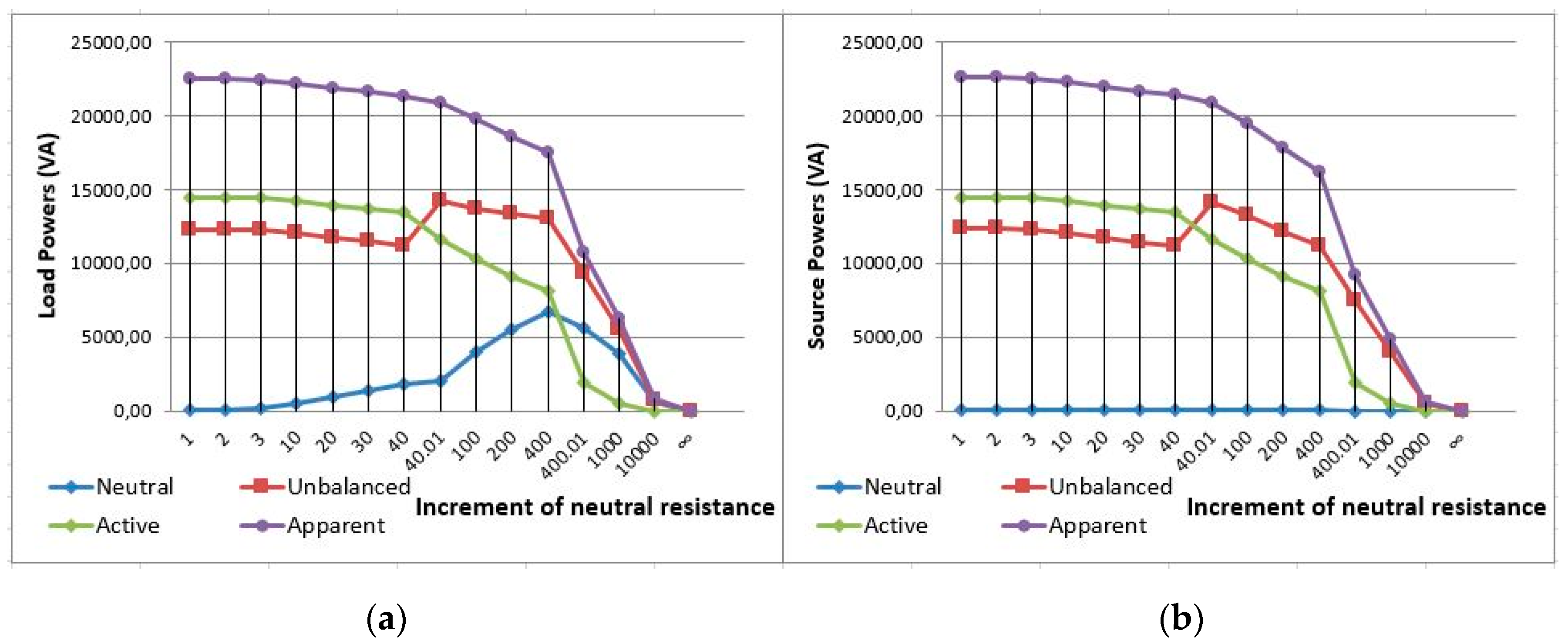
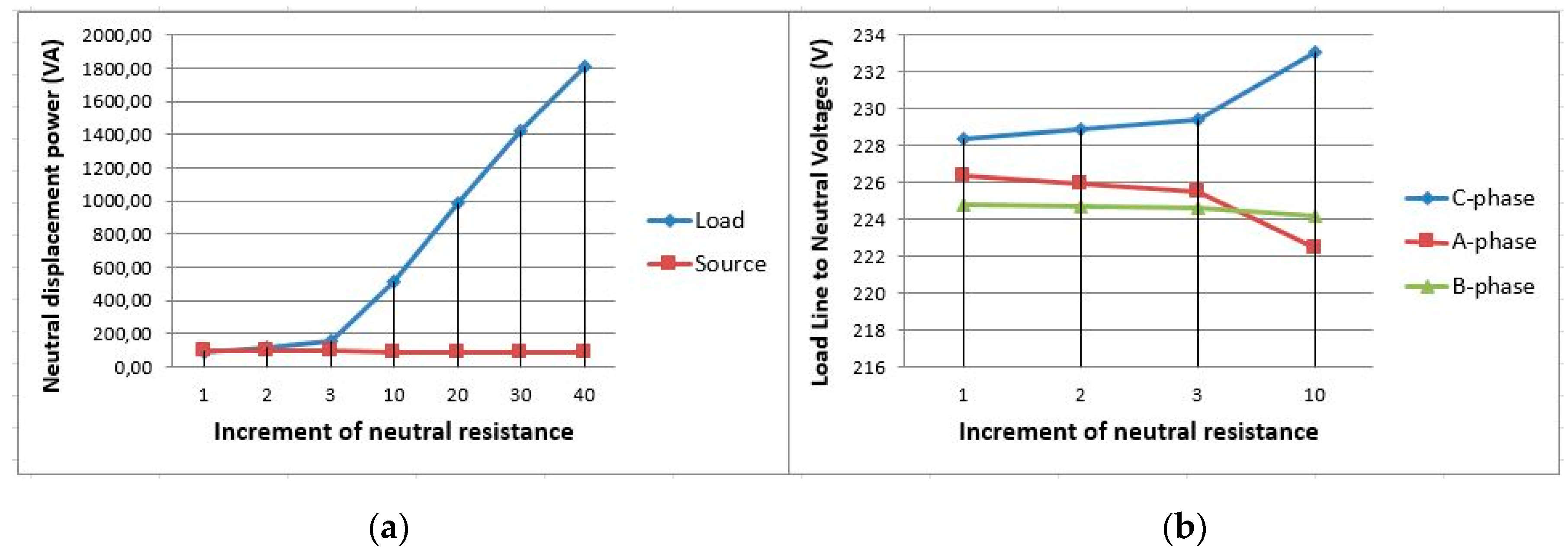
5. Application Example
6. Conclusions
7. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Steinmetz, C.P. Theory of Alternating Current Phenomena; McGraw: New York, NY, USA, 1897; pp. 150–157. [Google Scholar]
- Budeanu, I. Reactive and Fictitious Powers; The Rumanian National Institute Publ.: Bucharest, Romania, 1927. [Google Scholar]
- Czarnecki, L.S. What is wrong in the Budeanu concept of reactive and distortion power and why it should be abandoned. IEEE Trans. Instr. Meas. 1987, 36, 834–837. [Google Scholar] [CrossRef]
- Buchholz, F. Die Drehstrom-Scheinleistung bei Ungleichmas-siger Belastung Der Drei Zweige. Licht Und Kraft 1922, 2, 9–11. [Google Scholar]
- Fryze, S. Wirk, Blind, und Scheinleistung in elektrischen Stromkreisen mit nichtsinus-formigen Verlauf von Strom und Spannung. Elektrotechi 1932, 25, 596–599. [Google Scholar]
- Czarnecki, L.S. Orthogonal decomposition of the currents in a 3-phase non-linear asymmetrical circuit with non-sinusoidal voltage source. IEEE Trans. Instr. Meas. 1988, 37, 30–34. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Currents physical components (CPC) concept: A fundamental of power theory. Prezglad Elektrotech. 2008, 6, 28–37. [Google Scholar] [CrossRef]
- Czarnecki, L.S.; Bhattarai, P. Currents physical components (CPC) in three-phase systems with asymmetrical voltage. Prezglad Elektrotech. 2015, 6, 40–47. [Google Scholar] [CrossRef]
- IEEE Standard 1459–2010. IEEE Trial-Use Standard for the Measurement of Electric Power Quantities under Sinusoidal, Non-sinusoidal, Balanced or Undalanced Conditions; The Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2010; pp. 1016–5997. [Google Scholar]
- DIN 40110, Teil 2. Mehrleiter-Strmkreise; Beuth-Verlag: Berlin, Germany, 2002. [Google Scholar]
- Emanuel, A.E. Apparent power definitions for three-phase systems. IEEE Trans. Power Deliv. 1999, 14, 767–772. [Google Scholar] [CrossRef]
- Pajic, S.; Emanuel, A.E. Modern apparent power definitions: Theoretical versus practical approach. The general case. IEEE Trans. PWD 2006, 21, 1787–1792. [Google Scholar] [CrossRef]
- Emanuel, A.E. Power Definitions and the Physical Mechanism of Power Flow; John Wiley & Sons: Chichester, UK, 2010. [Google Scholar]
- Depenbrock, M. The FBD-Method, a generally applicable tool for analyzing power relations. IEEE Trans. PWS 1993, 8, 381–387. [Google Scholar] [CrossRef]
- Ferrero, A. Definition of electrical quantities commonly used in non-sinusoidal conditions. ETEP Eur. Trans. PW Eng. 1998, 8, 235–240. [Google Scholar] [CrossRef]
- Lyon, W. Discussion on report of joint committee. Trans. AIEE 1920, 39, 1515–1520. [Google Scholar]
- Curtis, H.L.; Silsbee, F.B. Definitions of Power and Related Quantities. Electr. Eng. 1935, 4, 394–404. [Google Scholar] [CrossRef]
- León-Martínez, V.; Giner-García, J.; Montañana-Romeu, J.; Cazorla-Navarro, A. Efficiency in electrical installations. New power definitions (in Spanish). Mundo Electron. 2001, 332, 28–32. [Google Scholar]
- Emanuel, A.E.; Orr, J.A. The effect of the neutral path impedance on voltage and current distortion. Part I: Symmetrical and balanced three-phase systems. In Proceedings of the 2004 11th International Conference on Harmonics and Quality Power, Lake Placid, NY, USA, 12–15 September 2004; pp. 186–190. [Google Scholar] [CrossRef]
- Emanuel, A.E.; Orr, J.A. The effect of the neutral path impedance on voltage and current distortion. Part II: Imbalanced three-phase systems. In Proceedings of the 2004 11th International Conference on Harmonics and Quality Power, Lake Placid, NY, USA, 12–15 September 2004; pp. 186–190. [Google Scholar] [CrossRef]
- PBlasco, A.; Montoya-Mira, R.; Díez, J.M.; Montoya, R.; Reig, M.J. Compensation of Reactive Power and Unbalanced Power in Three-Phase Three-Wire Systems Connected to an Infinite Power Network. Appl. Sci. 2020, 10, 113. [Google Scholar] [CrossRef] [Green Version]
- Akagi, H.; Kanazawa, Y.; Nabae, A. Instantaneous reactive power compensators comprising switching devices without energy storage components. IEEE Trans. Ind. Appl. 1984, 20, 625–630. [Google Scholar] [CrossRef]
- Willems, J.L.; Ghijselen, J.A. The Relation between the Generalized Apparent Power and the Voltage Reference. In Proceedings of the Sixth International Workshop on Power Definitions and Measurements under Non-sinusoidal Conditions, Milano, Italy, 13–15 October 2003; pp. 37–45. [Google Scholar]
- Czarnecki, L.S. Could Power Properties of Three-Phase Systems Be Described in Terms of the Poynting Vector? IEEE Trans. Power Deliv. 2006, 21, 339–344. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Physical Interpretation of the Reactive Power in Terms of the CPC Power Theory. Electr. Power Qual. Util. J. 2007, XIII, 89–95. [Google Scholar]
- Jeon, S.-J. Properties of the generalized power theory: Universality and portioning/augmentation properties. IET Gener. Transm. Distrib. 2015, 9, 2126–2134. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Critical comments on the conservative power theory (CPT). In Proceedings of the 2015 International School on Nonsinusoidal Currents and Compensation (ISNCC), Lagow, Poland, 5–18 June 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Artemenko, M.Y.; Batrak, L.M. The New Formula for Apparent Power and Power Losses of Three-Phase Four-Wire System. In Proceedings of the 2017 IEEE 37th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 18–20 April 2017; pp. 389–393. [Google Scholar] [CrossRef]
- León-Martínez, V.; Montañana-Romeu, J. Procedure for Determining the Condition of the Neutral Conductor in Electrical Installations and the Procedure for Implementation Thereof. Spanish Granted Patent ES 2588260 B2, 9 May 2017. [Google Scholar]
| Components | Instantaneous Power | Apparent Power | ||
|---|---|---|---|---|
| Total | ||||
| Fundamental | Total | |||
| Active | ||||
| Reactive | ||||
| Unbalanced | Total | |||
| Current imbalance | ||||
| Voltage imbalance | ||||
| Non-Fundamental | Total | |||
| Current distortion | ||||
| Voltage distortion | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
León-Martínez, V.; Montañana-Romeu, J.; Peñalvo-López, E.; Valencia-Salazar, I. Relationship between Buchholz’s Apparent Power and Instantaneous Power in Three-Phase Systems. Appl. Sci. 2020, 10, 1798. https://doi.org/10.3390/app10051798
León-Martínez V, Montañana-Romeu J, Peñalvo-López E, Valencia-Salazar I. Relationship between Buchholz’s Apparent Power and Instantaneous Power in Three-Phase Systems. Applied Sciences. 2020; 10(5):1798. https://doi.org/10.3390/app10051798
Chicago/Turabian StyleLeón-Martínez, Vicente, Joaquín Montañana-Romeu, Elisa Peñalvo-López, and Iván Valencia-Salazar. 2020. "Relationship between Buchholz’s Apparent Power and Instantaneous Power in Three-Phase Systems" Applied Sciences 10, no. 5: 1798. https://doi.org/10.3390/app10051798
APA StyleLeón-Martínez, V., Montañana-Romeu, J., Peñalvo-López, E., & Valencia-Salazar, I. (2020). Relationship between Buchholz’s Apparent Power and Instantaneous Power in Three-Phase Systems. Applied Sciences, 10(5), 1798. https://doi.org/10.3390/app10051798






