Quantum Many-Body Theory for Exciton-Polaritons in Semiconductor Mie Resonators in the Non-Equilibrium
Abstract
:1. Introduction
2. Theory
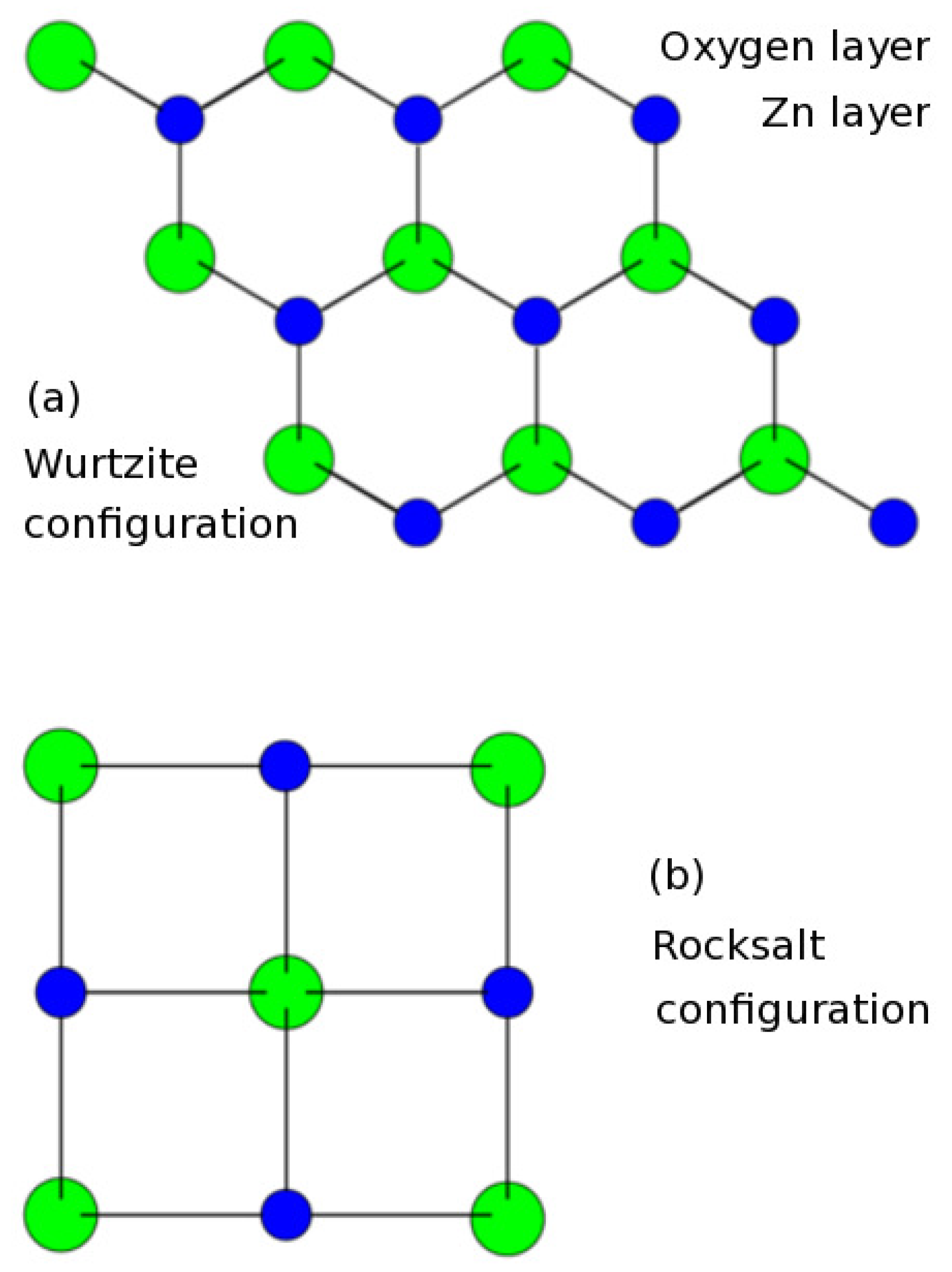
2.1. Hubbard Model for Excitons and Exciton-Polaritons
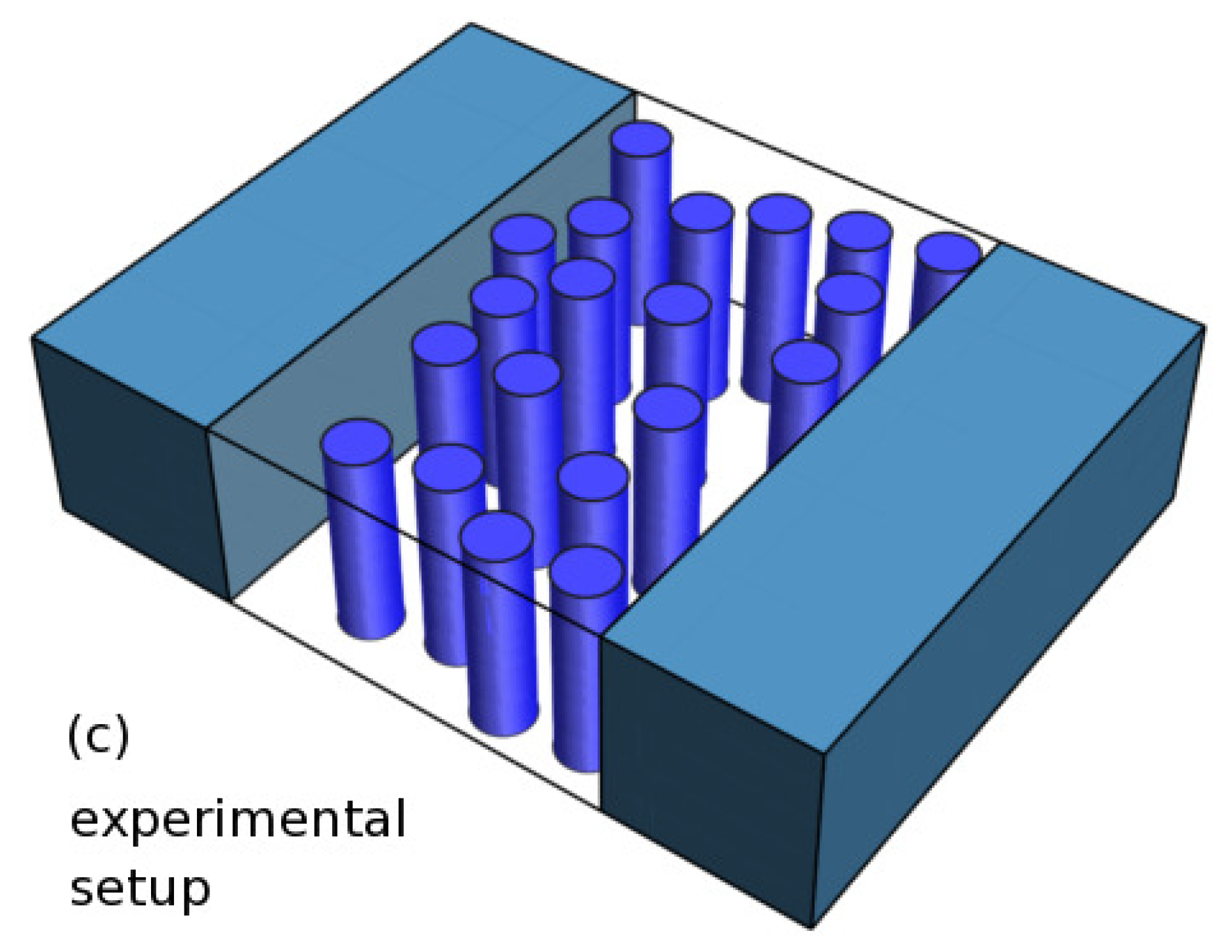
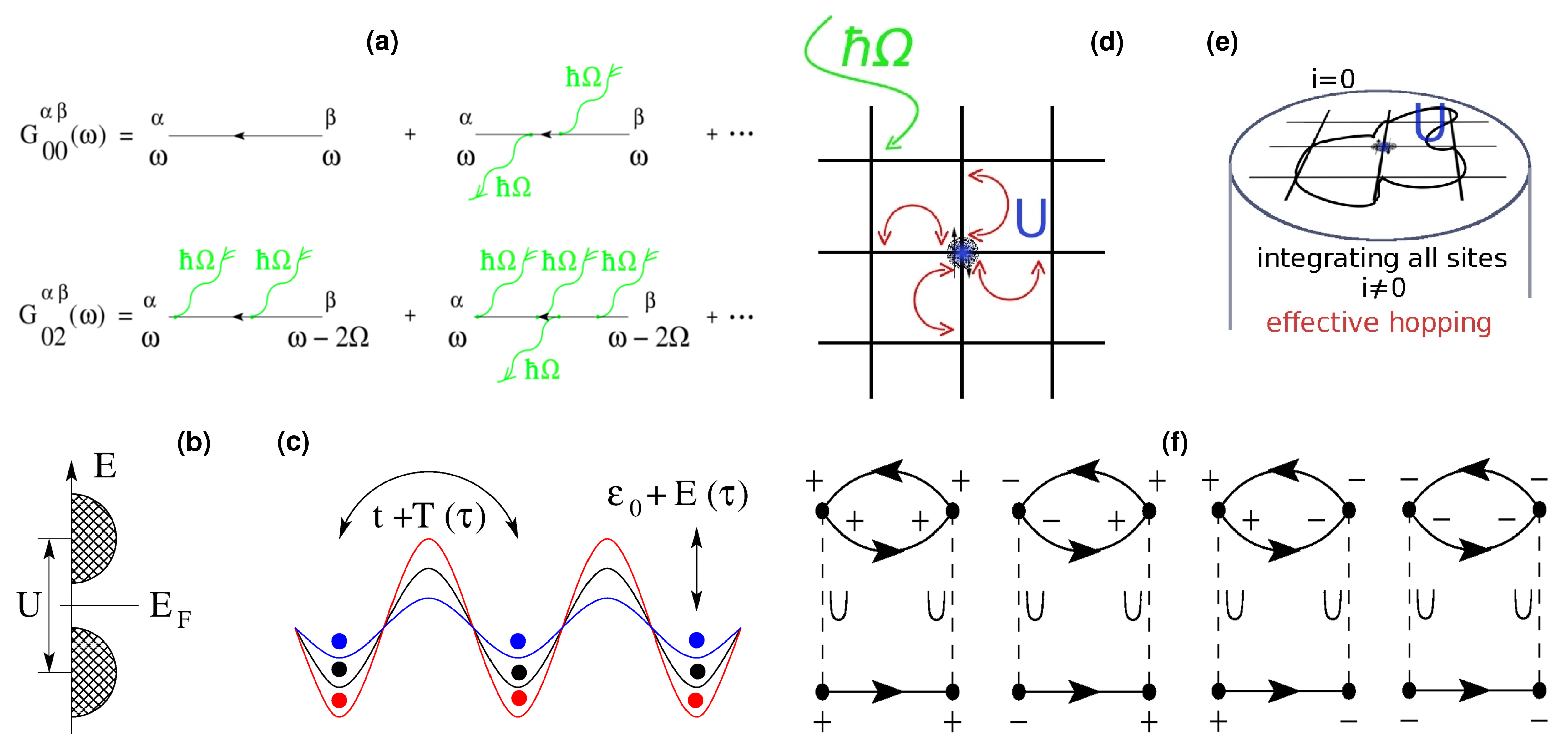
2.2. Dynamical Mean-Field Theory for Electromagnetically Driven Semiconductors in d = 3 Dimensions
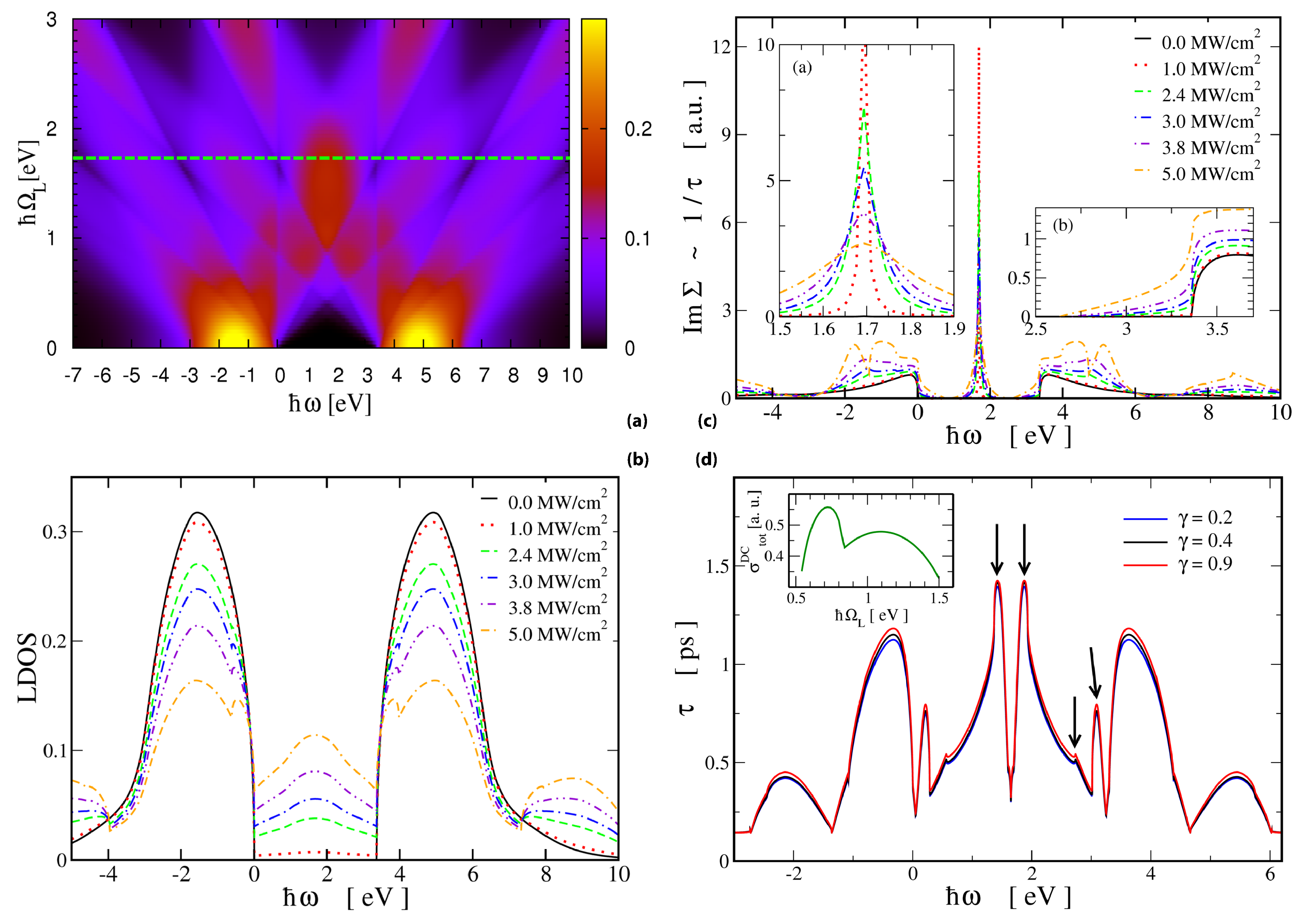
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yamamoto, Y. Half-matter, half-light amplifier. Nature 2000, 405, 629–630. [Google Scholar] [CrossRef]
- Imamoglu, A.; Ram, R.J.; Pau, S.; Yamamoto, Y. Nonequilibrium condensates and lasers without inversion: Exciton-polariton lasers. Phys. Rev. A 1996, 53, 4250–4253. [Google Scholar] [CrossRef] [PubMed]
- Zamfirescu, M.; Kavokin, A.; Gil, B.; Malpuech, G.; Kaliteevski, M. ZnO as a material mostly adapted for the realization of room-temperature polariton lasers. Phys. Rev. B 2002, 65, 161205(R). [Google Scholar] [CrossRef]
- Deng, H.; Weihs, G.; Santori, C.; Bloch, J.; Yamamoto, Y. Condensation of semiconductor microcavity exciton polaritons. Science 2002, 298, 199–202. [Google Scholar] [CrossRef] [Green Version]
- Kasprzak, J.; Richard, M.; Kundermann, S.; Baas, A.; Jeambrun, P.; Keeling, J.M.; Marchetti, F.M.; Szymanska, M.H.; Andre, R.; Staehli, J.L.; et al. Bose-Einstein condensation of exciton polaritons. Nature 2006, 443, 409–414. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.; Rahimi-Iman, A.; Kim, Y.N.; Fischer, J.; Savenko, I.G.; Amthor, M.; Lermer, M.; Wolf, A.; Worschech, L.; Kulakovskii, V.D.; et al. An electrically pumped polariton laser. Nature 2013, 497, 348–352. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Orosz, L.; Kamoun, O.; Bouchoule, S.; Brimont, C.; Disseix, P.; Guillet, T.; Lafosse, X.; Leroux, M.; Leymarie, J.; et al. Fabrication and characterization of a room-temperature ZnO polariton laser. Appl. Phys. Lett. 2013, 102, 191118. [Google Scholar] [CrossRef]
- Guillet, T.; Mexis, M.; Levrat, J.; Rossbach, G.; Brimont, C.; Bretagnon, T.; Gil, B.; Butte, R.; Grandjean, N.; Orosz, L.; et al. Polariton lasing in a hybrid bulk ZnO microcavity. Appl. Phys. Lett. 2011, 99, 161104. [Google Scholar] [CrossRef]
- Bajoni, D. Polariton lasers. Hybrid light-matter lasers without inversion. J. Phys. D Appl. Phys. 2012, 45, 313001. [Google Scholar] [CrossRef]
- Cao, H.; Zhao, Y.G.; Ho, S.T.; Seelig, E.W.; Wang, Q.H.; Chang, R.P.H. Random Laser Action in Semiconductor Powder. Phys. Rev. Lett. 1999, 82, 11–2278. [Google Scholar] [CrossRef] [Green Version]
- Niyuki, R.; Fujiwara, H.; Nakamura, T.; Ishikawa, Y.; Koshizaki, N.; Tsuji, T.; Sasaki, K. Double threshold behavior in a resonance-controlled ZnO random laser. APL Photonics 2017, 2, 036101. [Google Scholar] [CrossRef]
- Lu, T.-C.; Lai, Y.-Y.; Lan, Y.-P.; Huang, S.-W.; Chen, J.-R.; Wu, Y.-C.; Hsieh, W.-F.; Deng, H. Room temperature polariton lasing vs. photon lasing in a ZnO-based hybrid microcavity. Opt. Express 2012, 20, 5530. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, S.; Zhang, B.; Wang, Z.; Fischer, J.; Brodbeck, S.; Kamp, M.; Schneider, C.; Höfling, S.; Deng, H. Coherent Polariton Laser. Phys. Rev. X 2016, 6, 011026. [Google Scholar] [CrossRef] [Green Version]
- Lubatsch, A.; Frank, R. Evolution of Floquet Topological Quantum States in Driven Semiconductors. Eur. Phys. J. B 2019, 92, 215. [Google Scholar] [CrossRef] [Green Version]
- Lubatsch, A.; Frank, R. Behavior of Floquet Topological Quantum States in Optically Driven Semiconductors. Symmetry 2019, 11, 1246. [Google Scholar] [CrossRef] [Green Version]
- Chang, P.-C.; Lu, J.G. Temperature dependent conduction and UV induced metal-to-insulator transition in ZnO nanowires. Appl. Phys. Lett. 2008, 92, 212113. [Google Scholar] [CrossRef]
- Aghamalyan, N.R.; Aslanyan, T.A.; Vardanyan, E.S.; Kafadaryan, Y.A.; Hovsepyan, R.K.; Petrosyan, S.I.; Poghosyan, A.R. Metal-insulator electronic phase transitions in wide-gap ZnO semiconductors. J. Contemp. Phys. 2012, 47, 275–281. [Google Scholar] [CrossRef]
- Chang, P.-C.; Chien, C.-J.; Stichtenoth, D.; Ronning, C.; Lu, J.G. Finite size effect in ZnO nanowires. Appl. Phys. Lett. 2007, 90, 113101. [Google Scholar] [CrossRef] [Green Version]
- Shimada, R.; Xie, J.; Avrutin, V.; Özgür, Ü.; Morkovic, H. Cavity polaritons in ZnO-based hybrid microcavities. Appl. Phys. Lett. 2008, 92, 011127. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.; Xu, C.X.; Sun, X.W.; Zhang, X.H. Exciton-polariton microphotoluminescence and lasing from ZnO whispering-gallery mode microcavities. Appl. Phys. Lett. 2011, 98, 161110. [Google Scholar] [CrossRef]
- Duan, Q.; Xu, D.; Liu, W.; Lu, J.; Zhang, L.; Wang, J.; Wang, Y.; Gu, J.; Hu, T.; Xie, W.; et al. Polariton lasing of quasi-whispering gallery modes in a ZnO microwire. Appl. Phys. Lett. 2012, 103, 022103. [Google Scholar] [CrossRef]
- Razavi-Khosroshahi, H.; Edalati, K.; Wu, J.; Nakashima, Y.; Arita, M.; Ikoma, Y.; Sadakiyo, M.; Inagaki, Y.; Staykov, A.; Yamauchi, M.; et al. High-pressure zinc oxide phase as visible-light-active photocatalyst with narrow band gap. J. Mater. Chem. A 2017, 5, 20298–20303. [Google Scholar] [CrossRef]
- Huang, F.; Lin, Z.; Lin, W.; Zhang, J.; Ding, K.; Wang, Y.; Zheng, Q.; Zhan, Z.; Yan, F.; Chen, D.; et al. Research progress in ZnO singlecrystal: Growth, scientific understanding, and device applications. Chin. Sci. Bull. 2014, 59, 1235. [Google Scholar] [CrossRef]
- Park, W.I.; Jun, Y.H.; Jung, S.W.; Yi, G.-C. Excitonic emissions observed in ZnO single crystal nanorods. Appl. Phys. Lett. 2003, 82, 964–966. [Google Scholar] [CrossRef] [Green Version]
- Fritsch, D.; Schmidt, H.; Grundmann, M. Pseudopotential band structures of rocksalt MgO, ZnO, and Mg1-xZnxO. Appl. Phys. Lett. 2006, 88, 134104. [Google Scholar] [CrossRef]
- Dixit, H.; Saniz, R.; Lamoen, D.; Partoens, B. The quasiparticle band structure of zincblende and rocksalt ZnO. J. Phys. Condens. Matter 2010, 22, 125505. [Google Scholar] [CrossRef] [Green Version]
- Koster, R.S.; Changming, M.F.; Dijkstra, M.; van Blaaderen, A.; van Huis, M.A. Stabilization of Rock Salt ZnO Nanocrystals by Low-Energy Surfaces and Mg Additions: A First-Principles Study. J. Phys. Chem. C 2015, 119, 5648–5656. [Google Scholar] [CrossRef]
- Floquet, G. Sur les équations différentielles linéaires à coefficients périodiques. Ann. l’ Ecole Norm. Sup. 1883, 12, 47–88. [Google Scholar] [CrossRef] [Green Version]
- Grifoni, M.; Hänggi, P. Driven quantum tunneling. Phys. Rep. 1998, 304, 229–354. [Google Scholar] [CrossRef]
- Frank, R. Coherent control of Floquet-mode dressed plasmon polaritons. Phys. Rev. B 2012, 85, 195463. [Google Scholar] [CrossRef] [Green Version]
- Frank, R. Non-equilibrium polaritonics - Nonlinear effects and optical switching. Ann. Phys. 2013, 525, 66–73. [Google Scholar] [CrossRef] [Green Version]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13. [Google Scholar] [CrossRef] [Green Version]
- Lubatsch, A.; Kroha, J. Optically driven Mott-Hubbard systems out of thermodynamical equilibrium. Ann. Phys. 2009, 18, 863–867. [Google Scholar] [CrossRef]
- Frank, R. Quantum criticality and population trapping of fermions by non-equilibrium lattice modulations. New J. Phys. 2013, 15, 123030. [Google Scholar] [CrossRef] [Green Version]
- Frank, R. Population trapping and inversion in ultracold Fermi gases by excitation of the optical lattice-Non-equilibrium Floquet - Keldysh description. Appl. Phys. B 2013, 113, 41–47. [Google Scholar] [CrossRef] [Green Version]
- Faisal, F.H.M.; Kaminski, J.Z. Floquet-Bloch theory of high-harmonic generation in periodic structures. Phys. Rev. A 1997, 56, 748. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Self-consistent quantum field theory for the characterization of complex random media by short laser pulses. Phys. Rev. Res. 2020, in press. [Google Scholar]
- Forn-Diaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 2019, 91, 025005-1. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 1998, 37, 3759. [Google Scholar] [CrossRef] [Green Version]
- Jarell, M.; Freericks, J.K.; Pruschke, T. Optical conductivity of the infinite-dimensional Hubbard model. Phys. Rev. B 1995, 51, 11704. [Google Scholar] [CrossRef] [Green Version]
- Eder, R.; van den Brink, J.; Sawatzky, G.A. Intersite Coulomb interaction and Heisenberg exchange. Phys. Rev. B 1996, 54, 732(R). [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jauho, A.-P.; Johnsen, K. Dynamical Franz-Keldysh Effect. Phys. Rev. Lett. 1996, 76, 4576–4579. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nordstrom, K.B.; Johnsen, K.; Allen, S.J.; Jauho, A.-P.; Birnir, B.; Kono, J.; Noda, T.; Akiyama, H.; Sakaki, H. Excitonic Dynamical Franz-Keldysh Effect. Phys. Rev. Lett. 1998, 81, 457–460. [Google Scholar] [CrossRef] [Green Version]
- Johnsen, K.; Jauho, A.-P. Quasienergy Spectroscopy of Excitons. Phys. Rev. Lett. 1999, 83, 1207–1210. [Google Scholar] [CrossRef] [Green Version]
- Savrasov, S.Y.; Kotliar, G. Linear Response Calculations of Lattice Dynamics in Strongly Correlated Systems. Phys. Rev. Lett. 2003, 90, 056401-1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fiebig, M.; Fröhlich, D.; Lottermoser, T.; Pavlov, V.V.; Pisarev, R.V.; Weber, H.-J. Second Harmonic Generation in the Centrosymmetric Antiferromagnet NiO. Phys. Rev. Lett. 2001, 87, 137202-1. [Google Scholar] [CrossRef]
- Castell, M.R.; Wincott, P.L.; Condon, N.G.; Muggelberg, C.; Thornton, G.; Dudarev, S.L.; Sutton, A.P.; Briggs, G.A.D. Atomic-resolution STM of a system with strongly correlated electrons:NiO(001) surface structure and defect sites. Phys. Rev. B 1997, 55, 7859. [Google Scholar] [CrossRef] [Green Version]
- Gibbs, H.M.; Khitrova, G.; Koch, S.W. Exciton–polariton light–semiconductor coupling effects. Nat. Photonics 2011, 5, 275–282. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann Phys. (Berl.) 1908, 4, 377–445. [Google Scholar] [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. A 1961, 124, 1866. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. A Self-Consistent Quantum Field Theory for Random Lasing. Appl. Sci. 2019, 9, 2477. [Google Scholar] [CrossRef] [Green Version]
- Kalt, H.; Fallert, J.; Dietz, R.J.B.; Sartor, J.; Schneider, D.; Klingshirn, C. Random lasing in nanocrystalline ZnO powders. Phys. Status Solidi B 2010, 247, 1448–1452. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Coherent transport and symmetry breaking - laser dynamics of constrained granular matter. New J. Phys. 2014, 16, 083043. [Google Scholar] [CrossRef] [Green Version]
- Lubatsch, A.; Frank, R. Tuning the Quantum Efficiency of Random Lasers - Intrinsic Stokes-Shift and Gain. Sci. Rep. 2015, 5, 17000. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.-Y.; Chou, Y.-H.; Lan, Y.-P.; Lu, T.-C.; Wang, S.-C.; Yamamoto, Y. Crossover from polariton lasing to exciton lasing in a strongly couples ZnO microcavity. Sci. Rep. 2015, 6, 20581. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lubatsch, A.; Frank, R. Quantum Many-Body Theory for Exciton-Polaritons in Semiconductor Mie Resonators in the Non-Equilibrium. Appl. Sci. 2020, 10, 1836. https://doi.org/10.3390/app10051836
Lubatsch A, Frank R. Quantum Many-Body Theory for Exciton-Polaritons in Semiconductor Mie Resonators in the Non-Equilibrium. Applied Sciences. 2020; 10(5):1836. https://doi.org/10.3390/app10051836
Chicago/Turabian StyleLubatsch, Andreas, and Regine Frank. 2020. "Quantum Many-Body Theory for Exciton-Polaritons in Semiconductor Mie Resonators in the Non-Equilibrium" Applied Sciences 10, no. 5: 1836. https://doi.org/10.3390/app10051836
APA StyleLubatsch, A., & Frank, R. (2020). Quantum Many-Body Theory for Exciton-Polaritons in Semiconductor Mie Resonators in the Non-Equilibrium. Applied Sciences, 10(5), 1836. https://doi.org/10.3390/app10051836




