Numerical-Experimental Investigation into the Tensile Behavior of a Hybrid Metallic–CFRP Stiffened Aeronautical Panel
Abstract
:1. Introduction
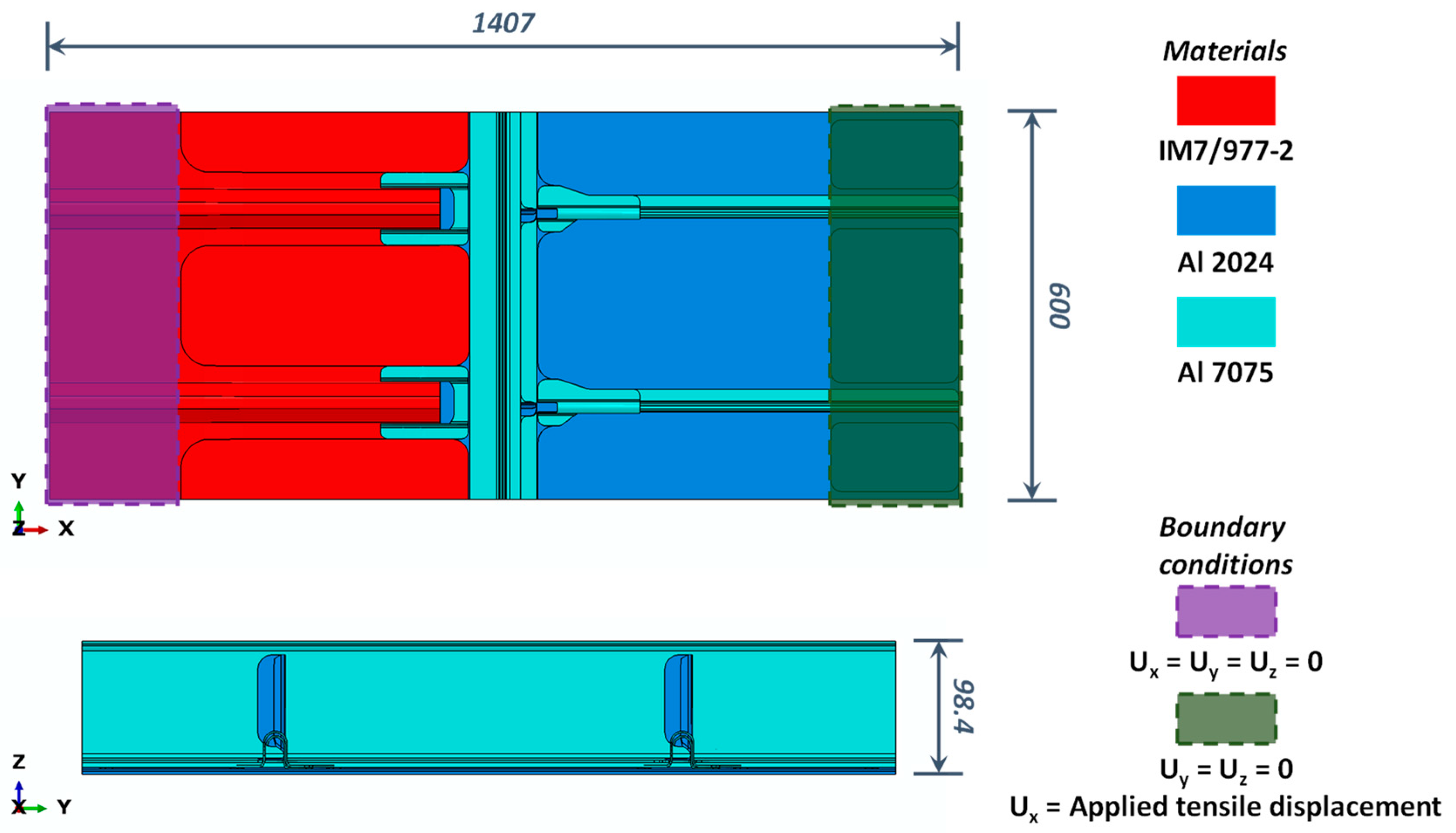
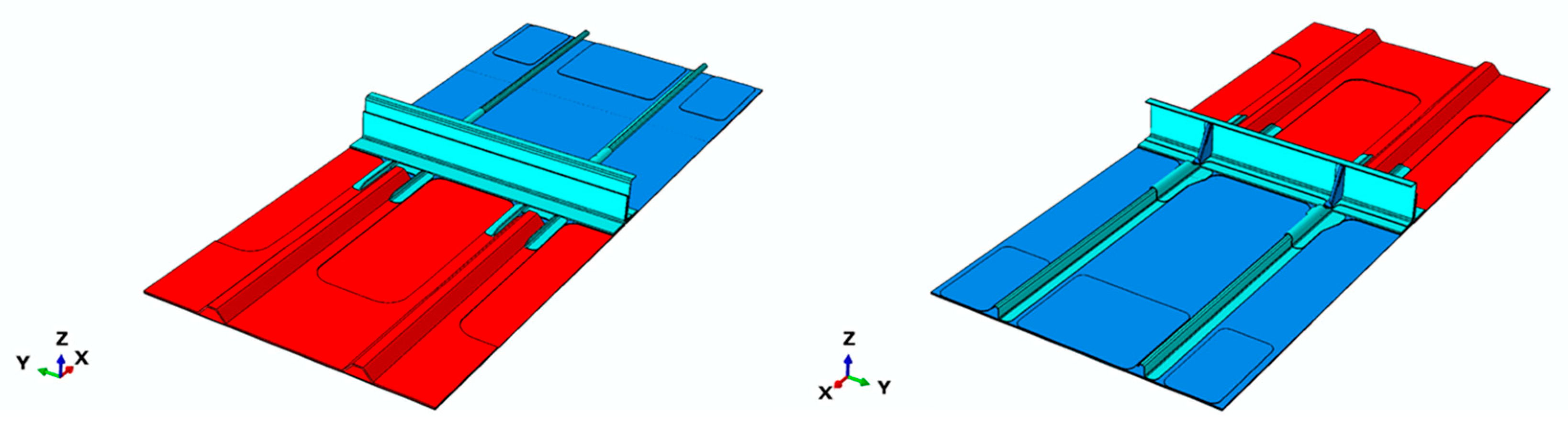
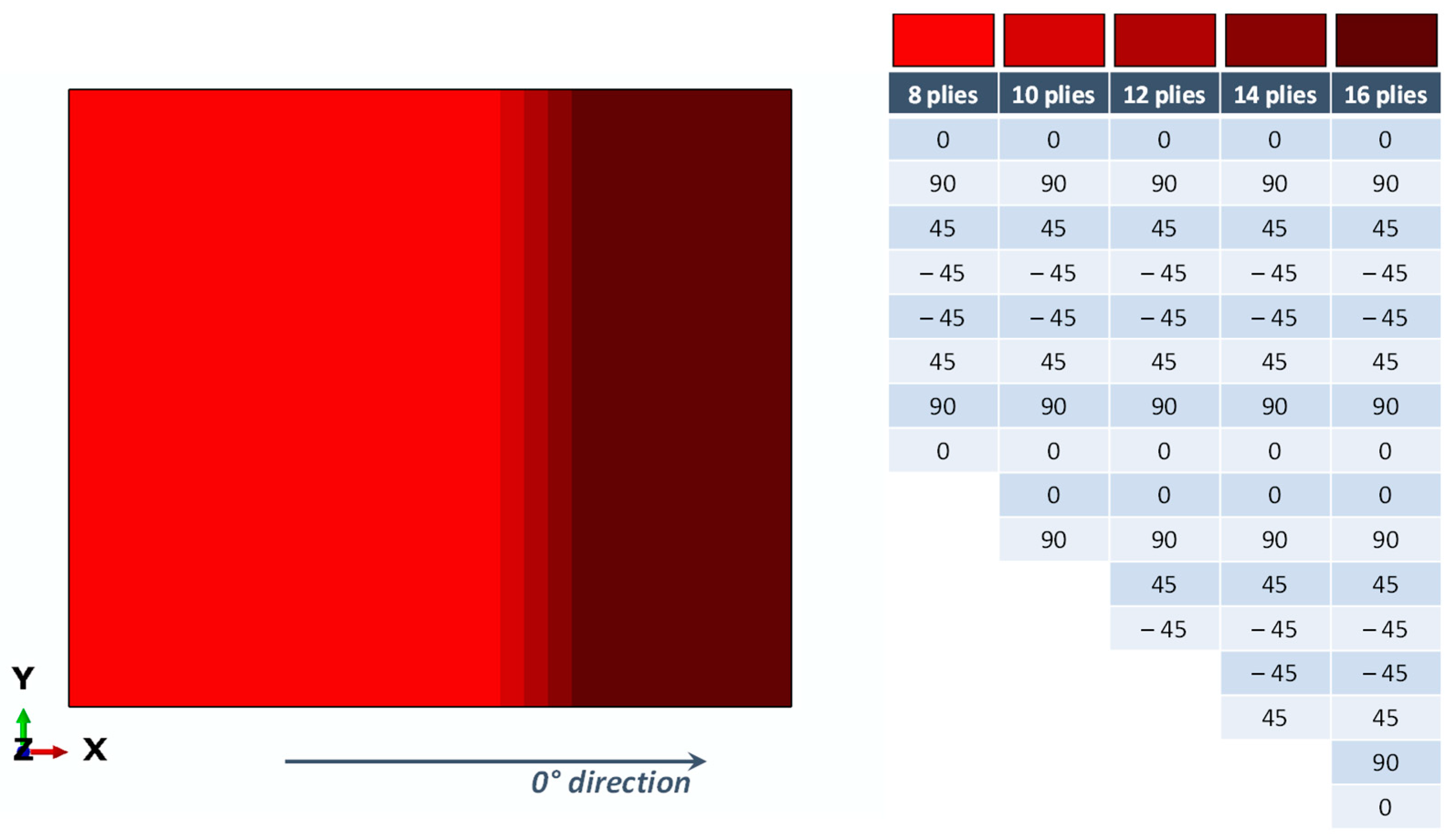
2. Test Case Description
3. The Experimental Setup
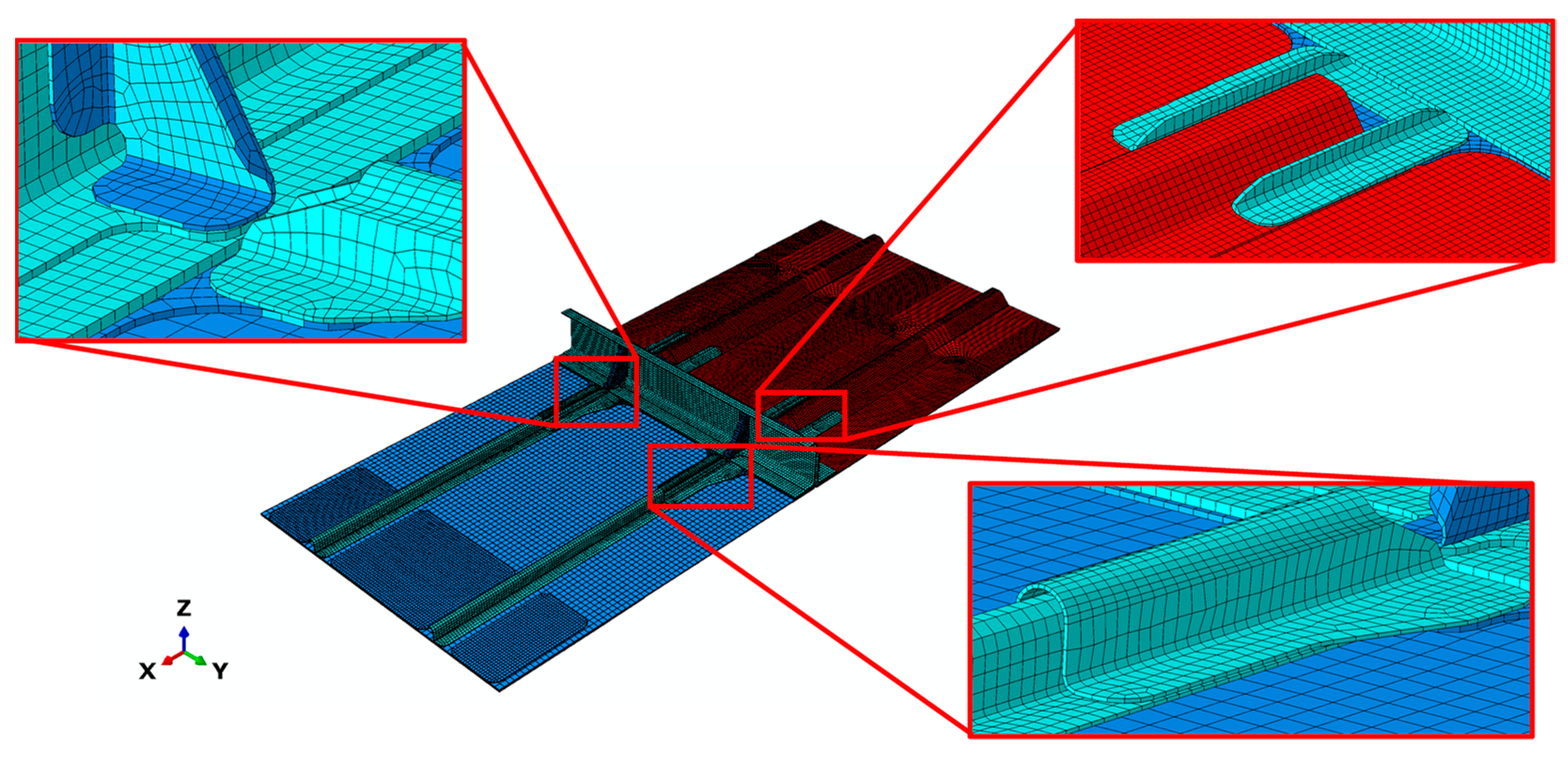
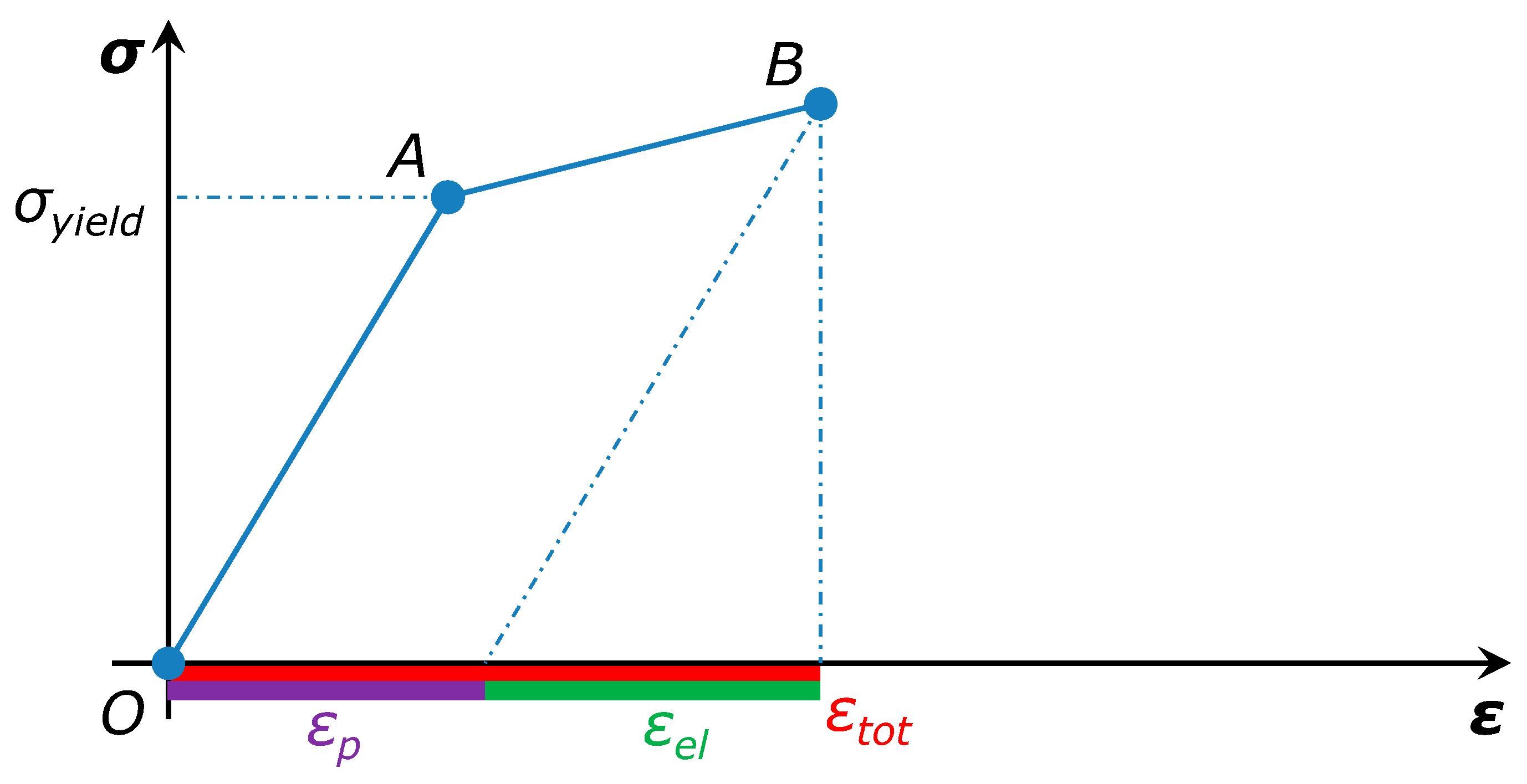
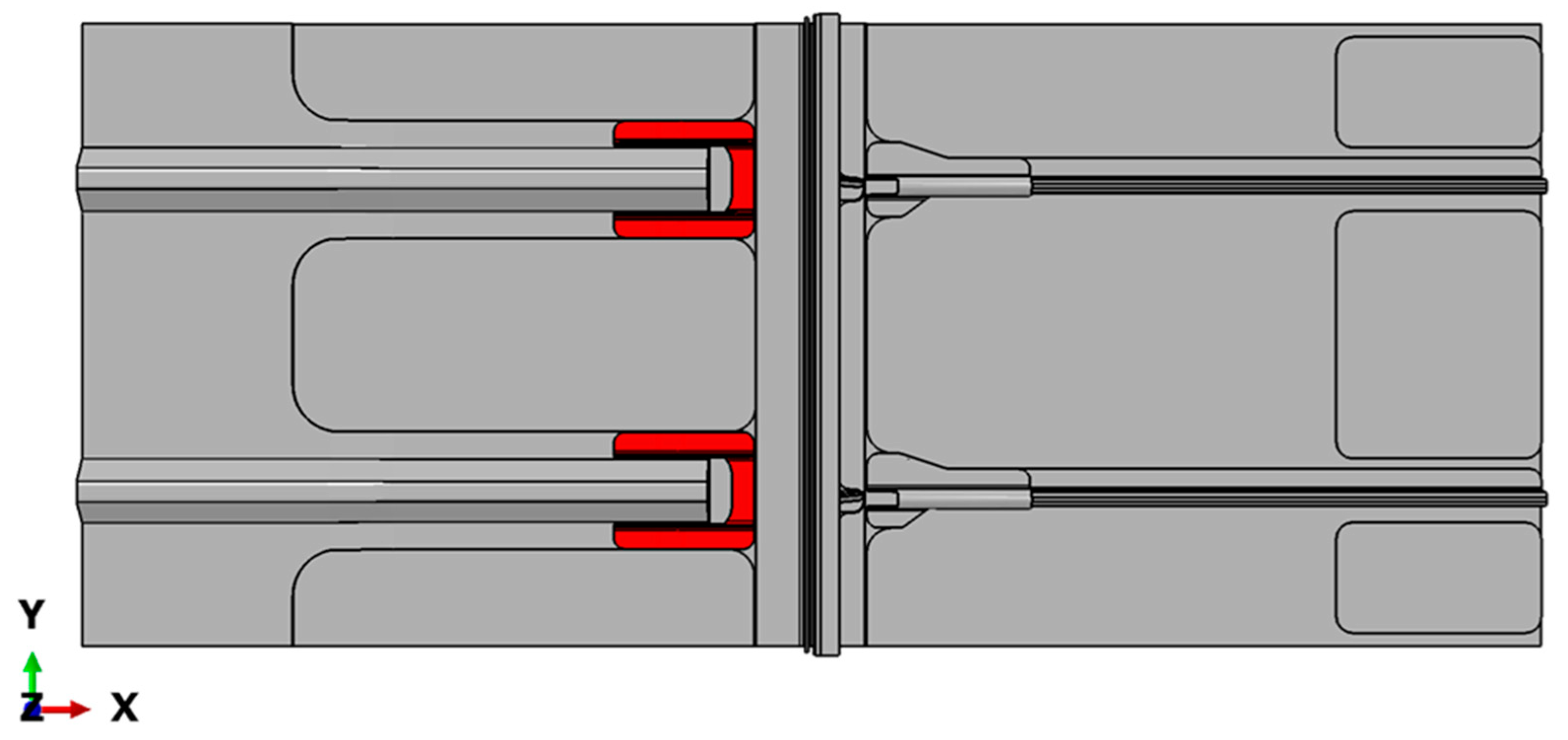
4. The Numerical Model
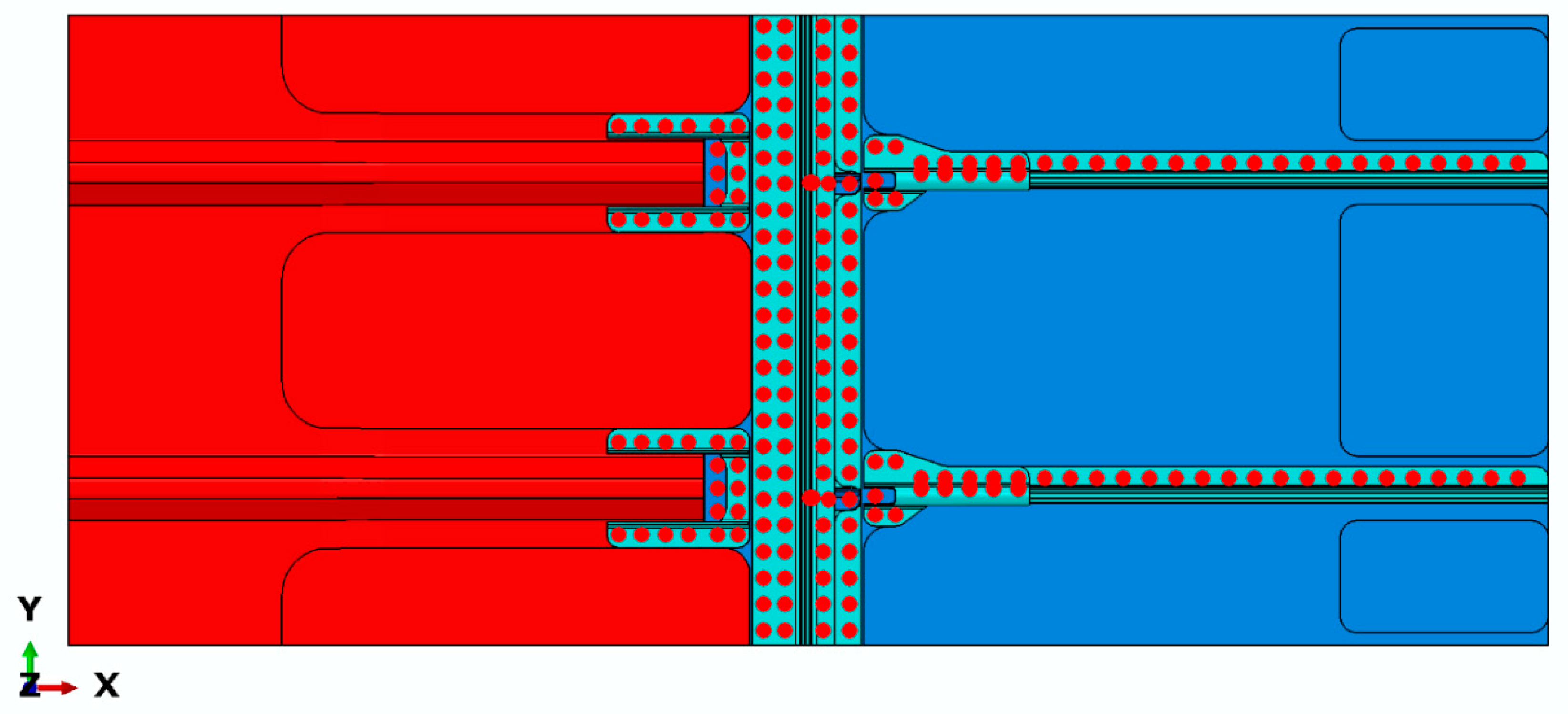
- Model with Tie: TIE constraints: this was used to connect the surfaces of the fastened subcomponents;
- Model with Fastener: the fasteners were numerically simulated by means of ABAQUS fastener connectors. An elastic behaviour was supposed for the fastener connectors, which were placed in the locations of the experimental test-case, reported in Figure 11.
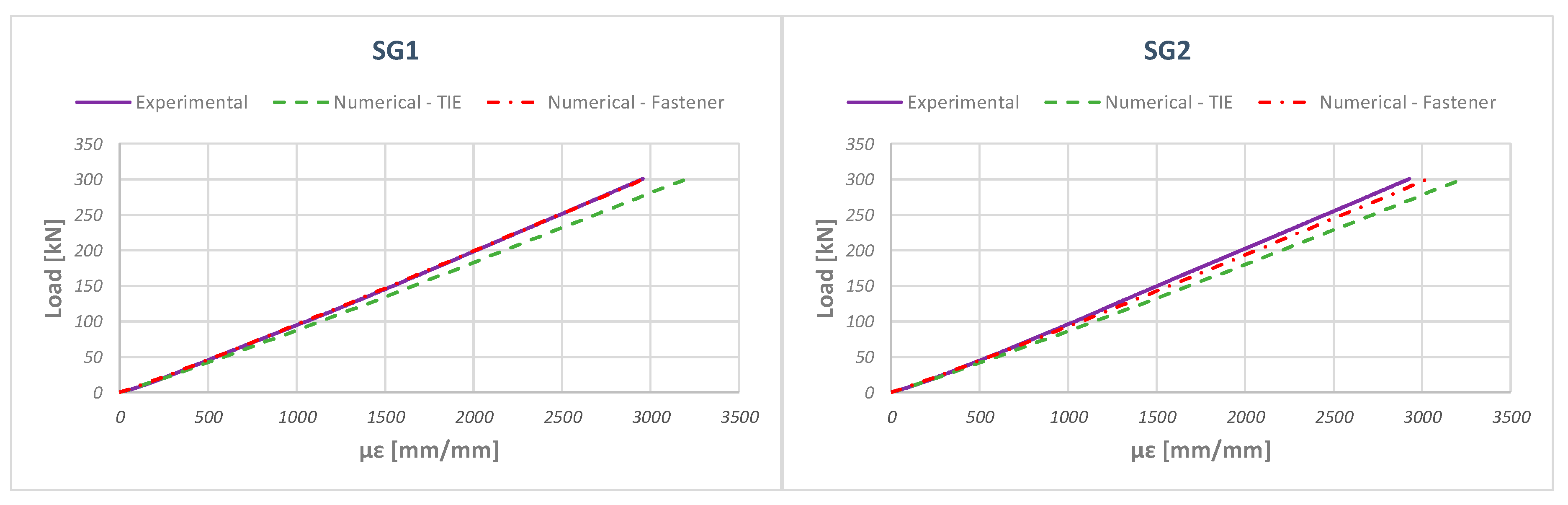
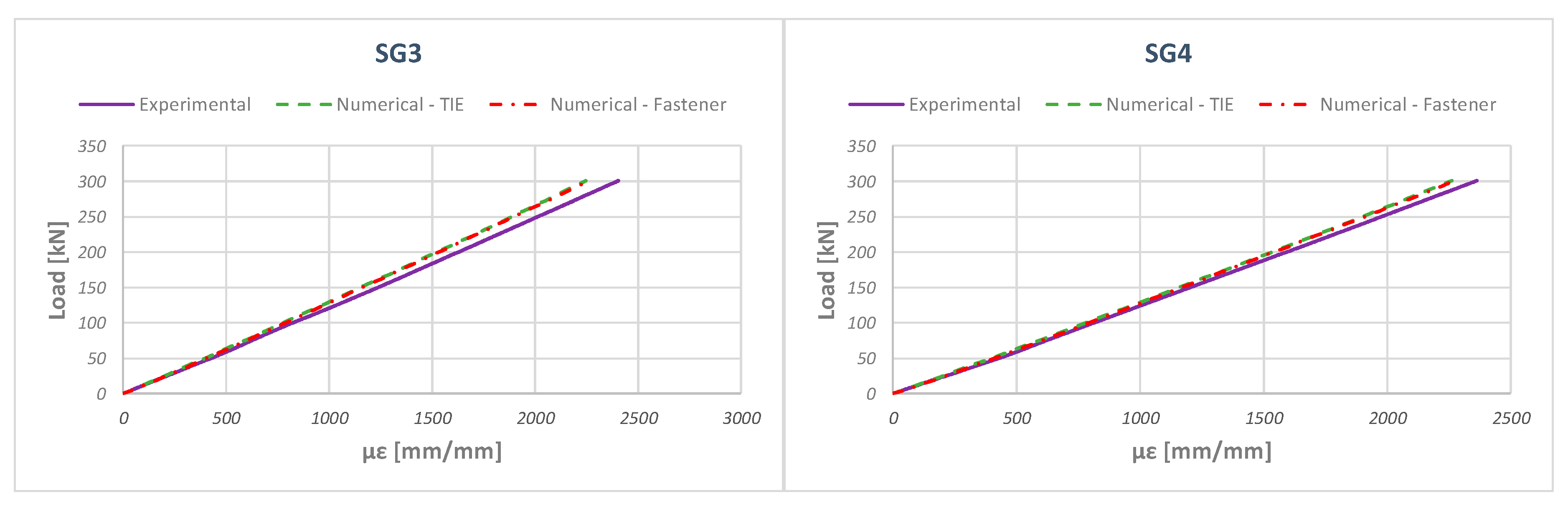
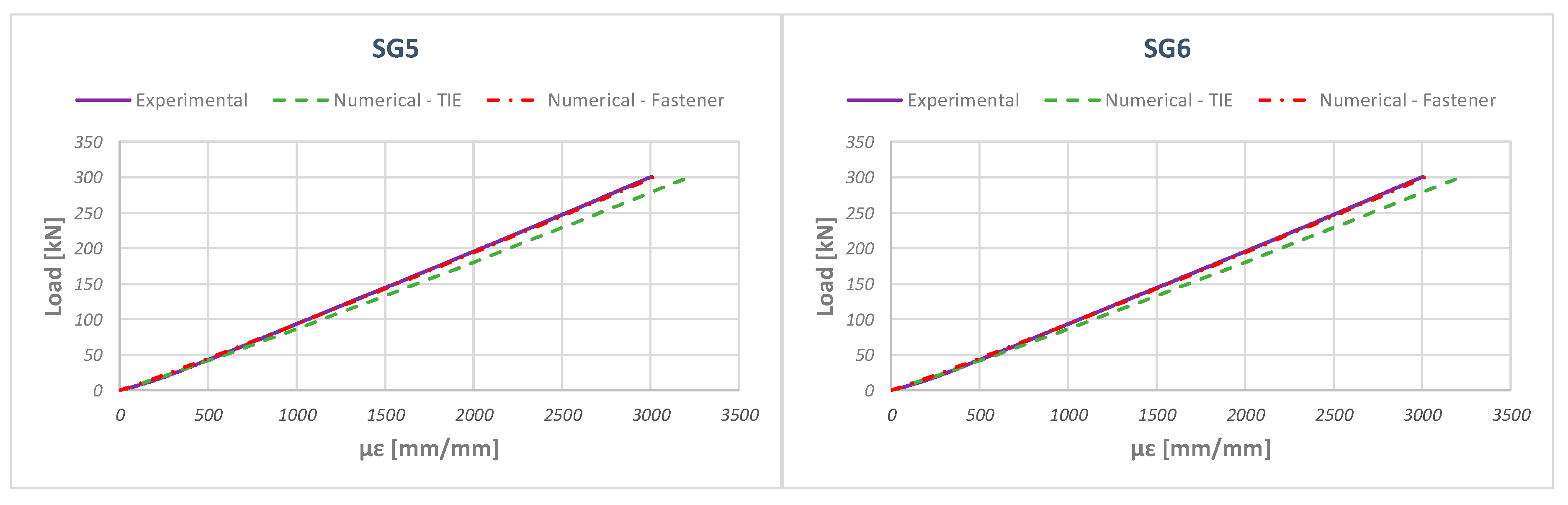
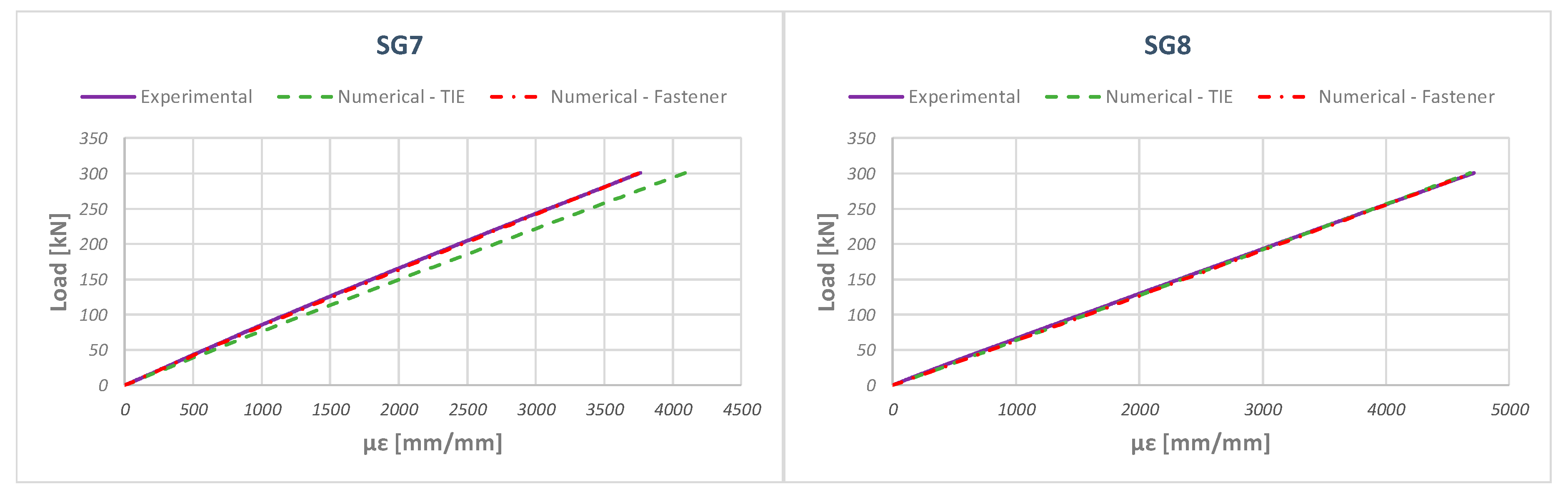
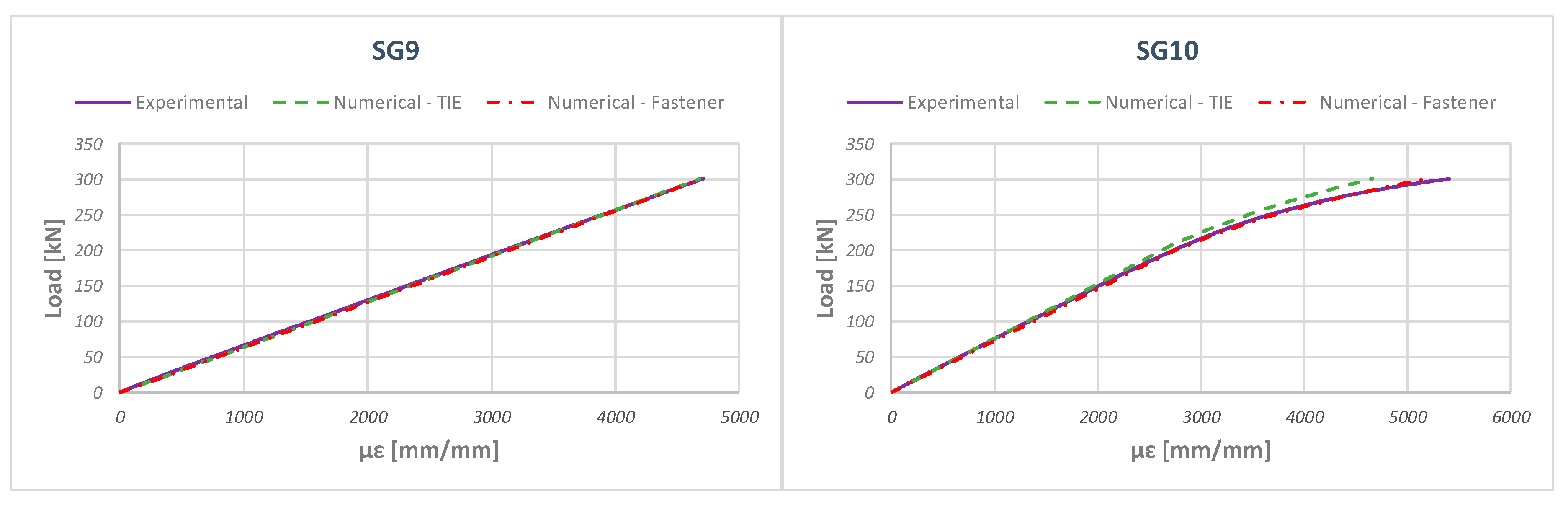
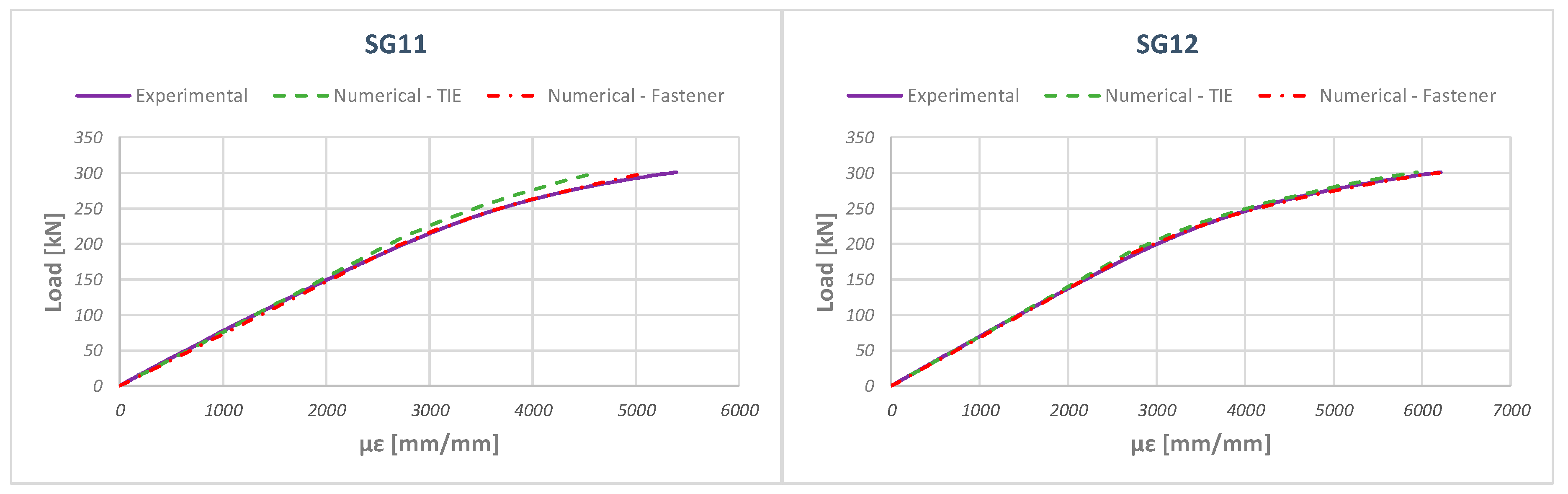
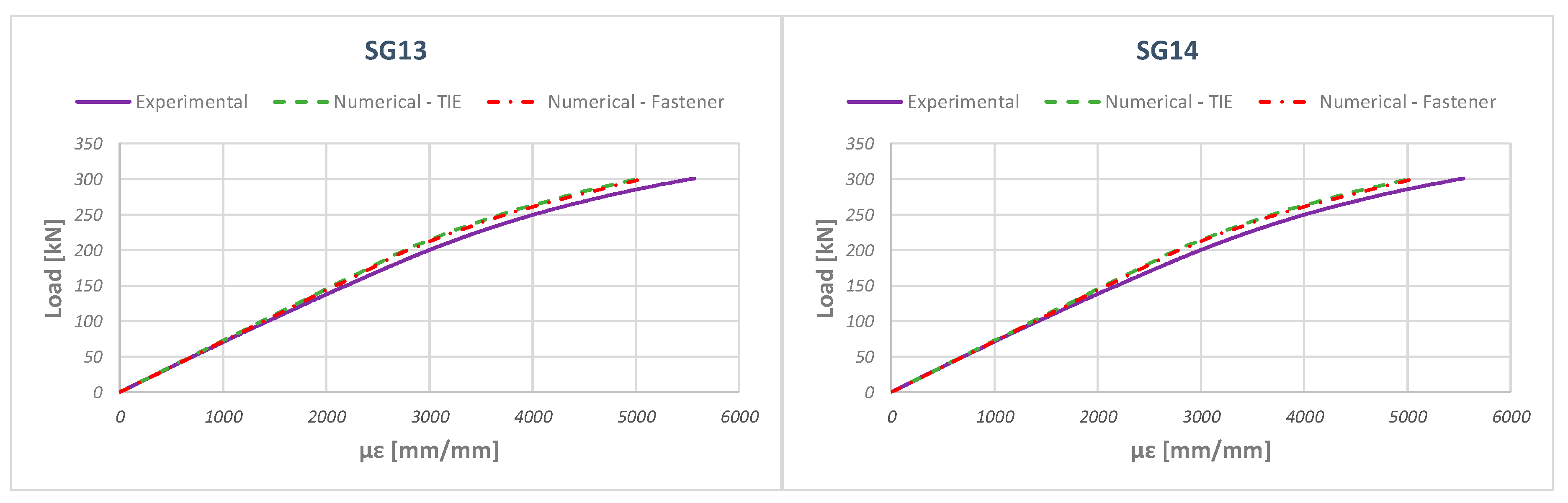
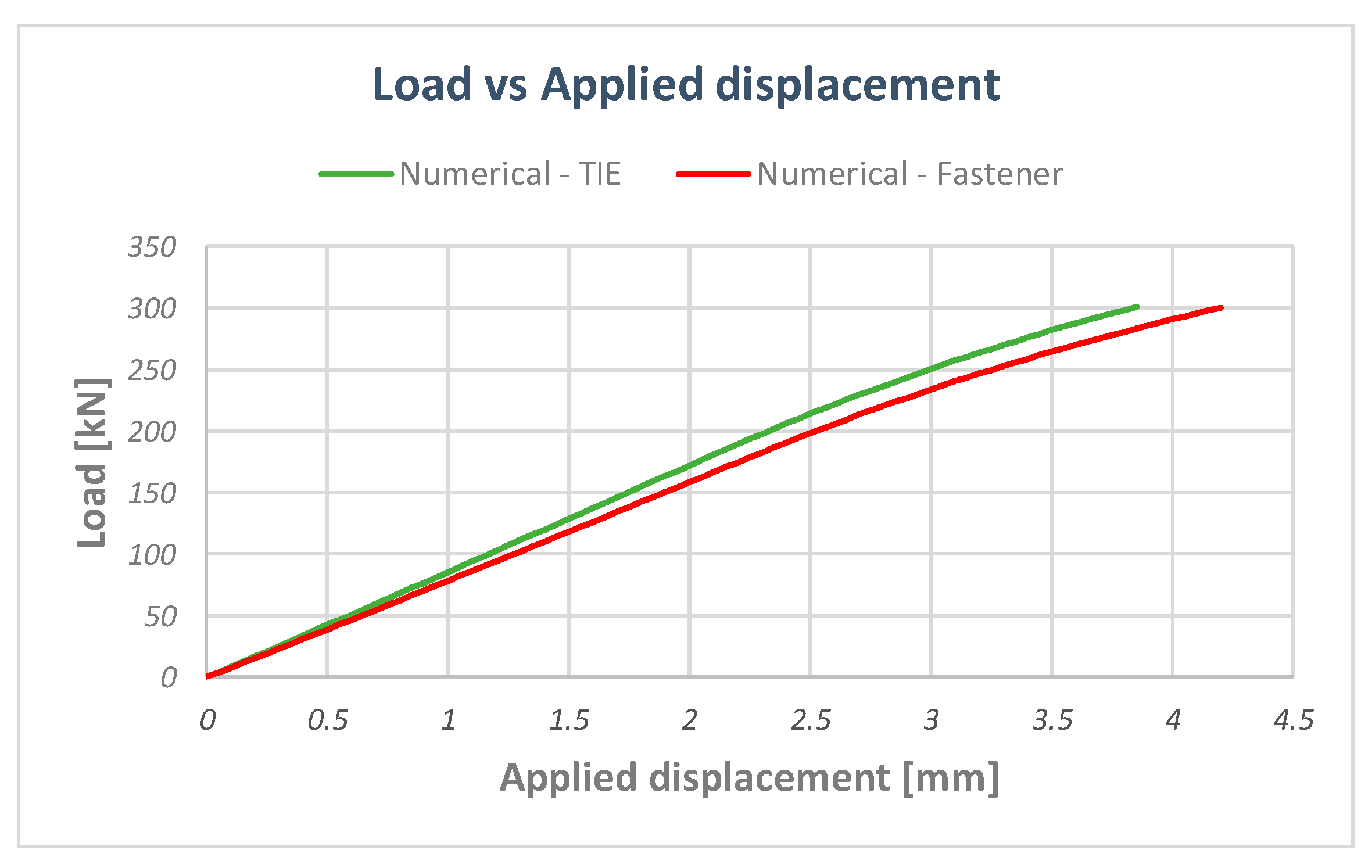
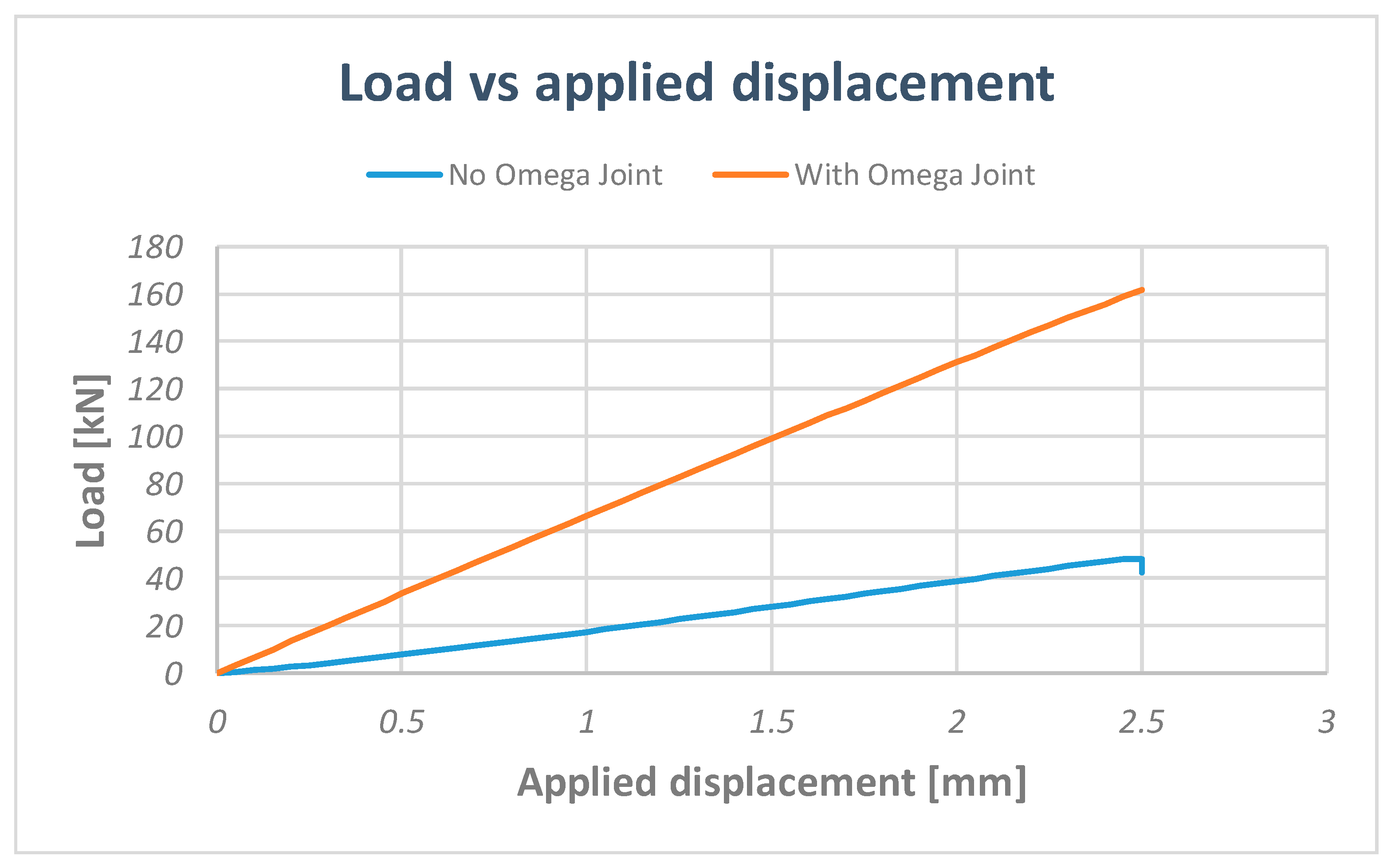
5. Numerical–Experimental Correlation
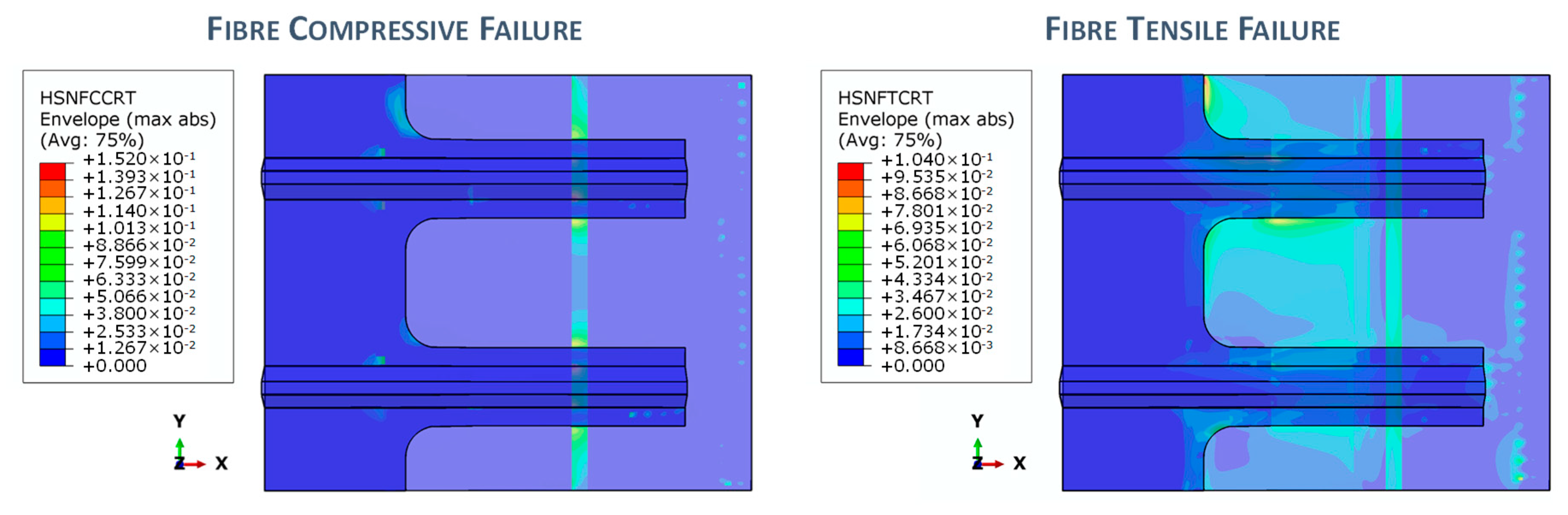
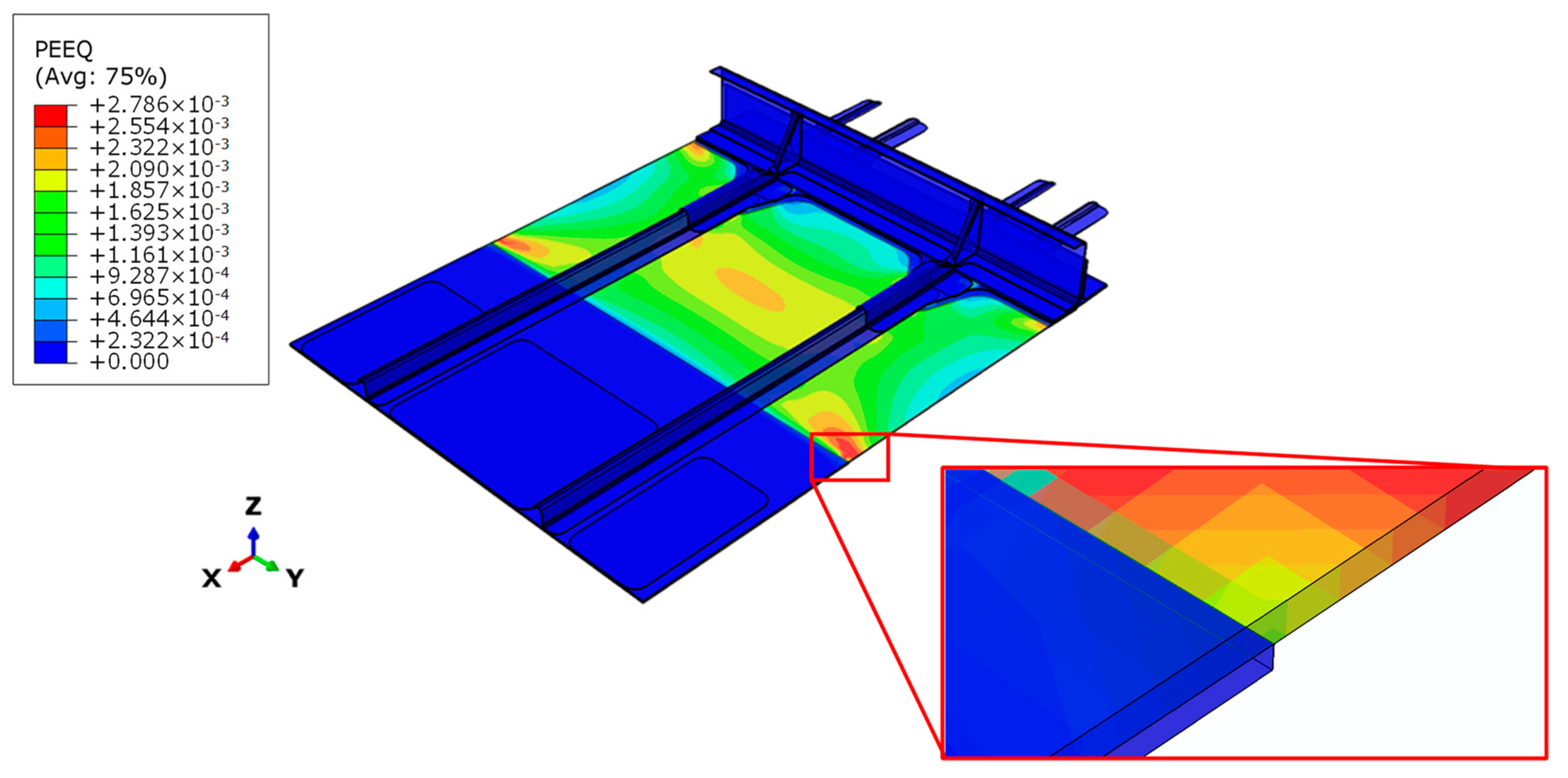
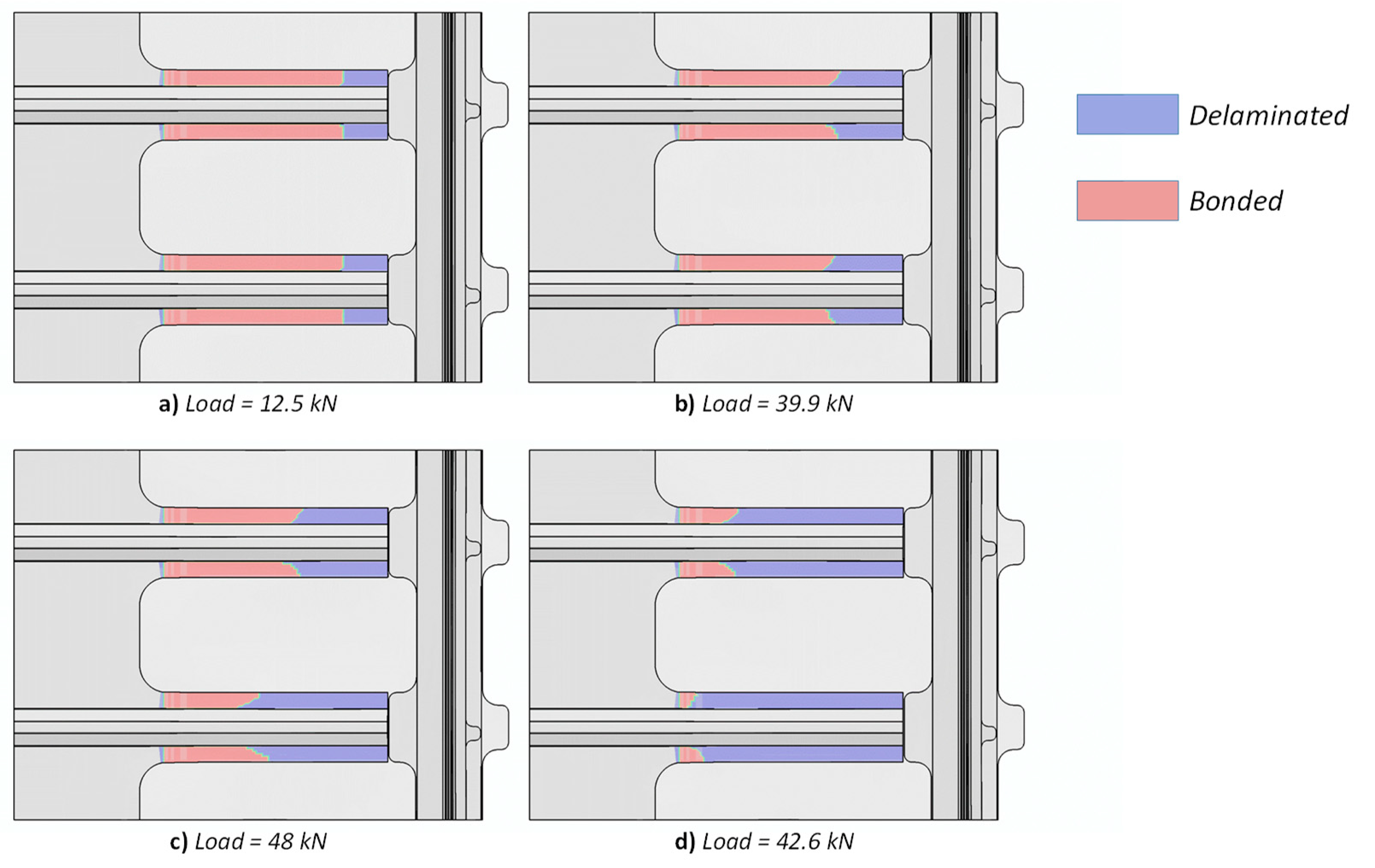
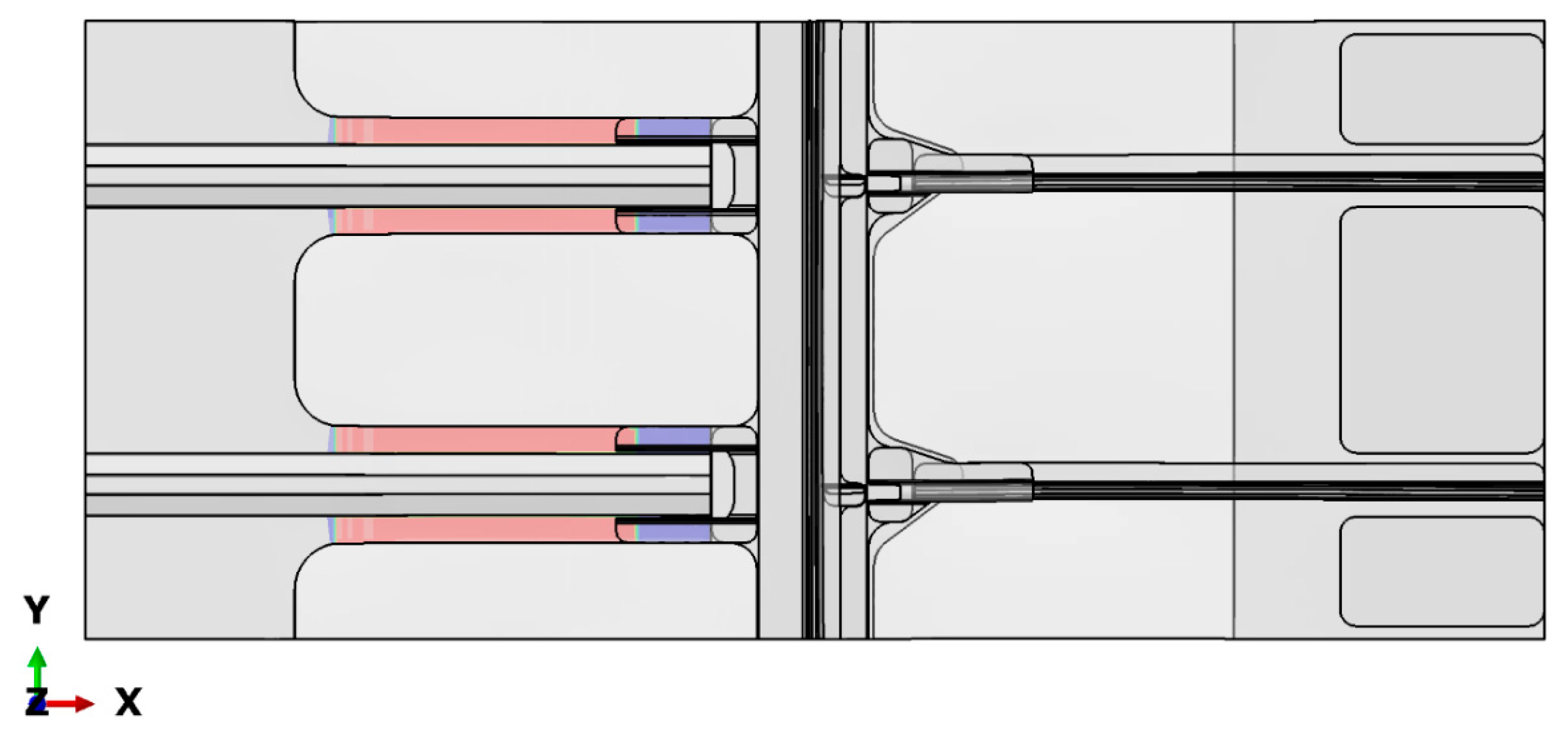
6. Sensitivity Analysis on the Inter-Laminar Damage Behaviour
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sellitto, A.; Riccio, A.; Russo, A.; Zarrelli, M.; Toscano, C.; Lopresto, V. Compressive behaviour of a damaged omega stiffened panel: Damage detection and numerical analysis. Compos. Struct. 2019, 209, 300–316. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Liu, W. Post-buckling progressive damage of CFRP laminates with a large-sized elliptical cutout subjected to shear loading. Compos. Struct. 2015, 128, 313–321. [Google Scholar] [CrossRef]
- Benedetti, I.; Gulizzi, V. A grain-scale model for high-cycle fatigue degradation in polycrystalline materials. Int. J. Fatigue 2018, 116, 90–105. [Google Scholar] [CrossRef]
- Benedetti, I.; Nguyen, H.; Soler-Crespo, R.A.; Gao, W.; Mao, L.; Ghasemi, A.; Wen, J.; Nguyen, S.; Espinosa, H.D. Formulation and validation of a reduced order model of 2D materials exhibiting a two-phase microstructure as applied to graphene oxide. J. Mech. Phys. Solids 2018, 112, 66–88. [Google Scholar] [CrossRef]
- Milazzo, A.; Benedetti, I.; Gulizzi, V. An extended Ritz formulation for buckling and post-buckling analysis of cracked multilayered plates. Compos. Struct. 2018, 201, 980–994. [Google Scholar] [CrossRef]
- Riccio, A.; Linde, P.; Raimondo, A.; Buompane, A.; Sellitto, A. On the use of selective stitching in stiffened composite panels to prevent skin-stringer debonding. Compos. Part B Eng. 2017, 124, 64–75. [Google Scholar] [CrossRef]
- Zhu, G.; Sun, G.; Liu, Q.; Li, G.; Li, Q. On crushing characteristics of different configurations of metal-composites hybrid tubes. Compos. Struct. 2017, 175, 58–69. [Google Scholar] [CrossRef]
- Zhu, G.; Sun, G.; Yu, H.; Li, S.; Li, Q. Energy absorption of metal, composite and metal/composite hybrid structures under oblique crushing loading. Int. J. Mech. Sci. 2018, 135, 458–483. [Google Scholar] [CrossRef]
- Kumar, P.; Rai, B. Delaminations of barely visible impact damage in CFRP laminates. Compos. Struct. 1993, 23, 313–318. [Google Scholar] [CrossRef]
- Rogge, M.D.; Leckey, C.A.C. Characterization of impact damage in composite laminates using guided wavefield imaging and local wavenumber domain analysis. Ultrasonics 2013, 53, 1217–1226. [Google Scholar] [CrossRef]
- Angelidis, N.; Irving, P.E. Detection of impact damage in CFRP laminates by means of electrical potential techniques. Compos. Sci. Technol. 2007, 67, 594–604. [Google Scholar] [CrossRef]
- Romano, F.; Di Caprio, F.; Mercurio, U. Compression after impact analysis of composite panels and equivalent hole method. Procedia Eng. 2016, 167, 182–189. [Google Scholar] [CrossRef]
- Borrelli, R.; Franchitti, S.; Di Caprio, F.; Mercurio, U.; Zallo, A. A repair criterion for impacted composite structures based on the prediction of the residual compressive strength. Procedia Eng. 2014, 88, 117–124. [Google Scholar] [CrossRef]
- Borrelli, R.; Franchitti, S.; Di Caprio, F.; Romano, F.; Mercurio, U. A numerical procedure for the virtual compression after impact analysis. Adv. Compos. Lett. 2015, 24, 57–67. [Google Scholar] [CrossRef]
- Perner, M.; Algermissen, S.; Keimer, R.; Monner, H.P. Avoiding defects in manufacturing processes: A review for automated CFRP production. Robot. Comput.-Integr. Manuf. 2016, 38, 82–92. [Google Scholar] [CrossRef]
- Ma, L.; Soleimani, M. Hidden defect identification in carbon fibre reinforced polymer plates using magnetic induction tomography. Meas. Sci. Technol. 2014, 25, 055404. [Google Scholar] [CrossRef]
- Hörrmann, S.; Adumitroaie, A.; Schagerl, M. The effect of ply folds as manufacturing defect on the fatigue life of CFRP materials. Frattura ed Integrita Strutturale 2016, 10, 76–81. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Lei, H.; Zhu, X.; Chen, H.; Wang, C.; Fang, D. Effect of manufacturing defect on mechanical performance of plain weave carbon/epoxy composite based on 3D geometrical reconstruction. Compos. Struct. 2018, 199, 38–52. [Google Scholar] [CrossRef]
- Pramanik, A. Developments in the non-traditional machining of particle reinforced metal matrix composites. Int. J. Mach. Tools Manuf. 2014, 86, 44–61. [Google Scholar] [CrossRef] [Green Version]
- Pramanik, A.; Basak, A.K.; Dong, Y.; Sarker, P.K.; Uddin, M.S.; Littlefair, G.; Dixit, A.R.; Chattopadhyaya, S. Joining of carbon fibre reinforced polymer (CFRP) composites and aluminium alloys—A review. Compos. Part A Appl. Sci. Manuf. 2017, 101, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Riccio, A.; Ricchiuto, R.; Di Caprio, F.; Sellitto, A.; Raimondo, A. Numerical investigation of constitutive material models on bonded joints in scarf repaired composite laminates. Eng. Fract. Mech. 2017, 173, 91–106. [Google Scholar] [CrossRef]
- Rhee, K.Y.; Choi, N.-S.; Park, S.-J. Effect of plasma treatment of aluminum on the bonding characteristics of aluminum-CFRP composite joints. J. Adhes. Sci. Technol. 2002, 16, 1487–1500. [Google Scholar] [CrossRef]
- Jumbo, F.; Ruiz, P.D.; Yu, Y.; Swallowe, G.M.; Ashcroft, I.A.; Huntley, J.M. Experimental and numerical investigation of mechanical and thermal residual strains in adhesively bonded joints. Strain 2007, 43, 319–331. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Li, Y. A method for predicting the curing residual stress for CFRP/Al adhesive single-lap joints. Int. J. Adhes. Adhes. 2013, 46, 7–13. [Google Scholar] [CrossRef]
- Ishii, K.; Imanaka, M.; Nakayama, H.; Kodama, H. Evaluation of the fatigue strength of adhesively bonded CFRP/metal single and single-step double-lap joints. Compos. Sci. Technol. 1999, 59, 1675–1683. [Google Scholar] [CrossRef]
- Biscaia, H.; Cardoso, J.; Chastre, C. A finite element based analysis of double strap bonded joints with CFRP and aluminium. Key Eng. Mater. 2017, 754, 237–240. [Google Scholar] [CrossRef]
- Ruiz, P.D.; Jumbo, F.; Huntley, J.M.; Ashcroft, I.A.; Swallowe, G.M. Experimental and numerical investigation of strain distributions within the adhesive layer in bonded joints. Strain 2011, 47, 88–104. [Google Scholar] [CrossRef]
- Tinkloh, S.; Wu, T.; Tröster, T.; Niendorf, T. A micromechanical-based finite element simulation of process-induced residual stresses in metal-CFRP-hybrid structures. Compos. Struct. 2020, 238, 111926. [Google Scholar] [CrossRef]
- Tsokanas, P.; Loutas, T.; Kotsinis, G.; Kostopoulos, V.; van den Brink, W.M.; Martin de la Escalera, F. On the fracture toughness of metal-composite adhesive joints with bending-extension coupling and residual thermal stresses effect. Compos. Part B Eng. 2020, 185, 107694. [Google Scholar] [CrossRef]
- Xiao, Y.; Ishikawa, T. Bearing strength and failure behavior of bolted composite joints (part I: Experimental investigation). Compos. Sci. Technol. 2005, 65, 1022–1031. [Google Scholar] [CrossRef]
- Xiao, Y.; Ishikawa, T. Bearing strength and failure behavior of bolted composite joints (part II: Modeling and simulation). Compos. Sci. Technol. 2005, 65, 1032–1043. [Google Scholar] [CrossRef]
- Irisarri, F.-X.; Laurin, F.; Carrere, N.; Maire, J.-F. Progressive damage and failure of mechanically fastened joints in CFRP laminates-Part I: Refined Finite Element modelling of single-fastener joints. Compos. Struct. 2012, 94, 2269–2277. [Google Scholar] [CrossRef]
- Irisarri, F.-X.; Laurin, F.; Carrere, N.; Maire, J.-F. Progressive damage and failure of mechanically fastened joints in CFRP laminates-Part II: Failure prediction of an industrial junction. Compos. Struct. 2012, 94, 2278–2284. [Google Scholar] [CrossRef]
- Madukauwa-David, I.D.; Drissi-Habti, M. Numerical simulation of the mechanical behavior of a large smart composite platform under static loads. Compos. Part B Eng. 2016, 88, 19–25. [Google Scholar] [CrossRef]
- Antony, S.; Drissi-Habti, M.; Raman, V. Numerical Analysis to Enhance Delamination Strength around Bolt Holes of Unidirectional Pultruded Large Smart Composite Platform. Adv. Mater. Sci. Eng. 2018, 2018, 3154904. [Google Scholar] [CrossRef] [Green Version]
- Benezech, L.; Landon, Y.; Rubio, W. Study of manufacturing defects and tool geometry optimisation for multi-material stack drilling. Adv. Mater. Res. 2012, 423, 1–11. [Google Scholar] [CrossRef]
- Zitoune, R.; Krishnaraj, V.; Sofiane Almabouacif, B.; Collombet, F.; Sima, M.; Jolin, A. Influence of machining parameters and new nano-coated tool on drilling performance of CFRP/Aluminium sandwich. Compos. Part B Eng. 2012, 43, 1480–1488. [Google Scholar] [CrossRef]
- Breziner, L.; Hutapea, P. Influence of harsh environmental conditions on CFRP-aluminum single lap joints. Aircr. Eng. Aerosp. Technol. 2008, 80, 371–377. [Google Scholar] [CrossRef]
- Coman, C.-D.; Pelin, G. Thermal effects on single-Lap, single-Bolt, hybrid metal—Composite joint stiffness. Incas Bull. 2018, 10, 75–88. [Google Scholar]
- Ueda, M.; Miyake, S.; Hasegawa, H.; Hirano, Y. Instantaneous mechanical fastening of quasi-isotropic CFRP laminates by a self-piercing rivet. Compos. Struct. 2012, 94, 3388–3393. [Google Scholar] [CrossRef]
- Hoang, N.-H.; Langseth, M.; Porcaro, R.; Hanssen, A.-G. The effect of the riveting process and aging on the mechanical behaviour of an aluminium self-piercing riveted connection. Eur. J. Mech. A/Solids 2011, 30, 619–630. [Google Scholar] [CrossRef]
- Hoang, N.-H.; Porcaro, R.; Langseth, M.; Hanssen, A.-G. Self-piercing riveting connections using aluminium rivets. Int. J. Solids Struct. 2010, 47, 427–439. [Google Scholar] [CrossRef] [Green Version]
- Pickin, C.G.; Young, K.; Tuersley, I. Joining of lightweight sandwich sheets to aluminium using self-pierce riveting. Mater. Des. 2007, 28, 2361–2365. [Google Scholar] [CrossRef]
- Landgrebe, D.; Jäckel, M.; Niegsch, R. Influence of process induced damages on joint strength when self-pierce riveting carbon fiber reinforced plastics with aluminum. Key Eng. Mater. 2015, 651–653, 1493–1498. [Google Scholar] [CrossRef]
- Rao, H.M.; Kang, J.; Huff, G.; Avery, K.; Su, X. Impact of rivet head height on the tensile and fatigue properties of lap shear self-pierced riveted CFRP to aluminum. SAE Int. J. Mater. Manuf. 2017, 10, 167–173. [Google Scholar] [CrossRef]
- Kweon, J.-H.; Jung, J.-W.; Kim, T.-H.; Choi, J.-H.; Kim, D.-H. Failure of carbon composite-to-aluminum joints with combined mechanical fastening and adhesive bonding. Compos. Struct. 2006, 75, 192–198. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Shibata, M.; Todoroki, A. Improving performance of GFRP/aluminum single lap joints using bolted/co-cured hybrid method. Compos. Part A Appl. Sci. Manuf. 2008, 39, 154–163. [Google Scholar] [CrossRef]
- Di Franco, G.; Zuccarello, B. Analysis and optimization of hybrid double lap aluminum-GFRP joints. Compos. Struct. 2014, 116, 682–693. [Google Scholar] [CrossRef] [Green Version]
- Fu, M.; Mallick, P.K. Fatigue of hybrid (adhesive/bolted) joints in SRIM composites. Int. J. Adhes. Adhes. 2001, 21, 145–159. [Google Scholar] [CrossRef]
- Di Franco, G.; Fratini, L.; Pasta, A. Analysis of the mechanical performance of hybrid (SPR/bonded) single-lap joints between CFRP panels and aluminum blanks. Int. J. Adhes. Adhes. 2013, 41, 24–32. [Google Scholar] [CrossRef]
- Barut, A.; Madenci, E. Analysis of bolted-bonded composite single-lap joints under combined in-plane and transverse loading. Compos. Struct. 2009, 88, 579–594. [Google Scholar] [CrossRef]
- Kapidžić, Z.; Nilsson, L.; Ansell, H. Finite element modeling of mechanically fastened composite-aluminum joints in aircraft structures. Compos. Struct. 2014, 109, 198–210. [Google Scholar] [CrossRef]
- Hochard, C.; Payan, J.; Bordreuil, C. A progressive first ply failure model for woven ply CFRP laminates under static and fatigue loads. Int. J. Fatigue 2006, 28, 1270–1276. [Google Scholar] [CrossRef]
- Guild, F.J.; Vrellos, N.; Drinkwater, B.W.; Balhi, N.; Ogin, S.L.; Smith, P.A. Intra-laminar cracking in CFRP laminates: Observations and modelling. J. Mater. Sci. 2006, 41, 6599–6609. [Google Scholar] [CrossRef]
- Reiner, J.; Feser, T.; Schueler, D.; Waimer, M.; Vaziri, R. Comparison of two progressive damage models for studying the notched behavior of composite laminates under tension. Compos. Struct. 2019, 207, 385–396. [Google Scholar] [CrossRef]
- Gong, W.; Chen, J.; Patterson, E.A. An experimental study of the behaviour of delaminations in composite panels subjected to bending. Compos. Struct. 2015, 123, 9–18. [Google Scholar] [CrossRef]
- Riccio, A.; Russo, A.; Sellitto, A.; Raimondo, A. Development and application of a numerical procedure for the simulation of the “Fibre Bridging” phenomenon in composite structures. Compos. Struct. 2017, 168, 104–119. [Google Scholar] [CrossRef]
- Lévêque, D.; Schieffer, A.; Mavel, A.; Maire, J.-F. Analysis of how thermal aging affects the long-term mechanical behavior and strength of polymer-matrix composites. Compos. Sci. Technol. 2005, 65, 395–401. [Google Scholar] [CrossRef]
- De Luca, A.; Caputo, F. A review on analytical failure criteria for composite materials. Aims Mater. Sci. 2017, 4, 1165–1185. [Google Scholar] [CrossRef]
- Khadyko, M.; Dumoulin, S.; Børvik, T.; Hopperstad, O.S. An experimental-numerical method to determine the work-hardening of anisotropic ductile materials at large strains. Int. J. Mech. Sci. 2014, 88, 25–36. [Google Scholar] [CrossRef]
- Frodal, B.H.; Dæhli, L.E.B.; Børvik, T.; Hopperstad, O.S. Modelling and simulation of ductile failure in textured aluminium alloys subjected to compression-tension loading. Int. J. Plast. 2019, 118, 36–69. [Google Scholar] [CrossRef]







| AA 2024–T42 | AA 7075–T62 | ||
|---|---|---|---|
| E [MPa] | ν [-] | E [MPa] | ν [-] |
| 72,400 | 0.33 | 71,700 | 0.33 |
| IMS/977-2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| E1 [MPa] | E2 = E3 [MPa] | G12 = G13 [MPa] | G23 [MPa] | ν12 [-] | GIC [kJ/m2] | GIIC = GIIIC [kJ/m2] | |||
| 152,310 | 8730 | 3940 | 2840 | 0.34 | 0.18 | 0.5 | |||
| XT [MPa] | XC [MPa] | YT [MPa] | YC [MPa] | ST [MPa] | SL [MPa] | GT1C [kJ/m2] | GT2C [kJ/m2] | GC1C [kJ/m2] | GC2C [kJ/m2] |
| 2700 | 1300 | 55 | 190 | 40 | 102 | 45 | 0.298 | 0.334 | 3.349 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sellitto, A.; Saputo, S.; Russo, A.; Innaro, V.; Riccio, A.; Acerra, F.; Russo, S. Numerical-Experimental Investigation into the Tensile Behavior of a Hybrid Metallic–CFRP Stiffened Aeronautical Panel. Appl. Sci. 2020, 10, 1880. https://doi.org/10.3390/app10051880
Sellitto A, Saputo S, Russo A, Innaro V, Riccio A, Acerra F, Russo S. Numerical-Experimental Investigation into the Tensile Behavior of a Hybrid Metallic–CFRP Stiffened Aeronautical Panel. Applied Sciences. 2020; 10(5):1880. https://doi.org/10.3390/app10051880
Chicago/Turabian StyleSellitto, Andrea, Salvatore Saputo, Angela Russo, Vincenzo Innaro, Aniello Riccio, Francesco Acerra, and Salvatore Russo. 2020. "Numerical-Experimental Investigation into the Tensile Behavior of a Hybrid Metallic–CFRP Stiffened Aeronautical Panel" Applied Sciences 10, no. 5: 1880. https://doi.org/10.3390/app10051880
APA StyleSellitto, A., Saputo, S., Russo, A., Innaro, V., Riccio, A., Acerra, F., & Russo, S. (2020). Numerical-Experimental Investigation into the Tensile Behavior of a Hybrid Metallic–CFRP Stiffened Aeronautical Panel. Applied Sciences, 10(5), 1880. https://doi.org/10.3390/app10051880








