Energy Efficient and Reliable Routing Algorithm for Wireless Sensors Networks
Abstract
:1. Introduction
- From the perspective of energy consumption reduction, DS-EERA establishes the node evaluation function. That is, the attributes of the nodes are considered comprehensively and abstracted into three indexes: transmission energy efficiency ratio, idleness degree and energy density factor.
- Considering the operation of each round of the network, we objectively determine the weight of each index based on the difference coefficient of entropy values.
- The application of DS evidence theory in node attributes fusion as routing is very few in WSN. DS-EERA regards three indexes as evidence, and determines whether the node can become the next hop as the recognition target. We innovatively apply DS fusion rules to the fuse the node indexes and take the fusion results as the basis of routing decisions.
- Significantly, the simulation results show that DS-EERA can not only reduce energy consumption effectively and prolong network lifetime in energy-constrained networks but also achieve lower packet loss rate and increase the reliability of data transmission.
2. Related Works
3. Network Model and Evidence Theory
3.1. Network Model
3.2. DS Evidence Theory
4. DS-EERA
4.1. Attribute Indexes
4.2. Weight Assignment
4.3. BPA Function Based on Triangular Membership Function
4.4. Fusion of Attribute Indexes and Routing Decision
| Algorithm 1 The Next Hop Selection |
| Input: Node , index weight , transmission energy efficiency ratio , idleness degree , energy density factor , the triangle membership function model . Output: The next hop 1: for // is the number of forward neighbor nodes of node i 2: j = 1, 3: According to G, traverse m: 4: , 5: find , , 6: Establish triangular membership function 7: Combine and corresponding weight to establish BPA function: 8: 9: Fuse the three indexes by Equations (17) and (18): 10: ,; , 11: if //criterion 12: 13: end if 14: end for 15: 16: Return j |
5. Simulation Results and Analysis
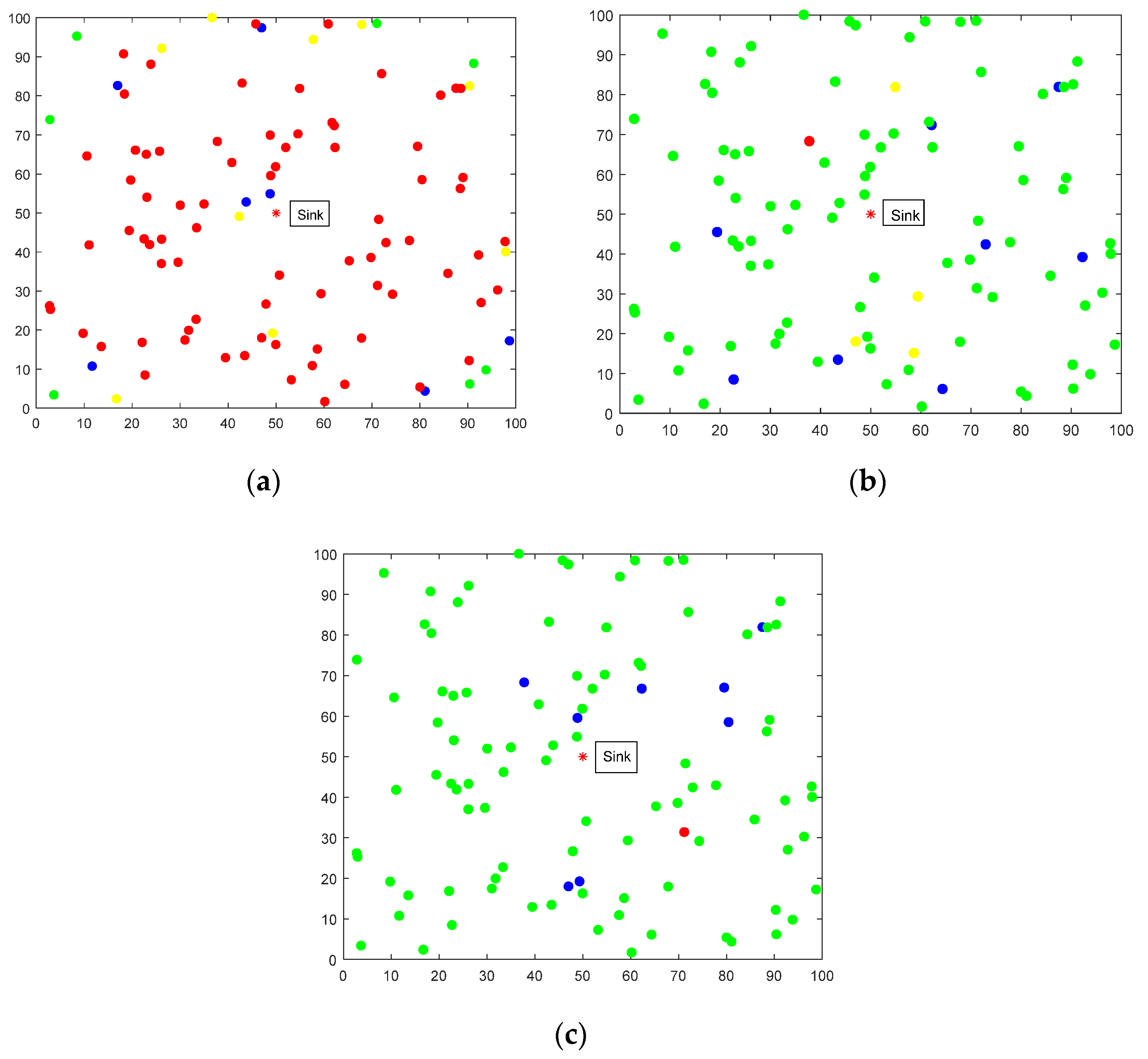
5.1. Average Packet Loss Rate
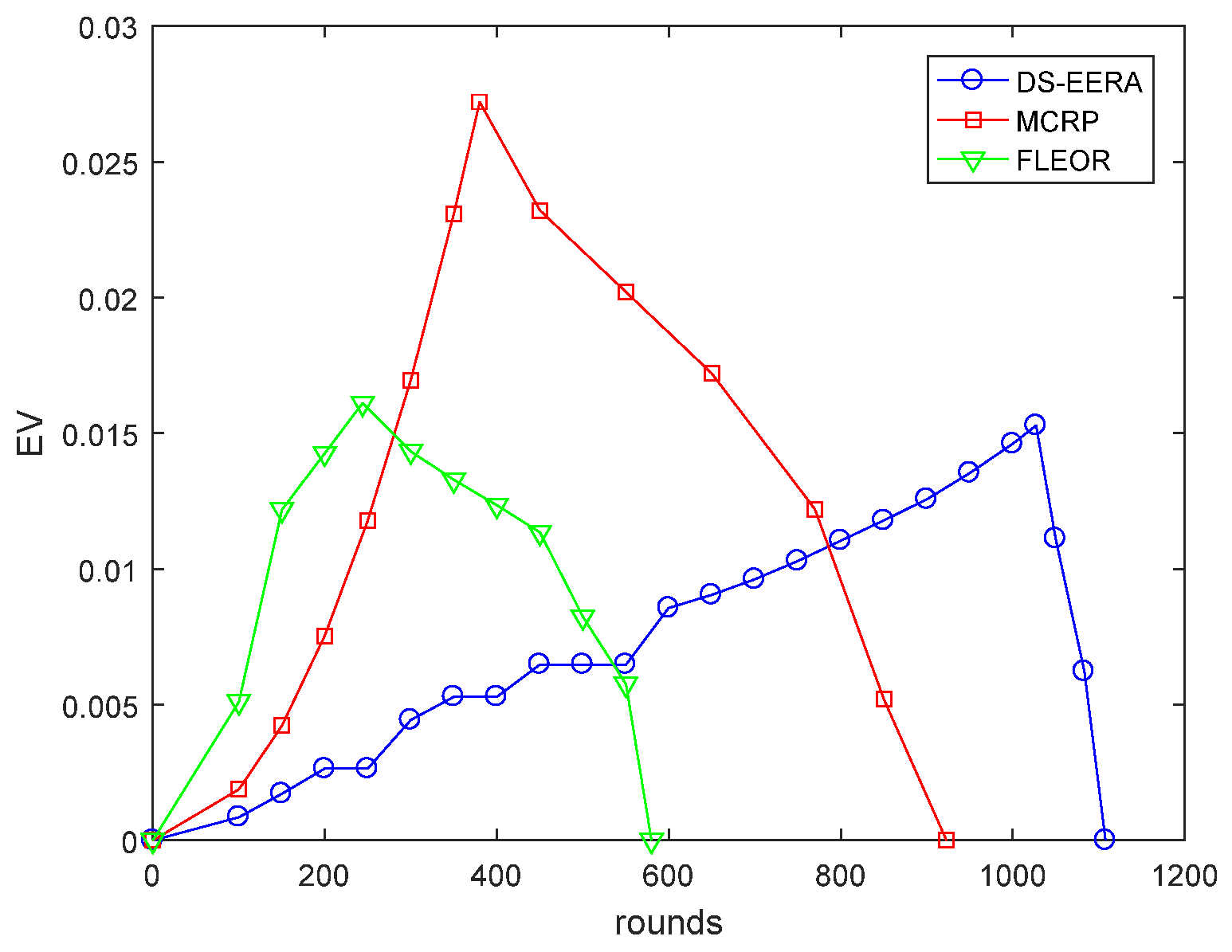
5.2. Energy Efficiency
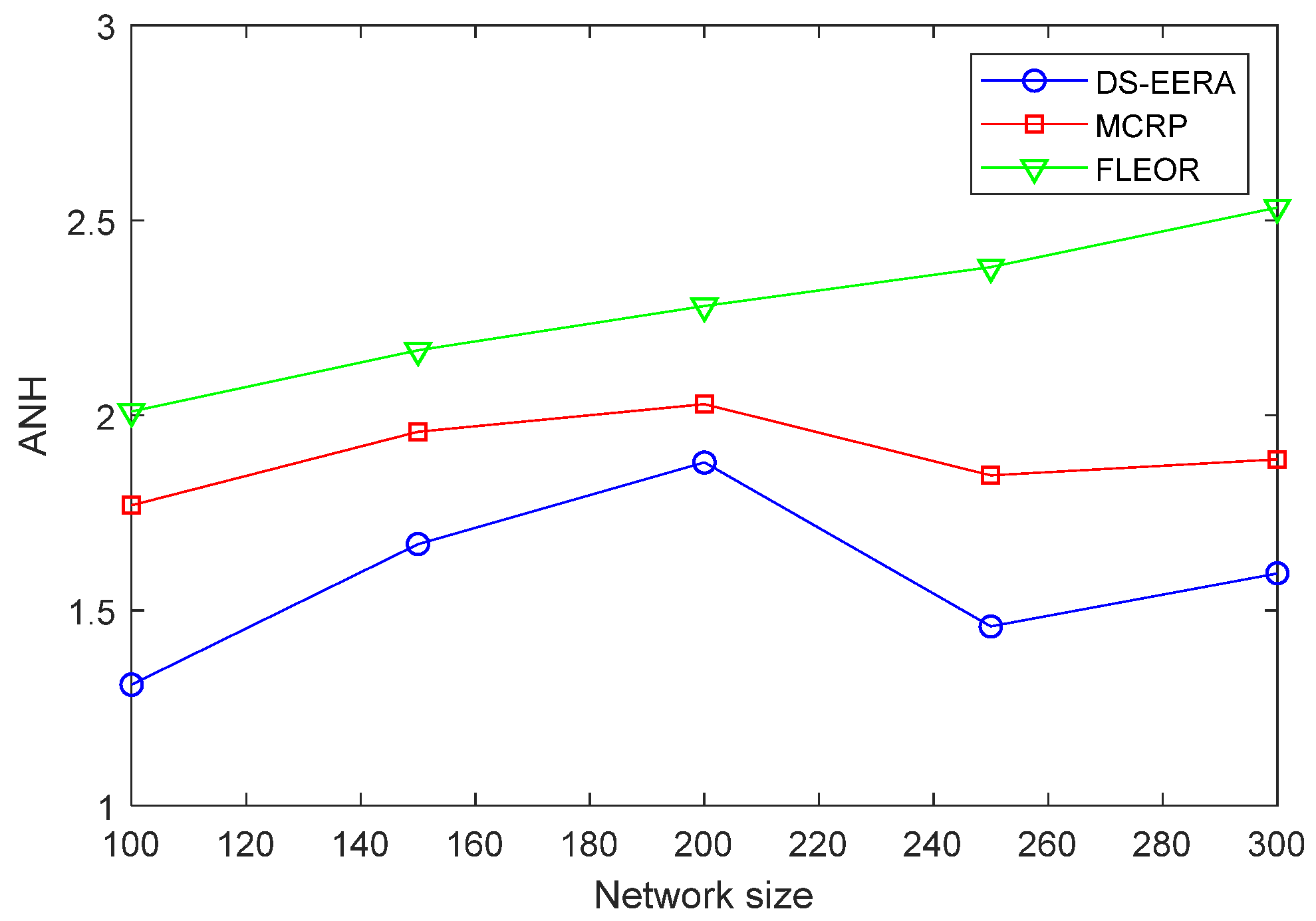
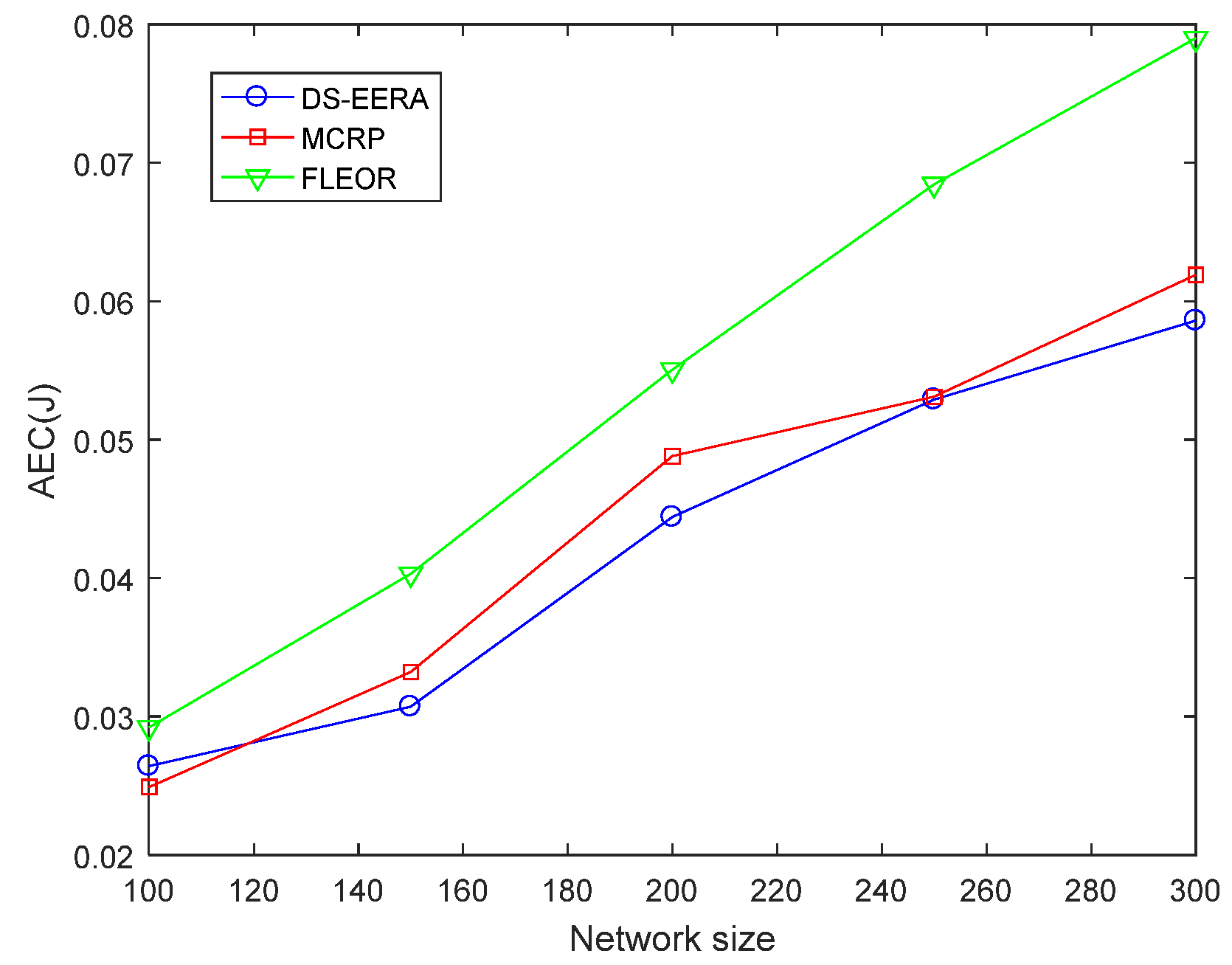
5.3. Average Number of Hops and Average Energy Consumption
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alhmiedat, T.; Taleb, A.A.; Bsoul, M. A Study on Threads Detection and Tracking Systems for Military Applications using WSNs. IJCA 2012, 40, 12–18. [Google Scholar]
- Mathur, P.; Nielsen, R.H.; Prasad, N.R.; Prasad, R. Cost Benefit Analysis of Utilizing Mobile Nodes in Wireless Sensor Networks. Wirel. Pers. Commun. 2015, 83, 2333–2346. [Google Scholar]
- Shen, J.; Wang, J.; Zhang, J.; Wang, S. Location-Aware Routing Protocol for Underwater Sensor Networks; Springer: Dordrecht, The Netherlands, 2013; pp. 609–617. [Google Scholar]
- Chen, S.; Lai, C.; Huang, Y.; Jeng, Y. Intelligent home-appliance recognition over IoT cloud network. In Proceedings of the 2013 9th International Wireless Communications and Mobile Computing Conference (IWCMC), Sardinia, Italy, 1–5 July 2013. [Google Scholar]
- Yan, J.; Zhou, M.; Ding, Z. Recent Advances in Energy-efficient Routing Protocols for Wireless Sensor Networks. IEEE Access 2016, 4, 5673–5686. [Google Scholar]
- Sergiou, C.; Vassiliou, V. Alternative path creation vs. data rate reduction for congestion mitigation in wireless sensor networks. In Proceedings of the 9th ACM/IEEE International Conference on Information Processing in Sensor Networks, Stockholm, Sweden, 12–16 April 2010. [Google Scholar]
- Demura, K.; Seto, A.; Sasaki, J. The forecasting an importation liberalization effect on the regional agriculture caused by the GATT Uruguay round: Simulation analysis using input-output in a macro model framework. Sensors 2017, 52, 15–27. [Google Scholar]
- Li, Y.; Shen, B.; Zhang, J.; Gan, X. Offloading in HCNs: Congestion-Aware Network Selection and User Incentive Design. IEEE Trans Wirel. Commun. 2017, 16, 6479–6492. [Google Scholar]
- Chiang, S.; Huang, C.; Chang, K. A Minimum Hop Routing Protocol for Home Security Systems Using Wireless Sensor Networks; IEEE Press: New York, NY, USA, 2007; Volume 53, pp. 1483–1489. ISBN 1558–4127. [Google Scholar]
- Ho, J.; Shih, H.; Liao, B.; Chu, S. A ladder diffusion algorithm using ant colony optimization for wireless sensor networks. Inf. Sci. 2012, 192, 204–212. [Google Scholar]
- Suh, Y.; Kim, K.; Shin, D.; Youn, H. Traffic-Aware Energy Efficient Routing (TEER) Using Multi-Criteria Decision Making for Wireless Sensor Network. In Proceedings of the 2015 5th International Conference on IT Convergence and Security (ICITCS), Kuala Lumpur, Malaysia, 24–27 August 2015. [Google Scholar]
- Zhang, D.; Li, G.; Zheng, K. An Energy-Balanced Routing Method Based on Forward-Aware Factor for Wireless Sensor Networks. IEEE Trans Ind. Inform. 2013, 10, 766–773. [Google Scholar]
- Ailian, J.; Lihong, Z. An Effective Hybrid Routing Algorithm in WSN: Ant Colony Optimization in combination with Hop Count Minimization. Sensors 2018, 18, 1020. [Google Scholar]
- Tang, L.; Lu, Z.; Cai, J.; Yan, J. An Equilibrium Strategy-Based Routing Optimization Algorithm for Wireless Sensor Networks. Sensors 2018, 18, 3477. [Google Scholar]
- Hajji, F.E.; Leghris, C.; Douzi, K. Adaptive Routing Protocol for Lifetime Maximization in Multi-Constraint Wireless Sensor Networks. J. Commun. Inf. Netw. 2018, 3, 67–83. [Google Scholar]
- Wang, X.; Li, D.; Zhang, X.; Cao, Y. MCDM-ECP: Multi Criteria Decision Making Method for Emergency Communication Protocol in Disaster Area Wireless Network. Appl. Sci. 2018, 8, 1165. [Google Scholar]
- Khan, B.M.; Bilal, R.; Young, R. Fuzzy-TOPSIS Based Cluster Head Selection in Mobile Wireless Sensor Networks. J. Electr. Syst. Inf. Technol. 2017, 5, 928–943. [Google Scholar]
- Jiang, H.; Sun, Y.; Sun, R.; Xu, H. Fuzzy-Logic-Based Energy Optimized Routing for Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. (IJDSN) 2013, 9, 264–273. [Google Scholar]
- Shah, B.; Iqbal, F.; Abbas, A.; Kim, K. Fuzzy Logic-Based Guaranteed Lifetime Protocol for Real-Time Wireless Sensor Networks. Sensors 2015, 15, 20373–20391. [Google Scholar]
- Sun, Z.; Zhang, Z.; Xiao, C.; Qu, G. D-S Evidence Theory Based Trust Ant Colony Routing in WSN. China Commun. 2018, 3, 27–41. [Google Scholar]
- Aitsaadi, N.; Aitsaadi, N.; Aitsaadi, N.; Oukhellou, L. Fusion-based surveillance WSN deployment using Dempster-Shafer theory. J. Netw. Comput. Appl. 2016, 64, 154–166. [Google Scholar]
- Yang, K.; Liu, S.; Li, X.; Wang, X. D-S Evidence Theory Based Trust Detection Scheme in Wireless Sensor Networks. Int. J. Technol. Hum. Interact. 2016, 12, 48–59. [Google Scholar]
- Sun, Z.; Wei, M.; Zhang, Z. Secure Routing Protocol based on Multi-objective Ant-colony-optimization for wireless sensor networks. Appl. Soft Comput. 2019, 77, 366–375. [Google Scholar]
- Chen, B.; Tao, X.; Yang, M.; Yu, C.; Pan, W. A Saliency Map Fusion Method Based on Weighted DS Evidence Theory. IEEE Access 2018, 6, 27346–27355. [Google Scholar]
- Fang, Y.; Jie, C.; Yuan, T. A Robust DS Combination Method Based on Evidence Correction and Conflict Redistribution. J. Sens. 2018, 2018, 1–12. [Google Scholar]
- Lv, Y.H.; Liu, Y.; Hua, J.F. A Study on the Application of WSN Positioning Technology to Unattended Areas. IEEE Access 2019, 7, 38085–38099. [Google Scholar]
- Ahmed, A.; Bakar, K.A.; Channa, M.I.; Haseeb, K.; Khan, A.W. TERP: A Trust and Energy Aware Routing Protocol for Wireless Sensor Network. IEEE Sens. J. 2015, 15, 1. [Google Scholar]
- Wang, Y.; Cheng, S.; Zhou, Y.; Peng, G.; Zhou, D.; Chao, C. Decision of air-to-air operation mode of airborne fire control radar based on DS evidence theory. Mod. Radar 2017, 39, 79–84. [Google Scholar]
- An, J.; Hu, M.; Fu, L.; Jan, J. A Novel Fuzzy Approach for Combining Uncertain Conflict Evidences in the Dempster-Shafer Theory. IEEE Access 2019, 7, 7481–7501. [Google Scholar]
- Ni, N.; Zhang, S.; Chen, X.; Zhang, X. Audit risk assessment based on entropy weight method and fuzzy analytic hierarchy process. Software 2018, 39, 254–259. [Google Scholar]
- Zhang, S.; Zhang, M.; Chi, G. Science and technology evaluation model and empirical research based on entropy weight method. J. Manag. 2010, 7, 34–42. [Google Scholar]
- Li, Y.; Gao, J.; Yu, Y.; Cao, T. An energy-based weight selection algorithm of monitor node in MANETs. In Proceedings of the 2017 International Conference on Computer, Information and Telecommunication Systems (CITS), Dalian, China, 21–23 July 2017. [Google Scholar]
- Shafer, G.A. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Kumar, N.; Vidyarthi, D.P. A Green Routing Algorithm for IoT-Enabled Software Defined Wireless Sensor Network. IEEE Sens. J. 2018, 18, 9449–9460. [Google Scholar]
- Yuan, Y.; Liu, W.; Wang, T.; Deng, Q.G.; Liu, A.F.; Song, H.B. Compressive Sensing-Based Clustering Joint Annular Routing Data Gathering Scheme for Wireless Sensor Networks. IEEE Access 2019, 7, 114639–114658. [Google Scholar]



| FN(i) | Indexes | Next Hop t = 1 | Non-Next Hop t = 2 | Fuzzy t = 3 |
|---|---|---|---|---|
| 0.0025 | 0.9900 | 0.0075 | ||
| a1 | 0.3775 | 0.2055 | 0.4170 | |
| 0.0099 | 0.9900 | 0.0001 | ||
| Fusion results | 0.00999625 | 0.9900 | 0.00000375 | |
| 0.9666 | 0.0110 | 0.0224 | ||
| a2 | 0.8125 | 0.0624 | 0.1251 | |
| 0.2307 | 0.3077 | 0.4616 | ||
| Fusion results | 0.9924 | 0.0055 | 0.0021 |
| Definition | Value |
|---|---|
| Simulation area (L × L) | 100 × 100 m2 |
| Network size (N) | 100~300 |
| Sink | (50, 50) |
| Maximum communication radius (R) | 30 m |
| Packets size | 1024 bits |
| Buffer size | 20 packets |
| Initial energy (E0) | 0.5 J |
| Data generation rate | 1024 bits/round |
| Energy consumed in electronics (Eelec) | 50 nJ/bit |
| Amplifier energy dissipation in free space (Efs) | 10 pJ/bit/m2 |
| Amplifier energy dissipation in multipath (Emp) | 0.0013 pJ/bit/m4 |
| Energy consumed in data aggregation (EDA) | 5 nJ/bit/signal |
| Distance threshold (dth) | 87 m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Lu, Z.; Fan, B. Energy Efficient and Reliable Routing Algorithm for Wireless Sensors Networks. Appl. Sci. 2020, 10, 1885. https://doi.org/10.3390/app10051885
Tang L, Lu Z, Fan B. Energy Efficient and Reliable Routing Algorithm for Wireless Sensors Networks. Applied Sciences. 2020; 10(5):1885. https://doi.org/10.3390/app10051885
Chicago/Turabian StyleTang, Liangrui, Zhilin Lu, and Bing Fan. 2020. "Energy Efficient and Reliable Routing Algorithm for Wireless Sensors Networks" Applied Sciences 10, no. 5: 1885. https://doi.org/10.3390/app10051885
APA StyleTang, L., Lu, Z., & Fan, B. (2020). Energy Efficient and Reliable Routing Algorithm for Wireless Sensors Networks. Applied Sciences, 10(5), 1885. https://doi.org/10.3390/app10051885





