Bearing Fault Diagnosis Using Grad-CAM and Acoustic Emission Signals
Abstract
1. Introduction
2. Proposed Method
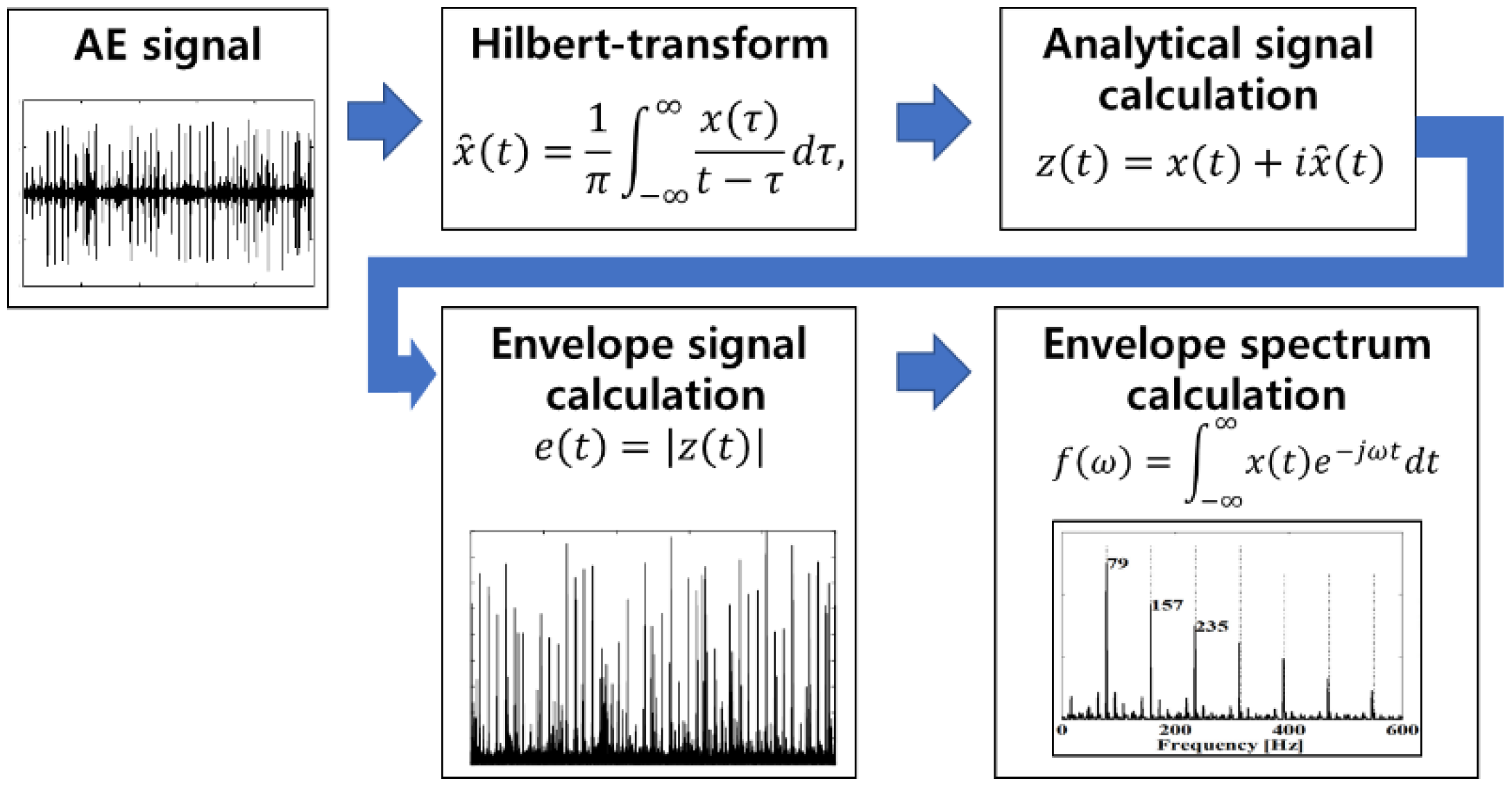
2.1. Envelope Analysis
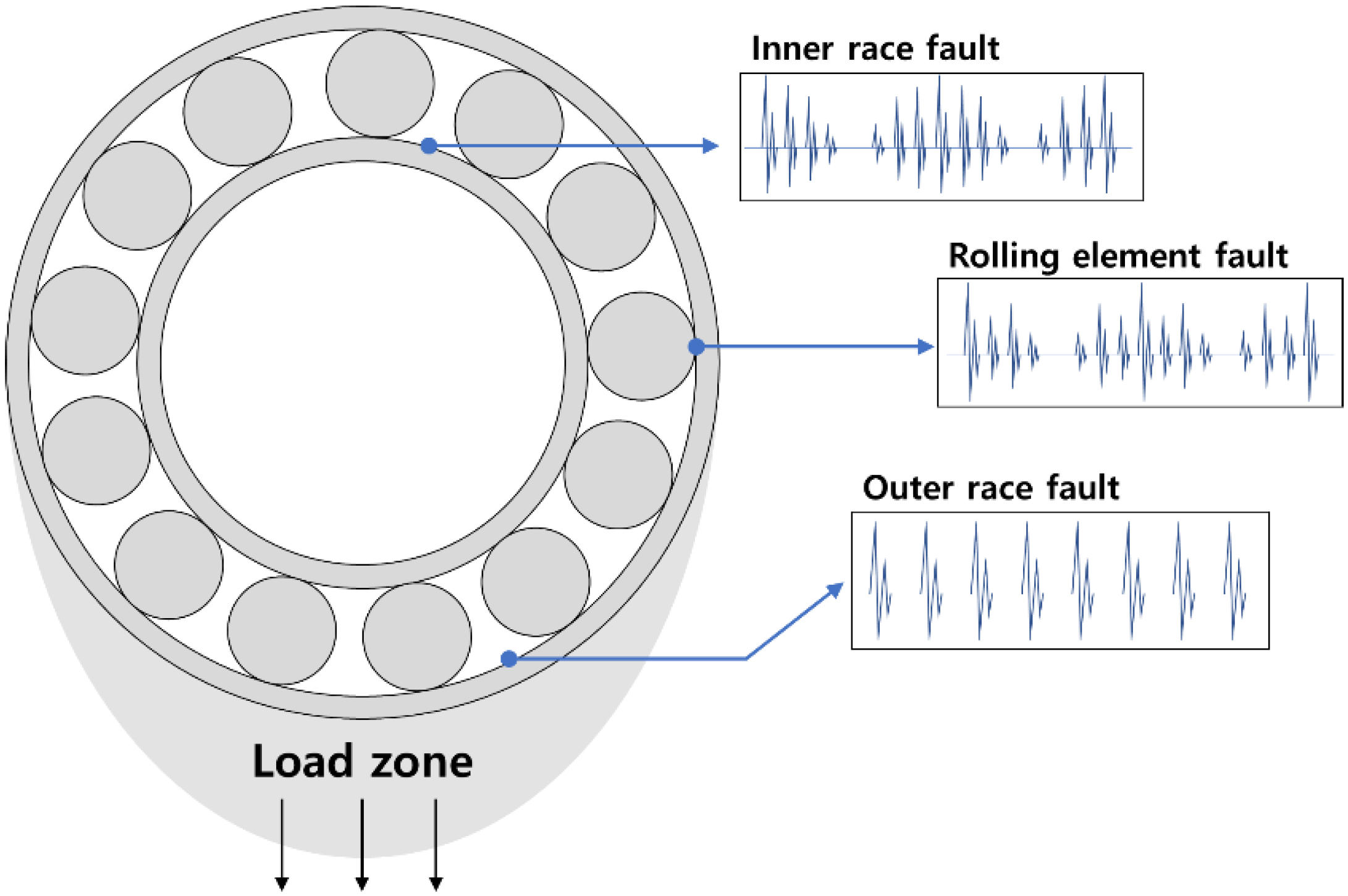
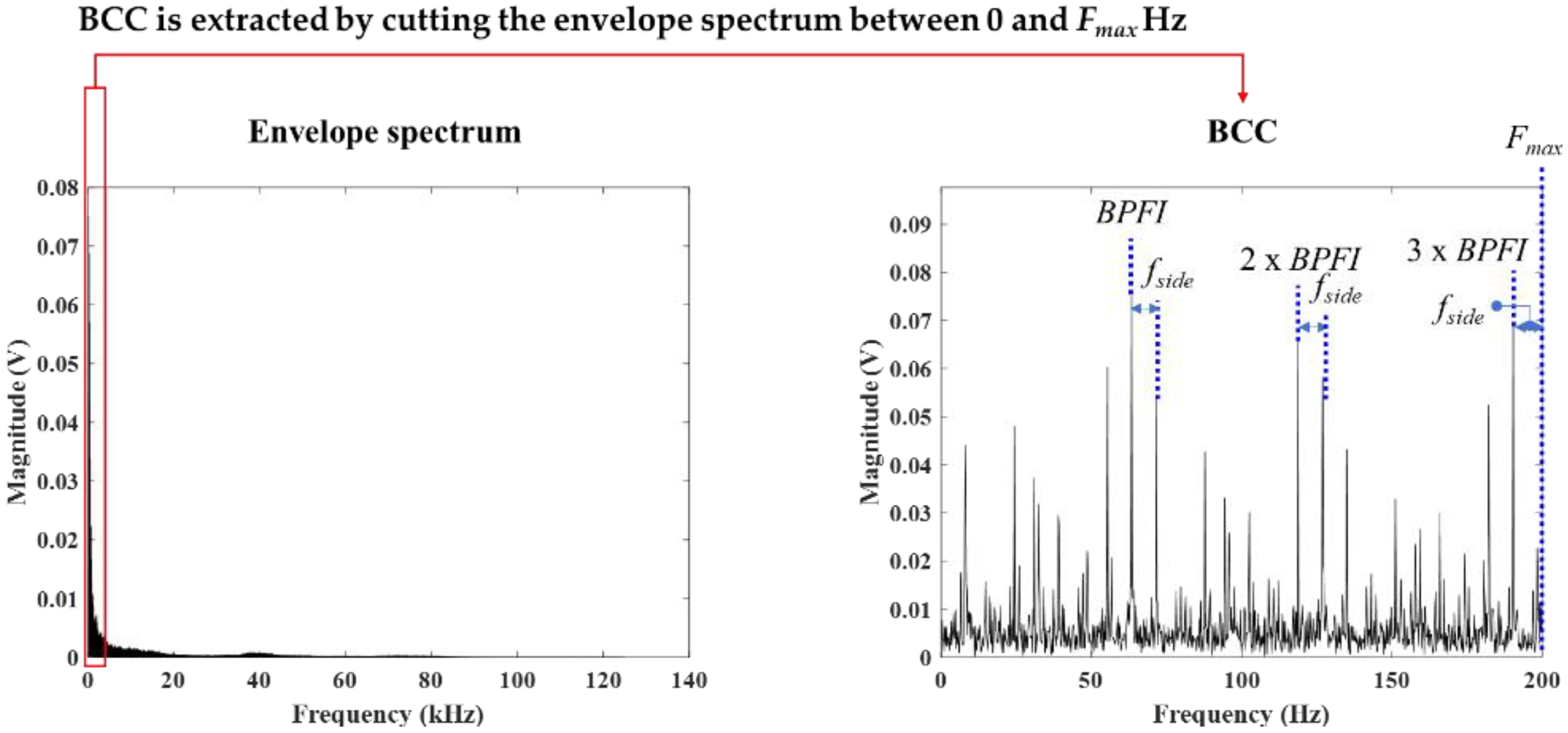
2.2. Bearing Characteristic Component Analysis
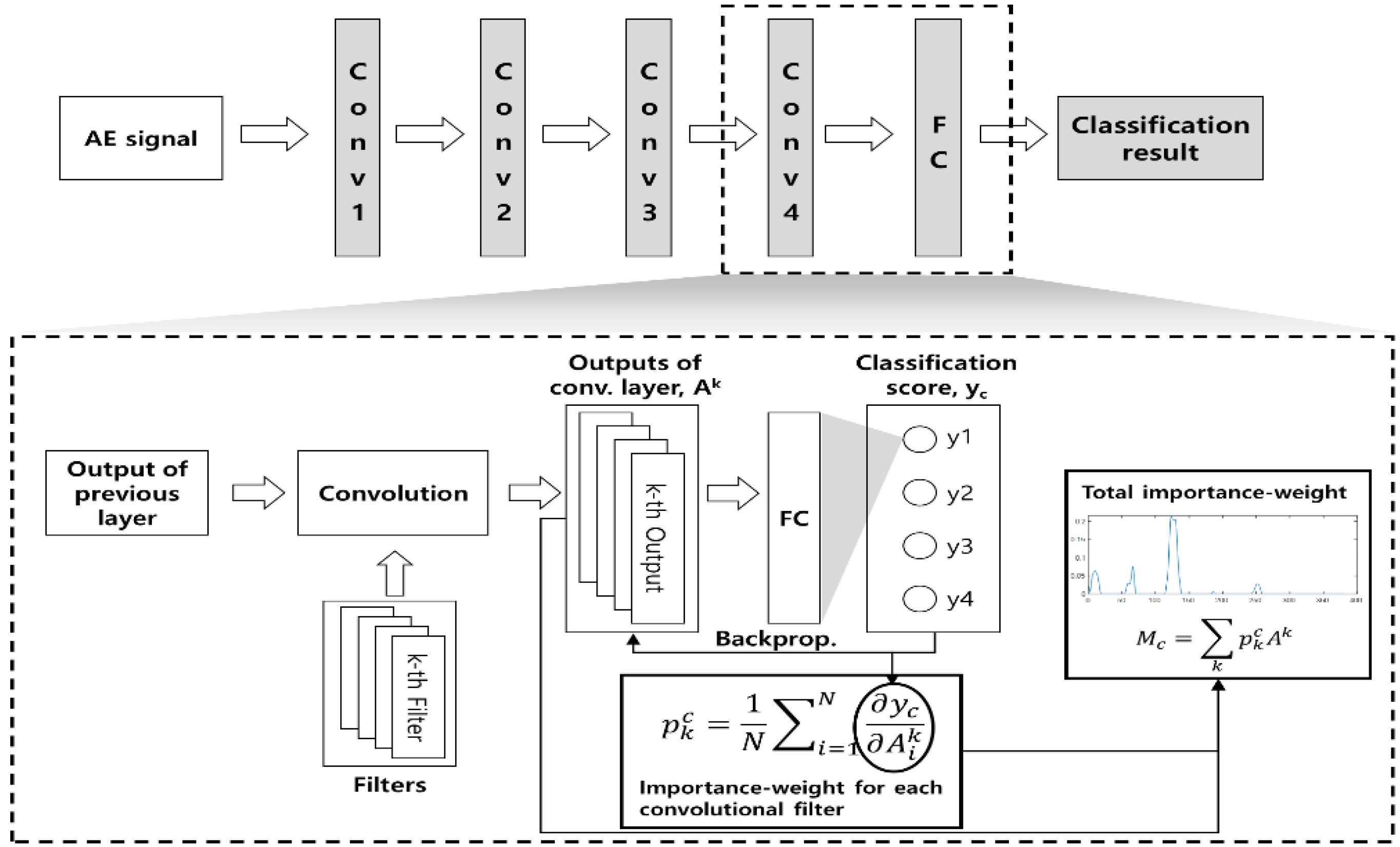
2.3. Training and Classification
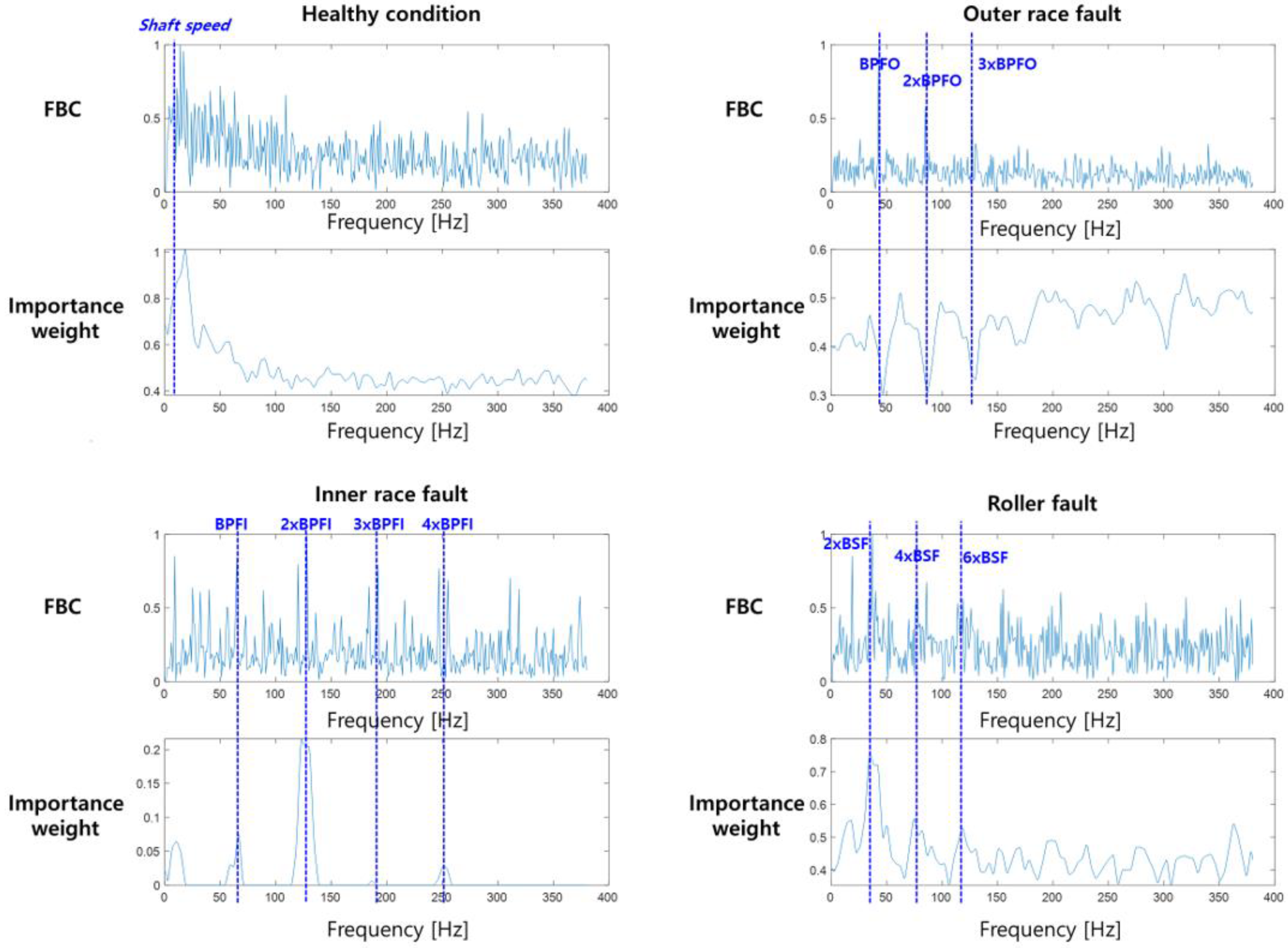
2.4. Importance-Weight Extraction
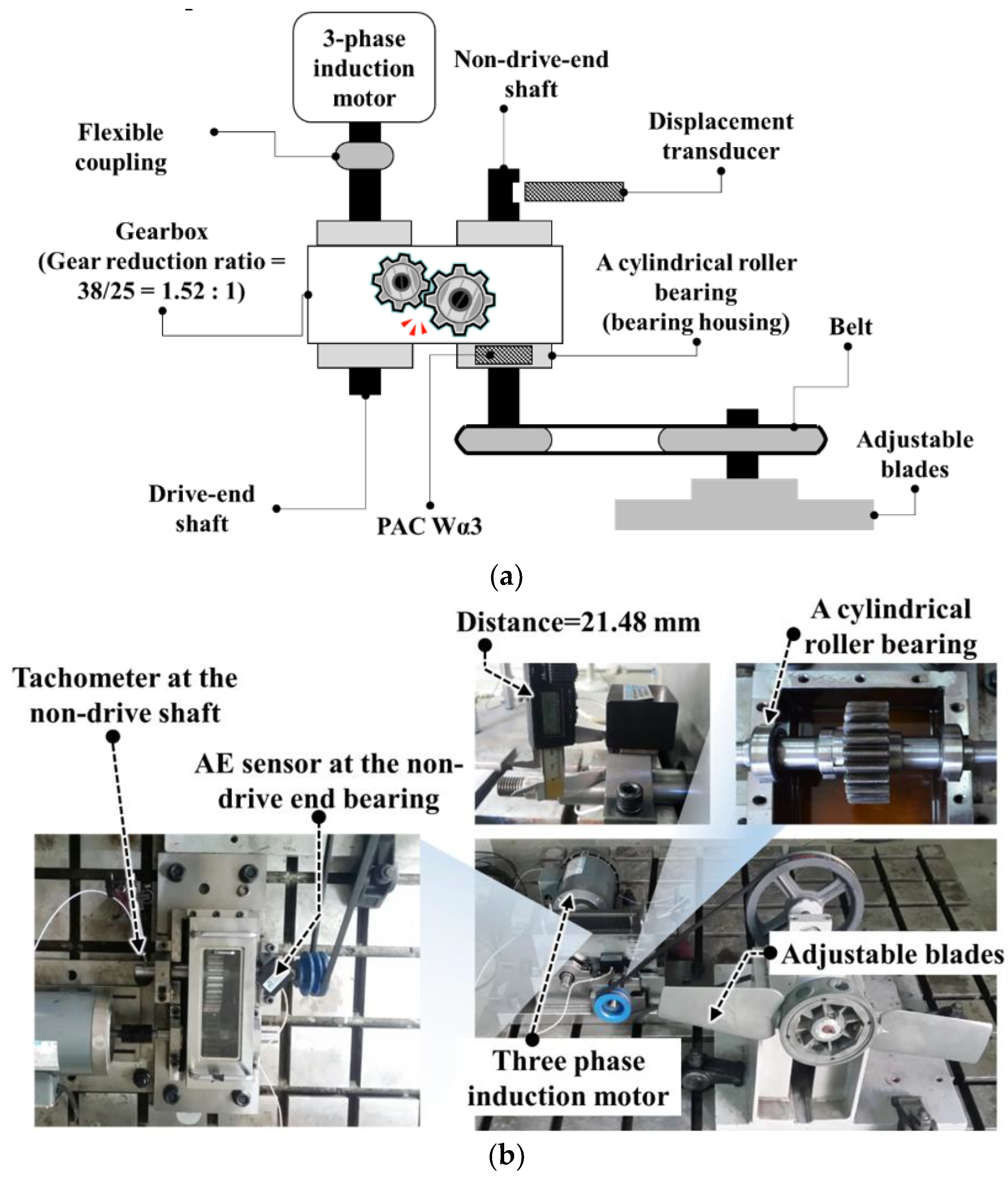
3. Experimental Setup and Data Acquisition
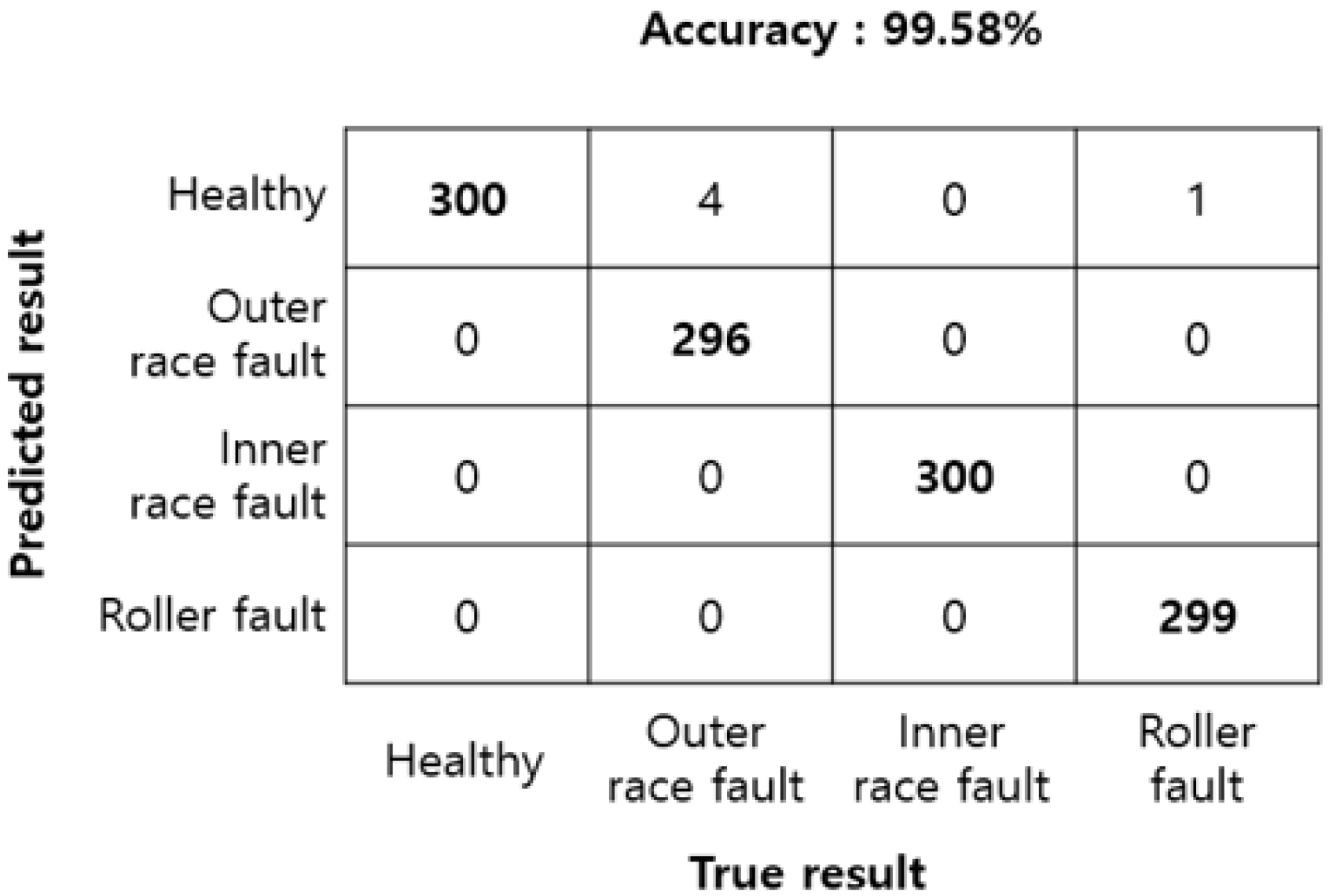
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| k-th output of a convolutional layer | |
| BCC | bearing characteristic components |
| the diameter of the rolling element of bearing | |
| BPFO | ball pass frequency on the outer race of bearing |
| BPFI | ball pass frequency on the inner race of bearing |
| BSF | ball spin frequency of bearing |
| a sample of envelope signal at the time, t | |
| the maximum frequency covering bearing characteristic frequencies and harmonics | |
| the magnitude of envelope spectrum at the frequency, | |
| The sideband of bearing characteristic frequency | |
| the importance-weight for the input data, | |
| the number of harmonics of bearing characteristic frequencies used in the proposed method | |
| the number of rolling elements | |
| normalized bearing characteristic components | |
| importance weight vector of k-th filter of a convolutional layer for class, c | |
| the pitch diameter of rolling element bearing | |
| shaft rotating speed | |
| a sample of signal at the time, t | |
| a sample of Hilbert-transformed signal at time, t | |
| the score of classification for class, c | |
| a sample of analytical signal at the time, t | |
| the contact angle of rolling element |
References
- Nandi, S.; Toliyat, H.A.; Li, X. Condition Monitoring and Fault Diagnosis of Electrical Motors—A Review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Elforjani, M.; Mba, D. Accelerated natural fault diagnosis in slow speed bearings with Acoustic Emission. Eng. Fract. Mech. 2010, 77, 112–127. [Google Scholar] [CrossRef]
- Tra, V.; Khan, S.A.; Kim, J.-M. Diagnosis of bearing defects under variable speed conditions using energy distribution maps of acoustic emission spectra and convolutional neural networks. J. Acoust. Soc. Am. 2018, 144, EL322–EL327. [Google Scholar] [CrossRef]
- Prosvirin, A.; Kim, J.; Kim, J.-M. Bearing Fault Diagnosis Based on Convolutional Neural Networks with Kurtogram Representation of Acoustic Emission Signals. In Advances in Computer Science and Ubiquitous Computing; Park, J.J., Loia, V., Yi, G., Sung, Y., Eds.; Springer: Singapore, 2018; pp. 21–26. [Google Scholar]
- Islam, M.R.; Uddin, J.; Kim, J.-M. Acoustic emission sensor network based fault diagnosis of induction motors using a gabor filter and multiclass support vector machines. Ad Hoc Sens. Wirel. Netw. 2016, 34, 273–287. [Google Scholar]
- Sun, H.; Wu, C.; Liang, X.; Zeng, Q. Identification of Multiple Faults in Gearbox Based on Multipoint Optional Minimum Entropy Deconvolution Adjusted and Permutation Entropy. Entropy 2018, 20, 850. [Google Scholar] [CrossRef]
- Li, Z.; Ma, J.; Wang, X.; Wu, J. MVMD-MOMEDA-TEO Model and Its Application in Feature Extraction for Rolling Bearings. Entropy 2019, 21, 331. [Google Scholar] [CrossRef]
- Cai, W.; Wang, Z. Application of an Improved Multipoint Optimal Minimum Entropy Deconvolution Adjusted for Gearbox Composite Fault Diagnosis. Sensors 2018, 18, 2861. [Google Scholar] [CrossRef] [PubMed]
- Wasmer, K.; Saeidi, F.; Meylan, B.; Le Quang, T.; Shevchik, S. When AE (Acoustic Emission) meets AI (Artificial Intelligence) II. In Proceedings of the EWGAE 2018, Senlis, France, 12–14 September 2018. [Google Scholar]
- Islam, M.M.M.; Kim, J.-M. Automated bearing fault diagnosis scheme using 2D representation of wavelet packet transform and deep convolutional neural network. Comput. Ind. 2019, 106, 142–153. [Google Scholar] [CrossRef]
- Hasan, M.J.; Islam, M.M.M.; Kim, J.-M. Acoustic spectral imaging and transfer learning for reliable bearing fault diagnosis under variable speed conditions. Measurement 2019, 138, 620–631. [Google Scholar] [CrossRef]
- Appana, D.K.; Prosvirin, A.; Kim, J.-M. Reliable fault diagnosis of bearings with varying rotational speeds using envelope spectrum and convolution neural networks. Soft Comput. 2018, 22, 6719–6729. [Google Scholar] [CrossRef]
- Tra, V.; Kim, J.; Kim, J.-M. Fault Diagnosis of Bearings with Variable Rotational Speeds Using Convolutional Neural Networks. In Advances in Computer Communication and Computational Sciences; Bhatia, S.K., Tiwari, S., Mishra, K.K., Trivedi, M.C., Eds.; Springer: Singapore, 2019; pp. 71–81. [Google Scholar]
- Duong, B.P.; Kim, J.-M. Fault Diagnosis of Multiple Combined Defects in Bearings Using a Stacked Denoising Autoencoder. In Advances in Computer Communication and Computational Sciences; Bhatia, S.K., Tiwari, S., Mishra, K.K., Trivedi, M.C., Eds.; Springer: Singapore, 2019; pp. 83–93. [Google Scholar]
- Tra, V.; Kim, J.; Khan, S.A.; Kim, J.-M. Bearing Fault Diagnosis under Variable Speed Using Convolutional Neural Networks and the Stochastic Diagonal Levenberg-Marquardt Algorithm. Sensors 2017, 17, 2834. [Google Scholar] [CrossRef] [PubMed]
- Appana, D.K.; Ahmad, W.; Kim, J.-M. Speed Invariant Bearing Fault Characterization Using Convolutional Neural Networks. In Multi-disciplinary Trends in Artificial Intelligence; Phon-Amnuaisuk, S., Ang, S.-P., Lee, S.-Y., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 189–198. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef]
- Wang, N.; Liu, X. Bearing Fault Diagnosis Method Based on Hilbert Envelope Demodulation Analysis. IOP Conf. Ser. Mater. Sci. Eng. 2018, 436, 012009. [Google Scholar]
- Kang, M.; Kim, J.; Wills, L.M.; Kim, J.-M. Time-Varying and Multiresolution Envelope Analysis and Discriminative Feature Analysis for Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 7749–7761. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Sainath, T.N.; Mohamed, A.; Kingsbury, B.; Ramabhadran, B. Deep convolutional neural networks for LVCSR. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8614–8618. [Google Scholar]
- Zhang, Z.; Sabuncu, M.R. Generalized cross entropy loss for training deep neural networks with noisy labels. In Proceedings of the the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December2018; pp. 8792–8802. [Google Scholar]




| Bearing Characteristic Frequency | Sideband (fside) |
|---|---|
| BPFO | No sideband |
| BPFI | Shaft speed |
| BSF | Fundamental train frequency 1 |
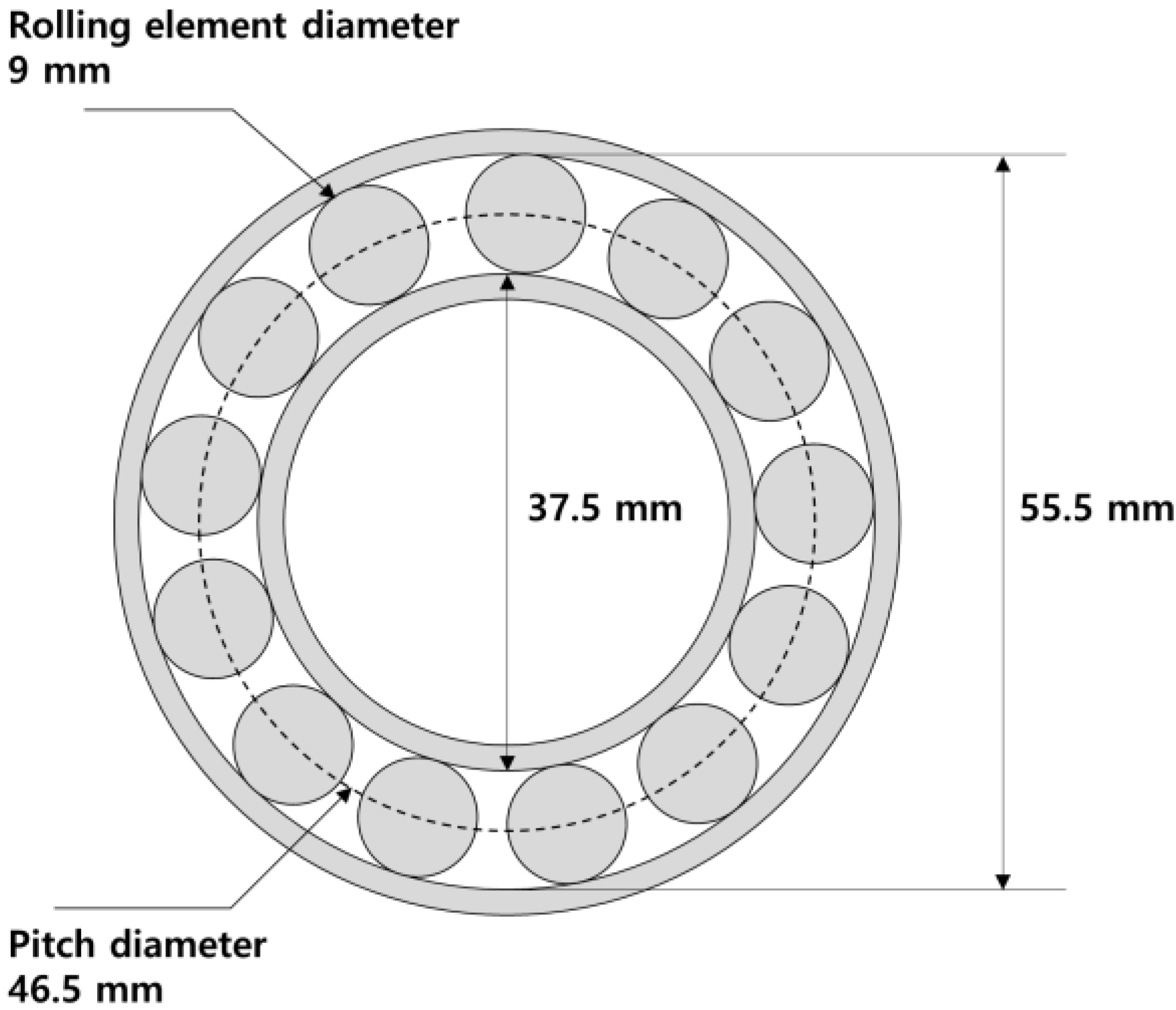
| Category | Symbol in Equations | Value (mm) |
|---|---|---|
| Pitch diameter | Pd | 46.5 |
| The diameter of rolling element | Bd | 9 |
| Contact angle of rolling element | θ | 0 |
| The number of rolling elements | Nb | 13 |
| Pitch diameter | Pd | 46.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Kim, J.-M. Bearing Fault Diagnosis Using Grad-CAM and Acoustic Emission Signals. Appl. Sci. 2020, 10, 2050. https://doi.org/10.3390/app10062050
Kim J, Kim J-M. Bearing Fault Diagnosis Using Grad-CAM and Acoustic Emission Signals. Applied Sciences. 2020; 10(6):2050. https://doi.org/10.3390/app10062050
Chicago/Turabian StyleKim, JaeYoung, and Jong-Myon Kim. 2020. "Bearing Fault Diagnosis Using Grad-CAM and Acoustic Emission Signals" Applied Sciences 10, no. 6: 2050. https://doi.org/10.3390/app10062050
APA StyleKim, J., & Kim, J.-M. (2020). Bearing Fault Diagnosis Using Grad-CAM and Acoustic Emission Signals. Applied Sciences, 10(6), 2050. https://doi.org/10.3390/app10062050






