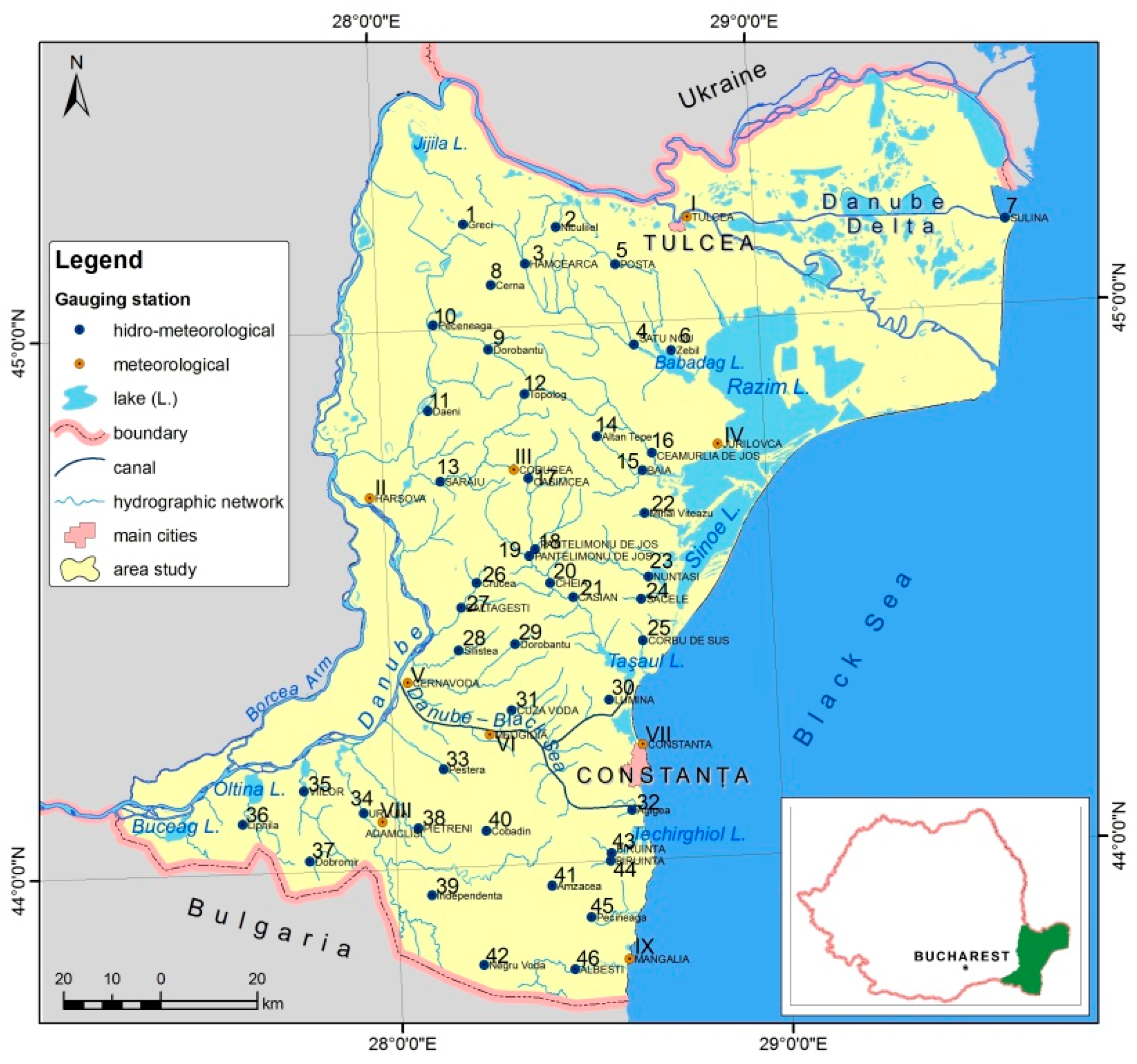
1. Introduction
Precipitation data analysis plays a major role in the process of making informed decisions for water resources management. Such data are gathered at monitoring stations scattered throughout a region. They are either not readily available for other locations or may be missing at certain time periods. These issues have negative influences on hydrological studies that rely on precipitation data as input. Therefore, spatial interpolation methods prove to be useful for estimating precipitation data at unsampled locations [
1].
Spatial interpolation methods are commonly used for the prediction of the values of environmental variables. Their specificity comes from incorporating information related to the geographic position of the sample data points. The most used methods are usually classified in the categories [
2,
3]: (1) deterministic methods (Nearest Neighbor, Inverse Distance Weighting (IDW), Splines, Classification and Regression methods), (2) geostatistical methods (Kriging (KG)) or (3) combined methods (regression combined with other interpolation methods and classification combined with other interpolation methods).
The importance of a successful spatial interpolation of precipitation before the hydrological modeling and a thorough review of different spatial interpolation methods for its modeling are presented in [
1]. Among them, IDW stands out as a real competitor. It builds estimates for environmental variables at a location, based on the values of those variables at some nearby sites and on the distances between that location and those where the variable is known.
The interpolation method often chosen by geoscientists is IDW, implemented in many Geographic Information Systems (GIS) packages [
4]. Its popularity is mainly due to its straightforward interpretability, easy computability and good prediction results. Still, the No Free Lunch theorem for optimization [
5] stands also in the case of spatial interpolation: no method stands out as being the best in all situations [
6]. In a study about the rainfall data in the Indian Himalayas, Kumari et al. [
7] performed a comparison of several interpolation methods, among which there were several variants of multivariate Kriging and IDW. It was shown that none of the methods performs best in all the studied cases. Principal Component Regression with the Residual correction (PCRR) method, IDW and the Multiple Linear Regression (MLR) methods were used to compare interpolated annual, daily and hourly precipitation and the spatial distribution of precipitation in the Xinxie catchment [
8], while the spatial distribution of precipitation deficit over Seyhan River basin using IDW is reported in [
9].
The basic IDW method is successfully employed in [
10] to estimate the rainfall distribution in a region of Iraq. The scenario uses incremental values for the power parameter, in the range from 1 to 5. A modified IDW method is investigated in [
11], where the elevation is also considered for estimating the values at unknown locations. A new method for estimating the regional precipitation (MPPM) has been introduced in [
12] and its performance has been tested against that of IDW and kriging. It was reported that MPPM avoids the problems that could appear in the application of kriging methods, as (i) the invertibility of the distance matrix, (ii) the high computational cost related to building the inverse of the distance matrix in the case of a high number of stations, (iii) the choice of the model for the estimation of theoretical variogram and (iv) the selection of the optimal parameters of the variogram model. It was shown that deterministic methods could be good competitors for spatial interpolation techniques, such as KG, performing better than the last ones in the study cases presented in [
12]. In an engineering setting, Gholipour et al. [
13] investigate a hybridization of IDW with a harmony search. The obtained metamodel significantly reduces the computational effort and improves the convergence rate. A genetic algorithm is used in [
6] to find the optimal order of distances in IDW.
An adaptive version of the IDW method is introduced in [
4], where the authors suggest that the spatial pattern of the sampled stations in the neighborhood could influence the weighting parameter. The algorithm selects the weights in IDW based on the stations’ density around the unsampled location. It gave better estimations than KG on the study cases. However, the choices of the membership functions and the number of relevant neighbors are heuristics, and there is no guarantee that they will perform well in other scenarios.
Some machine learning models were also investigated in [
3], with application to spatial interpolation of environmental variables. They are compared with several traditional spatial interpolation methods, among which is inverse distance squared. The study found that the combination of random forest and IDW, respectively random forest with OK were the best methods, with similar accuracies. At the same time, OK was found to perform similarly to IDW in the tested scenarios. A hybrid method that combines IDW with support vector machines is reported in [
14], applied to multiyear annual precipitation. In [
15], temporal predictions obtained with an ensemble approach are used as inputs to spatial interpolation by IDW, with improved overall results.
The main difficulty faced when applying IDW is setting the value of the power parameter. This is usually done before the algorithm is applied. The usual approach for searching for the optimal value of the power parameter is by exhaustive search, by sampling all possible values in a given interval, at a user chosen step size [
2]. The results of this method depend on the search window. The method is only guaranteed to find a local optimum [
2].
In this paper, we target the optimization of the process of setting the power parameter in IDW, using a nature-inspired metaheuristic—Particle Swarm Optimization. We automate the process of identifying the suitable parameter, while maintaining, if not optimizing, the prediction accuracy of the standard IDW method. Experiments are performed on maximum annual precipitation data gathered in the Dobrogea region (Romania). An evaluation of the proposed hybrid method is performed, against standard IDW and Kriging.
The paper structure is the following.
Section 2 begins with a brief presentation of the meteorological stations locations in the study area.
Section 2.2 and
Section 2.3 present the spatial interpolation methods IDW and KG. The Particle Swarm Optimization (PSO) metaheuristic is presented in
Section 2.4. The section ends with the presentation of the hybrid algorithm Optimizing IDW (OIDW), obtained by optimizing the β parameter of IDW with PSO. The experimental settings are described in
Section 3, while the results are discussed in
Section 4. The paper ends with the conclusion section.
3. Experimental Settings
The experiments were run using an improved deterministic PSO variant from [
30], which is among the most popular versions of the PSO algorithm [
31]. We are interested in assessing the quality of predictions for OIDW and compare them with the traditional grid search IDW (denoted, in the following. by IDW*).
The experiments were run in 2 scenarios:
(Scenario A)
First, we used PSO and grid search to identify a single β that minimizes the sum of prediction error over all stations. The β value identified is characteristic of the entire Dobrogea region, hence it can be useful to infer values at points where no recordings are available, for example. When the predicted values for a given station are computed, the weights in Formula (1) corresponding to that station are set to 0.
(Scenario B)
We used PSO and grid search to search a β for each station that minimizes the prediction error when the series from that station is estimated using the other series from the other stations.
For example, if we have ten stations, to estimate the precipitation at the station I, the series recorded at the stations II-X are used as input, while the series recorded at the station I are hold out as control values. Thus, they are used for comparison with the values computed by applying Formula (2) with the parameter β1 identified by OIDW. The β1 obtained minimizes the MSE for the station I. Another example: to estimate the values of the series from the station V, the series recorded at station I-IV and VI-X are used as an input, and a β5 is computed, corresponding to the minimum MSE for the station V, and so on.
Further, we refined the experimental settings by performing experiments in two stages. First, we employed a reduced dataset comprising the series from ten main meteorological stations. We will refer to these scenarios as (A1) and (B1). The same experiments were repeated with the extended dataset that contains all 51 series. We will refer to these scenarios as (A2) and (B2). Hence we obtained four scenarios. We took a special interest in type (A) experiments because they should yield a unique empirically determined β to be characteristic for the entire region.
For each scenario, 50 different runs of the PSO algorithm were performed. The default Mersenne twister randomizer with an initial seed of 0 was used in the experiments reported in the tables below.
Setting the PSO parameters to optimal values is a very difficult optimization problem by itself [
30,
32]. In our experiments, the PSO parameters are chosen to match those widely used in the literature [
30]:
The swarm size is 24,
Personal best influence is 2,
Global best influence is 2,
The inertia weight, decreasing during the iterations of the algorithm from 0.9 to 0.4,
The number of epochs (i.e., PSO iterations) is 100,
β is searched in the interval (1, 5).
The results are compared with those obtained by applying IDW and KG. For IDW, we identified the parameter β performing a grid search with the step-size of 10−4, in the interval [1.001, 5]. The grid search identifies the parameter β that yields the minimum prediction error (that will be listed in the results tables).
The experiments for OIDW and IDW* were performed in the Matlab environment, in Matlab R2012, on a computer with Intel Core i5 quad-core processor at 2.30 GHz with 8 GB RAM, using the PSO toolbox, available online [
33]. Matlab was also used for performing the IDW* computation (IDW with the grid search).
For KG, we used Ordinary Kriging and report the mean prediction error obtained. The Kriging algorithm was run using the
gstat,
sp,
spacetime,
automap and
geoR libraries from the R software. Different types of variograms (spherical, exponential, Gaussian, linear and power) were fit to the data, using
autofitVariogram (from
automap package) [
34] and the best one (in terms of the lowest MSE) was selected. While for using the
fit.
variogram function (from
gstat package) [
35] the user has to supply an initial guess (estimate) for the sill, range, etc. to fit a certain type of variogram, the use of the
autofitVariogram function (from
automap package) does not necessitate any initial guess.
autofitVariogram has the advantage to provide this estimate by computing it based on the data, and then calls the
fit.variogram function [
35]. So,
autofitVariogram automatically provides fit parameters (sill, nugget and range) of the best variogram. For a deeper insight on the variogram fitting, one can see the vignettes of the mentioned packages on the website of R software [
34,
35]. In our case, the fit variogram was of an exponential type, with the parameters sill = 144.9766 and range = 48,843.73.
To check if the MSE obtained in OIDW (A and B scenarios) and IDW* are not statistically different, the following statistical tests have been performed:
● The Anderson–Darling test [
36], for testing the null hypothesis of data series normality:
The series is Gaussian (has a normal distribution),
Against the alternative that:
The series is not Gaussian (has not a normal distribution).
● The Levene’s test [
36] for verifying the null hypothesis that:
The MSE series (from the scenarios A, B and IDW*) have the same variance,
Against the alternative that:
The MSE series do not have the same variance;
● The non-parametric Kruskal–Wallis test [
37], for checking the null hypothesis that:
The mean ranks of the groups of MSE series (from the scenarios A, B and IDW*) are the same.
Against the alternative:
The mean ranks of the groups are not the same.
● The non-parametric eqdist.etest test [
38], for verifying the null hypothesis that:
The MSE series (from the scenarios A, B and IDW*) have the same distribution,
Against the alternative:
The MSE series did not have the same distribution.
These nonparametric tests were selected because the normality hypothesis was rejected for some MSE series in A, B scenarios and IDW*. These tests were performed at the significance level of 5%, using the R software, version R 3.5.1.
4. Results and Discussion
- ➢
β values rounded up to 4 decimals (which are mean values for the β’s obtained over the 50 runs of the PSO algorithm);
- ➢
Standard deviations of the computed β values, denoted by st.dev.;
- ➢
Mean squared errors (MSE) of the series values obtained in the experiments. The MSE is the average squared difference between the estimated values and the actual values; it is a measure of a model’s quality (Formula (15)). The smaller the MSE, the better the model is.
- ➢
The time (in seconds) for running an experiment in the case of IDW*;
- ➢
The average run time (in seconds) over all the 50 experiments and the standard deviation of the time in the OIDW experiments.
PSO is a stochastic algorithm; hence, mean and standard deviations are reported for both the optimized parameter, and the time consumed by the algorithm. The standard deviation is a proof of the algorithm stability (i.e., when the standard deviation is very small it means that the algorithm converges in every run; hence, it is stable and reliable).
The results obtained using only the series recorded at the ten main stations in the experiments done in the scenario A1 are displayed in
Table 1, as follows: IDW* (columns 2–4), OIDW (columns 5–7) and KG (column 8). The values of the
β parameter are equal up to the fourth decimal in IDW* and OIDW. The average run time for IDW* is 82.19 times greater than that for running OIDW (column 4-60 s and column 7-0.73 s).
Table 2 displays the results of the experiments performed using the series recorded at the main meteorological station, in the scenario B1.
We remarked that the PSO convergence was very good. The standard deviations of time and β in the OIDW algorithm are of the order of 10−4, respectively 10−6, hence they are not reported individually in the table. The values identified by OIDW coincide with those identified by IDW*, by the 4th decimal. A significant difference appears in the computational time. In the scenario B1, the average computational time for an OIDW run is more than 60 times smaller than the time for a IDW* run.
In both scenarios (A1 and B1), OIDW found the optimum, as it was exhaustively identified by IDW. Moreover, the differences between the mean squared errors of the approximations computed with IDW using the
β values identified with grid search (IDW*) and OIDW were not statistically significant. Additionally, the MSEs associated to the IDW algorithms are almost identical; in some cases, these are better than those obtained by KG. The standard deviations of
β are very small in both scenarios. This signifies that the PSO search for
β is stable—PSO converged in all the 50 runs to very similar values. The average MSE are 30.9327 for IDW* and OIDW in scenario A1; 30.3704 for IDW* and 30.3718 for OIDW in scenario B1 and 31.022 for KG, respectively (
Table 1 and
Table 2). It was expected that OIDW in the scenario A1 (
Table 1) would yield larger prediction errors than the individual OIDW’s in the scenario B1 (
Table 2), since in B1 the algorithm tries to fit a much smaller number of data points.
Nevertheless, the differences with respect to KG are significant only in one case (e.g., Adamclisi). OIDW is run for each station in scenario B1, hence the computational times in
Table 2 add up, for a fair comparison; OIDW is run only once for the entire set in A1, with the time as reported in
Table 1. Therefore the time to run the experiments in scenario B1 is smaller than in A1 (1.31 times in for IDW* and 1.66 times for OIDW).
Table 3,
Table 4,
Table 5 and
Table 6 contain the results obtained in experiments performed using the 51 meteorological stations, in scenario A2 and B2, respectively. Results in
Table 3 prove that PSO converges to the optimal
β, as it was identified by grid search (standard deviation of 1.1813 × 10
−4).
For the main stations, the standard deviations are equal up to the third decimal for almost all the series. The computational effort, reported as run time, was significantly smaller (40 times) in the case of the OIDW algorithm (190 s for IDW* and 4.846 s for OIDW). The average MSE computed in A2 experiments were the following: 30.64324 (IDW*), 30.64315 (OIDW) and 30.876 (KG)—computed using the MSE for the main series; 31.0671 (IDW*), 31.0671(OIDW) and 29.5480 (KG)—computed using the MSE for the 41 secondary series and 30.9840 (IDW*), 30.9840 (OIDW) and 29.7924 (KG)—computed using all series. We found that the average MSE was smaller in all situations in scenario A2 for the main series, by comparison to scenario A1. The smallest average MSE in scenarios A1 and A2 corresponded to KG, when extracting only the secondary series (followed by the case when using all the series) for the MSE computation.
The results from
Table 5 reveal little to no difference between the
β’s identified by grid search and those identified by PSO search. Therefore, the MSE’s associated to the computed IDW approximations were identical. The significant difference comes from the computational time: PSO identified the optimal value 50 times faster than the grid search.
The MSE’s in scenario B2 are smaller in the experiments with 51 stations than those in the experiments with only ten main stations.
In scenario B1, when taking into account only the results for the main stations, they were as follows: 30.3704 vs. 29.22245 for IDW*, 30.37178 vs. 29.22245 for OIDW and 31.022 vs. 30.876 (
Table 7, rows 3 and 6). This was to be expected because the algorithms received far more information in the scenario B2 than in B1. On the other hand, from the same reason,
β st.dev in OIDW increased, while remaining very small.
All the results from
Table 7 that summarizes the average MSE in all experiments show similar performances of IDW*, OIDW and KG. None of the algorithms were the best in all situations, confirming the literature findings [
39].
Therefore, one can remark that OIDW yields competitive results in terms of MSE’s of estimated values when compared to KG. This is important because it proves OIDW to be a reliable method.
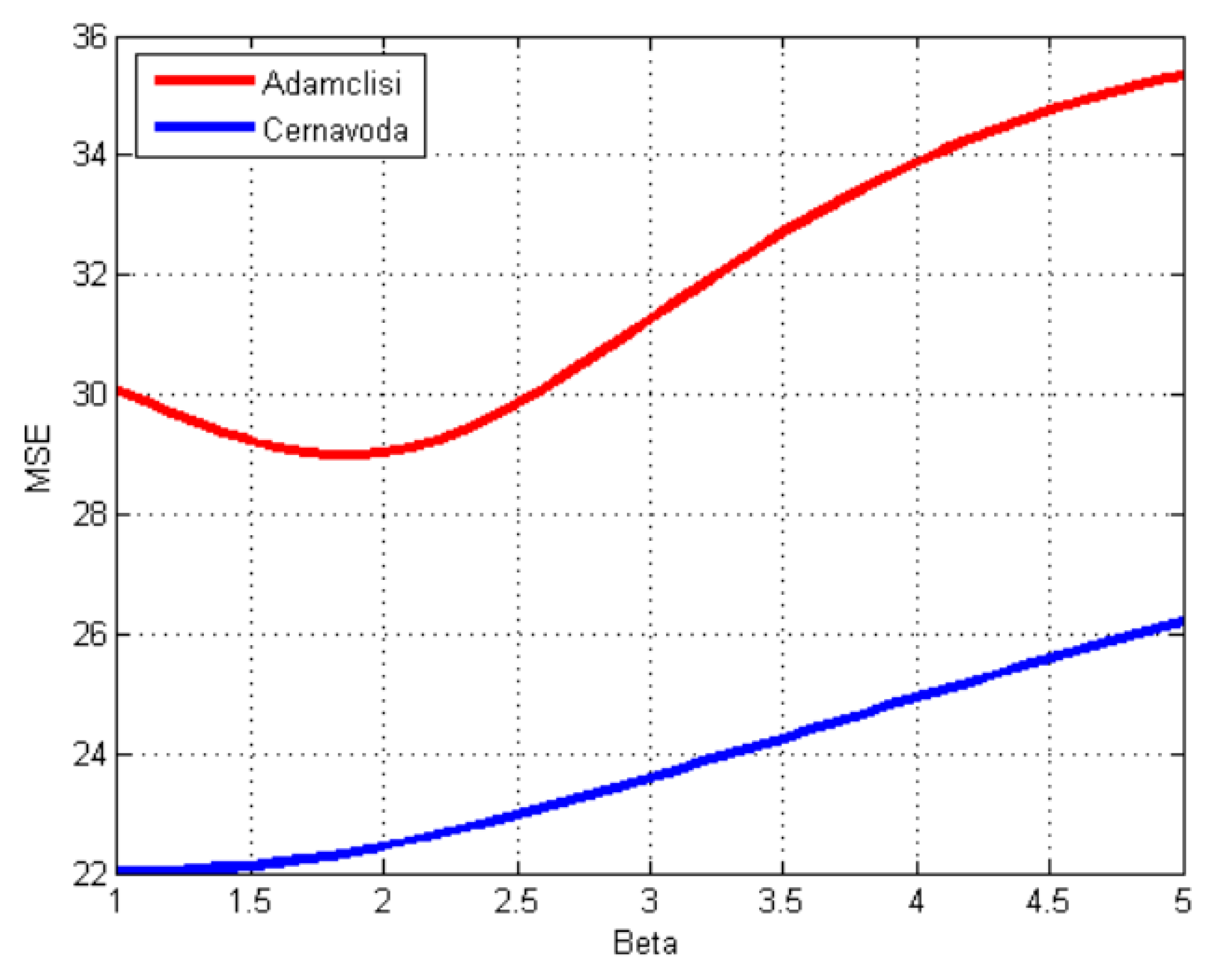
Finding the minimum MSE in the grid search is not straightforward because the MSE evolution patterns are different, as it is illustrated in
Figure 5, for two series, where the MSE is computed using all the series, with a grid search step of 10
−4. For Cernavoda, the trend is almost linear, while for Adamclisi, it decreases them it increases and presents an inflexion point.
Figure 6 depicts the dependence of the average MSE for all series as a function of
β. The chart has a similar behavior as for the Adamclisi series.
With respect to computational effort: for detecting the β that minimizes the MSE for fitting the values of a series in IDW* using a grid search with a step r, on an interval [a. b], the computation should be performed times (where [] is the integer part of the number inside the bracket). For example, for a grid search with a step of 0.1, IDW* was performed 50 times for each station, so 500 times when only the main stations were employed and 2550 times when all the 51 series were used.
Once again, taking into account the consumed time in scenarios A1 or A2, B1 or B2 is more convenient to run OIDW. This idea is supported by the fact that the β’s identified with OIDW in all the runs were identical to optimal values of β found by grid search IDW* up to the third digits (so, OIDW converged to a global optimum, in all cases).
OIDW performed better than KG in 60% of cases in scenario A1, in 80% of cases in scenario B1, and in 49.01% cases in scenarios A2 and B2. While in the scenarios A1 and B1, the OIDW MSE and KG MSE are comparable, in the A2 and B2 scenarios, there are some discrepancies between them, as for example, for Sulina, Cheia, Negureni, Pantelimon and Mihai Viteazu (in A2 and B2). This situation could be explained by the following reasons: (a) the low number of series used in A1 and B1 scenario, (b) the inhomogeneity of the stations on the in the Dobrogea region, (c) the climate differences on the different part of the region and (d) the possible anisotropy was not considered.
The results of the statistical tests on the SE series for OIDW and IDW* are presented in the following. The normality test for the MSE series corresponding to the experiments in scenarios A1, B1, OIDW, KG and IDW* from
Table 1 and
Table 2, A2, B2, IDW*, KG from
Table 3 and
Table 5, KG from
Table 3 +
Table 4 and KG from
Table 5 +
Table 6 could not reject the normality hypothesis. The same test led to the normality rejection for the IDW* MSE and OIDW MSE series corresponding to the secondary stations from
Table 4 and
Table 6, but not for OIDW MSE corresponding to all the series in
Table 3 +
Table 4 and
Table 5 +
Table 6.
A spatial map containing illustration the distribution of MSE in OIDW form B2 scenario (values from
Table 5 +
Table 6) is presented in
Figure 7. The highest MSEs correspond to the station near the region border, where the stations had few close neighbors.
To offer a different perspective of the OIDW performance, we computed the Mean Absolute Percentage Error (MAPE) and the Kling–Gupta efficiency (KGE).
The MAPE is given by the formula:
where
n is number of stations used in the IDW,
is the value predicted by IDW for the precipitation at station
i and
is the measured value for the precipitation at station
i.
The KGE coefficient is introduced in [
40]; it is defined by formula:
where:
where
is mean of the values resulted from the model,
is the mean of the recorded values,
is the standard deviation of the values resulted from the model and
standard deviation of the recorded values.
MAPE is a scale-independent indicator that could be used in order to compare the performance of a given method on separate data sets. The lower MAPE is, the better the model is. The KGE coefficient is dimensionless as well and has an ideal value of unity. Although, in this study, the models were calibrated using the MSE as the model calibration criterion, the KGE and MAPE provide further validation of the obtained models.
Table 8 provides the MAPE values together with the Root Mean Square Errors (RMSE =
and the KGE for the ten main stations.
Similar results for MAPE and KGE were obtained in the A2 and B2 scenarios, so we are not presenting them here.
The highest MAPE value (so the worst data fit) was noticed for the Sulina station in both scenarios. It was expected, since Sulina is situated 12 km offshore, in the Danube Delta, and the climate presents different particularities compared with the rest of Dobrogea region. The same was true for the KGE coefficient: its lowest values were obtained for the Sulina and Mangalia stations (the most isolated stations).
Since the values of both goodness-of-fit indicators, dimensional-RMSE and dimensionless-MAPE are small, and most of the KGE values are bigger that 0.5, it resulted in the OIDW performing well.
The Kruskal—Wallis test could not reject the null hypothesis, the corresponding
p-values being 0.9356 (
Table 1 and
Table 2), 0.8348 (
Table 3 +
Table 5), 0.6437 (
Table 4 +
Table 6) and 0.7519 (
Table 3,
Table 4,
Table 5 and
Table 6 all the stations), respectively. The eqdist.etest test applied to the same groups of series as in the previous test could not reject the hypothesis that each group of series has the same distribution, the corresponding
p-values being greater than the significance level of 5%.
Concluding, the MSE’s of the estimations obtained by OIDW, IDW* and KG were not significantly different.
When KG is not very straightforward to be applied and searching for the best parameter β for IDW with grid search is computationally intensive, OIDW proves to be a convenient and rapid to use solution.
Other optimization methods can be applied for the power parameter of IDW calibration, such as methods based on the Golden Section (GS) method, provided that the hypotheses of this method are satisfied. As an example, we tried to calibrate the parameter
β by this additional optimization method, namely by the fminbnd Matlab function [
41]. This function applies GS, followed by parabolic interpolation; the boundaries for the search are to be specified as parameters. In the experiments performed on the series from the ten main stations with the fminbnd method, we obtained an approximation of 1.1903
f or
with a duration of 1 s, with MSE = 30.75. The results are comparable in this situation with those obtained by both OIDW and IDW. The assumptions for this method include that the function to be minimized should be continuous, which is hardly the case in real world problems. Additionally, since in some situations the fminbnd fails to find the optimum (as in the case of independent stations, where there are local minima or when minimum lies on the boundary of the search domain [
41]), we consider that an extensive study should be done to compare our approach with that of fminbnd. The results will be communicated in another article.
5. Conclusions
The paper describes a hybrid PSO-IDW algorithm for the modeling of data; it is applied on maximum precipitation data in the experimental part. The algorithm is based on a well-known spatial interpolation method (IDW). Since the application of IDW makes use of the power parameter β, we proposed the use of the PSO algorithm to identify a suitable value for this parameter. Empirical results proved that the IDW performance was maintained, while the new method offered lower computational costs. Results of the IDW and OIDW were further compared to Kriging.
The optimization of IDW with PSO described in this paper offered an alternative to an exhaustive search for the problem of tuning the power parameter in the IDW method. In cases when the estimations provided by the traditional application of IDW are good, the results obtained with OIDW should preserve the quality of the prediction and be better in terms of computational effort.
Kriging is a powerful geostatistical method, suitable to be applied in certain cases, and its application assumes profound knowledge of spatial statistics. When the spatial correlation is strong and the variogram can depict well the spatial variability, the KG algorithm predicts very well. Even so, for our precipitation data, the results are not substantially better by KG, as it was the case for other environmental variables studied in [
17]. In cases where the nature of the input data does not support KG, instead of using IDW for prediction it is wiser to choose OIDW since it automates the process of identifying the appropriate power parameter, with smaller computational effort. Our approach also benefits from the advantages of the PSO algorithm: a simple implementation, robustness, small number of parameters to adjust and a high probability and efficiency in finding the global optima, fast convergence, short computational time and modeling accuracy. OIDW is easy to use by people that do not have statistical knowledge [
29,
42].
The limitations of IDW are preserved by OIDW: in locations with sparse neighbors (such as those near the borders of the study region), the errors for IDW simulated data are larger. While providing a solution for optimizing the IDW parameter, OIDW uses PSO, which has several parameters of its own that need to be set (e.g., swarm size, the weights in the Equations (7) and (8)). In our experiments, setting these parameters to values commonly used in the literature led to very good results.
The contribution of our paper was two-fold. For hydrologists, we introduced an optimization of a well-known and widely used spatial interpolation method—namely IDW. For the artificial intelligence community, we proved the utility of the application of the PSO metaheuristic on a parameter optimization problem.
The results obtained in our case study using time series data from 51 meteorological locations in the Dobrogea region (Romania) encouraged us to consider OIDW as a good choice for the spatial interpolation of precipitation data. Still, more experiments will be performed, using various types of environmental data and various measures of performance of the models, in order to decide the appropriateness of OIDW as a general spatial interpolator.