On the Use of Linear and Nonlinear Controls for Mechanical Systems Subjected to Friction-Induced Vibration
Abstract
:1. Introduction
2. Preamble
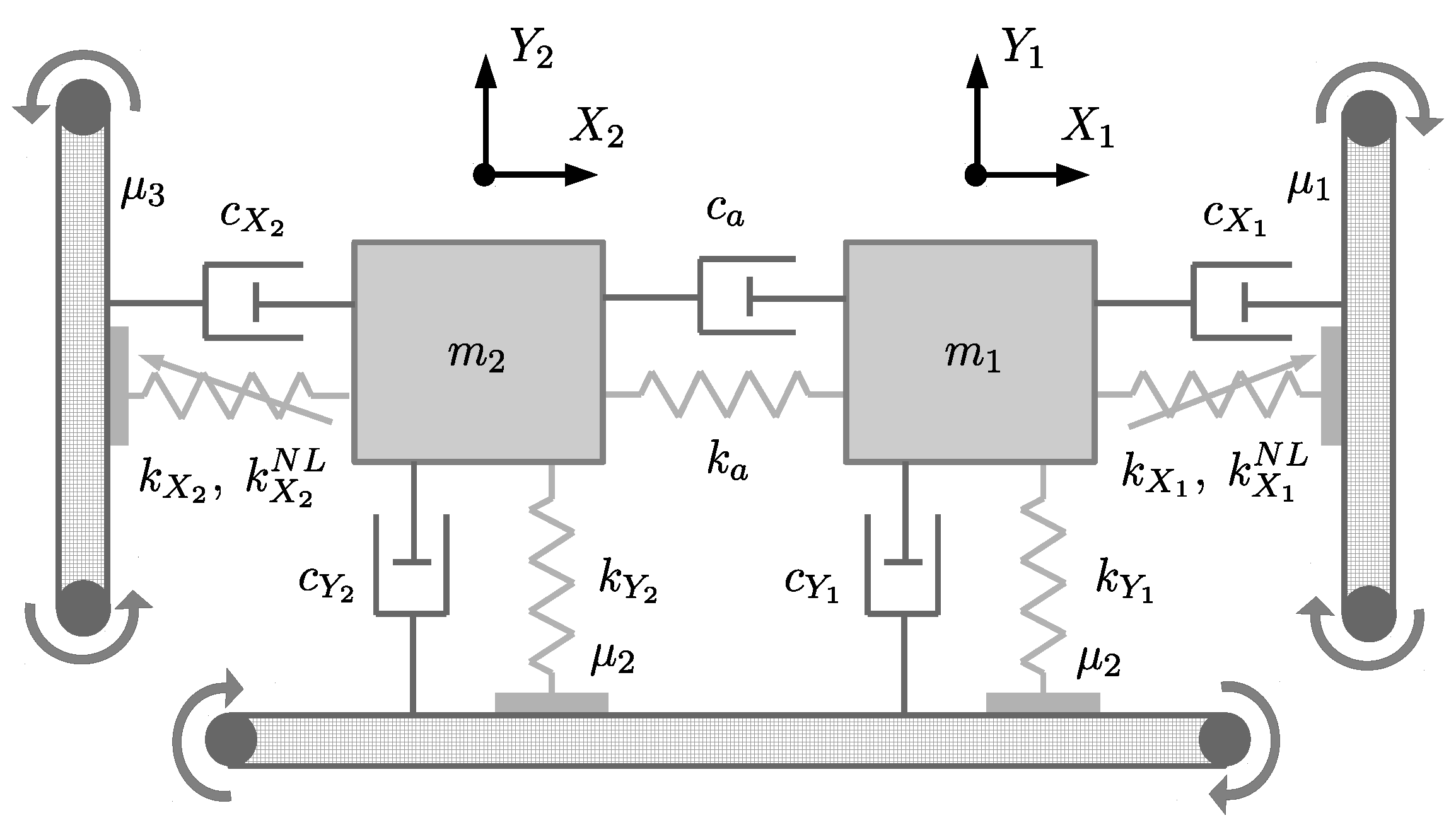
2.1. Mechanical System under Study
- The bands and the masses are supposed to be permanently in contact because of a preload applied to the system;
- The friction forces are determined with a classical Coulomb’s law and the friction coefficient at the different contacts is supposed to be constant and equal to . The tangential friction forces are related to the normal forces by the following formula: ;
- The stick-slip phenomenon is not taken into consideration;
- The belt runs at a constant speed and the relative velocity between the bands and the masses are positive so that the tangential friction forces do not change.
- To allow realistic results for the physical quantities observed (instability frequencies, vibration amplitudes, velocities, etc.) and thus test the relevance of the control in a context close to the engineering problem in the real world;
- To validate the control for a mechanical system subjected to more or less complex nonlinear behaviors (with mono or multi-instabilities in the presence of friction).
2.2. Stability Analysis, Transient and Self-Excited Vibrations
3. Active Control Design
3.1. Active Feedback Linearization
3.2. Linear Poles Placement
3.3. Numerical Simulations
- Case 1 for with only one unstable mode detected by CEA and the generation of self-sustaining periodic vibrational responses;
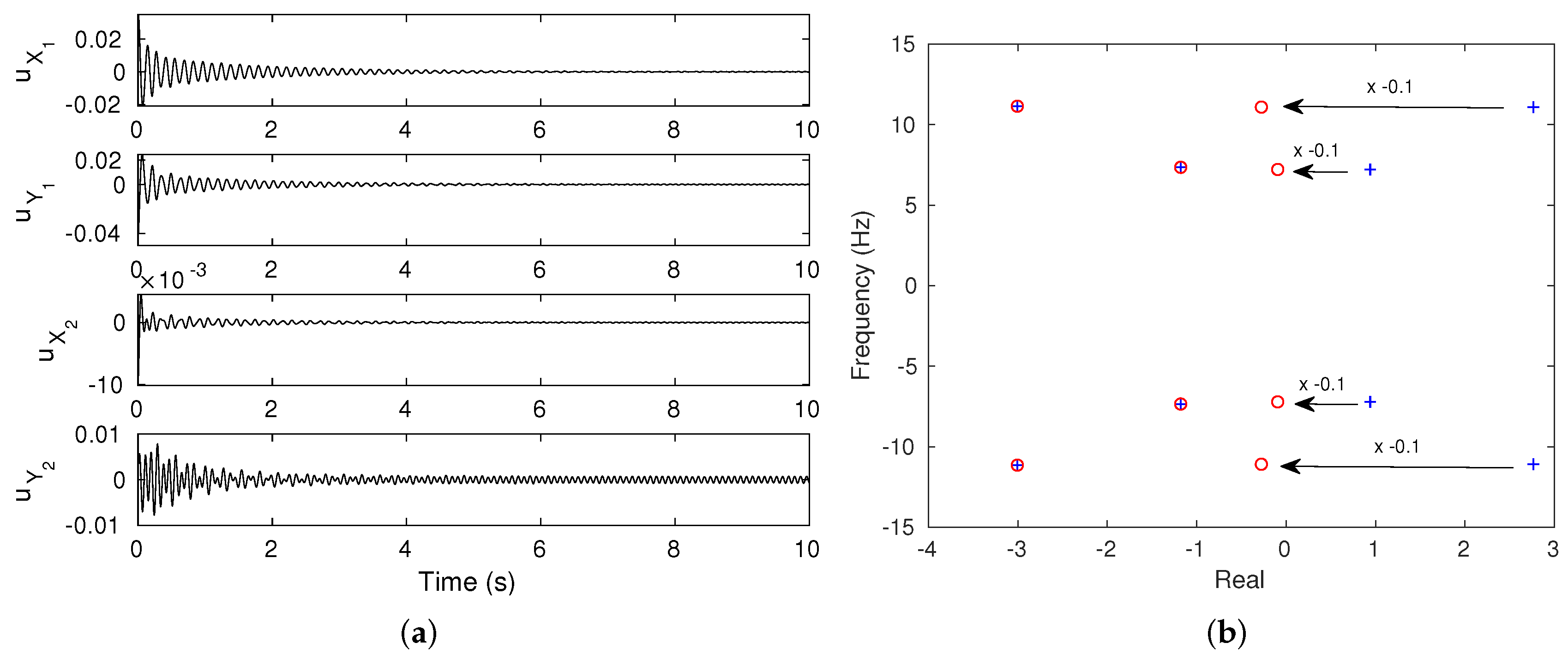
- Case 2 for with two unstable modes detected by CEA and a self-sustaining quasi-periodic motion.
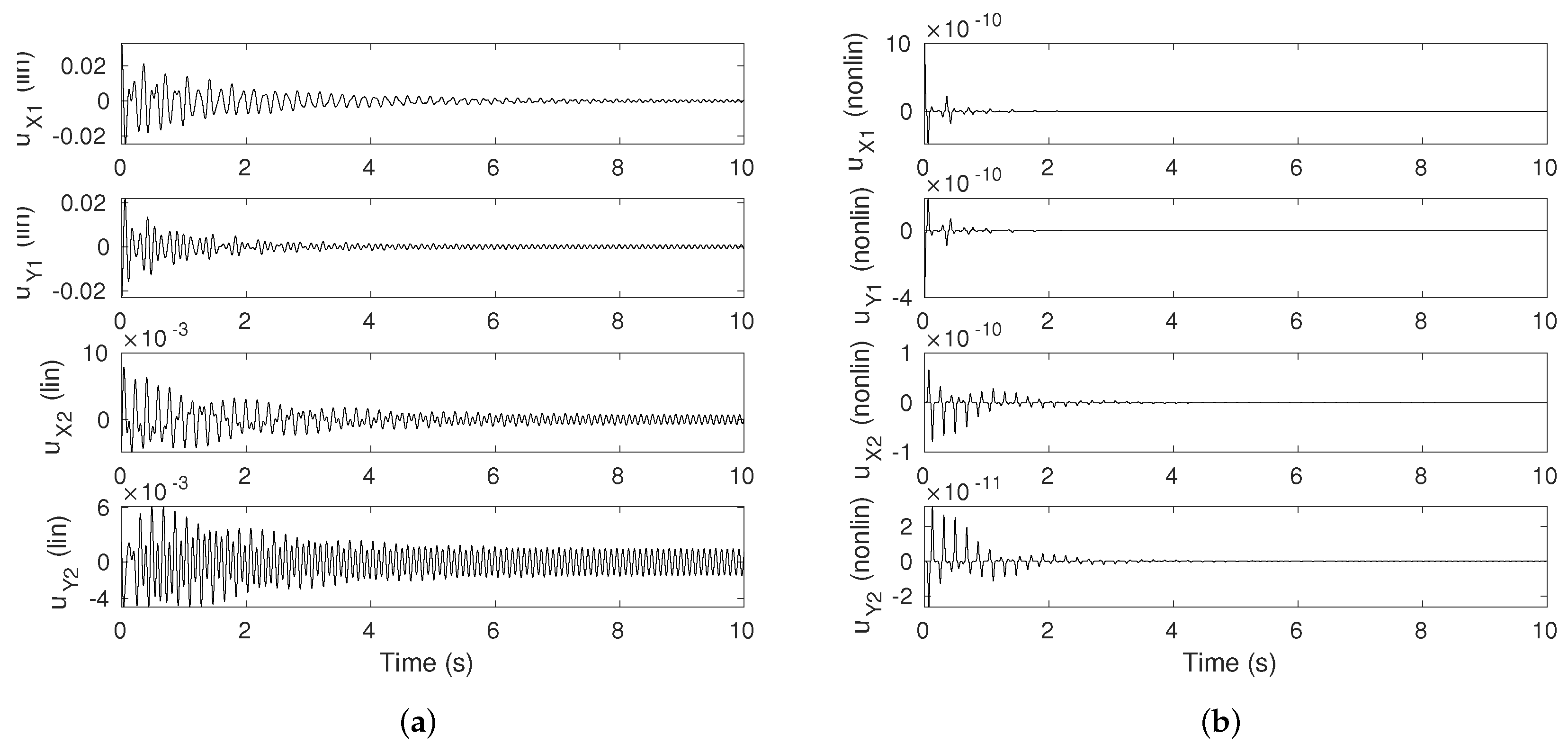
3.3.1. Contributions of Linear and Nonlinear Parts in the Control Vector for Different Values of
3.3.2. Influence of the Control Gain and Sensitivity of the Controller to the Signal-To-Noise Ratio (SNR)
4. Conclusions
- The use of active control makes it possible to significantly reduce periodic or quasi-periodic self-sustained vibrations (i.e., in the case of mechanical systems subjected to one or more unstable modes);
- The control gain has a significant influence on system control performances. This is particularly important in a practical case where the gain has to remain on physically feasible nominal values in terms of design particularly for the amplification and the actuation part;
- The robustness of the control to the signal-to-noise ratio is proven. For the proposed study, the control remains effective up to a minimum value equal to 15 dB;
- Using nonlinear active control seems useless in the present case. Effectively, due to the fact that the control is started at the beginning of the self-excited oscillations, a simple active control based on the linearized system dynamics at the equilibrium point is sufficient.
- Robustness of the control in the case of other inaccuracies possible in real systems, for example time delay, time discretization;
- Extension of control efficiency to a more real industrial brake system;
- Experimental validation of the potential of an active control design based on full and partial linearization feedback;
- Active control algorithm based on the receptance method to control the system without the knowledge of mechanical properties including nonlinearities in the case of experimental validation;
- Extension of the method in the case of stick-slip vibrations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kinkaid, N.; O’Reilly, O.; Papadopoulos, P. Automotive disc brake squeal. J. Sound Vib. 2003, 267, 105–166. [Google Scholar] [CrossRef]
- Ouyang, H.; Nack, W.; Yuan, Y.; Chen, F. Numerical analysis of automotive disc brake squeal: A review. Int. J. Veh. Noise Vib. 2005, 1, 207–231. [Google Scholar] [CrossRef]
- Crolla, D.; Lang, A. Brake noise and vibration—State of the art. Tribol. Ser. 1991, 18, 165–174. [Google Scholar]
- Papinniemi, A.; Lai, J.; Zhao, J.; Loader, L. Brake squeal: A literature review. Appl. Acoust. 2002, 63, 391–400. [Google Scholar] [CrossRef]
- Chatterjee, S. Non-linear control of friction-induced self-excited vibration. Int. J. Nonlinear Mech. 2007, 42, 459–469. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wang, D.H.; Chai, T.Y. Active control of friction-induced self-excited vibration using adaptive fuzzy systems. J. Sound Vib. 2011, 330, 4201–4210. [Google Scholar] [CrossRef]
- Snoun, C.; Bergeot, B.; Berger, S. Prediction of the dynamic behavior of an uncertain friction system coupled to nonlinear energy sinks using a multi-element generalized polynomial chaos approach. Eur. J. Mech. A-Solid 2020, 80, 103917. [Google Scholar] [CrossRef] [Green Version]
- Jakubczyk, B. Feedback Linearization of Discrete-Time-Systems. Syst. Control Lett. 1987, 9, 411–416. [Google Scholar] [CrossRef]
- Charlet, B.; Levine, J.; Marino, R. Sufficient Conditions for Dynamic State Feedback Linearization. SIAM J. Control Optim. 1991, 29, 38–57. [Google Scholar] [CrossRef]
- Nechak, L. Nonlinear control of friction-induced limit cycle oscillations via feedback linearization. Mech. Syst. Signal Process. 2019, 126, 264–280. [Google Scholar] [CrossRef]
- Jiffri, S.; Paoletti, P.; Cooper, J.E.; Mottershead, J.E. Feedback Linearisation for Nonlinear Vibration Problems. Shock Vib. 2014, 2014, 1–16. [Google Scholar] [CrossRef]
- Tehrani, M.G.; Wilmshurst, L.; Elliott, S.J. Receptance method for active vibration control of a nonlinear system. J. Sound Vib. 2013, 332, 4440–4449. [Google Scholar] [CrossRef]
- Liang, Y.; Yamaura, H.; Ouyang, H. Active assignment of eigenvalues and eigen-sensitivities for robust stabilization of friction-induced vibration. Mech. Syst. Signal Process. 2017, 90, 254–267. [Google Scholar] [CrossRef]
- Hu, X. On state observers for nonlinear systems. Syst. Control Lett. 1991, 17, 465–473. [Google Scholar] [CrossRef]
- Nechak, L. Nonlinear state observer for estimating and controlling of friction-induced vibrations. Mech. Syst. Signal Process. 2020, 139, 106588. [Google Scholar] [CrossRef]
- Dakel, M.; Sinou, J.J. Stability and nonlinear self-excited friction-induced vibrations for a minimal model subjected to multiple coalescence patterns. J. Vibroeng. 2017, 19, 604–628. [Google Scholar] [CrossRef]
- Denimal, E.; Nechak, L.; Sinou, J.J.; Nacivet, S. Kriging surrogate models for predicting the complex eigenvalues of mechanical systems subjected to friction-induced vibration. Shock Vib. 2016, 2016, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Denimal, E.; Nechak, L.; Sinou, J.J.; Nacivet, S. A novel hybrid surrogate model and its application on a mechanical system subjected to friction-induced vibration. J. Sound Vib. 2018, 434, 456–474. [Google Scholar] [CrossRef]
- Hulten, J. Brake Squeal-A Self-Exciting Mechanism with Constant Friction; Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 1993. [Google Scholar]
- Hulten, J. Friction phenomena related to drum brake squeal instabilities. In Proceedings of the ASME Design Engineering Technical Conferences, 16th Biennial Conference on Mechanical Vibration and Noise, Sacramento, CA, USA, 14–17 September 1997. [Google Scholar]
- Sinou, J.J. Transient non-linear dynamic analysis of automotive disc brake squeal–on the need to consider both stability and non-linear analysis. Mech. Res. Commun. 2010, 37, 96–105. [Google Scholar] [CrossRef] [Green Version]
- Valášek, M.; Olgac, N. Efficient eigenvalue assignments for general linear MIMO systems. Automatica 1995, 31, 1605–1617. [Google Scholar] [CrossRef]
 1st mode;
1st mode;  2nd mode;
2nd mode;  3rd mode;
3rd mode;  4th mode).
4th mode).
 1st mode;
1st mode;  2nd mode;
2nd mode;  3rd mode;
3rd mode;  4th mode).
4th mode).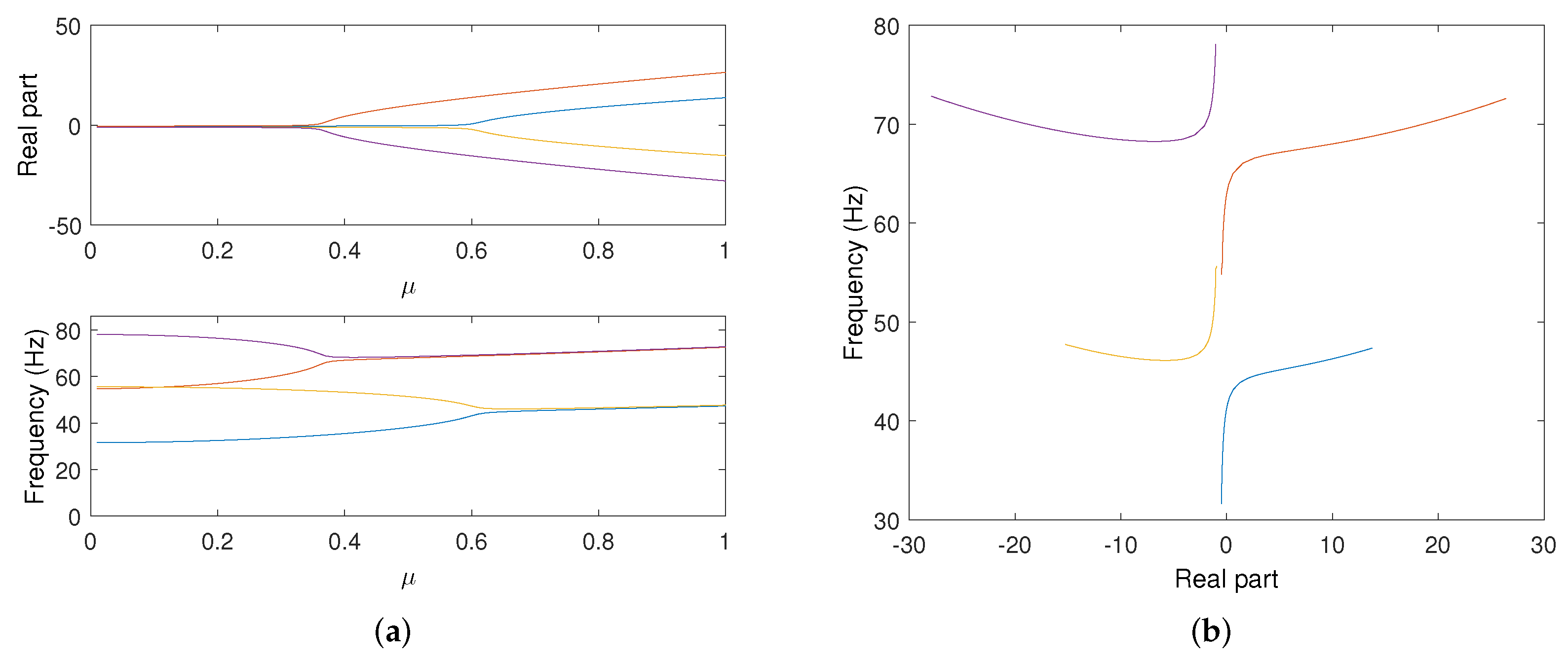


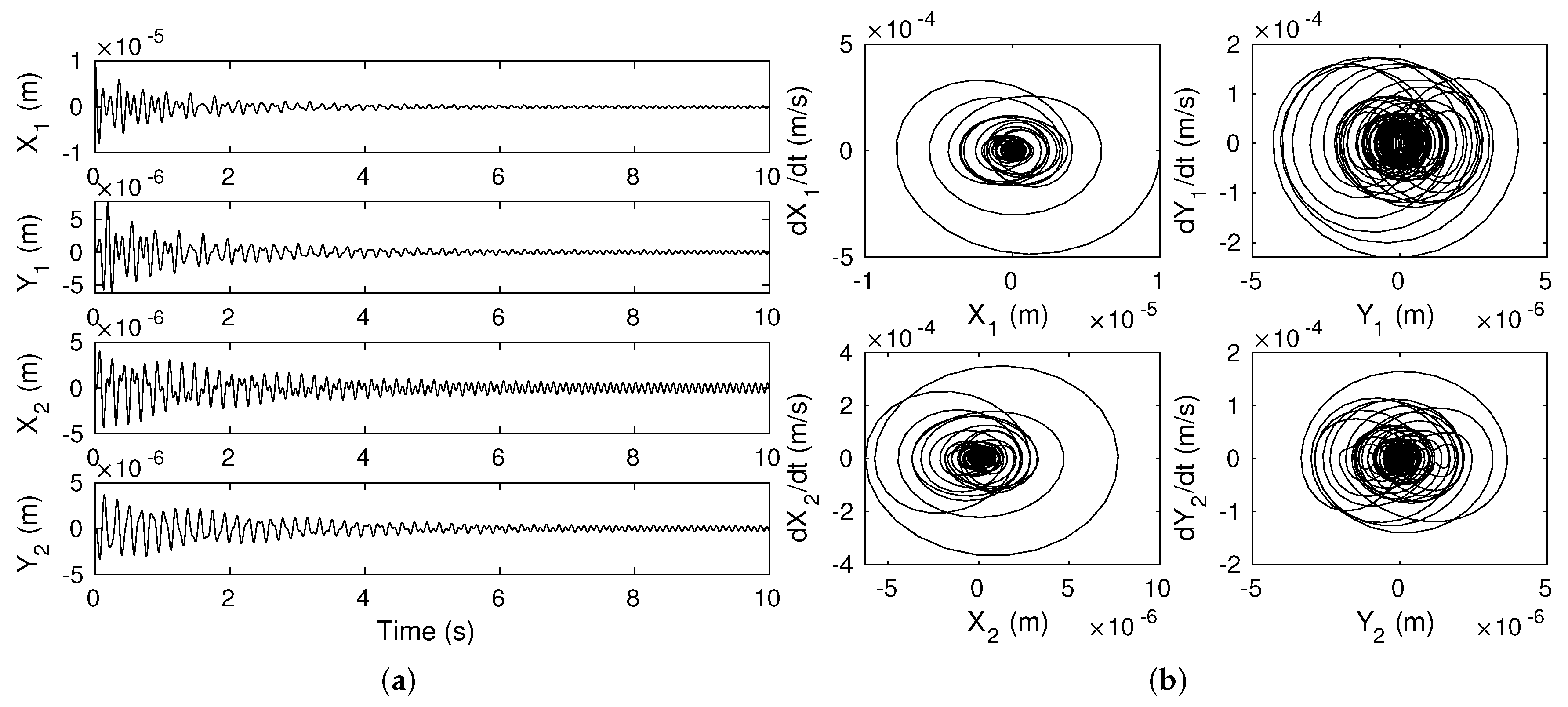
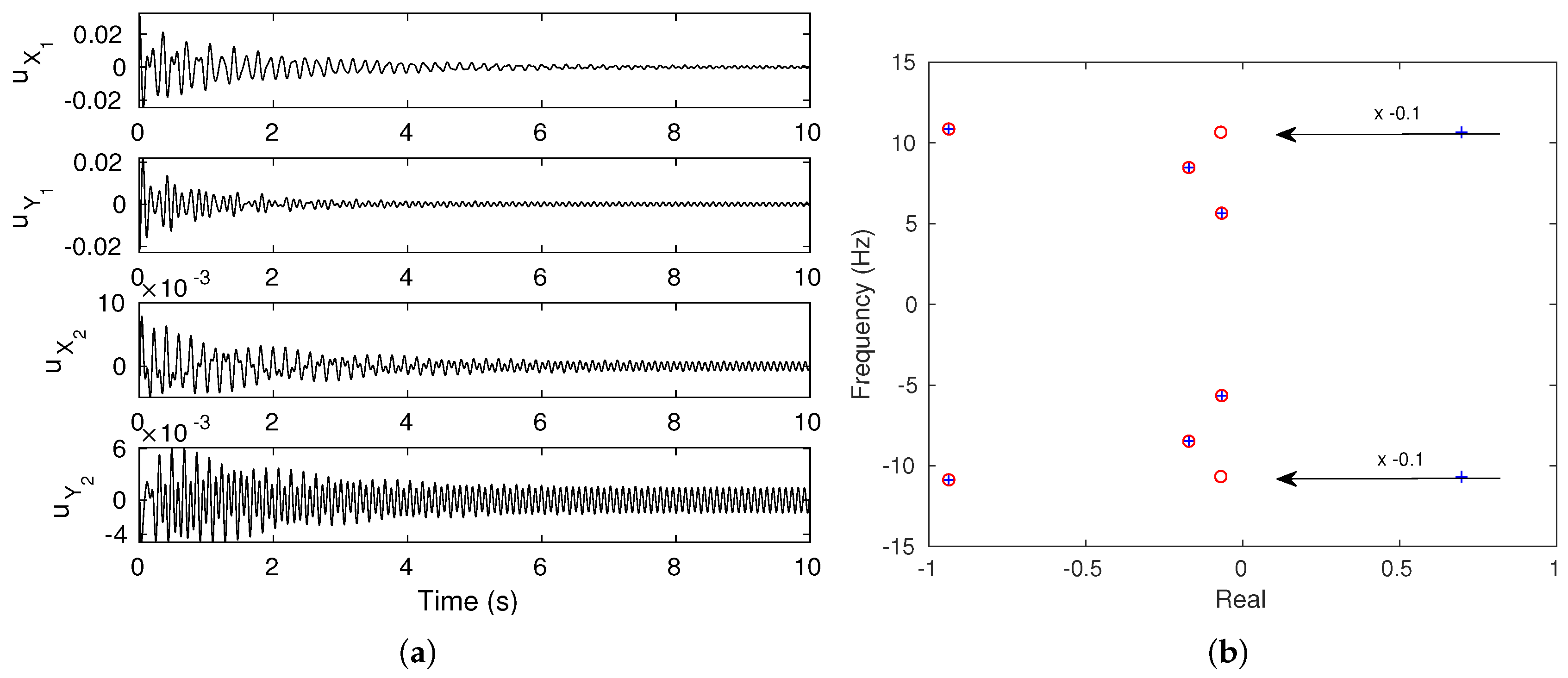


 uncontrolled;
uncontrolled;  controlled). (a) (b) .
controlled). (a) (b) .
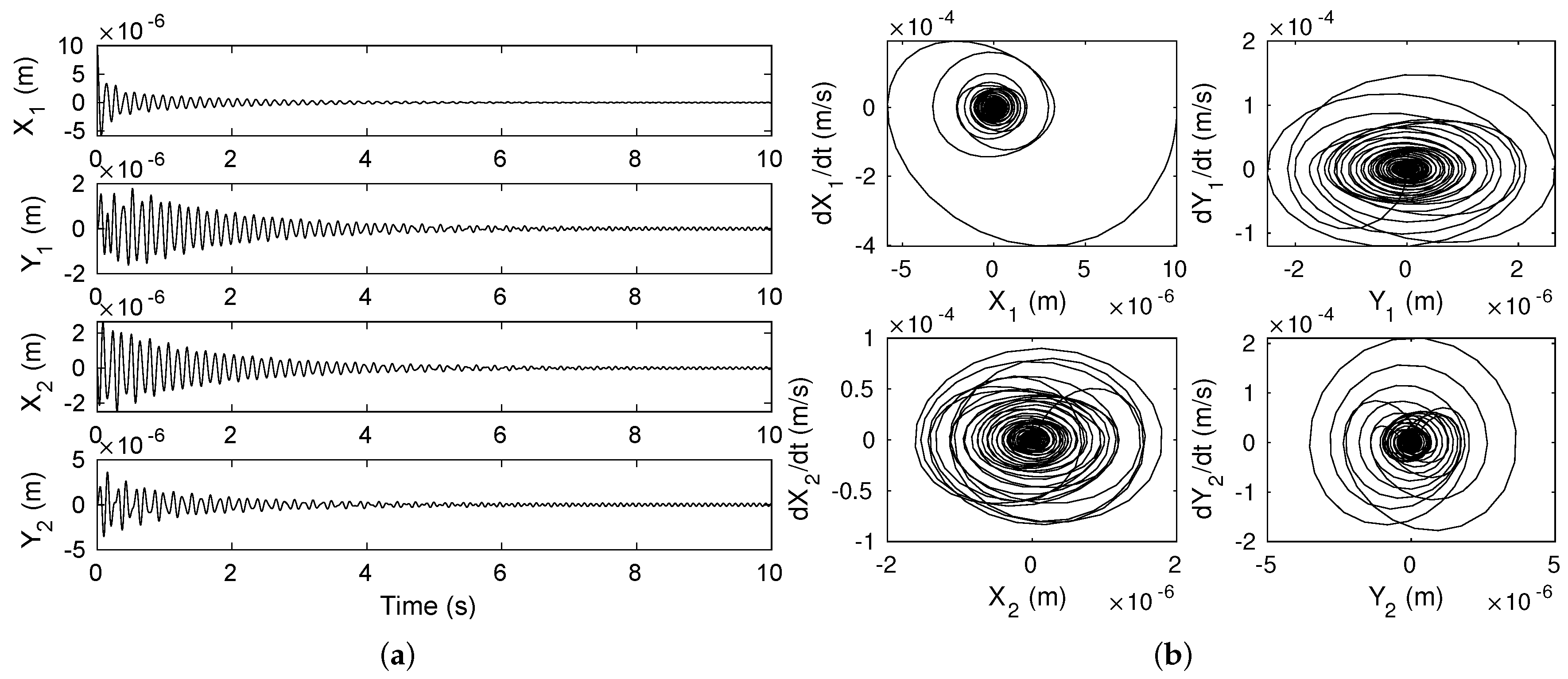
 uncontrolled;
uncontrolled;  controlled). (a) (b) .
controlled). (a) (b) .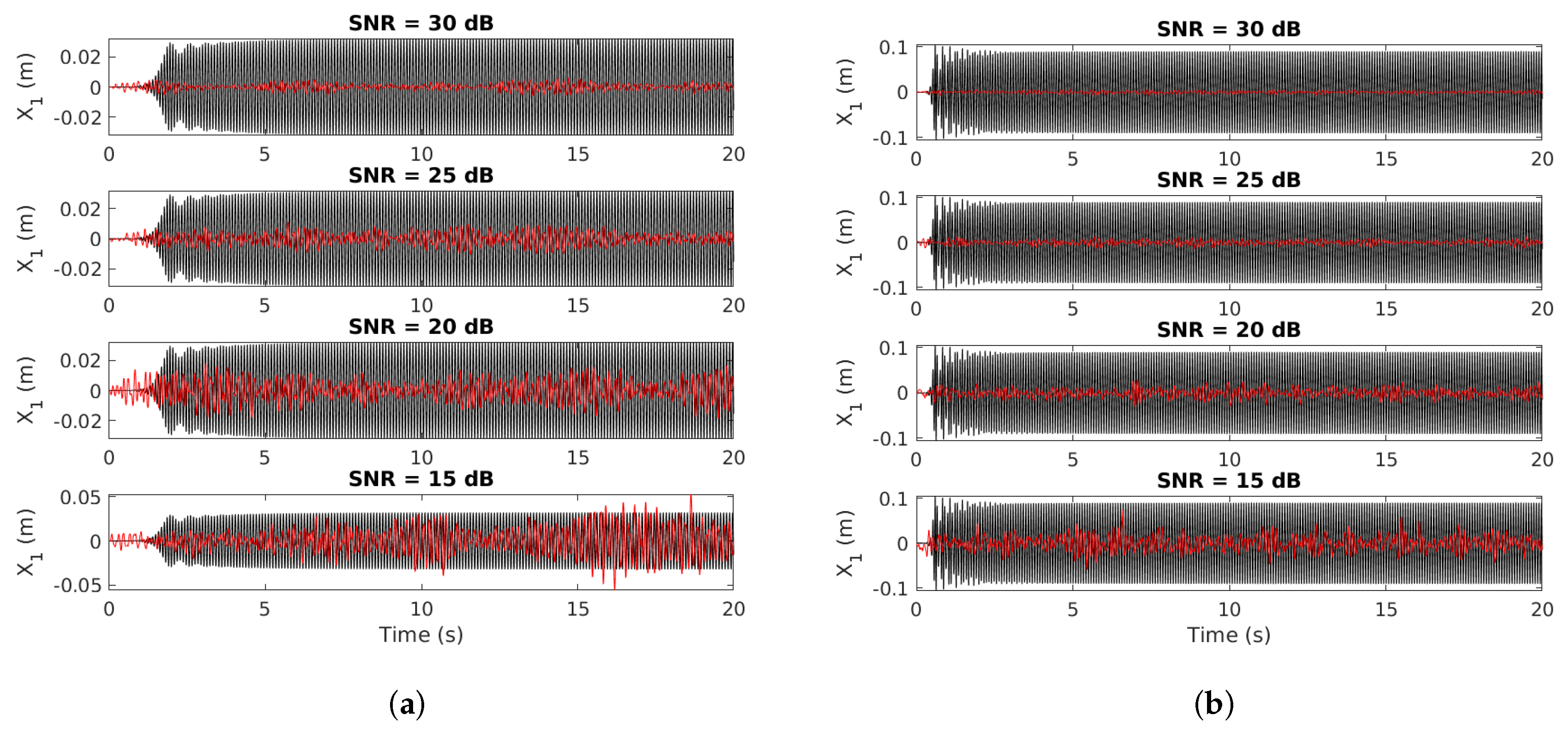
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chomette, B.; Sinou, J.-J. On the Use of Linear and Nonlinear Controls for Mechanical Systems Subjected to Friction-Induced Vibration. Appl. Sci. 2020, 10, 2085. https://doi.org/10.3390/app10062085
Chomette B, Sinou J-J. On the Use of Linear and Nonlinear Controls for Mechanical Systems Subjected to Friction-Induced Vibration. Applied Sciences. 2020; 10(6):2085. https://doi.org/10.3390/app10062085
Chicago/Turabian StyleChomette, Baptiste, and Jean-Jacques Sinou. 2020. "On the Use of Linear and Nonlinear Controls for Mechanical Systems Subjected to Friction-Induced Vibration" Applied Sciences 10, no. 6: 2085. https://doi.org/10.3390/app10062085
APA StyleChomette, B., & Sinou, J.-J. (2020). On the Use of Linear and Nonlinear Controls for Mechanical Systems Subjected to Friction-Induced Vibration. Applied Sciences, 10(6), 2085. https://doi.org/10.3390/app10062085





