Nonlinear Lamb Wave Micro-Crack Direction Identification in Plates with Mixed-Frequency Technique
Abstract
:1. Introduction
2. Basic Theory of Nonlinear Lamb Waves
2.1. Mode Selection of Lamb Wave
2.2. Nonlinear Lamb Wave Frequency-Mixing Excitation
2.3. Pulse Inversion Method of Frequency-Mixing Excitation
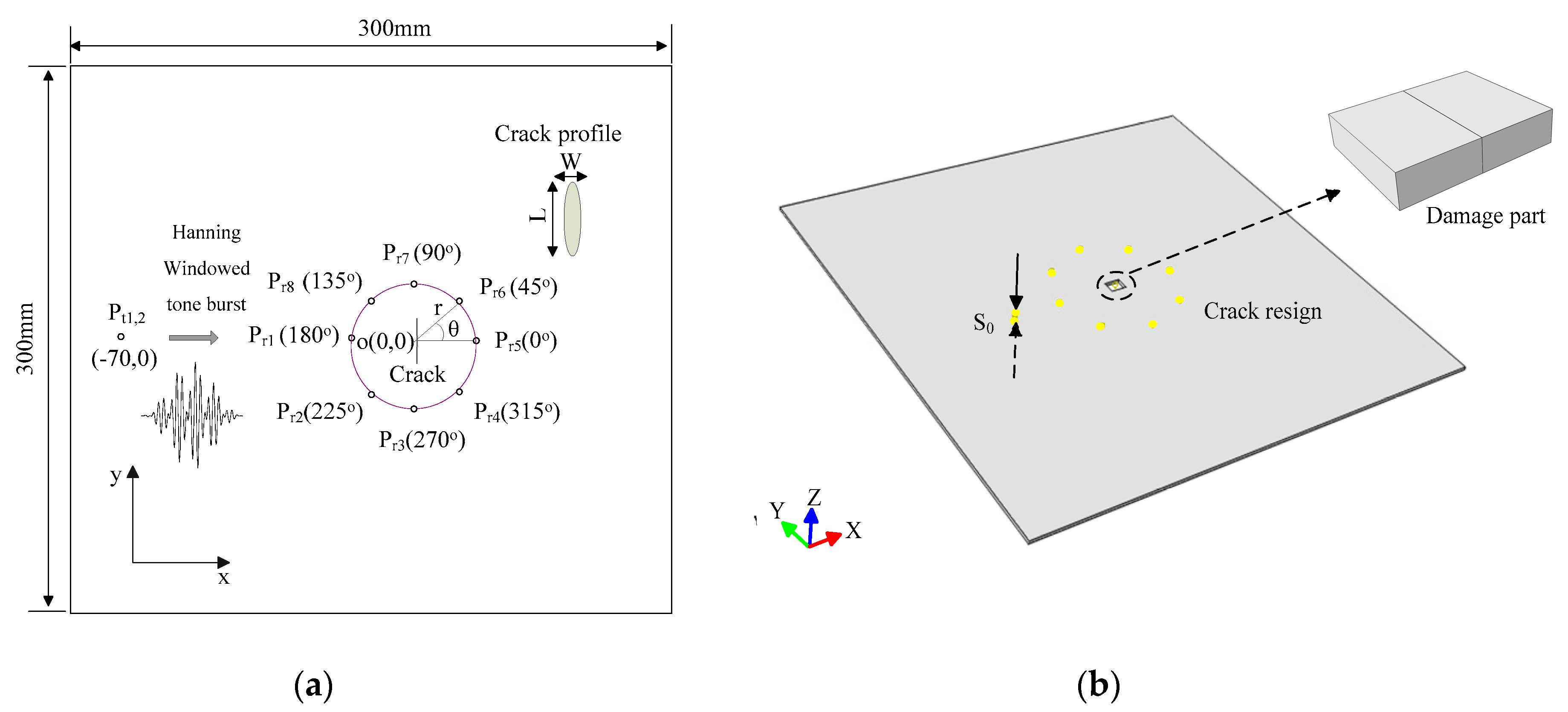
3. Three-Dimensional Finite-Element Simulation
3.1. 3D Models of an Aluminum Plate
3.1.1. Through-Thickness Micro-Crack Model
3.1.2. Buried Micro-Crack Model
3.2. Simulation Results and Analyses
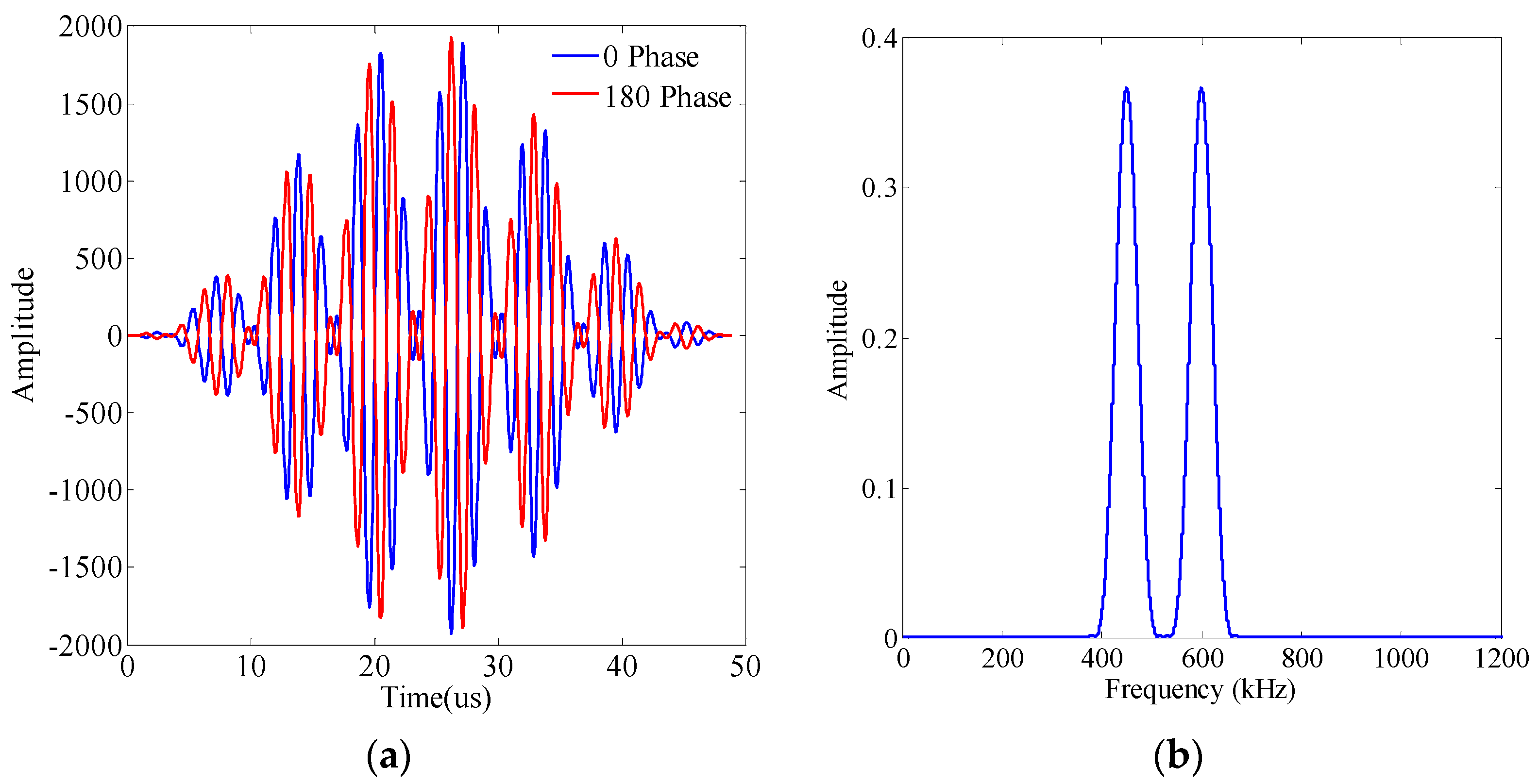
3.2.1. Signal Excitation and Processing
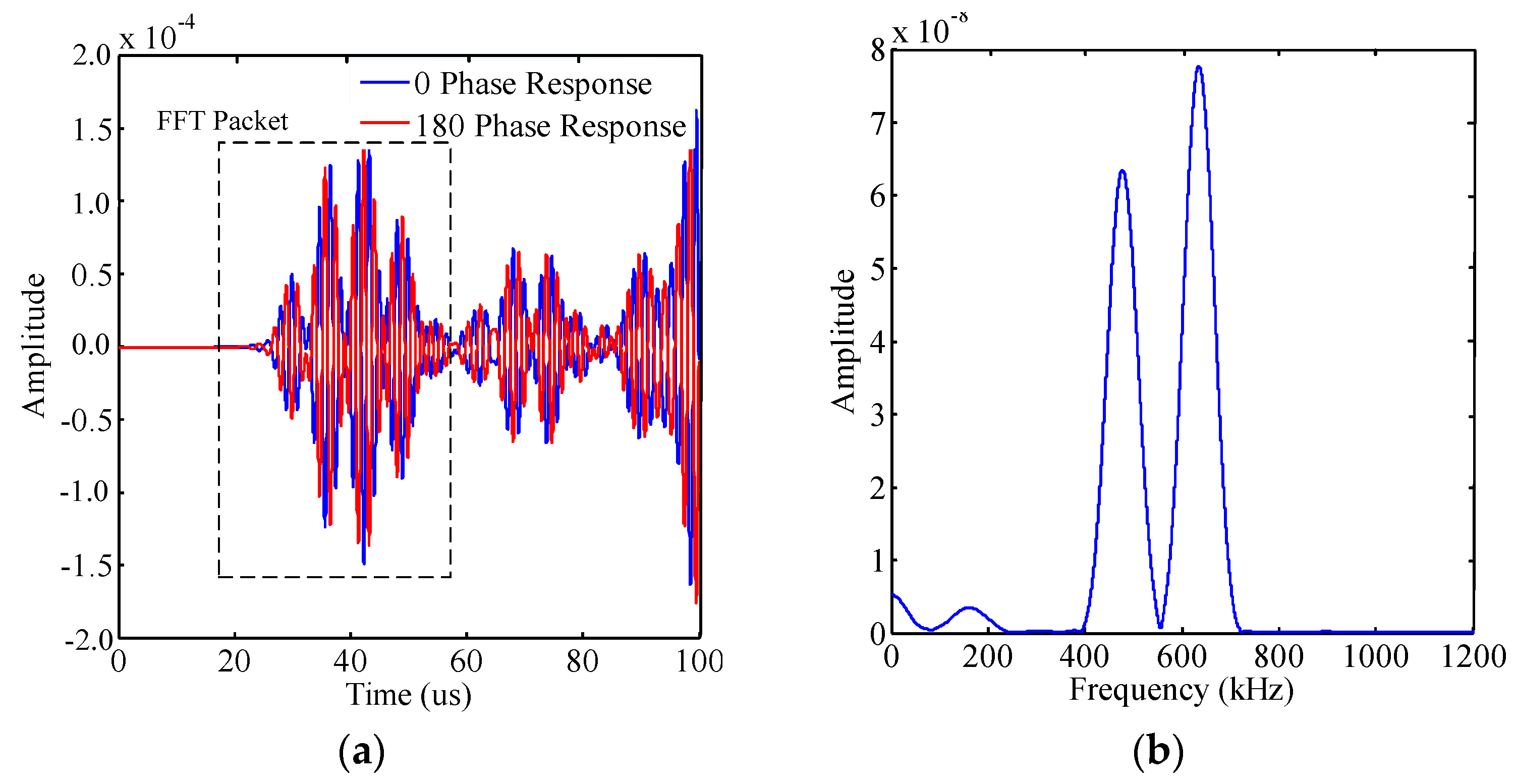
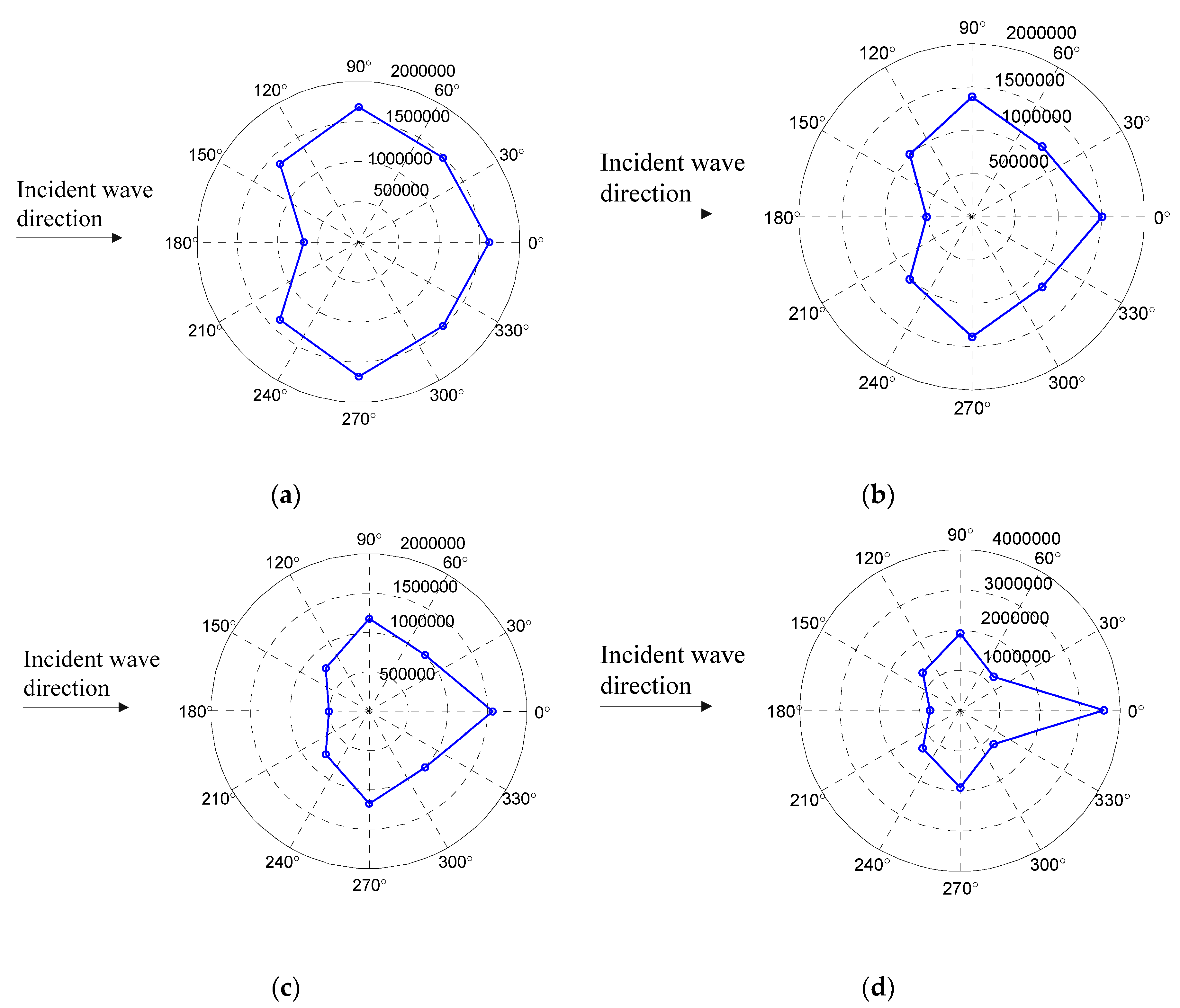
3.2.2. Through-Thickness Crack Simulation Results and Analyses
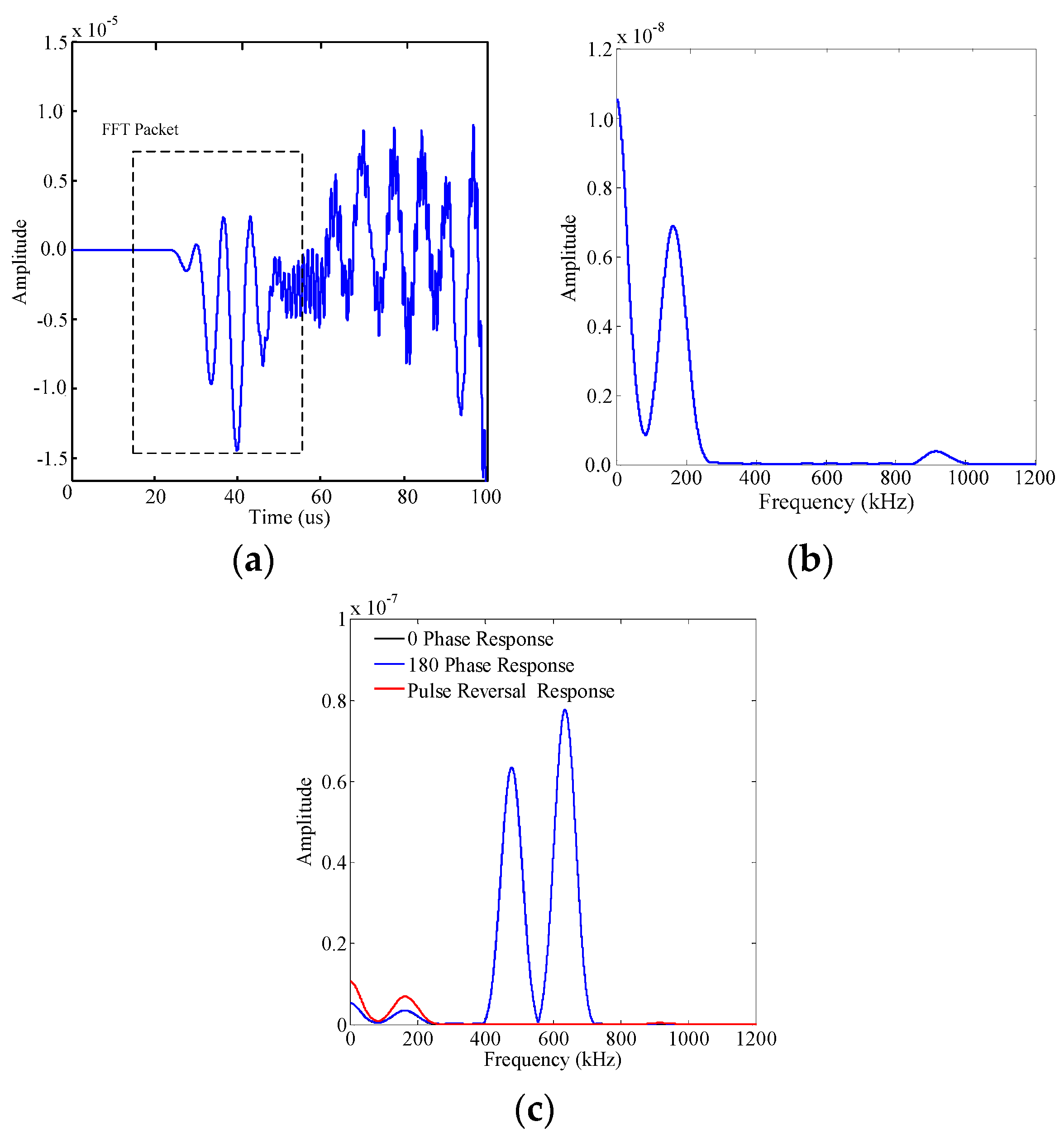
3.2.3. Buried Crack Model Simulation Results and Analyses
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sohn, H.; Lee, S.J. Lamb wave tuning curve calibration for surface-bonded piezoelectric transducers. Smart Mater. Struct. 2010, 19, 15007–15012. [Google Scholar] [CrossRef] [Green Version]
- Kundu, T.; Nakatani, H.; Takeda, N. Acoustic source localization in anisotropic plates. Ultrasonics 2012, 52, 740–746. [Google Scholar] [CrossRef] [PubMed]
- Gresil, M.; Giurgiutiu, V. Prediction of attenuated guided wave propagation in carbon fiber composites using Rayleigh damping model. J. Intell. Mater. Syst. Struct. 2015, 26, 2151–2169. [Google Scholar] [CrossRef]
- Mańka, M.; Rosiek, M.; Martowicz, A.; Stepinski, T.; Uhl, T. PZT-based tunable interdigital transducer for Lamb wave-based NDT and SHM. Mech. Syst. Signal Process. 2016, 78, 71–83. [Google Scholar] [CrossRef]
- Shan, S.; Cheng, L.; Li, P. Adhesive nonlinearity in Lamb wave-based structural health monitoring systems. Smart Mater. Struct. 2017, 26, 025019. [Google Scholar] [CrossRef]
- Ghadami, A.; Behzad, M.; Mirdamadi, H.R. Damage identification in multi-step waveguides using Lamb waves and scattering coefficients. Arch. Appl. Mech. 2018, 88, 1009–1026. [Google Scholar] [CrossRef]
- Amjad, U.; Jha, D.; Tara, K.S.; Grill, W. Determination of the stress dependence of the velocity of Lamb waves in aluminum plates. Proc. SPIE 2011, 10, 1133–1145. [Google Scholar]
- Ramadas, C.; Balasubramaniam, K.; Joshi, M.; Krishnamurthy, C.V. Interaction of guided Lamb waves with an asymmetrically located delamination in a laminated composite plate. Smart Mater. Struct. 2010, 19, 065009. [Google Scholar] [CrossRef]
- Zeng, L.; Lin, J.; Huang, L.P. A modified Lamb wave time-reversal method for health monitoring of composite structures. Sensors 2017, 17, 955. [Google Scholar] [CrossRef] [Green Version]
- Gao, A.; Gong, S. Harnessing mode conversion for spurious mode suppression in AlN laterally vibrating resonators. J. Microelectromech. Syst. 2016, 25, 450–458. [Google Scholar] [CrossRef]
- Ong, W.H.; Chiu, W.K.; Rose, L.R.F. Numerical simulation of cumulative nonlinear symmetric Lamb waves in an aluminum plate. Procedia Eng. 2017, 188, 217–224. [Google Scholar] [CrossRef]
- Hong, M.; Su, Z.; Wang, Q.; Li, C.; Qing, X.L. Modeling nonlinearities of ultrasonic waves for fatigue damage characterization: Theory, simulation, and experimental validation. Ultrasonics 2014, 54, 770–778. [Google Scholar] [CrossRef] [PubMed]
- Wan, X.; Tse, P.W.; Chen, J.; Xu, G.H.; Zhang, Q. Second-harmonic reflection and transmission from primary S0-mode Lamb wave interacting with a localized microscale damage in a plate: A numerical perspective. Ultrasonics 2018, 82, 57–71. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Liu, M.; Su, Z.; Xiao, Y. Quantitative evaluation of residual torque of a loose bolt based on wave energy dissipation and vibro-acoustic modulation: A comparative study. J. Sound Vib. 2016, 383, 156–170. [Google Scholar] [CrossRef]
- Yao, Y.; Wu, F.; Zhang, X.; Hou, Z. Lamb-wave band gaps in locally resonant phononic crystal strip waveguides. Phys. Lett. 2012, 376, 579–583. [Google Scholar] [CrossRef]
- Wan, X.; Zhang, Q.; Xu, G.; Tse, P.W. Numerical simulation of nonlinear Lamb waves used in a thin plate for detecting buried micro-cracks. Sensors 2014, 14, 8528–8546. [Google Scholar] [CrossRef] [Green Version]
- Li, F.L.; Zhao, Y.X.; Cao, P.; Hu, N. Mixing of ultrasonic Lamb waves in thin plates with quadratic nonlinearity. Ultrasonics 2018, 87, 33–43. [Google Scholar] [CrossRef]
- Wang, Y.K.; Guan, R.Q.; Lu, Y. Nonlinear Lamb waves for fatigue damage identification in FRP-reinforced steel plates. Ultrasonics 2017, 80, 80–87. [Google Scholar] [CrossRef]
- Hong, M.; Su, Z.Q.; Lu, Y.; Sohn, H.; Qing, X.L. Locating fatigue damage using temporal signal features of nonlinear Lamb waves. Mech. Syst. Signal Process. 2015, 60–61, 182–197. [Google Scholar] [CrossRef]
- Zhou, J.Y.; Li, X.; Qu, W.Z.; Lu, Y. Nonlinear Lamb wave-based DORT method for detection of fatigue cracks. NDT. E. Int. 2017, 92, 22–29. [Google Scholar] [CrossRef]
- Chen, Z.; Tang, G.; Zhao, Y.; Jacobs, L.J.; Qu, J. Mixing of collinear plane wave pulses in elastic solids with quadratic nonlinearity. J. Acoust. Soc. Am. 2014, 136, 2389–2404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, D.J.; Cho, Y.; Li, W.B. A feasibility study for a Lamb wave mixing nonlinear technique. AIP Conf. Proc. 2014, 1581, 662–666. [Google Scholar]
- Jiao, J.P.; Meng, X.J.; He, C.F.; Wu, B. Nonlinear Lamb wave-mixing technique for micro-crack detection in plates. NDT. E. Int. 2017, 85, 63–71. [Google Scholar]
- Zhai, G.; Jiang, T.; Kang, L. Analysis of multiple wavelengths of Lamb waves generated by meander-line coil EMATs. Ultrasonics 2014, 54, 632–636. [Google Scholar] [CrossRef]
- Courtney, C.R.P.; Neild, S.A.; Wilcox, P.D.; Drinkwater, B.W. Application of the bispectrum for detection of small nonlinearities excited sinusoidally. J. Sound Vib. 2010, 329, 4279–4293. [Google Scholar] [CrossRef] [Green Version]
- Jiao, J.; Sun, J.; Li, G.; Wu, B.; He, C.F. Evaluation of intergranular corrosion in austenitic stainless steel using collinear wave mixing method. NDT. E. Int. 2015, 69, 1–8. [Google Scholar]
- Krishnan, S.; Hamilton, J.D.; Donnel, M.O. Suppression of propagating second harmonic in ultrasound contrast imaging. IEEE. Trans. Ultrason. Ferroelectr. 1998, 45, 704–711. [Google Scholar] [CrossRef]
- Kim, J.Y.; Jacobs, L.J.; Qu, J.; Littles, J.W. Experimental characterization of fatigue damage in a nickel-base superalloy using nonlinear ultrasonic waves. J. Acoust. Soc. Am. 2006, 120, 1266–1273. [Google Scholar] [CrossRef]
- Yang, Y.; Ng, C.T.; Kotousov, A.; Sohn, H.; Lim, H.J. Second harmonic generation at fatigue cracks by low-frequency Lamb waves: Experimental and numerical studies. Mech. Syst. Signal Process. 2018, 99, 760–773. [Google Scholar] [CrossRef] [Green Version]
- Zou, F.; Rao, J.; Aliabadi, M. Highly accurate online characterization of cracks in plate-like structures. NDT. E. Int. 2017, 94, 1–12. [Google Scholar] [CrossRef]
- Jiao, J.P.; Liu, W.H.; He, C.F.; Zhang, J. Nonlinear Acoustic Interaction of Contact Interface. Exp. Mech. 2014, 54, 63–68. [Google Scholar] [CrossRef]








| Dimensions (Length × Width × Height) | Density ρ | Elasticity Modulus E | Poisson’s Ratio λ |
|---|---|---|---|
| 300 × 300 × 2 mm | 2700 kg/m3 | 70 GPa | 0.33 |
| Sequence Number (i) | Cycle (n) | f1 | f2 | f1 + f2 | f2 − f1 |
|---|---|---|---|---|---|
| 1 | 22 | 450 kHz | 600 kHz | 1050 kHz | 150 kHz |
| 2 | 22 | 470 kHz | 650 kHz | 1120 kHz | 180 kHz |
| 3 | 22 | 500 kHz | 700 kHz | 1200 kHz | 200 kHz |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, L.; Zou, M.; Wan, X.; Li, Y. Nonlinear Lamb Wave Micro-Crack Direction Identification in Plates with Mixed-Frequency Technique. Appl. Sci. 2020, 10, 2135. https://doi.org/10.3390/app10062135
Guan L, Zou M, Wan X, Li Y. Nonlinear Lamb Wave Micro-Crack Direction Identification in Plates with Mixed-Frequency Technique. Applied Sciences. 2020; 10(6):2135. https://doi.org/10.3390/app10062135
Chicago/Turabian StyleGuan, Liqiang, Mingxia Zou, Xili Wan, and Yifeng Li. 2020. "Nonlinear Lamb Wave Micro-Crack Direction Identification in Plates with Mixed-Frequency Technique" Applied Sciences 10, no. 6: 2135. https://doi.org/10.3390/app10062135
APA StyleGuan, L., Zou, M., Wan, X., & Li, Y. (2020). Nonlinear Lamb Wave Micro-Crack Direction Identification in Plates with Mixed-Frequency Technique. Applied Sciences, 10(6), 2135. https://doi.org/10.3390/app10062135





