Dynamics of the Global Stock Market Networks Generated by DCCA Methodology
Abstract
:Featured Application
Abstract
1. Introduction
2. Data
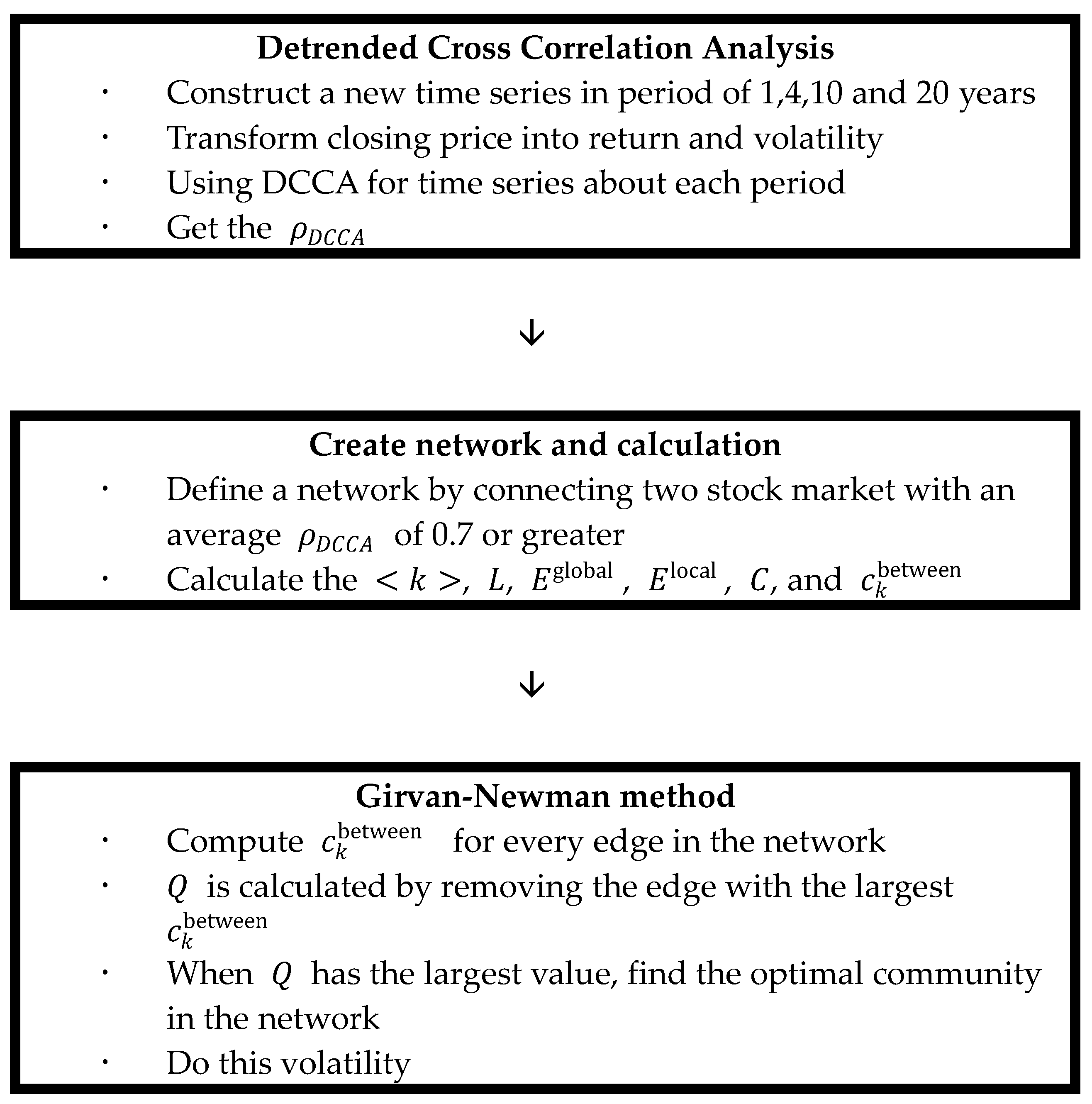
3. Methodology
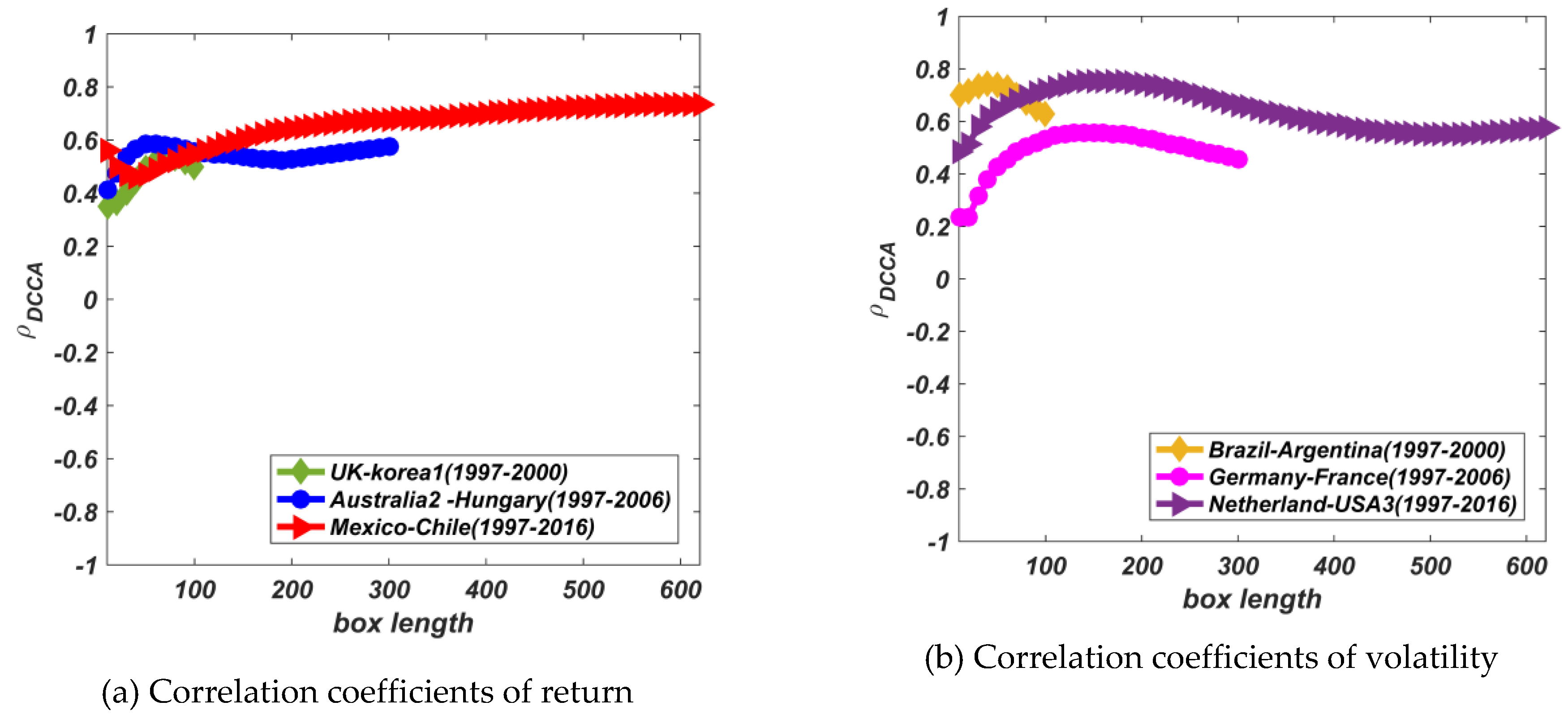
3.1. Detrended cross Correlation Analysis (DCCA)
3.2. Complex Network Analysis and Girvan-Newman Method
3.2.1. Degree
3.2.2. Characteristic Path Length
3.2.3. Efficiency
3.2.4. Clustering Coefficient
3.2.5. Betweenness Centrality
3.2.6. Modularity
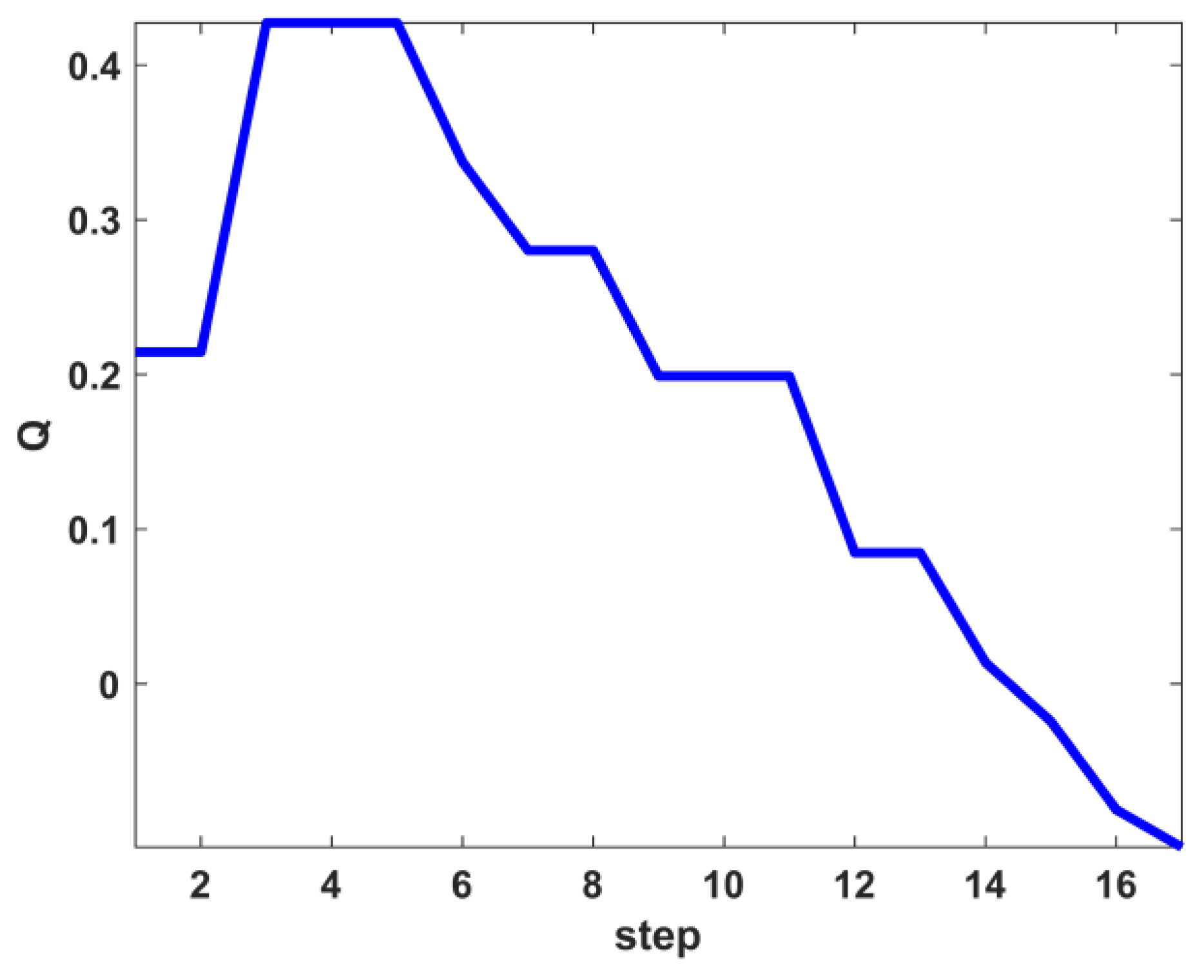
3.2.7. Girvan-Newman Method
3.2.8. Create Network Structure
4. Numerical Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Data | Year | |||||||
|---|---|---|---|---|---|---|---|---|
| Return | 1997 | 3.333 | 1.904 | 0.246 | 0.557 | 0.790 | USA1 | 0.109 |
| 1998 | 1.583 | 1.825 | 0.099 | 0.451 | 0.880 | USA2 | 0.067 | |
| 1999 | 0.750 | 2.172 | 0.061 | 0.090 | 0.433 | USA2 | 0.055 | |
| 2000 | 1.083 | 2.696 | 0.102 | 0.093 | 0.290 | Netherland | 0.121 | |
| 2001 | 4.583 | 1.445 | 0.263 | 0.488 | 0.819 | USA4 | 0.050 | |
| 2002 | 3.000 | 1.052 | 0.134 | 0.366 | 0.952 | Netherland | 0.001 | |
| 2003 | 1.666 | 1.400 | 0.089 | 0.304 | 0.825 | USA1 | 0.016 | |
| 2004 | 1.833 | 1.538 | 0.108 | 0.298 | 0.636 | USA2 | 0.022 | |
| 2005 | 1.250 | 1.166 | 0.059 | 0.312 | 0.937 | Netherland | 0.012 | |
| 2006 | 2.416 | 1.821 | 0.175 | 0.320 | 0.559 | USA2 | 0.090 | |
| 2007 | 7.000 | 1.766 | 0.437 | 0.726 | 0.836 | Netherland | 0.109 | |
| 2008 | 8.583 | 1.658 | 0.590 | 0.768 | 0.766 | Japan | 0.128 | |
| 2009 | 6.333 | 1.790 | 0.461 | 0.613 | 0.893 | Hong Kong | 0.356 | |
| 2010 | 6.750 | 2.012 | 0.519 | 0.662 | 0.708 | Korea1 | 0.192 | |
| 2011 | 5.166 | 2.384 | 0.395 | 0.557 | 0.678 | UK | 0.149 | |
| 2012 | 2.833 | 1.418 | 0.160 | 0.407 | 0.804 | USA2 | 0.060 | |
| 2013 | 1.500 | 1.530 | 0.088 | 0.297 | 0.766 | UK | 0.047 | |
| 2014 | 2.083 | 1.324 | 0.112 | 0.357 | 0.904 | USA1 | 0.024 | |
| 2015 | 2.666 | 1.657 | 0.179 | 0.396 | 0.706 | USA3 | 0.057 | |
| 2016 | 1.333 | 2.500 | 0.109 | 0.260 | 0.667 | Netherland | 0.095 | |
| Volatility | 1997 | 5.750 | 1.633 | 0.327 | 0.605 | 0.859 | France | 0.103 |
| 1998 | 0.666 | 1.384 | 0.038 | 0.097 | 0.583 | USA2 | 0.012 | |
| 1999 | 0.166 | 1.000 | 0.007 | 0.000 | 0.000 | - | - | |
| 2000 | 0.333 | 1.200 | 0.016 | 0.000 | 0.000 | Netherland | 0.004 | |
| 2001 | 2.000 | 2.620 | 0.152 | 0.353 | 0.663 | USA1 | 0.174 | |
| 2002 | 1.250 | 1.166 | 0.059 | 0.347 | 0.851 | USA1 | 0.004 | |
| 2003 | 0.667 | 1.200 | 0.032 | 0.222 | 0.888 | France | 0.008 | |
| 2004 | 0.750 | 1.357 | 0.041 | 0.097 | 0.583 | USA2 | 0.012 | |
| 2005 | 0.750 | 1.100 | 0.034 | 0.277 | 0.904 | Netherland | 0.002 | |
| 2006 | 0.833 | 1.000 | 0.036 | 0.291 | 1.000 | - | - | |
| 2007 | 2.167 | 3.441 | 0.182 | 0.457 | 0.617 | Argentina | 0.217 | |
| 2008 | 7.500 | 1.874 | 0.547 | 0.759 | 0.770 | Indonesia | 0.177 | |
| 2009 | 1.167 | 1.333 | 0.063 | 0.243 | 0.687 | USA2 | 0.020 | |
| 2010 | 3.083 | 1.990 | 0.238 | 0.481 | 0.711 | UK | 0.162 | |
| 2011 | 2.416 | 1.469 | 0.139 | 0.363 | 0.749 | USA2 | 0.033 | |
| 2012 | 0.833 | 1.000 | 0.036 | 0.291 | 1.000 | - | - | |
| 2013 | 0.667 | 1.384 | 0.038 | 0.097 | 0.583 | USA2 | 0.012 | |
| 2014 | 1.083 | 1.000 | 0.047 | 0.333 | 1.000 | - | - | |
| 2015 | 3.333 | 2.219 | 0.233 | 0.454 | 0.676 | Korea2 | 0.095 | |
| 2016 | 1.083 | 1.862 | 0.070 | 0.281 | 0.812 | USA2 | 0.049 | |
References
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [Green Version]
- Hu, K.; Ivanov, P.; Chen, Z.; Carpena, P.; Stanley, H.E. Effect of trends on detrended fluctuation analysis. Phys. Rev. E 2001, 64, 011114. [Google Scholar] [CrossRef] [Green Version]
- Podobnik, B.; Stanley, H.E. Detrended Cross-Correlation Analysis: A New Method for Analyzing Two Non-stationary Time Series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [Green Version]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef] [Green Version]
- Souma, W.; Fujiwara, Y.; Aoyama, H. Complex networks and economics. Physica A 2003, 324, 396–401. [Google Scholar] [CrossRef]
- Mason, O.; Verwoerd, M. Graph theory and networks in biology. IET Syst. Biol. 2007, 1, 89–119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Silva, E.; Stumpf, M.P. Complex networks and simple models in biology. J. R. Soc. Interface 2005, 2, 419–430. [Google Scholar] [CrossRef] [Green Version]
- McNally, R.J. Can network analysis transform psychopathology? Behav. Res. Ther. 2016, 86, 95–104. [Google Scholar] [CrossRef]
- Steinhaeuser, K.; Chawla, N.V.; Ganguly, A.R. Complex Networks in Climate Science: Progress, Opportunities and Challenges. In Proceedings of the 2011 Conference on Intelligent Data Understanding (CIDU 2011), Mountain View, CA, USA, 19–21 October 2011; pp. 16–26. [Google Scholar]
- Liu, J.; Li, M.; Pan, Y.; Lan, W.; Zheng, R.; Wu, F.-X.; Wang, J. Complex brain network analysis and its applications to brain disorders: A survey. Complexity 2017, 2017, 1–27. [Google Scholar] [CrossRef]
- Zebende, G.F. DCCA cross-correlation coefficient: Quantifying level of cross-correlation. Phys. A 2011, 390, 614–618. [Google Scholar] [CrossRef]
- Piao, L.; Fu, Z. Quantifying distinct associations on different temporal scales: Comparison of DCCA and Pearson methods. Sci. Rep. 2016, 6, 36759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Despalatovic, L.; Vojkovic, T.; Vukicevic, D. Community structure in networks: Improving the Girvan-Newman algorithm. In Proceedings of the 2014 37th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO 2014), Opatija, Croatia, 26–30 May 2014. [Google Scholar]
- Wu, S.; Tuo, M.; Xiong, D. Network Structure Detection and Analysis of Shanghai Stock Market. JIEMS J. Ind. Eng. Manag. 2015, 8, 383–398. [Google Scholar] [CrossRef] [Green Version]
- Silva, F.N.; Comin, C.H.; Peron, T.K.; Rodrigues, F.A.; Ye, C.; Wilson, R.C.; Hancock, E.; da F. Costa, L. Modular Dynamics of Financial Market Networks. arXiv 2015, arXiv:1501.05040. [Google Scholar]
- Yan, X.G.; Xie, C.; Wang, G.J. The stability of financial market networks. EPL Eur. Lett. 2014, 107, 48002. [Google Scholar] [CrossRef]
- Pereira, E.J.A.L.; Ferreira, P.J.S.; da Silva, M.F.; Miranda, J.G.V.; Pereira, H.B.B. Multiscale network for 20 stock markets using DCCA. Phys. A 2019, 529, 121542. [Google Scholar] [CrossRef]
- Piccardi, C.; Calatroni, L.; Bertoni, F. Clustering financial time series by network community analysis. Int. J. Mod. Phys. C 2011, 22, 35–50. [Google Scholar] [CrossRef]
- Tang, Y.; Xiong, J.J.; Jia, Z.-Y.; Zhang, Y.-C. Complexities in Financial Network Topological Dynamics: Modeling of Emerging and Developed Stock Markets. Complexity 2018, 2018, 31. [Google Scholar] [CrossRef] [Green Version]
- You, T.; Fiedor, P.; Hołda, A. Network Analysis of the Shanghai Stock Exchange Based on Partial Mutual Information. J. Risk Financ. Manag. 2015, 8, 266–284. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Xu, H.; Yu, J.; Wang, L. Linkage Effects Mining in Stock Market Based on Multi-Resolution Time Series Network. Information 2018, 9, 276. [Google Scholar] [CrossRef] [Green Version]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.-U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Ledenyov, D.O.; Ledenyov, V.O. On the accurate characterization of business cycles in nonlinear dynamic financial and economic systems. arXiv 2013, arXiv:1304.4807. [Google Scholar]
- Rak, R.; Drod, S.; Kwapie, J.; Owiȩcimka, P. Detrended cross-correlations between returns, volatility, trading activity, and volume traded for the stock market companies. Phys. Rev. E 2015, 112, 48001. [Google Scholar] [CrossRef] [Green Version]
- Horvatic, D.; Stanley, H.E.; Podobnik, B. Detrended cross-correlation analysis for non-stationary time series with periodic trends. EPL Eur. Lett. 2011, 94, 18007. [Google Scholar] [CrossRef] [Green Version]
- Kristoufek, L. Fractal approach towards power-law coherency to measure cross-correlations between time series. Commun. Nonlinear Sci. 2017, 50, 193–200. [Google Scholar] [CrossRef] [Green Version]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [Green Version]






| No | Nation | Stock Market | No | Nation | Stock Market |
|---|---|---|---|---|---|
| 1 | Argentina | MERVALS | 13 | Korea1 | KOSPI |
| 2 | Australia1 | AORD | 14 | Korea2 | KOSDAQ |
| 3 | Australia2 | S&P ASX200 | 15 | Mexico | IPC |
| 4 | Brazil | IBOVESPA | 16 | Netherland | AEX |
| 5 | Chile | IGPA | 17 | Pakistan | KSE100 |
| 6 | France | CAC40 | 18 | Singapore | STI |
| 7 | Germany | DAX | 19 | Taiwan | TAIMEX |
| 8 | Hong Kong | HANGSENG | 20 | USA1 | DOW |
| 9 | Hungary | BUX | 21 | USA2 | S&P500 |
| 10 | India | BSE SENSEX | 22 | USA3 | NASDAQ |
| 11 | Indonesia | IDX | 23 | USA4 | DOW TRANS |
| 12 | Japan | NIKKEI225 | 24 | UK | FTSE100 |
| Figure No. | Community | Stock Market |
|---|---|---|
| Figure 5a Return Network (1997–2000) | (G1) Europe | France, Germany, Netherland, UK |
| (G2) USA | USA1, USA2, USA3, USA4 | |
| (G3) Oceania | Australia1, Australia2 | |
| (G4) C./S. America | Argentina, Brazil, Mexico | |
| Figure 5b Volatility Network (1997–2000) | (G1) Europe | France, Germany, Netherland |
| (G2) USA | USA1, USA2, USA4 | |
| (G3) Oceania | Australia1, Australia2 | |
| (G4) C./S. America | Argentina, Brazil, Mexico | |
| Figure 5c Return Network (2001–2004) | (G1) Europe | France, Germany, Netherland, UK |
| USA | USA1, USA2, USA3, USA4 | |
| Oceania | Australia1, Australia2 | |
| (G2) Asia | Korea1, Korea2, Taiwan | |
| Figure 5d | (G1) Europe | France, Germany, Netherland, UK |
| Volatility Network | USA | USA1, USA2, USA3, USA4 |
| (2001-2004) | (G2) Oceania | Australia1, Australia2 |
| Figure 5e Return Network (2005–2008) | (G1) Europe | France, Germany, Netherland, UK |
| USA | USA1, USA2, USA3 | |
| Oceania | Australia1, Australia2 | |
| C./S. America | Brazil, Mexico | |
| Asia | Hong Kong, India, Japan | |
| Figure 5f Volatility Network (2005–2008) | (G1) Europe | France, Germany, Hungary, UK |
| USA | USA1, USA2, USA3 | |
| C./S. America | Argentina, Brazil, Mexico | |
| Asia | Hong Kong, Korea1 | |
| Figure 5g Return Network (2009–2012) | (G1) Europe | France, Germany, Netherland, UK |
| USA | USA1, USA2, USA3, USA4 | |
| Oceania | Australia1, Australia2 | |
| C./S. America | Brazil, Mexico | |
| Asia | Korea1 | |
| Figure 5h Volatility Network (2009–2012) | (G1) Europe | France, Germany, Netherland, UK |
| USA | USA1, USA2, USA3, USA4 | |
| C./S. America | Brazil, Mexico | |
| (G2) Asia | Hong Kong, Indonesia, Taiwan | |
| Figure 5i Return Network (2013–2016) | (G1) Europe | France, Germany, Netherland, UK |
| (G2) USA | USA1, USA2, USA3, USA4 | |
| (G3) Oceania | Australia1, Australia2 | |
| (G4) Asia | Hong Kong, Korea1 | |
| Figure 5j Volatility Network (2013–2016) | (G1) Europe | France, Germany, Netherland, UK |
| (G2) USA | USA1, USA2, USA3, USA4 | |
| (G3) Oceania | Australia1, Australia2 | |
| (G4) Asia | Korea1, Taiwan | |
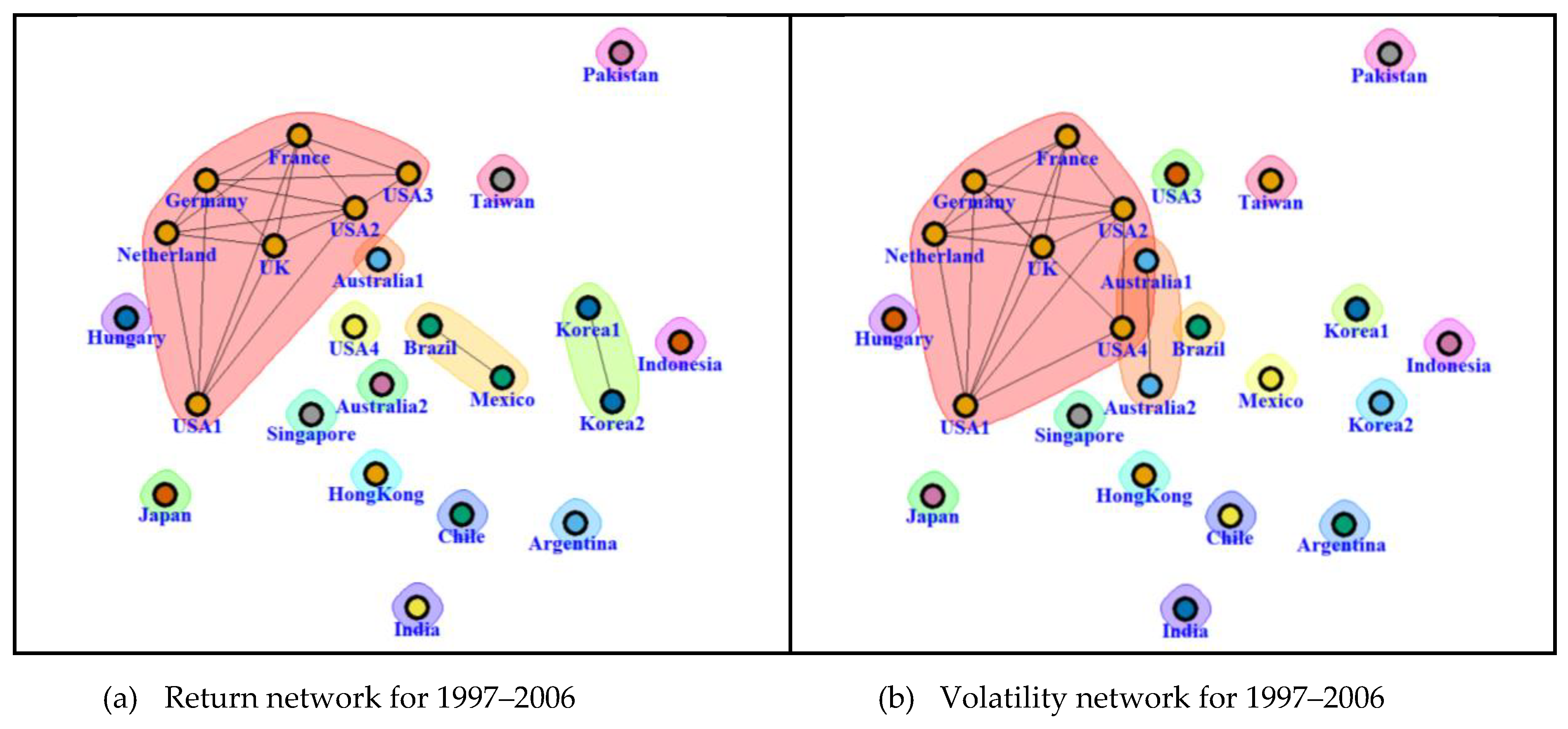
| Figure 6a Return Network (1997–2006) | (G1) Europe | France, Germany, Netherland, UK |
| USA | USA1, USA2, USA3 | |
| (G2) C./S. America | Brazil, Mexico | |
| (G3) Asia | Korea1, Korea2 | |
| Figure 6b | (G1) Europe | France, Germany, Netherland, UK |
| Volatility Network | USA | USA1, USA2, USA4 |
| (1997–2006) | (G2) Oceania | Australia1, Australia2 |
| Figure 6c Return Network (2007–2016) | (G1) Europe | France, Germany, Hungary, Netherland, UK |
| USA | USA1, USA2, USA3, USA4 | |
| Oceania | Australia1, Australia2 | |
| C. America | Mexico | |
| Asia | Hong Kong, Japan, Korea1, Taiwan | |
| Figure 6d Volatility Network (2007–2016) | (G1) Europe | France, Germany, Hungary, Netherland, UK |
| USA | USA1, USA2, USA3, USA4 | |
| Oceania | Australia1, Australia2 | |
| C./S. America | Argentina, Brazil, Chile, Mexico | |
| Asia | Hong Kong, India, Indonesia, Japan, Korea1, Korea2, Taiwan | |
| Figure 7a Return Network (1997–2016) | (G1) Europe | France, Germany, Netherland, UK |
| USA | USA1, USA2, USA3 | |
| Oceania | Australia1, Australia2 | |
| (G2) Asia | Korea1, Korea2 | |
| Figure 7b | (G1) Europe | France, Germany, Netherland, UK |
| Volatility Network | USA | USA1, USA2, USA4 |
| (1997–2016) | Oceania | Australia1, Australia2 |
| Data | Period | Year | |||||||
|---|---|---|---|---|---|---|---|---|---|
| return | 4 years | 1997-2000 | 1.250 | 1.812 | 0.079 | 0.361 | 0.866 | USA2 | 0.055 |
| 2001-2004 | 3.416 | 1.327 | 0.178 | 0.385 | 0.794 | USA3 | 0.036 | ||
| 2005-2008 | 5.916 | 1.888 | 0.411 | 0.558 | 0.728 | Korea1 | 0.130 | ||
| 2009-2012 | 6.750 | 1.726 | 0.473 | 0.620 | 0.787 | Hong Kong | 0.157 | ||
| 2013-2016 | 1.416 | 1.566 | 0.082 | 0.295 | 0.791 | Netherland | 0.024 | ||
| 10 years | 1997-2006 | 2.083 | 1.553 | 0.128 | 0.327 | 0.791 | UK | 0.035 | |
| 2007-2016 | 10.500 | 1.447 | 0.602 | 0.805 | 0.842 | Korea1 | 0.069 | ||
| 20 years | 1997-2016 | 4.833 | 1.737 | 0.341 | 0.508 | 0.785 | Hong Kong | 0.123 | |
| volatility | 4 years | 1997-2000 | 0.833 | 1.230 | 0.041 | 0.222 | 0.761 | France | 0.008 |
| 2001-2004 | 1.583 | 1.379 | 0.086 | 0.300 | 0.808 | USA1 | 0.013 | ||
| 2005-2008 | 11.083 | 1.380 | 0.619 | 0.814 | 0.862 | Netherland | 0.063 | ||
| 2009-2012 | 5.000 | 1.921 | 0.360 | 0.541 | 0.698 | Korea1 | 0.165 | ||
| 2013-2016 | 1.833 | 1.578 | 0.105 | 0.341 | 0.822 | USA1 | 0.024 | ||
| 10 years | 1997-2006 | 1.667 | 1.310 | 0.088 | 0.268 | 0.881 | USA2 | 0.028 | |
| 2007-2016 | 17.083 | 1.112 | 0.789 | 0.880 | 0.921 | Netherland | 0.008 | ||
| 20 years | 1997-2016 | 6.833 | 1.818 | 0.542 | 0.661 | 0.752 | Hong Kong | 0.260 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, K.-H.; Lim, G.; Min, S. Dynamics of the Global Stock Market Networks Generated by DCCA Methodology. Appl. Sci. 2020, 10, 2171. https://doi.org/10.3390/app10062171
Shin K-H, Lim G, Min S. Dynamics of the Global Stock Market Networks Generated by DCCA Methodology. Applied Sciences. 2020; 10(6):2171. https://doi.org/10.3390/app10062171
Chicago/Turabian StyleShin, Ki-Hong, Gyuchang Lim, and Seungsik Min. 2020. "Dynamics of the Global Stock Market Networks Generated by DCCA Methodology" Applied Sciences 10, no. 6: 2171. https://doi.org/10.3390/app10062171
APA StyleShin, K.-H., Lim, G., & Min, S. (2020). Dynamics of the Global Stock Market Networks Generated by DCCA Methodology. Applied Sciences, 10(6), 2171. https://doi.org/10.3390/app10062171






