Crown Wall Modifications as Response to Wave Overtopping under a Future Sea Level Scenario: An Experimental Parametric Study for an Innovative Composite Seawall
Abstract
:1. Introduction
1.1. Motivations and Perspective
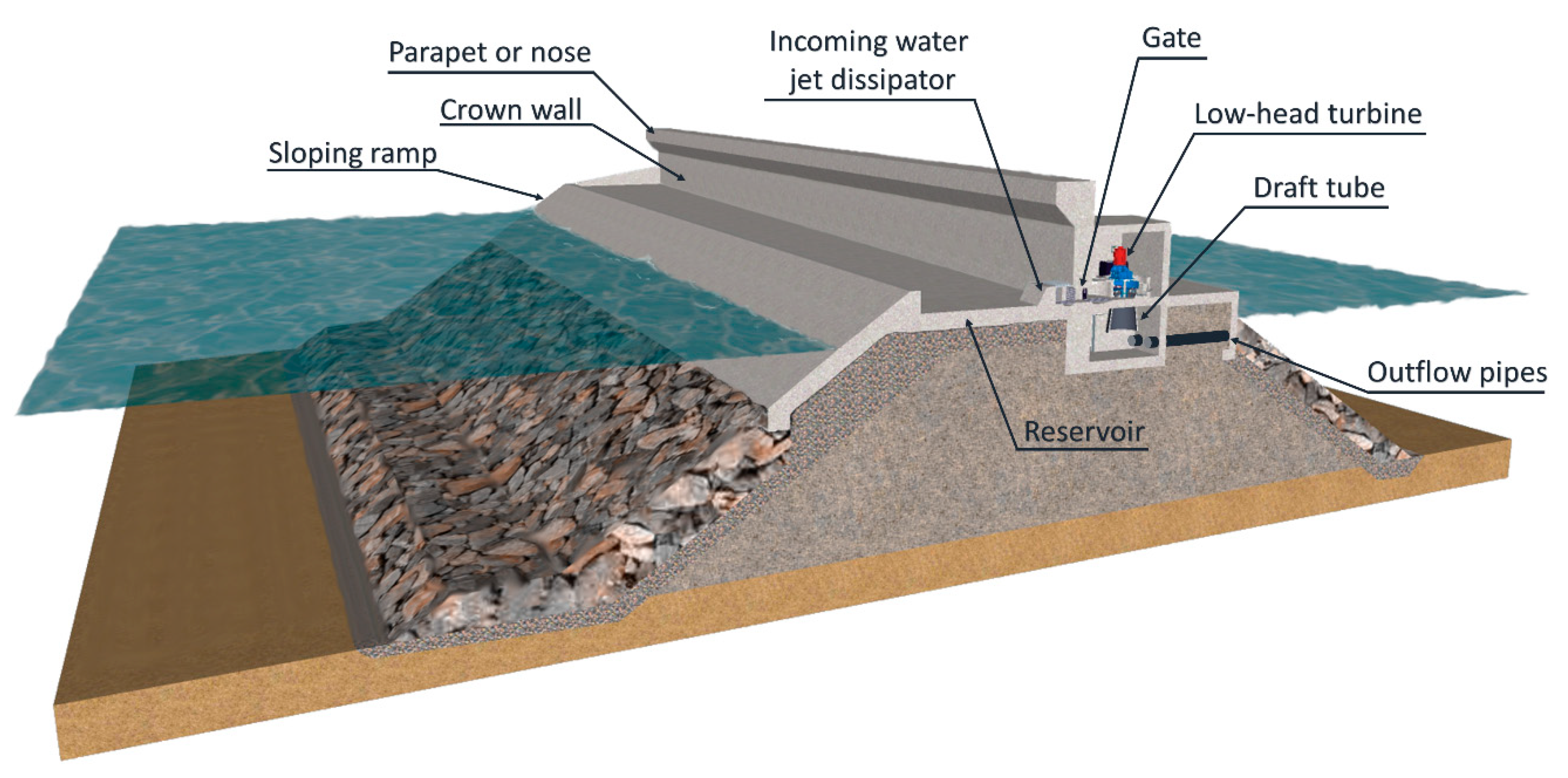
1.2. Technical Background
- An enhancement of the hydraulic safety level as compared to a traditional breakwater;
- The lowering of the OBREC crest height to provide lower visual impact on the city skyline;
- An increase of the potential energy to be converted because the up-rushing waves are redirected into the reservoir;
- An effective and economically feasible solution to counter the effects derived by the SLR.
2. Materials and Methods
2.1. Laboratory Model
2.2. Geometry of the Nose
2.3. Sea-Level-Rise Scenario
2.4. Wave Characteristics and Experimental Program
- Five tests for the small nose configuration, under the actual water level;
- Five tests for the small nose configuration, with water level after SLR;
- Five tests for the large nose configuration, with water level after SLR;
- Five for the extra-large configuration, with water level after SLR.
3. Results
3.1. Nose Effect
3.2. Average Wave Overtopping Discharge
3.3. New Equation to Account for the Increase of the Nose Dimension
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Falcão, A.F.D.O. Wave energy utilization: A review of the technologies. Renew. Sust. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Azzellino, A.; Lanfredi, C.; Contestabile, P.; Ferrante, V.; Vicinanza, D. Strategic environmental assessment to evaluate WEC projects in the perspective of the environmental cost-benefit analysis. In Proceedings of the Twenty-First International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Buccino, M.; Dentale, F.; Salerno, D.; Contestabile, P.; Calabrese, M. The use of CFD in the analysis of wave loadings acting on seawave slot-cone generators. Sustainability 2016, 8, 1255. [Google Scholar] [CrossRef] [Green Version]
- Contestabile, P.; Vicinanza, D. Coastal Defence Integrating Wave-Energy-Based Desalination: A Case Study in Madagascar. J. Mar. Sci. Eng. 2018, 6, 64. [Google Scholar] [CrossRef] [Green Version]
- Di Lauro, E.; Lara, J.L.; Maza, M.; Losada, I.J.; Contestabile, P.; Vicinanza, D. Stability analysis of a non-conventional breakwater for wave energy conversion. Coast. Eng. J. 2019, 145, 36–52. [Google Scholar] [CrossRef]
- Vicinanza, D.; Cappietti, L.; Ferrante, V.; Contestabile, P. Estimation of the wave energy in the Italian offshore. J. Coast. Res. 2011, 64, 613–617. [Google Scholar]
- Contestabile, P.; Di Lauro, E.; Galli, P.; Corselli, C.; Vicinanza, D. Offshore wind and wave energy assessment around Malè and Magoodhoo Island (Maldives). Sustainability 2017, 9, 613. [Google Scholar] [CrossRef] [Green Version]
- Palma, G.; Contestabile, P.; Mizar Formentin, S.; Vicinanza, D.; Zanuttigh, B. Design optimization of a multifunctional wave energy device. In Progress in Renewable Energies Offshore, Proceedings of the 2nd International Conference on Renewable Energies Offshore (RENEW2016), Lisbon, Portugal, 24–26 October 2016; CRC Press: Boca Raton, FL, USA, 2016; p. 235. [Google Scholar]
- Aderinto, T.; Li, H. Review on Power Performance and Efficiency of Wave Energy Converters. Energies 2019, 12, 4329. [Google Scholar] [CrossRef] [Green Version]
- Vicinanza, D.; Margheritini, L.; Contestabile, P.; Kofoed, J.P.; Frigaard, P. Seawave Slot-cone Generator: An innovative caisson breakwaters for energy production. In Coastal Engineering 2008—Proceedings of the 31st International Conference; World Scientific Publishing: Singapore, 2009; pp. 3694–3705. [Google Scholar]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Climate Change: How Do We Know? Available online: https://climate.nasa.gov/evidence/ (accessed on 10 January 2020).
- Demirbilek, Z. Sea level rise and impacts on engineering practice. Ocean Eng. 2013, 71, 1–2. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modelling of Extreme Values; Springer Series in Statistics; Springer: London, UK, 2001; p. 208. [Google Scholar]
- Galiatsatou, P.; Prinos, P.; Sanchez-Arcilla, A. Estimation of extremes: Conventional versus Bayesian techniques. J. Hydraul. Res. 2008, 46, 211–223. [Google Scholar] [CrossRef]
- Chini, N.; Stansby, P.K. Extreme values of coastal wave overtopping accounting for climate change and sea level rise. Coast. Eng. 2012, 65, 27–37. [Google Scholar] [CrossRef]
- Weisse, R.; Bellafiore, D.; Menéndez, M.; Méndez, F.; Nicholls, R.J.; Umgiesser, G.; Willems, P. Changing extreme sea levels along European coasts. Coast. Eng. 2014, 87, 4–14. [Google Scholar] [CrossRef] [Green Version]
- Vicinanza, D.; Di Lauro, E.; Contestabile, P.; Gisonni, C.; Lara, J.L.; Losada, I.J. Review of innovative harbor breakwaters for wave-energy conversion. J. Waterw. Port. Coast. 2019, 145, 1–18. [Google Scholar] [CrossRef]
- Vicinanza, D.; Contestabile, P.; Nørgaard, J.; Lykke Andersen, T. Innovative rubble mound breakwaters for overtopping wave energy conversion. Coast. Eng. 2014, 88, 154–170. [Google Scholar] [CrossRef]
- Patrizi, N.; Pulselli, R.M.; Neri, E.; Niccolucci, V.; Vicinanza, D.; Contestabile, P.; Bastianoni, S. Lifecycle environmental impact assessment of an overtopping wave energy converter embedded in breakwater systems. Front. Energy Res. 2019, 7, 32. [Google Scholar] [CrossRef] [Green Version]
- Contestabile, P.; Iuppa, C.; Di Lauro, E.; Cavallaro, L.; Lykke Andersen, T.; Vicinanza, D. Wave loadings acting on innovative rubble mound breakwater for overtopping wave energy conversion. Coast. Eng. 2017, 122, 60–74. [Google Scholar] [CrossRef]
- Contestabile, P.; Ferrante, V.; Di Lauro, E.; Vicinanza, D. Full-scale prototype of an overtopping breakwater for wave energy conversion. In Proceedings of the 35th Conference on Coastal Engineering, Antalya, Turkey, 17–20 November 2016; p. 35. [Google Scholar]
- Formentin, S.M.; Palma, G.; Contestabile, P.; Vicinanza, D.; Zanuttigh, B. 2DV RANS-VOF numerical modeling of a multi-functional harbour structure. In Proceedings of the 35th Conference on Coastal Engineering, Antalya, Turkey, 17–20 November 2016; p. 35. [Google Scholar]
- Palma, G.; Mizar Formentin, S.; Zanuttigh, B.; Contestabile, P.; Vicinanza, D. Numerical Simulations of the Hydraulic Performance of a Breakwater-Integrated Overtopping Wave Energy Converter. J. Mar. Sci. Eng 2019, 7, 38. [Google Scholar] [CrossRef] [Green Version]
- Di Lauro, E.; Contestabile, P.; Vicinanza, D. Non-conventional overtopping breakwater for energy conversion. In Advances in Renewable Energies Offshore: Proceedings of the 3rd International Conference on Renewable Energies Offshore (RENEW2018), Lisbon, Portugal, 8–10 October 2018; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Contestabile, C.; Crispino, G.; Di Lauro, E.; Ferrante, V.; Gisonni, C.; Vicinanza, D. Overtopping breakwater for wave energy conversion: Review of state of art, recent advancements and what lies ahead. Renew. Energy 2020, 147, 705–718. [Google Scholar] [CrossRef]
- Molines, J.; Bayon, A.; Gómez-Martín, M.E.; Medina, J.R. Influence of parapets on wave overtopping on mound breakwaters with crown walls. Sustainability 2019, 11, 7109. [Google Scholar] [CrossRef] [Green Version]
- Capel, A. Wave run-up and overtopping reduction by block revetments with enhanced roughness. Coast. Eng. 2015, 104, 76–92. [Google Scholar] [CrossRef]
- Kisacik, D.; Tarakcioglu, G.O.; Baykal, C. Stilling wave basins for overtopping reduction at an urban vertical seawall—The Kordon seawall at Izmir. Ocean Eng. 2019, 185, 82–99. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B. Eurotop Manual—Manual on Wave Overtopping of Sea Defences and Related Structures: An Overtopping Manual Largely Based on European Research, but for Worldwide Application, 2nd ed.; Environment Agency: Bristol, UK, 2018. [Google Scholar]
- U.S. Army Corps of Engineers. Coastal Engineering Manual—Part V; U.S. Army Corps of Engineers: Washington, DC, USA, 2008.
- Franco, L. Ancient Mediterranean harbours: A heritage to preserve. Ocean Coast. Manag. 1996, 30, 115–151. [Google Scholar] [CrossRef]
- Burcharth, H.F.; Lykke-Andersen, T. Overtopping of rubble mound breakwaters with front reservoir. In Proceedings of the 30th International Conference on Coastal Engineering, San Diego, CA, USA, 3–8 September 2006; pp. 4605–4615. [Google Scholar]
- Franco, L.; Gentilomo, M.; Noli, A.; Passacantando, G. Constructional aspects of some large rubble mound breakwaters in northern Africa. In Advances in Coastal Structures and Breakwaters, Proceedings of the Conference on Coastal Structures and Breakwaters, London, England, 1995; Thomas Telford, Ltd.: London, UK, 1996; pp. 158–173. [Google Scholar]
- Kortenhaus, A.; Pearson, J.; Bruce, T.; Allsop, N.W.H.; van der Meer, J.W. Influence of parapets and recurves on wave overtopping and wave loading of complex vertical walls. In Proceedings of the Conference on Coastal Structures, Portland, OR, USA, 26–30 August 2003; pp. 369–381. [Google Scholar]
- Pearson, J.; Bruce, T.; Allsop, W.; Kortenhaus, A.; van der Meer, J.W. Effectiveness of recurve wave walls in reducing wave overtopping on seawalls and breakwaters. In Proceedings of the 29th International Conference on Coastal Engineering, Lisbon, Portugal, 19–24 September 2004; Smith, J.M., Ed.; World Scientific Publishing: Singapore, 2005; pp. 4404–4416. [Google Scholar]
- Van Doorslaer, K.; De Rouck, J. Reduction on wave overtopping on a smooth dike by means of a parapet. In Proceedings of the 32nd International Conference on Coastal Engineering, Shanghai, China, 30 June–5 July 2010; Smith, J.M., Lynett, P., Eds.; Coastal Engineering Research Council: Long Beach, CA, USA, 2010. [Google Scholar]
- Van Doorslaer, K.; De Rouck, J. Wave overtopping over sea dikes and impact forces on storm walls. In Proceedings of the 9th International Conference on Coastal and Port Engineering in Developing Countries, Rio de Janeiro, Brazil, 16–21 October 2016. [Google Scholar]
- Martinelli, L.; Ruol, P.; Volpato, M.; Favaretto, C.; Castellino, M.; De Girolamo, P.; Franco, L.; Romano, A.; Sammarco, P. Experimental investigation on non-breaking wave forces and overtopping at the recurved parapets of vertical breakwaters. Coast. Eng. 2018, 141, 52–67. [Google Scholar] [CrossRef]
- Vicinanza, D.; Nørgaard, J.H.; Contestabile, P.; Andersen, T.L. Wave loadings acting on overtopping breakwater for energy conversion. J. Coast. Res. 2013, 65, 1669–1674. [Google Scholar] [CrossRef]
- Iuppa, C.; Contestabile, P.; Cavallaro, L.; Foti, E.; Vicinanza, D. Hydraulic performance of an innovative breakwater for overtopping wave energy conversion. Sustainability 2016, 8, 1226. [Google Scholar] [CrossRef] [Green Version]
- Hay, C.C.; Morrow, E.; Kopp, R.E.; Mitrovica, J.X. Probabilistic reanalysis of twentieth-century sea-level rise. Nature 2015, 517, 481–484. [Google Scholar] [CrossRef] [PubMed]
- Church, J.A.; White, N.J. Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef] [Green Version]
- Nerem, R.S.; Chambers, D.; Choe, C.; Mitchum, G.T. Estimating Mean Sea Level Change from the TOPEX and Jason Altimeter Missions. Mar. Geod. 2010, 33, 435–446. [Google Scholar] [CrossRef]
- Parris, A.; Bromirski, P.; Burkett, V.; Cayan, D.; Culver, M.; Hall, J.; Horton, R.; Knuuti, K.; Moss, R.; Obeysekera, J.; et al. Global Sea Level Rise Scenarios for the US National Climate Assessment; NOAA Technical Report No. OAR CPO-1; National Oceanic And Atmospheric Administration: Silver Spring, MD, USA, 2012.
- Church, J.A.; Clark, P.U. Sea level change. In Climate Change 2013: The Physical Science Basis; Chapter 13; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Sweet, W.V.; Kopp, R.E.; Weaver, C.P.; Obeysekera, J.; Horton, R.M.; Thieler, E.R.; Zervas, C. Global and Regional Sea Level Rise Scenarios for the United States; NOAA Technical Report No. NOS CO-OPS 083; NOAA/NOS Center for Operational Oceanographic Products and Services: Silver Spring, MD, USA, 2017.
- Hinkel, J.; Jaeger, C.; Nicholls, R.J.; Lowe, J.; Renn, O.; Peijun, S. Sea-level rise scenarios and coastal risk management. Nat. Clim. Change 2015, 5, 188–190. [Google Scholar] [CrossRef]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea-level rise by 2100. Science 2013, 342, 1445. [Google Scholar] [CrossRef] [Green Version]
- Hauer, M.E.; Evans, J.M.; Mishra, D.R. Millions projected to be at risk from sea-level rise in the continental United States. Nat. Clim. Change 2016, 6, 691–695. [Google Scholar] [CrossRef]
- Sierra, J.P. Economic impact of overtopping and adaptation measures in Catalan ports due to sea level rise. Water 2019, 11, 1440. [Google Scholar] [CrossRef] [Green Version]
- Christensen, O.B.; Yang, S.; Boberg, F.; Fox Maule, C.; Thejll, P.; Olesen, M.; Drews, M.; Danielsen Sørup, H.J.; Christensen, J.H. Scalability of regional climate change in Europe for high-end scenarios. Clim. Res. 2015, 64, 25–38. [Google Scholar] [CrossRef] [Green Version]
- Jevrejeva, S.; Jackson, L.P.; Riva, R.E.; Grinsted, A.; Moore, J.C. Coastal sea level rise with warming above 2 C. Proc. Natl. Acad. Sci. USA 2016, 113, 13342–13347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Science for Environment Policy. Available online: https://ec.europa.eu/environment/integration/research/newsalert/pdf/rapid_significant_sea_level_rise_expected_two_degree_plus_global_warming_486na1_en.pdf (accessed on 10 January 2020).
- Frigaard, P.; Andersen, T.L. Technical Background Material for the Wave Generation Software Awasys 5; DCE Technical Report No. 64; Aalborg University: Aalborg, Denmark, 2010. [Google Scholar]
- Andersen, T.L.; Clavero, M.; Frigaard, P.; Losada, M.; Puyol, J. A new active absorption system and its performance to linear and non-linear waves. Coast. Eng. 2016, 114, 47–60. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP); Hydraulic Engineering Report No. 12; Deutches Hydrographisches Institut: Hamburg, Germany, 1973; p. 95.
- Victor, L.; Troch, P. Wave overtopping at smooth impermeable steep slopes with low crest freeboards. J. Waterw. Port. Coast. Ocean Eng. 2012, 138, 372–385. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Bruce, T. New physical insights and design formulas on wave overtopping at sloping and vertical structures. J. Waterw. Port. Coast. Ocean Eng. 2013, 140, 04014025. [Google Scholar] [CrossRef] [Green Version]
- Van Doorslaer, K.; De Rouck, J.; Audenaert, S.; Duquet, V. Crest modifications to reduce wave overtopping of non-breaking waves over a smooth dike slope. Coast. Eng. 2015, 101, 69–88. [Google Scholar] [CrossRef]
- Castellino, M.; Sammarco, P.; Romano, A.; Martinelli, L.; Ruol, P.; Franco, L.; De Girolamo, P. Large impulsive forces on recurved parapets under non-breaking waves. A numerical study. Coast. Eng. 2018, 136, 1–15. [Google Scholar] [CrossRef]











| Rc (m) | dw (m) | Rr (m) | ΔBrs (m) | hres (m) | hw (m) | |
|---|---|---|---|---|---|---|
| min | 0.147 | 0.192 | 0.045 | 0.300 | 0.300 | 0.197 |
| max | 0.227 | 0.192 | 0.125 | 0.300 | 0.300 | 0.197 |
| Hm0 (m) | h (m) | h’ (m) | r (m) | Tp (s) | Tm−1,0 (s) | Lm−1,0 (m) | sm−1,0 (-) | |
|---|---|---|---|---|---|---|---|---|
| Min | 0.08 | 0.27 | 0.30 | 1.11 | 1.46 | 1.40 | 3.05 | 0.014 |
| Max | 0.12 | 0.27 | 0.30 | 1.11 | 2.56 | 2.19 | 7.47 | 0.029 |
| Equation (3) [30] | Equation (4) [58] | Equations (3), (5) and (6) [59] | |
|---|---|---|---|
| NSE | 0.46 | −1.81 | 0.36 |
| MAE | 3.35 × 10−4 | 1.98 × 10−3 | 3.13 × 10−4 |
| RMSE | 1.04 × 10−3 | 2.38 × 10−3 | 1.13 × 10−3 |
| NRMSE | 2.61 | 0.97 | 4.51 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contestabile, P.; Crispino, G.; Russo, S.; Gisonni, C.; Cascetta, F.; Vicinanza, D. Crown Wall Modifications as Response to Wave Overtopping under a Future Sea Level Scenario: An Experimental Parametric Study for an Innovative Composite Seawall. Appl. Sci. 2020, 10, 2227. https://doi.org/10.3390/app10072227
Contestabile P, Crispino G, Russo S, Gisonni C, Cascetta F, Vicinanza D. Crown Wall Modifications as Response to Wave Overtopping under a Future Sea Level Scenario: An Experimental Parametric Study for an Innovative Composite Seawall. Applied Sciences. 2020; 10(7):2227. https://doi.org/10.3390/app10072227
Chicago/Turabian StyleContestabile, Pasquale, Gaetano Crispino, Sara Russo, Corrado Gisonni, Furio Cascetta, and Diego Vicinanza. 2020. "Crown Wall Modifications as Response to Wave Overtopping under a Future Sea Level Scenario: An Experimental Parametric Study for an Innovative Composite Seawall" Applied Sciences 10, no. 7: 2227. https://doi.org/10.3390/app10072227








