Design, Experiment, and Improvement of a Quasi-Zero-Stiffness Vibration Isolation System
Abstract
:1. Introduction
2. The QZS Vibration Isolation System
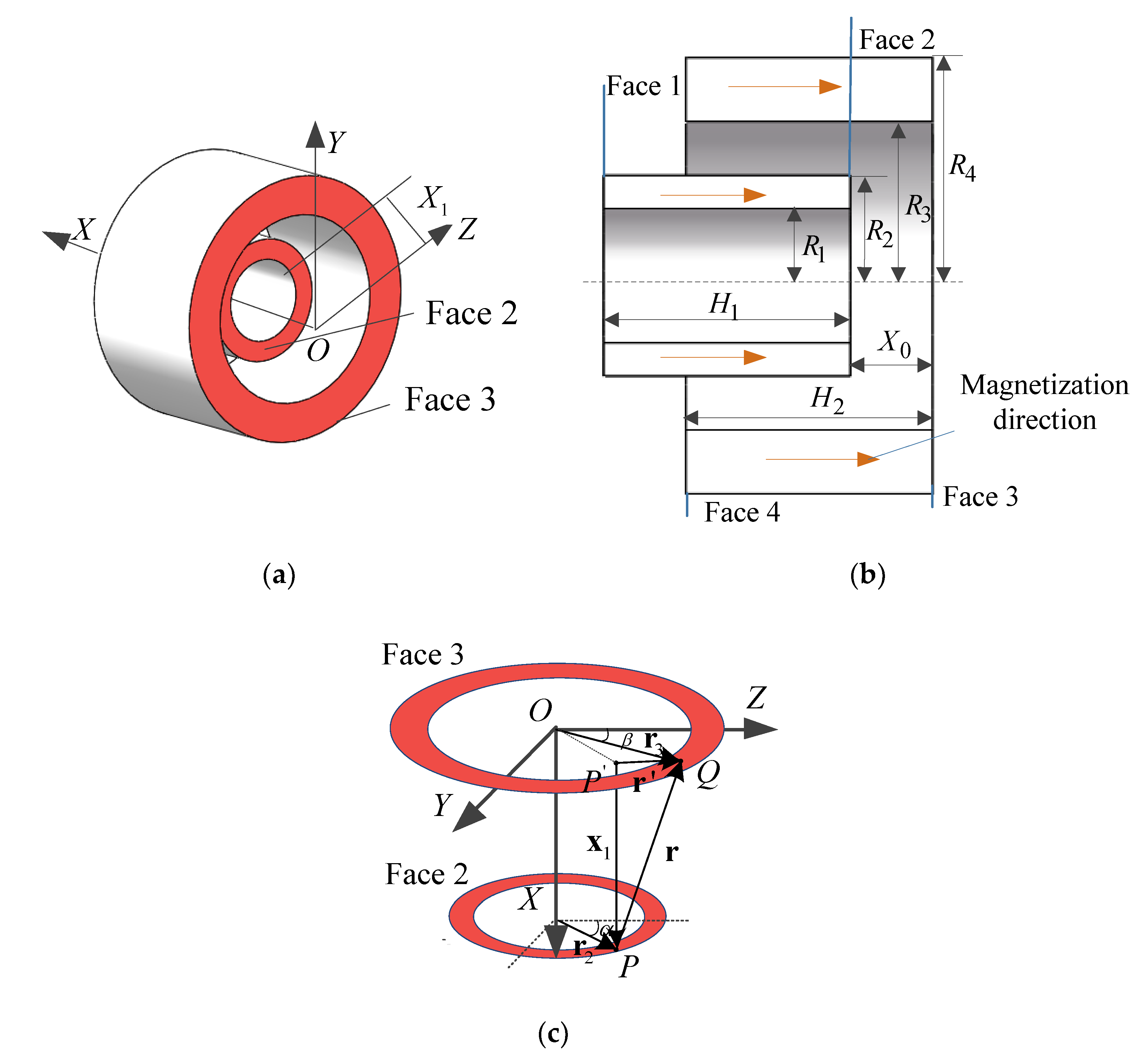
2.1. Force–Displacement Characteristic of the Two Coupled Magnet Springs
2.2. Analysis of the Stiffness of the Two Coupled Magnet Springs
2.3. Stiffness of the QZS Vibration Isolation System
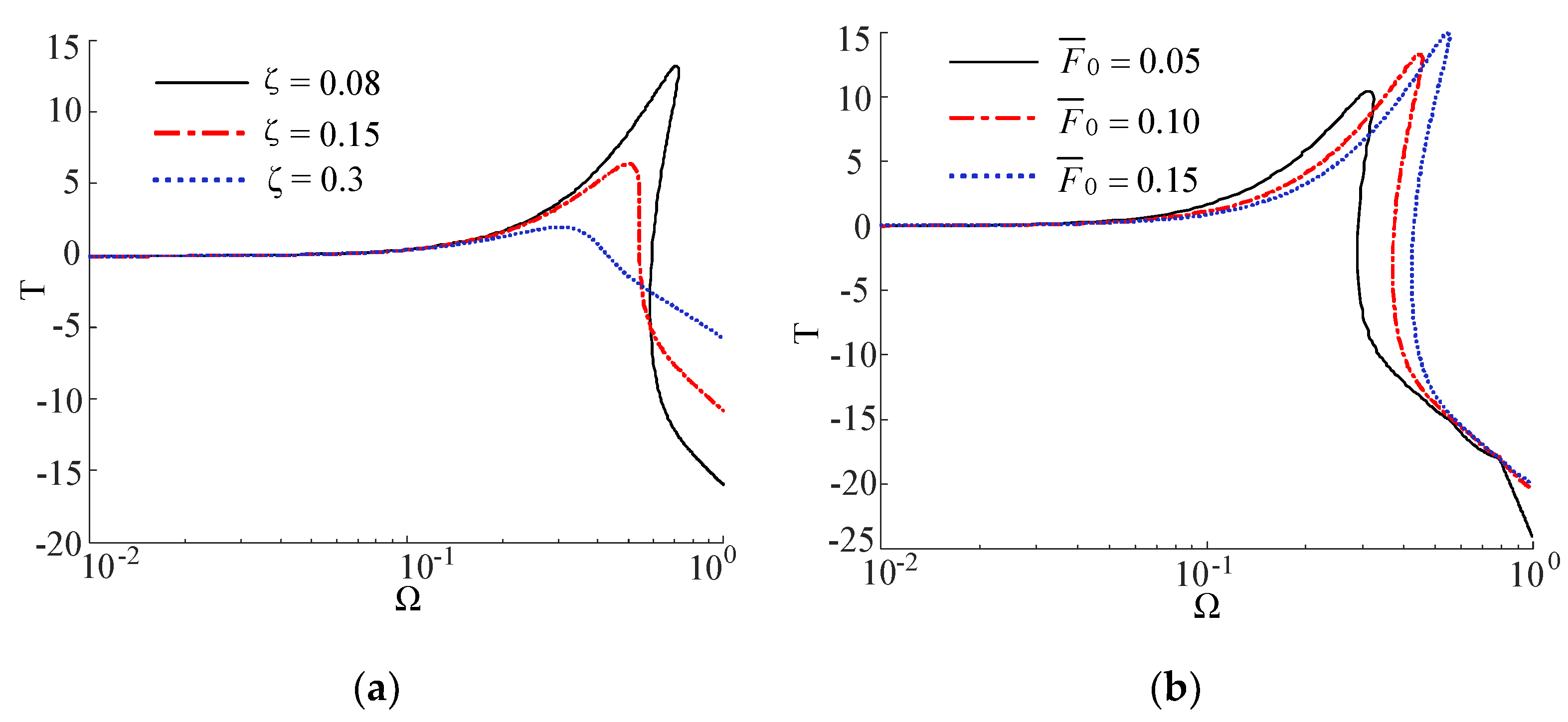
3. Dynamic Analysis of the QZS System
4. Experimental Setup and Results
4.1. Experimental Apparatus
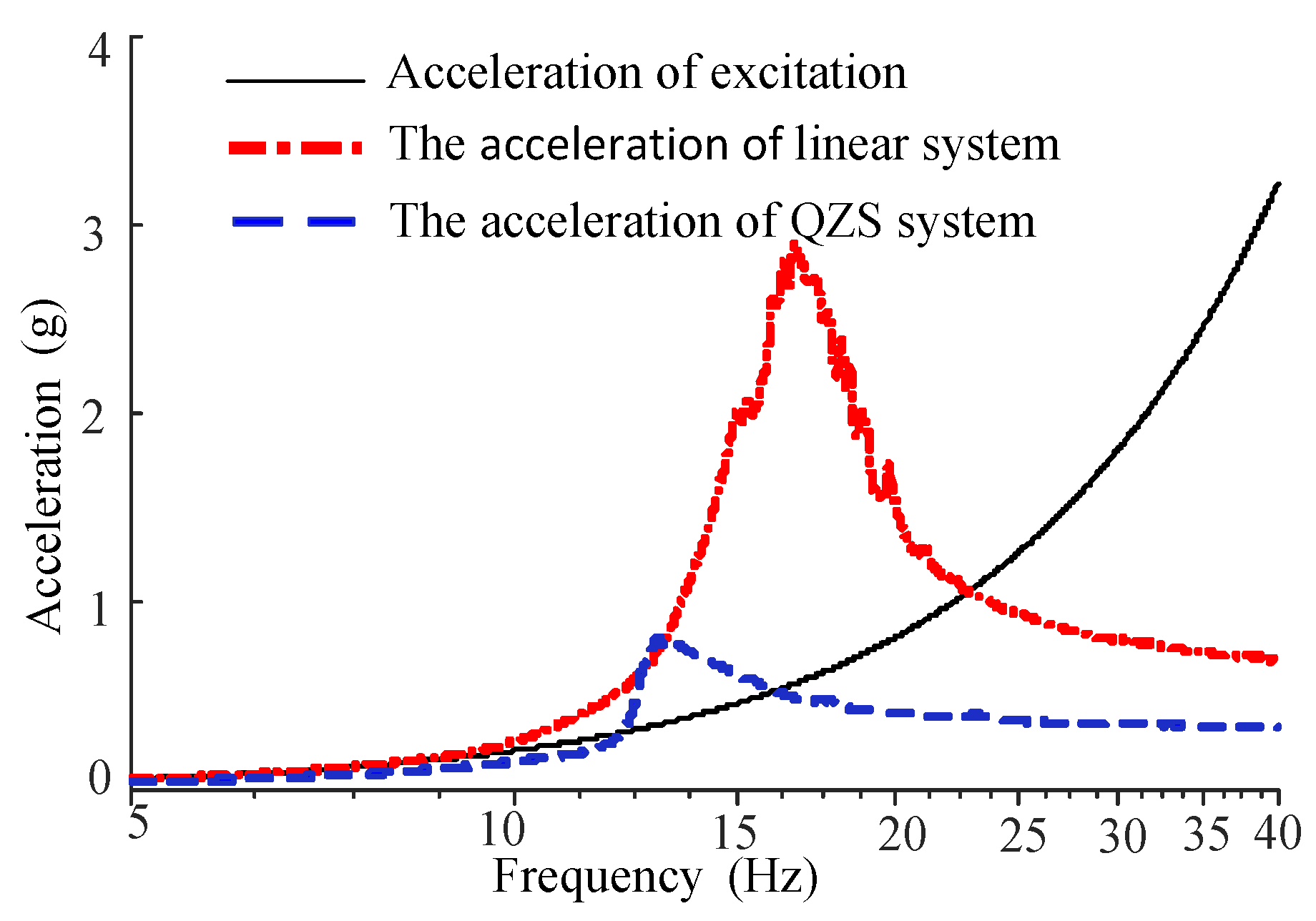
4.2. Experimental Results
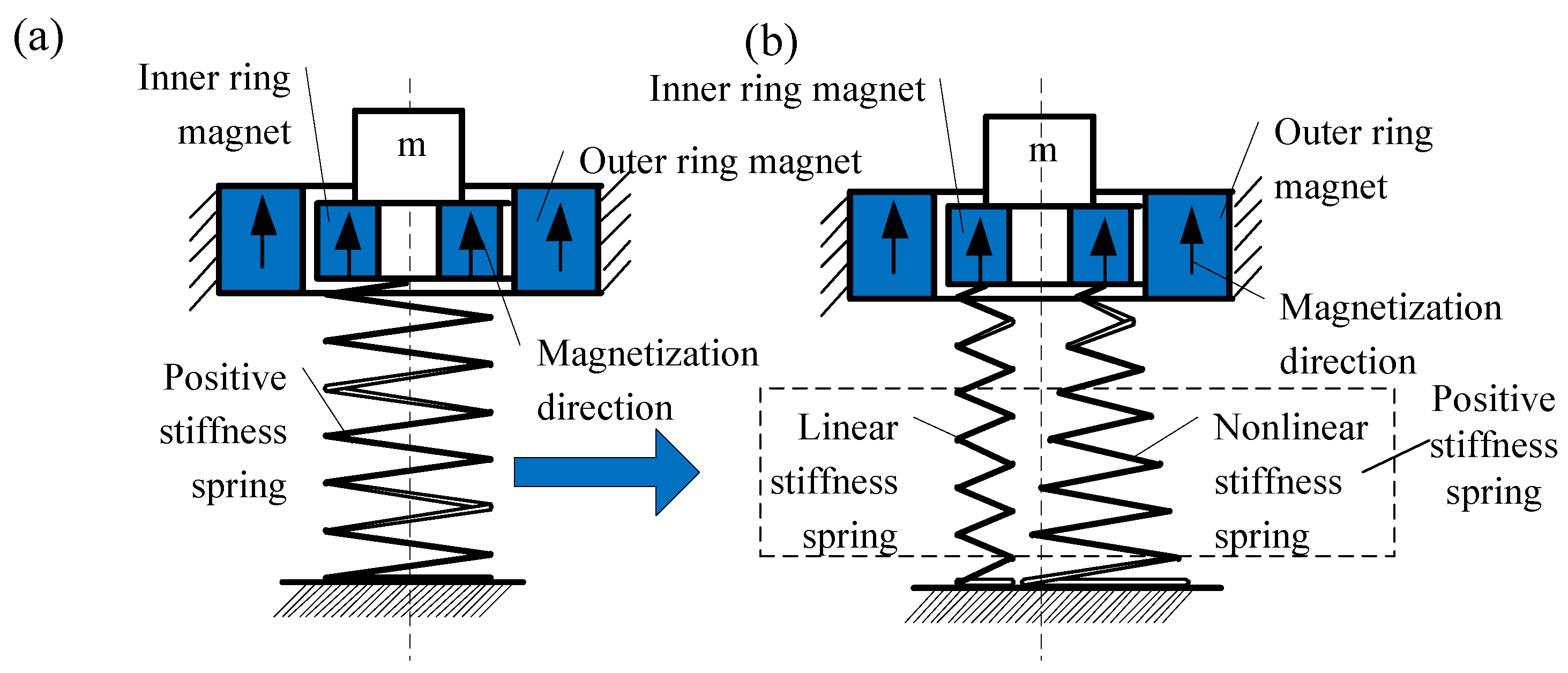
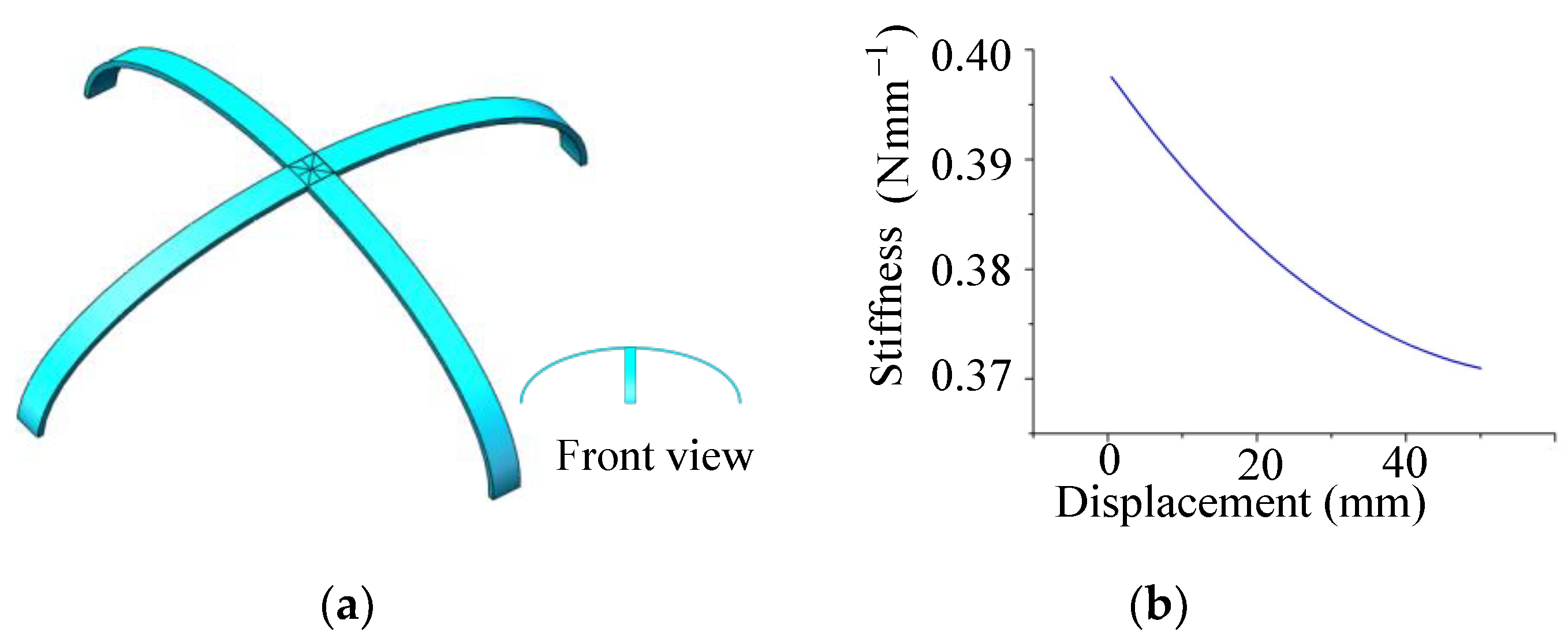
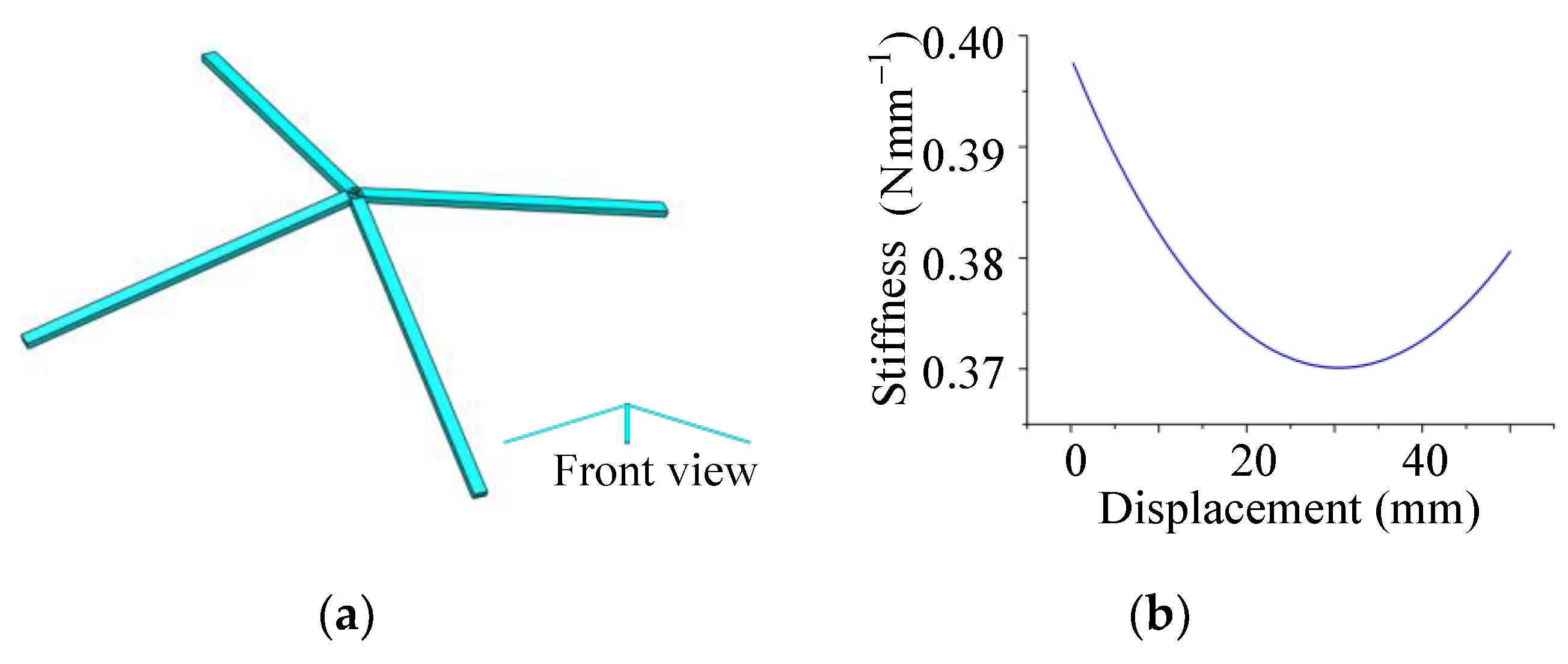
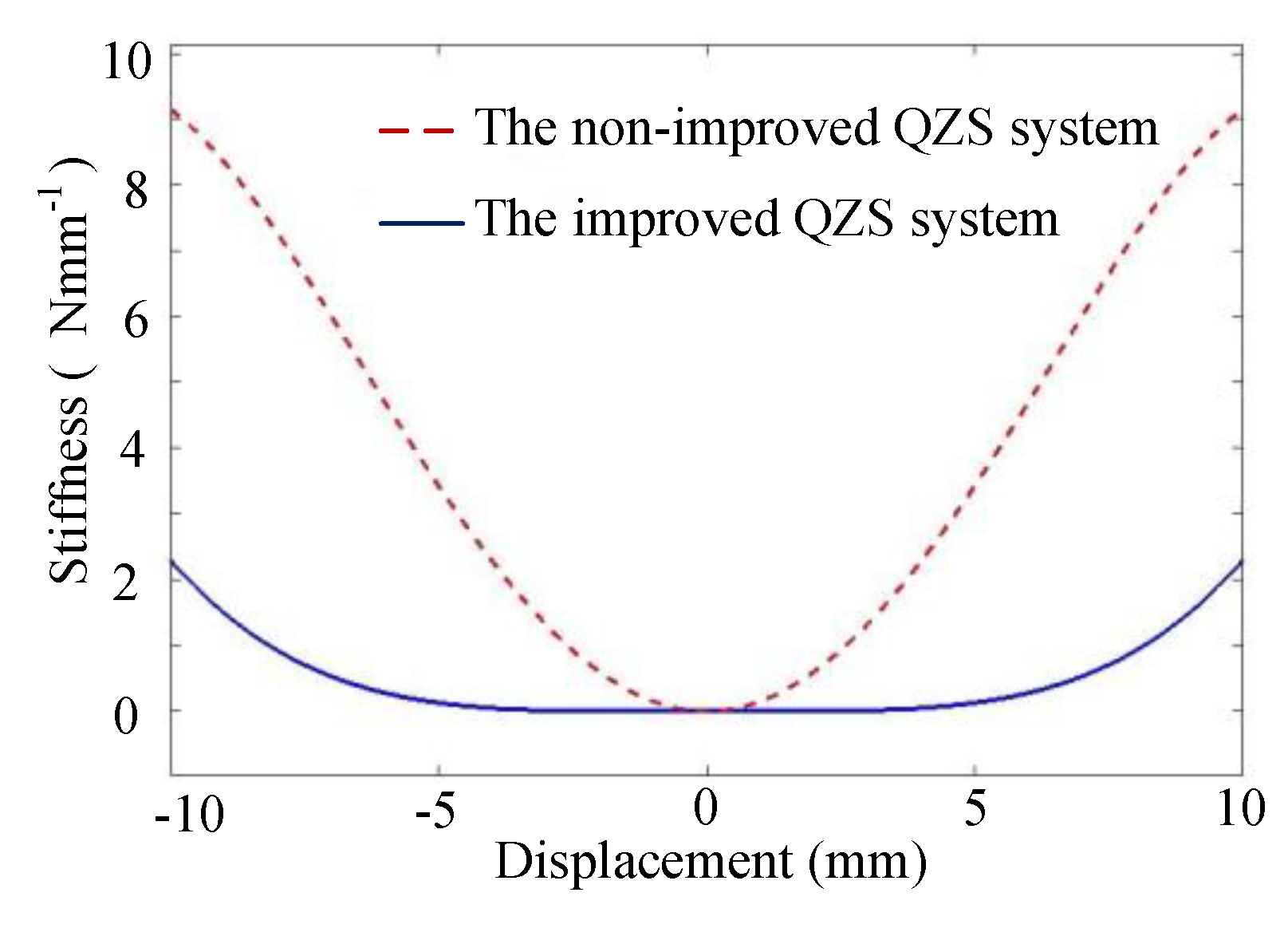
5. The Improvement of the QZS System
5.1. Ways to Improve Under a Wide Range of Loads
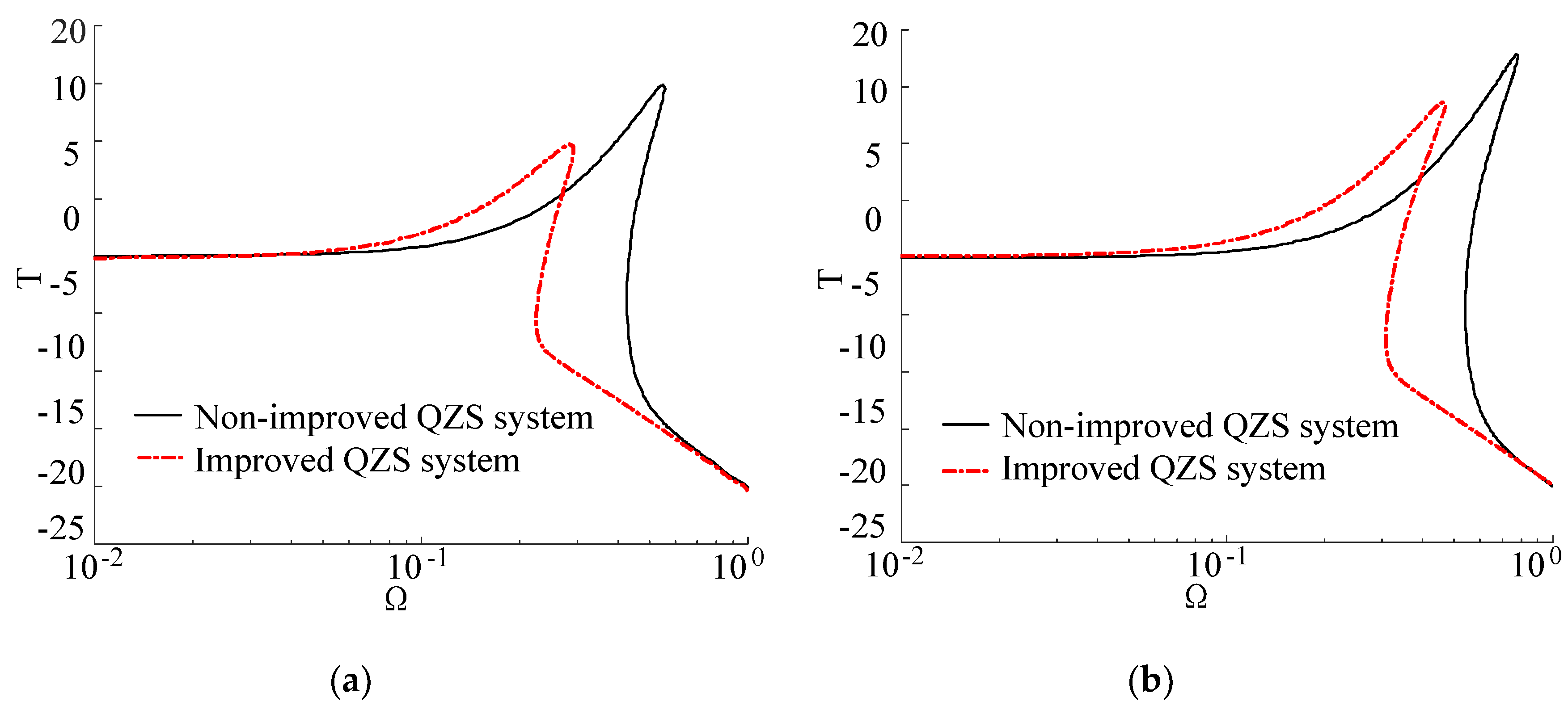
5.2. Dynamic Analysis for the Improved System
6. Discussions and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ibrahim, R.A. Recent advances in nonlinear passive vibration isolators. J. Sound Vibr. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Ledezma, R.D.F.; Tapia, G.P.E.; Ferguson, N.; Bennan, M.; Tang, B. Recent advances in shock vibration isolation: An overview and future possibilities. Appl. Mech. Rev. 2019, 71, 060802. [Google Scholar] [CrossRef]
- Ahn, H.J.; Lim, S.H.; Park, C. An integrated design of quasi-zero stiffness mechanism. J. Mech. Sci. Technol. 2016, 30, 1071–1075. [Google Scholar] [CrossRef]
- Valeev, A.; Tokarev, A.; Zotov, A. Material with quasi-zero stiffness for vibration isolation in civil and industrial structures and buildings. Int. IOP Conf. Ser: Earth Environ. Sci. 2019, 272, 032048. [Google Scholar] [CrossRef]
- Sorokin, V.N.; Kalashnikov, B.A.; Efimov, I.Y. Dynamics of anti-vibration mount with quasi-zero stiffness. Int. J. Mod. Phys. Conf. Ser. 2019, 1210, 012135. [Google Scholar] [CrossRef]
- Sadeghi, S.; Li, S. Harnessing the quasi-zero stiffness from fluidic origami for low frequency vibration isolation. In Proceedings of the ASME Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Snowbird, UT, USA, 18–21 September 2017; pp. 3754–3763. [Google Scholar]
- Yan, L.; Gong, X. Experimental study of vibration isolation characteristics of a geometric anti-spring isolator. Appl. Sci. 2017, 7, 711. [Google Scholar] [CrossRef] [Green Version]
- Valeev, A. Vibration isolating plate with quasi-zero effect. Mater. Today Proc. 2018, 5, 688–692. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vibr. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J.; Waters, T.P. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic. J. Sound Vibr. 2008, 315, 700–711. [Google Scholar] [CrossRef]
- Ishida, S.; Suzuki, K.; Shimosaka, H. Design and experimental analysis of origami-inspired vibration isolator with quasi-zero-stiffness characteristic. J. Vib. Acoust. Trans. ASM 2017, 139, 051004. [Google Scholar] [CrossRef]
- Sun, X.; Jing, X. Multi-direction vibration isolation with quasi-zero stiffness by employing geometrical nonlinearity. Mech. Syst. Signal Proc. 2015, 62–63, 149–163. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Xu, D.; Ouyang, H.; Duan, Y. Force transmissibility of a two-stage vibration isolation system with quasi-zero stiffness. Nonlinear Dyn. 2017, 87, 633–646. [Google Scholar] [CrossRef]
- Vo, N.Y.P.; Le, T.D. Static Analysis of Low Frequency Isolation Model Using Pneumatic Cylinder with Auxiliary Chamber. Int. J. Precis. Eng. Manuf. 2020, 346, 1–17. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat. J. Sound Vibr. 2011, 330, 6311–6335. [Google Scholar] [CrossRef]
- Abbasi, A.; Khadem, S.E.; Bab, S. Vibration control of a continuous rotating shaft employing high-static low-dynamic stiffness isolators. J. Vib. Control 2018, 24, 760–783. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Jr, V.L. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Lu, Z.; Brennan, M.J.; Chen, L.Q. On the transmissibility of nonlinear vibration isolation system. J Sound Vib. 2016, 375, 28–37. [Google Scholar] [CrossRef]
- Fulcher, B.A.; Shahan, D.W.; Haberman, M.R.; Seepersad, C.C.; Wilson, P.S. Analytical and experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems. J. Vib. Acoust. Trans. ASM 2014, 136, 031009. [Google Scholar] [CrossRef]
- Ishida, S.; Uchida, H.; Shimosaka, H.; Hagiwara, I. Design and numerical analysis of vibration isolators with quasi-zero-stiffness characteristics using bistable foldable structures. J. Vib. Acoust. Trans. ASM 2017, 139, 3. [Google Scholar] [CrossRef]
- Lan, C.C.; Yang, S.A.; Wu, Y.S. Design and experiment of a compact quasi-zero-stiffness isolator capable of a wide range of loads. J. Sound Vibr. 2014, 333, 4843–4858. [Google Scholar] [CrossRef]
- Sun, X.; Jing, X.; Cheng, L.; Xu, J. A 3-D quasi-zero-stiffness-based sensor system for absolute motion measurement and application in active vibration control. IEEE ASME Trans. Mechatron. 2015, 20, 254–262. [Google Scholar]
- Kim, J.; Jeon, Y.; Um, S.; Park, U.; Kim, K.S.; Kim, S. A novel passive quasi-zero stiffness isolator for ultra-precision measurement systems. Int. J. Precis. Eng. Manuf. 2019, 20, 1573–1580. [Google Scholar] [CrossRef]
- Naeeni, I.P.; Ghayour, M.; Keshavarzi, A.; Moslemi, A. Theoretical analysis of vibration pickups with quasi-zero-stiffness characteristic. Acta Mech. 2019, 230, 3205–3220. [Google Scholar] [CrossRef]
- Xu, J.; Sun, X. A multi-directional vibration isolator based on quasi-zero-stiffness structure and time-delayed active control. Int. J. Mech. Sci. 2015, 100, 126–135. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Shin, K. On the design of a high-static–low-dynamic stiffness isolator using linear mechanical springs and magnets. J. Sound Vibr. 2008, 315, 712–720. [Google Scholar] [CrossRef]
- Wu, W.; Chen, X.; Shan, Y. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness. J. Sound Vibr. 2014, 333, 2958–2970. [Google Scholar] [CrossRef]
- Sun, X.; Wang, F.; Xu, J. Analysis, design and experiment of continuous isolation structure with Local Quasi-Zero-Stiffness property by magnetic interaction. Int. J. Non-Linear Mech. 2019, 116, 289–301. [Google Scholar] [CrossRef]
- Robertson, W.S.; Kidner, M.R.F.; Cazzolato, B.S.; Zander, A.C. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation. J. Sound Vibr. 2009, 326, 88–103. [Google Scholar] [CrossRef]
- Xu, D.; Yu, Q.; Zhou, J.; Bishop, S.R. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vibr. 2013, 332, 3377–3389. [Google Scholar] [CrossRef]
- Zhu, T.; Cazzolato, B.; Robertson, W.S.P.; Zander, A. Vibration isolation using six degree-of-freedom quasi-zero stiffness magnetic levitation. J. Sound Vibr. 2015, 358, 48–73. [Google Scholar] [CrossRef]
- Mofidian, S.M.; Bardaweel, H. Displacement transmissibility evaluation of vibration isolation system employing nonlinear-damping and nonlinear-stiffness elements. J. Vib. Control 2018, 24, 4247–4259. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Luo, Y.; Yan, B.; Ma, C. Design and experiment of a high-static–low-dynamic stiffness isolator using a negative stiffness magnetic spring. J. Sound Vibr. 2016, 360, 31–52. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Q.; Xu, D.; Zhang, M. Modeling of axial magnetic force and stiffness of ring-shaped permanent-magnet passive vibration isolator and its vibration isolating experiment. IEEE Trans. Magn. 2012, 48, 2228–2238. [Google Scholar] [CrossRef]
- Inamoto, K.; Ishida, S. Improved feasible load range and its effect on the frequency response of origami-inspired vibration isolators with quasi-zero-stiffness characteristics. J. Vib. Acoust. Trans. ASM 2019, 141, 021004. [Google Scholar] [CrossRef]
- Dao, T.P.; Huang, S.C. A compact quasi-zero stiffness vibration isolator using flexure-based spring mechanisms capable of tunable stiffness. In Proceedings of the 18th International Conference on Applied Mechanics, London, UK, 25–26 August 2016; pp. 1572–1581. [Google Scholar]
- Kim, K.R.; You, Y.H.; Ahn, H.J. Optimal design of a QZS isolator using flexures for a wide range of payload. Int. J. Precis. Eng. Manuf. 2013, 14, 911–917. [Google Scholar] [CrossRef]
- Gatti, G. Statics and dynamics of a nonlinear oscillator with quasi-zero stiffness behaviour for large deflections. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105143. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C.; Brown, T. Design of a quasi-zero stiffness isolation system for supporting different loads. J. Sound Vibr. 2020, 115198. [Google Scholar] [CrossRef]
- Ravaud, R.; Lemarquand, G.; Lemarquand, V. Force and stiffness of passive magnetic bearings using permanent magnets, Part 1: Axial magnetization. IEEE Trans. Magn. 2009, 45, 2996–3002. [Google Scholar] [CrossRef] [Green Version]












| Parameters | Value |
|---|---|
| The inner diameter of the inner magnetic ring D1 | 10 mm |
| The outer diameter of the inner magnetic ring D2 | 30 mm |
| The inner diameter of the outer magnetic ring D3 | 60 mm |
| The outer diameter of the outer magnetic ring D4 | 80 mm |
| Remanence | 1.24 T |
| The stiffness of the linear spring | 7500 N/m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Xin, W.; Ning, Y.; Li, B.; Hu, Y. Design, Experiment, and Improvement of a Quasi-Zero-Stiffness Vibration Isolation System. Appl. Sci. 2020, 10, 2273. https://doi.org/10.3390/app10072273
Wang S, Xin W, Ning Y, Li B, Hu Y. Design, Experiment, and Improvement of a Quasi-Zero-Stiffness Vibration Isolation System. Applied Sciences. 2020; 10(7):2273. https://doi.org/10.3390/app10072273
Chicago/Turabian StyleWang, Shuai, Wenpen Xin, Yinghao Ning, Bing Li, and Ying Hu. 2020. "Design, Experiment, and Improvement of a Quasi-Zero-Stiffness Vibration Isolation System" Applied Sciences 10, no. 7: 2273. https://doi.org/10.3390/app10072273




