Raman 2D Peak Line Shape in Epigraphene on SiC
Abstract
:1. Introduction
2. Materials and Methods
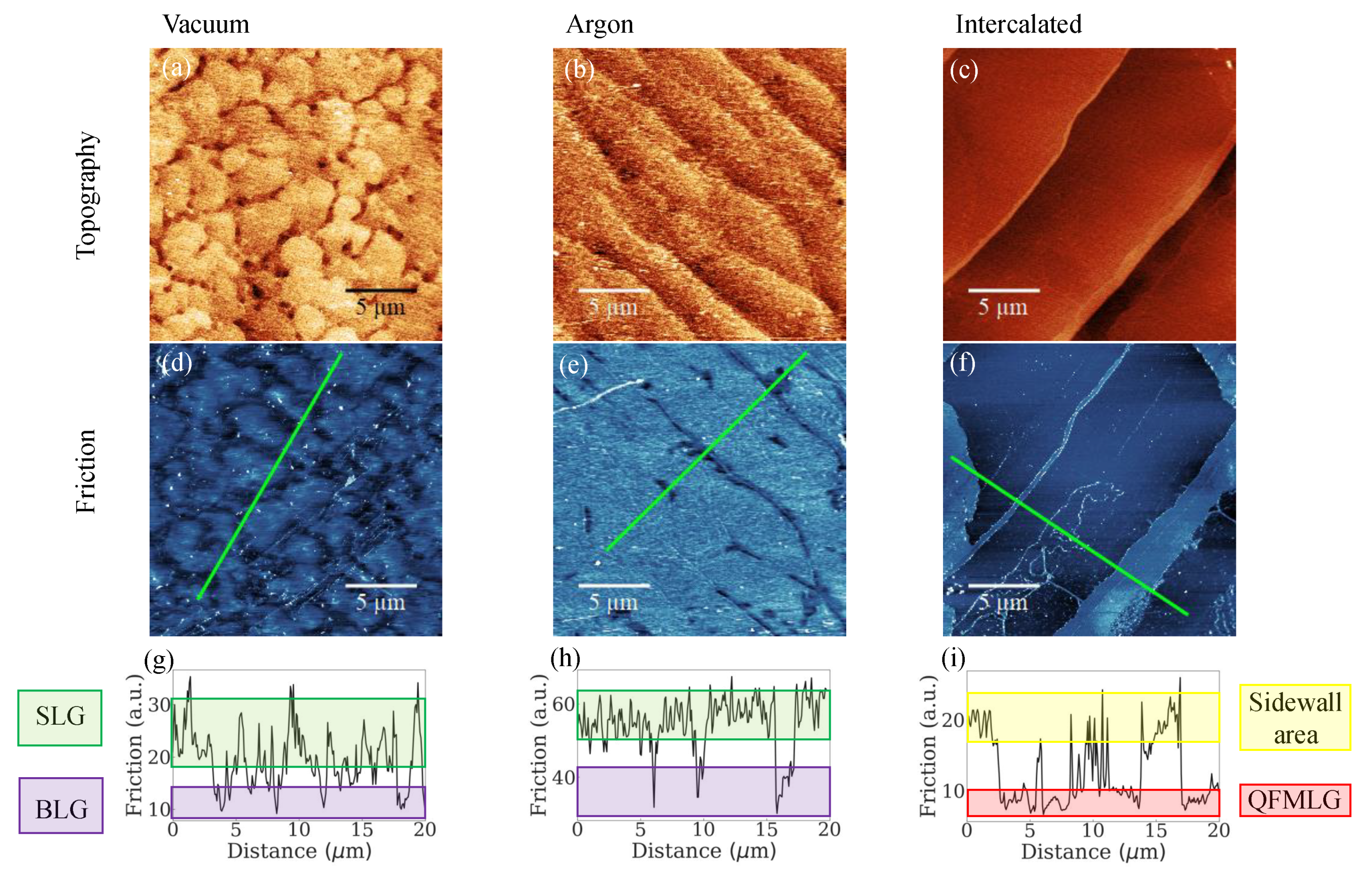
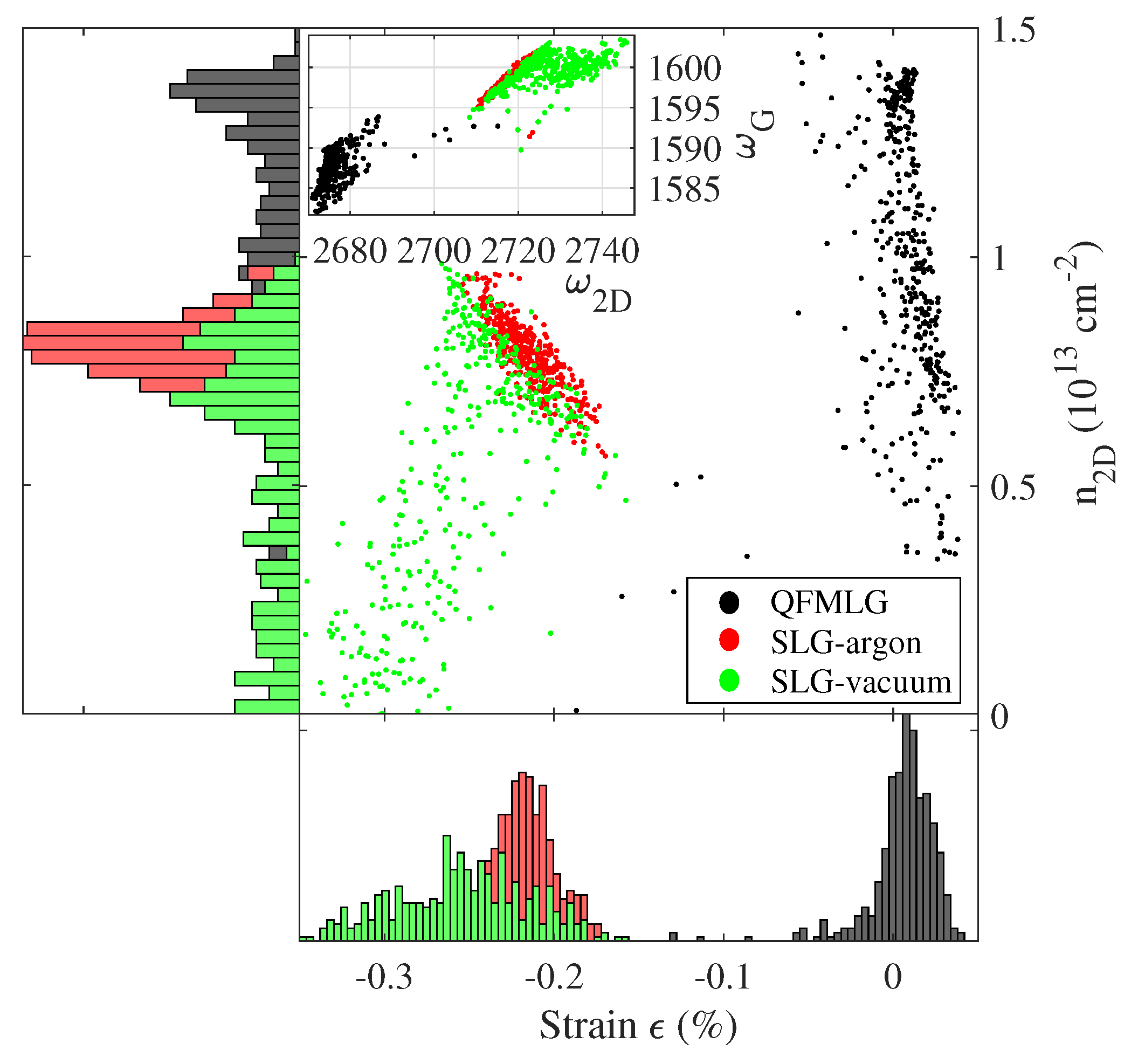
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SLG | single layer graphene |
| QFMLG | Quasi free-standing monolayer graphene |
| SLG-Ar | Single layer graphene grown in argon |
| SLG-vac | Single layer graphene grown in vacuum |
| AFM | Atomic Force Microscopy |
| LFM | Lateral Force Microscopy |
| DOF | Degrees of freedom |
| RSS | Residual Sum of Squares |
| FWHM | Full Width at Half Maximum |
| CDF | Cumulative distribution function |
References
- Tang, B.; Guoxin, H.; Gao, H. Raman Spectroscopic Characterization of Graphene. Appl. Spectrosc. Rev. 2010, 45, 369–407. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Basko, D.M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8, 235–246. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar] [CrossRef]
- Park, J.S.; Reina, A.; Saito, R.; Kong, J.; Dresselhaus, G.; Dresselhaus, M.S. G ‘ band Raman spectra of single, double and triple layer graphene. Carbon 2009, 47, 1303–1310. [Google Scholar] [CrossRef]
- Schmidt, D.A.; Ohta, T.; Beechem, T.E. Strain and charge carrier coupling in epitaxial graphene. Phys. Rev. B 2011, 84, 235422. [Google Scholar] [CrossRef] [Green Version]
- Nicolle, J.; Machon, D.; Poncharal, P.; Pierre-Louis, O.; San-Miguel, A. Pressure-Mediated Doping in Graphene. Nano Lett. 2011, 11, 3564–3568. [Google Scholar] [CrossRef]
- Das, A.; Pisana, S.; Chakraborty, B.; Piscanec, S.; Saha, S.K.; Waghmare, U.V.; Novoselov, K.S.; Krishnamurthy, H.R.; Geim, A.K.; Ferrari, A.C.; et al. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 2008, 3, 210–215. [Google Scholar] [CrossRef] [Green Version]
- Childres, I.; Jauregui, L.A.; Chen, Y.P. Raman spectra and electron-phonon coupling in disordered graphene with gate-tunable doping. J. Appl. Phys. 2014, 116, 233101. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Zhang, Y.; Kim, P.; Pinczuk, A. Electric field effect tuning of electron-phonon coupling in graphene. Phys. Rev. Lett. 2007, 98, 166802. [Google Scholar] [CrossRef] [Green Version]
- Dresselhaus, M.S.; Jorio, A.; Souza Filho, A.G.; Saito, R. Defect characterization in graphene and carbon nanotubes using Raman spectroscopy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 5355–5377. [Google Scholar] [CrossRef]
- Liu, J.; Li, Q.; Zou, Y.; Qian, Q.; Jin, Y.; Li, G.; Jiang, K.; Fan, S. The Dependence of Graphene Raman D-band on Carrier Density. Nano Lett. 2013, 13, 6170–6175. [Google Scholar] [CrossRef] [PubMed]
- Maultzsch, J.; Reich, S.; Thomsen, C. Double-resonant Raman scattering in graphite: Interference effects, selection rules, and phonon dispersion. Phys. Rev. B 2004, 70, 155403. [Google Scholar] [CrossRef] [Green Version]
- Cancado, L.; Takai, K.; Enoki, T.; Endo, M.; Kim, Y.; Mizusaki, H.; Jorio, A.; Coelho, L.; Magalhaes-Paniago, R.; Pimenta, M. General equation for the determination of the crystallite size L-a of nanographite by Raman spectroscopy. Appl. Phys. Lett. 2006, 88, 163106. [Google Scholar] [CrossRef]
- Cancado, L.G.; Jorio, A.; Martins Ferreira, E.H.; Stavale, F.; Achete, C.A.; Capaz, R.B.; Moutinho, M.V.O.; Lombardo, A.; Kulmala, T.S.; Ferrari, A.C. Quantifying Defects in Graphene via Raman Spectroscopy at Different Excitation Energies. Nano Lett. 2011, 11, 3190–3196. [Google Scholar] [CrossRef] [Green Version]
- Niyogi, S.; Bekyarova, E.; Itkis, M.E.; Zhang, H.; Shepperd, K.; Hicks, J.; Sprinkle, M.; Berger, C.; Lau, C.N.; de Heer, W.A.; et al. Spectroscopy of Covalently Functionalized Graphene. Nano Lett. 2010, 10, 4061–4066. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Coh, S.; Tan, L.Z.; Regan, W.; Yuk, J.M.; Chatterjee, E.; Crommie, M.F.; Cohen, M.L.; Louie, S.G.; Zettl, A. Raman Spectroscopy Study of Rotated Double-Layer Graphene: Misorientation-Angle Dependence of Electronic Structure. Phys. Rev. Lett. 2012, 108, 246103. [Google Scholar] [CrossRef] [Green Version]
- Kunc, J.; Rejhon, M.; Hlidek, P. Hydrogen intercalation of epitaxial graphene and buffer layer probed by mid-infrared absorption and Raman spectroscopy. AIP Adv. 2018, 8, 045015. [Google Scholar] [CrossRef] [Green Version]
- Rejhon, M.; Kunc, J. ZO phonon of a buffer layer and Raman mapping of hydrogenated buffer on SiC(0001). J. Raman Spectrosc. 2019, 50, 465–473. [Google Scholar] [CrossRef]
- Basko, D.M. Calculation of the Raman G peak intensity in monolayer graphene: Role of Ward identities. New J. Phys. 2009, 11, 095011. [Google Scholar] [CrossRef]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron-phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 2006, 97, 187401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robinson, J.A.; Wetherington, M.; Tedesco, J.L.; Campbell, P.M.; Weng, X.; Stitt, J.; Fanton, M.A.; Frantz, E.; Snyder, D.; VanMil, B.L.; et al. Correlating Raman Spectral Signatures with Carrier Mobility in Epitaxial Graphene: A Guide to Achieving High Mobility on the Wafer Scale. Nano Lett. 2009, 9, 2873–2876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palmer, J.; Kunc, J.; Hu, Y.; Hankinson, J.; Guo, Z.; Berger, C.; de Heer, W.A. Controlled epitaxial graphene growth within removable amorphous carbon corrals. Appl. Phys. Lett. 2014, 105, 023106. [Google Scholar] [CrossRef] [Green Version]
- Frank, O.; Mohr, M.; Maultzsch, J.; Thomsen, C.; Riaz, I.; Jalil, R.; Novoselov, K.S.; Tsoukleri, G.; Parthenios, J.; Papagelis, K.; et al. Raman 2D-Band Splitting in Graphene: Theory and Experiment. ACS Nano 2011, 5, 2231–2239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, M.; Yan, H.; Heinz, T.F.; Hone, J. Probing Strain-Induced Electronic Structure Change in Graphene by Raman Spectroscopy. Nano Lett. 2010, 10, 4074–4079. [Google Scholar] [CrossRef]
- Mohiuddin, T.M.G.; Lombardo, A.; Nair, R.R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.M.; Galiotis, C.; Marzari, N.; et al. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Gruneisen parameters, and sample orientation. Phys. Rev. B 2009, 79, 205433. [Google Scholar] [CrossRef]
- Yoon, D.; Son, Y.W.; Cheong, H. Strain-Dependent Splitting of the Double-Resonance Raman Scattering Band in Graphene. Phys. Rev. Lett. 2011, 106, 155502. [Google Scholar] [CrossRef] [Green Version]
- Robinson, J.A.; Puls, C.P.; Staley, N.E.; Stitt, J.P.; Fanton, M.A.; Emtsev, K.V.; Seyller, T.; Liu, Y. Raman Topography and Strain Uniformity of Large-Area Epitaxial Graphene. Nano Lett. 2009, 9, 964–968. [Google Scholar] [CrossRef] [Green Version]
- Neumann, C.; Reichardt, S.; Venezuela, P.; Droegeler, M.; Banszerus, L.; Schmitz, M.; Watanabe, K.; Taniguchi, T.; Mauri, F.; Beschoten, B.; et al. Raman spectroscopy as probe of nanometre-scale strain variations in graphene. Nat. Commun. 2015, 6, 8429. [Google Scholar] [CrossRef] [Green Version]
- Grodecki, K.; Bozek, R.; Strupinski, W.; Wysmolek, A.; Stepniewski, R.; Baranowski, J.M. Micro-Raman spectroscopy of graphene grown on stepped 4H-SiC (0001) surface. Appl. Phys. Lett. 2012, 100, 261604. [Google Scholar] [CrossRef]
- Hass, J.; de Heer, W.A.; Conrad, E.H. The growth and morphology of epitaxial multilayer graphene. J. Phys. Condensed Matter 2008, 20, 323202. [Google Scholar] [CrossRef]
- De Heer, W.A.; Berger, C.; Ruan, M.; Sprinkle, M.; Li, X.; Hu, Y.; Zhang, B.; Hankinson, J.; Conrad, E. Large area and structured epitaxial graphene produced by confinement controlled sublimation of silicon carbide. Proc. Natl. Acad. Sci. USA 2011, 108, 16900–16905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Emtsev, K.V.; Bostwick, A.; Horn, K.; Jobst, J.; Kellogg, G.L.; Ley, L.; McChesney, J.L.; Ohta, T.; Reshanov, S.A.; Roehrl, J.; et al. Towards wafer-size graphene layers by atmospheric pressure graphitization of silicon carbide. Nat. Mater. 2009, 8, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Yazdi, G.R.; Iakimov, T.; Yakimova, R. Epitaxial Graphene on SiC: A Review of Growth and Characterization. Crystals 2016, 6, 53. [Google Scholar] [CrossRef] [Green Version]
- Riedl, C.; Coletti, C.; Iwasaki, T.; Zakharov, A.A.; Starke, U. Quasi-Free-Standing Epitaxial Graphene on SiC Obtained by Hydrogen Intercalation. Phys. Rev. Lett. 2009, 103, 246804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hassan, J.; Winters, M.; Ivanov, I.G.; Habibpour, O.; Zirath, H.; Rorsman, N.; Janzen, E. Quasi-free-standing monolayer and bilayer graphene growth on homoepitaxial on-axis 4H-SiC(0001) layers. Carbon 2015, 82, 12–23. [Google Scholar] [CrossRef] [Green Version]
- Emtsev, K.V.; Speck, F.; Seyller, T.; Ley, L.; Riley, J.D. Interaction, growth, and ordering of epitaxial graphene on SiC{0001} surfaces: A comparative photoelectron spectroscopy study. Phys. Rev. B 2008, 77, 155303. [Google Scholar] [CrossRef] [Green Version]
- Speck, F.; Jobst, J.; Fromm, F.; Ostler, M.; Waldmann, D.; Hundhausen, M.; Weber, H.B.; Seyller, T. The quasi-free-standing nature of graphene on H-saturated SiC(0001). Appl. Phys. Lett. 2011, 99, 122106. [Google Scholar] [CrossRef] [Green Version]
- Kunc, J.; Rejhon, M.; Belas, E.; Dedic, V.; Moravec, P.; Franc, J. Effect of Residual Gas Composition on Epitaxial Growth of Graphene on SiC. Phys. Rev. Appl. 2017, 8, 044011. [Google Scholar] [CrossRef] [Green Version]
- Ida, T.; Ando, M.; Toraya, H. Extended pseudo-Voigt function for approximating the Voigt profile. J. Appl. Crystallogr. 2000, 33, 1311–1316. [Google Scholar] [CrossRef]
- Thompson, P.; Cox, D.; Hastings, J. Rietveld Refinement of Debye-Scherrer Synchrotron X-ray Data from Al2O3. J. Appl. Crystallogr. 1987, 20, 79–83. [Google Scholar] [CrossRef] [Green Version]
- Fromm, F.; Oliveira, M.H., Jr.; Molina-Sanchez, A.; Hundhausen, M.; Lopes, J.M.J.; Riechert, H.; Wirtz, L.; Seyller, T. Contribution of the buffer layer to the Raman spectrum of epitaxial graphene on SiC(0001). New J. Phys. 2013, 15, 043031. [Google Scholar] [CrossRef] [Green Version]
- Filleter, T.; McChesney, J.L.; Bostwick, A.; Rotenberg, E.; Emtsev, K.V.; Seyller, T.; Horn, K.; Bennewitz, R. Friction and Dissipation in Epitaxial Graphene Films. Phys. Rev. Lett. 2009, 102, 086102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Norimatsu, W.; Kusunoki, M. Formation process of graphene on SiC (0001). Physica E 2010, 42, 691–694. [Google Scholar] [CrossRef]
- Berger, C.; Conrad, E.H.; de Heer, W.A. Epigraphene: Epitaxial graphene on silicon carbide. arXiv 2017, arXiv:1704.00374. [Google Scholar]
- Sprinkle, M.; Ruan, M.; Hu, Y.; Hankinson, J.; Rubio-Roy, M.; Zhang, B.; Wu, X.; Berger, C.; de Heer, W.A. Scalable templated growth of graphene nanoribbons on SiC. Nat. Nanotechnol. 2010, 5, 727–731. [Google Scholar] [CrossRef]
- Baringhaus, J.; Aprojanz, J.; Wiegand, J.; Laube, D.; Halbauer, M.; Huebner, J.; Oestreich, M.; Tegenkamp, C. Growth and characterization of sidewall graphene nanoribbons. Appl. Phys. Lett. 2015, 106, 043109. [Google Scholar] [CrossRef]
- Lazzeri, M.; Mauri, F. Nonadiabatic Kohn anomaly in a doped graphene monolayer. Appl. Phys. Lett. 2006, 97, 266407. [Google Scholar] [CrossRef] [Green Version]
- De Jong, T.A.; Krasovskii, E.E.; Ott, C.; Tromp, R.M.; van der Molen, S.J.; Jobst, J. Intrinsic stacking domains in graphene on silicon carbide: A pathway for intercalation. Phys. Rev. Mater. 2018, 2, 104005. [Google Scholar] [CrossRef] [Green Version]
- Pearce, R.; Tan, X.; Wang, R.; Patel, T.; Gallop, J.; Pollard, A.; Yakimova, R.; Hao, L. Investigations of the effect of SiC growth face on graphene thickness uniformity and electronic properties. Surf. Topogr. Metrol. Properties 2015, 3, 015001. [Google Scholar] [CrossRef]





| Sample | DOF | RSS | RSS | F | p |
|---|---|---|---|---|---|
| QFMLG | 163 | 3.6 | 4.9 | 1000 | 1 |
| SLG-Ar | 162 | 5.8 | 8.4 | 932 | 1 |
| SLG-vac | 163 | 8.0 | 1.5 | 675 | 1 |
| Sample | Sample Position | FWHM (cm) | (cm) | (cm) |
|---|---|---|---|---|
| QFMLG | 1 | 21.1 | 10.53 ± 0.12 | 10.13 ± 0.12 |
| 2 | 21.1 | 10.56 ± 0.13 | 10.06 ± 0.13 | |
| 3 | 25.3 | 11.16 ± 0.16 | 11.24 ± 0.15 | |
| 4 | 23.2 | 10.94 ± 0.17 | 11.06 ± 0.16 | |
| Argon grown | 1 | 33.6 | 14.8 ± 0.4 | 16.3 ± 0.3 |
| 2 | 31.5 | 13.7 ± 0.3 | 15.4 ± 0.3 | |
| 3 | 29.4 | 13.9 ± 0.2 | 14.7 ± 0.2 | |
| 4 | 33.6 | 12.1 ± 0.6 | 17.6 ± 0.5 | |
| Vacuum grown | 1 | 35.7 | 14.9 ± 0.5 | 17.5 ± 0.4 |
| 2 | 31.5 | 13.5 ± 0.3 | 15.5 ± 0.2 | |
| 3 | 35.6 | 14.8 ± 0.4 | 17.7 ± 0.4 | |
| 4 | 31.4 | 13.7 ± 0.3 | 16.4 ± 0.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kunc, J.; Rejhon, M. Raman 2D Peak Line Shape in Epigraphene on SiC. Appl. Sci. 2020, 10, 2354. https://doi.org/10.3390/app10072354
Kunc J, Rejhon M. Raman 2D Peak Line Shape in Epigraphene on SiC. Applied Sciences. 2020; 10(7):2354. https://doi.org/10.3390/app10072354
Chicago/Turabian StyleKunc, Jan, and Martin Rejhon. 2020. "Raman 2D Peak Line Shape in Epigraphene on SiC" Applied Sciences 10, no. 7: 2354. https://doi.org/10.3390/app10072354
APA StyleKunc, J., & Rejhon, M. (2020). Raman 2D Peak Line Shape in Epigraphene on SiC. Applied Sciences, 10(7), 2354. https://doi.org/10.3390/app10072354




