Development and Application of a Pre-Corrected Fast Fourier Transform Accelerated Multi-Layer Boundary Element Method for the Simulation of Shallow Water Acoustic Propagation
Abstract
1. Introduction
2. Numerical Method
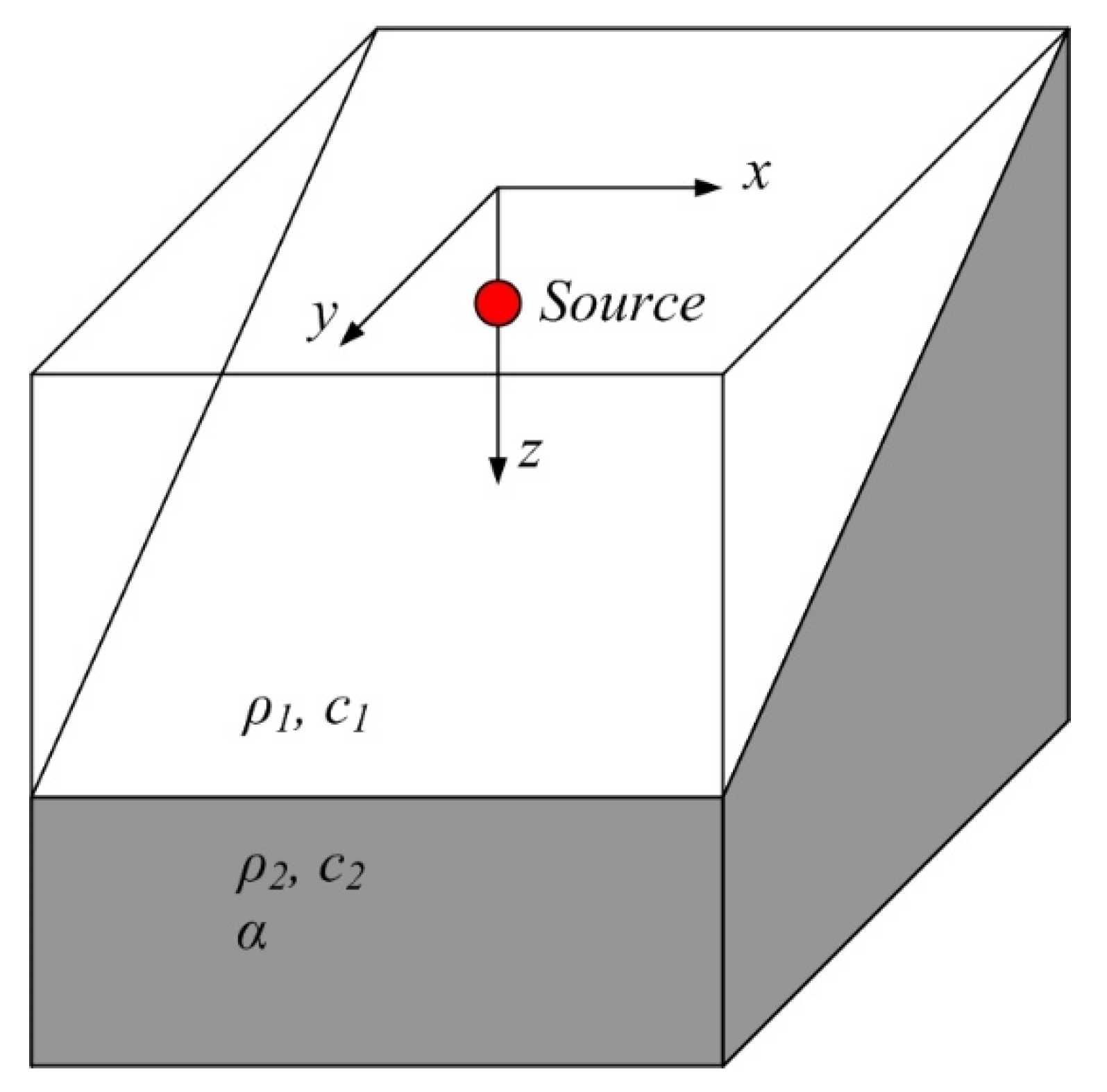
2.1. Formulation of the Boundary Element Method
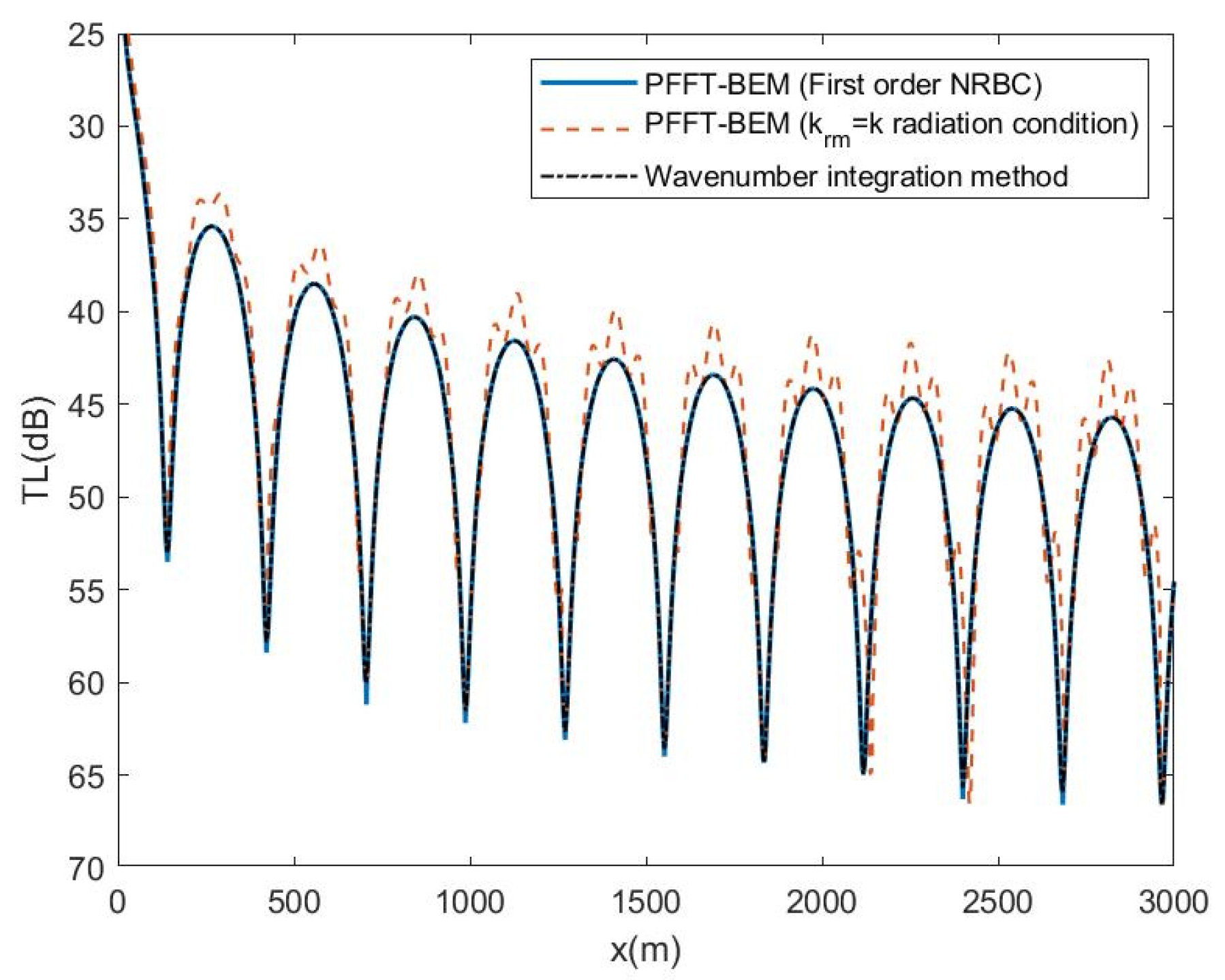
2.2. Non-Reflecting Boundary Condition
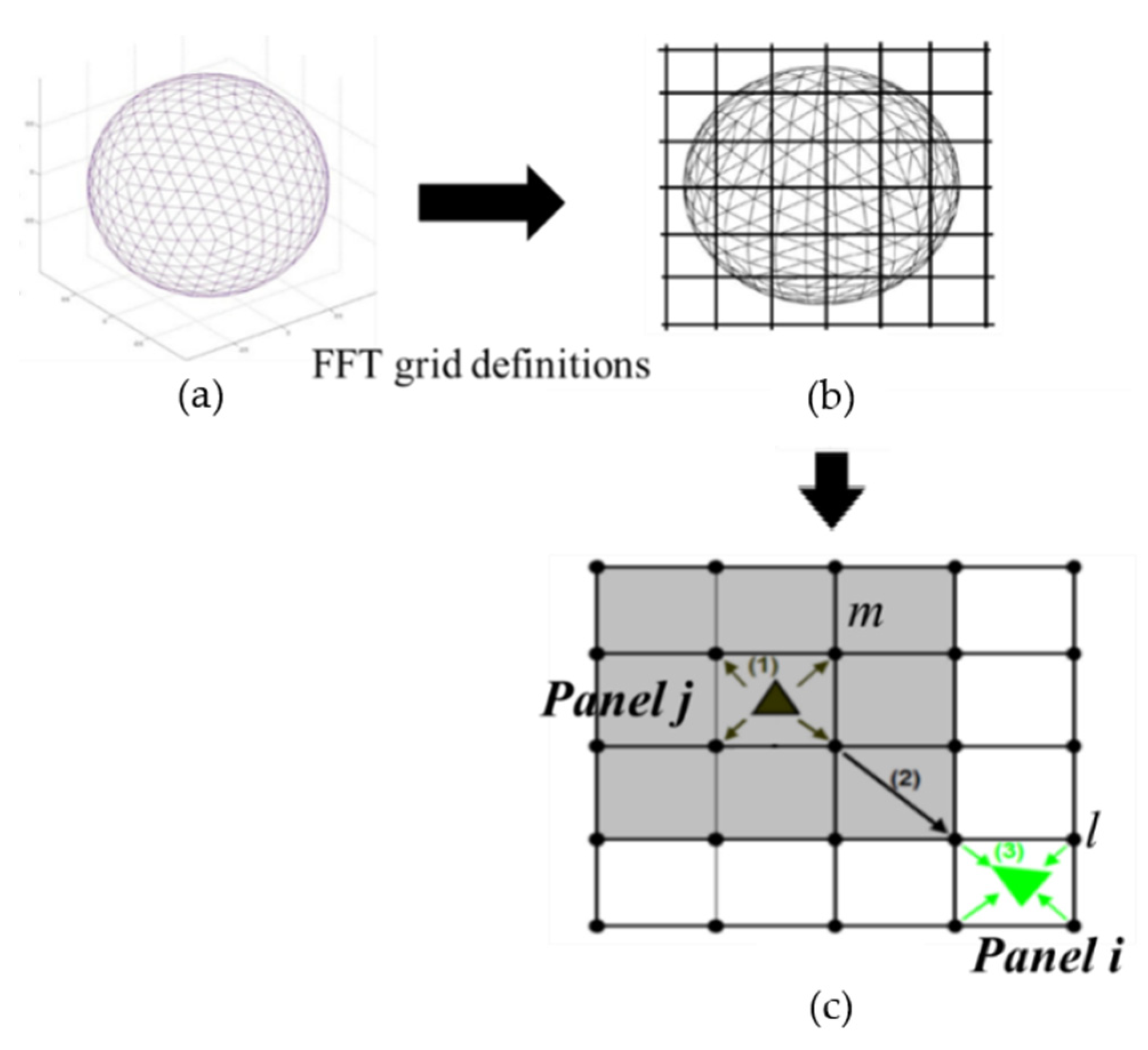
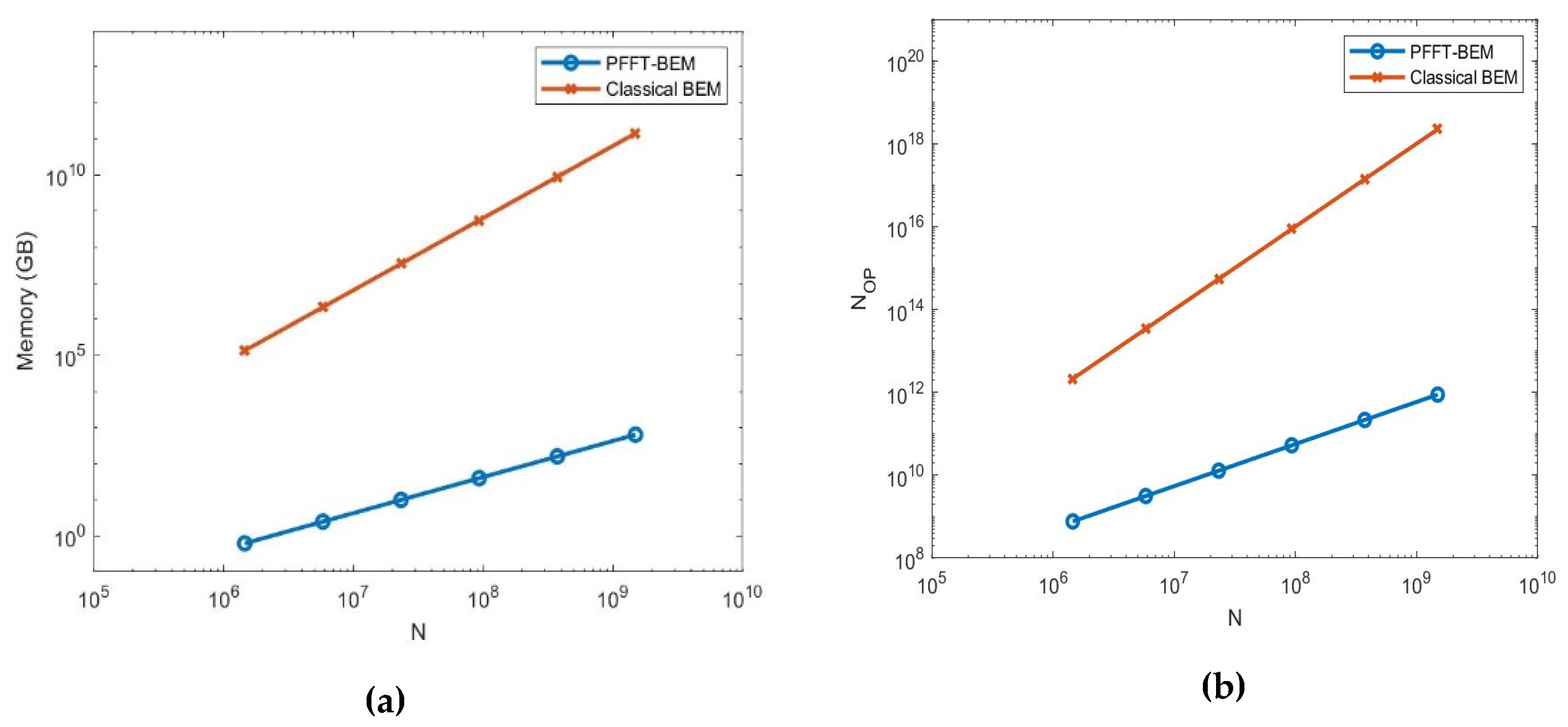
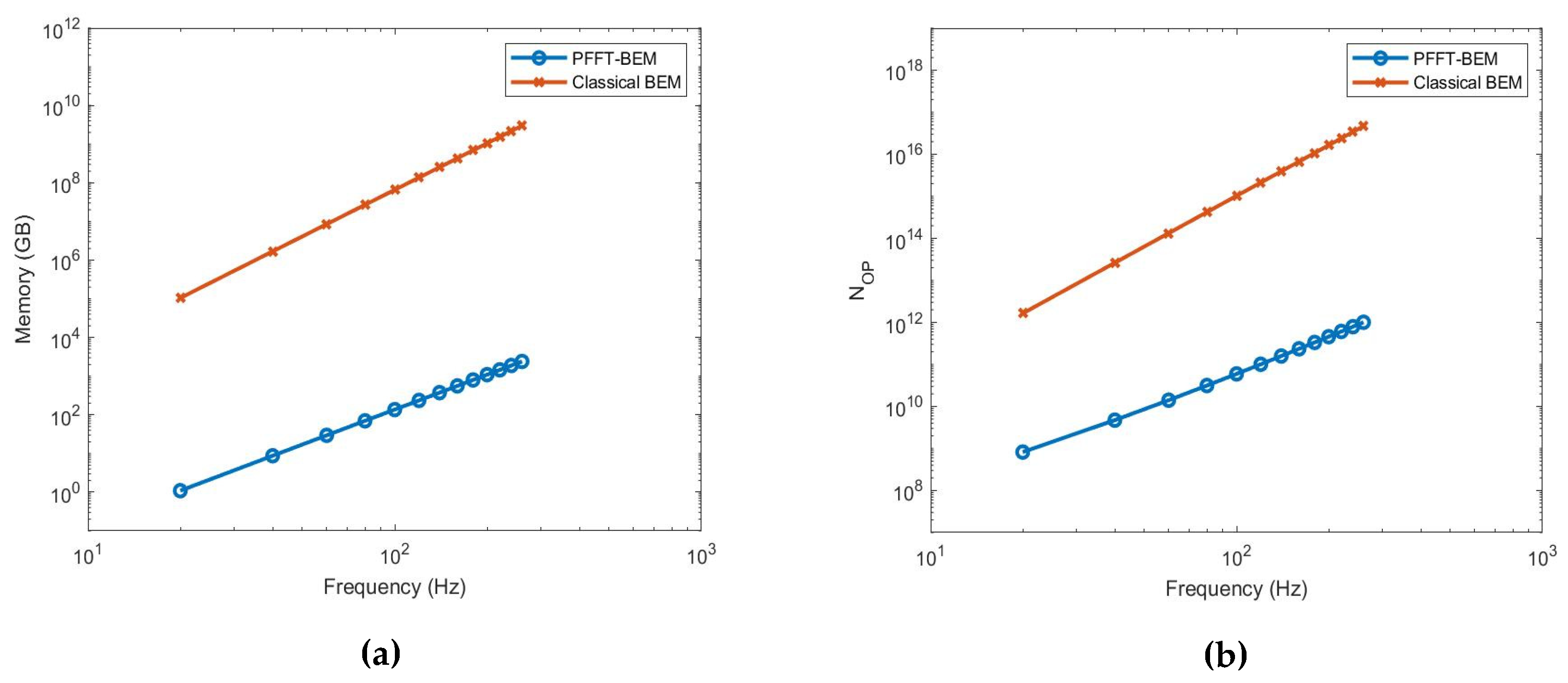
2.3. Evaluation of [A]{x} Pre-Corrected Fast Fourier Transform Method
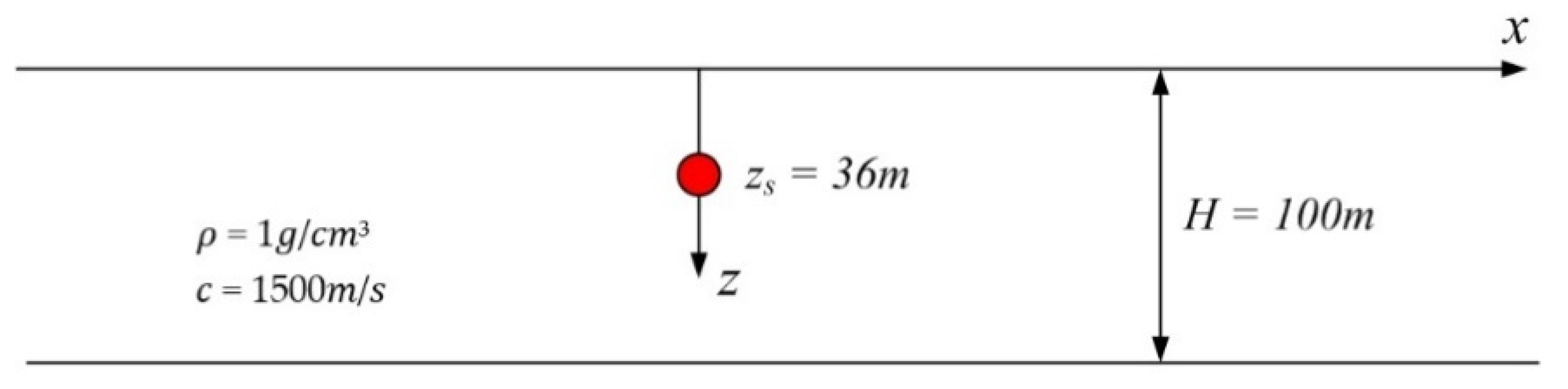
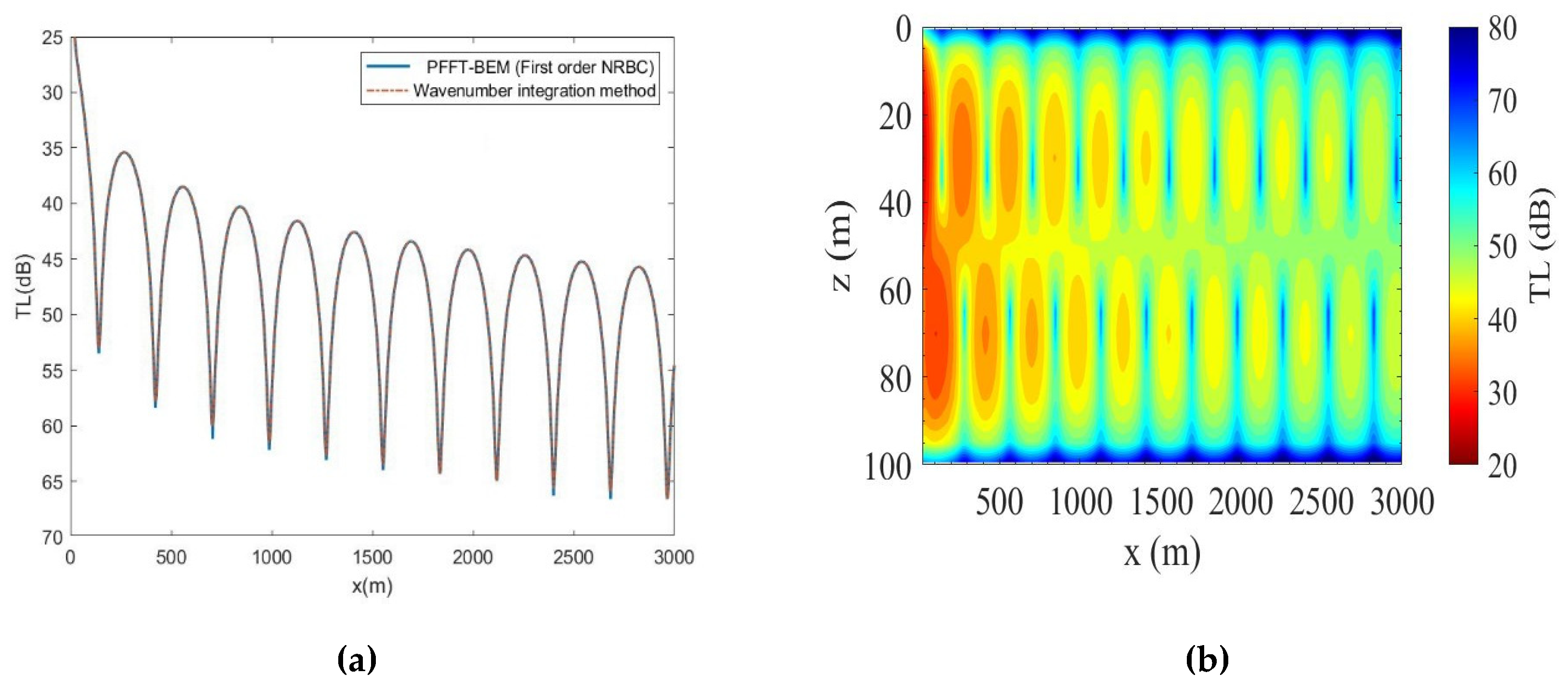
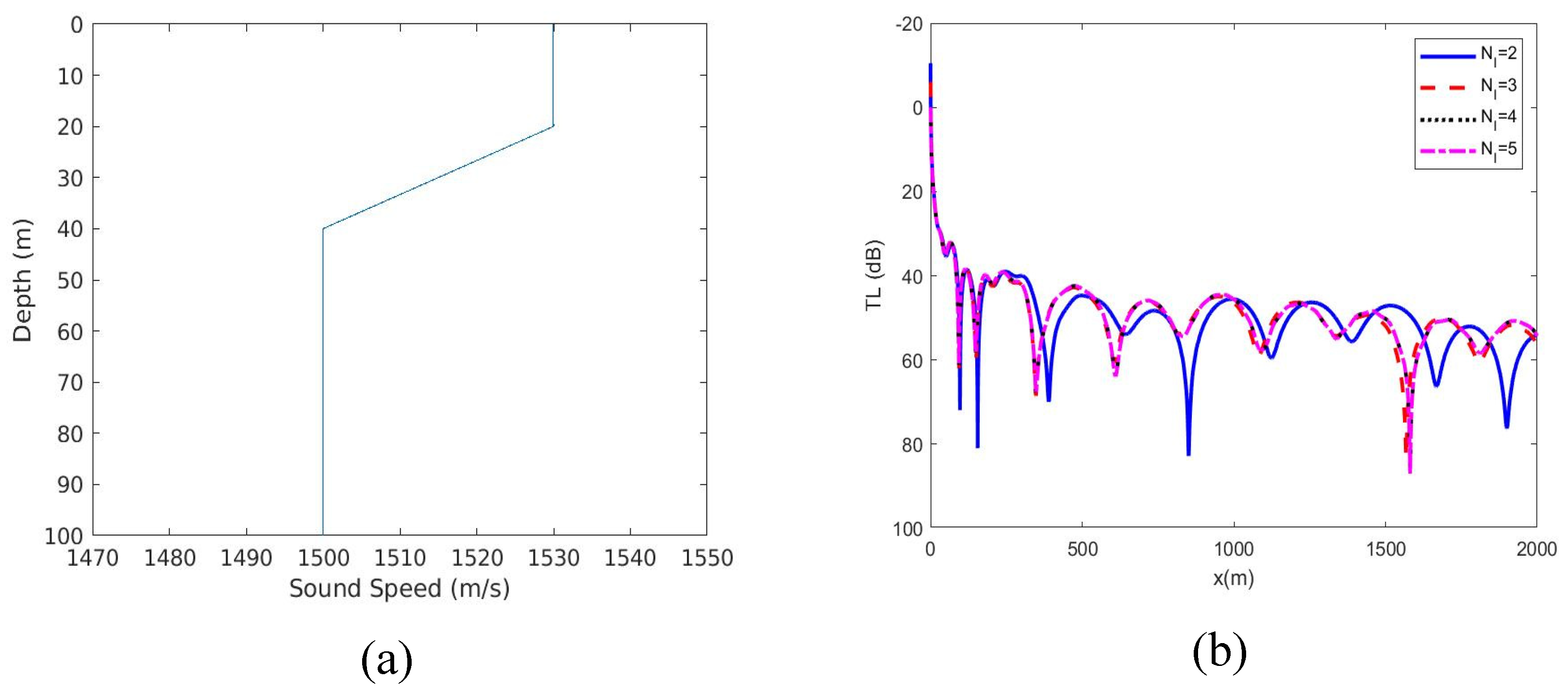
3. Validation of Multi-Layer PFFT-BEM Solutions
4. Applications of 3D PFFT-BEM
4.1. Model Comparisons of the PFFT-BEM with the 3D Parabolic Equation Method
4.1.1. Formulation and Assumptions of the PE Method
- Higher-order term effects: the higher-order terms of the square root operator are small and negligible;
- Backscattering effects: only forward scattering is included (no backscattering effects);
- Large slope effects: only pressure continuity is satisfied across the marching vertical boundaries.
4.1.2. Higher-Order Term Effects: Acoustical Society of America (ASA) Wedge
4.1.3. Backscattering Effects: 3D Seamount
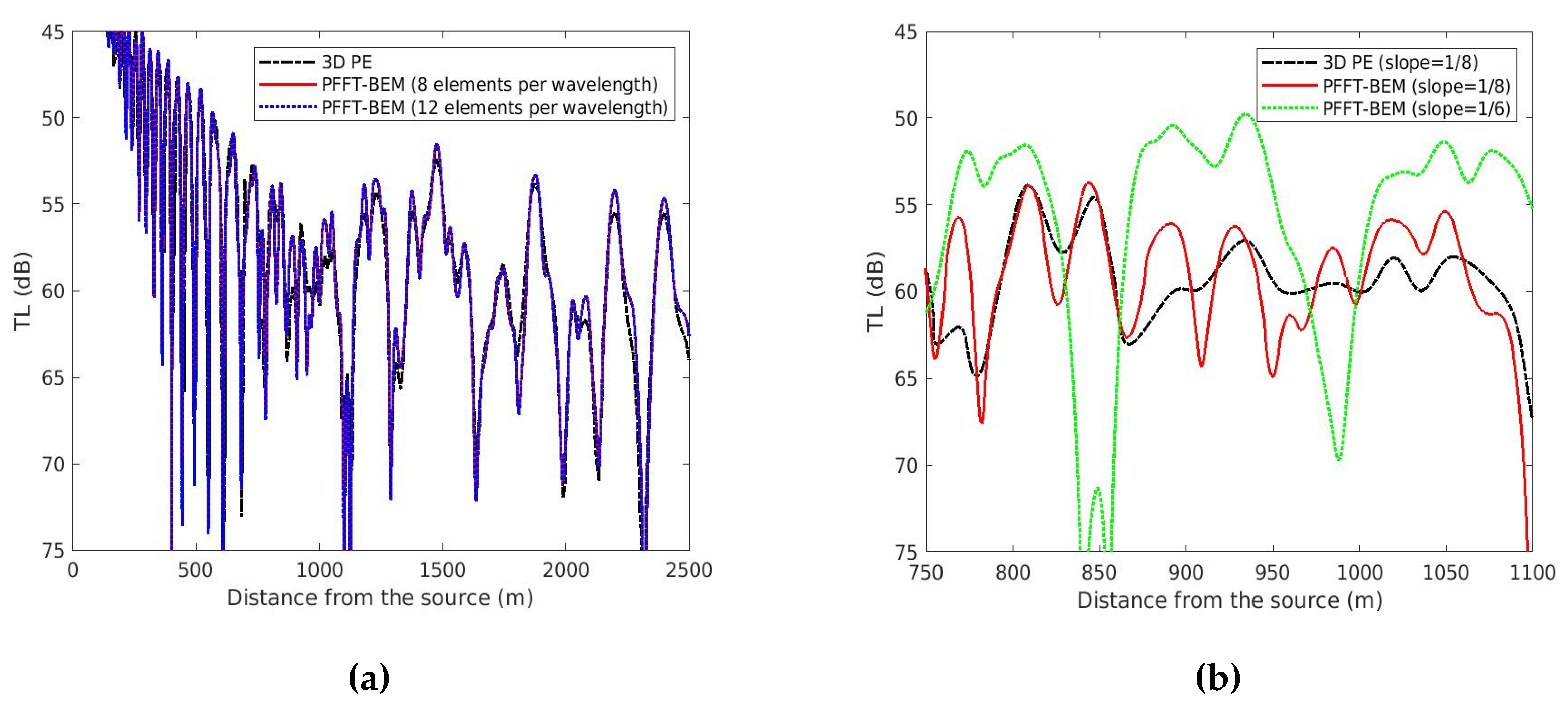
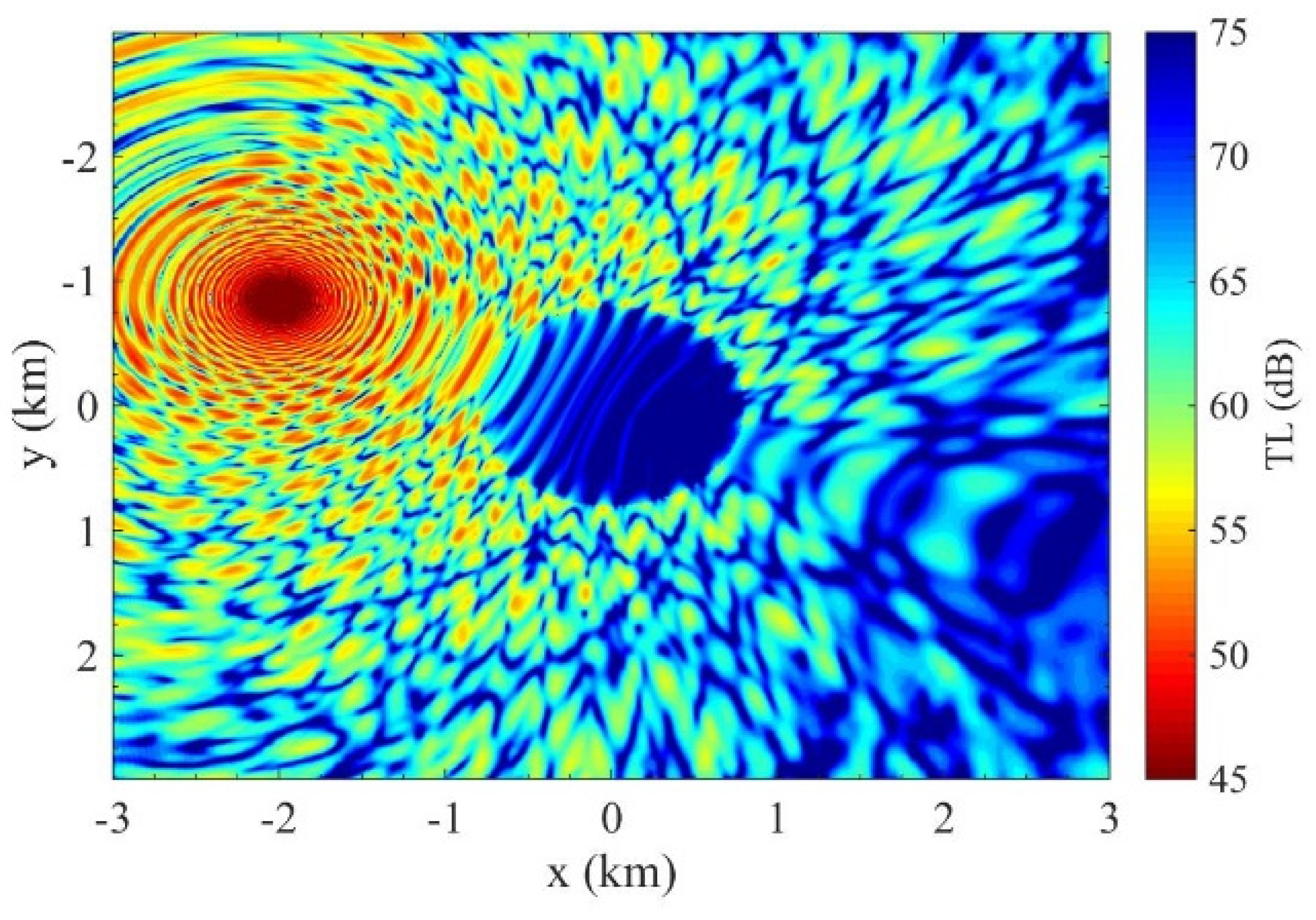
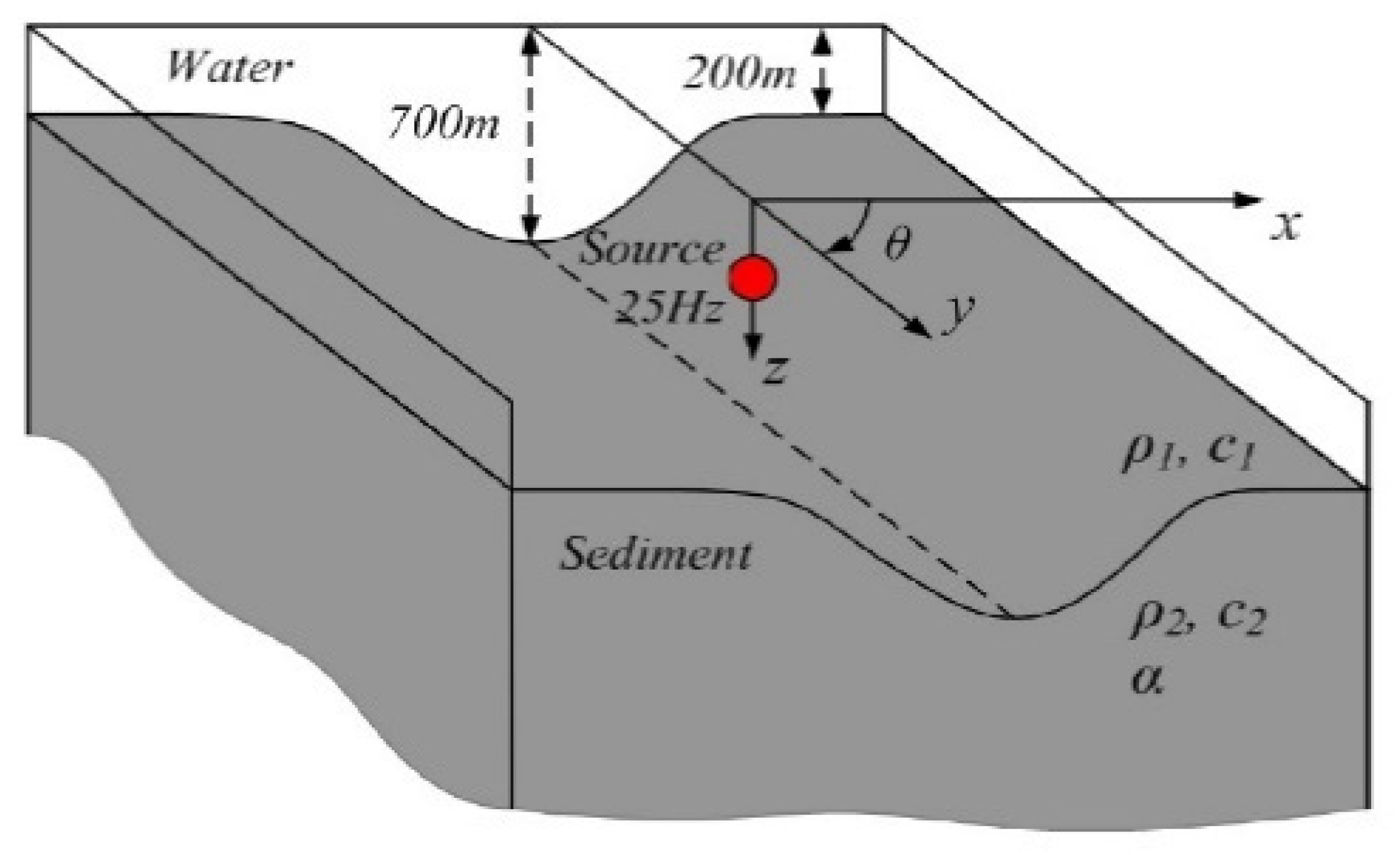
4.1.4. Large Slope Effects: Gaussian Canyon
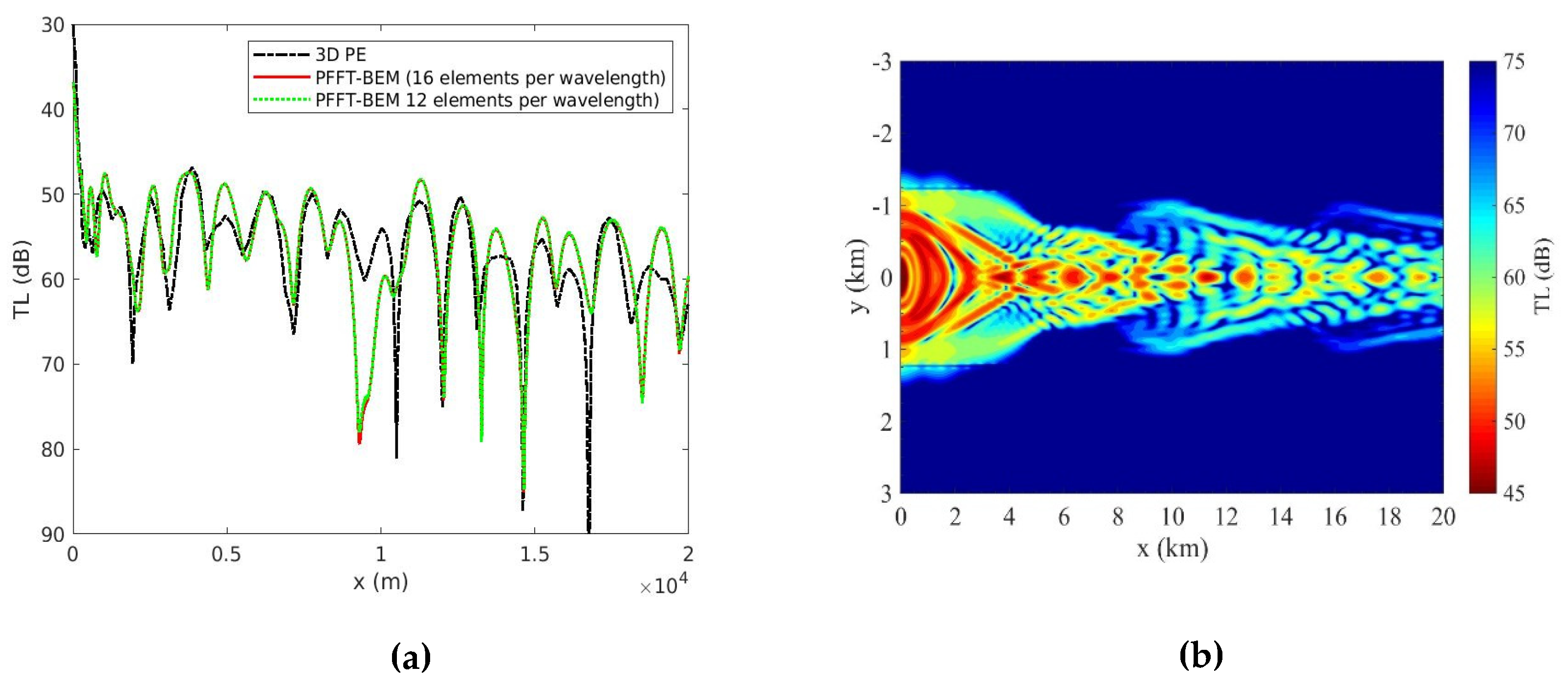
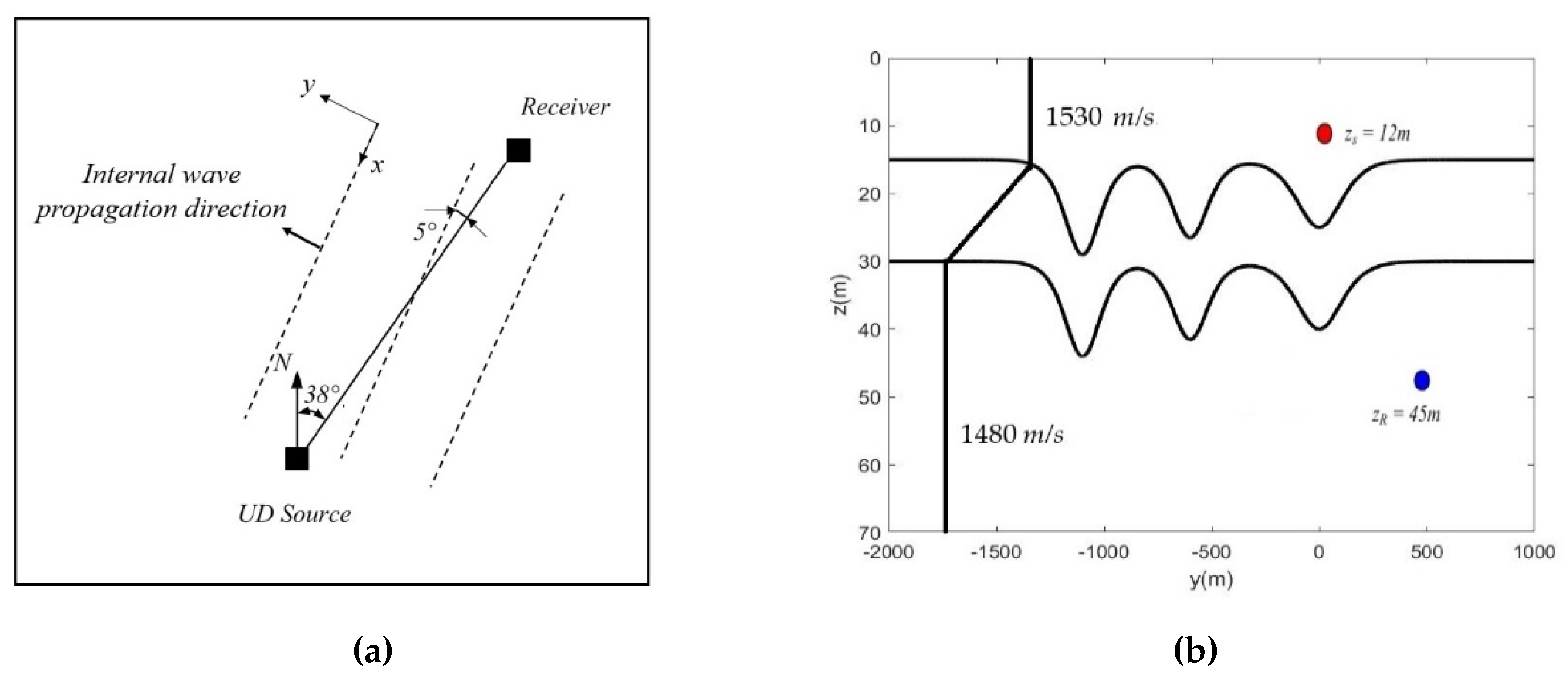
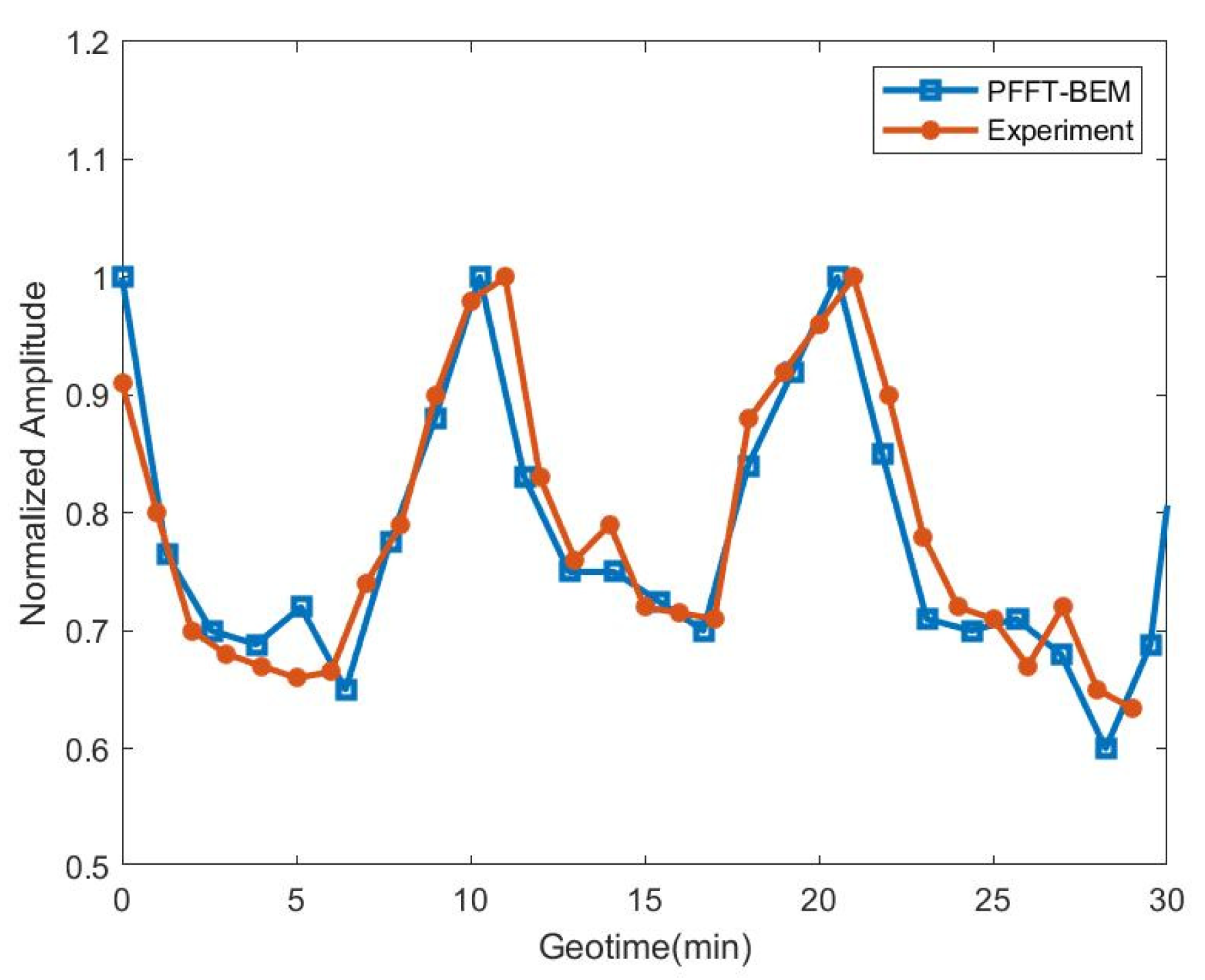
4.2. Prediction of Sound Scattering by Traveling Internal Waves
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luo, W.; Schmidt, H. Three-dimensional propagation and scattering around a conical seamount. J. Acoust. Soc. Am. 2009, 125, 52–65. [Google Scholar] [CrossRef]
- Taroudakis, M.I. A coupled-mode formulation for the solution of the Helmholtz equation in water in the presence of a conical seamount. J. Comput. Acoust. 1996, 4, 101–121. [Google Scholar] [CrossRef]
- Shmelev, A.A.; Lynch, J.F.; Lin, Y.-T.; Schmidt, H. Three-dimensional coupled mode analysis of internal-wave acoustic ducts. J. Acoust. Soc. Am. 2014, 135, 2497–2512. [Google Scholar] [CrossRef]
- Porter, M.B. The Bellhop Manual and User’s Guide: Preliminary Draft; Heat, light, and Sound Res. Inc.: La Jolla, CA, USA, 2011. [Google Scholar]
- Tappert, F.D. The parabolic approximation method. In Wave Propagation and Underwater Acoustics; Springer: Berlin/Heidelberg, Germany, 1977; pp. 224–287. [Google Scholar]
- Lingevitch, J.F.; Collins, M.D.; Mills, M.J.; Evans, R.B. A two-way parabolic equation that accounts for multiple scattering. J. Acoust. Soc. Am. 2002, 112, 476–480. [Google Scholar] [CrossRef] [PubMed]
- Collins, M.D.; Evans, R.B. A two-way parabolic equation for acoustic backscattering in the ocean. J. Acoust. Soc. Am. 1992, 91, 1357–1368. [Google Scholar] [CrossRef]
- Zhu, D.; Bjørnø, L. A three-dimensional, two-way, parabolic equation model for acoustic backscattering in a cylindrical coordinate system. J. Acoust. Soc. Am. 2000, 108, 889–898. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.R.; White, J.K. A precorrected-FFT method for electrostatic analysis of complicated 3-D structures. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1997, 16, 1059–1072. [Google Scholar] [CrossRef]
- Yan, H.; Liu, Y. An efficient high-order boundary element method for nonlinear wave–wave and wave-body interactions. J. Comput. Phys. 2011, 230, 402–424. [Google Scholar] [CrossRef]
- Li, C.; Campbell, B.K.; Liu, Y.; Yue, D.K. A fast multi-layer boundary element method for direct numerical simulation of sound propagation in shallow water environments. J. Comput. Phys. 2019, 392, 694–712. [Google Scholar] [CrossRef]
- Bayliss, A.; Turkel, E. Radiation boundary conditions for wave-like equations. Commun. Pure Appl. Math. 1980, 33, 707–725. [Google Scholar] [CrossRef]
- Givoli, D. High-order local non-reflecting boundary conditions: A review. Wave Motion 2004, 39, 319–326. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Vendhan, C.P.; Diwan, G.C.; Bhattacharyya, S.K. Finite-element modeling of depth and range dependent acoustic propagation in oceanic waveguides. J. Acoust. Soc. Am. 2010, 127, 3319–3326. [Google Scholar] [CrossRef] [PubMed]
- Harris, P.J.; Chen, K. On efficient preconditioners for iterative solution of a Galerkin boundary element equation for the three-dimensional exterior Helmholtz problem. J. Comput. Appl. Math. 2003, 156, 303–318. [Google Scholar] [CrossRef][Green Version]
- Balay, S.; Abhyankar, S.; Adams, M.; Brown, J.; Brune, P.; Buschelman, K.; Dalcin, L.; Dener, A.; Eijkhout, V.; Gropp, W.; et al. PETSc Users Manual; Technical Report for Argonne National Laboratory: Alexandra, VA, USA, 2019.
- Kuperman, W.A.; Lynch, J.F. Shallow-water acoustics. Phys. Today 2004, 57, 55–61. [Google Scholar] [CrossRef]
- Lin, Y.-T.; Duda, T.F.; Newhall, A.E. Three-dimensional sound propagation models using the parabolic-equation approximation and the split-step Fourier method. J. Comput. Acoust. 2013, 21, 1250018. [Google Scholar] [CrossRef]
- Sturm, F. Numerical study of broadband sound pulse propagation in three-dimensional oceanic waveguides. J. Acoust. Soc. Am. 2005, 117, 1058–1079. [Google Scholar] [CrossRef]
- Feit, M.; Fleck, J. Light propagation in graded-index optical fibers. Appl. Opt. 1978, 17, 3990–3998. [Google Scholar] [CrossRef]
- Collins, M.D. An energy-conserving parabolic equation for elastic media. J. Acoust. Soc. Am. 1993, 94, 975–982. [Google Scholar] [CrossRef]
- Lin, Y.-T.; Collis, J.M.; Duda, T.F. A three-dimensional parabolic equation model of sound propagation using higher-order operator splitting and Padé approximants. J. Acoust. Soc. Am. 2012, 132, EL364–EL370. [Google Scholar] [CrossRef]
- Sturm, F. Leading-order cross term correction of three-dimensional parabolic equation models. J. Acoust. Soc. Am. 2016, 139, 263–270. [Google Scholar] [CrossRef]
- Deane, G.; Buckingham, M. An analysis of the three-dimensional sound field in a penetrable wedge with a stratified fluid or elastic basement. J. Acoust. Soc. Am. 1993, 93, 1319–1328. [Google Scholar] [CrossRef]
- Apel, J.R.; Badiey, M.; Chiu, C.-S.; Finette, S.; Headrick, R.; Kemp, J.; Lynch, J.F.; Newhall, A.; Orr, M.H.; Pasewark, B.H.; et al. An overview of the 1995 SWARM shallow-water internal wave acoustic scattering experiment. IEEE J. Ocean. Eng. 1997, 22, 465–500. [Google Scholar] [CrossRef]
- Headrick, R.H.; Lynch, J.F.; Kemp, J.N.; Newhall, A.E.; von der Heydt, K.; Apel, J.; Badiey, M.; Chiu, C.; Finette, S.; Orr, M.; et al. Acoustic normal mode fluctuation statistics in the 1995 SWARM internal wave scattering experiment. J. Acoust. Soc. Am. 2000, 107, 201–220. [Google Scholar] [CrossRef] [PubMed]
- Badiey, M.; Katsnelson, B.G.; Lynch, J.F.; Pereselkov, S.; Siegmann, W.L. Measurement and modeling of three-dimensional sound intensity variations due to shallow-water internal waves. J. Acoust. Soc. Am. 2005, 117, 613–625. [Google Scholar] [CrossRef] [PubMed]
- Headrick, R.H. Analysis of Internal Wave induced Mode Coupling Effects on the 1995 SWARM Experiment Acoustic Transmissions; Woods Hole Oceanographic Institution MA: Woods Hole, MA, USA, 1997. [Google Scholar]
- Shmelev, A.A. Three-Dimensional Acoustic Propagation through Shallow Water Internal, Surface Gravity and Bottom Sediment Waves. Ph.D. Thesis, Massachusetts Institute of Technology Joint Program in Applied Ocean Science, Cambridge, MA, USA, September 2011. [Google Scholar]
- Duda, T.F.; Preisig, J.C. A modeling study of acoustic propagation through moving shallow-water solitary wave packets. IEEE J. Ocean. Eng. 1999, 24, 16–32. [Google Scholar] [CrossRef]
- Robinson, S.P.; Lepper, P.A.; Hazelwood, R.A. Good Practice Guide for Underwater Noise Measurement; Technical Report for National Physics Laboratory: Teddington, UK, March 2014. [Google Scholar]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Lian, J. Development and Application of a Pre-Corrected Fast Fourier Transform Accelerated Multi-Layer Boundary Element Method for the Simulation of Shallow Water Acoustic Propagation. Appl. Sci. 2020, 10, 2393. https://doi.org/10.3390/app10072393
Li C, Lian J. Development and Application of a Pre-Corrected Fast Fourier Transform Accelerated Multi-Layer Boundary Element Method for the Simulation of Shallow Water Acoustic Propagation. Applied Sciences. 2020; 10(7):2393. https://doi.org/10.3390/app10072393
Chicago/Turabian StyleLi, Chengxi, and Jijian Lian. 2020. "Development and Application of a Pre-Corrected Fast Fourier Transform Accelerated Multi-Layer Boundary Element Method for the Simulation of Shallow Water Acoustic Propagation" Applied Sciences 10, no. 7: 2393. https://doi.org/10.3390/app10072393
APA StyleLi, C., & Lian, J. (2020). Development and Application of a Pre-Corrected Fast Fourier Transform Accelerated Multi-Layer Boundary Element Method for the Simulation of Shallow Water Acoustic Propagation. Applied Sciences, 10(7), 2393. https://doi.org/10.3390/app10072393





