Blind Image Deconvolution Algorithm Based on Sparse Optimization with an Adaptive Blur Kernel Estimation

Abstract

Image blurs are a major source of degradation in an imaging system. There are various blur types, such as motion blur and defocus blur, which reduce image quality significantly. Therefore, it is essential to develop methods for recovering approximated latent images from blurry ones to increase the performance of the imaging system. In this paper, an image blur removal technique based on sparse optimization is proposed. Most existing methods use different image priors to estimate the blur kernel but are unable to fully exploit local image information. The proposed method adopts an image prior based on nonzero measurement in the image gradient domain and introduces an analytical solution, which converges quickly without additional searching iterations during the optimization. First, a blur kernel is accurately estimated from a single input image with an alternating scheme and a half-quadratic optimization algorithm. Subsequently, the latent sharp image is revealed by a non-blind deconvolution algorithm with the hyper-Laplacian distribution-based priors. Additionally, we analyze and discuss its solutions for different prior parameters. According to the tests we conducted, our method outperforms similar methods and could be suitable for dealing with image blurs in real-life applications.

1. Introduction

Image deblurring is important in many fields, such as surveillance, traffic control, astronomy, and remote sensing [1,2,3]. Blurs occur due to a variety of reasons, such as moving objects, focus issues, and atmospheric turbulence. They significantly deteriorate the quality of the image. The blurring procedure is always described by a point spread function (PSF), also known as blur kernel. When the PSF is known, the blur can be removed by conventional deconvolution methods, such as Weiner filtering and the Lucy–Richardson algorithm. However, when the PSF is unknown, the issue constitutes a blind-deconvolution problem, which is a notoriously vague inverse problem that has perplexed the scientific community for decades.

Therefore, recovering an approximated latent image from a blurred observation is essential for improving the performance of an imaging system, in addition to having several applications [4,5,6]. One approach to handle this problem is to build parameterized models for specific blur types, i.e., employ motion length and angle to describe a motion blur, the radius of a disk to model the defocus blur, and a Gaussian model to simulate the atmospheric turbulence blur. Subsequently, Dash and Majhi suggested a radial basis function neural network with image features based on the magnitude of Fourier coefficients to estimate the motion lengths [7]. Jalobeanu et al. exploited the maximum likelihood estimator on the entire dataset available to estimate the parameters for a Gaussian model [8]. Kumar et al. utilized the Tchebycheff moment to estimate the variance of a Gaussian model [9]. Yin and Hussain combined the non-Gaussianity measures for independent component analysis to estimate the parameters for the motion length, disk radius, and turbulence degrees [10].

However, the methods based on parameter estimation fail when dealing with a random PSF. Because the blind deconvolution problem is ambiguous, it could be regularized by some image priors, which favor the original nature of images over noisy and blurry ones. In this perspective, numerous image priors have been proposed in recent years. The Gaussian prior is one of the simplest and most commonly used priors because it implements ridge regularization in the image gradient domain as the penalty term in the cost functions and turns the problem into a quadratic convex optimization problem, which can be solved by a number of numerical methods [11]. However, the Gaussian prior is not adequately effective because natural images are mainly non-Gaussian [12,13].

Recent advances in digital image processing and sparse representation have led to the development of new methods based on the statistical characteristics of natural images. Fergus et al. asserted that the distribution of gradient magnitudes of a natural image has a heavy tail and sharp top, and proposed an effective method based on the variational Bayesian approach [14]. Levin et al. introduced a hyper-Laplacian prior to the image gradient and used the iterative reweighted least squares to solve the cost function [15]. Joshi et al. put forward a prior on local color statistics with the hyper-Laplacian prior for denoising and deblurring [16]. Wang et al. proposed a prior based on total variation [17]. Xu and Jia combined the total variation with an ${\mathbf{\ell }}_{\mathbf{1}}$ constraint deconvolution method to efficiently reduce outliers and preserve image structures [18]. Pan et al. restored the latent image in the dark channel [19]. Yang et al. proposed an ${\mathbf{\ell }}_{\mathbf{1}}$-based constrained method combined with a genetic algorithm to restore a clear image [20]. These methods adopt the ${\mathbf{\ell }}_{\mathbf{p}}$-norm or quasi-norm forms as the image priors, which achieve high quality results.

Furthermore, learning-based methods are also practical approaches in this field. Zhu et al. proposed a method that reveals the priors from Gibbs sampling [21]. Roth et al. adopted the fields of experts to learn image priors with contrastive divergence [22]. Raj et al. proposed an image prior based on a Markov random field [23]. Schuler et al. used a multi-layer perceptron to learn an image deconvolution scheme on a dataset of natural images with large quantities [24]. Zhang et al. trained a set of convolutional neural network priors, which act as a constraint of model-based optimization methods to cope with the image restoration problems [25].

In this paper, we propose a deblurring framework consisting of two stages. First, an accurate blur kernel is estimated from an input blurry image via a nonzero constrained function as the image prior. Compared to the conventional sparsity-based techniques, the optimization procedure of our method has a lower computational complexity due to the analytical solution of the mathematical model. Subsequently, we propose a deconvolution algorithm on sparse representation for latent image restoration. Experimental results and comparisons indicate that our method outperforms others.

This study makes a novel contribution to the literature as summarized below:

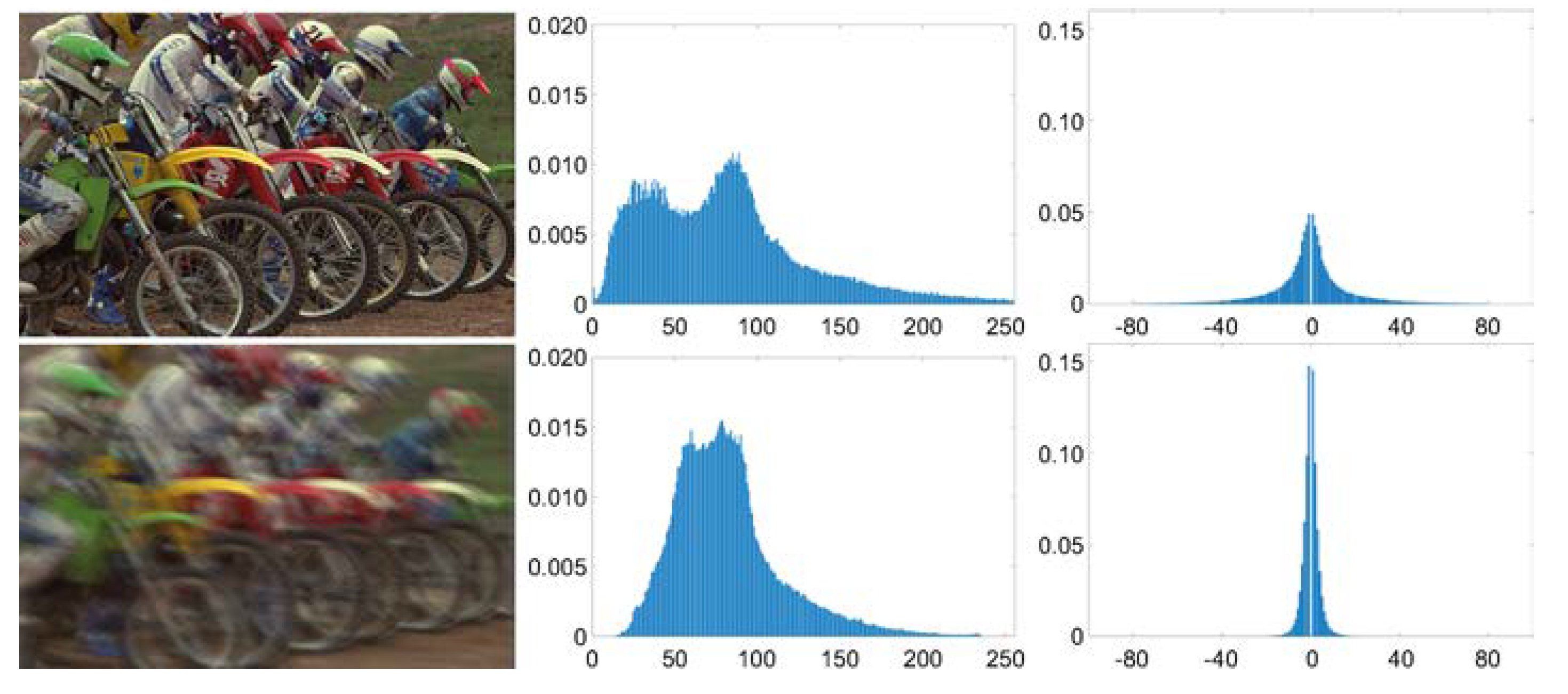
• An image prior based on nonzero measurement on four orientations of the image gradient domain is proposed. The image histogram charts show that the frequency of nonzero values in the gradient domain of a blurry image is far more than that in a clear one, and the nonzero measurement is suitable for a constraint for image deblurring. The solution for the cost function with the proposed image prior is also analyzed and discussed.
• The blur kernel is obtained under a ridge regularization on the PSF because the measurements on an image are enough to estimate the blur kernel in the maximum a posteriori (MAP) framework. During the optimization, we propose a solution based on a conjugate gradient method combined with Newton’s method; this solution could prevent us from calculating the inversion of a Hessian matrix and solve the cost function efficiently.
• Considering the statistical features of natural images, we presented a non-blind image deconvolution algorithm by applying the concept of hyper-Laplacian distribution-based prior. Its target image is constrained by an ${\mathbf{\ell }}_{\mathit{p}}$ quasi-norm in the cost function. We analyze and discuss the solutions for different $\mathit{p}$ values.
• We tested our method on both simulated motion blurs and atmospheric turbulence blurs in real-life applications. In addition, we comparatively analyzed our method, in terms of the cost durations, estimated accuracy of the blur kernels, and quality assessment of the restored images, and adopted several approaches related to blur removal.

The remainder of this paper is organized as follows: Section 2 introduces the imaging system and the principle of image blurs. Subsequently, we present the details of our proposed deblurring method, including the blur kernel estimation technique and the image deconvolution algorithm. The results of the experiments and comparative analysis performed are described in Section 3. Section 4 summarizes the study and presents concluding remarks.

2. Materials and Methods

Image blur is one of the most common phenomena of image degradations, which can generally be regarded as a linear, shift-invariant system. Furthermore, it can be expressed by a convolution model as follows [14,15,16,17,18,19,20]:

$$\mathit{g}=\mathit{k}\otimes \mathit{f}+\mathit{\eta }$$

(1)

where $\mathit{f}$ and $\mathit{g}$ represent the original and observed blurry images, respectively; $\mathit{k}$ is the blur kernel; the symbol “$\otimes$” represents the convolution operator; and $\mathit{\eta }$ stands for the additive noise generated during image acquisition or transmission.

2.1. Image Prior and Our Method’s Framework

From previous studies a practical framework of blind image deblurring is the blind iterative deconvolution algorithm [15,16,17,18,19]. Its fundamental principle is expressed as follows:

$$\left(\widehat{\mathit{f}},\widehat{\mathit{k}}\right)=\mathit{arg}\underset{\mathit{f},\mathit{k}}{\mathit{min}}\parallel \mathit{k}\otimes \mathit{f}-\mathit{g}{\parallel }_2^2+{\alpha }_1{P}_{\mathit{f}}+{\alpha }_2{P}_{\mathit{k}}$$

(2)

where the first term, $\parallel \mathit{k}\otimes \mathit{f}-\mathit{g}{\parallel }_2^2$, is the data fidelity term which indicates the prior of the additive noise $\mathit{\eta }$ in Equation (1), $P_{\mathit{f}}$ and $P_{\mathit{k}}$ represent the priors of the original image and the blur kernel, respectively, while ${\alpha }_1$ and ${\alpha }_2$ are their corresponding weights.

For the image prior model, we assume that the first-order derivatives of the image $\mathit{f}$ in four directions are represented in Equation (3) by:

$$\{\begin{array}{l}{\nabla }_1\mathit{f}\left(x,y\right)=\mathit{f}\left(x,y\right)-\mathit{f}\left(x,y+1\right)\\ {\nabla }_2\mathit{f}\left(x,y\right)=\mathit{f}\left(x,y\right)-\mathit{f}\left(x+1,y\right)\\ {\nabla }_3\mathit{f}\left(x,y\right)=\mathit{f}\left(x,y\right)-\mathit{f}\left(x+1,y+1\right)\\ {\nabla }_4\mathit{f}\left(x,y\right)=\mathit{f}\left(x,y\right)-\mathit{f}\left(x-1,y-1\right)\end{array}$$

(3)

where $x$ and $y$ represent the coordinates of a digital image; and the operator ${\nabla }_n$ with $n\in N=\left\{1,2,3,4\right\}$ indicates the image gradients in four orientations: 0, $\mathsf{\pi }/2$, $\mathsf{\pi }/4$, and $3\mathsf{\pi }/4$, respectively. In the following context, the images and blur kernels are represented by lexicographic order, which is to list every pixel in raster scan order as one long vector [26]. This process is convenient for analysis and mathematical calculations.

In this paper, to measure the image sparsity, we utilized the nonzero measurement in the image gradient domain in the four orientations as the image prior, and we defined the prior as follows:

$$P_{\mathit{f}}={\displaystyle \sum }_{i\in \Omega }\left(1-\delta \left(\left|{\nabla }_1{\mathit{f}}_i\right|+\left|{\nabla }_2{\mathit{f}}_i\right|+\left|{\nabla }_3{\mathit{f}}_i\right|+\left|{\nabla }_4{\mathit{f}}_i\right|\right)\right)$$

(4)

where the subscript $i$ represents the $i$th element of the image gradient domain in lexicographic order discussed above, and $\mathsf{\Omega }$ is the support domain of the images. Notation $|\cdot |$ represents the magnitude. The function $\delta \left(m\right)$ is the Kronecker delta function, which returns 0 if $m\ne 0$ and 1 if $m=0$. In general, Equation (4) aims at counting the number of nonzero elements in image gradient domains in four orientations.

In Figure 1, the first column shows an example of a clear image and a blurry one. The statistical charts in the second column constitute their corresponding image histograms. It shows that the pixel intensities are more concentrated in the blurred image, which implies that the gradient domain of the blurred image has a better sparsity than that of the clear one. The third column shows the statistical charts of nonzero values in the gradient domain in four orientations (${\nabla }_1+{\nabla }_2+{\nabla }_3+{\nabla }_4$), which confirms that the frequencies of nonzero values of the blurred image in gradient domain are higher than those in the clear image.

In the view of MAP, the estimators can get closer to the true values on the condition of more measurements. Since the size of the blur kernel is far smaller than that of the images, the observed image $\mathit{g}$ supplies enough measurements for estimating the blur kernel alone [27]. Thus, the blind deconvolution problem of solving Equation (2) can be transformed into an alternating scheme, i.e., the blur kernel should be estimated at first, and then the latent sharp image can be acquired by a non-blind deconvolution method.

2.2. Estimation of Blur Kernel and the Intermediate Latent Image

To estimate the blur kernel, Equation (2) can be divided into two parts as follows:

$$\{\begin{array}{c}\widehat{\mathit{f}}=\mathit{arg}\underset{\mathit{f}}{\mathit{min}}\parallel \mathit{k}\otimes \mathit{f}-\mathit{g}{\parallel }_2^2+{\alpha }_1{P}_{\mathit{f}}\\ \widehat{\mathit{k}}=\mathit{arg}\underset{\mathit{k}}{\mathit{min}}\parallel \mathit{k}\otimes \mathit{f}-\mathit{g}{\parallel }_2^2+{\alpha }_2{P}_{\mathit{k}}\end{array}$$

(5)

where the two subproblems above are solved alternately. Their solutions are represented in the following section. In addition, to avoid the algorithm’s converging to local minimums, we adopt a coarse-to-fine scheme during the blur kernel estimation. The image pyramid technique is applied to generate the target image from the coarsest level to the finest level [26]. Figure 2 shows the framework of the proposed method.

2.2.1. Solve $\mathit{f}$ with a Given $\mathit{k}$

As discussed in Section 2.1, we use a notation in the form of a norm constraint $\parallel \nabla {\mathit{f}\parallel }_{\mathrm{c}}$ to represent the image prior $P_{\mathit{f}}$ proposed in Equation (4) for simplicity. Then, the first subproblem of Equation (5) can be written as:

$$\widehat{\mathit{f}}=\mathit{arg}\underset{\mathit{f}}{\mathit{min}}\parallel \mathit{k}\otimes \mathit{f}-\mathit{g}{\parallel }_2^2+{\alpha }_1{\parallel \nabla \mathit{f}\parallel }_c$$

(6)

where the result of $\mathit{f}$ is an intermediate variable that is used for estimating an accurate blur kernel. Furthermore, it cannot be regarded as the deblurring result because it loses multiple image details and retains only the outlines. The above mentioned minimization can be solved via the split Bergman iteration. With auxiliary variable $\mathit{u}=\left(u^1, u^2,u^3,u^4\right)$ the cost function of Equation (6) turns into another optimization problem:

$$\underset{\mathit{f},\mathit{u}}{\mathit{min}}\parallel \mathit{k}\otimes \mathit{f}-\mathit{g}{\parallel }_2^2+{\beta }_1\parallel \nabla \mathit{f}-\mathit{u}{\parallel }_2^2+{\alpha }_1{\parallel \mathit{u}\parallel }_c$$

(7)

where $\nabla \mathit{f}=\left({\nabla }_1\mathit{f}, {\nabla }_2\mathit{f},{\nabla }_3\mathit{f},{\nabla }_4\mathit{f}\right)$ represents the collection of the gradient in the four orientations, and the intermediate coefficient, ${\beta }_1$, is varied during the optimization process. The optimization of $\mathit{f}$ in Equation (7) converges to the solution of Equation (6) as ${\beta }_1$ approaches to infinity. The alternating scheme of the subproblem is described as follows:

$$\{\begin{array}{l}\widehat{\mathit{u}}=\mathit{arg}\underset{\mathit{u}}{\mathit{min}}{\parallel \mathit{u}\parallel }_c+\frac{{\beta }_1}{{\alpha }_1}\parallel \nabla \mathit{f}-\mathit{u}{\parallel }_2^2\\ \widehat{\mathit{f}}=\mathit{arg}\underset{\mathit{f}}{\mathit{min}}\parallel \mathit{k}\otimes \mathit{f}-\mathit{g}{\parallel }_2^2+{\beta }_1\parallel \nabla \mathit{f}-\mathit{u}{\parallel }_2^2\end{array}$$

(8)

where the result value of $\widehat{\mathit{f}}$ represents the intermediate latent image.

Considering the $i$th element of $\mathit{u}$ and $\nabla \mathit{f}$, the $\widehat{\mathit{u}}$-subproblem in the first part of Equation (8) can be expressed as:

$$\widehat{\mathit{u}}={\displaystyle \sum }_{i\in \Omega }\left(\mathit{arg}\underset{{\mathit{u}}_i}{\mathit{min}}1-\delta \left({\displaystyle \sum }_{n\in N}\left|u_i^n\right|\right)+\frac{{\beta }_1}{{\alpha }_1}{\displaystyle \sum }_{n\in N}{\left({\nabla }_n{\mathit{f}}_i-u_i^n\right)}^2\right)$$

(9)

where the bold variable ${\mathit{u}}_i=\left(u_i^1, u_i^2,u_i^3,u_i^4\right)$ to be minimized under the “$\mathit{arg}min$” function represents the $i$th element of $\mathit{u}$. It can be seen from the above equation that the solution of Equation (9) is able to be acquired via element-wise optimization.

Let $\Psi \left({\mathit{u}}_i\right)$ represent the minimization problem, i.e., the “$\mathit{arg}min$” function, for the $i$th element in the right-hand side of Equation (9), and it can be expanded as follows:

$$\Psi \left({\mathit{u}}_i\right)=\{\begin{array}{ll}\frac{{\beta }_1}{{\alpha }_1}{\displaystyle {\displaystyle \sum }_{n\in N}}{\left({\nabla }_n{\mathit{f}}_i\right)}^2& ,{\mathit{u}}_i=\mathbf{0}\left(\forall n:u_i^n=0\right)\hfill \\ 1+\frac{{\beta }_1}{{\alpha }_1}{\displaystyle {\displaystyle \sum }_{n\in N}}{\left({\nabla }_n{\mathit{f}}_i-u_i^n\right)}^2\hfill & ,{\mathit{u}}_i\ne \mathbf{0} \left(\exists n:u_i^n\ne 0\right)\hfill \end{array}$$

(10)

It can be seen from Equation (10) that when ${\mathit{u}}_i\ne \mathbf{0}$, the inequality $\Psi \left({\mathit{u}}_i\right)\ge 1$ always holds. As a result, when $\Psi \left(\mathbf{0}\right)>1$, the minimum of $\Psi \left({\mathit{u}}_i\right)$ is $1$; when $\Psi \left(\mathbf{0}\right)\le 1$, the minimum of $\Psi \left({\mathit{u}}_i\right)$ is $\Psi \left(\mathbf{0}\right)$.

The optimization of Equation (10) is discussed as follows:

(1) When $\Psi \left(\mathbf{0}\right)>1$, the solution for $\Psi \left({\mathit{u}}_i\right)=1$ is ${\mathit{u}}_i=\nabla \mathit{f}$.

(2) When $\Psi \left(\mathbf{0}\right)\le 1$, $\Psi \left({\mathit{u}}_i\right)$ reaches the minimum when ${\mathit{u}}_i=\mathbf{0}$.

Overall, the solution for Equation (9) is obtained in Equation (11) as follows:

$${\widehat{\mathit{u}}}_i=\{\begin{array}{ll}\left({\nabla }_1\mathit{f}, {\nabla }_2\mathit{f},{\nabla }_3\mathit{f},{\nabla }_4\mathit{f}\right)\hfill & ,\frac{{\beta }_1}{{\alpha }_1}{\displaystyle {\displaystyle \sum }_{n\in N}}{\left({\nabla }_n{\mathit{f}}_i\right)}^2>1\hfill \\ \hfill & \hfill \\ \left(0,0,0,0\right)\hfill & ,otherwise\hfill \end{array}$$

(11)

As to the $\widehat{\mathit{f}}$-subproblem in the second part of Equation (8), it is a convex quadratic optimization problem whose solution can be achieved in frequency domain as follows:

$$\widehat{F}=\frac{G\circ K^{*}+{\beta }_1{{\displaystyle \sum }}_{n\in N}{D}_n\circ U_n^{*}}{K\circ K^{*}+{\beta }_1{{\displaystyle \sum }}_{n\in N}{D}_n\circ D_n^{*}}$$

(12)

where $F$, $G$, $K$, and $U_n$ stand for the discrete Fourier transform (DFT) of $\mathit{f}$, $\mathit{g}$, $\mathit{k}$, and ${\mathit{u}}_n$; $D_n$ is the DFT of the differential operators in the four orientations; notation $\circ$ is the Hadamard product; and the superscript $*$ represents the complex conjugation. Generally, the denominator should be adjusted to the floating-point relative accuracy depending on the platform to avoid any divide by zero cases in practical implementations.

2.2.2. Solve $\mathit{k}$ with a given $\mathit{f}$

As the differential operations are linear, the blurs in the image gradient domains also satisfy the convolution model in Equation (1). Moreover, the blur kernel $\mathit{k}$ can be estimated with more accuracy in the gradient domain than directly solving the second subproblem in Equation (5) with pixel intensities [28]. In the following contexts, the analytical solution for the $\mathit{k}$-subprolem is discussed in the matrix form, and the second part of Equation (5) can be rewritten as:

$$\widehat{\mathit{K}}=\mathit{arg}\underset{\mathit{K}}{\mathit{min}}{\left(\mathit{F}\mathit{K}-\mathit{G}\right)}^T\left(\mathit{F}\mathit{K}-\mathit{G}\right)+{\alpha }_2{\mathit{K}}^T\mathit{K}$$

(13)

where $\mathit{F}=\left({\mathit{F}}_1+{\mathit{F}}_2+{\mathit{F}}_3+{\mathit{F}}_4\right)$ and $\mathit{G}=\left({\mathit{G}}_1+{\mathit{G}}_2+{\mathit{G}}_3+{\mathit{G}}_4\right)$; ${\mathit{G}}_n$ and ${\mathit{G}}_n$ with $n\in N$ represent the block circulant matrices with circulant blocks generated from $\nabla \mathit{f}$ and $\nabla \mathit{g}$; and $\mathit{K}$ is rearranged from $\mathit{k}$ in a vector form so as to transform the convolution operation to the matrix multiplication [26,29].

The optimization of the above equation is a least squares problem, and its closed-form solution can be achieved with the help of fast Fourier transform. However, the division and truncation in the frequency domain will lead to the amplification of both noise and estimation error. However, in this paper, we solve the optimization problem in the pixel domain directly with an effective conjugate gradient method combined with Newton’s method.

Let $ℬ\left(\mathit{K}\right)$ stand for the “$\mathit{arg}min$” function in the right-hand side of Equation (13), then its gradient $\nabla ℬ\left(\mathit{K}\right)$ and Hessian matrix $\mathit{H}$ are calculated in Equation (14) as follows:

$$\{\begin{array}{l}\nabla B\left(\mathit{K}\right)=2{\mathit{F}}^T\mathit{F}\mathit{K}-2{\mathit{F}}^T\mathit{G}+2{\alpha }_2\mathit{K}\\ \\ \mathit{H} =2{\mathit{F}}^T\mathit{F}+2{\alpha }_2\mathit{I}\end{array}$$

(14)

where $\mathit{I}$ is an identity matrix of the same size as ${\mathit{F}}^T\mathit{F}$, and the variable $\mathit{K}$ is eliminated in the Hessian matrix when calculating their second-order partial derivatives. The solution of $\mathit{K}$ can be achieved by Newton’s descent method. Furthermore, since $ℬ\left(\mathit{K}\right)$ is quadratic, the searching process converges within only one iteration [30]. Assume the starting point is ${\mathit{K}}_0=\mathbf{0}$, then the minimum is achieved for:

$$\begin{array}{ll}\widehat{\mathit{K}}& ={\mathit{K}}_0-{\mathit{H}}^{-1}\nabla ℬ\left({\mathit{K}}_0\right)\\ & =2{\mathit{H}}^{-1}{\mathit{F}}^T\mathit{G}\end{array}$$

(15)

Considering that the computation of the inverse of the Hessian matrix $\mathit{H}$ directly is very complicated and impracticable, and computing the inversion ${\mathit{H}}^{-1}$ is not the final aim, the solution of Equation (15) can be converted to the following form:

$$\mathit{H}\widehat{\mathit{K}}=2{\mathit{F}}^T\mathit{G}.$$

(16)

It can be seen that Equation (16) is a linear system of equations; it can be solved by the conjugate descent method effectively. During the alternating optimization, it should be noted that the blur kernel must be kept positive and normalized so as to satisfy the property of a PSF. As a result, the negative elements of the estimated $\mathit{K}$ are set to zero, and its elements, $K_i$, are then normalized to hold ${\displaystyle \sum }{K}_i$ = 1.

2.3. Image Restoration

With the estimated blur kernel $\mathit{k}$ from the above method, the latent image can be revealed by nonblind deconvolution algorithms, such as Wiener filtering and the Lucy–Richardson method, which were introduced decades ago. These deconvolution algorithms are classic and have been widely implemented in many fields. However, they are sensitive to noise, especially when the blur kernels are estimated incorrectly, and the ringing effect is unavoidable. Therefore, inspired by the kernel estimation discussed above, the sparse representation techniques can also be applied in the restoration of the latent image. Based on the statistical character of natural images in recent studies, the distributions of image gradient domains tend to have heavy tails and sharp tops, which means that most of their distribution is on small values, but the probability of large values is much greater compared to the Gaussian distribution [14,15,16,17,18,19]. Therefore, the hyper-Laplacian distribution-based prior can be used as a regularization term in the cost function as follows:

$$\widehat{\mathit{f}}=\mathit{arg}\underset{\mathit{f}}{\mathit{min}}\parallel \mathit{k}\otimes \mathit{f}-\mathit{g}{\parallel }_2^2+{\alpha }_2{\parallel \left({\nabla }_x\mathit{f}, {\nabla }_y\mathit{f}\right)\parallel }_p$$

(17)

where $p$ is derived from the hyper-Laplacian model, which signifies the slope of the exponential term of the density function. In Equation (17), it becomes the constraint term as a quasi-norm form, ${\parallel \cdot \parallel }_p$, as shown above. ${\nabla }_x\mathit{f}$ and ${\nabla }_y\mathit{f}$ are the image gradient domains in the horizontal ($x$-axis), and vertical ($y$-axis), respectively. The optimization can be solved by half-quadratic penalty method similar to that of Equation (7). With auxiliary variable $\mathit{v}=\left(v_x, v_y\right)$, the alternating scheme is shown as follows:

$$\{\begin{array}{l}\widehat{\mathit{v}}=\mathit{arg}\underset{\mathit{v}}{\mathit{min}}{\parallel v\parallel }_p+\frac{{\beta }_2}{{\alpha }_2}\parallel \left({\nabla }_x\mathit{f}, {\nabla }_y\mathit{f}\right)-{(v_x, v_y)\parallel }_2^2\\ \widehat{\mathit{f}}=\mathit{arg}\underset{\mathit{f}}{\mathit{min}}\parallel \mathit{k}\otimes \mathit{f}-\mathit{g}{\parallel }_2^2+{\beta }_2\parallel \left({\nabla }_x\mathit{f}, {\nabla }_y\mathit{f}\right)-{(v_x, v_y)\parallel }_2^2\end{array}$$

(18)

The solutions for the $\widehat{\mathit{v}}$-subproblem vary with different $p$ values. In particular, when $p=1$, the analytical solution can be obtained in Equation (19) by the soft thresholding algorithm [17] as follows:

$$\widehat{\mathit{v}}=sgn\left(\mathit{v}\right)\max \left\{\mathbf{0}, \left|\mathit{v}\right|-T\right\}$$

(19)

where $T={\alpha }_2/\left(2{\beta }_2\right)$ is the threshold and $sgn(\cdot )$ represents the signum function.

It should be noted that the solutions in the horizontal and vertical orientation have the same form in the following Equation (20)–(22), therefore the subscripts related to orientations are omitted for briefness and convenience.

In general, for an arbitrary $p$, the minimization problem can be solved by setting the derivative of the $\widehat{v}$-subproblem to zero. Therefore, for the $i$th element of $v$ and $\nabla \mathit{f}$ in horizontal orientation, we get:

$$p{\left|v_i\right|}^{p-1}sgn\left(v_i\right)+\frac{2{\beta }_2}{{\alpha }_2}\left(v_i-\nabla {\mathit{f}}_i\right)=0$$

(20)

In particular, when $p=0.5$, the $\widehat{\mathit{v}}$-subproblem in Equation (18) can be simplified to a cubic function:

$$v_i^3-2\nabla {\mathit{f}}_i{v}_i^2+\nabla {\mathit{f}}_i^2{\mathit{u}}_i-{\left(\frac{{\alpha }_2}{4{\beta }_2}\right)}^{2}sgn\left(v_i\right)=0$$

(21)

which can be solved using Cardano’s formula [31].

When $p=2/3$, the $\widehat{\mathit{v}}$-subproblem in Equation (18) can be expanded as a quartic function:

$$v_i^4-3\nabla {\mathit{f}}_i{v}_i^3+3\nabla {\mathit{f}}_i^2{v}_i^2-\nabla {\mathit{f}}_i^3{v}_i-{\left(\frac{{\alpha }_2}{3{\beta }_2}\right)}^3=0$$

(22)

which can be solved using Ferrari’s and Descartes’ solutions [31].

For some special cases where $p>1$, analytical solutions can be referred to in [32]. However, for the remaining $p$ values, no analytical solution exists, and the Newton–Raphson root finding method is more effective [30].

The $\widehat{\mathit{f}}$-subproblem is similar to Equation (12) and, hence, its solution can also be determined in the frequency domain in Equation (23), as follows:

$$\widehat{\mathit{f}}=IDFT\left[\frac{G\circ K^{*}+{\beta }_2{V}_x\circ D_x^{*}+{\beta }_2{V}_y\circ D_y^{*}}{K\circ K^{*}+{\beta }_2{D}_x\circ D_x^{*}+{\beta }_2{D}_y\circ D_y^{*}}\right]$$

(23)

where “IDFT” stands for the inverse discrete Fourier transform operation; $V_x$ and $V_y$ stand for the DFT of $v_x$ and $v_y$, respectively; and $D_x$ and $D_y$ is the DFT of the differential operators in horizontal orientation, ${\nabla }_x$, and vertical, ${\nabla }_y$, respectively. The treatment for zero denominator is the same as that in Equation (12).

2.4. Smooth the Image Boundaries

When processing a digital image in the frequency domain via DFT, this indicates that the pixel domain is assumed to be periodical. This means that the top and bottom of the image are connected similar to the left and right sides. In practice, the image size should be expanded to a proper size and be padded with zeroes or other values to avoid aliasing, according to the Nyquist sampling criterion, which dramatically reduces the smoothness of the padded image.

One approach to address this issue is to pre-process the image to be symmetric when padding, and then use the “edgetaper” function in MATLAB, which only blurs the edges of the input image with a specified PSF and keeps the center region. In this way, the pixel values in the boundary are equal to the weighted sum of the original image and become differentiable. However, this method cannot ensure ${\mathrm{C}}^2$ continuity. In this paper, we padded the images by minimizing the summation of second-order partial derivatives of the image borders to satisfy the 2nd-order smoothness. This technique was also referred to by Liu and Jia [33].

3. Results and Discussion

In this section, the proposed deblurring method is verified by both simulated motion-blurred images and atmospheric turbulence blur in real-life applications. For simulations, the test images were taken from the Kodak Lossless True Color Image Suite [34], and were numbered as “Img01,” “Img02,” etc., for ease of comprehension. Figure 3 shows examples of the ground truth images for which the testing process is outlined in the following subsections.

We compared the proposed method with several other blind image deblurring methods. Shan et al. used both the image gradient domain and pixel domain in the cost function for the data fitting term, together with a natural image prior and uniform prior [35]. Cho and Lee used the shock filter and bilateral filter with multiple orientations of images to enhance the structures, with the aim of ensuring that the histograms of the gradient domain of the reconstructed images are similar to those of the original [36]. Krishnan et al. proposed an image prior model based on a piecewise function that approximates the statistical characteristics of natural images using a sparsity representation technique [37]. They solved the deblurring problem using an iterative shrinkage-thresholding algorithm. Wu and Su used the graph Laplacian matrix as the cost function and obtained the clear image by an iterative solution [38].

3.1. Comparisons of Blur Kernel Estimations

The ground truth of blur kernels was taken from Levin et al. who represent a variety of PSFs of motion blurs in daily life. Blur kernels are numbered as “(a),” “(b),” etc., for convenience [27]. Their sizes range from 13 × 13 to 27 × 27 and their support domain varied from 10 to 25 pixels. The labels and sizes are listed in the first two lines in

Table 1. Comparison results of the blur kernel estimation. The cost durations are recorded in seconds, and the best results of mean square error (MSE) are shown in bold.

PSF	Number	(a)	(b)	(c)	(d)	(e)	(f)	(g)	(h)
	Size	$19\times 19$	$17\times 17$	$15\times 15$	$27\times 27$	$13\times 13$	$21\times 21$	$23\times 23$	$23\times 23$
Method in [35]	Duration	64.572	63.431	56.714	81.508	50.356	67.938	69.447	74.999
	MSE	0.6182	0.2592	0.2259	0.1062	0.6942	0.2656	0.1457	0.0975
Method in [36]	Duration	6.9690	6.9370	6.8580	7.5930	6.1690	7.0620	7.0930	7.3120
	MSE	0.4893	0.3763	0.3722	0.0977	0.7499	0.2036	0.0867	0.1339
Method in [37]	Duration	95.979	56.916	35.043	211.07	25.636	110.29	131.32	143.96
	MSE	0.6249	0.7617	0.2892	0.3221	0.4817	0.3404	0.1711	0.4252
Method in [38]	Duration	71.577	70.950	65.525	126.08	58.953	77.165	110.45	119.04
	MSE	0.5624	0.3650	0.1807	0.1364	0.2374	0.2312	0.1012	0.1525
Proposed method	Duration	14.702	14.327	13.796	28.076	13.171	18.061	21.624	21.653
	MSE	0.4823	0.1540	0.1024	0.0675	0.1110	0.1161	0.0627	0.0821

.

3.2. Comparison of Deblurring Results.

The first row of Figure 4 shows the eight ground truth blur kernels. To evaluate the effectiveness of blur kernel estimation, a test image, namely “Img21,” was artificially blurred by the eight ground truth blur kernels, therefore eight simulated blurred images were obtained. Subsequently, these blurred images were used as the inputs of the proposed method and other methods discussed above.

To evaluate the blur kernel estimation more objectively, the mean square errors (MSE) of the estimated blur kernels were calculated and are listed in Table 1. The cost durations for the deblurring methods were also recorded. Our method was implemented in MATLAB, and the comparisons were assessed using a Windows platform with an Intel Xeon E5-2620 v4 CPU (2.1 GHz, 8 cores) and 32 GB RAM. The comparison results are shown in Figure 4.

Table 1 shows that the proposed method achieves faster convergence than most of the other methods. Because the method in [36] adopts the fast Fourier transform technique both in the kernel estimation and in the deblurring process, we estimated the blur kernel in the pixel domain directly, using the conjugate descent method. Although our estimation of the blur kernels required more time, we avoided truncation and division operations in the high-frequency domain; this effectively improved the estimation accuracy. In practice, the estimated blur kernels of our method achieved the best visual effects and achieved the lowest MSE as shown in the last row of Figure 4 and Table 1.

In our experiments, to evaluate our method and compare it with other similar ones, we used the peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) as the full-reference image quality assessment (FRIQA) parameters, which are shown in Equations (24) and (25).

The PSNR [39] is a conventional indicator that is widely employed for measuring the quality of image reconstruction:

$$PSNR\left(\mathit{x},\mathit{y}\right)=10\lg \frac{L^2}{MSE\left(\mathit{x},\mathit{y}\right)},$$

(24)

where $x$ and $y$ represent the reference image and deblurred result, respectively, $MSE\left(x,y\right)=x-y_2^2$ represents the mean square error between them, and $L$ stands for the image dynamic range.

The SSIM [39] is a full-reference metric for measuring the similarity between two images, $x$ and $y$, and is defined as follows:

$$SSIM\left(\mathit{x},\mathit{y}\right)=\frac{\left(2\overline{\mathit{x}}\overline{\mathit{y}}+C_1\right)\left(2{\sigma }_{\mathit{x}\mathit{y}}+C_2\right)}{\left({\overline{\mathit{x}}}^2+{\overline{\mathit{y}}}^2+C_1\right)\left({\sigma }_{\mathit{x}}^2+{\sigma }_{\mathit{y}}^2+C_2\right)}$$

(25)

where $\overline{x}$ and $\overline{y}$ are the mean values, ${\sigma }_x$ and ${\sigma }_y$ are the standard deviations, and ${\sigma }_{xy}$ is the cross-covariance. Furthermore, $C_1={(k_{1}L)}^2$ and $C_2={(k_{2}L)}^2$ are factors used to ensure stability in case of division with a small denominator, with $k_1=0.01$ and $k_2=0.03$ in general.

An example of “Img02” blurred by kernel “(b)” and the deblurring results are shown in Figure 5. The white ball and the latch, as well as the wood grains and cracks, are blurred and indistinct, as shown in Figure 5a. The deblurring method described in [35] significantly reduces the blur in Figure 5b, but the result is still unsatisfying. The methods described in [36,37] introduce the ringing effect, both around the ball and wood cracks, as they are obvious in Figure 5c,d. This phenomenon is reduced by the method described in [38] as shown in Figure 5e. However, wood grains in the image are not clear enough. In contrast, as it can be seen in Figure 5f, the proposed method restores both the texture and the background.

Figure 6 shows an image, namely, “Img07,” blurred by kernel “(a).” As can be seen in Figure 6b, the deblurring method described in [35] reduced some of the blurriness; however, the visual effect is still lacking. Particularly, the shutters in the background are still not clear enough, and the estimated blur kernel shown in the top left is a little rough when compared with others. Moreover, as it can be seen in Figure 6c,d, the method described in [36,37] restored the sharpness, but introduced strong artifacts, especially around the petals and leaves. These limitations were overcome by the method described in [38] (see Figure 6e), as well as by the proposed method (see Figure 6f), which restored most of the details, and the shape of its estimated blur kernel is the closest to the ground truth data.

Figure 7 shows another example blurred by kernel “(f)”; the image here is “Img21.” The lighthouse and cabins are blurred and unclear in Figure 7a. As can be seen in Figure 7b, the deblurring method described in [35] reduced some of the blurriness; however, the visual effect is still lacking. In addition, as can be seen in Figure 7c, the method described in [36] restored the sharpness but introduced strong artifacts along the roofs and the white tower. In Figure 7d, because the method described in [37] estimated a blur kernel with numerous outliers, its deblurring result is not as good as the others. The limitation was partially overcome by the method described in [38]. There were still, however, some outliers in the estimated blur kernel shown in Figure 7e; the general outlines of the kernel were estimated correctly. In contrast, the proposed method not only estimated the most appropriate blur kernel, but also obtained a clear result with high quality.

Table 2. Full-reference image quality assessment data of the comparison results of Figure 5, Figure 6 and Figure 7.

Test Images	FRIQA	Method in [35]	Method in [36]	Method in [37]	Method in [38]	Proposed Method
“RedDoor.png”	PSNR	28.660	26.126	27.126	28.633	28.986
	SSIM	0.9751	0.9570	0.9660	0.9764	0.9787
“Flowers.png”	PSNR	27.411	26.082	27.429	27.826	28.240
	SSIM	0.9049	0.9120	0.9173	0.9122	0.9177
“Lighthouse.png”	PSNR	25.197	24.297	24.887	25.577	25.841
	SSIM	0.8816	0.8724	0.8651	0.8791	0.8867

lists the original FRIQA data of a comparative analysis performed on the examples. For all of these—“Img02,” “Img07,” and “Img21,”—the PSNR and SSIM were the highest for the proposed method.

More comprehensive comparisons were carried out on all 24 tested images in the Kodak Lossless True Color Image Suite, which was introduced at the beginning of Section 3 [34]. The statistics related to the PSNR and SSIM, as determined from a comparative analysis of all the simulated motion-blurred images, are shown in Figure 8 and Figure 9, respectively. In the deconvolution procedure, any slight noise or outliers in an estimated blur kernel can cause errors in the image gray values; the shapes and offsets of the blur kernels can also affect the pixel positions in the deblurred results. In addition, the testing ground truth images were wrapped with gray or black boundaries. As the PSNR value is based on the MSE of the images, it mainly depends on image contrast and gray scales. Additionally, the SSIM value uses the image absolute means and the standard deviations. These two metrics have their advantages and make up for each other’s shortcomings. In this paper, therefore, we use both metrics to evaluate the deblurring results. As can be seen in Figure 8 and Figure 9, the PSNR values of our results for “Img03” and “Img10” are lower than others, but their SSIM values are the highest. Similarly, the phenomena of “Img04” and “Img22”, with lower SSIM values, but the highest PSNR values, derive from the same reasons. Once again, it can be seen that the proposed method was superior to other methods in most cases.

3.3. Real-Life Applications

In building and infrastructure construction, a theodolite is used to measure angles between designated visible points in the vertical and horizontal planes. In special tasks, however, such as long-range detection in the morning, the imaging quality is greatly reduced by atmospheric turbulence. In our project, a customized theodolite equipped with a high-speed camera was used to capture photo sequences (in gray scale) of targets over 1.5 kilometers away in the open air of a military base. The photographs were taken early in the morning on a sunny day in autumn. The focal length of the camera was 2000 mm; the exposure time was 4 ms; and the frequency was 50 frames per second. Some examples of the targets captured over long distances are shown in this paper. The deblurring results obtained using this method are shown in Figure 10, Figure 11 and Figure 12. In Figure 10a, the numeric character on the watchtower is dim and illegible, and the stairs are unclear. In Figure 11a and Figure 12a, the edges of the chimney and the signal pole are indistinct. Figure 10f clearly shows that the character on the watchtower and the outlines of the stairs are more detailed. The area around the edges of the chimney and pole are clearer than in the images obtained using other methods, as shown in Figure 11f and Figure 12f.

To evaluate the deblurring methods for images without ground truth, we used the Blind Image Quality Index (BIQI) and the Spatial-Spectral Entropy-based Quality (SSEQ) index as the non-reference image quality assessments (NRIQA). Both of these constitute a scoring mechanism: a 2-D image is inputted and then a score is outputted (100 represents the worst quality while 0 represents the best). The BIQI was proposed based on distorted image statistics (DIS), and the proposers found that the distortions of natural images have unique characteristics using DIS, and the images can be classified into distortion categories via these characteristics; details can be obtained from [40]. The SSEQ index utilizes down-sampled responses as inputs, then a local entropy feature vector of twelve dimensions can be extracted, and the image quality scores are generated from these features via a learning-based method [41].

Table 3. Non-reference image quality assessment data of the comparison results of Figure 10, Figure 11 and Figure 12.

Test Images	NRIQA	Method in [35]	Method in [36]	Method in [37]	Method in [38]	Proposed Method
“Tower.bmp”	BIBQ	46.347	38.829	41.496	39.855	37.293
	SSEQ	37.831	46.839	40.268	36.637	35.693
“Chimney.bmp”	BIBQ	57.800	52.974	58.437	52.889	51.953
	SSEQ	69.902	52.127	59.659	49.884	33.326
“Pole.bmp”	BIBQ	52.357	45.612	46.507	45.246	41.586
	SSEQ	45.693	52.588	44.672	39.171	37.514

shows the original NRIQA data of a comparative analysis performed on the examples.

4. Conclusions

In this paper, we proposed and evaluated an image deblurring method based on sparse representation. We determined the image prior based on the nonzero measurement in the gradient domain of natural images, which is an efficient prior for blur kernel estimation. We optimized the cost function via the split Bergman iteration that turned the non-convex problem into an alternating scheme, and the blur kernel could be estimated correctly in a coarse-to-fine manner for avoiding local minima. Subsequently, we revealed the latent image through a similar technique with the help of the hyper-Laplacian distribution-based prior with the estimated blur kernel. In the interim, to reduce ringing effects, we preprocessed the image boundaries to achieve second-order smoothness. Moreover, the deblurring algorithm converged quickly owing to the analytical solutions of the subproblems. The results of experiments and comparative analysis shows that the proposed method can obtain improved results compared with other similar deblurring methods. In addition, our method is effective when dealing with atmospheric turbulence blurs in real-life applications. Because our deblurring framework is based on a linear system, it works well on spatially invariant blurs in most scenarios. In the future, the deblurring model can be extended to nonlinear blurs for wider applications.