1. Introduction
The development of alternative energy sources is becoming increasingly necessary in Korea to prepare for an era of hefty oil prices, as Korea faces energy and resource shortages and imports approximately 97% of its fossil fuels. The post-Kyoto Protocol, which is in effect since 2013, limits the rate of emission of greenhouse gases. In 2000, Korea’s CO
2 emissions amounted to 480.4 million tons, making Korea the ninth highest CO
2-emitting country worldwide. Most of the greenhouse gases emitted come from energy consumption [
1,
2,
3].
The Korean government initiated a program known as law section 11 to reduce the consumption of fossil fuels. The program promotes the supply of renewable energy by enforcing the use of renewable energy systems for more than 5% of the total construction cost for public buildings whose floor space is more than 3000 m
2. Moreover, the Korean government set up a plan in 2000 for stimulating the consumption of renewable energy in order to increase the renewable energy share of the total energy consumption to 5% by 2018 [
4]. Geothermal energy, defined as thermal energy generated and stored in the ground, is considered to be a relatively clean and inexhaustible source of renewable energy. Geothermal energy comes mainly from the breakdown of natural radioactive isotopes of uranium, thorium, and potassium. The average heat flow on the surface of the earth is 82 W/m, and the total heat loss is approximately 42 × 10
6 MW. The estimated total thermal energy from the surface of the earth to a depth of 10 km is 1.3 × 10
27 J, which corresponds to burning of 3 × 10
17 barrels of oil.
The heat content of rocks on the Earth’s surface is the largest source of geothermal energy. The highest hundreds of meters of crust are not a geothermal reservoir in the classical sense, but the temperature in the area is too low for immediate use. Adjusting only the heat pump gives access to this wide range of resources, which increases the temperature of the heat carrier fluid. The most extensive technique to utilize shallow geothermal resources involves borehole heat exchangers (BHE) with geothermal heat pumps [
5,
6].
After inserting the BHE into the drilled hole, the borehole is grouted by mixing sand, cement, and bentonite. An important role of boreholes is that thermal contact is a very important factor to ensure sufficient heat transfer properties between the borehole wall and the water circulation system to prevent vertical movement of water. [
7]. A thermal response test (TRT) requires suitable measuring equipment to select the thermal performance of the BHE. This test takes into account the overall heat transfer characteristics including groundwater effects and other disturbance factors. The first approach for the constant heat injection or extraction is provided by Morgensen [
8] and is based on the line source method [
9]. Firstly, mobile TRT devices were deployed in Sweden [
10] and the United States [
11]. After this period, analytical methods were greatly improved in several countries [
10,
11,
12]. However, it is more practical than standardized TRT measurements, and it contributes in an easy-to-use way, further reducing TRT costs. The thermal performance characteristics of the ground are measured in a laboratory, but the results are generally inaccurate with some errors. These methods tend to ignore site conditions, such as groundwater effects and grouting materials. [
13]. For actual measurement, it is necessary to select a test suitable for local conditions and prepare to compare the thermal performance of various BHE types of underground heat exchangers [
14]. The literature allows you to find references to the appropriate number of geothermal system heat pumps (GSHP) and BHEs in the field, design, economic analysis and standard booklets [
7,
15,
16,
17,
18,
19]. Various BHE types (single U type, double U type, coaxial type) and grouting materials are used in GSHP systems. The thermal conductivity and length for BHE in one place should be the same in continuous testing, whereby only BHE type and grouting material can be changed. Ground thermal conductivity (l) and thermal resistance (Rb) for different coaxial BHE types and grouting materials were obtained. To the best of the authors’ knowledge, field studies of this combination are yet to be conducted in the literature. The effectiveness of thermal bore hole resistance was evaluated against the GSHP’s coefficient of performance (COP) and could not be ignored.
The previous study’s standing column well (SCW) [
20,
21] showed that the SCW can reduce the overall borehole length compared to a conventional closed-loop system consisting of a single U-tube heat exchanger. In addition, the improvement of the performance of the SCW can be improved by utilizing groundwater, and some groundwater from the well is discharged (exhausted) without being completely recycled to the SCW system. Groundwater bleeding regulates the well temperature by inducing a flow toward the well. Rees et al.’s [
22] parametric research showed that bleeding rate is one of the most important parameters affecting SCW performance, and integrating a bleeding strategy into SCW can significantly reduce depth, capital cost, and life-cycle cost compared to no bleeding. Numerical studies of previous models of standing column wells [
23,
24,
25] made many assumptions about heat transfer between the various components of the well.
There are relatively few design tools and simulation models available for SCW systems [
22,
26,
27]. Standing column wells are in limited use since the development of geothermal heat pump systems; however, in recent years, overall performance improved in areas with adequate hydrological and geological conditions, attracting more attention [
22,
28,
29,
30]. In addition, many studies using single- and multi-well standing column wells were carried out recently, and studies reported that the efficiency is improved by using a plurality of SCW systems and using bleeding of water rather than a sealed heat exchanger.
In recent years, SCW systems, which are more efficient than sealed type, are increasingly installed in areas where geological properties and groundwater utilization conditions are suitable [
31,
32]. The focus of attention on these systems is not only due to the high thermal efficiency of the SCW system, but also because the SCW system requires less construction area than the enclosed system, which is of primary importance in urban areas. In the case of the SCW system, a numerical analysis model is being developed by applying finite volume and finite element methods in consideration of complex underground heat and groundwater circulation [
33,
34,
35,
36]. However, these numerical models cannot be reflected in hourly simulation programs or designs because calculations are too complicated and conditions over time are too heavy. Therefore, it is often simplified by an empirical approach and approximation from real design. This is why the direction and performance of recent research focused on the development of models that simplify the SCW system [
37,
38,
39].
The groundwater heat pump system using groundwater extracted from the same well hole and being recovered into the same well hole in a semi-open loop arrangement was widely known as the SCW (standing column well) system. The ground heat exchangers in these systems consist of vertical boreholes filled with groundwater up to the groundwater level [
40,
41]. In an open-loop pipe circuit, water is circulated from the well through a heat pump to return to the same well, and, for most of the year, the system works by recirculating water between the well and the heat pump. However, during the peak temperature period, only a portion of the flow can be returned to the well, and the rest can be drained to “bleed” some water from the system [
41]. This leads to groundwater flow from the surrounding formation to the well. This system in case of bleeding cools the wells and surrounding grounds during heat removal in the summer and heats the wells and surrounding grounds during heat extraction in the winter. The open SCW system according to the circulating water ratio of this bleeding showed that the effective thermal conductivity characteristics are superior to the existing SCW [
42,
43].
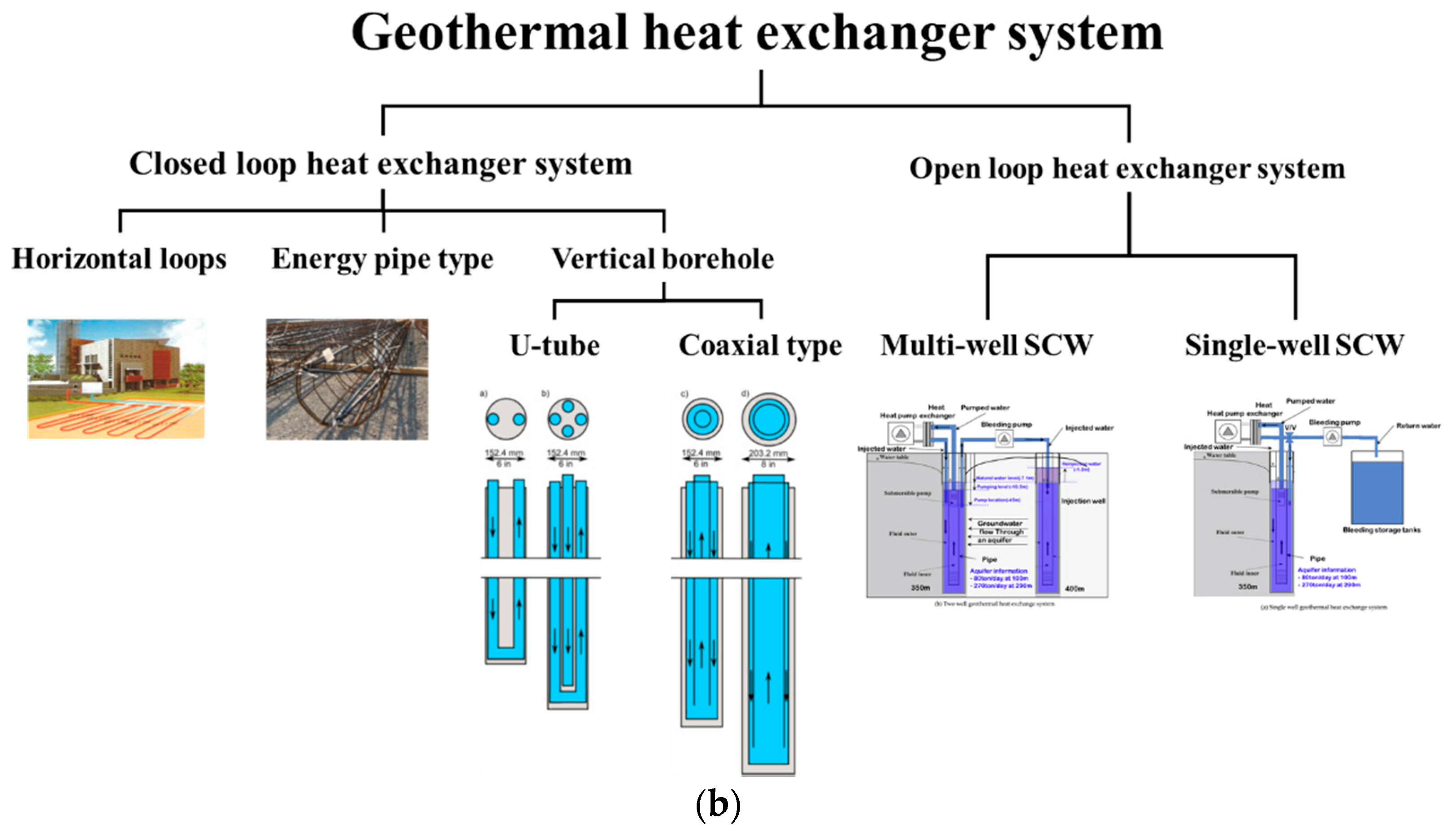
A schematic diagram of geothermal heat exchange systems is shown in
Figure 1. The geothermal heat exchanger system is divided into two types: closed type and open type. The sealed heat exchanger is divided into surface water loops, wells to groundwater, and ground heat exchangers in vertical bores and horizontal loops. In addition, the open heat exchanger is divided into a single-well and a multi-well SCW system.
In this study, we compared, analyzed, and investigated the effective thermal conductivity of a borehole geothermal heat exchanger system and the effective thermal conductivity not applied when bleeding single-well SCWs are used. We also investigated the heat transfer characteristics during the bleeding of two-well SCWs, where water is injected from one clearing hole to the returning hole according to the bleeding rate. To compare the characteristics of closed and open heat exchangers, single- and two-well heat exchangers, for the effective thermal conductivity coefficient in the same borehole with the same depth, we intend to generate basic data on the basis and performance of geothermal heat exchanger design. The geothermal heat exchanger was characterized and the thermal performance was compared under these three conditions.
2. In Situ Thermal Response Test
Several techniques can be employed to predict the thermal conductivity of a GHEX design. The easiest approach is to use the standard value of the rock where the GHEX is located. However, this method may require expensive samples and may not provide a full profile of the field. Mogenson [
8] presented a thermal response test (TRT) for estimating the ground value of underground thermal conductivity and the thermal resistance of a borehole system. The general method of TRT adopts a system in which the heat medium fluid circulates through the Hall system at a constant heat injection rate, as shown in
Figure 2. The thermal response is then recorded continuously. After data acquisition, the temperature data are compared with mathematical models such as the source model [
44,
45,
46,
47,
48]) or cylindrical source model [
44,
45,
46,
49,
50].
Figure 3 consists of the trailer-type transport system used in this study [
52,
53,
54,
55,
56]. In addition, a schematic diagram of the experimental set-up of the SCW system showing the thermal response of the test equipment shown in
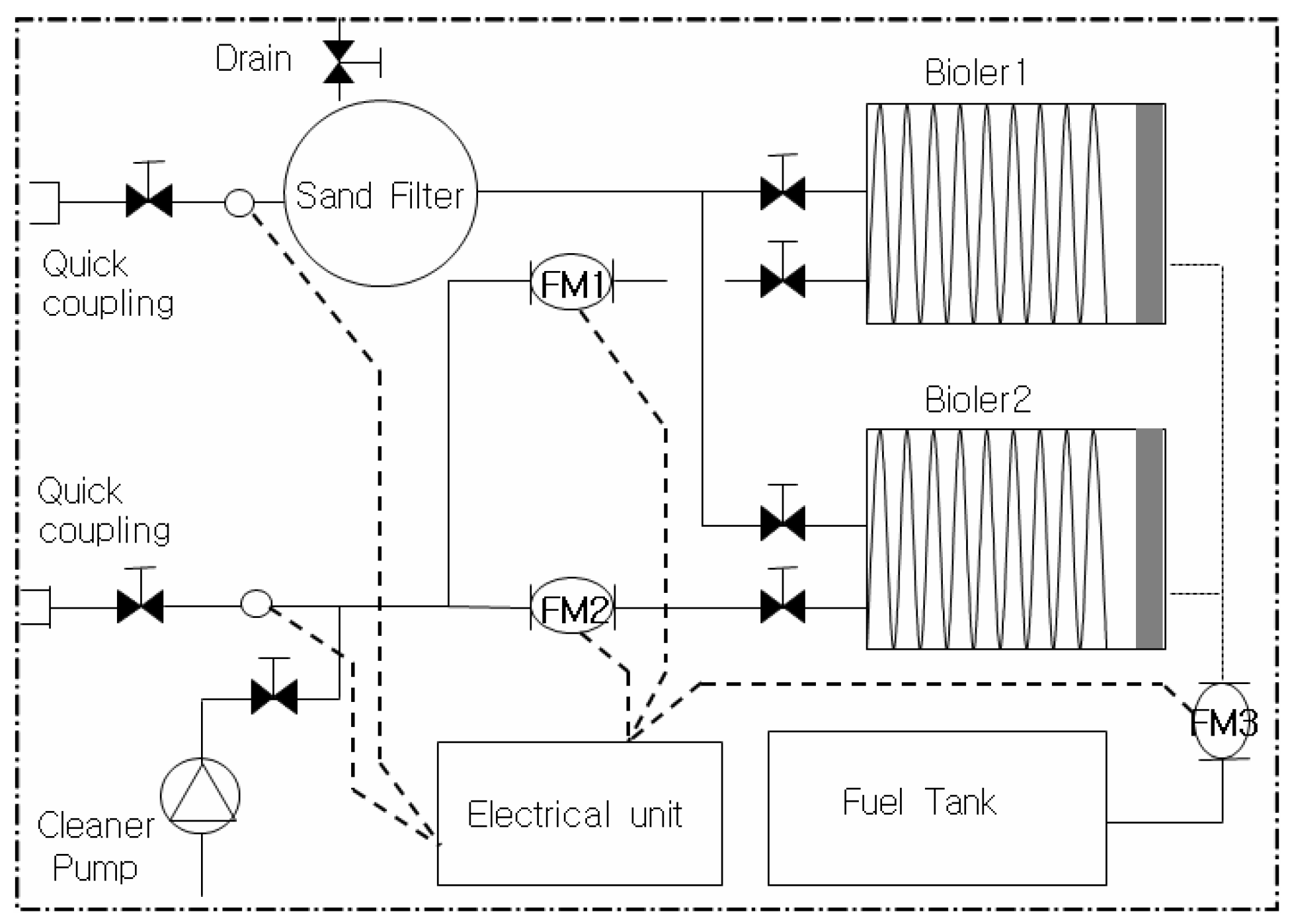
Figure 4 is shown. In the test set-up (Agilent 34970A), a measurement program (LabView) and a flow meter were used to measure temperature and flow. Control circuits and temperature sensors were installed on each pipe at the inlet/outlet, including boilers and filters. Each device used an instrument that was calibrated at the factory or regularly. The boiler capacity provided 84 kW (42 kW × 2 units) of oil condensation. The flow rate of the circulating fluid was measured using a flow meter (Macnaught). In addition, a return pipe flow meter (water meter) was installed and the bleeding rate was controlled to measure the bleeding rate of the measuring device without introducing water into the SCW system.
Table 1 shows the components installed in the experimental and measurement devices used in this study.
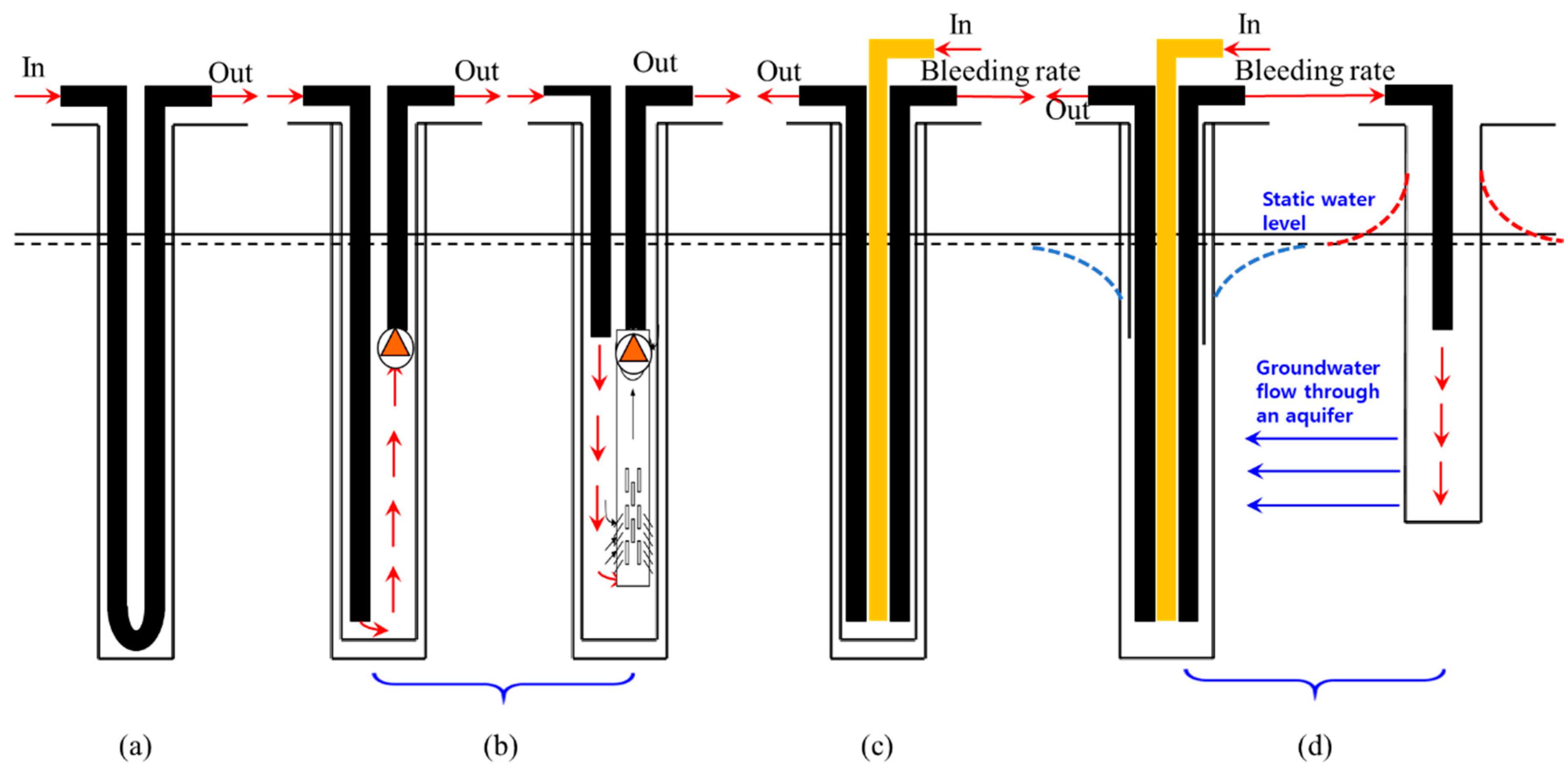
Figure 5 shows the behavior of the closed borehole and single/two-well SCW systems according to the exponential and exponential used in this study, as well as the position of the return pipe. The groundwater heat exchanger under test is of type SCW, eight inches in diameter and 350 m and 400 m deep. It has a PVC inner casing and a top extraction/bottom circulation structure. During the drilling process, water intake was observed to increase significantly at depths of 80–100 m and 270–290 m. The maximum quantity analyzed was found to be in the range of 600–800 tons/day based on the groundwater impact survey results, and the stable withdrawal capacity was found to be in the range of 200–250 tons/day.
Table 2 shows the bleeding percentage used in this study. The bleeding rates of 10% and 25% have absorption capacities of 80 tons/day and 200 tons/day (0.06 m
3/min and 0.13 m
3/min), respectively. In this study, the characteristics of single-well and two-well underground heat exchangers were compared. We also evaluate the thermal performance of a two-well system and a single-well system underground heat exchanger when there is no discharge rate and when returning from the inlet and re-injecting the discharge into the wells [
40,
41,
42].