Stepwise Intelligent Diagnosis Method for Rotor System with Sliding Bearing Based on Statistical Filter and Stacked Auto-Encoder
Abstract
:1. Introduction
- The proposed method can automatically learn useful fault information with the deep structure of SAE, which cannot depend on rich experiments and professional knowledge to implement intelligent fault diagnosis. Moreover, the statistical filter in the proposed method can attenuate noise effects to extract the sensitive feature further, and it can sensitively reflect the symptoms of the equipment states.
- The proposed method effectively distinguishes five kinds of conditions through the stepwise intelligent diagnosis with the SAE after filtering. Although the various faults similarities in sliding bearing are higher than others in rotor system, it can accurately and efficiently distinguish them in a large number of signals.
- The detail relationship between fault feature and fault type in sliding bearing can be described with the data mining capabilities owning to SAE, which is not affected by the negative impact of the data dimension. Therefore, it can objectively and effectively improve the diagnosis accuracy and enhances the robustness of the proposed method.
2. Basic Theory
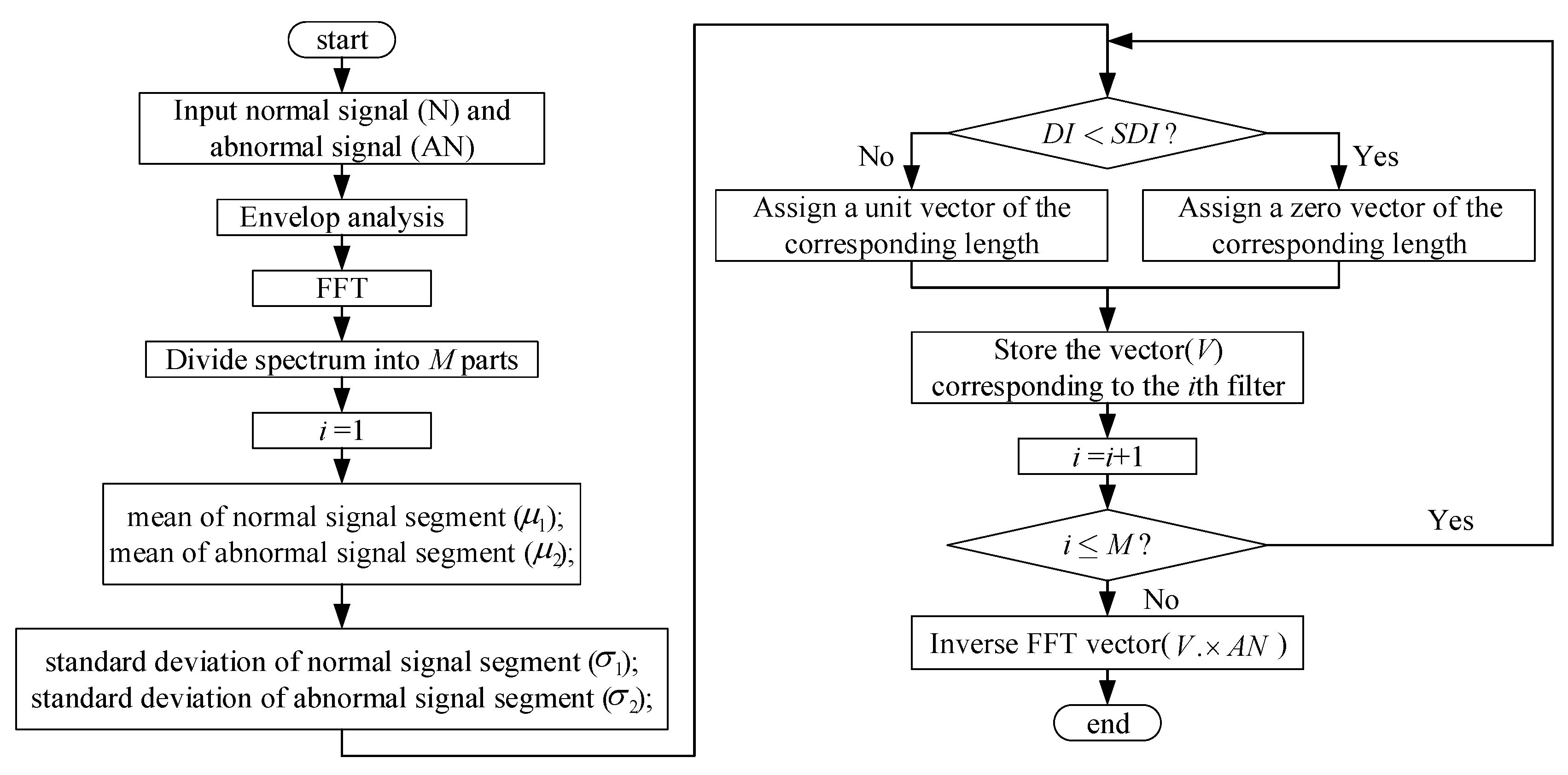
2.1. Basic Concept of the Statistical Filter
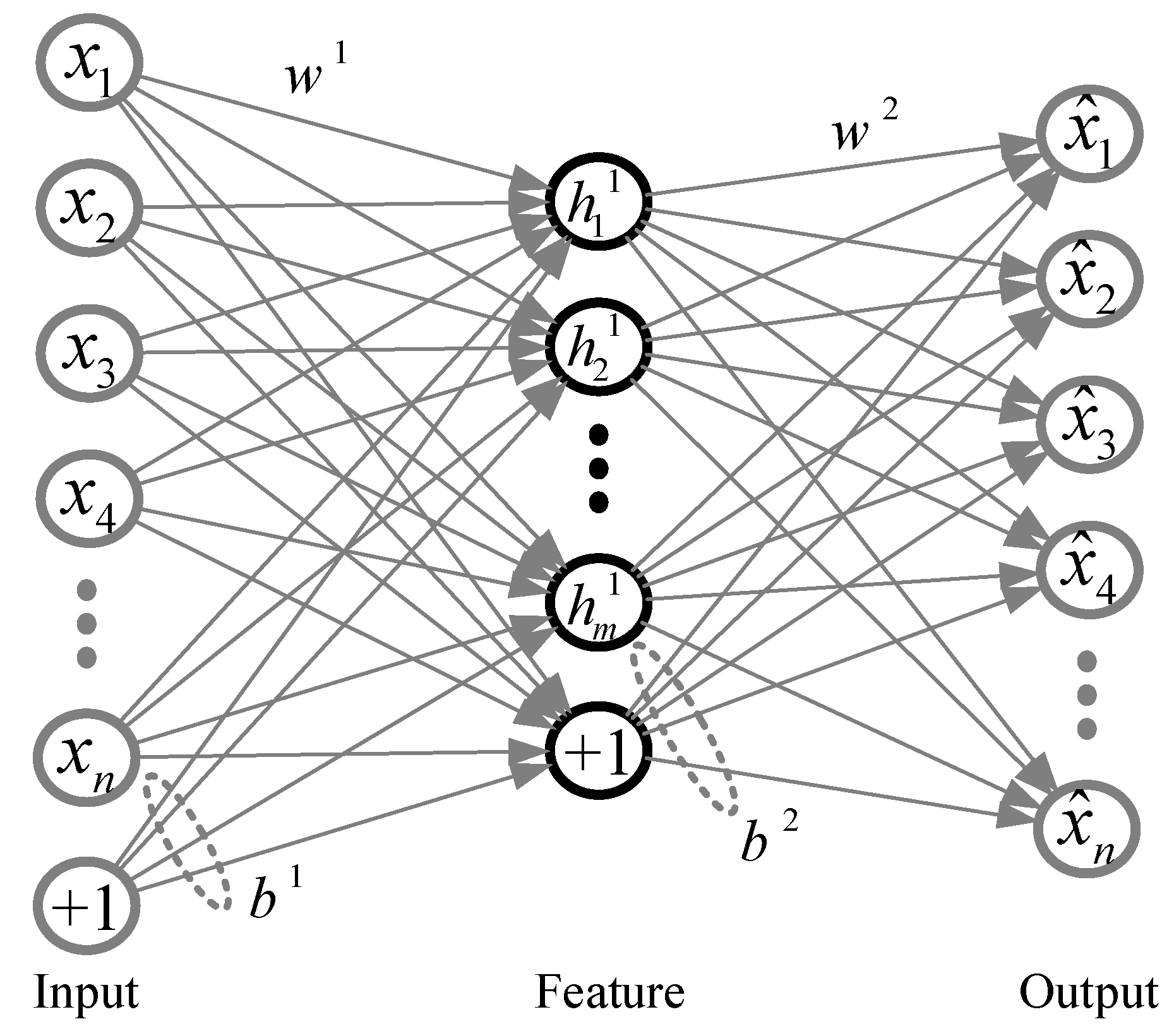
2.2. Framework of Auto-Encoder
2.3. Stepwise Intelligent Diagnosis Method Based on SAE
2.4. Proposed Method
- Raw signals of sliding bearing in normal state and 4 kinds of abnormal states using professional experimental platform with sensors;
- Filter noise with the statistical filter between normal state and each abnormal state;
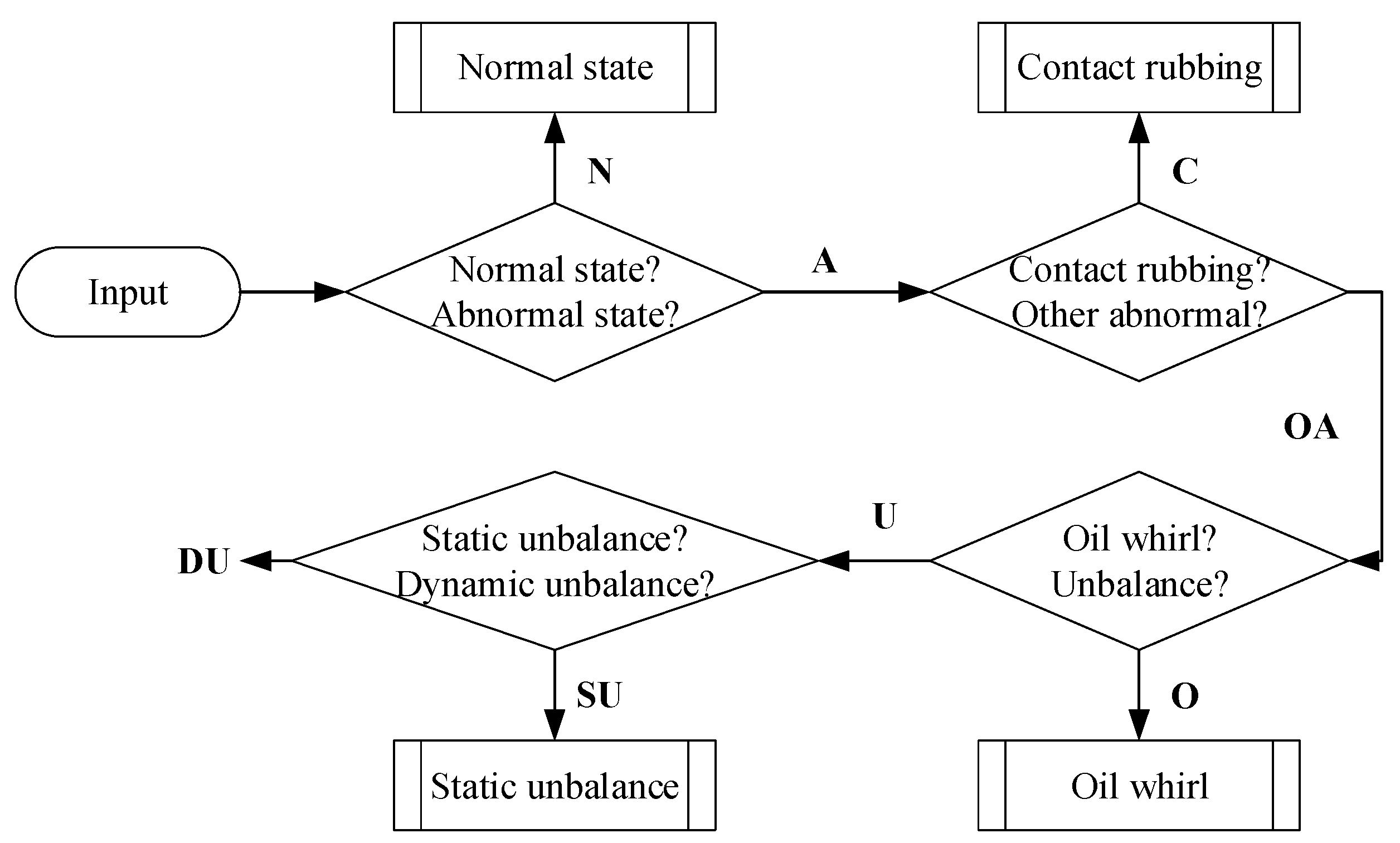
- Decompose five kinds of bearing states into four groups according to Figure 4 and perform the stepwise bearing fault diagnosis with SAE to distinguish two states at each time;
- Establish the deep hierarchical structure with the rule of greedy training, where the auto-encoders are utilized to obtain characteristics of the training sets; output the diagnosis results and stop diagnosis until distinguishing the static unbalance and dynamic unbalance.
- Apply the testing sets to confirm the accuracy of the fault diagnosis with the trained SAE.
3. Experiment Setup and Data Acquisition
4. Results and Discussion
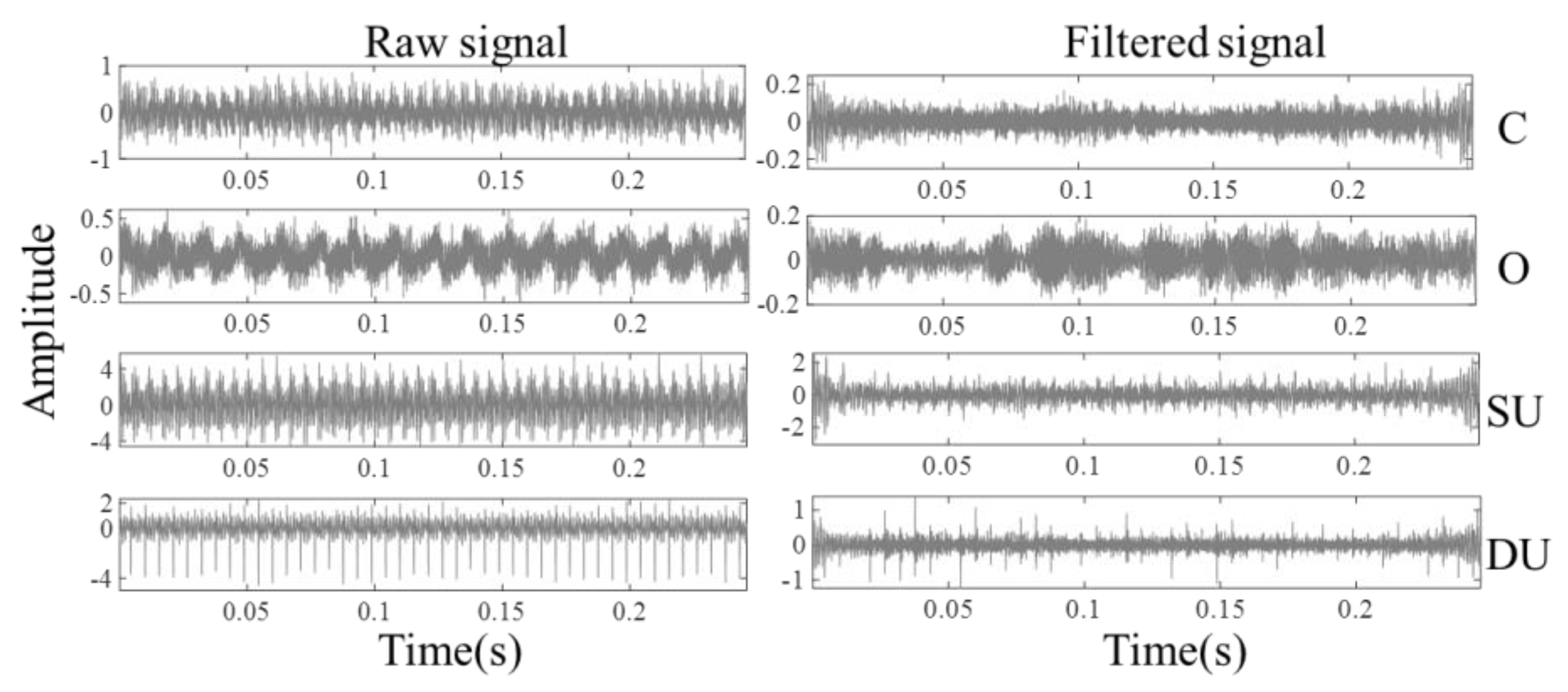
4.1. Data Preprocess with Statistical Filter
4.2. Stepwise Intelligent Fault Diagnosis Based on SAE
4.2.1. Description of Data in Stepwise Process
- There are five kinds of sliding bearing signal (normal state, contact rubbing, oil whirl, static unbalance, and dynamic unbalance) in this experiment and they are one-dimension data whose length is 1,000,000; moreover, the statistical filter is utilized to filter the noise and obtain the new data that marked as normal state , contact rubbing , oil whirl , static unbalance and dynamic unbalance ;
- The data can be reconstructed into a matrix and the number of rows of the matrix is 8192 (213 = 8192), and it fully contains the amount of data generated by one rotation of the sliding bearing; the column of the matrix change with the stepwise intelligent diagnosis to keep same size of two groups (two states of bearing). For example, the length of the contact rubbing state is 983,040 (8192 × 120), and the other three states are 327,680 (8192 × 40); similarly, the length of the oil whirl state is 983,040 (8192 × 120), and the other two states are 491,520 (8192 × 60);
- Two sets of data (group1 and group2) in stepwise fault diagnosis are marked as and . The train data (100 × 8192) is above 80% in the first half of and similarly (100 × 8192) is also above 80% in the first half of and the remaining data is test data. Therefore, the train data and the test data in this experiment are (200 × 8192) and (40 × 8192), respectively;
- The data labels are marked as [0, 1] according to the group 1 and group 2, respectively. Then the label data are expanded to vectors according to and and they are marked as (200 × 1) and (40 × 1). Therein, the first half of the vectors is 0 and remaining values are 1.
4.2.2. Process of SAE Learning
4.2.3. Validation Results
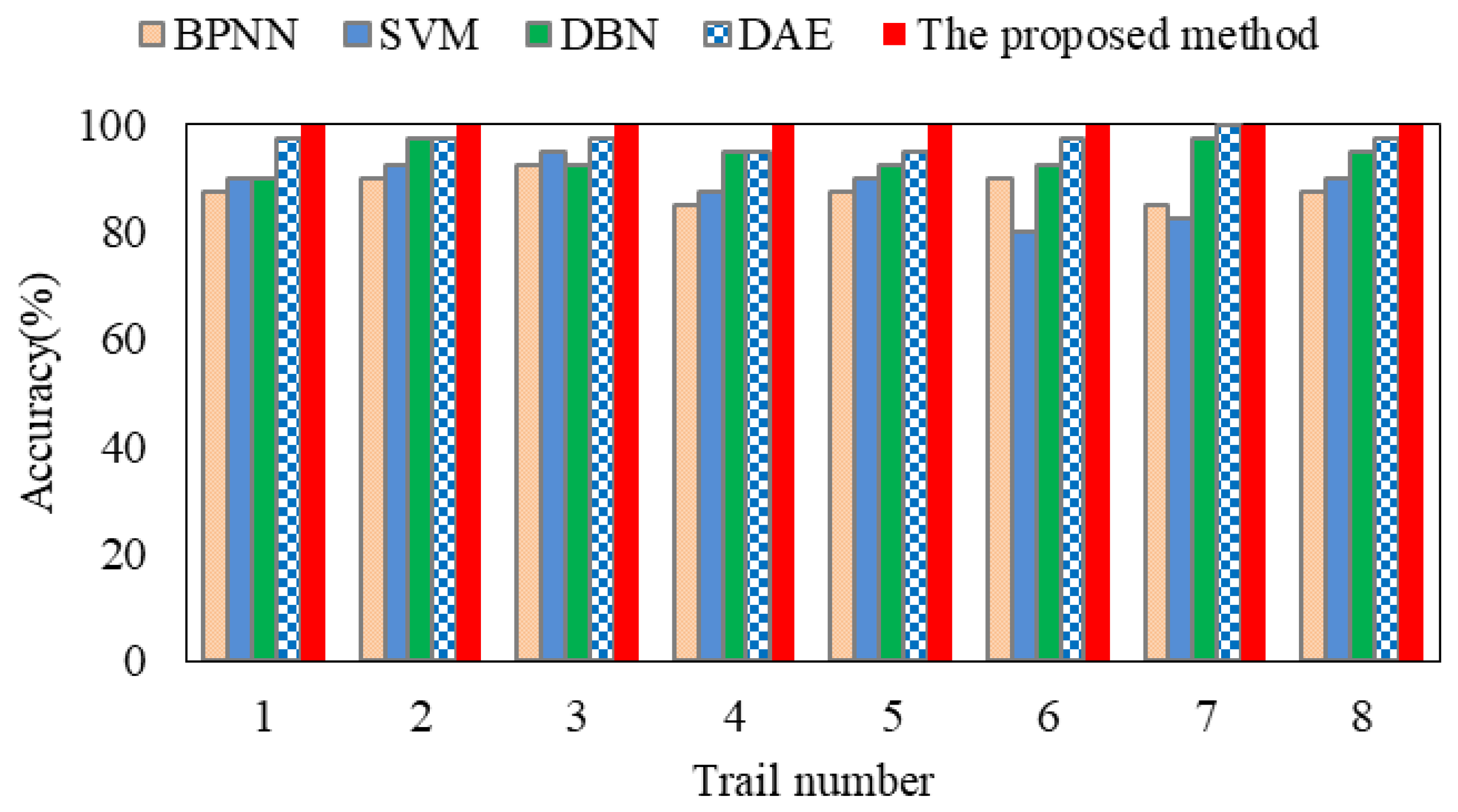
5. Comparative Experiment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guo, M.; Li, W.; Yang, Q.; Zhao, X.; Tang, Y. Amplitude filtering characteristics of singular value decomposition and its application to fault diagnosis of rotating machinery. Measurement 2020, 154, 107444. [Google Scholar] [CrossRef]
- Zernin, M.V.; Mishin, A.V.; Rybkin, N.N.; Shil’Ko, S.V.; Ryabchenko, T.V. Consideration of the multizone hydrodynamic friction, the misalignment of axes, and the contact compliance of a shaft and a bush of sliding bearings. J. Frict. Wear 2017, 38, 242–251. [Google Scholar] [CrossRef]
- Vincent, B.; Maspeyrot, P.; Frêne, J. Cavitation in noncircular journal bearings. Wear 1997, 207, 122–127. [Google Scholar] [CrossRef]
- Yan, X.; Liu, Y.; Zhang, W.; Jia, M.; Wang, X. Research on a Novel Improved Adaptive Variational Mode Decomposition Method in Rotor Fault Diagnosis. Appl. Sci. 2020, 10, 1696. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Dong, F.; Ding, E.-J.; Wu, S.; Fan, C. Rolling Bearing Fault Diagnosis Using Modified LFDA and EMD with Sensitive Feature Selection. IEEE Access 2018, 6, 3715–3730. [Google Scholar] [CrossRef]
- Shi, J.; Du, G.; Ding, R.; Zhu, Z. Time Frequency Representation Enhancement via Frequency Matching Linear Transform for Bearing Condition Monitoring under Variable Speeds. Appl. Sci. 2019, 9, 3828. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Cai, Z.; Ding, K. An enhanced bearing fault diagnosis method based on TVF-EMD and a high-order energy operator. Meas. Sci. Technol. 2018, 29, 095108. [Google Scholar] [CrossRef]
- Song, L.; Wang, H.; Chen, P. Vibration-Based Intelligent Fault Diagnosis for Roller Bearings in Low-Speed Rotating Machinery. IEEE Trans. Instrum. Meas. 2018, 67, 1887–1899. [Google Scholar] [CrossRef]
- Song, L.; Wang, H.; Chen, P. Step-by-Step Fuzzy Diagnosis Method for Equipment Based on Symptom Extraction and Trivalent Logic Fuzzy Diagnosis Theory. IEEE Trans. Fuzzy Syst. 2018, 26, 3467–3478. [Google Scholar] [CrossRef]
- Glowacz, A. Acoustic fault analysis of three commutator motors. Mech. Syst. Signal Process. 2019, 133, 106226. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, J.; Xu, J.; Deng, W. Fault Diagnosis Method Based on Principal Component Analysis and Broad Learning System. IEEE Access 2019, 7, 99263–99272. [Google Scholar] [CrossRef]
- Agrawal, P.; Jayaswal, P. Diagnosis and Classifications of Bearing Faults Using Artificial Neural Network and Support Vector Machine. J. Inst. Eng. (India) Ser. C 2019, 101, 61–72. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z. Identification of Load Categories in Rotor System Based on Vibration Analysis. Sensors 2017, 17, 1676. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, H.; Diao, Y.; Wu, W.; Zhang, J.; Ma, M.; Zhong, X. A high-speed D-CART online fault diagnosis algorithm for rotor systems. Appl. Intell. 2019, 50, 29–41. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, X.; Kou, L.-L.; Qin, Y.; Zhao, Y.; Tsui, K.-L. A simple and fast guideline for generating enhanced/squared envelope spectra from spectral coherence for bearing fault diagnosis. Mech. Syst. Signal Process. 2019, 122, 754–768. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.-Q. Multi-Layer domain adaptation method for rolling bearing fault diagnosis. Signal Process. 2019, 157, 180–197. [Google Scholar] [CrossRef] [Green Version]
- Krolczyk, G.M.; Li, Z.; Antonino-Daviu, J.A. Fault Diagnosis of Rotating Machine. Appl. Sci. 2020, 10, 1961. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zhang, W.; Peng, G.; Liu, S. Bearing Fault Diagnosis Using Fully-Connected Winner-Take-All Autoencoder. IEEE Access 2017, 6, 6103–6115. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, L.-B.; Duan, L. A novel fusion diagnosis method for rotor system fault based on deep learning and multi-sourced heterogeneous monitoring data. Meas. Sci. Technol. 2018, 29, 115005. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Oh, H.; Jung, J.H.; Jeon, B.C.; Youn, B.D. Scalable and Unsupervised Feature Engineering Using Vibration-Imaging and Deep Learning for Rotor System Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 3539–3549. [Google Scholar] [CrossRef]
- Li, K.; Chen, P.; Wang, S. An Intelligent Diagnosis Method for Rotating Machinery Using Least Squares Mapping and a Fuzzy Neural Network. Sensors 2012, 12, 5919–5939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liao, Z.; Song, L.; Chen, P.; Zuo, S. An automatic filtering method based on an improved genetic algorithm—with application to rolling bearing fault signal extraction. IEEE Sens. J. 2017, 17, 1. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, H.; Zhao, K.; Li, X. An adaptive deep transfer learning method for bearing fault diagnosis. Measurement 2020, 151, 107227. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Understanding and improving deep learning-based rolling bearing fault diagnosis with attention mechanism. Signal Process. 2019, 161, 136–154. [Google Scholar] [CrossRef]
- Rao, M.; Li, Q.; Wei, D.; Zuo, M.J. A deep bi-directional long short-term memory model for automatic rotating speed extraction from raw vibration signals. Measurement 2020, 21, 107719. [Google Scholar] [CrossRef]
- Zhao, W.; Hua, C.; Dong, D.; Ouyang, H. A Novel Method for Identifying Crack and Shaft Misalignment Faults in Rotor Systems under Noisy Environments Based on CNN. Sensors 2019, 19, 5158. [Google Scholar] [CrossRef] [Green Version]






| Rotating Speed | Number | State | Description |
|---|---|---|---|
| 5400(RPM) | 1,000,000 | Normal (N) | / |
| Contact rubbing (C) | Bolt contact the rotation axis; | ||
| Oil whirl (O) | Rotation frequency is greater than the natural frequency; | ||
| Static unbalance (SU) | One flange is loaded with 1 hammer with masses of 10 g; | ||
| Dynamic unbalance (DU) | Two flanges are loaded with 2 hammers with masses of 10 g and angle is 180°; |
| No. | Group 1 | Group 2 |
|---|---|---|
| 1 | N (983,040) | C+O+SU+DU; (each state is 245,760) |
| 2 | C (983,040) | O+SU+DU; (each state is 327,680) |
| 3 | O (983,040) | SU+DU; (each state is 491,520) |
| 4 | SU (983,040) | DU (each state is 983,040) |
| No. of Hidden Layers | No. of Neurons in Hidden Layer | No. of Iterations |
|---|---|---|
| 4 | 4000-2000-500-30 | 2000 |
| Learning rate | Momentum | Masked fraction |
| 0.9 | 0.5 | 0 |
| Input: Output: | The 5 Kinds of Sliding Bearing Signal Bearing Fault Diagnosis Result |
|---|---|
| /*Raw signal preprocessed*/ | |
| The raw signal preprocessed with statistical filter and obtain new signal , , , , ; | |
| /*SAE training process*/ | |
| Construct data according to Table 2 and obtain and ; | |
| Mark label data as [0,1] according to , ; | |
| Divide the train data and ; and test data , ; | |
| /Auto-encoder (Unsupervised learning)/ | |
| Construct AE-1, AE-2, AE-3 and AE-4; Obtain and by inputting the train data () to AE-1(8192-4000-8192); | |
| Obtain and by inputting to AE-2 (4000-2000-4000); | |
| Obtain and by inputting to AE-3 (2000-500-2000); | |
| Obtain and by inputting to AE-4 (500-30-500); | |
| /Network classification process (supervised learning)/ | |
| Build a neural network architecture: 8192-4000-2000-500-30-1; | |
| Enter , , , and into the network to initialize parameters; Assign output layer weight randomly and obtain the actual output ; | |
| Perform the gradient descent to fine-tune the globally ; | |
| Get SAE training model; | |
| /*SAE testing process*/ | |
| The test data is substituted into the above-mentioned trained classification model for fault identification, and the identification results are outputted and compared with . | |
| Method A | Method B | Method C | |
|---|---|---|---|
| Accuracy | 85% | 62.5% | 25% |
| Standard deviation | 0.1045 | 1.0085 | 2.3574 |
| Method | No. of Hidden Layers | No. of Neurons in Hidden Layer | No. of Iterations |
|---|---|---|---|
| BPNN | 3 | 7-12-1 | 1000 |
| SVM | Function | Type of SVM | |
| sigmoid kernel function | epsilon-SVR | ||
| Method | No. of Hidden Layers | No. of Neurons in Hidden Layer | No. of Iterations |
|---|---|---|---|
| DBN | 4 | 4000-2000-500-30 | 2000 |
| Learning Rate | Momentum | ||
| 0.9 | 0.5 | 1 | |
| DAE | No. of Hidden Layers | No. of Neurons in Hidden Layer | No. of Iterations |
| 4 | 4000-2000-500-30 | 2000 | |
| Learning Rate | Momentum | Masked Fraction | |
| 0.9 | 0.5 | 0.5 |
| Parameter ( is Frequency (Hz) and is the Frequency Transformation) |
| ; |
| ;; |
| ; |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Liao, Z.; Ozaki, Y.; Chen, P. Stepwise Intelligent Diagnosis Method for Rotor System with Sliding Bearing Based on Statistical Filter and Stacked Auto-Encoder. Appl. Sci. 2020, 10, 2477. https://doi.org/10.3390/app10072477
Tang H, Liao Z, Ozaki Y, Chen P. Stepwise Intelligent Diagnosis Method for Rotor System with Sliding Bearing Based on Statistical Filter and Stacked Auto-Encoder. Applied Sciences. 2020; 10(7):2477. https://doi.org/10.3390/app10072477
Chicago/Turabian StyleTang, Haihong, Zhiqiang Liao, Yayoi Ozaki, and Peng Chen. 2020. "Stepwise Intelligent Diagnosis Method for Rotor System with Sliding Bearing Based on Statistical Filter and Stacked Auto-Encoder" Applied Sciences 10, no. 7: 2477. https://doi.org/10.3390/app10072477





