Smoothing and Differentiation of Kinematic Data Using Functional Data Analysis Approach: An Application of Automatic and Subjective Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Derivation of Smooth Functions
2.3. Regression Analysis and Roughness Penalty
2.4. Cross-Validation and Generalized Cross-Validation
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. R Code A1
| times < −seq(0, 1, len = 100) |
| rng < −c(0, 1) |
| length(rng) == 1 |
| breaks = seq(rng[1], rng[2], len = 100) |
| rng < −range(breaks) |
| nbreaks < −length(breaks) |
| breaks[1] = rng[1] |
| breaks[nbreaks] = rng[2] |
| norder < −3 |
| nbasis < −nbreaks + norder − 3 |
| sum(is.na(as.numeric(rng))) == 0 |
| fdobj < −create.bspline.basis(rng, nbasis, norder, names = “bspl”) |
| Data < −smooth.basisPar(times,datac,6,Lfdobj = int2Lfd(4),lambda = 1*10^−12)$fd |
Appendix A.2. R Code A2
| cvfit = cv.glmnet(x, y, nfolds = 10, alpha = 1, lambda = seq(0, 1, by = 0.0001)) |
| plot(cvfit) |
Appendix A.3. R Code A3
| plotGCVRMSE.fd = function(lamlow, lamhi, lamdel, x, argvals, y, fdParobj, wtvec = NULL, fdnames = NULL, covariates = NULL) |
| {loglamvec = seq(lamlow, lamhi, lamdel) |
| loglamout = matrix(0, length(loglamvec), 4) |
| m = 0 |
| for (loglambda in loglamvec) |
| { m = m + 1 |
| Loglamout[m, 1] = loglambda |
| fdParobj$lambda = 10^ (loglambda) |
| smoothlist = smooth.basis(argvals, y, fdParobj, wtvec = wtvec, fdnames = fdnames, |
| Covariates = covariates) |
| xfd = smoothlist$fd |
| loglamout[m, 2] = smoothlist$df |
| loglamout[m, 3] = sqrt(mean((eval.fd(argvals, xfd) − x)^2)) |
| loglamout[m, 4] = mean(smoothlist$gcv) } |
| cat (“log10 lambda, deg. freedom, RMSE, gcv\n”) |
| for (i in 1:m) { |
| cat(format(round(loglamout[i,],3))) |
| cat(“\n”) |
| par(mfrow = c(3,1)) |
| plot(loglamvec, loglamout[,2], type = “b”) |
| title(“Degrees of freedom”) |
| plot(loglamvec, loglamout[,3], type = “b”) |
| title(“RMSE”) |
| plot(loglamvec, loglamout[,4], type = “b”) |
| title(“Mean gcv”) |
| return(loglamout) |
| } |
| n = 100 |
| norder = 6 |
| nbasis = 100 + norder |
| basisobj = create.bspline.basis(c(0, 1),nbasis) |
| lambda = 10^(−4.5) |
| fdParobj = fdPar(fdobj = basisobj, Lfdobj = 2, lambda = lambda) |
| smoothlist = smooth.basis(x, y, fdParobj) |
| xfd = smoothlist$fd |
| df = smoothlist$df |
| gcv = smoothlist$gcv |
| RMSE = sqrt(mean((eval.fd(x, xfd) − x)^2)) |
| cat(round(c(df,RMSE,gcv),3),”\n”) |
| sum(gcv) |
| plotfit.fd(y, x, xfd) |
| points(x,x, pch = “*”) |
| loglamout = plotGCVRMSE.fd(−12, −3, 1, x, x, y, fdParobj) |
Appendix B




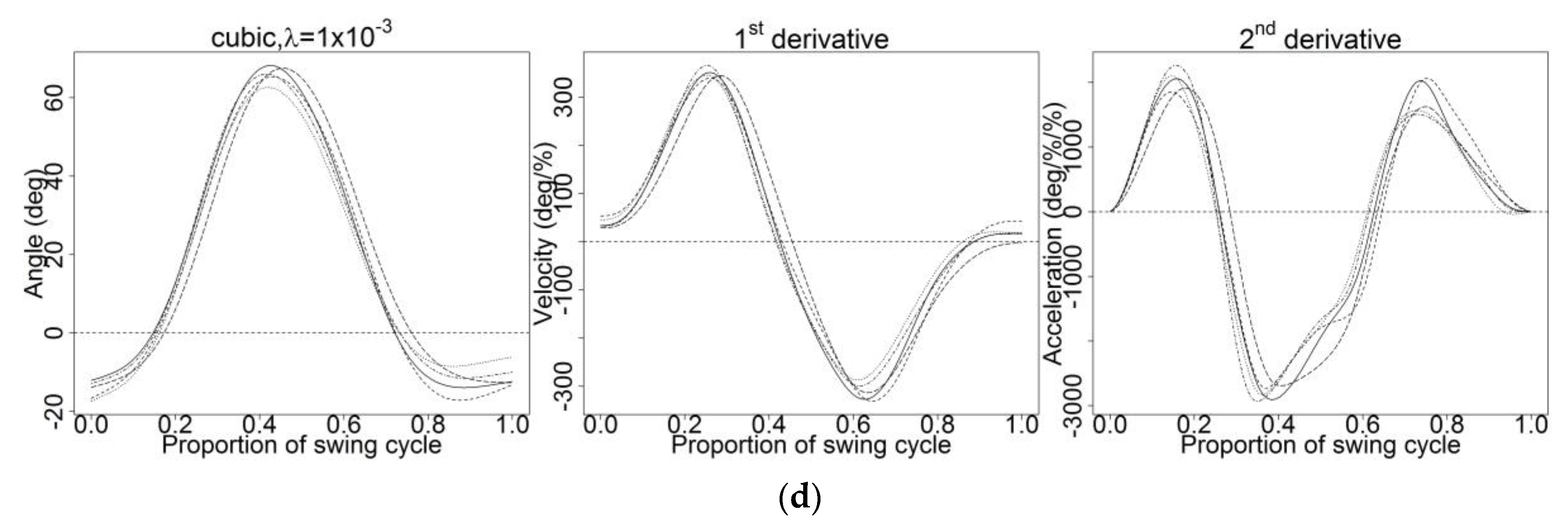


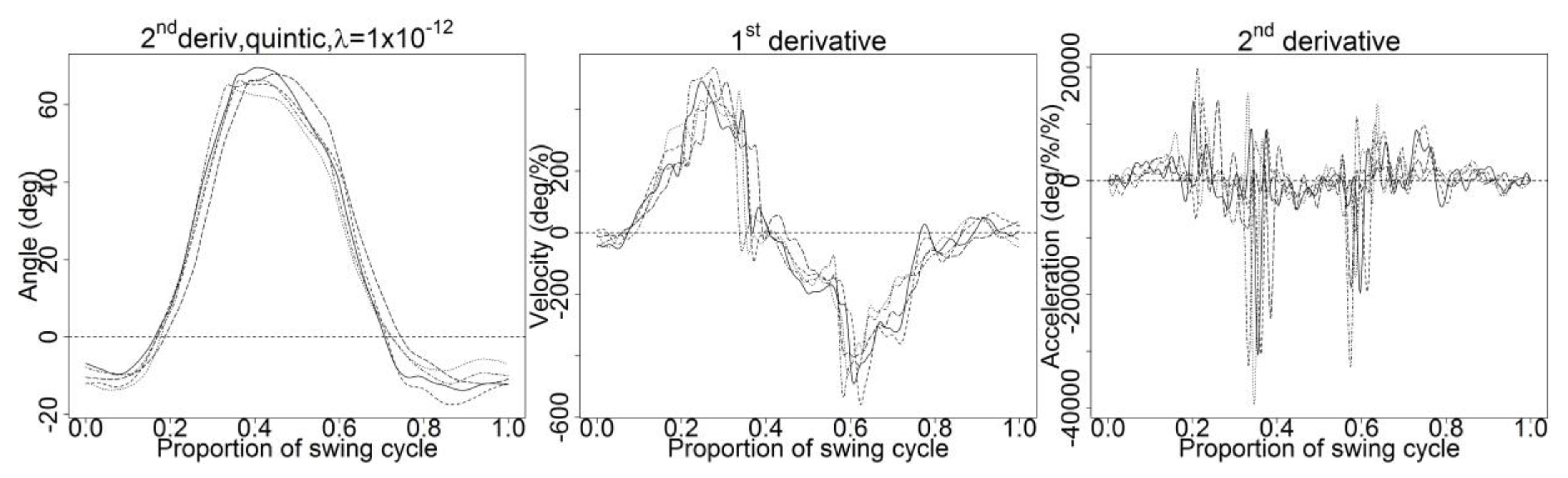
References
- Robertson, G.; Caldwell, G.; Hamill, J.; Kamen, G.; Whittlesey, S. Research Methods in Biomechanics, 2nd ed.; Human Kinetics: Champaign, IL, USA, 2014. [Google Scholar]
- Zernicke, R.F.; Caldwell, G.; Roberts, E.M. Fitting biomechanical data with cubic spline functions. Res. Q. Am. All. Health Phys. Educ. Rec. 1976, 47, 9–19. [Google Scholar] [CrossRef]
- McLaughlin, T.M.; Dillman, C.J.; Lardner, T.J. Biomechanical analysis with cubic spline functions. Res. Q. Am. All. Health Phys. Educ. Rec. 1977, 48, 569–582. [Google Scholar] [CrossRef]
- Pezzack, J.C.; Norman, R.W.; Winter, D.A. An assessment of derivative determining techniques used for motion analysis. J. Biomech. 1977, 10, 377–382. [Google Scholar] [CrossRef]
- Miller, D.I.; Nelson, R.C. Biomechanics of Sport; Lea and Febiger: Philadelphia, PA, USA, 1973. [Google Scholar]
- Wood, G.A.; Jennings, L.S. On the use of spline functions for data smoothing. J. Biomech. 1979, 12, 477–479. [Google Scholar] [CrossRef]
- Vint, P.F.; Hinrichs, R.N. Endpoint error in smoothing and differentiating raw kinematic data: An evaluation of four popular methods. J. Biomech. 1996, 29, 1637–1642. [Google Scholar] [CrossRef]
- Phillips, S.J.; Roberts, E.M. Spline solution to terminal zero acceleration problems in biomechanical data. Med. Sci. Sports Exerc. 1983, 15, 382–387. [Google Scholar] [CrossRef]
- Vaughan, C.L. Smoothing and differentiation of displacement-time data: An application of splines and digital filtering. Int. J. Bio-Med. Comput. 1982, 13, 375–386. [Google Scholar] [CrossRef]
- Woltring, H.J. On optimal smoothing and derivative estimation from noisy displacement data in biomechanics. Hum. Mov. Sci. 1985, 4, 229–245. [Google Scholar] [CrossRef]
- D’amico, M.; Ferrigno, G. Technique for the evaluation of derivatives from noisy biomechanical displacement data using a model-based bandwidth-selection procedure. Med. Biol. Eng. Comput. 1990, 28, 407–415. [Google Scholar] [CrossRef]
- Lanshammar, H. On practical evaluation of differentiation techniques for human gait analysis. J. Biomech. 1982, 15, 99–105. [Google Scholar] [CrossRef]
- Burkholder, T.J.; Lieber, R.L. Stepwise regression is an alternative to splines for fitting noisy data. J. Biomech. 1996, 29, 235–238. [Google Scholar] [CrossRef]
- Donoghue, O.A.; Harrison, A.J.; Coffey, N.; Hayes, K. Functional data analysis of running kinematics in chronic Achilles tendon injury. Med. Sci. Sports Exerc. 2008, 40, 1323–1335. [Google Scholar] [CrossRef]
- Dona, G.; Preatoni, E.; Cobelli, C.; Rodano, R.; Harrison, A.J. Application of functional principal component analysis in race walking: An emerging methodology. Sports Biomech. 2009, 8, 284–301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramsay, J.; Hooker, G.; Graves, S. Functional Data Analysis with R and MATLAB; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Crane, E.; Childers, D.; Gerstner, G.; Rothman, E. Functional Data Analysis for Biomechanics. In Theoretical Biomechanics; Vaclav, K., Ed.; InTech: Rijeka, Croatia, 2011; pp. 77–92. [Google Scholar]
- Ryan, W.; Harrison, A.; Hayes, K. Functional data analysis of knee joint kinematics in the vertical jump. Sports Biomech. 2006, 5, 121–138. [Google Scholar] [CrossRef] [PubMed]
- Harrison, A.J.; Ryan, W.; Hayes, K. Functional data analysis of joint coordination in the development of vertical jump performance. Sports Biomech. 2007, 6, 199–214. [Google Scholar] [CrossRef] [PubMed]
- Page, A.; Ayala, G.; Leon, M.T.; Peydro, M.F.; Prat, J.M. Normalizing temporal patterns to analyze sit-to-stand movements by using registration of functional data. J. Biomech. 2006, 39, 2526–2534. [Google Scholar] [CrossRef] [PubMed]
- Epifanio, I.; Ávila, C.; Page, Á.; Atienza, C. Analysis of multiple waveforms by means of functional principal component analysis: Normal versus pathological patterns in sit-to-stand movement. Med. Biol. Eng. Comput. 2008, 46, 551–561. [Google Scholar] [CrossRef]
- Donoghue, O.; Harrison, A.J.; Coffey, N.; Hayes, K. Functional data analysis of the kinematics of gait in subjects with a history of Achilles tendon injury. In Proceedings of the 24th International Symposium on Biomechanics in Sports, Salzburg, Austria, 14–18 July 2006; Schwameder, H., Strutzenberger, G., Fastenbauer, V., Lindinger, S., Müller, E., Eds.; International Society of Biomechanics in Sports: University of Salzburg, Salzburg, Austria, 2007. [Google Scholar]
- Coffey, N.; Harrison, A.J.; Donoghue, O.A.; Hayes, K. Common functional principal components analysis: A new approach to analyzing human movement data. Hum. Mov. Sci. 2011, 30, 1144–1166. [Google Scholar] [CrossRef]
- Godwin, A.; Takahara, G.; Agnew, M.; Stevenson, J. Functional data analysis as a means of evaluating kinematic and kinetic waveforms. Theoretical Issues Ergon. Sci. 2010, 11, 489–503. [Google Scholar] [CrossRef]
- Din, W.R.W.; Rambely, A.S.; Jemain, A.A. Load carriage analysis for Malaysian military using functional data analysis technique: Trial experiment. In Proceedings of the 2011 Fourth International Conference on Modeling, Simulation and Applied Optimization, Kuala Lumpur, Malaysia, 19–21 April 2011; IEEE: Kuala Lumpur, Malaysia, 2011; pp. 1–8. [Google Scholar]
- Din, W.R.W.; Rambely, A.S.; Jemain, A.A. Smoothing of GRF data using functional data analysis technique. Int. J. Appl. Math. Stat. 2013, 47, 70–77. [Google Scholar]
- Din, W.R.W.; Rambely, A.S. Functional data analysis on ground reaction force of military load carriage increment. In Proceedings of the 3rd International Conference on Mathematical Sciences, Kuala Lumpur, Malaysia, 17–19 December 2013; AIP Publishing: Kuala Lumpur, Malaysia, 2014. [Google Scholar]
- Din, W.R.W.; Rambely, A.S.; Jemain, A.A. Load carriage analysis for military using functional data analysis technique: Registration and permutation test. Int. J. Basic Appl. Sci. 2015, 4, 1–9. [Google Scholar]
- Marras, W.S.; Lavender, S.A.; Leurgans, S.E.; Fathallah, F.A.; Ferguson, S.A.; Gary Allread, W.; Rajulu, S.L. Biomechanical risk factors for occupationally related low back disorders. Ergonomics 1995, 38, 377–410. [Google Scholar] [CrossRef] [PubMed]
- Allread, W.G.; Marras, W.S.; Burr, D.L. Measuring trunk motions in industry: Variability due to task factors, individual differences, and the amount of data collected. Ergonomics 2000, 43, 691–701. [Google Scholar] [CrossRef] [PubMed]
- Dunk, N.M.; Keown, K.J.; Andrews, D.M.; Callaghan, J.P. Task variability and extrapolated cumulative low back loads. Occup. Ergon. 2005, 5, 149–159. [Google Scholar]
- Woltring, H.J. A Fortran package for generalized, cross-validatory spline smoothing and differentiation. Adv. Eng. Softw. 1986, 8, 104–113. [Google Scholar] [CrossRef]
- Woltring, H.J. Smoothing and differentiation techniques applied to 3-D data. In Three-Dimensional Analysis of Human Movement; Allard, P., Stokes, I.A.F., Blanchi, J., Eds.; Human Kinetics: Champaign, IL, USA, 1995; pp. 79–99. [Google Scholar]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar]
- De Boor, C. A Practical Guide to Splines, Revised ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Ramsay, J.O.; Silverman, B.W. Applied Functional Data Analysis: Methods and Case Studies; Springer: New York, NY, USA, 2002. [Google Scholar]
- Warmenhoven, J.; Harrison, A.; Robinson, M.A.; Vanrenterghem, J.; Bargary, N.; Smith, R.; Cobley, S.; Draper, C.; Pataky, T. A force profile analysis comparison between functional data analysis, statistical parametric mapping and statistical non-parametric mapping in on-water single sculling. J. Sci. Med. Sport. 2018, 21, 1100–1105. [Google Scholar] [CrossRef] [Green Version]
- Eilers, P.H.; Marx, B.D. Flexible smoothing with B-splines and penalties. Stat. Sci. 1996, 11, 89–102. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis; Springer: New York, NY, USA, 1997. [Google Scholar]
- Craven, P.; Wahba, G. Smoothing noisy data with spline functions. Numer. Math. 1979, 31, 377–403. [Google Scholar] [CrossRef]







| Degrees of Freedom (df) | RMSE | GCV | |
|---|---|---|---|
| −12 | 100 | 35.859 | 0.038 |
| −11 | 100 | 35.859 | 0.038 |
| −10 | 100 | 35.859 | 0.037 |
| −9 | 98 | 35.859 | 0.036 |
| −8 | 86 | 35.858 | 0.032 |
| −7 | 60 | 35.858 | 0.046 |
| −6 | 36 | 35.852 | 0.146 |
| −5 | 21 | 35.824 | 0.578 |
| −4 | 12 | 35.667 | 2.637 |
| −3 | 7 | 34.839 | 14.704 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zin, M.A.M.; Rambely, A.S.; Ariff, N.M.; Ariffin, M.S. Smoothing and Differentiation of Kinematic Data Using Functional Data Analysis Approach: An Application of Automatic and Subjective Methods. Appl. Sci. 2020, 10, 2493. https://doi.org/10.3390/app10072493
Zin MAM, Rambely AS, Ariff NM, Ariffin MS. Smoothing and Differentiation of Kinematic Data Using Functional Data Analysis Approach: An Application of Automatic and Subjective Methods. Applied Sciences. 2020; 10(7):2493. https://doi.org/10.3390/app10072493
Chicago/Turabian StyleZin, Muhammad Athif Mat, Azmin Sham Rambely, Noratiqah Mohd Ariff, and Muhammad Shahimi Ariffin. 2020. "Smoothing and Differentiation of Kinematic Data Using Functional Data Analysis Approach: An Application of Automatic and Subjective Methods" Applied Sciences 10, no. 7: 2493. https://doi.org/10.3390/app10072493
APA StyleZin, M. A. M., Rambely, A. S., Ariff, N. M., & Ariffin, M. S. (2020). Smoothing and Differentiation of Kinematic Data Using Functional Data Analysis Approach: An Application of Automatic and Subjective Methods. Applied Sciences, 10(7), 2493. https://doi.org/10.3390/app10072493





