Reciprocating Compressor Multi-Fault Classification Using Symbolic Dynamics and Complex Correlation Measure
Abstract
:1. Introduction
- Novel application in PHM of the Complex Correlation Measure (CCM) derived from the Poincaré plot of the vibration signal for extracting useful features for accurate classification of multi-fault in valves and roller bearings.
- Novel application of Symbolic Dynamics (SD) for classification of multi-fault of valves and roller bearings.
- Accurate classification of 13 different combined fault conditions (multi-fault scenario) of valves and roller bearing.
- Accurate classification of 17 fault conditions of valves in a reciprocating compressor.
- Comparison of three different set of features extracted from vibration signal for classifying the set of multi-fault previously mentioned.
- Comparison of two high performance Random Forest (RF) models applied to the problem of multi-fault classification of valves and roller bearings in a reciprocating compressor.
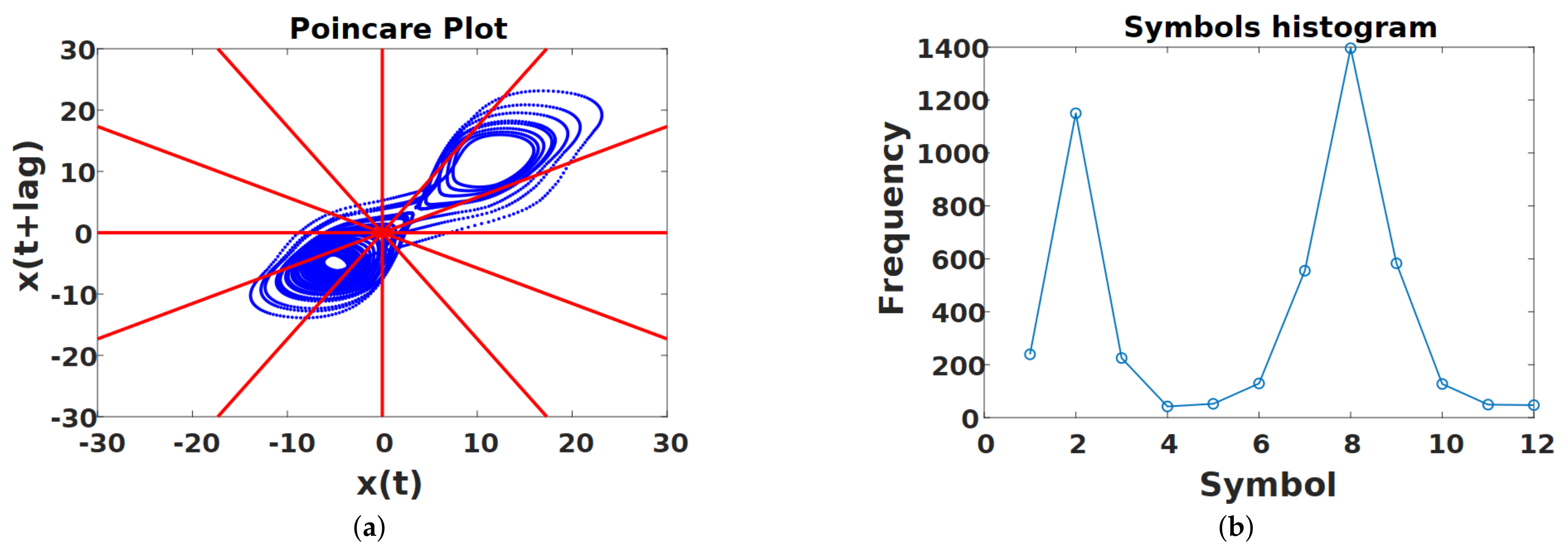
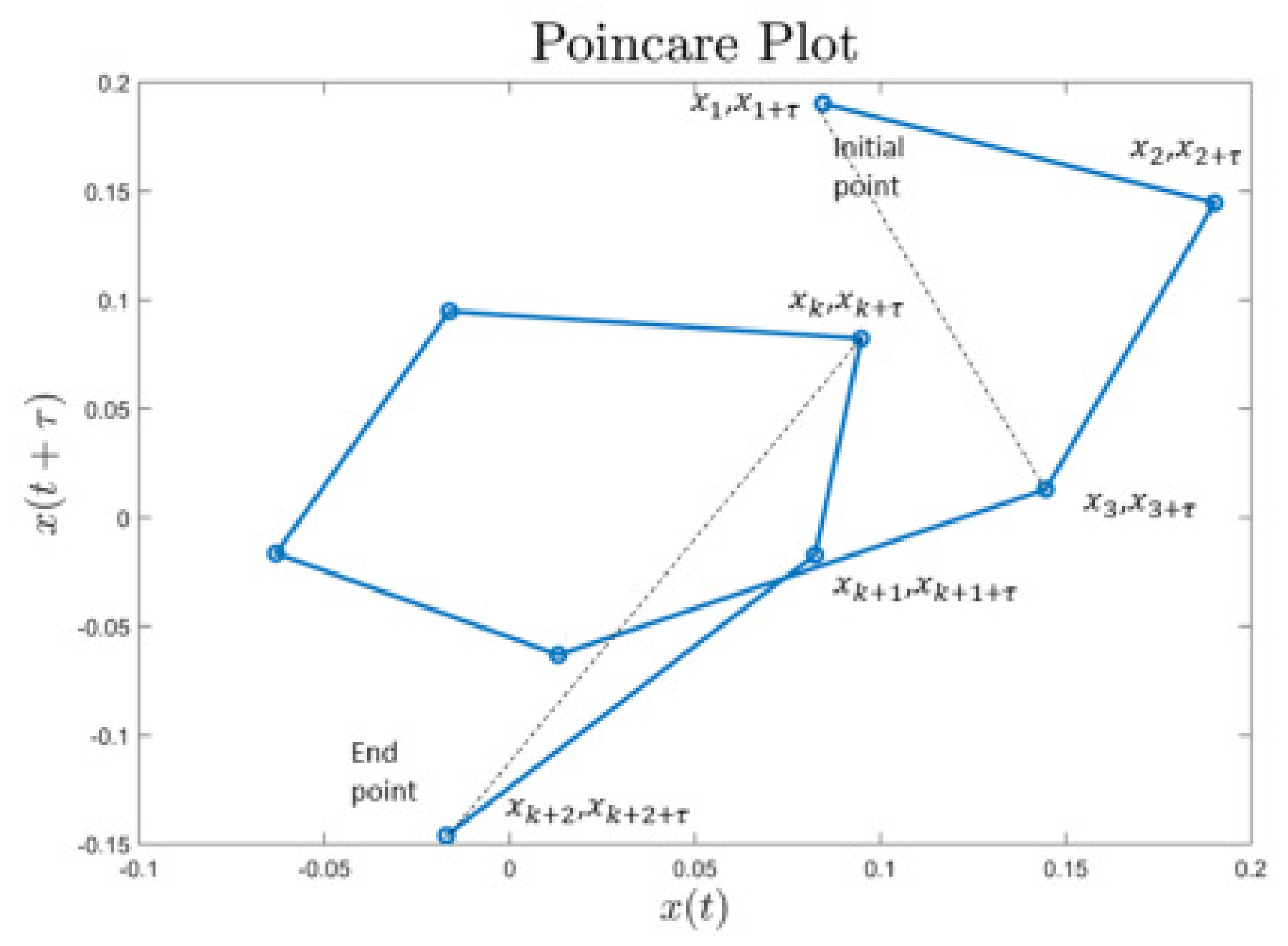
2. Poincaré Plot and Their Features
2.1. Poincaré Plot
2.2. Symbolic Dynamics
2.3. Complex Correlation Measure
3. Random Forest
3.1. Ensemble Bagged Trees
3.2. Ensemble Subspace k-Nearest Neighbors
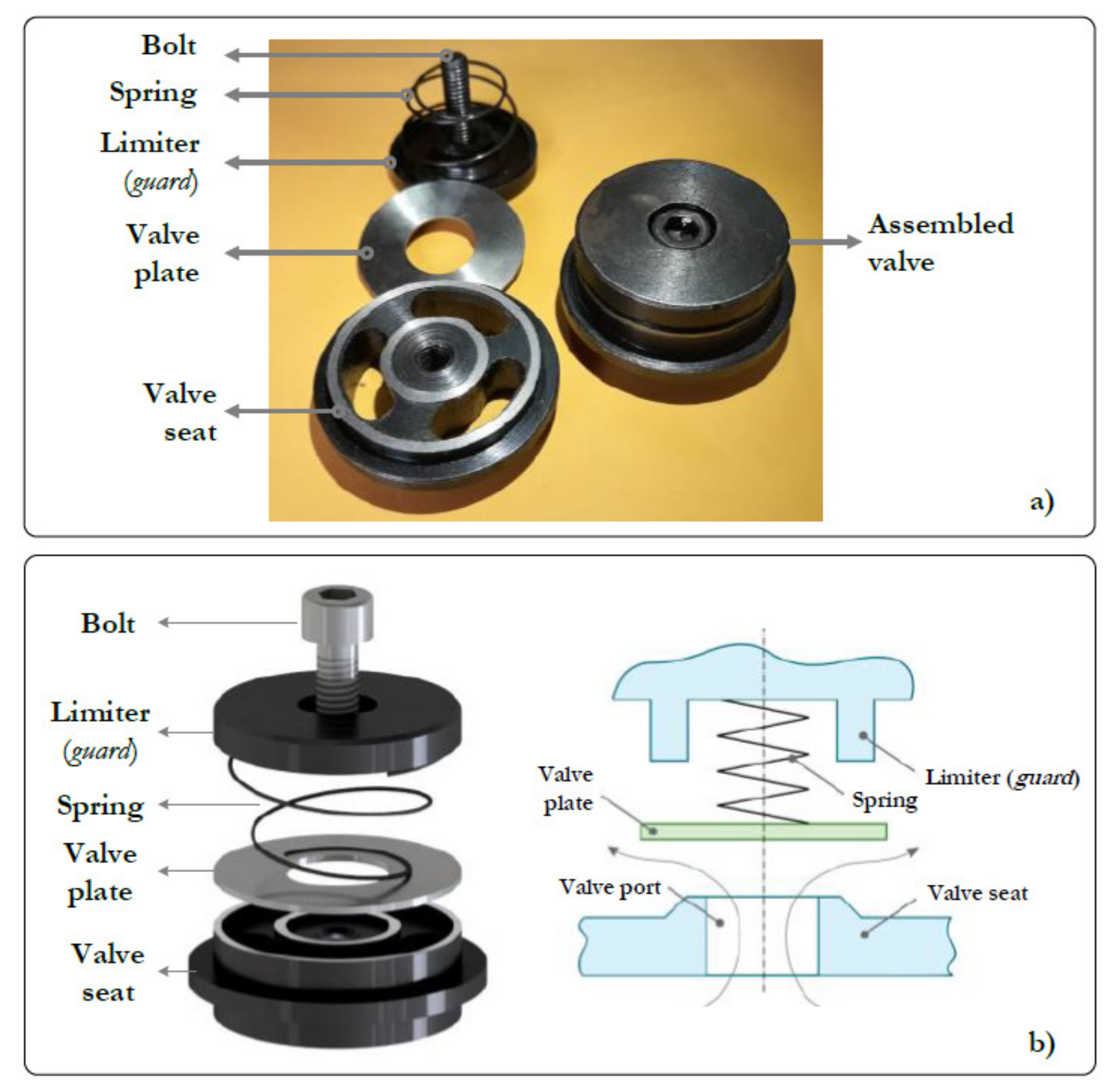
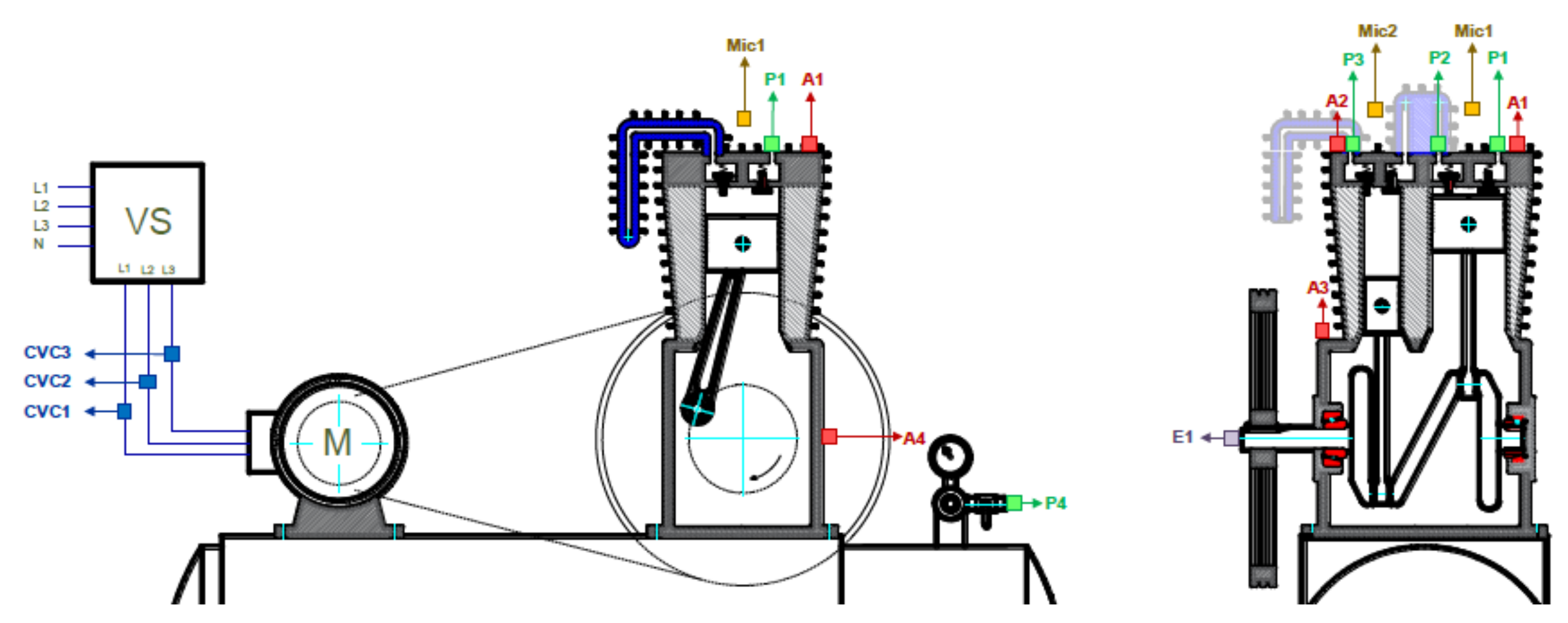
4. Experimental Test-Bed
4.1. Reciprocating Compressor
4.2. Dataset Vibration Signal Acquisition
5. Feature Extraction
5.1. Symbolic Dynamics
5.2. Complex Correlation Measure
5.3. Statistical Features
6. Multi-Fault Classification
Parameters Selection
7. Results
8. Discussion
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PHM | Prognostics and Health Management |
| SVM | Support Vector Machines |
| LSTM | Long Short-Term Memory model |
| CCM | Complex Correlation Measure |
| RF | Random Forest |
| CART | Classification And Regression Tree |
| OOB | Out of the Bag |
| EDM | Electrical Discharge Machining |
| SD | Symbolic Dynamics |
| EBT | Ensemble Bagged Tree |
| k-NN | k-Nearest Neighbors |
| ESK | Ensemble Subspace k-NN |
References
- Liu, Y.; Duan, L.; Yuan, Z.; Wang, N.; Zhao, J. An Intelligent Fault Diagnosis Method for Reciprocating Compressors Based on LMD and SDAE. Sensors 2019, 19, 1041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Gao, A.; Zheng, S.; Peng, X. Experimental investigation of the fault diagnosis of typical faults in reciprocating compressor valves. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2285–2299. [Google Scholar] [CrossRef]
- Aravinth, S.; Sugumaran, V. Air compressor fault diagnosis through statistical feature extraction and random forest classifier. Prog. Ind. Ecol. Int. J. 2018, 12, 192–205. [Google Scholar] [CrossRef]
- Pichler, K.; Lughofer, E.; Pichler, M.; Buchegger, T.; Klement, E.P.; Huschenbett, M. Fault detection in reciprocating compressor valves under varying load conditions. Mech. Syst. Signal Process. 2016, 70, 104–119. [Google Scholar] [CrossRef]
- Khan, S.; Yairi, T. A review on the application of deep learning in system health management. Mech. Syst. Signal Process. 2018, 107, 241–265. [Google Scholar] [CrossRef]
- Wang, H.; Dong, F.; Zhou, X.; Wang, H.; Zhu, X.; Song, L.; Guo, Q. Fault Diagnosis of Reciprocating Compressor Using Component Estimating Empirical Mode Decomposition and De-Dimension Template With Double-Loop Correction Algorithm. IEEE Access 2019, 7, 90630–90639. [Google Scholar] [CrossRef]
- Lei, N.; Tang, Y.; Lei, Y. A fault diagnosis approach of reciprocating compressor gas valve based on local mean decomposition and autoregressive-generalized autoregressive conditional heteroscedasticity model. J. Vibroeng. 2016, 18, 838–848. [Google Scholar]
- Li, Y.; Wang, J.; Zhao, H.; Song, M.; Ou, L. Fault Diagnosis Method Based on Modified Multiscale Entropy and Global Distance Evaluation for the Valve Fault of a Reciprocating Compressor. Stroj. Vestn./J. Mech. Eng. 2019, 65, 123–135. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Jiang, K.; Wang, Q.; Wang, X.; Zhou, Y. Quantitative Evaluation on Valve Leakage of Reciprocating Compressor Using System Characteristic Diagnosis Method. Appl. Sci. 2020, 10, 1946. [Google Scholar] [CrossRef] [Green Version]
- Guerra, C.J.; Kolodziej, J.R. A data-driven approach for condition monitoring of reciprocating compressor valves. J. Eng. Gas Turbines Power 2014, 136, 1–13. [Google Scholar] [CrossRef]
- Cui, H.; Zhang, L.; Kang, R.; Lan, X. Research on fault diagnosis for reciprocating compressor valve using information entropy and SVM method. J. Loss Prev. Process. Ind. 2009, 22, 864–867. [Google Scholar] [CrossRef]
- Qin, Q.; Jiang, Z.N.; Feng, K.; He, W. A novel scheme for fault detection of reciprocating compressor valves based on basis pursuit, wave matching and support vector machine. Measurement 2012, 45, 897–908. [Google Scholar] [CrossRef]
- Xiao, S.; Liu, S.; Jiang, F.; Song, M.; Cheng, S. Nonlinear dynamic response of reciprocating compressor system with rub-impact fault caused by subsidence. J. Vib. Control. 2019, 25, 1737–1751. [Google Scholar] [CrossRef]
- Xiao, S.; Zhang, H.; Liu, S.; Jiang, F.; Song, M. Dynamic behavior analysis of reciprocating compressor with subsidence fault considering flexible piston rod. J. Mech. Sci. Technol. 2018, 32, 4103–4124. [Google Scholar] [CrossRef]
- Tufillaro, N.B.; Abbott, T.; Reilly, J. An Experimental Approach to Nonlinear Dynamics and Chaos; Addison-Wesley: Redwood City, CA, USA, 1992. [Google Scholar]
- Tucker, W. Computing accurate Poincaré maps. Phys. D Nonlinear Phenom. 2002, 171, 127–137. [Google Scholar] [CrossRef]
- Soleimani, A.; Khadem, S. Early fault detection of rotating machinery through chaotic vibration feature extraction of experimental data sets. Chaos Solitons Fractals 2015, 78, 61–75. [Google Scholar] [CrossRef]
- Trendafilova, I.; Manoach, E. Vibration-based damage detection in plates by using time series analysis. Mech. Syst. Signal Process. 2008, 22, 1092–1106. [Google Scholar] [CrossRef] [Green Version]
- Grebogi, C.; Ott, E.; Yorke, J.A. Chaos, strange attractors, and fractal basin boundaries in nonlinear dynamics. Science 1987, 238, 632–638. [Google Scholar] [CrossRef] [Green Version]
- Cabrera, D.; Guamán, A.; Zhang, S.; Cerrada, M.; Sánchez, R.V.; Cevallos, J.; Long, J.; Li, C. Bayesian approach and time series dimensionality reduction to LSTM-based model-building for fault diagnosis of a reciprocating compressor. Neurocomputing 2020, 380, 51–66. [Google Scholar] [CrossRef]
- Alligood, K.T.; Sauer, T.D.; Yorke, J.A. Chaos: An Introduction to Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Wu, S.T.; Campos, S.P.; de Aguiar, M.A. Scientific visualization of Poincarémaps. Comput. Graph. 1998, 22, 209–216. [Google Scholar] [CrossRef]
- Brennan, M.; Palaniswami, M.; Kamen, P. Do existing measures of Poincare plot geometry reflect nonlinear features of heart rate variability? IEEE Trans. Biomed. Eng. 2001, 48, 1342–1347. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Rao, C.; Sarkar, S.; Ray, A.; Yasar, M. Comparative evaluation of symbolic dynamic filtering for detection of anomaly patterns. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 3052–3057. [Google Scholar]
- Medina, R.; Macancela, J.C.; Lucero, P.; Cabrera, D.; Cerrada, M.; Sánchez, R.V.; Vásquez, R.E. Vibration signal analysis using symbolic dynamics for gearbox fault diagnosis. Int. J. Adv. Manuf. Technol. 2019, 104, 2195–2214. [Google Scholar] [CrossRef]
- Du, Q.; Faber, V.; Gunzburger, M. Centroidal Voronoi tessellations: Applications and algorithms. SIAM Rev. 1999, 41, 637–676. [Google Scholar] [CrossRef] [Green Version]
- Thäle, C. A first attempt to fractal mosaics. In Proceedings of the European Congress of Stereology and Image Analysis (ECS10), Milan, Italy, 22–26 June 2009; pp. 342–348. [Google Scholar]
- Lind, D.; Marcus, B.; Douglas, L.; Brian, M. An Introduction to Symbolic Dynamics and Coding; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Karmakar, C.K.; Khandoker, A.H.; Gubbi, J.; Palaniswami, M. Complex Correlation Measure: A novel descriptor for Poincaré plot. Biomed. Eng. Online 2009, 8, 17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Stine, R. An introduction to bootstrap methods: Examples and ideas. Sociol. Methods Res. 1989, 18, 243–291. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Strobl, C.; Boulesteix, A.L.; Augustin, T. Unbiased split selection for classification trees based on the Gini index. Comput. Stat. Data Anal. 2007, 52, 483–501. [Google Scholar] [CrossRef] [Green Version]
- Qin, X.; Li, Q.; Dong, X.; Lv, S. The fault diagnosis of rolling bearing based on ensemble empirical mode decomposition and random forest. Shock Vib. 2017, 2017, 2623081. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Gul, A.; Perperoglou, A.; Khan, Z.; Mahmoud, O.; Miftahuddin, M.; Adler, W.; Lausen, B. Ensemble of a subset of kNN classifiers. Adv. Data Anal. Classif. 2018, 12, 827–840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, R.V.; Lucero, P.; Vásquez, R.E.; Cerrada, M.; Macancela, J.C.; Cabrera, D. Feature ranking for multi-fault diagnosis of rotating machinery by using random forest and KNN. J. Intell. Fuzzy Syst. 2018, 34, 3463–3473. [Google Scholar] [CrossRef]
- Jelinek, H.F.; Khandoker, A.H.; Quintana, D.; Imam, M.H.; Kemp, A. Complex correlation measure as a sensitive indicator of risk for sudden cardiac death in patients with depression. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; pp. 809–812. [Google Scholar]
















| Label | Valve, 2S–DV | Bearings, B1 |
|---|---|---|
| P1 | Healthy | Healthy |
| P2 | Valve seat wear | Inner race crack |
| P3 | Corrosion of valve plate | Inner race crack |
| P4 | Fracture of valve plate | Inner race crack |
| P5 | Broken Spring | Inner race crack |
| P6 | Valve seat wear | Roller element crack |
| P7 | Corrosion of valve plate | Roller element crack |
| P8 | Fracture of valve plate | Roller element crack |
| P9 | Broken Spring | Roller element crack |
| P10 | Valve seat wear | Outer race crack |
| P11 | Corrosion of valve plate | Outer race crack |
| P12 | Fracture of valve plate | Outer race crack |
| P13 | Broken Spring | Outer race crack |
| Features | Model | A1 | A2 | A3 |
|---|---|---|---|---|
| Statistical | EBT | 100 | 100 | 100 |
| ESK | 100 | 100 | 100 | |
| SD | EBT | 100 | 100 | 100 |
| ESK | 100 | 100 | 100 | |
| CCM | EBT | 99.4 | 96.8 | 94.2 |
| ESK | 100 | 100 | 99.4 |
| Fault Condition | Sensitivity | Specificity | F1-Score |
|---|---|---|---|
| P1 | 0.92 | 1.00 | 0.96 |
| P2 | 1.00 | 1.00 | 1.00 |
| P3 | 1.00 | 1.00 | 1.00 |
| P4 | 1.00 | 0.99 | 0.96 |
| P5 | 1.00 | 0.99 | 0.96 |
| P6 | 0.92 | 1.00 | 0.96 |
| P7 | 0.92 | 0.99 | 0.92 |
| P8 | 0.85 | 0.99 | 0.88 |
| P9 | 1.00 | 0.99 | 0.96 |
| P10 | 1.00 | 1.00 | 1.00 |
| P11 | 1.00 | 1.00 | 1.00 |
| P12 | 0.79 | 0.99 | 0.85 |
| P13 | 0.90 | 0.98 | 0.82 |
| Features | Model | A1 | A2 | A3 | A4 |
|---|---|---|---|---|---|
| Statistical | EBT | 73.2 | 83.5 | 73.4 | 74.4 |
| ESK | 52.6 | 61.7 | 57.2 | 49.0 | |
| SD | EBT | 100 | 100 | 100 | 100 |
| ESK | 100 | 100 | 100 | 100 | |
| CCM | EBT | 91.7 | 98.7 | 95.3 | 97.9 |
| ESK | 97.8 | 99.8 | 97.8 | 99.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerrada, M.; Macancela, J.-C.; Cabrera, D.; Estupiñan, E.; Sánchez, R.-V.; Medina, R. Reciprocating Compressor Multi-Fault Classification Using Symbolic Dynamics and Complex Correlation Measure. Appl. Sci. 2020, 10, 2512. https://doi.org/10.3390/app10072512
Cerrada M, Macancela J-C, Cabrera D, Estupiñan E, Sánchez R-V, Medina R. Reciprocating Compressor Multi-Fault Classification Using Symbolic Dynamics and Complex Correlation Measure. Applied Sciences. 2020; 10(7):2512. https://doi.org/10.3390/app10072512
Chicago/Turabian StyleCerrada, Mariela, Jean-Carlo Macancela, Diego Cabrera, Edgar Estupiñan, René-Vinicio Sánchez, and Ruben Medina. 2020. "Reciprocating Compressor Multi-Fault Classification Using Symbolic Dynamics and Complex Correlation Measure" Applied Sciences 10, no. 7: 2512. https://doi.org/10.3390/app10072512
APA StyleCerrada, M., Macancela, J.-C., Cabrera, D., Estupiñan, E., Sánchez, R.-V., & Medina, R. (2020). Reciprocating Compressor Multi-Fault Classification Using Symbolic Dynamics and Complex Correlation Measure. Applied Sciences, 10(7), 2512. https://doi.org/10.3390/app10072512







