Practical Control of a Cold Milling Machine using an Adaptive PID Controller
Abstract
:Featured Application
Abstract
1. Introduction
2. Control Model
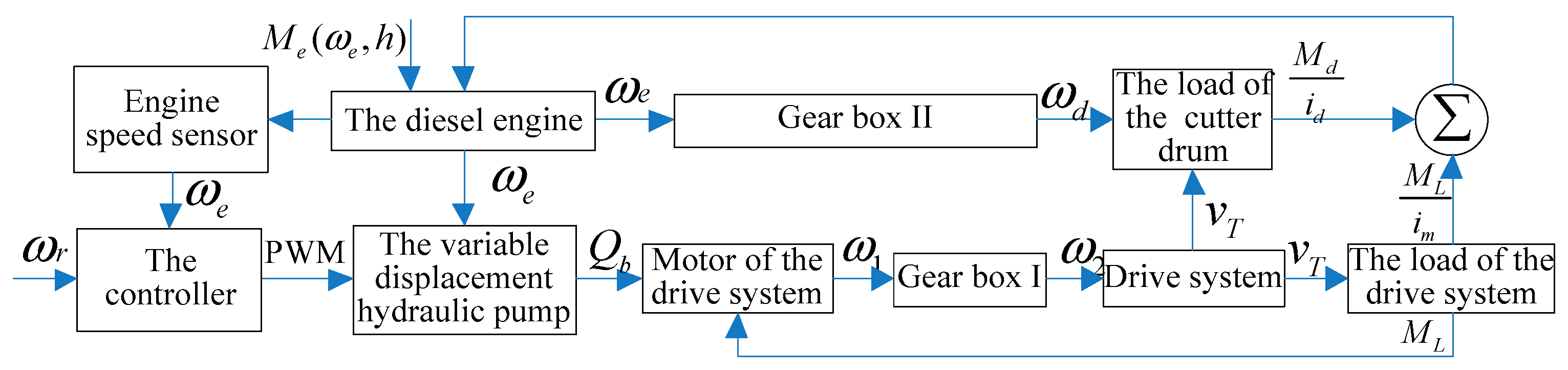
2.1. Control System Overview
2.2. System Model
2.2.1. Engine Model
2.2.2. Model of Drive System
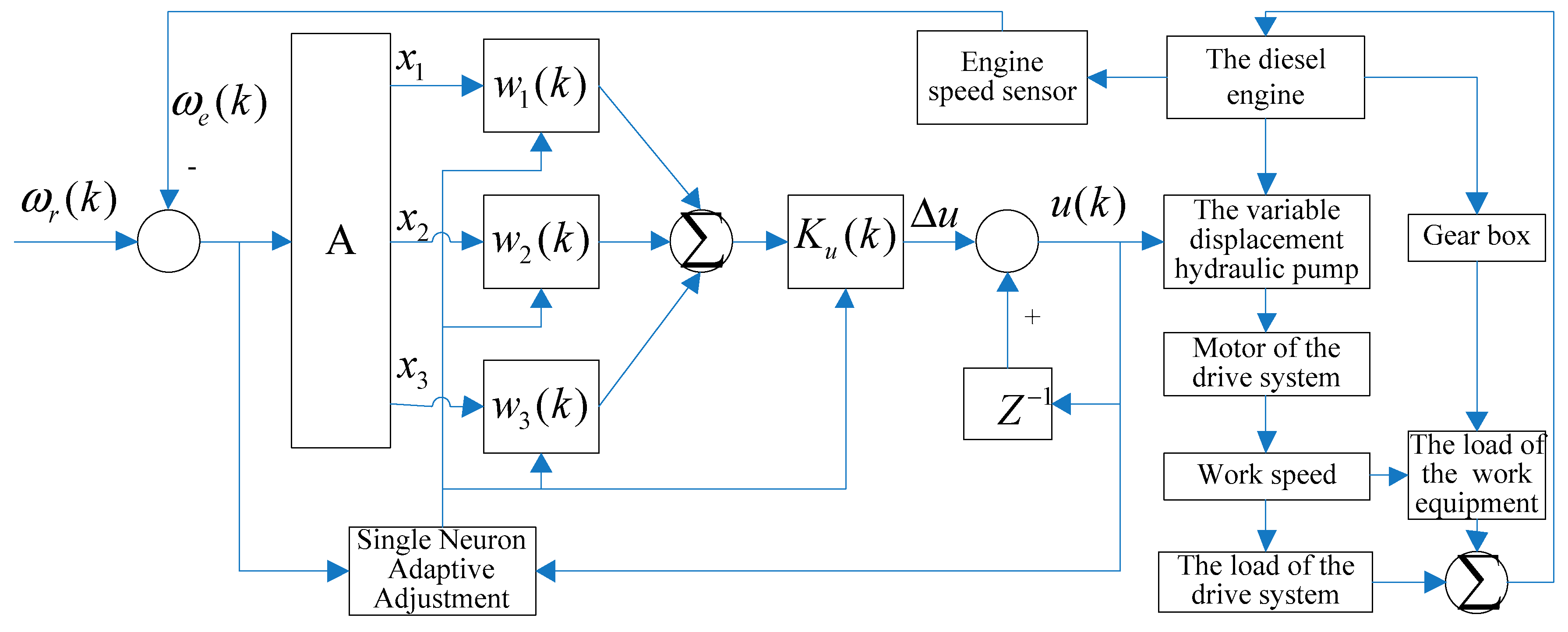
3. The Proposed Adaptive PID Controller
4. Simulation Redults
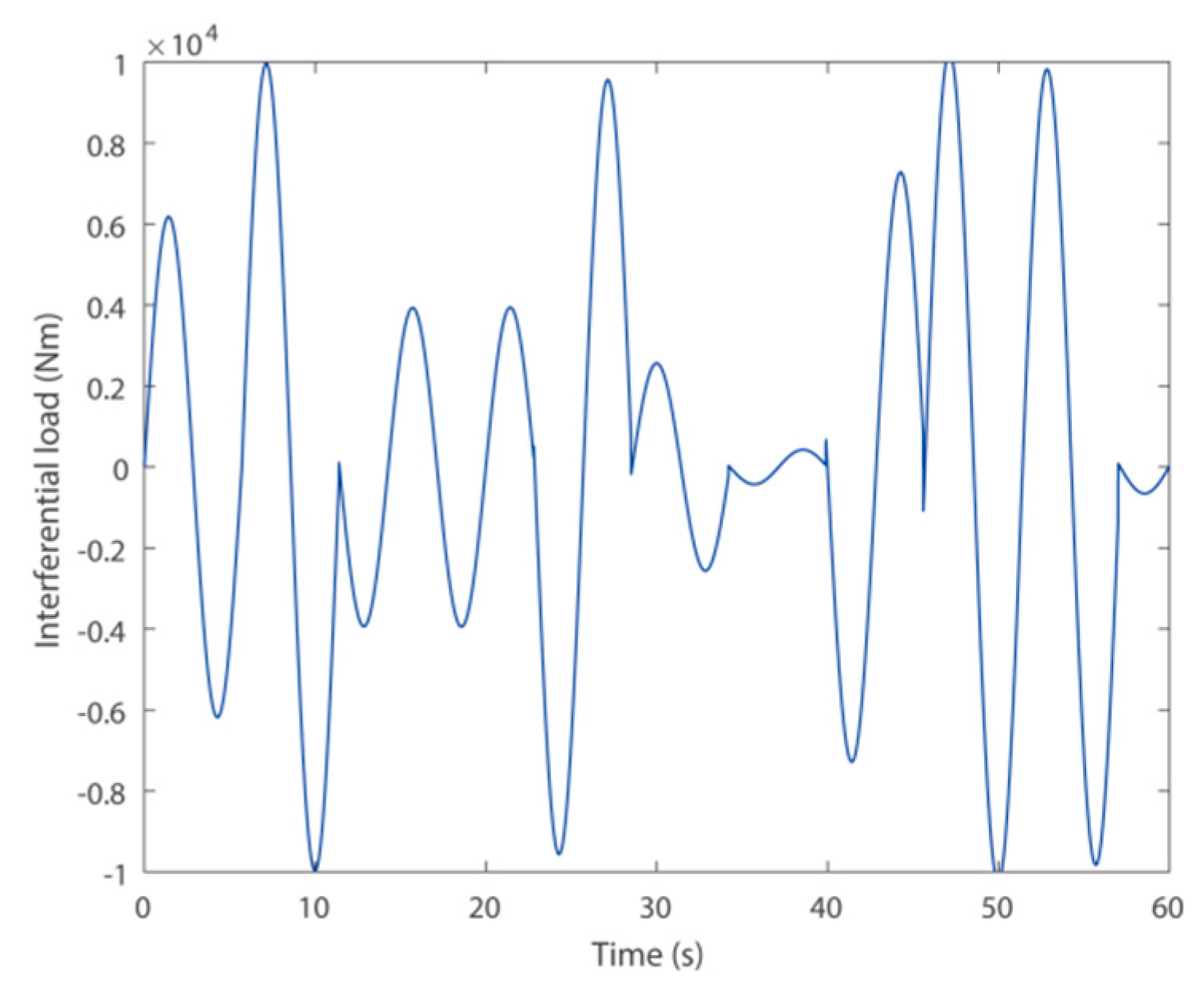
4.1. Parameters’ Confirmation in the Model of the Cold Milling Machine
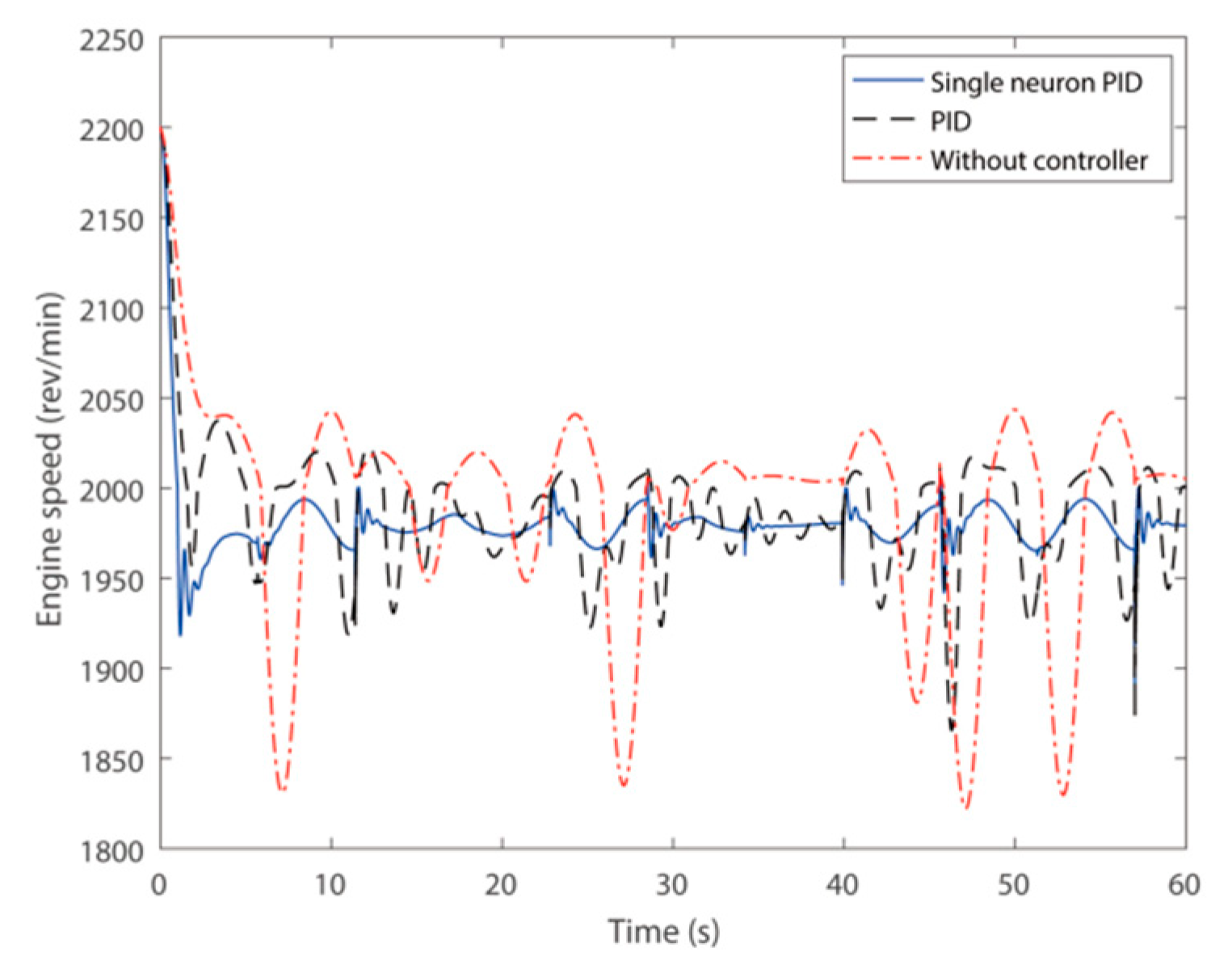
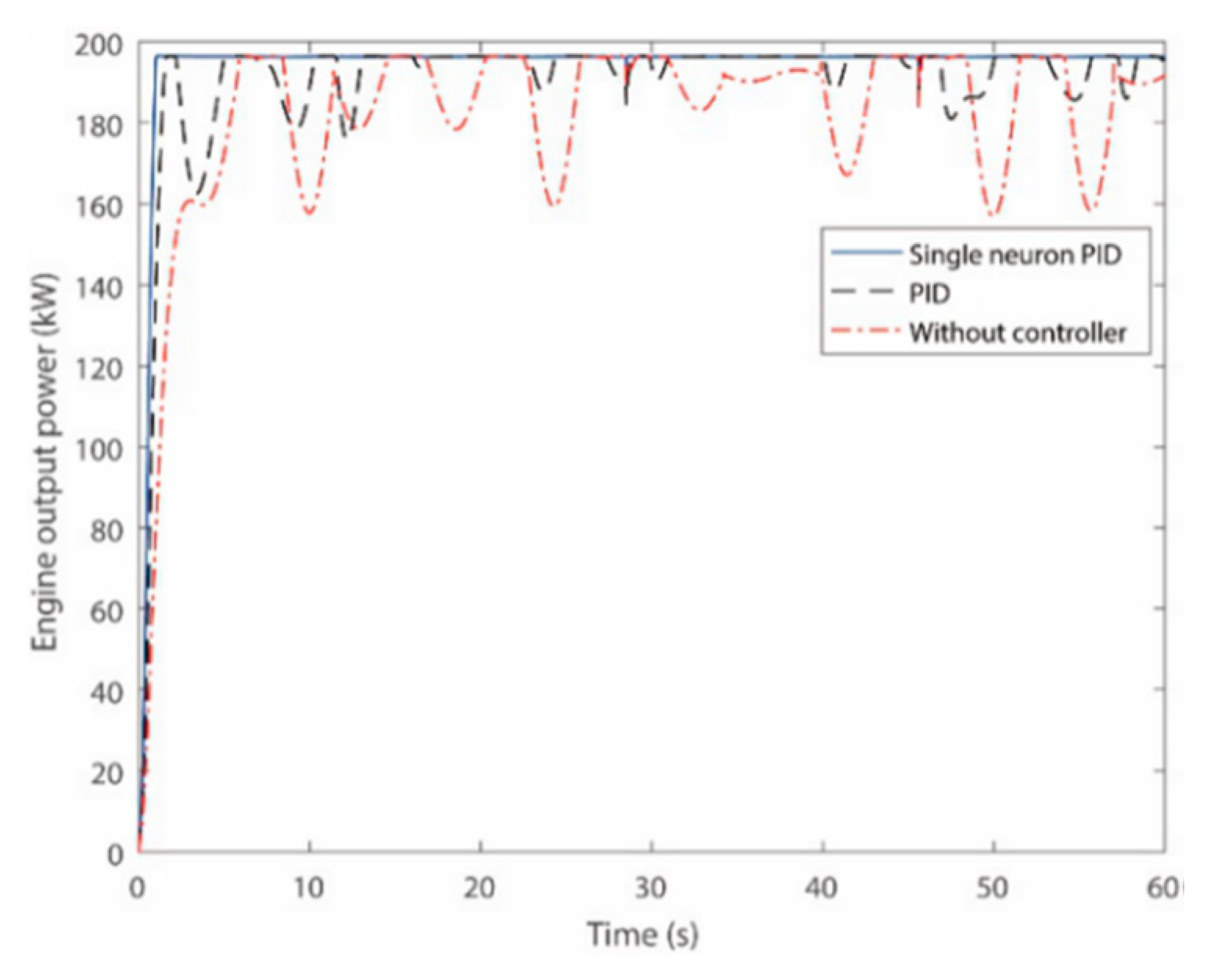
4.2. Simulation Results
5. Field Test
5.1. Field Test Setup
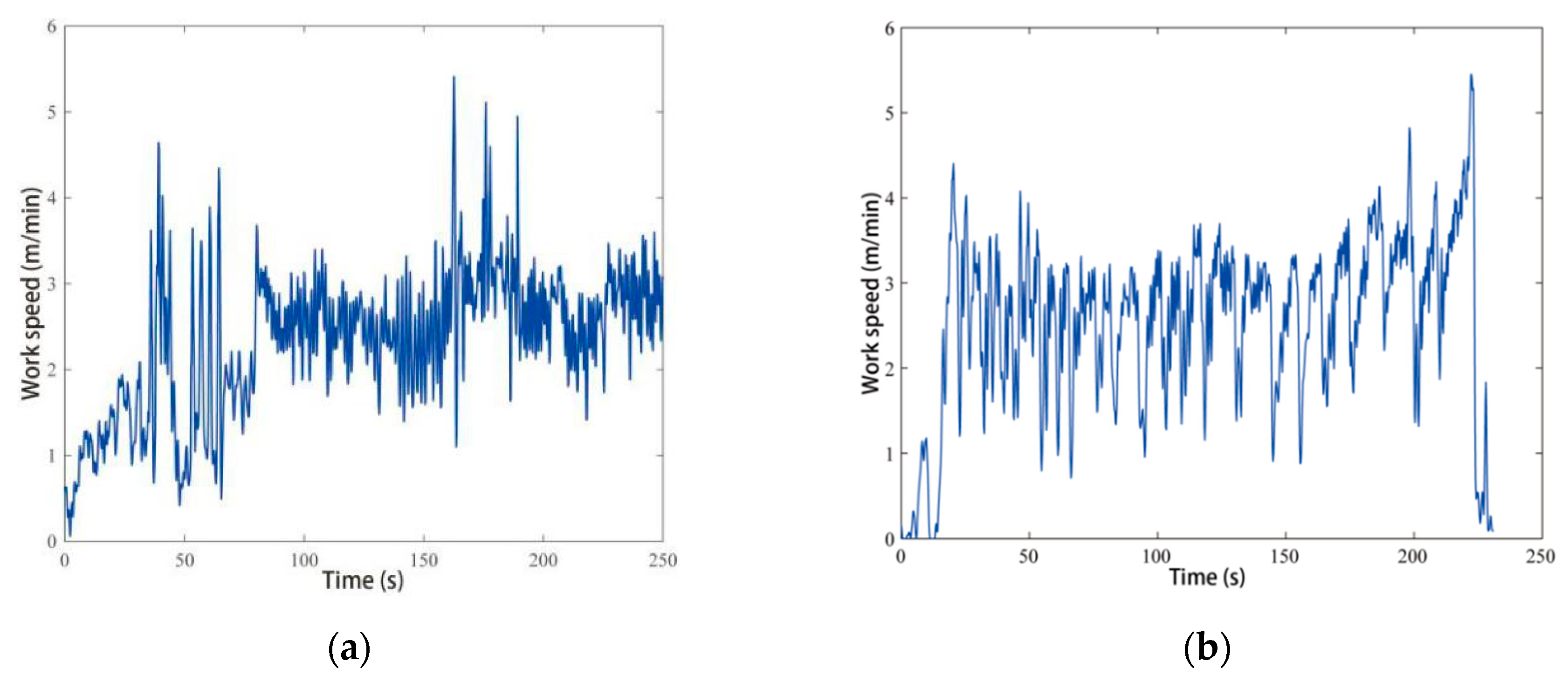
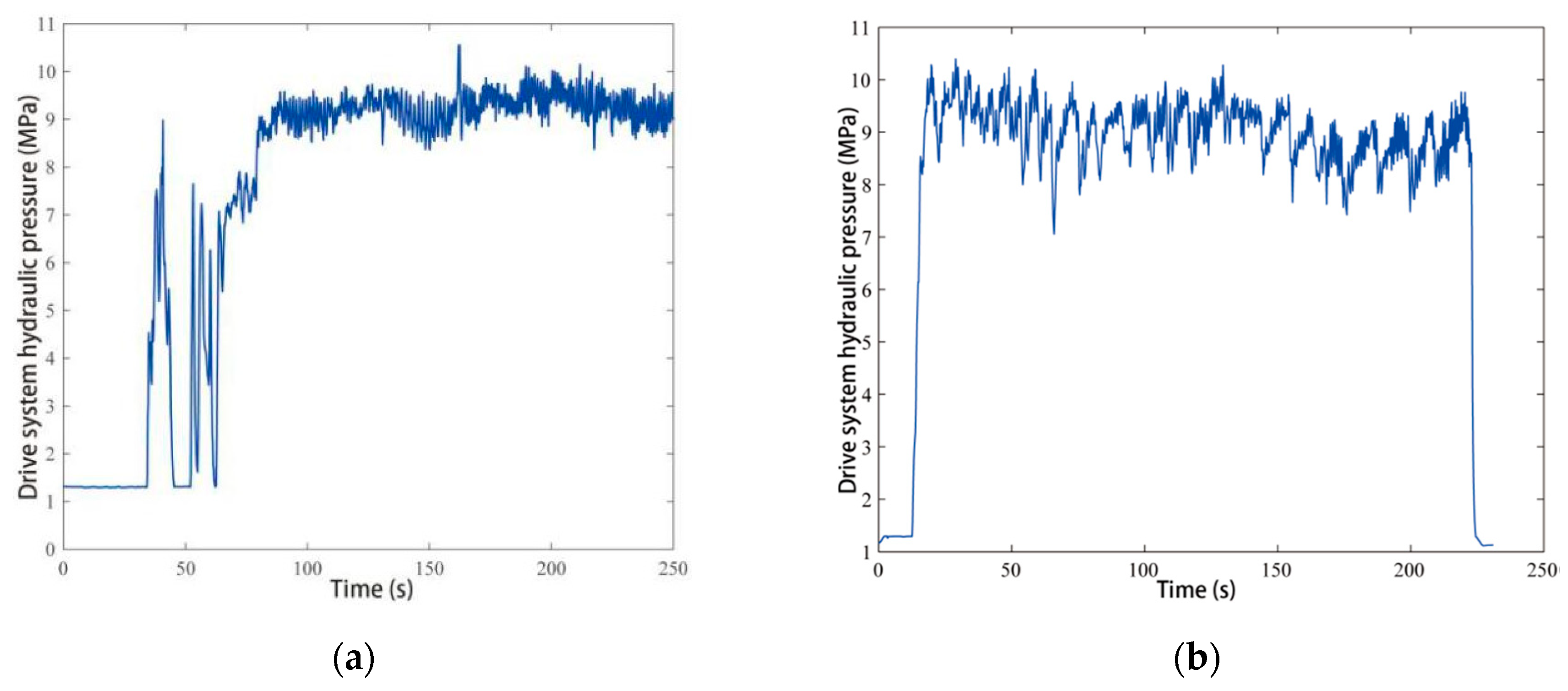
5.2. Field Test Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Q. The Study on Milling Drum System of Road Cold Miller. Master’s Thesis, Dept. Mech. Eng., Xi’an University of Technology, Xi’an, China, 2006. [Google Scholar]
- Guo, Y.; Duan, M. Computer Simulation of Load Fluctuation of Milling Cylinder of Pavement Planer. J. Hunan Univ. Sci. Technol. Nat. Sci. Ed. 2007, 24, 17–20. [Google Scholar]
- Gu, H.; Jiao, S.; Xiao, A.C. Analysis and Test on Asphalt Milling Machine Cutting Load Characteristic. China J. Highw. Transp. 2012, 25, 154–158. [Google Scholar]
- Wang, A.; Li, Z.; Yao, H. Discussion of automatic power apportioning of milling machine. Road Mach. Constr. Mech. 2005, 22, 34–36. [Google Scholar]
- Long, J. Study on Working Principle and Power Allocation of Tracked Milling Machine. Road Mach. Constr. Mech. 2010, 27, 73–75. [Google Scholar]
- Chen, Y.; Zou, X.; Yang, Y. Design of Digital Control System of Hydraulic Milling Machine. Mech. Eng. Autom. 2012, 19, 123–125. [Google Scholar]
- Yuan, F. Design of Traveling Control System for Milling Machine Based on DSP. Road Mach. Constr. Mech. 2010, 27, 79–81. [Google Scholar]
- Ma, P.; Hu, Y.; Zhang, X. Research on adaptive power control parameter of a cold milling machine. Simul. Model. Pract. Theory 2008, 16, 1136–1144. [Google Scholar]
- Ma, P.; Hu, Y.; Zhang, Z. The dynamical model of a cold milling machine and its adaptive power control simulation. Simulation 2011, 87, 809–817. [Google Scholar]
- Atherton, D.P. PID controller tuning. Comput. Control. Eng. J. 1999, 10, 44–50. [Google Scholar]
- Nasr, M.B.; Chtourou, M. Neural network control of nonlinear dynamic systems using hybrid algorithm. Appl. Soft Comput. 2014, 24, 423–431. [Google Scholar]
- Kumara, N.; Panwarb, V.; Sukavanam, N.; Sharma, S.P.; Borm, J.H. Neural network-based nonlinear tracking control of kinematic ally redundant robot manipulators. Math. Comput. Model. 2011, 53, 1889–1901. [Google Scholar]
- Ge, S.S.; Hong, F.; Lee, T.H. Adaptive neural network control of nonlinear systems with unknown time delays. IEEE Trans. Autom. Control. 2003, 48, 2004–2010. [Google Scholar]
- Yang, Q.; Yang, Z.; Sun, Y. Universal Neural Network Control of MIMO Uncertain Nonlinear Systems. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1163–1169. [Google Scholar]
- Baloochy, B. A Robust Approach in Nonlinear Fuzzy Control of Chemical Process. Chem. Eng. Res. Bull. 2013, 16, 45–60. [Google Scholar]
- Sofianos, N.A.; Boutalis, Y.S. Robust adaptive multiple models based fuzzy control of nonlinear systems. Neurocomputing 2016, 173, 1733–1742. [Google Scholar]
- Harb, A.M.; Smadi, I.A. Tracking control of DC motors via mimo nonlinear fuzzy control. Chaos Solitons Fractals 2009, 42, 702–710. [Google Scholar]
- He, Z.; Ji, X. Nonlinear robust control of integrated vehicle dynamics. Veh. Syst. Dyn. 2012, 50, 247–280. [Google Scholar]
- Tian, B.; Fan, W.; Zong, Q.; Wang, J.; Wang, F. Nonlinear robust control for reusable launch vehicles in reentry phase based on time-varying high order sliding mode. J. Frankl. Inst. 2013, 350, 1787–1807. [Google Scholar]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. Robust Nonlinear Control for Path Tracking of a Quad-Rotor Helicopter. Asian J. Control. 2015, 17, 142–156. [Google Scholar]
- Isidori, A.; Marconi, L.; Serrani, A. Robust nonlinear motion control of a helicopter. IEEE Trans. Autom. Control. 2003, 48, 413–426. [Google Scholar]
- Abdeddaim, S.; Betka, A.; Drid, S.; Becherif, M. Implementation of MRAC controller of a DFIG based variable speed grid connected wind turbine. Energy Convers. Manag. 2014, 79, 281–288. [Google Scholar]
- Mirkin, B.; Gutman, P.-O.; Shtessel, Y. Coordinated decentralized sliding mode MRAC with control cost optimization for a class of nonlinear systems. J. Frankl. Inst. 2012, 349, 1364–1379. [Google Scholar]
- Zilletti, M.; Elliott, S.J.; Gardonio, P.; Rustighi, E. Experimental implementation of a self-tuning control system for decentralized velocity feedback. J. Sound Vib. 2012, 331, 1–14. [Google Scholar]
- Wang, R.; Chen, L.; Wang, D. Self-tuning Control on Integrated System of EPS and SAS Based on Pole Placement. Procedia Eng. 2011, 16, 271–277. [Google Scholar]
- Yao, H. The Hydraulic Dynamics and Control Mechanism of Construction Vehicles; China Communications Press: Beijing, China, 2006. [Google Scholar]
- Hu, Y.; Ma, P.; Zhang, X. Modelling and simulating of cold milling machine. J. Chang’an Univ. Nat. Sci. Ed. 2008, 28, 92–95. [Google Scholar]
- Galichet, S.; Foulloy, L. Fuzzy controllers: synthesis and equivalences. IEEE Trans. Fuzzy Syst. 1995, 3, 140–148. [Google Scholar]
- Ding, J.; Xu, Y. Single Neuron Adaptive PID Controller and its Applications. Control Eng. China 2004, 11, 27–30. [Google Scholar]
- Yadav, R.; Kalra, P.K.; John, J. Time series prediction with single multiplicative neuron model. Appl. Soft Comput. 2007, 7, 1157–1163. [Google Scholar]
- Cai, Z. Intelligent Control, 2nd ed.; Publishing House of Electronics Industry: Beijing, China, 2004. [Google Scholar]
- He, L.; Wan, Z.; Cheng, L.; Liao, X. Simulink simulation of single neuron PID and smith predictive control based on the s-Function. In Proceedings of the 2013 Third International Conference on IMCCC, Shenyang, China, 21–23 September 2013; pp. 1548–1551. [Google Scholar]
- Zhao, X.; Jiao, Y. Single Neuron Self-Adaptive PSD Control and Its Application in Reheat Steam Temperature Control System. Chin. Soc. Elec. Eng. 2001, 21, 93–96. [Google Scholar]
- Cheng, Q.; Wan, D.; Huang, L. The Single Neuron Adaptive PID/PSD Controller of Ship Autopilot. J. Southeast Univ. 1997, 27, 133–137. [Google Scholar]
- Astrom, K.J.; Hagglund, T. PID Controllers: Theory, Design and Tuning, 2nd ed.; Instrument Society of America: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Jiao, S. Research on the Hydraulic Drive and Control Systems of an Asphalt Concrete Spreader. Ph.D Thesis, Dept. Mech. Eng. Chang’an University, Xi’an, China, 2002; pp. 36–51. [Google Scholar]
- Lei, T. New Manual of Hydraulic Engineering; Beijing Institute of Technology Press: Beijing, China, 1998; pp. 3–6. [Google Scholar]
- Zeng, W.; Zhao, M.; He, T. Working performance for asphalt road plane milling machine. J. Chang’an Univ. Nat. Sci. Ed. 2004, 24, 58–61. [Google Scholar]







| Variable | Value | Variable | Value |
|---|---|---|---|
| ie | 1 | h | 100% |
| J(kg·m2) | 0.459 | Rg (m) | 0.34 |
| Dm(m3/rad) | 4.16 × 10−5 | Jd(kg·m2) | 0.536 |
| βe(MPa) | 1.25 × 103 | V0(m) | 1.27 × 10−5 |
| τs (MPa) | 2.55 | Cm(m−5·(N·s)−1) | 1.4 × 10−12 |
| nmax (rev·min−1) | 2200 | Zd | 112 |
| nH (rev·min−1) | 2000 | nMmax (rev·min−1) | 1400 |
| P H (kW) | 196 | Mmax (Nm) | 1140 |
| R0 (m) | 0.34 | M H (Nm) | 937 |
| B (m) | 1.3 | F f (N) | 2800 |
| Rd (m) | 0.46 | k | 0.607 |
| KP (m3·rad−1) | 1.59 × 10−4 | kd | 0.9 |
| β(rad) | 0.174 | kmd | 2 |
| ae(m) | 0.08 | γ0(rad) | 0.209 |
| ap(m) | 0.08 | im | 230 |
| id | 12.5 | ηP | 2.6 |
| m(kg) | 20,000 | ηD | 0.05 |
| ηI | 1.25 | w1 | 0.3 |
| Ku0 | 0.065 | w3 | 0.01 |
| w2 | 0.13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, F.; Hu, Y.; Ma, P.; Zhang, X.; Li, Z. Practical Control of a Cold Milling Machine using an Adaptive PID Controller. Appl. Sci. 2020, 10, 2516. https://doi.org/10.3390/app10072516
Meng F, Hu Y, Ma P, Zhang X, Li Z. Practical Control of a Cold Milling Machine using an Adaptive PID Controller. Applied Sciences. 2020; 10(7):2516. https://doi.org/10.3390/app10072516
Chicago/Turabian StyleMeng, Fanwei, Yongbiao Hu, Pengyu Ma, Xuping Zhang, and Zhixiong Li. 2020. "Practical Control of a Cold Milling Machine using an Adaptive PID Controller" Applied Sciences 10, no. 7: 2516. https://doi.org/10.3390/app10072516
APA StyleMeng, F., Hu, Y., Ma, P., Zhang, X., & Li, Z. (2020). Practical Control of a Cold Milling Machine using an Adaptive PID Controller. Applied Sciences, 10(7), 2516. https://doi.org/10.3390/app10072516





