Transient Study of Flow and Cavitation Inside a Bileaflet Mechanical Heart Valve
Abstract
:1. Introduction
2. Method and Validation
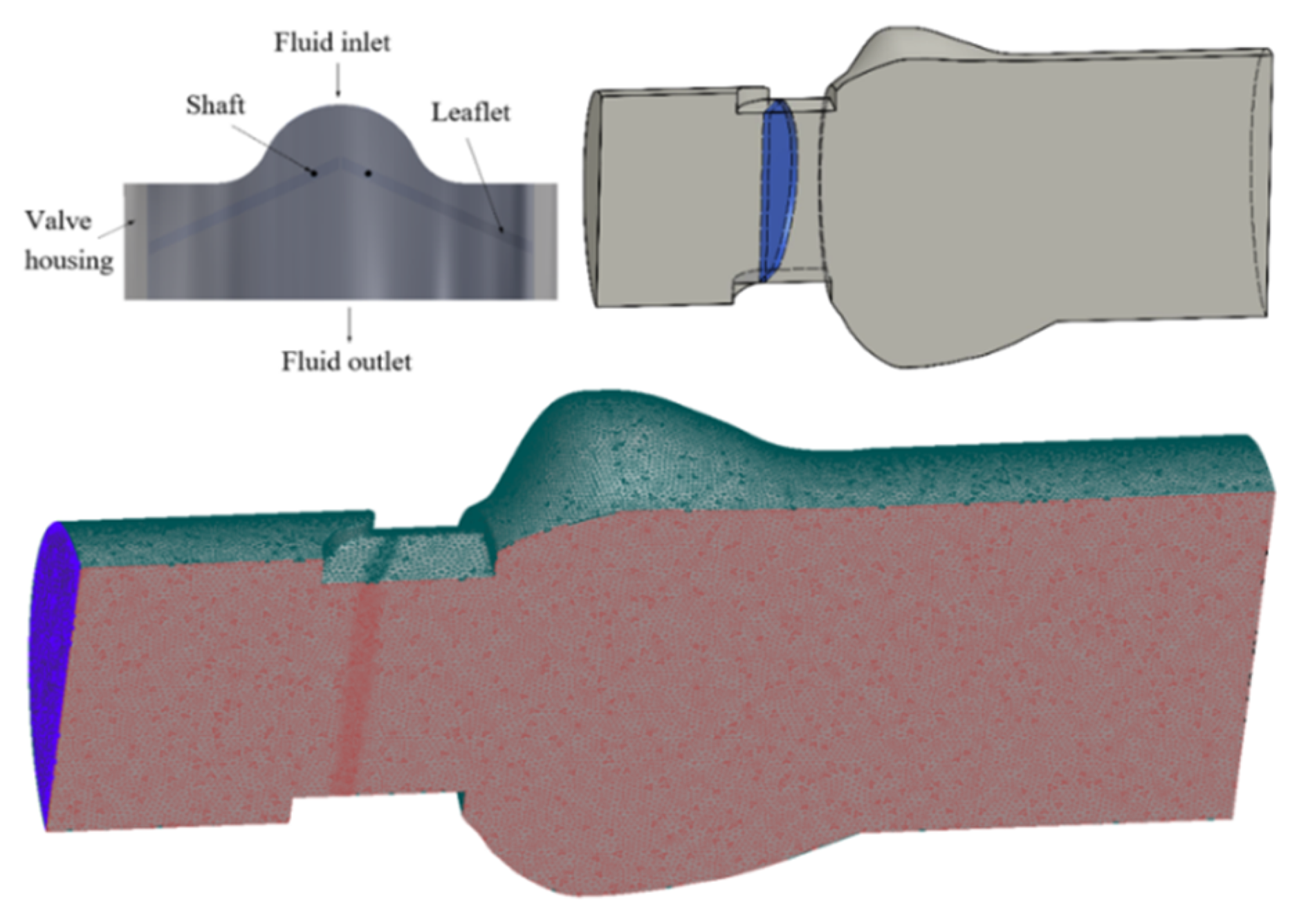
2.1. Geometric Model
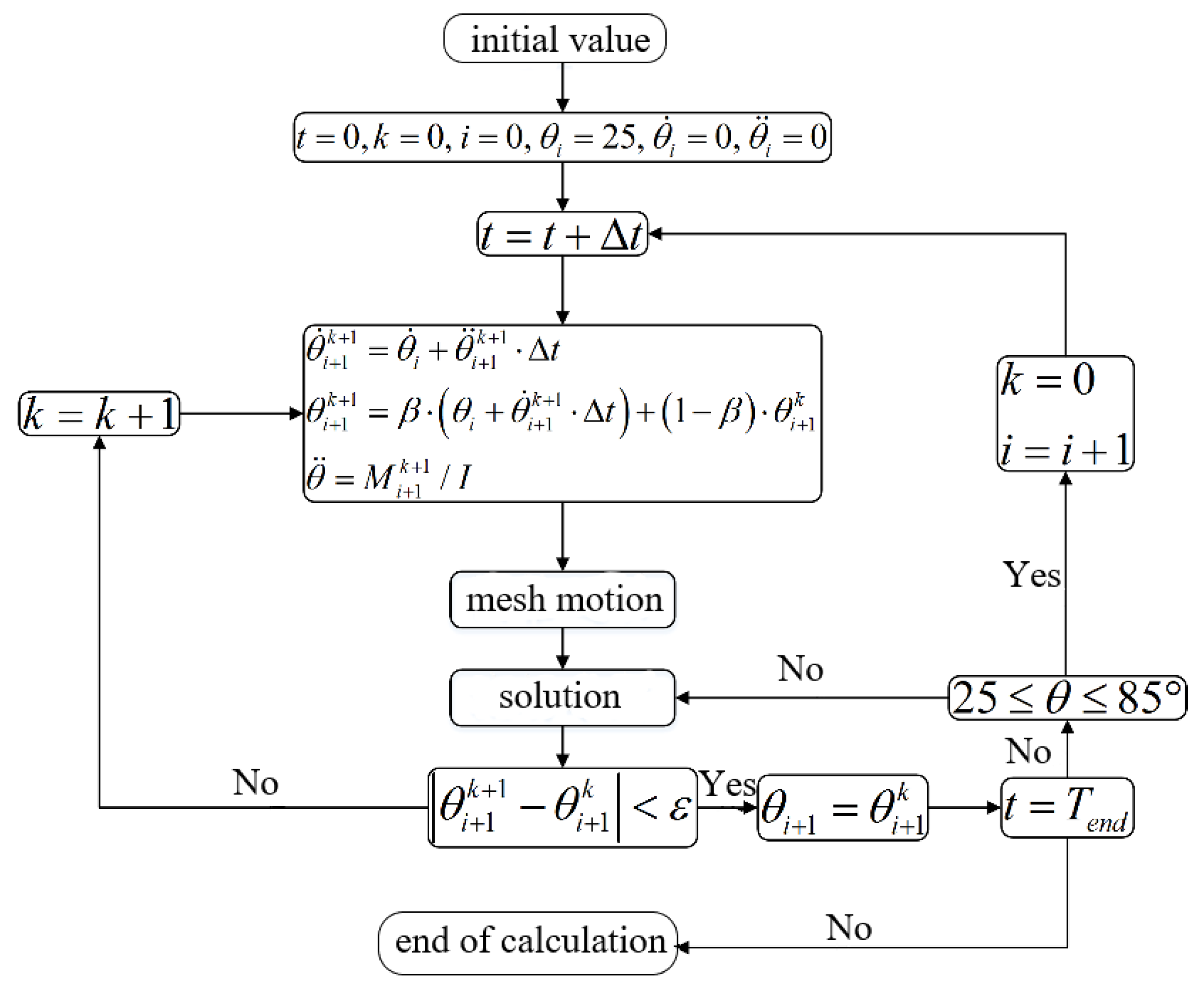
2.2. Numerical Model
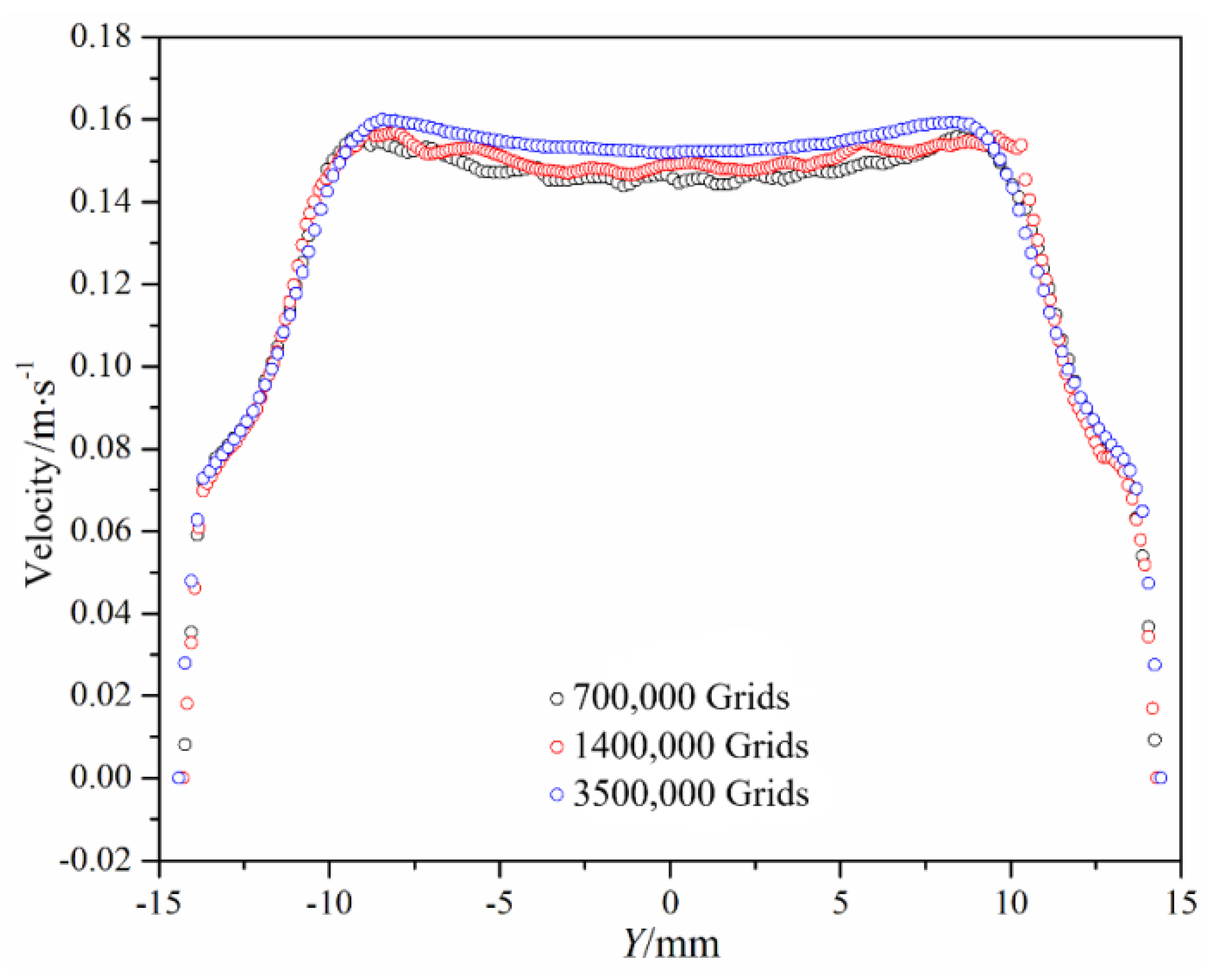
2.3. Experimental Validation
3. Results and Discussion
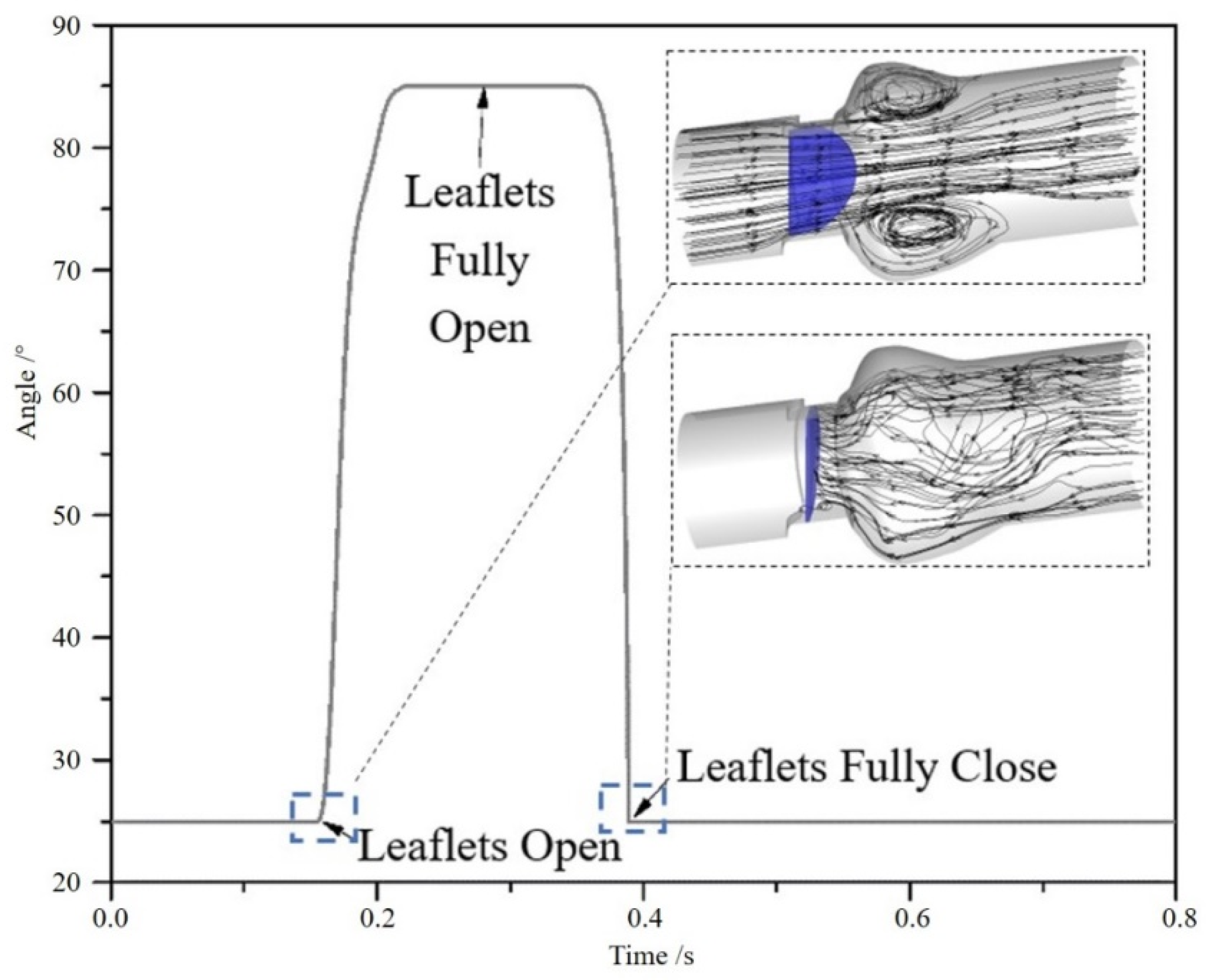
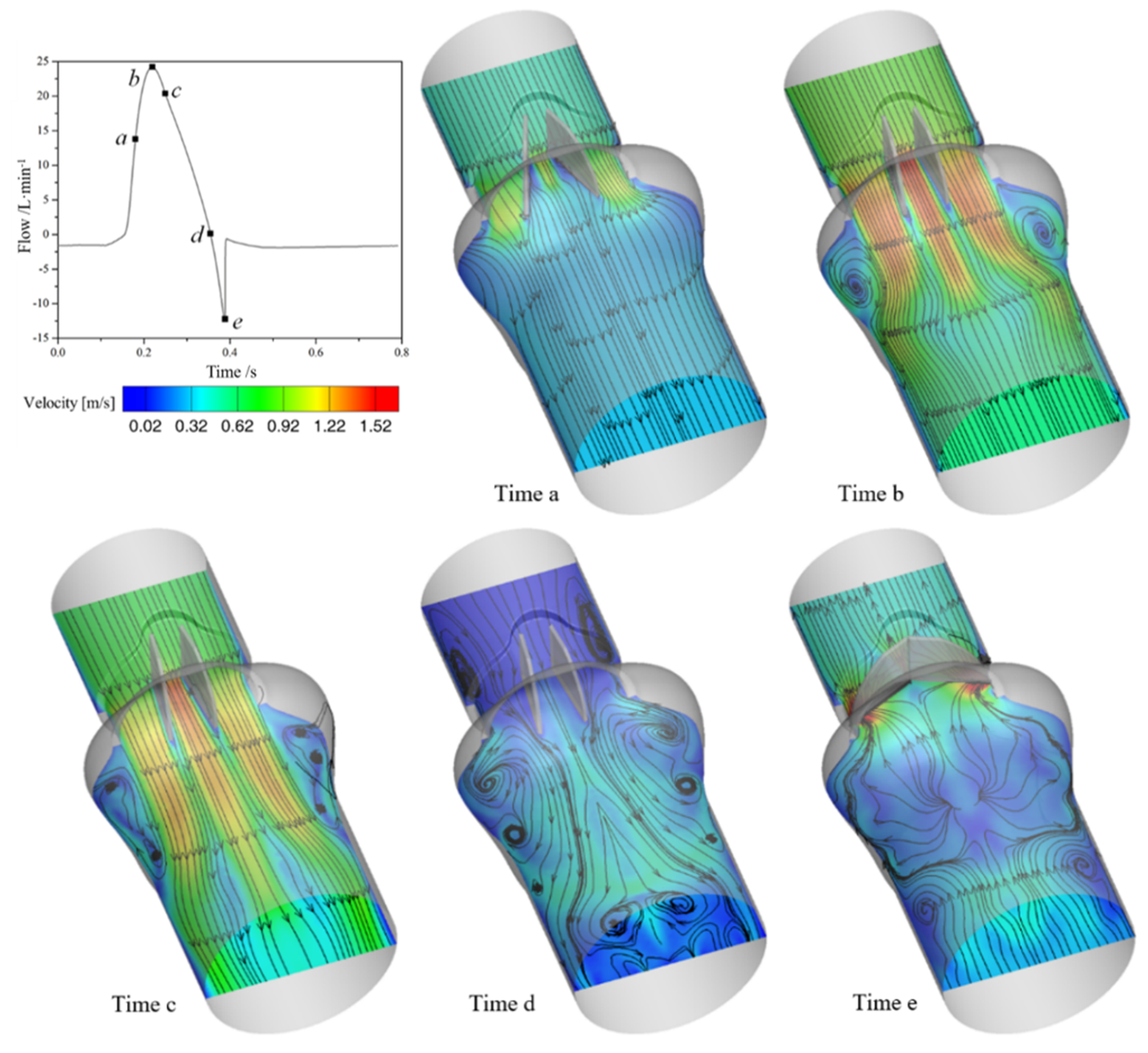
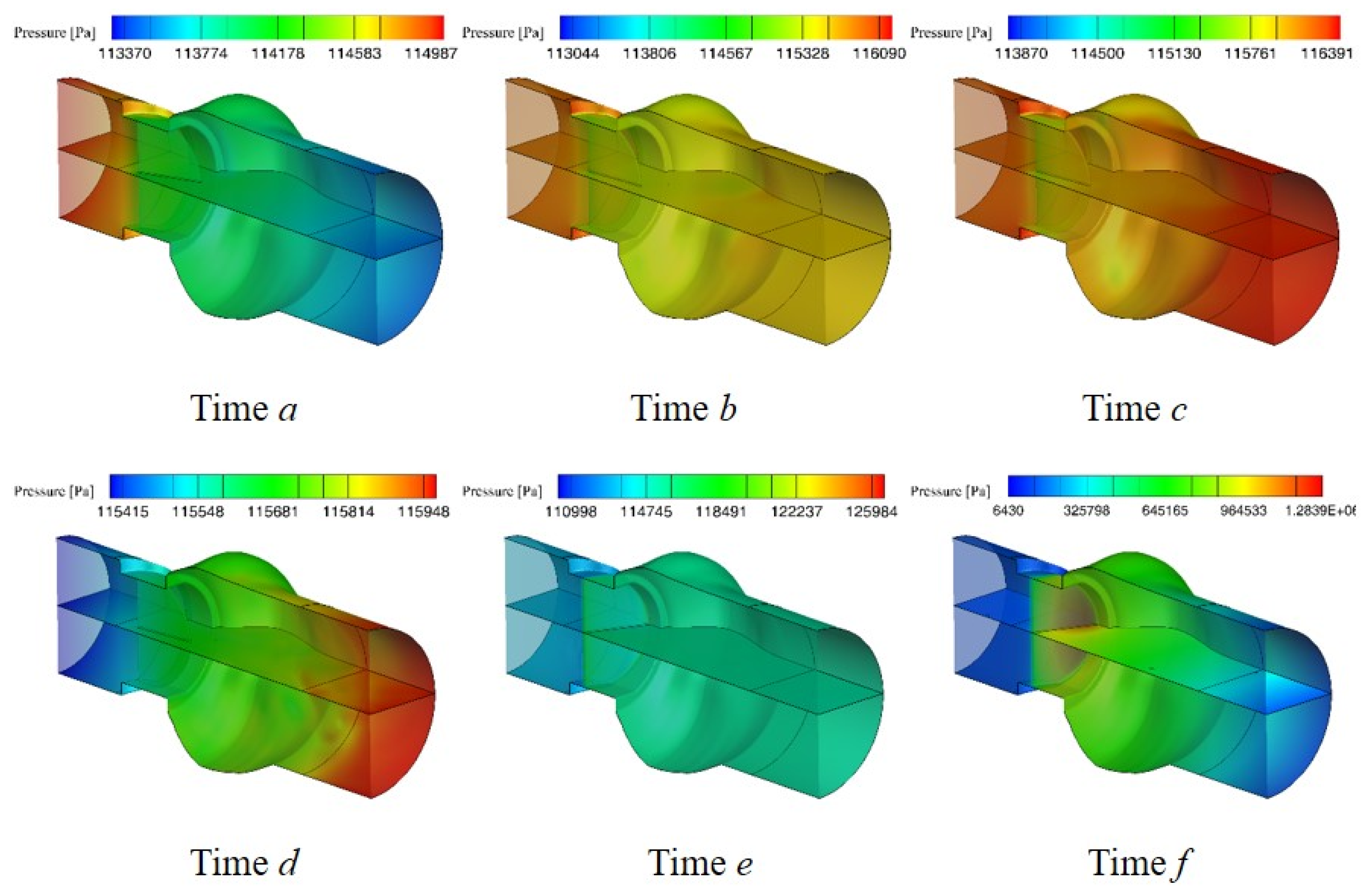
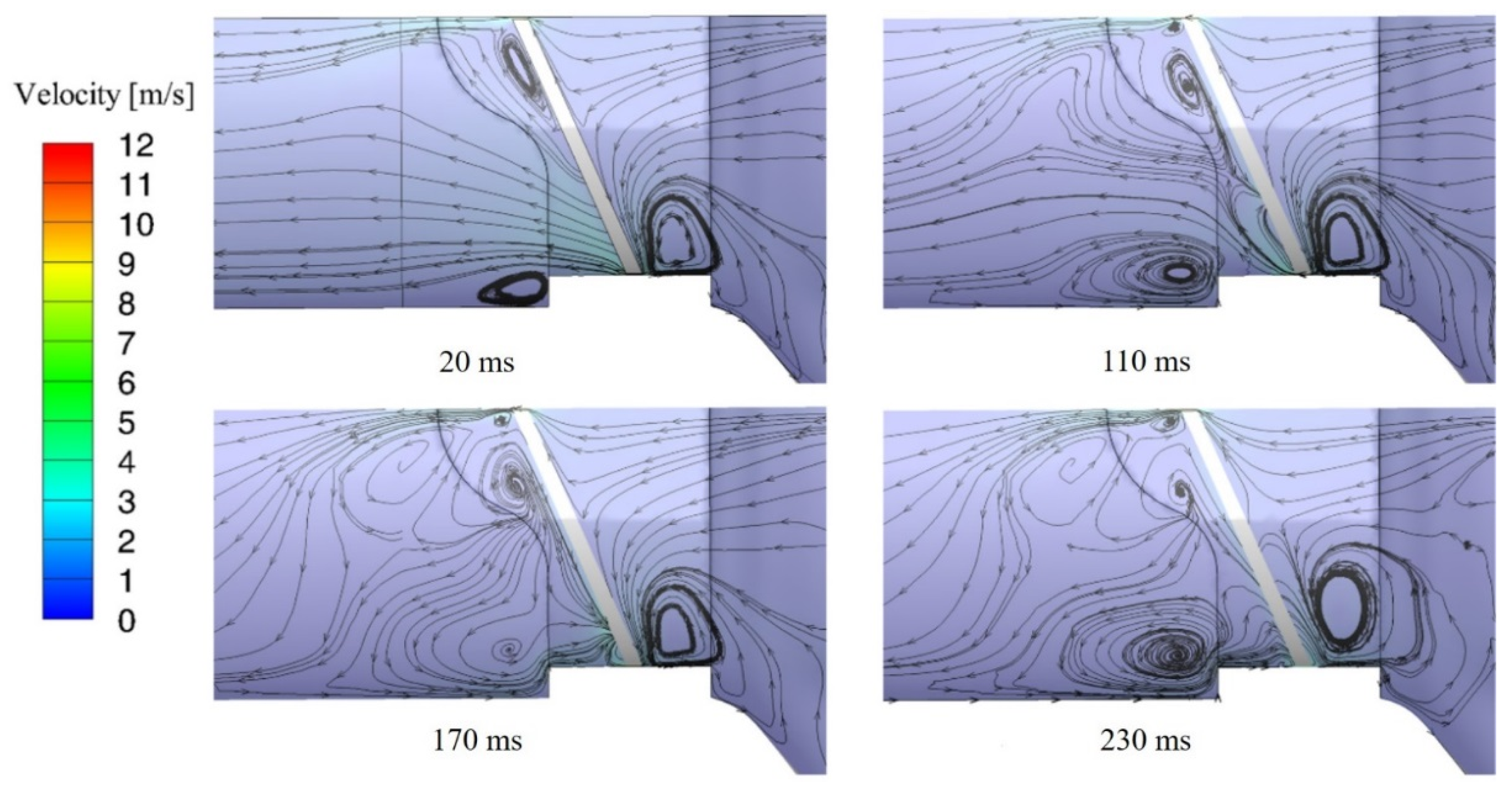
3.1. Flow Characteristics of the Bileaflet Mechanical Heart Valve
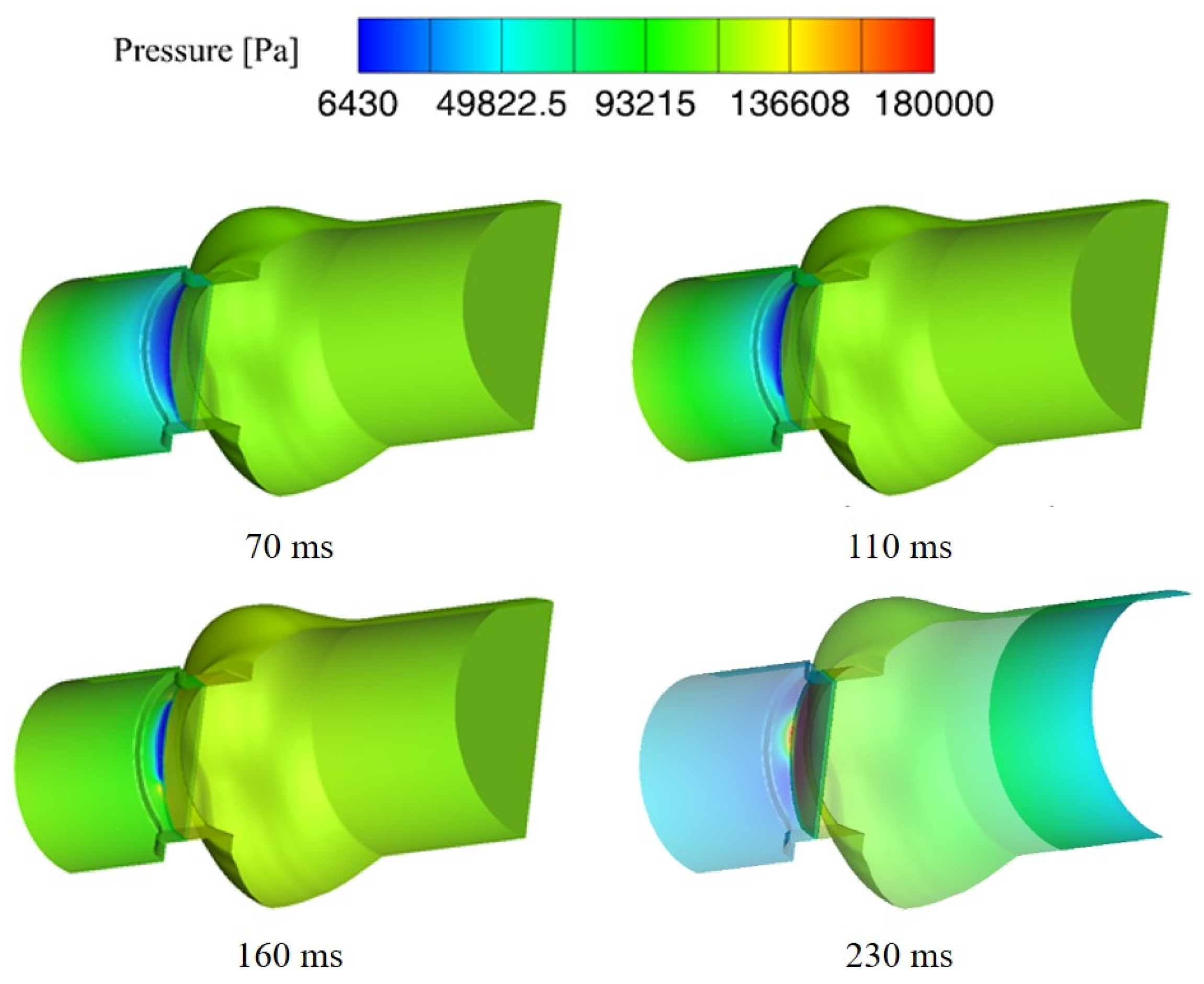
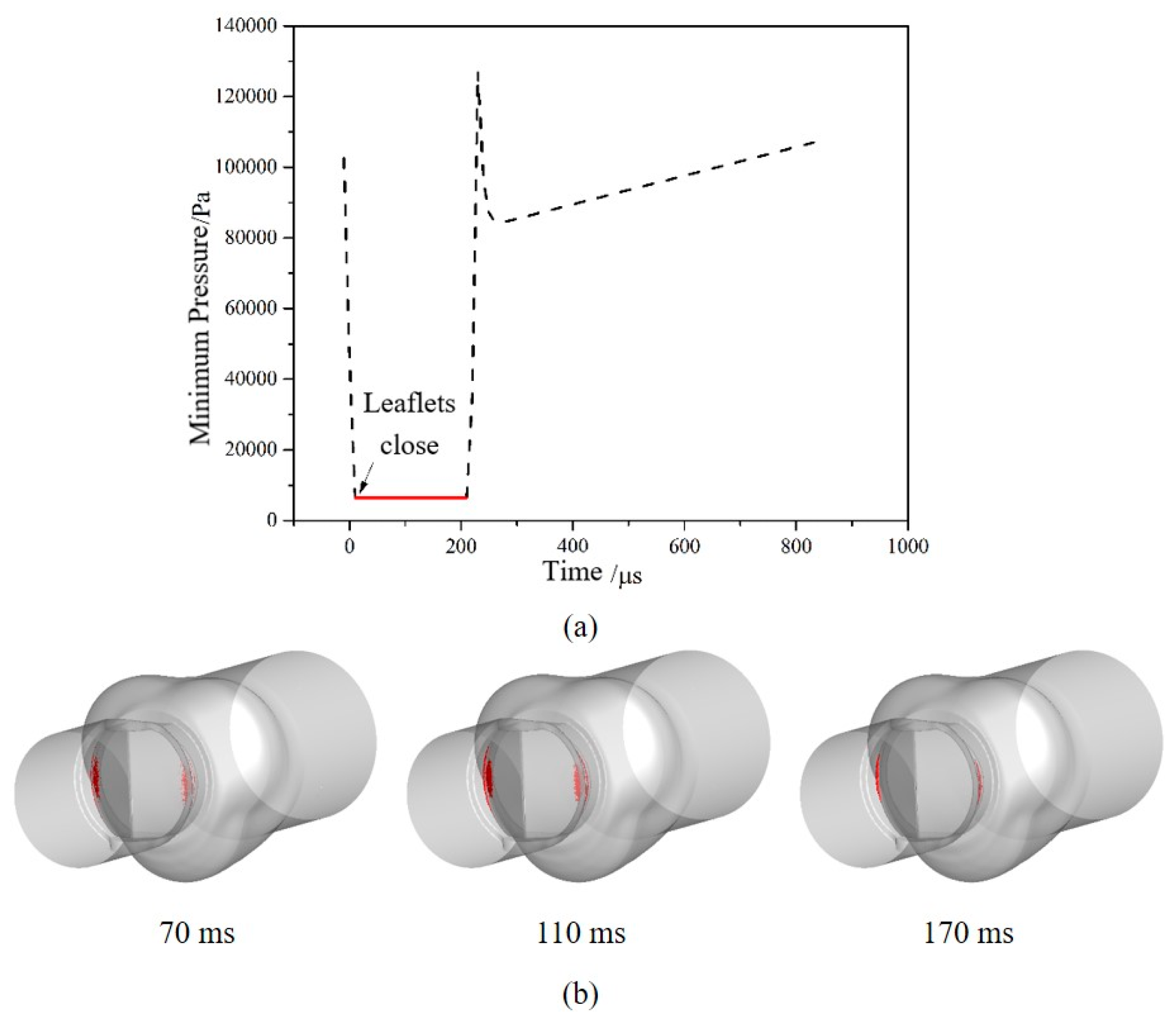
3.2. Cavitation Characteristics of the Bileaflet Mechanical Heart Valve
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dangas, G.D.; Weitz, J.I.; Giustino, G.; Makkar, R.; Mehran, R. Prosthetic Heart Valve Thrombosis. J. Am. Coll. Cardiol. 2016, 68, 2670–2689. [Google Scholar] [CrossRef]
- Del Gaudio, C.; Gasbarroni, P.L.; Romano, G.P. Experimental investigations on the fluid-mechanics of an electrospun heart valve by means of particle image velocimetry. J. Mech. Behav. Biomed. Mater. 2016, 64, 229–239. [Google Scholar] [CrossRef] [PubMed]
- Qian, J.-Y.; Chen, M.-R.; Gao, Z.-X.; Jin, Z.-J. Mach number and energy loss analysis inside multi-stage Tesla valves for hydrogen decompression. Energy 2019, 179, 647–654. [Google Scholar] [CrossRef]
- Tao, J.; Lin, Z.; Ma, C.; Ye, J.; Zhu, Z.; Li, Y.; Mao, W. An Experimental and Numerical Study of Regulating Performance and Flow Loss in a V-Port Ball Valve. J. Fluids Eng. 2019, 142, 142. [Google Scholar] [CrossRef]
- Luraghi, G.; Wu, W.; De Gaetano, F.; Matas, J.F.R.; Moggridge, G.D.; Serrani, M.; Stasiak, J.; Costantino, M.L.; Migliavacca, F. Evaluation of an aortic valve prosthesis: Fluid-structure interaction or structural simulation? J. Biomech. 2017, 58, 45–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qian, J.-Y.; Chen, M.-R.; Liu, X.-L.; Qian, J.-Y. A numerical investigation of the flow of nanofluids through a micro Tesla valve. J. Zhejiang Univ. A 2018, 20, 50–60. [Google Scholar] [CrossRef]
- Qian, J.-Y.; Wu, J.-Y.; Gao, Z.-X.; Wu, A.; Jin, Z.-J. Hydrogen decompression analysis by multi-stage Tesla valves for hydrogen fuel cell. Int. J. Hydrogen Energy 2019, 44, 13666–13674. [Google Scholar] [CrossRef]
- Abu Bakar, H.; Abas, A.; Mokhtar, N.H.; Razak, N.; Hamid, M.N.B.A. Particle Image Velocimetry and Finite Volume Method Study of Bi-leaflet Artificial Heart Valve. J. Appl. Fluid Mech. 2018, 11, 1365–1375. [Google Scholar] [CrossRef]
- Kadhim, S.K.; Nasif, M.S.; Al-Kayiem, H.H.; Al-Waked, R. Computational fluid dynamics simulation of blood flow profile and shear stresses in bileaflet mechanical heart valve by using monolithic approach. J. Soc. Comput. Simul. 2017, 94, 93–104. [Google Scholar] [CrossRef] [Green Version]
- Hafizah, M.N.; Aizat, A. Simulation of blood flow in different configurations design of bi-leaflet mechanical heart valve. IOP Conf. Ser. Mater. Sci. Eng. 2018, 370, 012065. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Kuan, Y.H.; Chen, P.-Y.; Ge, L.; Sotiropoulos, F.; Yoganathan, A.P.; Leo, H.L. Experimentally Validated Hemodynamics Simulations of Mechanical Heart Valves in Three Dimensions. Cardiovasc. Eng. Technol. 2011, 3, 88–100. [Google Scholar] [CrossRef] [Green Version]
- Bark, D.L.; Vahabi, H.; Bui, H.; Movafaghi, S.; Moore, B.; Kota, A.K.; Popat, K.; Dasi, L.P. Hemodynamic Performance and Thrombogenic Properties of a Superhydrophobic Bileaflet Mechanical Heart Valve. Ann. Biomed. Eng. 2016, 45, 452–463. [Google Scholar] [CrossRef] [Green Version]
- De Tullio, M.D.; Nam, J.; Pascazio, G.; Balaras, E.; Verzicco, R. Computational prediction of mechanical hemolysis in aortic valved prostheses. Eur. J. Mech. B/Fluids 2012, 35, 47–53. [Google Scholar] [CrossRef]
- Sturla, F.; Votta, E.; Stevanella, M.; Conti, C.A.; Redaelli, A. Impact of modeling fluid–structure interaction in the computational analysis of aortic root biomechanics. Med Eng. Phys. 2013, 35, 1721–1730. [Google Scholar] [CrossRef]
- Querzoli, G.; Fortini, S.; Espa, S.; Melchionna, S. A laboratory model of the aortic root flow including the coronary arteries. Exp. Fluids 2016, 57, 134. [Google Scholar] [CrossRef]
- Susin, F.M.; Espa, S.; Toninato, R.; Fortini, S.; Querzoli, G. Integrated strategy for in vitro characterization of a bileaflet mechanical aortic valve. Biomed. Eng. Online 2017, 16, 29. [Google Scholar] [CrossRef] [Green Version]
- Hanafizadeh, P.; Mirkhani, N.; Davoudi, M.R.; Masouminia, M.; Sadeghy, K. Non-Newtonian Blood Flow Simulation of Diastolic Phase in Bileaflet Mechanical Heart Valve Implanted in a Realistic Aortic Root Containing Coronary Arteries. Artif. Organs 2016, 40, E179–E191. [Google Scholar] [CrossRef]
- Haya, L.; Tavoularis, S. Effects of bileaflet mechanical heart valve orientation on fluid stresses and coronary flow. J. Fluid Mech. 2016, 806, 129–164. [Google Scholar] [CrossRef]
- Taehyup, H.; Chang, N.K. A numerical analysis of the blood flow around the bileaflet mechanical heart valves with different rotational implantation angles. J. Hydrodyn. 2011, 23, 607–614. [Google Scholar]
- Abbas, S.S.; Nasif, M.S.; Said, M.A.M.; Kadhim, S.K. Numerical investigation on effect of aortic root geometry on flow induced structural stresses developed in a bileaflet mechanical heart valve. J. Phys. Conf. Ser. 2017, 908, 12039. [Google Scholar] [CrossRef]
- Abbas, S.S.; Nasif, M.S.; Said, M.A.M.; Al-Waked, R.; Kadhim, S.K. Numerical investigation on effect of leaflet thickness on structural stresses developed in a bileaflet mechanical heart valve for its sustainable manufacturing. MATEC Web Conf. 2017, 131, 4004. [Google Scholar] [CrossRef] [Green Version]
- Kheradvar, A.; Pedrizzetti, G. Vortex Formation in the Cardiovascular System. Vortex Form. Cardiovasc. Syst. 2012, 3, 45–73. [Google Scholar]
- Kheradvar, A.; Assadi, R.; Falahatpisheh, A.; Sengupta, P.P. Assessment of Transmitral Vortex Formation in Patients with Diastolic Dysfunction. J. Am. Soc. Echocardiogr. 2012, 25, 220–227. [Google Scholar] [CrossRef]
- Domenichini, F.; Pedrizzetti, G.; Baccani, B. Three-dimensional filling flow into a model left ventricle. J. Fluid Mech. 2005, 539, 179. [Google Scholar] [CrossRef]
- Qian, J.-Y.; Hou, C.-W.; Wu, J.-Y.; Gao, Z.-X.; Qian, J.-Y. Aerodynamics analysis of superheated steam flow through multi-stage perforated plates. Int. J. Heat Mass Transf. 2019, 141, 48–57. [Google Scholar] [CrossRef]
- Li, C.-P.; Lu, P.-C. Numerical comparison of the closing dynamics of a new trileaflet and a bileaflet mechanical aortic heart valve. J. Artif. Organs 2012, 15, 364–374. [Google Scholar] [CrossRef]
- Mirkhani, N.; Davoudi, M.R.; Hanafizadeh, P.; Javidi, D.; Saffarian, N. On-X Heart Valve Prosthesis: Numerical Simulation of Hemodynamic Performance in Accelerating Systole. Cardiovasc. Eng. Technol. 2016, 7, 223–237. [Google Scholar] [CrossRef]
- Forleo, M.; Dasi, L.P. Effect of Hypertension on the Closing Dynamics and Lagrangian Blood Damage Index Measure of the B-Datum Regurgitant Jet in a Bileaflet Mechanical Heart Valve. Ann. Biomed. Eng. 2013, 42, 110–122. [Google Scholar] [CrossRef]
- Kuan, Y.H.; Kabinejadian, F.; Nguyen, V.-T.; Su, B.; Yoganathan, A.P.; Leo, H.L. Comparison of hinge microflow fields of bileaflet mechanical heart valves implanted in different sinus shape and downstream geometry. Comput. Methods Biomech. Biomed. Eng. 2014, 18, 1785–1796. [Google Scholar] [CrossRef]
- Simon, H.A.; Ge, L.; Borazjani, I.; Sotiropoulos, F.; Yoganathan, A.P. Simulation of the Three-Dimensional Hinge Flow Fields of a Bileaflet Mechanical Heart Valve Under Aortic Conditions. Ann. Biomed. Eng. 2009, 38, 841–853. [Google Scholar] [CrossRef] [Green Version]
- Klusak, E.; Bellofiore, A.; Loughnane, S.; Quinlan, N. High-Resolution Measurements of Velocity and Shear Stress in Leakage Jets From Bileaflet Mechanical Heart Valve Hinge Models. J. Biomech. Eng. 2015, 137, 111008. [Google Scholar] [CrossRef]
- Shadden, S.C.; Astorino, M.; Gerbeau, J.-F. Computational analysis of an aortic valve jet with Lagrangian coherent structures. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 017512. [Google Scholar] [CrossRef] [Green Version]
- Shahriari, S.; Maleki, H.; Hassan, I.; Kadem, L. Evaluation of shear stress accumulation on blood components in normal and dysfunctional bileaflet mechanical heart valves using smoothed particle hydrodynamics. J. Biomech. 2012, 45, 2637–2644. [Google Scholar] [CrossRef]
- Qian, J.-Y.; Gao, Z.-X.; Hou, C.-W.; Jin, Z.-J. A comprehensive review of cavitation in valves: Mechanical heart valves and control valves. Bio-Design Manuf. 2019, 2, 119–136. [Google Scholar] [CrossRef]
- Lu, L.; Xie, S.; Yin, Y.; Ryu, S. Experimental and numerical analysis on the surge instability characteristics of the vortex flow produced large vapor cavity in u-shape notch spool valve. Int. J. Heat Mass Transf. 2020, 146, 118882. [Google Scholar] [CrossRef]
- Rambod, E.; Beizaie, M.; Shusser, M.; Milo, S.; Gharib, M. A physical model describing the mechanism for formation of gas microbubbles in patients with mitral mechanical heart valves. Ann. Biomed. Eng. 2000, 27, 774–792. [Google Scholar] [CrossRef]
- Simcha, M.; Edmond, R.; Chaim, G. Mitral mechanical heart valves: In vitro studies of their closure, vortex and microbubble formation with possible medical implications. Eur. J. Cardio-Thorac. Surg. 2003, 24, 364–370. [Google Scholar]
- Qian, J.-Y.; Li, X.-J.; Wu, Z.; Jin, Z.-J.; Sunden, B. A comprehensive review on liquid–liquid two-phase flow in microchannel: Flow pattern and mass transfer. Microfluid. Nanofluidics 2019, 23, 116. [Google Scholar] [CrossRef]
- Bluestein, D.; Einav, S.; Hwang, N.H. A squeeze flow phenomenon at the closing of a bileaflet mechanical heart valve prosthesis. J. Biomech. 1994, 27, 1369–1378. [Google Scholar] [CrossRef]
- Jin, Z.-J.; Qiu, C.; Jiang, C.-H.; Wu, J.-Y.; Qian, J.-Y. Effect of valve core shapes on cavitation flow through a sleeve regulating valve. J. Zhejiang Univ. A 2020, 21, 1–14. [Google Scholar] [CrossRef]
- Choi, C.R.; Kim, C.N. Numerical Analysis on the Hemodynamics and Leaflet Dynamics in a Bileaflet Mechanical Heart Valve Using a Fluid-Structure Interaction Method. ASAIO J. 2009, 55, 428–437. [Google Scholar] [CrossRef]
- Lee, H.; Homma, A.; Taenaka, Y. Hydrodynamic Characteristics of Bileaflet Mechanical Heart Valves in an Artificial Heart: Cavitation and Closing Velocity. Artif. Organs 2007, 31, 532–537. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.-q.; Gao, Z.-x.; Jin, Z.-j.; Qian, J.-y. Transient Study of Flow and Cavitation Inside a Bileaflet Mechanical Heart Valve. Appl. Sci. 2020, 10, 2548. https://doi.org/10.3390/app10072548
Li W-q, Gao Z-x, Jin Z-j, Qian J-y. Transient Study of Flow and Cavitation Inside a Bileaflet Mechanical Heart Valve. Applied Sciences. 2020; 10(7):2548. https://doi.org/10.3390/app10072548
Chicago/Turabian StyleLi, Wen-qing, Zhi-xin Gao, Zhi-jiang Jin, and Jin-yuan Qian. 2020. "Transient Study of Flow and Cavitation Inside a Bileaflet Mechanical Heart Valve" Applied Sciences 10, no. 7: 2548. https://doi.org/10.3390/app10072548
APA StyleLi, W.-q., Gao, Z.-x., Jin, Z.-j., & Qian, J.-y. (2020). Transient Study of Flow and Cavitation Inside a Bileaflet Mechanical Heart Valve. Applied Sciences, 10(7), 2548. https://doi.org/10.3390/app10072548







