Decision of Water Quality Measurement Locations for the Identification of Water Quality Problems under Emergency Link Pipe Operation
Abstract
1. Introduction
2. Methodologies
2.1. Objectives and Assumptions
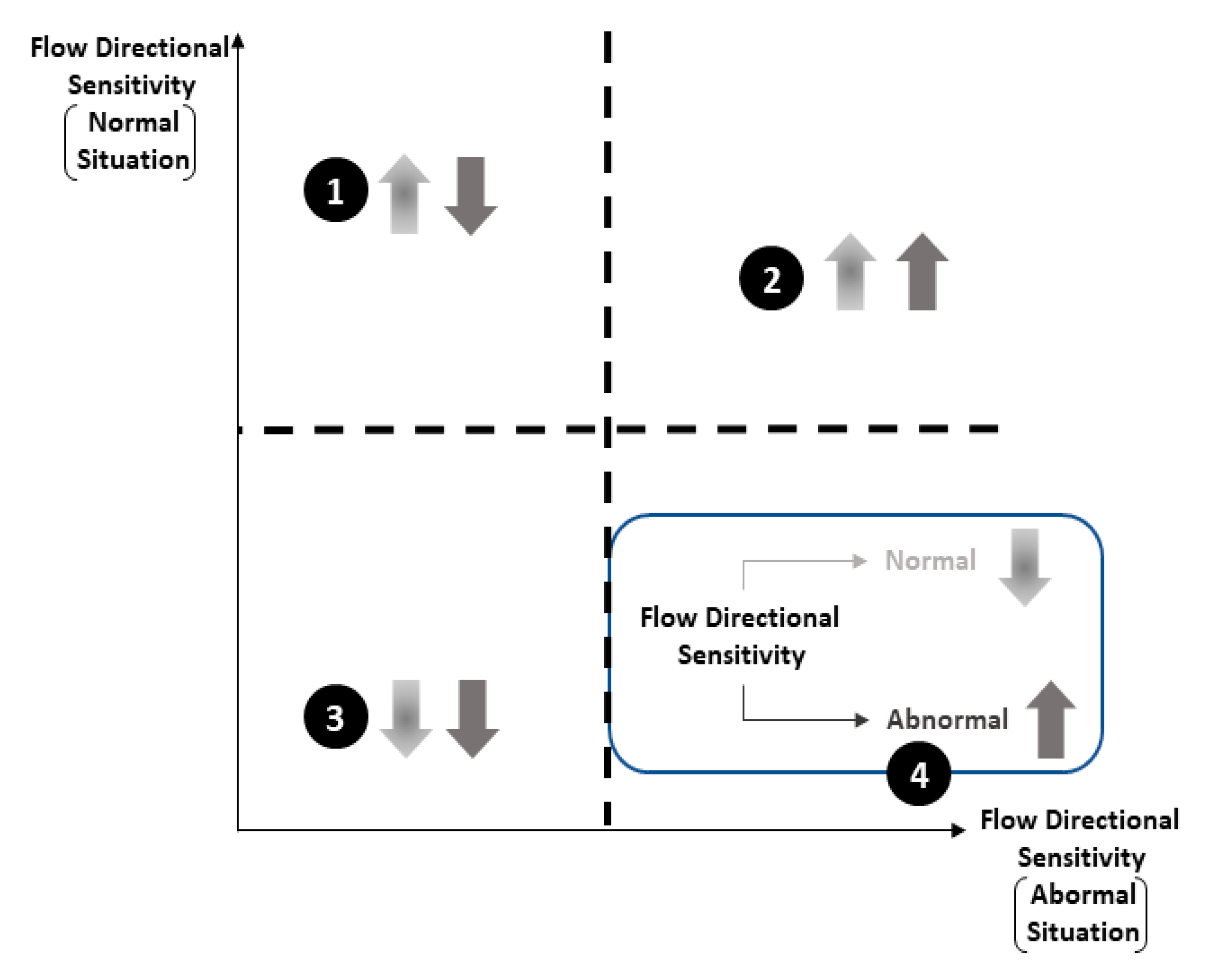
2.2. Water Quality Sensor Location Decision
3. Abnormal Scenarios
3.1. Target Pipe Network
3.2. Water Quality Measurement Location Decision Scenario
4. Application and Results
4.1. Emergency Scenario Application Result
4.2. Decision Result of Water Sensor Installation Pipeline
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- South Korea’s Ministry of Environment (MOE). Water-Supply Statistics; MOE: Sejong, Korea, 2019.
- MOE. The Causes and Future Plans of Turbid Water Incident in Incheon; Official brief report; MOE: Sejong, Korea, 2019.
- Waterworks Seoul Metropolitan Government, Korea. A Case Study of Accidents in Water Distribution Networks; Seoul Metropolitan Government: Seoul, Korea, 2010.
- Kessler, A.; Avi, O.; Gideon, S. Detecting accidental contaminations in municipal water networks. J. Water Resour. Plan. Manag. 1998, 124, 192–198. [Google Scholar] [CrossRef]
- Ostfeld, A.; Elad, S. Optimal layout of early warning detection stations for water distribution systems security. J. Water Resour. Plan. Manag. 2004, 130, 377–385. [Google Scholar] [CrossRef]
- Alzamora, F.M.; Ayala, H.B. Optimal sensor location for detecting contamination events in water distribution systems using topological algorithms. In Proceedings of the 8th Annual Water Distribution System Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Krause, A.; Leskovec, J.; Isovitsch, S.; Xu, J.; Guestrin, C.; VanBriesen, J.; Small, M.; Fischbeck, P. Optimizing sensor placements in water distribution systems using submodular function maximization. In Proceedings of the 8th Annual Water Distribution System Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- De Winter, C.; Palleti, V.R.; Worm, D.; Kooij, R. Optimal placement of imperfect water quality sensors in water distribution networks. Comput. Chem. Eng. 2019, 121, 200–211. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Sensor network design proposal for the battle of the water sensor networks (BWSN). In Proceedings of the 8th Annual Water Distribution System Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Preis, A.; Avi, O. Contamination source identification in water systems: A hybrid model trees–linear programming scheme. J. Water Resour. Plan. Manag. 2006, 132, 263–273. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar]
- Piazza, S.; Blokker, E.M.; Freni, G.; Puleo, V.; Sambito, M. Impact of diffusion and dispersion of contaminants in water distribution networks modelling and monitoring. Water Supply 2020, 20, 46–58. [Google Scholar] [CrossRef]
- Sambito, M.; Di Cristo, C.; Freni, G.; Leopardi, A. Optimal water quality sensor positioning in urban drainage systems for illicit intrusion identification. J. Hydroinformatics 2020, 22, 46–60. [Google Scholar] [CrossRef]
- Tsakiris, G.; Spiliotis, M. Uncertainty in the analysis of urban water supply and distribution systems. J. Hydroinformatics 2017, 19, 823–837. [Google Scholar] [CrossRef][Green Version]
- Mukherjee, R.; Diwekar, U.M.; Vaseashta, A. Optimal sensor placement with mitigation strategy for water network systems under uncertainty. Comput. Chem. Eng. 2017, 103, 91–102. [Google Scholar] [CrossRef]
- Xu, J.; Fischbeck, P.S.; Small, M.J.; VanBriesen, J.M.; Casman, E. Identifying Sets of Key Nodes for Placing Sensors in Dynamic Water Distribution Networks. J. Water Resour. Plann. Manag. 2008, 134, 378–385. [Google Scholar] [CrossRef]
- Xu, J.; Johnson, M.P.; Fischbeck, P.S.; Small, M.J.; van Briesen, J.M. Robust placement of sensors in dynamic water distribution systems. Eur. J. Oper. Res. 2010, 202, 707–716. [Google Scholar] [CrossRef]
- Krause, A.; Leskovec, J.; Guestrin, C.; VanBriesen, J.; Faloutsos, C. Efficient Sensor Placement Optimization for Securing Large Water Distribution Networks. J. Water Resour. Plann. Manag. 2008, 134, 516–526. [Google Scholar] [CrossRef]
- Watson, J.P.; Murray, R.; Hart, W.E. Formulation and Optimization of Robust Sensor Placement Problems for Drinking Water Contamination Warning Systems. J. Infrastruct. Syst. 2009, 15, 330–339. [Google Scholar] [CrossRef]
- Tryby Michael, E.; Marco, P.; Ranjithan, S.R. Monitoring design for source identification in water distribution systems. J. Water Resour. Plann. Manag. 2010, 136, 637–646. [Google Scholar] [CrossRef]
- Aral, M.M.; Guan, J.; Maslia, M.L. Optimal Design of Sensor Placement in Water Distribution Networks. J. Water Resour. Plann. Manag. 2010, 136, 5–18. [Google Scholar] [CrossRef]
- Cozzolinoa, L.; Mortea, R.D.; Palumbob, A.; Pianeseb, D. Stochastic approaches for sensors placement against intentional contaminations in water distribution systems. Civil Eng. Environ. Syst. 2011, 28, 75–98. [Google Scholar] [CrossRef]
- Koch, M.W.; McKenna, S.A. Distributed Sensor Fusion in Water Quality Event Detection. J. Water Resour. Plann. Manag. 2011, 137, 10–19. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di Nardo, A.; Greco, R.; Creaco, E.; Scala, A. Topological Placement of Quality Sensors in Water-Distribution Networks without the Recourse to Hydraulic Modeling. J. Water Resour. Plan. Manag. 2020, 146, 04020030. [Google Scholar] [CrossRef]
- De Winter, C.; Palleti, V.R.; Worm, D.; Kooij, R. Measuring imperfections of water quality sensors in water distribution networks. Meas. Sci. Technol. 2019, 30, 095101. [Google Scholar] [CrossRef]
- Di Nardo, A.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G.F.; Scala, A. Sensor placement in water distribution networks based on spectral algorithms. EPiC Ser. Eng. 2018, 3, 593–600. [Google Scholar]
- Yoo, D.G.; Chung, G.; Sadollah, A.; Kim, J.H. Applications of network analysis and multi-objective genetic algorithm for selecting optimal water quality sensor locations in water distribution networks. KSCE J. Civ. Eng. 2015, 19, 2333–2344. [Google Scholar] [CrossRef]
- Rossman, L. EPANet2 User’s Manual; US Environmental Protection Agency: Washington, DC, USA, 2000.
- Ronald, A.; Chadderton, G.; Christensen, L.; Henry-Unrath, P. Implementation and Optimization of Distribution Flushing Programs; AWWA Research Foundation; AWWA: Washington, DC, USA, 1992. [Google Scholar]
- South Korea’s Ministry of Environment (MOE). Water Supply System Standards; MOE: Sejong, Korea, 2010.
- Xanthopulos, Z.; Melachrinoudis, E.; Solomon, M.M. Interactive Multiobjective Group Decision Making with Interval Parameters. Manag. Sci. 2000, 46, 1721–1732. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water distribution reliability: Simulation methods. J. Water Resour Plann Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef]
- Cullinane, M.J.; Lansey, K.E.; Mays, L.W. Optimisationavailability-based design of water distribution networks. J. Hydraul. Eng. 1992, 118, 420–441. [Google Scholar] [CrossRef]
- Yoo, D.G.; Yoon, J.S.; Lee, H.M.; Kang, D.; Kim, J.H. Development and Application of Leakage Detection Model for Water Distribution Networks Considering Uncertainty Analysis. J. Korean Soc. Hazard Mitig. 2014, 14, 177–185. [Google Scholar] [CrossRef]






| Case Number | Abnormal Scenario | Normal Scenario | |
|---|---|---|---|
| Problematic Reservoir | Connected Reservoir | ||
| 1 | RES 1 (Block 1) | RES 2 (Block 2) | Demand Pattern (24 h) |
| 2 | RES 2 (Block 2) | RES 1 (Block 1) | Demand Pattern (24 h) |
| 3 | RES 2 (Block 2) | RES 3 (Block 3) | Demand Pattern (24 h) |
| 4 | RES 2 (Block 2) | RES 1 (Block 1) RES 3 (Block 3) | Demand Pattern (24 h) |
| 5 | RES 3 (Block 3) | RES 2 (Block 2) | Demand Pattern (24 h) |
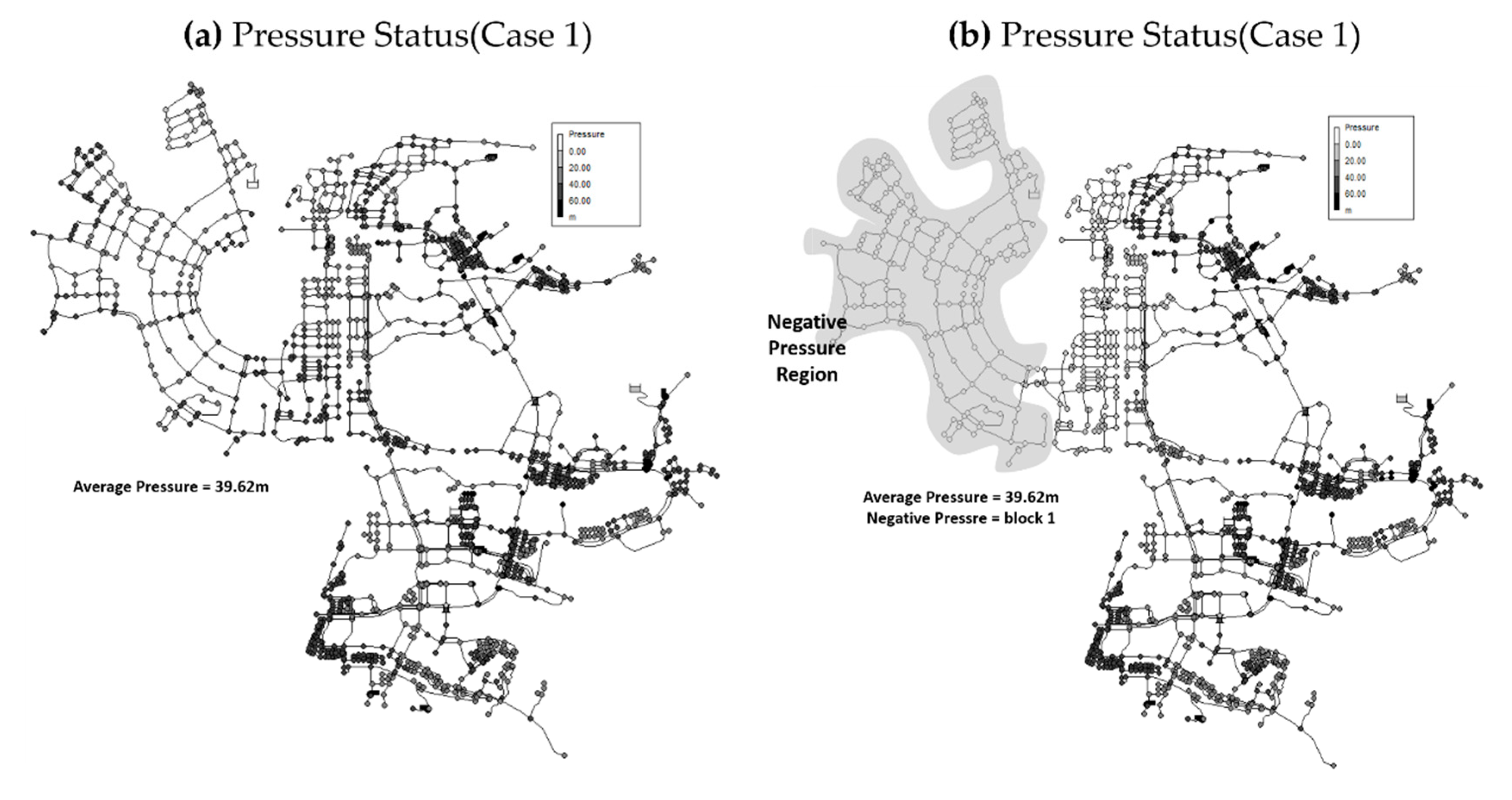
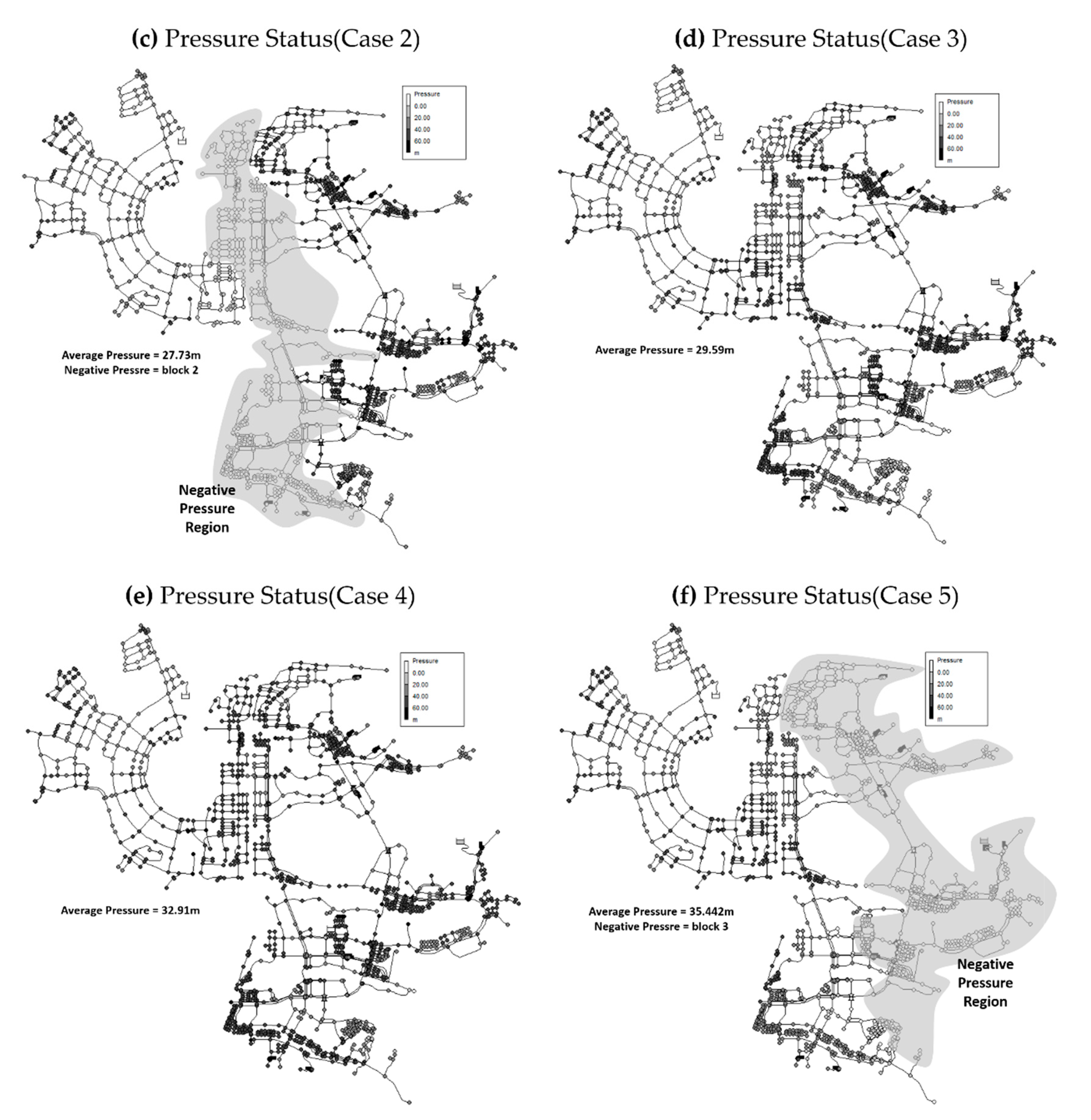
| Block Number | Pressure(m) | |||||
|---|---|---|---|---|---|---|
| Normal Situation | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |
| Block 1 | 39.62 | −18.81 | 29.82 | 38.12 | 39.23 | 38.67 |
| Block 2 | 43.13 | 20.17 | −89.22 | 17.92 | 23.82 | 32.21 |
| Block 3 | 36.11 | 35.27 | 35.22 | 32.74 | 35.67 | −94.28 |
| Average | 39.62 | 12.21 | −8.06 | 29.59 | 32.91 | −7.80 |
| Case Number | Pipe Name | Located Block | Abnormal Situation Sensitivity (X-Axis) | Normal Situation Sensitivity (Y-Axis) | Distance (1,0) |
|---|---|---|---|---|---|
| 1 | LG-96 | Block 2 | 0.64 | 0.48 | 0.6 |
| 3 | LE-90 | Block 2 | 0.48 | 0 | 0.52 |
| LG056(4) | Block 2 | 0.48 | 0 | 0.52 | |
| LE-108 | Block 2 | 0.48 | 0 | 0.52 | |
| 4 | #D744 | Block 1 | 0.96 | 0 | 0.04 |
| #D568 | Block 1 | 0.96 | 0 | 0.04 | |
| #D680 | Block 1 | 0.96 | 0 | 0.04 | |
| SA-25 | Block 1 | 0.96 | 0 | 0.04 | |
| LE-99-3 | Block 2 | 0.96 | 0 | 0.04 |
| Priority | Pipe Name | Abnormal Situation Sensitivity (X-Axis) | Normal Situation Sensitivity (Y-Axis) | Distance (1,0) |
|---|---|---|---|---|
| 1 | #D744 | 0.96 | 0 | 0.04 |
| #D568 | 0.96 | 0 | 0.04 | |
| #D680 | 0.96 | 0 | 0.04 | |
| SA-25 | 0.96 | 0 | 0.04 | |
| LE-99-3 | 0.96 | 0 | 0.04 | |
| 2 | LB-67 | 0.88 | 0 | 0.12 |
| LG072(5) | 0.88 | 0 | 0.12 | |
| #D685 | 0.88 | 0 | 0.12 | |
| 3 | #D686 | 0.8 | 0 | 0.2 |
| 4 | #D666 | 0.72 | 0 | 0.28 |
| SA-24 | 0.72 | 0 | 0.28 | |
| LA-03 | 0.72 | 0 | 0.28 | |
| LE-75 | 0.72 | 0 | 0.28 | |
| MP-24 | 0.72 | 0 | 0.28 | |
| MP-23 | 0.72 | 0 | 0.28 | |
| MP-22 | 0.72 | 0 | 0.28 | |
| LE-74-2 | 0.72 | 0 | 0.28 | |
| LE-94 | 0.72 | 0 | 0.28 | |
| 5 | LG-106 | 0.64 | 0 | 0.36 |
| LB-66 | 0.64 | 0 | 0.36 | |
| LB-62 | 0.64 | 0 | 0.36 | |
| LB-60 | 0.64 | 0 | 0.36 | |
| SA-43 | 0.64 | 0 | 0.36 | |
| #D740 | 0.64 | 0 | 0.36 | |
| #D623 | 0.64 | 0 | 0.36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.W.; Yoo, D.G. Decision of Water Quality Measurement Locations for the Identification of Water Quality Problems under Emergency Link Pipe Operation. Appl. Sci. 2020, 10, 2707. https://doi.org/10.3390/app10082707
Lee CW, Yoo DG. Decision of Water Quality Measurement Locations for the Identification of Water Quality Problems under Emergency Link Pipe Operation. Applied Sciences. 2020; 10(8):2707. https://doi.org/10.3390/app10082707
Chicago/Turabian StyleLee, Chan Wook, and Do Guen Yoo. 2020. "Decision of Water Quality Measurement Locations for the Identification of Water Quality Problems under Emergency Link Pipe Operation" Applied Sciences 10, no. 8: 2707. https://doi.org/10.3390/app10082707
APA StyleLee, C. W., & Yoo, D. G. (2020). Decision of Water Quality Measurement Locations for the Identification of Water Quality Problems under Emergency Link Pipe Operation. Applied Sciences, 10(8), 2707. https://doi.org/10.3390/app10082707






