Effect of Displacement Current on the Finite-Difference Modeling of Natural Source Electromagnetic Diffusion
Abstract
:1. Introduction
2. Materials and Methods
2.1. Basic Theory
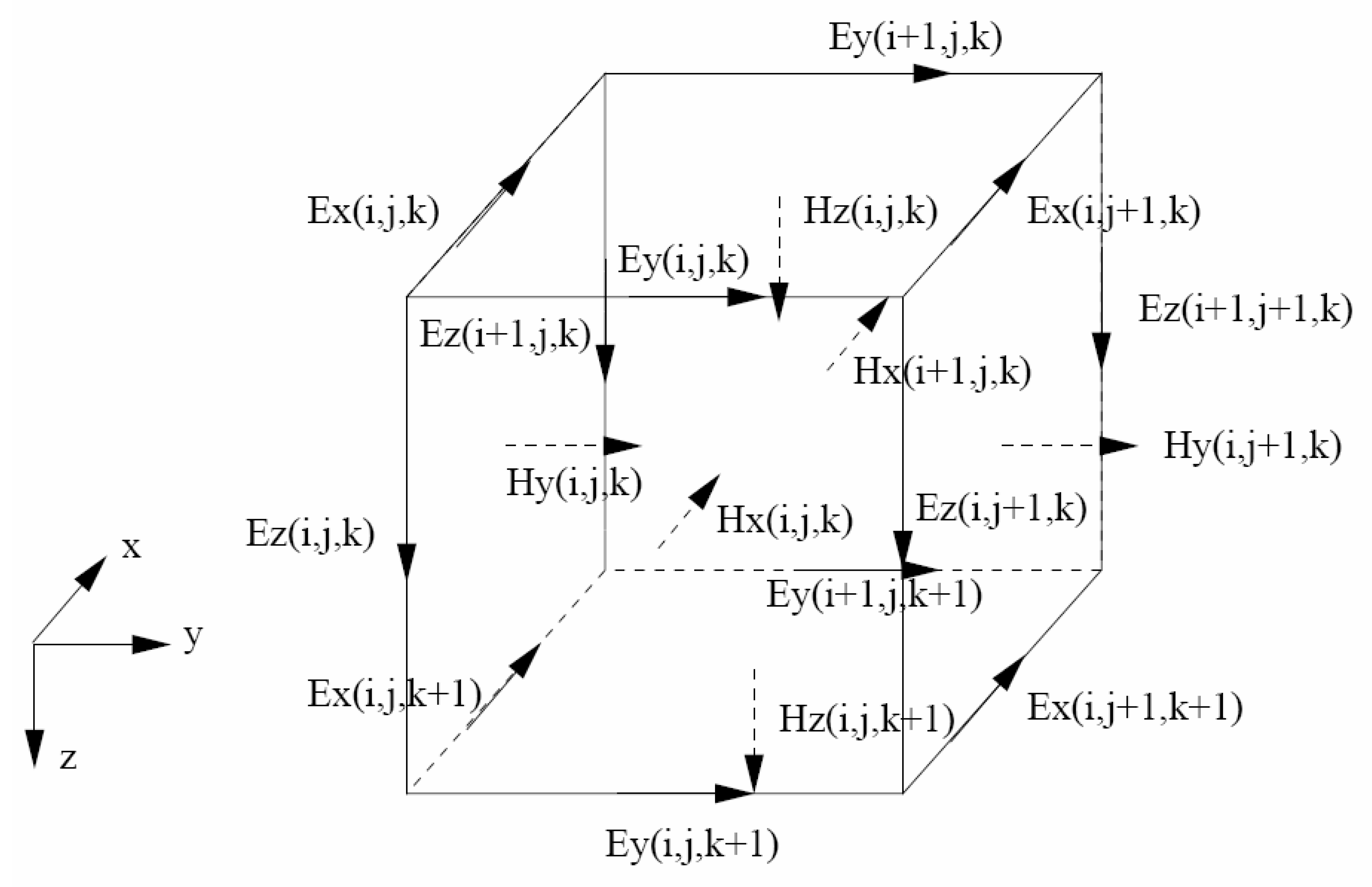
2.2. Finite-Difference Discretization
3. Results
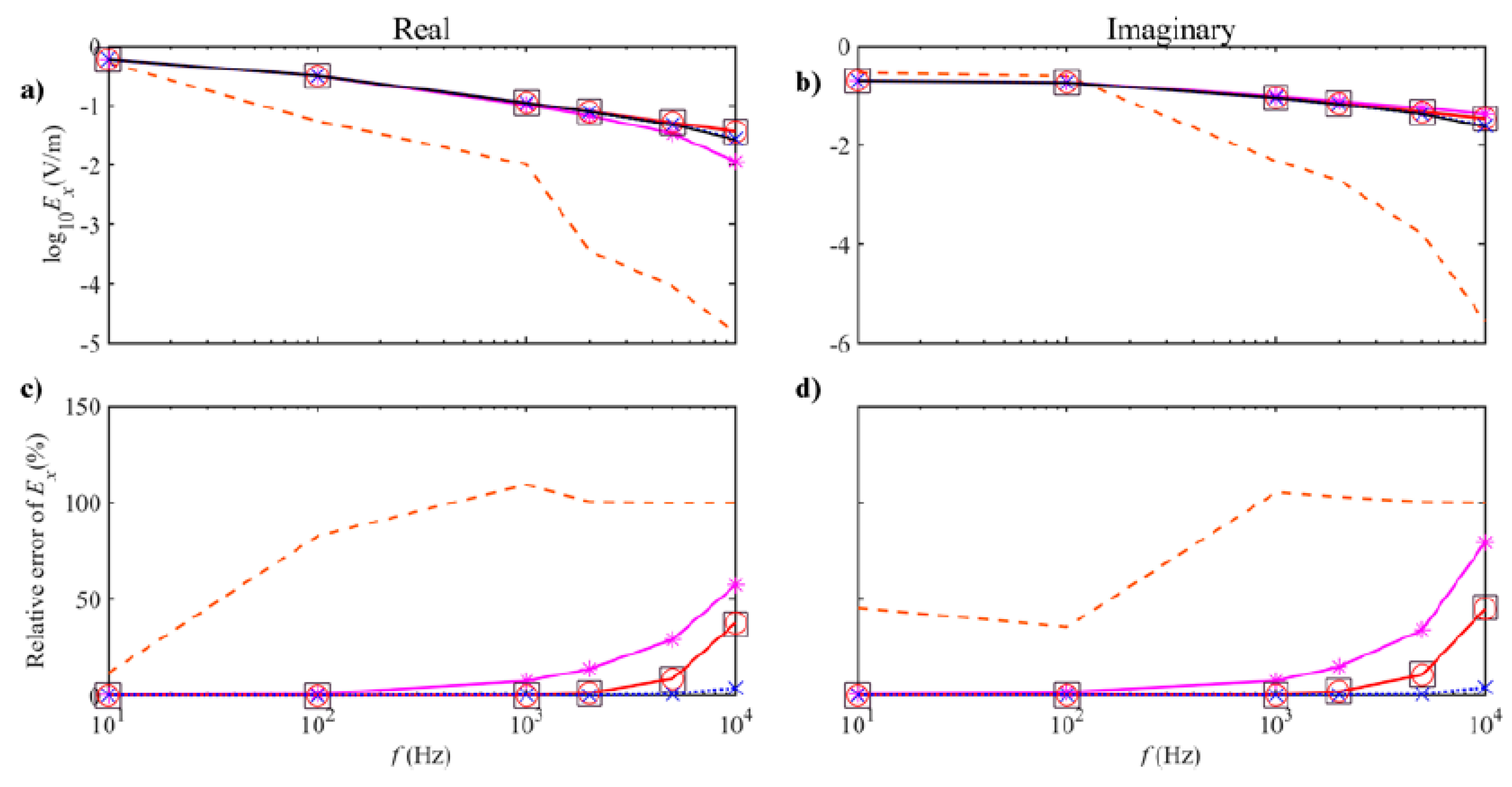
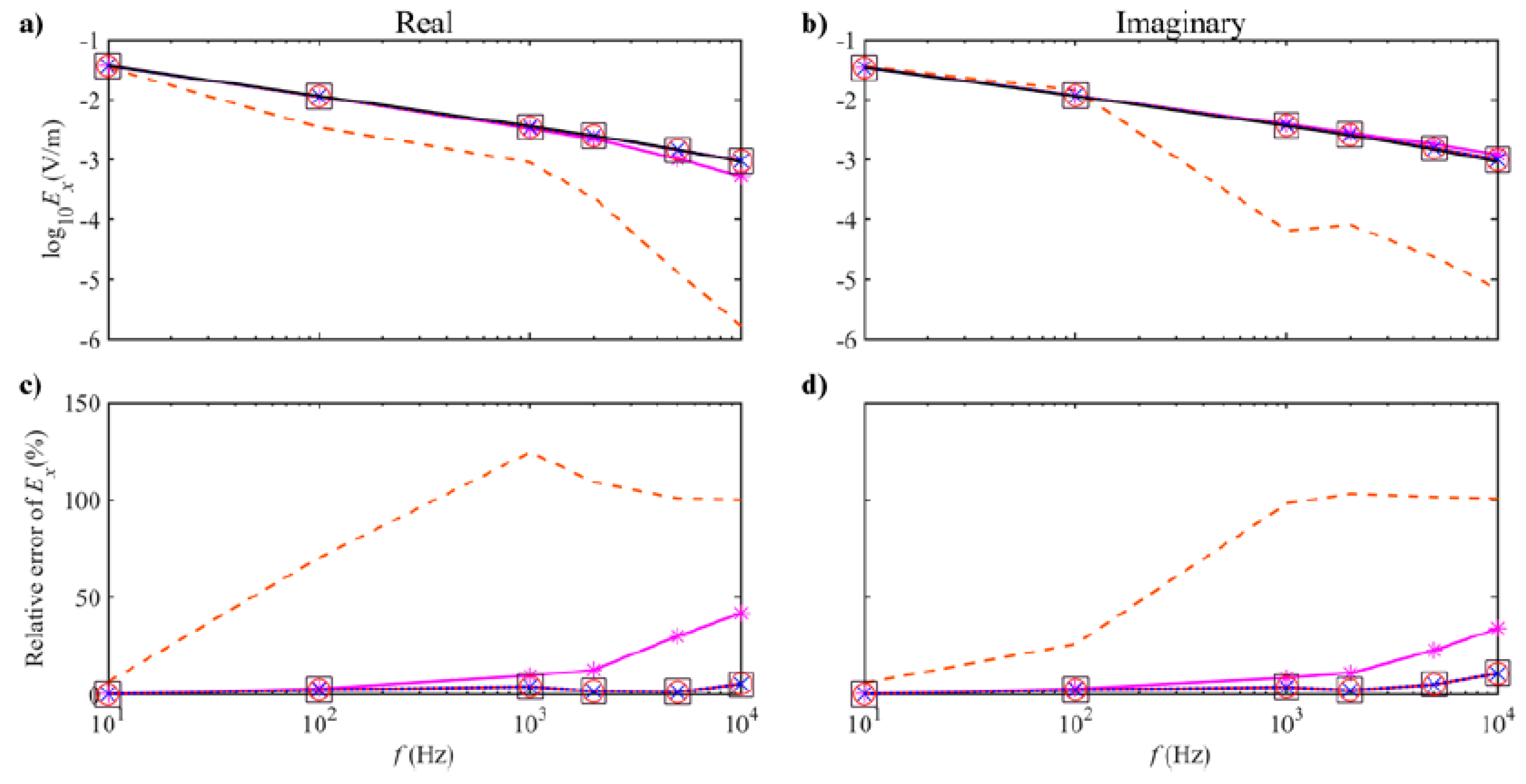
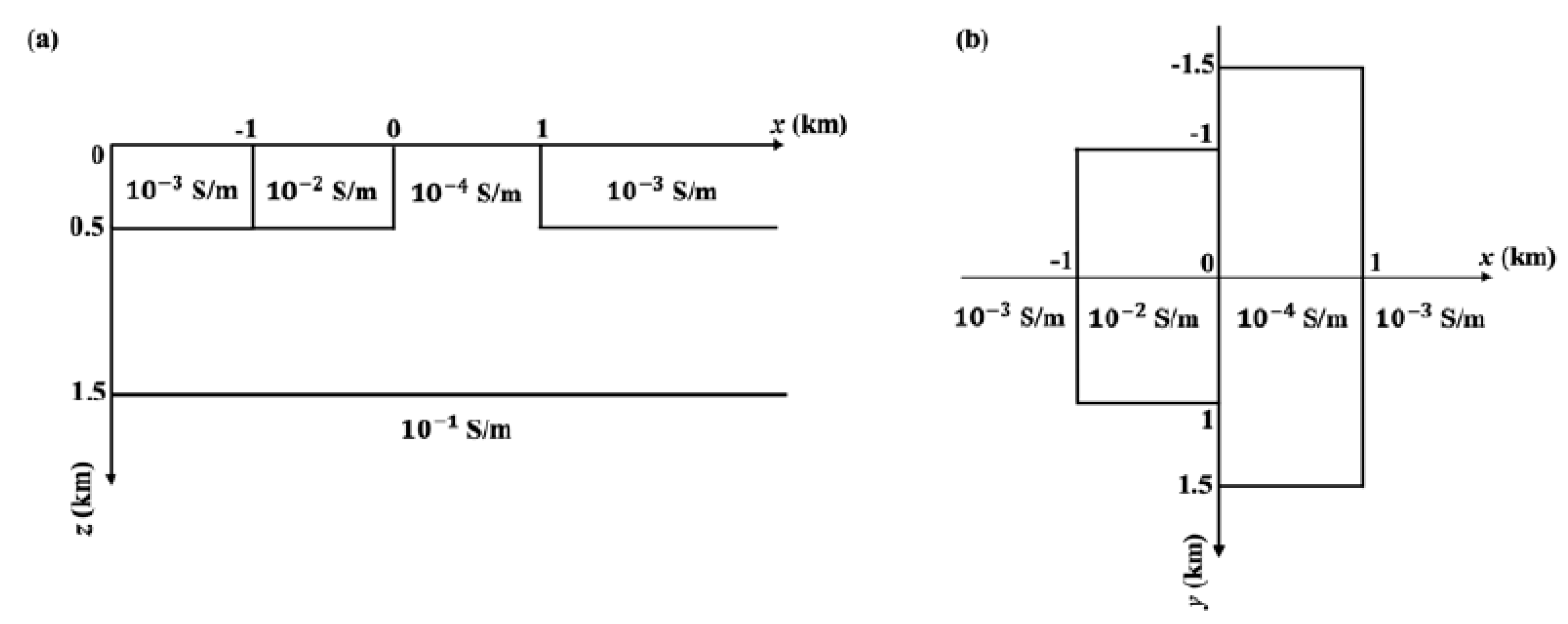
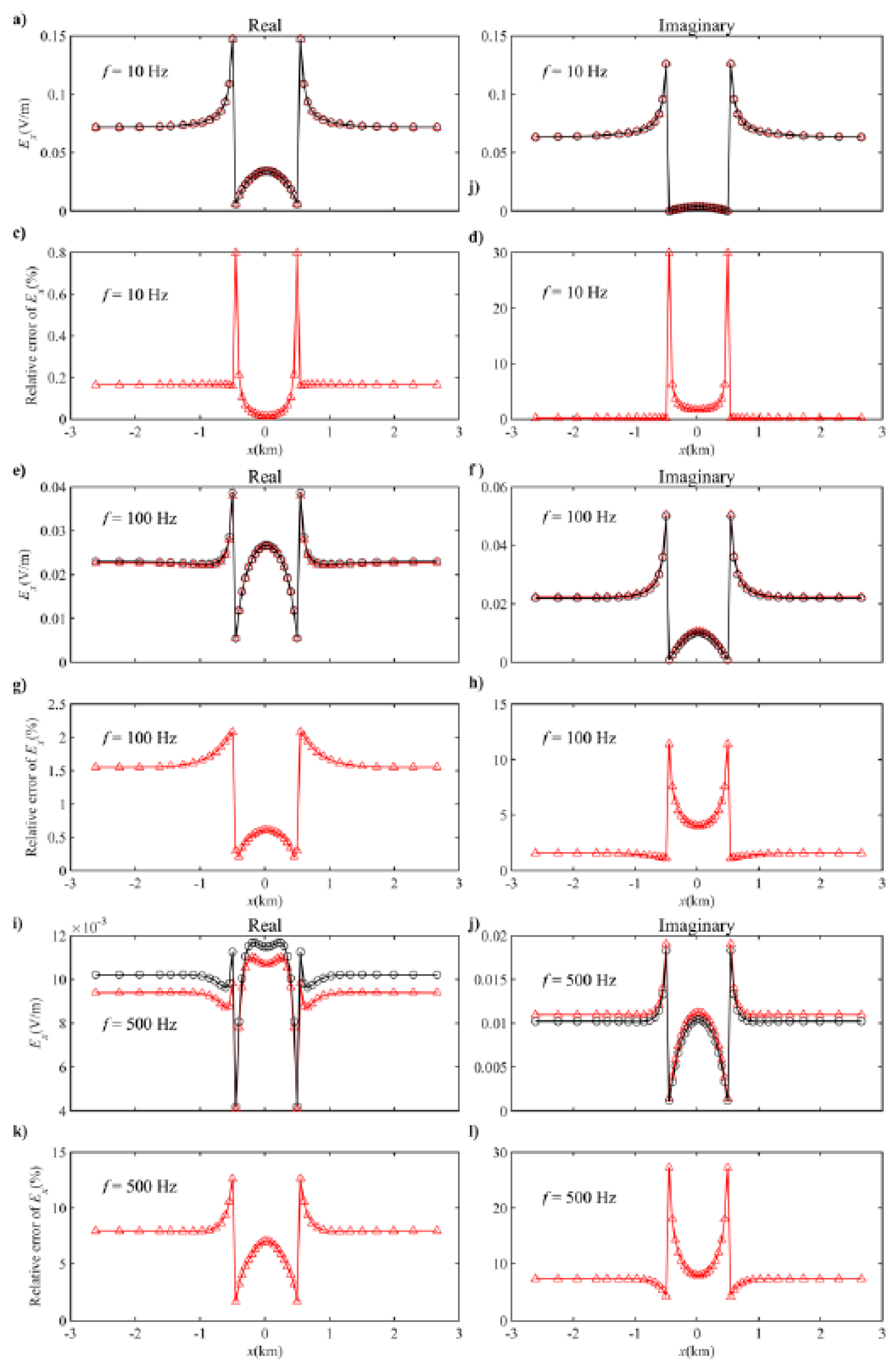
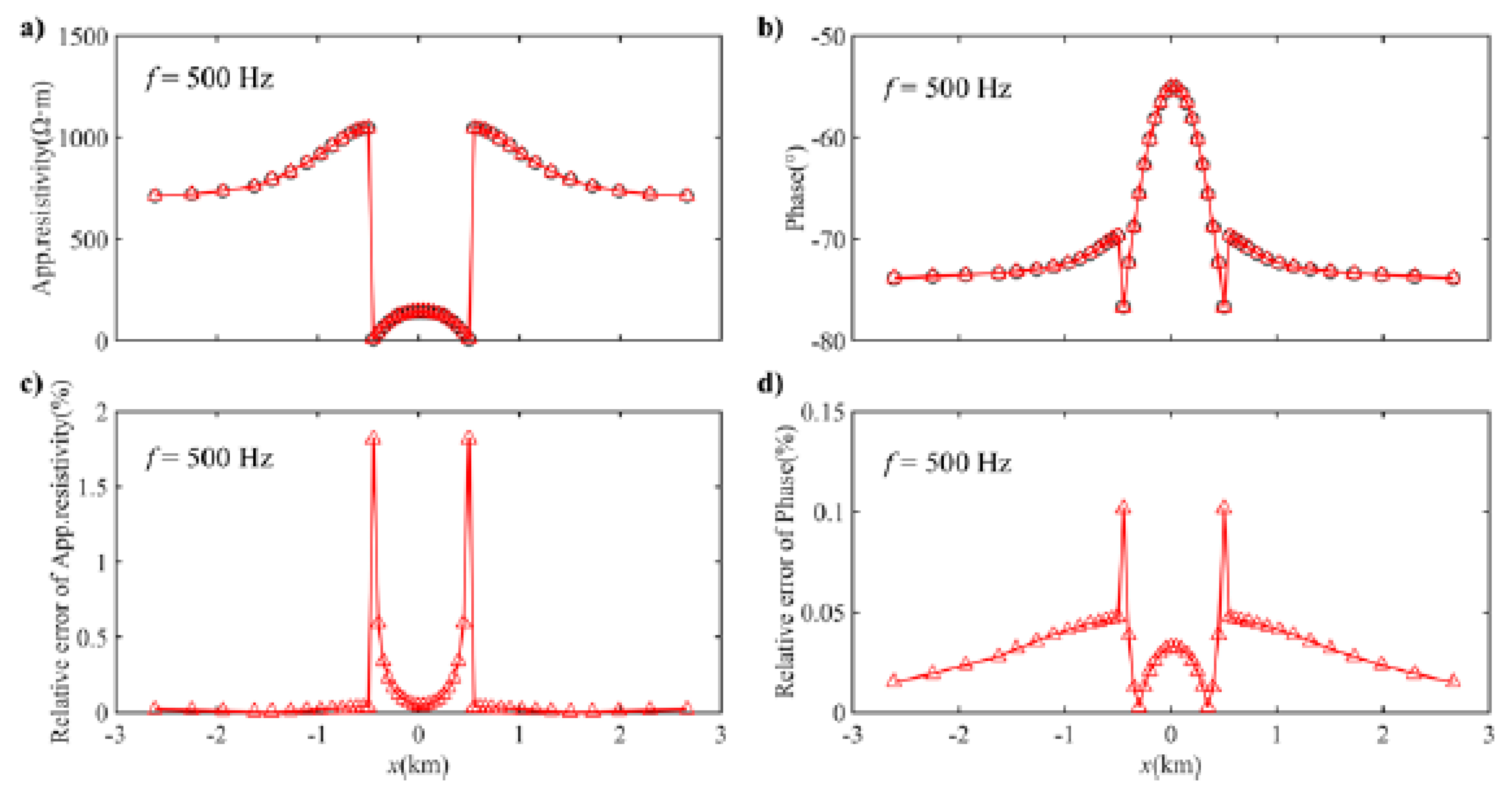
3.1. Simple 1D Models
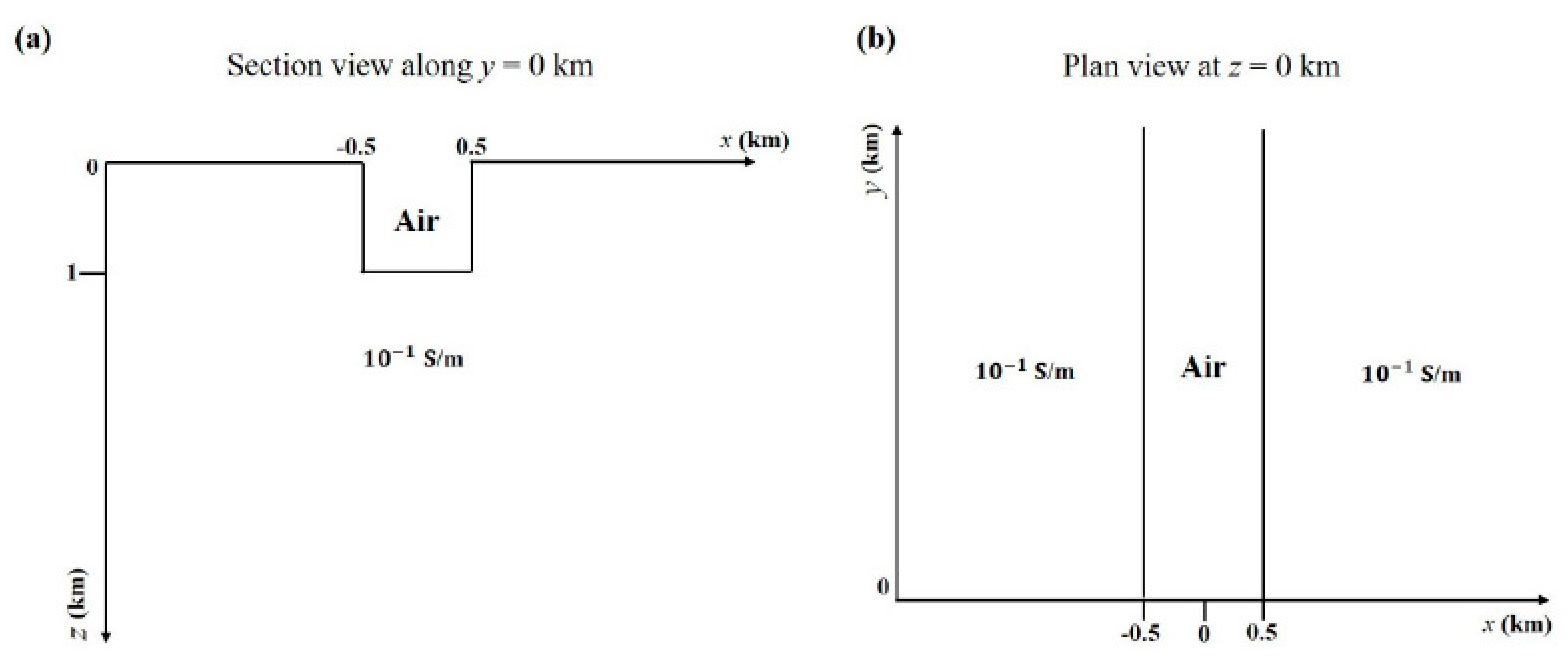
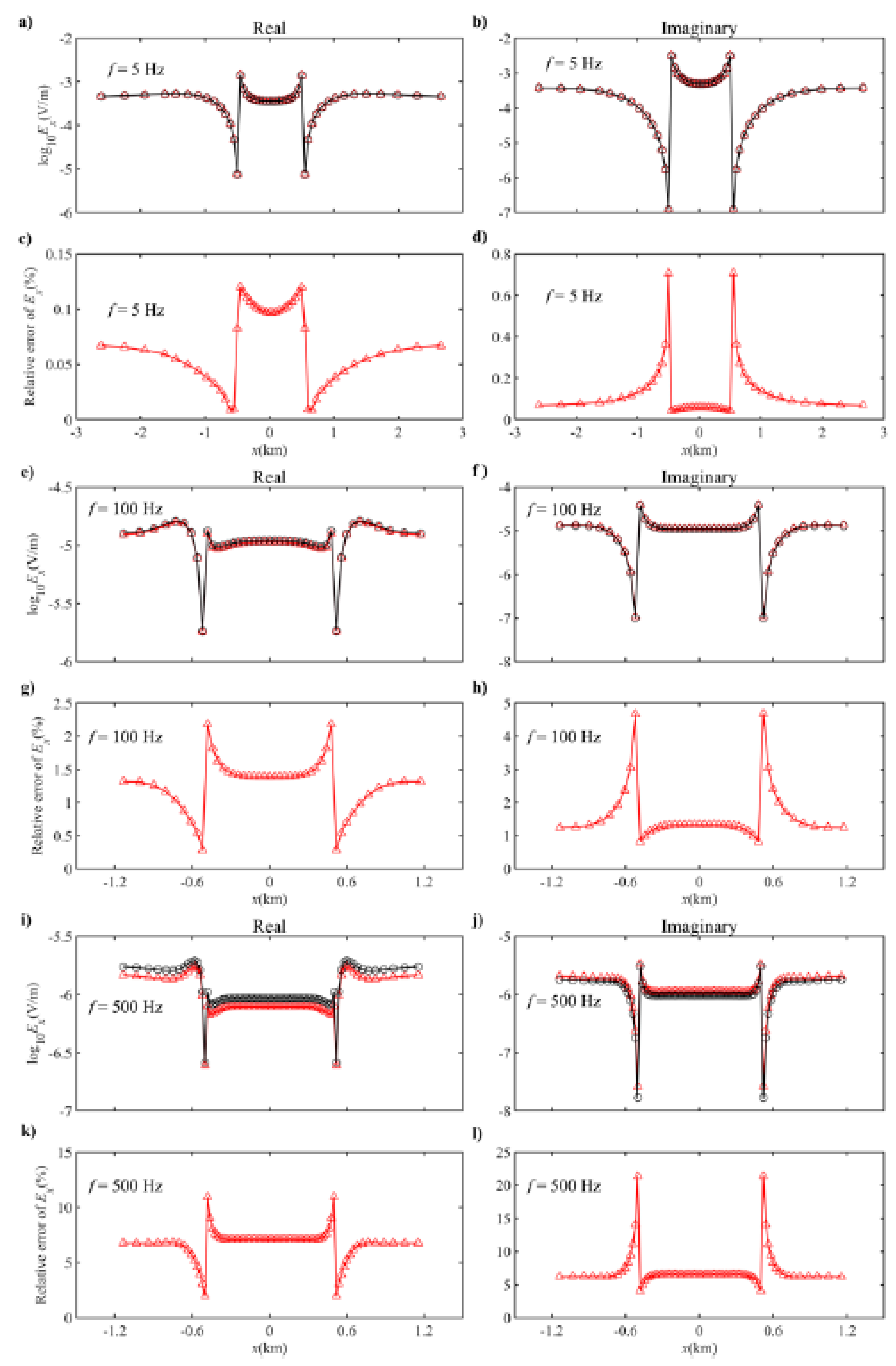
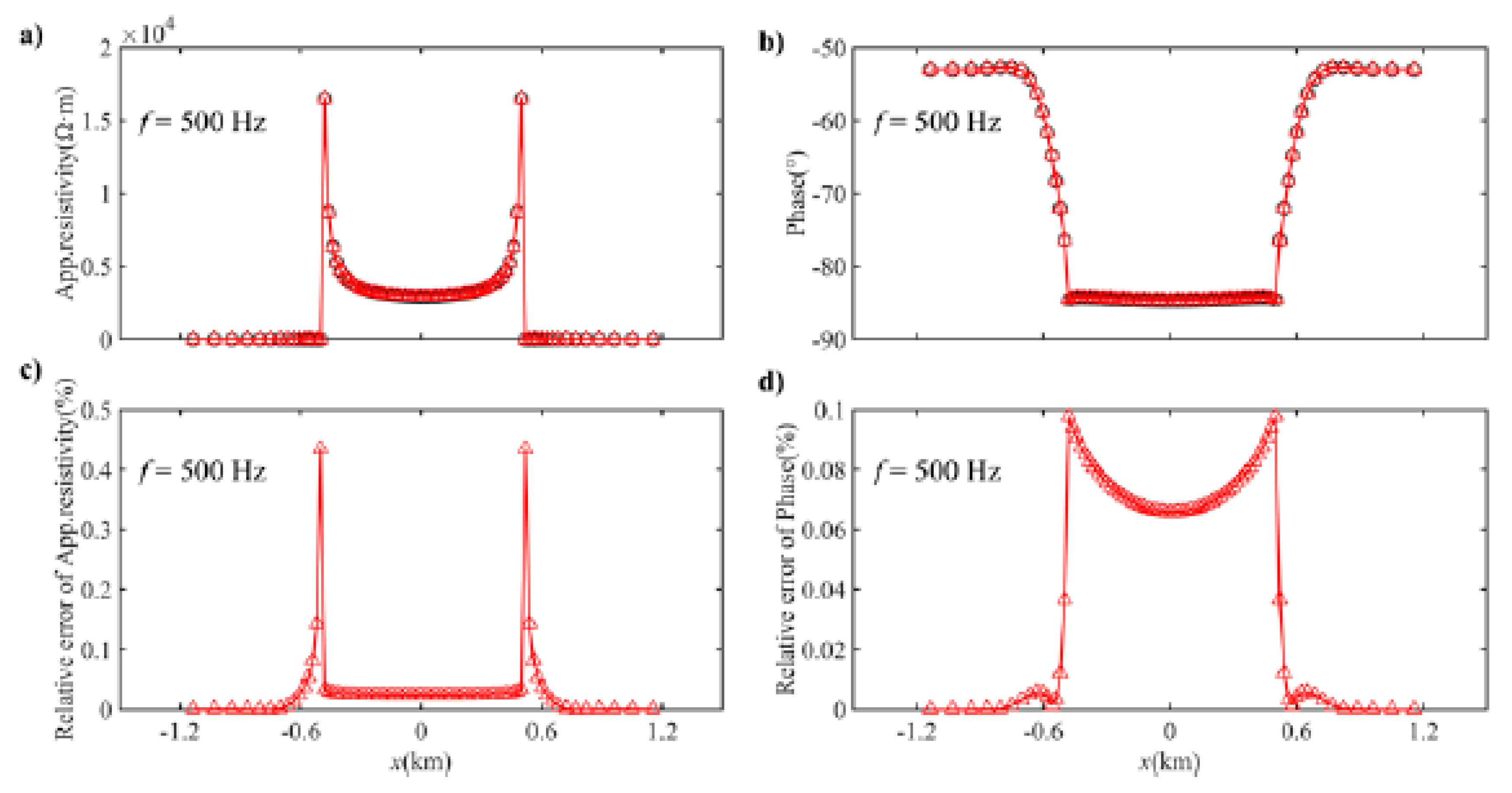
3.2. 3D Flat Model
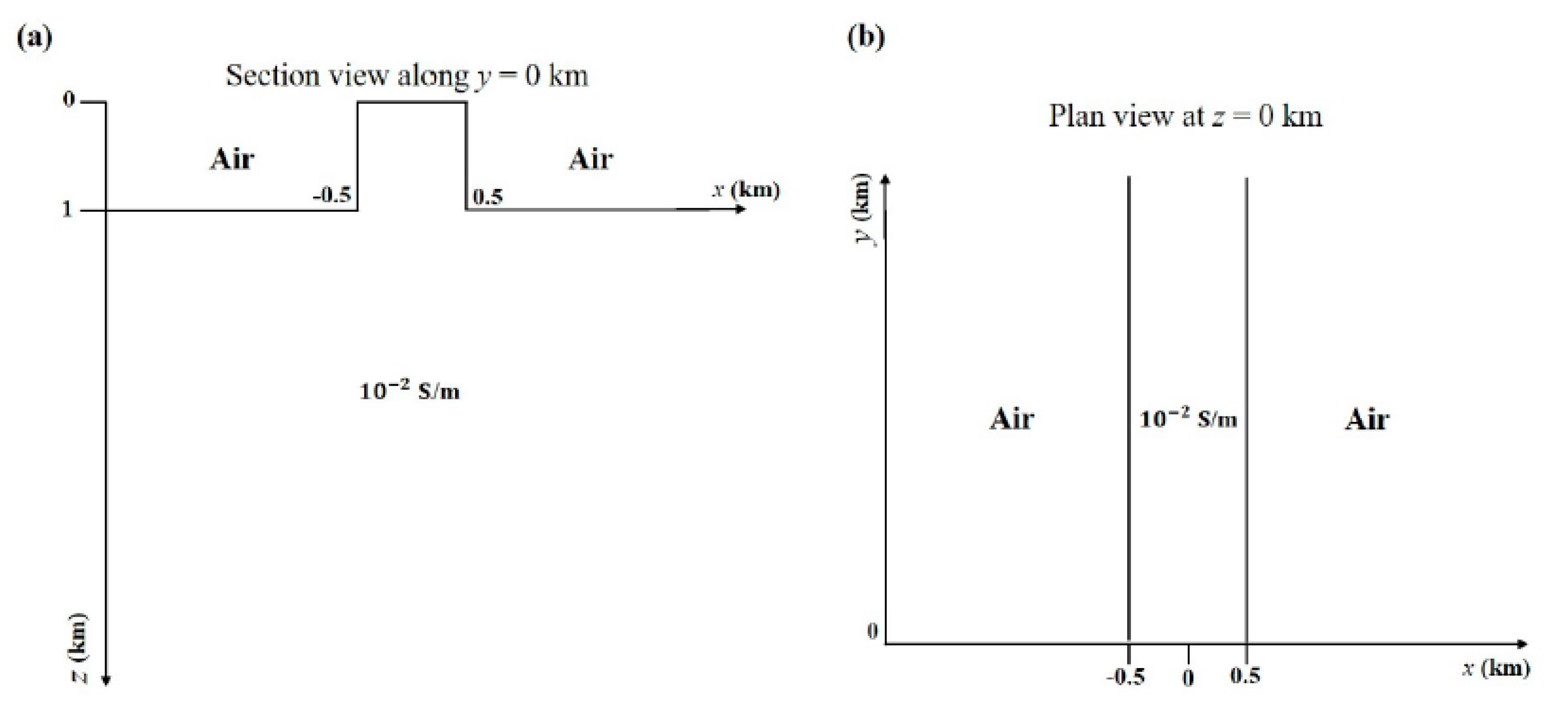
3.3. Models with Topography
3.3.1. Canyon Model
3.3.2. Steep Hill Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ward, S.H.; Hohmann, G.W. Electromagnetic theory for geophysical applications. In Electromagnetic Methods in Applied Geophysics: Volume 1, Theory; Society of Exploration Geophysicists: Tulsa, Oklahoma, 1988; pp. 130–311. [Google Scholar]
- Zhdanov, M.S.; Lee, S.K.; Yoshioka, K. Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity. Geophysics 2006, 71, 333–345. [Google Scholar] [CrossRef]
- Vozoff, K. Electromagnetic methods in applied geophysics. Geophys. Surv. 1980, 4, 9–29. [Google Scholar] [CrossRef]
- Avdeev, D.B. Three-dimensional electromagnetic modelling and inversion from theory to application. Surv. Geophys. 2005, 26, 767–799. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Craven, J.A. Three-dimensional inversion of magnetotelluric data for mineral exploration: An example from the McArthur River uranium deposit, Saskatchewan, Canada. J. Appl. Geophys. 2009, 68, 450–458. [Google Scholar] [CrossRef]
- Zhang, K.; Wei, W.; Lu, Q.; Dong, H.; Li, Y. Theoretical assessment of 3-D magnetotelluric method for oil and gas exploration: Synthetic examples. J. Appl. Geophys. 2014, 106, 23–36. [Google Scholar] [CrossRef]
- Beka, T.I.; Smirnov, M.; Birkelund, Y.; Senger, K.; Bergh, S.G. Analysis and 3D inversion of magnetotelluric crooked profile data from central Svalbard for geothermal application. Tectonophysics 2016, 686, 98–115. [Google Scholar] [CrossRef]
- Newman, G.A.; Alumbaugh, D.L. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophys. J. Int. 2000, 140, 410–424. [Google Scholar] [CrossRef] [Green Version]
- Xiang, E.; Guo, R.; Dosso, S.E.; Liu, J.; Dong, H.; Ren, Z. Efficient hierarchical trans-dimensional Bayesian inversion of magnetotelluric data. Geophys. J. Int. 2018, 213, 1751–1767. [Google Scholar] [CrossRef]
- Miensopust, M.P.; Queralt, P.; Jones, A.G.; The 3D MT Modellers. Magnetotelluric 3-D inversion—A review of two successful workshops on forward and inversion code testing and comparison. Geophys. J. Int. 2013, 193, 1216–1238. [Google Scholar] [CrossRef] [Green Version]
- Ren, Z.; Kalscheuer, T.; Greenhalgh, S.; Maurer, H. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophys. J. Int. 2013, 194, 700–718. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liu, J.; Liu, R.; Guo, R.; Feng, D. Frequency-domain magnetotelluric footprint analysis for 3D earths. J. Geophys. Eng. 2019, 16, 1151–1163. [Google Scholar] [CrossRef] [Green Version]
- Wannamaker, P.E. Advances in three-dimensional magnetotelluric modeling using integral equations. Geophysics 1991, 56, 1716–1728. [Google Scholar] [CrossRef]
- Avdeev, D.; Knizhnik, S. 3D integral equation modeling with a linear dependence on dimensions. Geophysics 2009, 74, 89–94. [Google Scholar] [CrossRef]
- Newman, G.A.; Alumbaugh, D.L. Three-dimensional induction logging problems, Part 2: A finite-difference solution. Geophysics 2002, 67, 484–491. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Miensopust, M.P. Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction. J. Appl. Geophys. 2011, 75, 699–710. [Google Scholar] [CrossRef]
- da Silva, N.V.; Morgan, J.V.; MacGregor, L.; Warner, M. A finite element multifrontal method for 3D CSEM modeling in the frequency domain. Geophysics 2012, 77, 101–115. [Google Scholar] [CrossRef]
- Ansari, S.; Farquharson, C.G. 3D finite-element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids. Geophysics 2014, 79, 149–165. [Google Scholar] [CrossRef]
- Liu, J.; Liu, P.; Tong, X. Three-dimensional Land FD-CSEM Regularized Inversion Based on Edge Finite-element Method. J. Environ. Eng. Geophys. 2018, 23, 211–222. [Google Scholar]
- Liu, R.; Guo, R.; Liu, J.; Liu, Z. An Efficient Footprint-Guided Compact Finite Element Algorithm for 3-D Airborne Electromagnetic Modeling. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1809–1813. [Google Scholar] [CrossRef]
- Mackie, R.L.; Smith, J.T.; Madden, T.R. Three-dimensional electromagnetic modeling using finite difference equations: The magnetotelluric example. Radio Sci. 1994, 29, 923–935. [Google Scholar] [CrossRef]
- Siripunvaraporn, W.; Egbert, G.; Lenbury, Y. Numerical accuracy of magnetotelluric modeling: A comparison of finite difference approximations. Earth Planets Space 2002, 54, 721–725. [Google Scholar] [CrossRef] [Green Version]
- Streich, R. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data: Direct solution and optimization for high accuracy. Geophysics 2009, 74, 95–105. [Google Scholar] [CrossRef]
- Kelbert, A.; Meqbel, N.; Egbert, G.D.; Tandon, K. ModEM: A modular system for inversion of electromagnetic geophysical data. Comput. Geosci. 2014, 66, 40–53. [Google Scholar] [CrossRef]
- Li, J.; Liu, J.; Egbert, G.D.; Liu, R.; Guo, R.; Pan, K. An efficient preconditioner for 3-D finite difference modeling of the electromagnetic diffusion process in the frequency domain. IEEE Trans. Geosci. Remote Sensi. 2019, 58, 500–509. [Google Scholar] [CrossRef]
- Varilsuha, D.; Candansayar, M.E. 3D magnetotelluric modeling by using finite-difference method: Comparison study of different forward modeling approaches. Geophysics 2018, 83, 51–60. [Google Scholar] [CrossRef]
- Um, E.S.; Harris, J.M.; Alumbaugh, D.L. An iterative finite element time-domain method for simulating three-dimensional electromagnetic diffusion in earth. Geophys. J. Int. 2012, 190, 871–886. [Google Scholar] [CrossRef] [Green Version]
- Cai, H.; Hu, X.; Li, J.; Endo, M.; Xiong, B. Parallelized 3D CSEM modeling using edge-based finite element with total field formulation and unstructured mesh. Comput. Geosci. 2017, 99, 125–134. [Google Scholar] [CrossRef]
- Liu, R.; Guo, R.; Liu, J.; Ma, C.; Guo, Z. A hybrid solver based on the integral equation method and vector finite-element method for 3D controlled-source electromagnetic method modeling. Geophysics 2018, 83, 319–333. [Google Scholar] [CrossRef]
- Egbert, G.D.; Kelbert, A. Computational recipes for electromagnetic inverse problems. Geophys. J. Int. 2012, 189, 251–267. [Google Scholar] [CrossRef] [Green Version]

| f (Hz) | σ (S/m) | σ/ωε | σ (S/m) | σ/ωε |
|---|---|---|---|---|
| 1 × 10−1 | 1 × 10−2 | 1.8 × 109 | 1 × 10−6 | 1.8 × 105 |
| 1 × 100 | 1 × 10−2 | 1.8 × 108 | 1 × 10−6 | 1.8 × 104 |
| 1 × 101 | 1 × 10−2 | 1.8 × 107 | 1 × 10−6 | 1.8 × 103 |
| 1 × 102 | 1 × 10−2 | 1.8 × 106 | 1 × 10−6 | 1.8 × 102 |
| 1 × 103 | 1 × 10−2 | 1.8 × 105 | 1 × 10−6 | 1.8 × 101 |
| 1 × 104 | 1 × 10−2 | 1.8 × 104 | 1 × 10−6 | 1.8 × 100 |
| 1 × 10−1 | 1 × 10−4 | 1.8 × 107 | 1 × 10−8 | 1.8 × 103 |
| 1 × 100 | 1 × 10−4 | 1.8 × 106 | 1 × 10−8 | 1.8 × 102 |
| 1 × 101 | 1 × 10−4 | 1.8 × 105 | 1 × 10−8 | 1.8 × 101 |
| 1 × 102 | 1 × 10−4 | 1.8 × 104 | 1 × 10−8 | 1.8 × 100 |
| 1 × 103 | 1 × 10−4 | 1.8 × 103 | 1 × 10−8 | 1.8 × 10-1 |
| 1 × 104 | 1 × 10−4 | 1.8 × 102 | 1 × 10−8 | 1.8 × 10-2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Y.; Liu, J.; Liu, R.; Liu, Z.; Guo, R.; Cao, C. Effect of Displacement Current on the Finite-Difference Modeling of Natural Source Electromagnetic Diffusion. Appl. Sci. 2020, 10, 2744. https://doi.org/10.3390/app10082744
Xue Y, Liu J, Liu R, Liu Z, Guo R, Cao C. Effect of Displacement Current on the Finite-Difference Modeling of Natural Source Electromagnetic Diffusion. Applied Sciences. 2020; 10(8):2744. https://doi.org/10.3390/app10082744
Chicago/Turabian StyleXue, Yahui, Jianxin Liu, Rong Liu, Zhuo Liu, Rongwen Guo, and Chuanghua Cao. 2020. "Effect of Displacement Current on the Finite-Difference Modeling of Natural Source Electromagnetic Diffusion" Applied Sciences 10, no. 8: 2744. https://doi.org/10.3390/app10082744





